Camera Model Identification with SPAIR-Swin and Entropy based Non-Homogeneous Patches
Abstract
Source camera model identification (SCMI) plays a pivotal role in image forensics with applications including authenticity verification and copyright protection. For identifying the camera model used to capture a given image, we propose SPAIR-Swin, a novel model combining a modified spatial attention mechanism and inverted residual block (SPAIR) with a Swin Transformer. SPAIR-Swin effectively captures both global and local features, enabling robust identification of artifacts such as noise patterns that are particularly effective for SCMI. Additionally, unlike conventional methods focusing on homogeneous patches, we propose a patch selection strategy for SCMI that emphasizes high-entropy regions rich in patterns and textures. Extensive evaluations on four benchmark SCMI datasets demonstrate that SPAIR-Swin outperforms existing methods, achieving patch-level accuracies of 99.45%, 98.39%, 99.45%, and 97.46% and image-level accuracies of 99.87%, 99.32%, 100%, and 98.61% on the Dresden, Vision, Forchheim, and Socrates datasets, respectively. Our findings highlight that high-entropy patches, which contain high-frequency information such as edge sharpness, noise, and compression artifacts, are more favorable in improving SCMI accuracy. Code will be made available upon request.
Index Terms— Entropy, Patch Extraction, Source Camera Model Identification, Swin Transformer
1 Introduction
In recent times, devices for capturing and conveniently sharing photographs; such as smartphones, tablets, and network connected digital cameras; have become widely available and increasingly affordable, resulting in a proliferation in images. The widespread use of digital images has also underscored the need for image forensics, particularly in applications where images serve as evidence in criminal investigations and judicial proceedings. Source camera model identification (SCMI) has emerged as an important subfield of digital image forensics, where the objective is to determine the camera model that was used to capture a given image [1, 2].
Image metadata, available in EXIF headers [3] of typical file formats such as JPEG, contains camera model information. However, such metadata is vulnerable to easy removal and manipulation, particularly in illicit use scenarios. It is crucial to develop SCMI methods that identify the camera model from the image by relying on fingerprints/traces indicative of the camera model that remain within images. SCMI methods aim to detect camera model-specific artifacts introduced during the image acquisition process and subsequent processing stages within the complex optics and image processing pipelines of camera devices. Conventional methods for SCMI have utilized features related to color filter array (CFA) demosaicing, interpolation traces, Auto-White Balance, JPEG compression, etc. Recent deep learning-based CMI methods are data-driven and rely on labeled training images to train neural networks for extracting camera model-specific features [4], [5], [6], [7], [8], [9]. While these methods can achieve high accuracy, consistent performance across different SCMI datasets remains an issue. This work addresses this challenge by proposing SPAIR-Swin - an SCMI method based on the modified SPatial Attention with an Inverted Residual (SPAIR) block and the Swin Transformer.
Unlike deep learning based vision tasks, resizing images is not suitable for forensic tasks due to loss of critical information. Therefore, SCMI methods employ a patch-based strategy to extract multiple patches from an image and preserve the noise characteristics in the patch region. In this work, we propose a patch extraction strategy based on entropy that focuses on more informative patches. Entropy quantifies uncertainty and randomness, encapsulating the unique sensor noise and processing characteristics of different cameras. By prioritizing patches with higher entropy, we can extract highly discriminative camera model specific features. Furthermore, the SPAIR block enhances camera model-specific artifacts, aiding the Swin Transformer in camera model identification. Due to its sliding window attention mechanism, the Swin Transformer can focus on global information and local features of an image patch and utilizes these enhanced artifacts to perform the final classification. Extensive experiments on different SCMI datasets demonstrate that SPAIR-Swin model with our proposed entropy based patch selection strategy provides superior performance compared with prior state of the art methods.
The main contributions of this work are as follows:
-
•
We propose SPAIR-Swin, an architecture integrating SPAIR block and Swin Transformer [10] for robust and enhanced source camera model identification.
-
•
We propose a patch extraction strategy using entropy to prioritize informative regions and improve the identification of the source camera model.
-
•
We propose the SPAIR block, a unique combination of a modified spatial attention and inverted residual blocks [11], which significantly improves feature learning and identification.
-
•
We conducted a comprehensive comparative study of seven different SCMI methods across four SCMI datasets.
The remainder of the paper is organized as follows. An overview of related work is present in Section 2. In Section 3, we introduce the proposed patch extraction strategy and SPAIR-Swin model. Section 4 describes the evaluations datasets used for the experiments. Section 5 provides a comprehensive and extensive analysis of the performance of the proposed method and a comparison with state-of-the-art methods. Section 6 concludes the paper.
2 Related Works
A number of methods have been proposed for SCMI, which are surveyed in [2]. Traditional methods extract hand-crafted features from the images and perform further inference on these features. Kharrazi et al. [9] transformed each image into a numerical feature vector via extraction from the wavelet domain or computation in the spatial domain to identify cameras using supervised learning. Lukas et al. [12] studied sensor noise patterns in images to distinguish unique camera characteristics. Later research investigated various features, such as sensor noise statistics [13], dust particles on the sensor [14], and combined feature sets [15]. Many of these hand-crafted feature-based methods utilize trained support vector machines (SVMs) classifiers for SCMI based on the features. Bondi et al. [4] developed a deep learning method using convolutional neural networks (CNN) for camera model identification (CMI). Their method consists of four convolutional layers to extract features, followed by two fully connected layers for refinement. These extracted features are then fed into linear binary support vector machines (SVMs) for final camera model classification. The final multi-class SCMI classification is realized using pairwise, one-versus-one, training of two-class SVMs. Yao et al. [16] utilized a more intricate deep learning model comprising 11 convolutional layers to extract complex characteristics specific to individual cameras.
Current state-of-the-art deep learning based SCMI methods employs CNN-based feature extractors followed by classification using fully connected layers. Chen et al. [17] employed a ResNet34 model for the SCMI. Ferreira et al. [8] improved CMI by combining Inception architecture and three CNNs for feature extraction. Rafi et al. [6] introduced RemNet, a CNN model designed for CMI on unseen and heavily post-processed images. It includes data-adaptive pre-processing remnant blocks that adjust to image manipulations. Liu et al. [18] investigated the use of the Res2Net module [19] for pre-processing, paired with a VGG16-based [20] CMI classifier. Bennabhaktula et al. [5] devised a data classification system using a seven-layer Convolutional Neural Network (CNN) model. They also used a limited convolutional layer to pre-process the data. Sychandaran et al. [21] employed a residual network consisting of different residual networks for the SCMI. Huan et al. [22] developed a novel patch-level compact deep network for efficient camera model identification. This network incorporates a patch extraction scheme based on a Uniform Local Binary Pattern (ULBP) to obtain complete texture information.
Each deep learning-based SCMI method employed a different patch selection strategy designed by considering the proposed model. Bondi et al. [4] proposed patching strategies based on mean and standard deviation, extracting 32 patches per image with a size of . Yao et al.. [16] retrieved 256 patches per image of size from the central of the image. Liu et al. [18] proposed a strategy to retrieve 128 patches per image of size , where 64 patches are calculated based on the quality measures described by Bondi et al. [4], and the remaining 64 are obtained using K-means clustering. Rafi et al. [6] retrieved 20 patches of size based on [4] and [23]. Sychandran et al. [21] used a patch size of . Bennabhaktula et al. [5] proposed a method to extract homogeneous patches based on the standard deviation and extracted 400 overlapping patches per image with a size of . Huan et al. [22] proposed a patching strategy using a uniform local binary pattern (ULBP) and retrieved 150 patches of size .
3 Methodology
The proposed pipeline incorporating the entropy-based patching strategy, the SPAIR block, and the SPAIR-Swin architecture for source camera model identification is illustrated in Fig. 1. Individual modules in the pipeline are described in the following subsections.
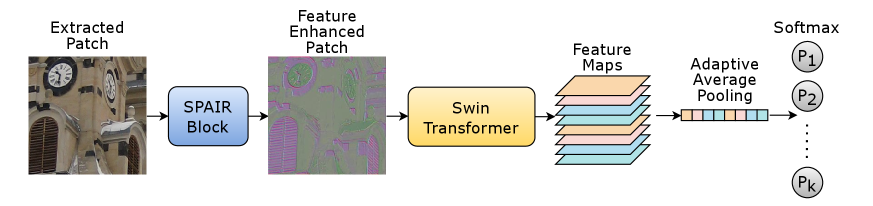
3.1 Entropy based Patch Extraction
In deep learning applications, before processing, images are typically resized to a fixed size that can be handled efficiently using the parallelism available in hardware. Although resizing preserves semantic content for vision-related tasks, it is sub-optimal for forensics, including SCMI, because it can suppress or eliminate subtle features indicative of the camera model that are unrelated to the image semantic content. Instead of scaling, SCMI methodologies therefore use fixed size patches cropped from the input image for use in deep learning pipelines. The selection of image regions for the extraction of patches plays a critical role in determining the performance of SCMI algorithms. A good selection strategy can better isolate regions carrying camera model information and enhance the generalization performance.
We propose a patch extraction strategy based on entropy, which is illustrated in Fig. 2. By partitioning the images into non-overlapping patches, the model can focus more on the regions with higher information content that contain sensor noise patterns like PRNU noise, chromatic aberrations, and demosaicing artifacts. We argue these high-entropy regions are likely to hold various textures and patterns well-suited for source camera identification.

Areas with higher entropy correlate to regions containing variations in pixel intensity and often such areas contain sensor-specific noise patterns relevant for identifying cameras. Entropy based selection preferably retains patches with high frequency noise that are critical for SCMI, in contrast with traditional discrete cosine transforms (DCT) based JPEG compression methods that tend to discard high-frequency noise. By concentrating on non-homogeneous patches that capture the most discriminative features, our method facilitates the extraction of robust camera fingerprints.
Specifically, our patch selection is based on the (first-order) entropy is computed for an -bit grayscale image patch as
| (1) |
where, denotes the fraction of pixels in the patch having a grayscale intensity . First, the source image is center-cropped to maintain the overall composition of the image. The purpose of center cropping is to ensure the image is evenly divisible by the patch size, preserving the central content while removing peripheral details from the boundary areas.Then, non-overlapping patches are extracted by using a sliding window with a stride of pixels along horizontal and vertical directions. A patch size of is used as a balanced choice to capture global and local features. This size maintains crucial information and is suitable for the SWIN Transformer architecture. Following the patch extraction, we compute the entropy of each patch using Equation (1). Patches are then sorted in descending order of entropy and the patches with the highest entropy are chosen. Empirically, the parameter is determined to optimize the trade-off between information richness and computational requirements. In Section 5, we analyze the effect of different values of on model performance and determine the optimal configuration that maximizes the discriminative capability of our model without adding redundancy.
3.2 Proposed SPAIR Block for Enhanced Feature Extraction
To extract features useful for SCMI from individual image patches, we proposed a SPAIR block that combines an Inverted Residual Block [11] with a modified spatial attention block [24]. The SPAIR block makes use of spatial attention to focus on distinctive features of interest by amplifying camera-specific features whereas the Inverted Residual Block utilizes its expansion layer and depthwise convolutions to retain information and to focus on unique channel-wise patterns.
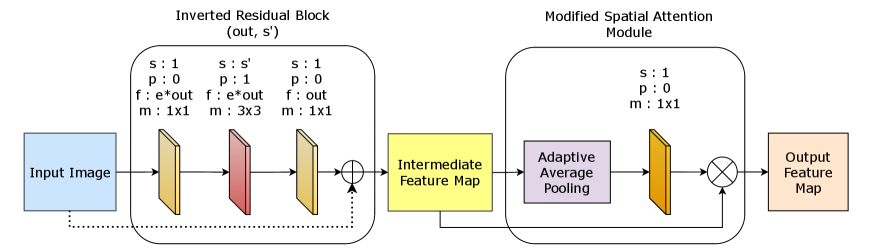
The Inverted Residual Block [11] is commonly used in many deep convolutional neural networks (CNNs). Its lightweight nature helps to create feature maps efficiently as it utilizes point-wise convolutions for dimensionality reduction and expansion. This is followed by a depth-wise separable convolution that significantly reduces the computational cost compared to the standard convolution. This combination promotes efficient feature learning while maintaining spatial information. The initial input is added to the output of the second convolution layer before passing it to modified spatial attention module. This residual connection helps with the gradient flow during training.
Unlike traditional modified spatial attention module [24], which uses both Max Pooling and Average Pooling, we simplify the process by focusing only on Average Pooling to reduce the redundancy while still capturing global features. The softmax layer utilized at the end ensures that attention features are globally distributed across the entire spatial dimension, enabling our model to focus on the most discriminative features. This targeted attention mechanism helps to suppress irrelevant background content and focus on global noise patterns that differentiate the camera models. By selectively improving informative regions, SPAIR aims to extract more discriminative features that effectively distinguish images captured by different cameras.
3.3 Swin Transformer
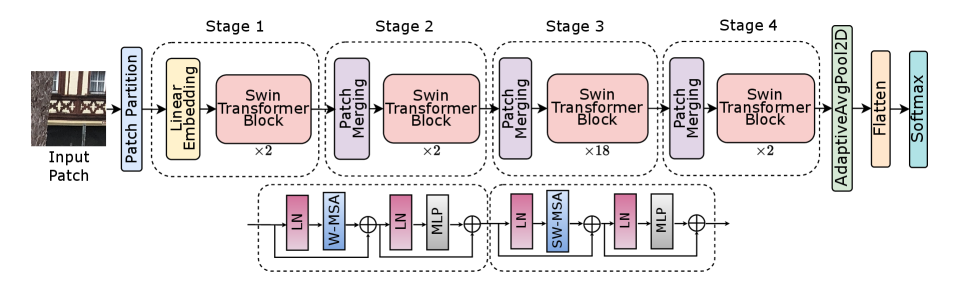
The output of the SPAIR block is processed by a Swin Transformer [10]. The Swin Transformer is a hierarchical transformer model designed specifically for computer vision/image processing that is more efficient than the initial proposals for vision transformers. The embedded patches are converted to tokens that form the base of the input to the transformer. Positional encoding is added to the tokens to supply spatial information for the model to be aware of the position of patches relative to each other. Another unconventional characteristic of the Swin Transformer is the low-cost manner in which it accommodates multi-scale features. Tokens at lower levels represent fine-grained details, whereas tokens at higher levels capture more abstract and global features. The final feature maps are obtained by combining all tokens which gives an overall view of the input features. These features obtained are then entered into the classification head.
4 Experimental Setup: Datasets, Metrics, and Baseline
4.1 Datasets
To assess the robustness and generalizability of the proposed SCMI method, we perform experiments on four large publicly available datasets: Dresden [25], Vision [26], Forchheim [27], and Socrates [28]. The selection of smartphone image datasets is significant as most images these days are acquired from smartphone cameras. Table 1 shows a summary of the datasets used. Before discussing the experiments, we outline the pertinent details of each of these datasets:
- •
-
•
The Vision dataset [26] includes images captured with various smartphone cameras. It comprises original images distributed over camera devices and contains identical camera models. We combine these classes for our experiments.
-
•
The Forchheim dataset [27] includes scenes taken with different brands of smartphones. It has images taken under various conditions, which include changes in lighting parameters, ambient light, and imaging parameters. Two out of the camera devices are identical, indicating that two models have more than one device, which are merged for Source Camera Model Identification tests. Consequently, there are different camera devices. This study focuses on native camera images that are labeled original (orig.) in [27].
-
•
The Socrates [28] is the largest dataset in terms of number of camera devices and models, containing images taken with different camera models. This dataset offers a rich variety of scenarios and authenticity, with images captured by individual smartphone users.
4.2 Setup
All the experiments are performed on a GHz AMD EPYC , core processor with GB RAM and an Nvidia A GPU with GB memory. Images in the dataset are split in an ratio. Splitting is performed before patching to ensure that the derived patches are present in either the training or the test set. The PyTorch [30] framework was used for implementation. A pre-trained Small Swin Transformer [10] is used that has a batch size of . AdamW [31] optimizer is used that has an initial learning rate of . All models were trained for epochs, at which point, they exhibited convergence in training loss, except for our proposed model which showed convergence around epochs.
4.3 Evaluation Metrics
To evaluate the proposed method, we measured Image Level Accuracy (ILA) and Patch Level Accuracy (PLA). The evaluation was carried out with a total of images collected by camera devices. For the image, , , and denote the specific image, the actual camera model, and the predicted camera model, respectively. Furthermore, the number of patches has been extracted from the image. For the patch of the image, and represent the actual and predicted camera models, respectively, for that patch image. PLA and ILA are computed as
where is the indicator function and corresponds to the camera model with the maximum number of votes according to the patch-level predictions of the image and its mathematical formulation is .
For comprehensive analysis across the datasets, we also used F1-score where unweighted mean was used to compute a single value for ease of understanding and visualization.
4.4 Baselines
We compare the performance of the proposed method against several competing methods for Camera Model Identification (CMI), specifically those proposed by Chen et al. [17], Liu et al. [18], Rafi et al. [6], Bennabhaktula et al. [5], Sychandran et al. [21], and Huan et al. [22]. Chen et al. [17] employed a CNN-based method without pre-processing strategies while all other SCMI methods utilized varied pre-processing strategies to enhance image features. This variety of methodological frameworks enhances comparative analysis by highlighting the strengths and limitations of each method in the context of source camera model identification.
5 Results and Analysis
The performance of the proposed SPAIR-Swin method is examined in detail. For the comparative analysis, extensive experiments were conducted to compare the proposed approach with the baselines outlined in Section 4.4, utilizing four distinct datasets detailed in Section 4.1.
| Dataset Methods | Dresden [25] | Vision [26] | Forchheim [27] | Socrates [28] | ||||
|---|---|---|---|---|---|---|---|---|
| ILA | PLA | ILA | PLA | ILA | PLA | ILA | PLA | |
| Chen et al. [17] | 94.33 | - | 87.48 | - | 48.91 | - | 77.31 | - |
| Liu et al. [18] | 97.30 | 92.63 | 95.33 | 86.52 | 97.19 | 85.37 | 96.25 | 88.59 |
| Rafi et al. [6] | 99.42 | 96.16 | 98.73 | 92.38 | 99.23 | 89.55 | 95.89 | 84.36 |
| Bennabhaktula et al. [5] | 98.76 | 96.96 | 97.71 | 93.53 | 95.02 | 90.30 | 93.06 | 87.50 |
| Sychandran et al. [21] | 94.29 | 82.00 | 79.47 | 65.00 | 63.35 | 47.03 | 43.94 | 38.72 |
| Huan et al. [22] | 97.65 | 95.10 | 95.38 | 90.47 | 93.87 | 83.74 | 93.43 | 86.35 |
| Proposed | 99.87 | 99.45 | 99.32 | 98.39 | 100 | 99.45 | 98.61 | 97.46 |
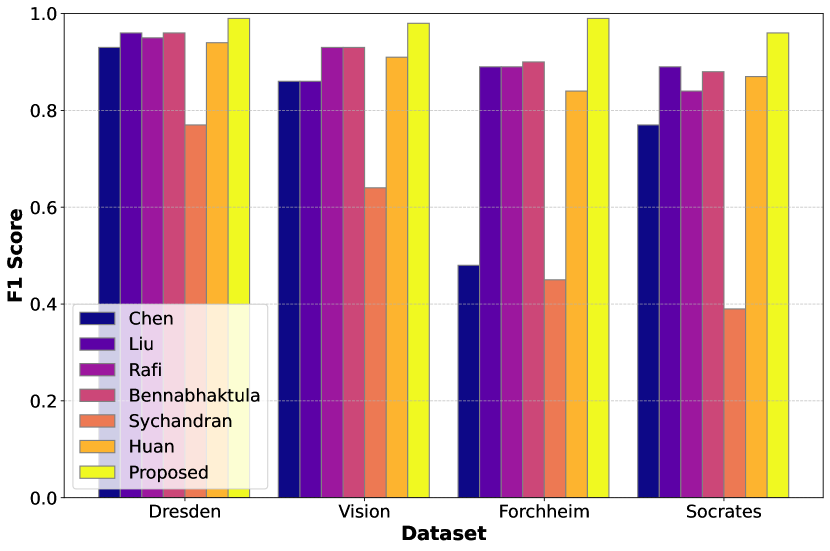
Table 2 presents the performance, in terms of ILA and PLA, of various Camera Model Identification (CMI) methods, including our proposed approach. The best scores are highlighted in bold and it is noted that the proposed approach outperforms all competing methods across all four datasets. Our proposed method achieves an average absolute improvement over baseline methods in terms of ILA by , , , and , and in terms of PLA by , , , and on the Dresden [25], Vision [26], Forchheim [27], and Socrates [28] datasets, respectively. Furthermore, Figure 5 presents a comparative analysis of patch-level F1-scores across four datasets, demonstrating that the proposed method improves classification performance by achieving a higher F1-score and reducing incorrect predictions. These results highlight the effectiveness of the proposed approach.
5.1 Validation of Patch Selection Strategy
This section provides a comprehensive analysis in order to demonstrate the efficacy of the proposed patch selection strategy. The key motivation for selecting non-homogeneous patches, i.e., high-entropy patches, is their ability to capture camera-specific features that are unevenly distributed across the image. These features include sensor noise, demosaicing patterns, and compression signatures, which are prominently found in parts with complex textures, edges, and high-frequency component areas.
| Dataset Methods | Dresden [25] | Vision [26] | Forchheim [27] | Socrates [28] | ||||
|---|---|---|---|---|---|---|---|---|
| Methods | Original | Proposed | Original | Proposed | Original | Proposed | Original | Proposed |
| Patch Level Accuracy (PLA) | ||||||||
| Liu et al. [18] | 92.63 | 96.81 | 86.52 | 93.58 | 85.37 | 94.09 | 88.59 | 91.78 |
| Rafi et al. [6] | 96.16 | 97.12 | 92.38 | 92.42 | 89.55 | 91.90 | 84.36 | 87.95 |
| Bennabhaktula et al. [5] | 96.96 | 97.54 | 93.53 | 94.57 | 90.30 | 91.61 | 87.50 | 91.78 |
| Sychandran et al. [21] | 82.00 | 85.49 | 65.00 | 65.77 | 47.03 | 62.81 | 38.72 | 38.96 |
| Huan et al. [22] | 95.10 | 99.18 | 90.47 | 97.47 | 83.74 | 98.01 | 86.35 | 94.16 |
| Image Level Accuracy (ILA) | ||||||||
| Liu et al. [18] | 97.30 | 98.10 | 95.33 | 97.45 | 97.19 | 98.85 | 96.25 | 96.56 |
| Rafi et al. [6] | 99.42 | 99.78 | 98.73 | 98.39 | 99.23 | 99.49 | 95.89 | 96.36 |
| Bennabhaktula et al. [5] | 98.76 | 99.56 | 97.71 | 98.26 | 95.02 | 98.34 | 93.06 | 96.36 |
| Sychandran et al. [21] | 94.29 | 96.81 | 79.47 | 82.61 | 63.35 | 83.91 | 43.94 | 44.82 |
| Huan et al. [22] | 97.65 | 99.96 | 95.38 | 99.27 | 93.87 | 100 | 93.43 | 98.05 |
Table 3 presents the comparative results of various baseline methods experimented across four different datasets with their respective native patch selection strategy and the proposed patch selection strategy while keeping all the experimental settings consistent with the original studies, which include the model and training pipelines, their respective hyperparameters, the number of patches, and patch sizes. The results demonstrate the effectiveness of the proposed entropy-based patch extraction in enhancing camera model identification performance across various state-of-the-art methods. It can be observed, baseline methods with our proposed patch selection strategy achieve an average relative PLA improvement of , , , and , and an average relative ILA improvement of , , , and over their native patch selection strategy on the Dresden [25], Vision [26], Forchheim [27], and Socrates [28] datasets, respectively. Notably, all studies show improvements in both PLA and ILA across all the datasets, except for a marginal ILA loss of in Liu et al.[18]. The relative gains are massive especially in calibration using difficult datasets like Forchheim which contains a high amount of similar images, and Socrates which has fewer samples per camera model and the highest classes for identification. For example, the method developed by Huan et al., experiences a drastic change in PLA from to for the Forchheim [27] data set and from to of the Socrates [28] dataset. These improvements are statistically significant across all the methodologies and datasets considered, demonstrating the consistency and expansiveness of the proposed patch extraction strategy.
| Dataset | Homogeneous | Non Homogeneous |
|---|---|---|
| Patch Level Accuracy (PLA) | ||
| Dresden [25] | 99.25 | 99.45 |
| Vision [26] | 97.90 | 98.39 |
| Forchheim [27] | 98.81 | 99.45 |
| Socrates [28] | 96.25 | 97.46 |
| Image Level Accuracy (ILA) | ||
| Dresden [25] | 99.91 | 99.87 |
| Vision [26] | 98.81 | 99.32 |
| Forchheim [27] | 99.87 | 100 |
| Socrates [28] | 97.12 | 98.61 |
Table 4 shows the performance of the proposed CMI method by considering both scenarios: (1) using homogeneous patches and (2) using non-homogeneous patches. The higher patch-level accuracy is achieved by using the non-homogeneous patches, as their high-entropy regions contain rich textures, edges, and structural details, effectively captured by the shifted window multi-head self-attention module of Swin Transformers. The modified spatial attention mechanism assigns weights to emphasize distinctive regions, aiding camera-specific feature extraction. In contrast, homogeneous patches, being uniform, offer fewer distinguishing features, making artifact isolation for SCMI more challenging. Moreover, the improvement in image-level precision, except for a marginal decline on Dresden [25], highlights the advantage of high-entropy patches.
| # Patches Dataset | 15 | 20 | 30 | 60 |
|---|---|---|---|---|
| Patch Level Accuracy (PLA) | ||||
| Dresden [25] | 99.18 | 99.45 | 99.23 | 99.19 |
| Vision [26] | 97.74 | 98.39 | 98.22 | 98.35 |
| Forchheim [27] | 98.67 | 99.45 | 99.20 | 99.18 |
| Socrates [28] | 96.57 | 97.46 | 96.96 | 96.97 |
| Image Level Accuracy (ILA) | ||||
| Dresden [25] | 99.82 | 99.87 | 99.91 | 99.68 |
| Vision [26] | 99.19 | 99.32 | 98.89 | 99.19 |
| Forchheim [27] | 99.74 | 100.00 | 99.87 | 99.61 |
| Socrates [28] | 97.63 | 98.61 | 98.35 | 98.45 |
An ablation analysis was conducted to determine the optimal number of patches for maximizing the proposed model’s performance, while addressing underfitting and overfitting. These patches must also be non-redundant about the information they convey as well as the patches should be high in quality. Table 5 shows that increasing the number of patches from 15 to 20 consistently improved both patch-level accuracy (PLA) and image-level accuracy (ILA) across four datasets. Overall, the best results are achieved when the number of high-entropy patches selected per image is 20. Increasing the number of such patches to 30 or 60 results in performance drop in most of the cases.
6 Conclusion
This paper introduced a novel Source Camera Model Identification (SCMI) framework, utilizing SPAIR-Swin which integrates SPAIR block with the Swin Transformer. The architecture effectively captures global and local features present in the image and provide a robust SCMI method. The use of the entropy-based patch selection enables the model to concentrate on areas of higher information content (higher entropy) and thus discriminate between discriminative camera-specific features such as sensor noise and demosaicing artifacts. Spatial Attention Inverted Residual Blocks (SPAIR) further boost the learning of features by combining it with the Swin Transformer, which contains efficient hierarchical self-attention adapted for robust classification. The experiments highlighted the superior performance of our method on four publicly available standard datasets, achieving state-of-the-art accuracy in both patch level (PLA) and image level (ILA). We demonstrated that our entropy-based patch extraction strategy worked well with most existing SCMI methods, and ablation studies signified the efficacy of the proposed method. We confirm the potential of the SPAIR-Swin model as a powerful method for SCMI, pointing the way toward future research in digital image forensics.
References
- [1] Chijioke Emeka Nwokeji, Akbar Sheikh-Akbari, Anatoliy Gorbenko, and Iosif Mporas, “Source camera identification techniques: A survey,” Journal of Imaging, vol. 10, no. 2, pp. 31, 2024.
- [2] Pengpeng Yang, Daniele Baracchi, Rongrong Ni, Yao Zhao, Fabrizio Argenti, and Alessandro Piva, “A survey of deep learning-based source image forensics,” Journal of Imaging, vol. 6, no. 3, pp. 9, 2020.
- [3] Matthew C. Stamm, Min Wu, and K. J. Ray Liu, “Information Forensics: An Overview of the First Decade,” IEEE Access, vol. 1, pp. 167–200, 2013.
- [4] Luca Bondi, Luca Baroffio, David Güera, Paolo Bestagini, Edward J Delp, and Stefano Tubaro, “First steps toward camera model identification with convolutional neural networks,” IEEE Signal Processing Letters, vol. 24, no. 3, pp. 259–263, 2016.
- [5] Guru Swaroop Bennabhaktula, Enrique Alegre, Dimka Karastoyanova, and George Azzopardi, “Camera model identification based on forensic traces extracted from homogeneous patches,” Expert Systems with Applications, vol. 206, pp. 117769, 2022.
- [6] Abdul Muntakim Rafi, Thamidul Islam Tonmoy, Uday Kamal, QM Jonathan Wu, and Md Kamrul Hasan, “RemNet: remnant convolutional neural network for camera model identification,” Neural Computing and Applications, vol. 33, pp. 3655–3670, 2021.
- [7] Kapil Rana, Puneet Goyal, and Gaurav Sharma, “Dual-branch convolutional neural network for robust camera model identification,” Expert Systems with Applications, vol. 238, pp. 121828, 2024.
- [8] Anselmo Ferreira, Han Chen, Bin Li, and Jiwu Huang, “An inception-based data-driven ensemble approach to camera model identification,” in 2018 IEEE International Workshop on Information Forensics and Security (WIFS). IEEE, 2018, pp. 1–7.
- [9] Mehdi Kharrazi, Husrev T Sencar, and Nasir Memon, “Blind source camera identification,” in 2004 International Conference on Image Processing, 2004. ICIP’04. IEEE, 2004, vol. 1, pp. 709–712.
- [10] Ze Liu, Yutong Lin, Yue Cao, Han Hu, Yixuan Wei, Zheng Zhang, Stephen Lin, and Baining Guo, “Swin Transformer: Hierarchical vision transformer using shifted windows,” in Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2021, pp. 10012–10022.
- [11] Mark Sandler, Andrew Howard, Menglong Zhu, Andrey Zhmoginov, and Liang-Chieh Chen, “MobileNetV2: Inverted residuals and linear bottlenecks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 4510–4520.
- [12] Jan Lukas, Jessica Fridrich, and Miroslav Goljan, “Digital camera identification from sensor pattern noise,” IEEE Transactions on Information Forensics and Security, vol. 1, no. 2, pp. 205–214, 2006.
- [13] Kai San Choi, Edmund Y Lam, and Kenneth KY Wong, “Source camera identification using footprints from lens aberration,” in Digital photography II. SPIE, 2006, vol. 6069, pp. 172–179.
- [14] Ahmet Emir Dirik, Husrev Taha Sencar, and Nasir Memon, “Digital single lens reflex camera identification from traces of sensor dust,” IEEE Transactions on Information Forensics and Security, vol. 3, no. 3, pp. 539–552, 2008.
- [15] Amel Tuama, Frédéric Comby, and Marc Chaumont, “Camera model identification based machine learning approach with high order statistics features,” in 2016 24th European Signal Processing Conference (EUSIPCO). IEEE, 2016, pp. 1183–1187.
- [16] Hongwei Yao, Tong Qiao, Ming Xu, and Ning Zheng, “Robust multi-classifier for camera model identification based on convolution neural network,” IEEE Access, vol. 6, pp. 24973–24982, 2018.
- [17] Yunshu Chen, Yue Huang, and Xinghao Ding, “Camera model identification with residual neural network,” in 2017 IEEE International Conference on Image Processing (ICIP). IEEE, 2017, pp. 4337–4341.
- [18] Yunxia Liu, Zeyu Zou, Yang Yang, Ngai-Fong Bonnie Law, and Anil Anthony Bharath, “Efficient source camera identification with diversity-enhanced patch selection and deep residual prediction,” Sensors, vol. 21, no. 14, pp. 4701, 2021.
- [19] Shang-Hua Gao, Ming-Ming Cheng, Kai Zhao, Xin-Yu Zhang, Ming-Hsuan Yang, and Philip Torr, “Res2Net: A new multi-scale backbone architecture,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 43, no. 2, pp. 652–662, 2019.
- [20] Karen Simonyan and Andrew Zisserman, “Very deep convolutional networks for large-scale image recognition,” in International Conference on Learning Representations (ICLR), 2015.
- [21] CS Sychandran and R Shreelekshmi, “SCCRNet: a framework for source camera identification on digital images,” Neural Computing and Applications, vol. 36, no. 3, pp. 1167–1179, 2024.
- [22] Sijie Huan, Yunxia Liu, Yang Yang, and Ngai-Fong Bonnie Law, “Camera model identification based on dual-path enhanced ConvNeXt network and patches selected by uniform local binary pattern,” Expert Systems with Applications, vol. 241, pp. 122501, 2024.
- [23] Pengpeng Yang, Rongrong Ni, Yao Zhao, and Wei Zhao, “Source camera identification based on content-adaptive fusion residual networks,” Pattern Recognition Letters, vol. 119, pp. 195–204, 2019.
- [24] Sanghyun Woo, Jongchan Park, Joon-Young Lee, and In So Kweon, “CBAM: Convolutional block attention module,” in Proceedings of the European conference on computer vision (ECCV), 2018, pp. 3–19.
- [25] Thomas Gloe and Rainer Böhme, “The Dresden image database for benchmarking digital image forensics,” in Proceedings of the 2010 ACM Symposium on Applied Computing, 2010, pp. 1584–1590.
- [26] Dasara Shullani, Marco Fontani, Massimo Iuliani, Omar Al Shaya, and Alessandro Piva, “VISION: a video and image dataset for source identification,” EURASIP Journal on Information Security, vol. 2017, no. 1, pp. 1–16, 2017.
- [27] Benjamin Hadwiger and Christian Riess, “The Forchheim image database for camera identification in the wild,” in Pattern Recognition. ICPR International Workshops and Challenges: Virtual Event, January 10–15, 2021, Proceedings, Part VI. Springer, 2021, pp. 500–515.
- [28] Chiara Galdi, Frank Hartung, and Jean-Luc Dugelay, “SOCRatES: A Database of Realistic Data for SOurce Camera REcognition on Smartphones.,” in Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), 2019, pp. 648–655.
- [29] Matthias Kirchner and Thomas Gloe, “Forensic camera model identification,” Handbook of Digital Forensics of Multimedia Data and Devices, pp. 329–374, 2015.
- [30] Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, et al., “PyTorch: An imperative style, high-performance deep learning library,” Advances in Neural Information Processing Systems, vol. 32, 2019.
- [31] Ilya Loshchilov and Frank Hutter, “Decoupled weight decay regularization,” in 7th International Conference on Learning Representations (ICLR), 2019.