*captionUnknown document class \WarningFilter*subcaptionUnknown document class
Calibration and Correctness of
Language Models for Code
Abstract
Machine learning models are widely used, but can also often be wrong. Users would benefit from a reliable indication of whether a given output from a given model should be trusted, so a rational decision can be made whether to use the output or not. For example, outputs can be associated with a confidence measure; if this confidence measure is strongly associated with likelihood of correctness, then the model is said to be well-calibrated.
A well-calibrated confidence measure can serve as a basis for rational, graduated decision-making on how much review and care is needed when using generated code. Calibration has so far been studied in mostly non-generative (e.g., classification) settings, especially in software engineering. However, generated code can quite often be wrong: Given generated code, developers must decide whether to use directly, use after varying intensity of careful review, or discard model-generated code. Thus, calibration is vital in generative settings.
We make several contributions. We develop a framework for evaluating the calibration of code-generating models. We consider several tasks, correctness criteria, datasets, and approaches, and find that, by and large, generative code models we test are not well-calibrated out of the box. We then show how calibration can be improved using standard methods, such as Platt scaling. Since Platt scaling relies on the prior availability of correctness data, we evaluate the applicability and generalizability of Platt scaling in software engineering, discuss settings where it has good potential for practical use, and settings where it does not. Our contributions will lead to better-calibrated decision-making in the current use of code generated by language models, and offers a framework for future research to further improve calibration methods for generative models in software engineering.
Index Terms:
LLMs, Calibration, Confidence MeasureI Introduction
Generative large language models (LLMs) are now widely-used for code completion in IDEs. However, LLMs make mistakes: they can generate known buggy code [1], or code with risky vulnerabilities [2, 3]. Despite these risks, LLM “copilots” [4] are growing in popularity—thus there is a growing concern that bad LLM-generated code could be integrated into widely-used software. Given that LLMs might generate buggy code, how should a developer decide whether generated code is correct or not?
One possibility is to use the confidence, or probability assigned to the generated code by the LLM itself.
Consider a developer who asks Gpt-3.5 to complete some unfinished code. For example, given the prefix
def clear(self, tag: Optional[Hashable] = None) -> None:
the model generates the completion
self.jobs[:] = [job for job in self.jobs if job.tag != tag]
with an average per-token confidence of 91%, suggesting high confidence (based on its training) that the code is a likely completion for the given prefix. However, this code is known to be buggy! In fact, when we test thousands of line completions, in cases where the average probability was greater than 90%, only 52% actually passed test cases. One can also find reverse examples, where the LLM has very little confidence, but the generated code is actually correct.
We make two observations. First, since LLMs can make mistakes, users would benefit from a reliable indication of confidence that the generated code is actually correct. Second, such indications of confidence, when well-aligned with actual correctness, can support well-justified software quality control measures, and thus improve the reliability of the AI4SE ecosystem. When an LLM-offered code suggestion is accompanied by a numerical “confidence” signal e.g., a probability measure, then this signal should be well-aligned with the likelihood that the code is actually correct. Such a measure is said to be well-calibrated.
Calibration has been studied in other settings e.g., classically in weather prediction and recently for software-related classification tasks [5]. In this paper, we study the calibration of generative111We note that the notion of correctness for generative tasks is quite different than for classification tasks, where the output is a label, rather than a sequence of tokens. large language models, when used in practical software engineering settings, such as line-level code completion, function synthesis, and code-repair.
A well-calibrated confidence measure would support rational risk-management in the development process, and help quality-improvement processes. For example, a development team might reasonably adopt a policy that: a) generated code associated with high confidence could be reviewed lightly and quickly accepted; b) suggestions with a medium confidence value should be reviewed more carefully before acceptance; and c) suggestions with a low confidence value should be simply rejected or the prompt should be adjusted.
Despite its importance and widespread use of LLMs in software engineering, the correctness and calibration of code-generating models currently is not well understood. In particular, it is currently unknown whether confidence measures provided by the LLMs themselves align well with actual code correctness.
This paper does an empirical study of the calibration of code-generating models using several prior techniques and explores approaches for improving calibration further. To this end, we describe an evaluation framework for the calibration of code-generating language models. We instantiate the framework for different tasks, e.g., code synthesis, code completion, and program repair, using different correctness criteria (exact-match w.r.t. a reference solution and correctness-modulo-testing), and by applying the framework to different models. Based on this framework, we evaluate well-established techniques for estimating how a model’s confidence align with actual correctness; then, based on our findings, we present improvements over existing techniques.
Our work yields several findings:
-
•
The alignment of confidence measures provided by LLMs with standard notions of code correctness is poor, when evaluated on realistic datasets across different tasks, including completion, synthesis, and automated program repair. We observe generally high (Expected Calibration Error, described in Section III-C) across all settings, ranging from to , suggesting intrinsic LLM confidences are poor predictors of code correctness.
-
•
We evaluate several reflective approaches to improve this alignment, and also confidence rescaling using known correctness labels. While rescaling generally improves calibration, reflective methods are rather inconsistent, working better in some settings than others.
-
•
Finally, we focus on the most widely-used SE task for LLMs, viz. code completion, and use the instructable Gpt-3.5 model, and few-shotting, in a reflective setting, and show that calibration improves substantially from the skill score222Brier Skill score, which we explain below in § III-C. of to a much higher level of .
Our work considers the important problem of providing developers with a reliable indication of whether generated code is correct, and (especially for the widely-used task of code completion) offers an approach, using BM25-aided [6] few-shotting, that has potential practical value.
I-A Research Agenda
Code LLMs are perhaps mostly widely-used for code suggestion/completion; other tasks include code synthesis and program repair.
We evaluate the output for two different notions of correctness, viz., exact-match with known correct code, and second, passing all given tests.
In general, the levels of alignment between the intrinsic confidence (viz., directly provided by the LLM) and correctness is poor. This indicates need for better approaches to calibration. We then explore several engineering responses to the problem, listed in the following research questions. First, we consider the standard approach of confidence rescaling, using Platt scaling.
While confidence rescaling can help remedy over- and under-confidence, it does require some data to determine the parameters of the scaling function. We also analyze and discuss some considerations in obtaining this data, specifically for code-generation tasks.
Next, we investigate the possibility that the model is able to better calibrate upon reflection. We ask the model (using a separate reflective prompt) to consider its own generated code and judge its confidence in the quality.
Finally we investigate few-shotting, to see whether it helps calibration for the widely used task of code completion.
II Background
II-A Calibration
This concept originates in prediction problems like weather forecasting. Consider a weather model predicting a 70% confidence (probability) of rain the next day. If we ran this model for a while, and observed rain in 70% of the days where a forecast with 70% confidence was made, then we call it a well-calibrated model. A well-calibrated model’s confidence in a given output, is quite close to the empirical relative frequency (likelihood) with which the output is actually correct.
With well-calibrated rain-forecasting, a user has options for a rational response: at 20% confidence of rain, one might take a hat; at higher confidences, one might take an umbrella; if even higher, one might take the bus rather than walk, etc. From an earlier work by [7]: given a model , an input and true, expected correct output , a model output , (note that we won’t always have ) and a output probability provided by the model, a perfectly calibrated model satisfies the following condition
| (1) |
In other words, if we have perfectly-calibrated confidence (the model’s calculated probability of its prediction that the output is ), then this value equals the empirical fraction p of the cases where the actual output correctly matches the prediction . Usually these probabilities don’t perfectly match; there are various measures of the deviation, including Brier Score [8] and (Expected Calibration Error) [9]
II-B Why Calibration Matters for Code
Even powerful LLMs can make mistakes [1], potentially leading users to accept incorrect code. A well-calibrated confidence signal could help developers manage [4, 10] this risk. Consider the confidence associated with generated code. A well-calibrated high-value of would indicate a high empirical probabilty p that the code is correct, and so it could be simply accepted; a low value would indicate higher risk that the code is incorrect, and so should be rejected. A poorly calibrated model may lead to either unnecessary rejection of likely correct code, or ill-advised acceptance of likely incorrect code. We note that good calibration allows more nuanced, effective quality-control (Q-C) decisions, beyond simple binary decisions e.g., carefully review each token of generated code, perhaps by several people, vs. just use it. Such a well-calibrated quality-control process has been used in medicine e.g., for elder-care [11], and for decision-making in cancer-care [12]. Given the cost & consequences of properly addressing software quality, and the potential benefits of LLM-generated code, a well-calibrated confidence signal is highly desirable.
III Research Methodology
We consider three generative tasks i.e., function synthesis, line-level code completion, and program repair, where generative LLMs are directly applicable and widely-used (e.g., completion in Copilot). In this section, we will discuss the tasks, datasets, models, and methodology of our approach.
III-A Code Correctness
When evaluating calibration, we need a notion of correctness. For (non-generative) models outputting labels, classes, True/False, etc. correctness is simply an exact-match with ground-truth correct label. Exact-match could also be viewed as a notion of correctness for code, e.g., with defect repair, where there is a known, incorrect “buggy” version, and a known “fixed” version. Generated code is correct only if it matches exactly the fixed version, given an appropriate prompt. However, this approach is overly strict; the generated code might match exactly, but still pass all tests. Other notions of correctness exist: code-review, formal verification, etc. We use test cases provided with the code as our preferred indication of correctness, as tests are widely used, and are easily automated.
III-B Confidence Measures
We usually calculate a confidence measure (or probability) , associated with generated output code . We consider two categories of measures: intrinsic probability, which is calculated by the generative LLM per se, and reflective probability, obtained by re-invoking the model, instructing it to estimate its confidence in the correctness of the code just generated (see Figure A1 for prompts). Our measures include:
- Average Token Probability
-
(Intrinsic, ) For an output sequence of tokens , we collect the associated model probabilities , and then compute the mean .
- Generated Sequence Probability
-
(Intrinsic, ) The full generated sequence confidence is calculated as the product of probabilities, .
- Verbalized Self-Ask
-
[15, 16, 17] (Reflective, ) We instruct the model to reflect jointly on the prompt, and the model-generated code, and then output a numeric value of its confidence in the generated code.
Extra logic is implemented for when the model fails to output a probability (discussed further in Understanding effects of verbalized retry failures).
- Question Answering Logit
-
[18] (Reflective, and ) In this case, rather than prompting for a numerical score (as above), we ask for a TRUE or FALSE answer. The probability associated with the TRUE token is taken to be the confidence measure. Additionally, we extend this approach using normalization: the model can assign probability mass to multiple possible expressions of TRUE or FALSE or even other variations (e.g, “ True”, “ true”, “ ”, ). Thus when extending to the normalized form (Ask T/F N), we take the fraction of probability mass “True” assigned between only “True” and “False”.
Our experiments consider the four above: average token probability, generated sequence probability, verbalized self-evaluation, and question answering logit. In addition, as a baseline, we also used the length of the generated sequence. The length baseline is calculated based on the number of characters in the generated sequence, scaled such that is the shortest value in the dataset, and is the longest.
For reflective measures, we expected that a code generation model should perform well (and provide well-calibrated confidence scores for correctness): first, for synthesis, given just a good natural language description (without tests), of the desired function; second, for completion & bug-fixing, given the surrounding context. In both settings, we measure correctness using available hidden test cases. We also note that including hidden or failing tests in an LLM prompt is not common experimental practice for the tasks we analyze. [19, 20, 21].
III-C Measures of Calibration
Using model’s confidence in its generated output, and a way of determining correctness, one can compute measures of calibration. Calibration measures conceptually arise from the Reliability Plot, which plots correctness vs. confidence
Two reliability plots illustrating this method are shown in Figure 1. 1(a) is for token-level code completions from Codex; it shows the observed proportion of exact-match correct tokens (y-axis) vs. the predicted probability i.e., confidence as per the language model, based on bucketing observations into subsets . Here, there are buckets, equally spaced by confidence measure. Each bucket has an associated bar whose height indicates the proportion (value ) of correct samples in the bucket. The closer the bars in each are to the diagonal line, the better the calibration.
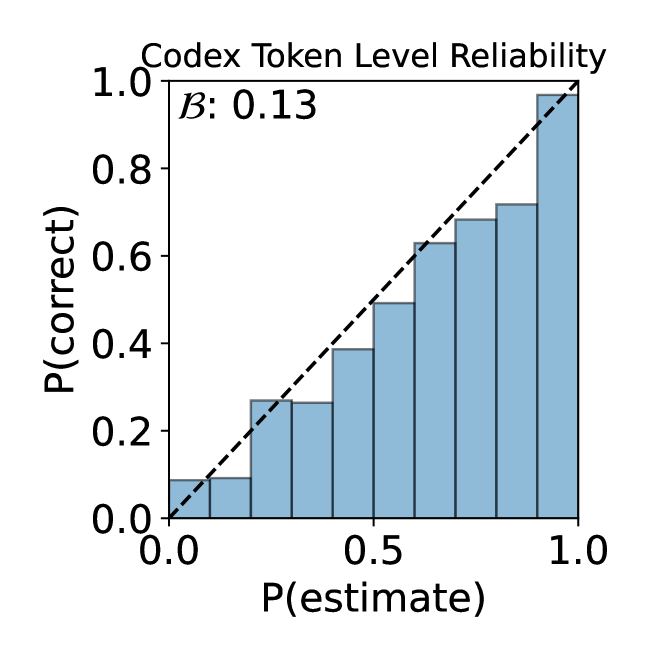

We note here that Codex is a large model, well-trained on the task of token-level completion; thus, it is both well-calibrated and generally correct on the simple token-level completion task. However, for notions of correctness farther from the training objective, such as line-level code completion and test-passing, Codex’s intrinsic probability may not be as well-calibrated. An example (1(b)) where the confidence is not well-calibrated is Gpt-3.5 for line completion using verbalized confidence (i.e., asking it to write its confidence; see Section III-B).
We study two measures of calibration: Brier Score [8] and [9]. Both measure the deviation from perfect calibration. As before (following [22]), we assume a model , input , actual desired output , and model prediction . In our case, both and are code, rather than a single label. Calibration measures indicate the extent to which the deviations of from the desired are actually aligned with the model’s confidence in its output, .
From the calibration plot, with the evaluation set bucketed into subsets . We estimate correctness in each bucket as the fraction of predictions in that bucket which are “correct” (as discussed in § III-A); confidence is the average estimated probability from the model in that bucket:
| (2) | ||||
| (3) |
where the model generates the code with confidence (probability) , and indicates that the generated code is correct, as per the operative experimental definition. For a perfectly calibrated , we would have . In practice, we observe deviations from this ideal. Expected Calibration Error () [9] is a typical measure of calibration, calculated as the weighted average of these deviations.
| (4) |
is intuitive, but can mislead; as seen below, a naïve predictor whose confidence is always the base rate would yield a deceptively low value. An alternative measure, the Brier score, [8] avoids this issue; it is calculated as follows: \useshortskip
| (5) |
One can achieve an optimal Brier of when confidently estimating when the code is correct, and estimating when the code is incorrect for each sample.
For comparison, consider using the Unskilled Reference Brier Score, , attainable by a naïve, “unskilled” model, which simply assigns the base-rate as its confidence for every prediction. Here, all prediction confidence values are in one bin, the value ; and the empirical correctness in this single bin is the base rate ; so which is misleading (thus exemplifying one of the weaknesses of ). The closed-form Brier Score for this unskilled predictor is: \useshortskip
| (6) |
In a 50-50 coinflip scenario (assuming heads is correct), a naïve predictor that randomly guesses correct with 50% confidence receives . Higher base rates yield lower ; e.g., for the MBPP dataset [20], Gpt-3.5 generates test-passing solutions for about 72% of the programming problems; here always guessing correct with 72% confidence results in . With well-calibrated confidence scores, a “skilled” model can achieve Brier Scores lower than this unskilled value; if a model does worse, it is indicative of poor calibration. Thus, one commonly reports a Skill Score (), calculated thus: \useshortskip
| (7) |
Positive (perfect score = 1.0) indicates improvement over baseline ; negative indicates worse calibration than the baseline. Small positive values of can sometimes indicate good skill. For example, the Deutsche Wetterdienst (German weather forecasting service) considers 0.05 Skill Score to be a minimum threshold for a good forecast quality444www.dwd.de/EN/ourservices/seasonals_forecasts/forecast_reliability.htm. As another data point, the American data journalism site 538 reports a skill of around 0.13 in forecasting World Cup games555projects.fivethirtyeight.com/checking-our-work/, which is in the range of what we observe in our experiments for best case code generation by LLMs; but these LLM performance numbers are just a starting point, and can be expected to improve in the future. (Equation 4) and Brier Score (Equation 5) serve slightly different purposes: the Brier Score is calculated for each sample, and measures both the ability to correctly discriminate output categories, and calibration of the output probability. The measures just calibration; but it can be misleadingly low, as noted above for the unskilled predictor. Additionally binning must be done carefully, since it can affect scores [23].
III-D Rescaling Approaches
Machine learning models are not always calibrated. [22] discuss ways of rescaling probability estimates to better match observations. A common approach is Platt scaling [24], where a logistic regression is fit to the logit values of the prediction i.e., the of the measured confidence probability. This optimizes two parameters, a linear scaling multiplier and a bias i.e., intercept, that shifts the value.
To reduce the likelihood that the scaling overfits & skews our results, we rescale over five folds; i.e., we fit a logistic regression on a random of data and apply it to of data, before sliding over and doing each combination of .
Besides Platt scaling, temperature rescaling has also been used [25, 18, 22]: this approach applies a scalar multiplier on the logits representing each class e.g., a multiclass image classifier. In our binary confidence case, this has similar expressivity to Platt scaling without an intercept. Other approaches include histogram binning [26], isotonic regression [27], inter alia [22, 28]. These approaches are more parameterized; given the data limitations in our experimental setup e.g., a few hundred examples in function synthesis, they pose higher risk of overfitting.
As we discuss in Section IV, Platt scaling does improve calibration, with some caveats.
III-E Tasks & Dataset
| Task | Dataset | Dataset Size |
|
Confidence Measure |
|
||||
|---|---|---|---|---|---|---|---|---|---|
| Function synthesis | HumanEval | 164 | Test-passing Correctness | Average Token Probability, Generated Sequence Probability, Verbalized Self-Evaluation, Question Answering Logit | Brier Score, | ||||
| MBBP Func | 880 | ||||||||
| Line-level Completion | DyPyBench | 1,988 | Test-passing Correctness, EM | ||||||
| Program Repair | Defects4J 1-line | 120 | |||||||
| ManySStubs4j | 3,000 | Exact-Match (EM) |
III-E1 Function Synthesis
This task aims to generate Python functions from “Docstrings”.666Docstrings are code comments that explain the code’s purpose and usage. Further discussed in § III-E2. Correctness is determined by functional testing.
We use HumanEval [19] and MBPP [20] datasets (see Figure A2 for sample prompts and model output). One caveat: the samples in these datasets largely constitute artificial problems, specifically assembled to test the code-synthesis capacity of LLMs; measurements (both accuracy and calibration) over these datasets may not generalize to real-world software development. Even so, these datasets provide a valuable datapoint for assessing model calibration.
We restructure all MBPP problems into a function synthesis task by placing the prompt inside the tested method as a Docstring, making it comparable to HumanEval. Additionally we exclude approximately 75 problems where the reference solution fails to pass the provided test cases777Due to either buggy reference code/tests, or possibly missing environment/networking/compute-time requirements..
III-E2 Line-level Code Completion
Code completion is currently the most important and widely-deployed generative task, with tools like GitHub Copilot [19]. Completion performance has been studied at both the token and line levels [29, 30, 31, 32]. However, calibration for this vital, widely-deployed task has so far not been evaluated in detail
The current decoder-only GPT models [33, 19] are already trained to generate the next token at low average cross-entropy given all the prior tokens, following the condition . Unsurprisingly, we found such autoregressively-trained models are per se well-calibrated at the token level. In this work, we will primarily focus on line-level completion. While several datasets exist for this problem [34, 35], we use DyPyBench [36], a new dataset consisting of 50 popular open-source Python projects, including test suites for these projects. The test suites allow a test-correctness measure, in addition to the highly restrictive exact-match (viz., the original line).
DyPyBench consists of complex real-world projects, each with hundreds of thousands of lines of Python code, and totaling over 2.2 million lines of Python code. We ran all test suites for each project with coverage reporting enabled, extracted all functions from the projects, following [37], and selected 1,988 functions with at least 3 lines in the body, test coverage, and at least one line in the “Docstring”.
III-E3 Program Repair
Program repair is a well-studied problem in software engineering [38]. Several studies report that LLMs are effective at this task [39, 21, 40]. However, LLM calibration for program repair is not well-understood. This paper focuses on small, pre-localized single-line bugs. We leverage the widely-used Defects4J dataset [41], which includes real-world examples of buggy programs, with fixes and test-sets. We extract 120 single-line bugs from Defects4J dataset. However, with only 120 samples, we may not obtain a comprehensive view of calibration. Therefore, we included another dataset, ManySStubs4J [42] (abbr. SStubs), which consists of single-line repairs. Following the setup of the SStubs dataset, the bug might be localized to a sub-expression of the line888Note, due to data processing errors, 3 Defects4J examples have slightly mis-localized bugs. We leave these as-is, reasoning that model confidence should be robustly well-calibrated even with slight localization noise, ideally giving a lower confidence of a fix if the location is noisy.. We sample (uniformly at random) 3,000 examples from this dataset. SStubs does not provide test-sets; so the only evaluation metric available is the exact-matching of the generated text to the ground truth bug-free text.
III-F The Models
We explore confidence calibration for three code generation models. These include OpenAI Gpt-3.5 999The gpt-3.5-turbo-instruct model, https://platform.openai.com/docs/models/gpt-3-5-turbo, OpenAI Codex [19], and CodeGen2-16B [43]. We sample from the models with temperature of 0, consistent with the reality that busy developers typically look at just the first suggestion in the completion [44]. For function synthesis task, temperature zero is most accurate and is fairly standard practice when doing pass@1 with only one solution to generate and present [19, 13].
IV Results
We begin with a brief overview of the findings on the correctness- & confidence- measures of LLMs on the various tasks, and then provide detailed results on the calibration-related research questions.
| All Pass@1 | Exact-Match | |||||
| CodeGen2 | Codex | |||||
| GPT-3.5 | CodeGen2 | Codex | GPT-3.5 | |||
| SStubs | - | - | - | 0.73% | 27.77% | 20.27% |
| DyPyBench | 28.84% | 32.96% | 33.22% | 19.68% | 23.60% | 23.96% |
| Defects4J | 0.00% | 23.33% | 19.17% | 0.00% | 19.17% | 15.00% |
| HumanEval | 23.17% | 47.24% | 64.60% | - | - | - |
| MBPP | 29.08% | 61.79% | 72.04% | - | - | - |
IV-A RQ 1: How well are language models’ confidence in their output aligned with the empirical correctness of their output, specifically for common generative tasks, viz. function synthesis, line-level code completion, and program repair?
IV-A1 Overall Correctness
Correctness performance rate of the various models on the various tasks and datasets, are presented in Table II. Specifically, we report the fraction of samples passing all test cases for a given model and dataset, and the percentage of exact-matches. We found that Gpt-3.5 worked well for both function synthesis (HumanEval and MBPP), and line-level code completion, whilst Codex generally performed well on program repair. The DyPyBench benchmark reflects the most popular use of LLMs, viz., for code completion.
IV-A2 Correctness: Test-passing vs. Exact-match
As per § III-A, we evaluate correctness both on test-passing and exact-match. Our experiment included two datasets (Defects4J and DyPyBench), where both methods of measuring correctness were available. Since Defects4J consists of only 120 samples, we present the results for DyPyBench; in this case, as per Table II, Gpt-3.5 performed best, with approximately 33% of generated code passing all available tests, and approximately 24% matching exactly.
In this setting (DyPyBench/Gpt-3.5), we cross-tabulate performance across the two correctness-measuring methods. We note that approximately half the test-passing generations did not match the original code exactly; furthermore 6.89% of the cases where the code matched exactly, did not pass all the test cases. Upon careful study we found that these tests were “flaky”, depending on network conditions, execution order, and other variable execution environment conditions. This aligns with [36], the author of this dataset, who observed an overall failure rate, but noted that 31 out of 50 projects had zero failed tests. This illustrates the relative merits/demerits of each correctness-evaluating approach, in practical SE settings. Since the correctness performance is different with these two notions of correctness, the calibration is also different, as we see below.
IV-A3 Confidence Measures
As might be expected, the two intrinsic measures & are usually somewhat, and sometimes strongly, positively correlated with each other within the same model, dataset, and task.
| Line Completion | Function Synthesis | Program Repair | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DyPyBench | HumanEval | MBPP | Defects4J | SStubs | ||||||||||||
| Model | Metric | |||||||||||||||
| GPT-3.5 | Total Prob | 0.23 | -0.03 | 0.15 | 0.62 | -1.70 | 0.63 | 0.71 | -2.50 | 0.71 | 0.25 | -0.63 | 0.28 | 0.24 | -0.50 | 0.25 |
| Avg Prob | 0.41 | -0.87 | 0.46 | 0.27 | -0.18 | 0.23 | 0.22 | -0.09 | 0.14 | 0.68 | -3.39 | 0.73 | 0.64 | -2.94 | 0.69 | |
| Ask T/F | 0.25 | -0.13 | 0.16 | 0.34 | -0.47 | 0.37 | 0.33 | -0.64 | 0.38 | 0.15 | +0.05 | 0.04 | 0.16 | -0.01 | 0.04 | |
| Ask T/F N | 0.25 | -0.15 | 0.15 | 0.23 | +0.01 | 0.19 | 0.22 | -0.11 | 0.16 | 0.20 | -0.30 | 0.24 | 0.22 | -0.34 | 0.23 | |
| Verbalize | 0.43 | -0.92 | 0.42 | 0.28 | -0.24 | 0.22 | 0.24 | -0.17 | 0.17 | 0.58 | -2.72 | 0.60 | 0.50 | -2.09 | 0.53 | |
| Length | 0.44 | -0.99 | 0.46 | 0.23 | -0.03 | 0.15 | 0.22 | -0.10 | 0.16 | 0.53 | -2.43 | 0.60 | 0.53 | -2.26 | 0.60 | |
| Unskilled | 0.22 | 0.00 | 0.00 | 0.23 | 0.00 | 0.00 | 0.20 | 0.00 | 0.00 | 0.15 | 0.00 | 0.00 | 0.16 | 0.00 | 0.00 | |
| [dashed] Codex | Total Prob | 0.23 | -0.02 | 0.16 | 0.44 | -0.77 | 0.45 | 0.60 | -1.52 | 0.60 | 0.25 | -0.39 | 0.24 | 0.20 | 0.00 | 0.09 |
| Avg Prob | 0.46 | -1.07 | 0.50 | 0.34 | -0.38 | 0.35 | 0.24 | -0.03 | 0.19 | 0.66 | -2.68 | 0.69 | 0.58 | -1.90 | 0.62 | |
| Ask T/F | 0.24 | -0.09 | 0.12 | 0.37 | -0.47 | 0.36 | 0.49 | -1.06 | 0.50 | 0.18 | +0.01 | 0.07 | 0.19 | +0.03 | 0.02 | |
| Ask T/F N | 0.23 | -0.06 | 0.07 | 0.32 | -0.29 | 0.30 | 0.42 | -0.79 | 0.43 | 0.25 | -0.41 | 0.27 | 0.23 | -0.14 | 0.18 | |
| Verbalize | 0.38 | -0.74 | 0.35 | 0.42 | -0.67 | 0.40 | 0.38 | -0.61 | 0.33 | 0.47 | -1.65 | 0.50 | 0.43 | -1.14 | 0.42 | |
| Length | 0.43 | -0.95 | 0.45 | 0.44 | -0.77 | 0.44 | 0.56 | -1.35 | 0.56 | 0.50 | -1.79 | 0.55 | 0.56 | -1.78 | 0.59 | |
| Unskilled | 0.22 | 0.00 | 0.00 | 0.25 | 0.00 | 0.00 | 0.24 | 0.00 | 0.00 | 0.18 | 0.00 | 0.00 | 0.20 | 0.00 | 0.00 | |
| [dashed] CodeGen2 | Total Prob | 0.21 | -0.02 | 0.15 | 0.23 | -0.30 | 0.23 | 0.29 | -0.41 | 0.29 | - | - | - | - | - | - |
| Avg Prob | 0.44 | -1.16 | 0.50 | 0.60 | -2.39 | 0.66 | 0.58 | -1.80 | 0.61 | - | - | - | - | - | - | |
| Ask T/F | 0.23 | -0.10 | 0.14 | 0.25 | -0.38 | 0.24 | 0.25 | -0.19 | 0.21 | - | - | - | - | - | - | |
| Ask T/F N | 0.33 | -0.59 | 0.35 | 0.39 | -1.19 | 0.45 | 0.39 | -0.88 | 0.43 | - | - | - | - | - | - | |
| Verbalize | 0.42 | -1.04 | 0.41 | 0.43 | -1.39 | 0.42 | 0.40 | -0.94 | 0.38 | - | - | - | - | - | - | |
| Length | 0.47 | -1.28 | 0.51 | 0.38 | -1.14 | 0.42 | 0.33 | -0.58 | 0.28 | - | - | - | - | - | - | |
| Unskilled | 0.21 | 0.00 | 0.00 | 0.18 | 0.00 | 0.00 | 0.21 | 0.00 | 0.00 | - | - | - | - | - | - |
IV-A4 Calibration without Rescaling
Table III presents the results for Line Completion, Function Synthesis, and Program Repair for each model and the raw confidence measure, without any rescaling method. We find raw confidence measures are poorly calibrated, with inconsistent exceptions. In fact, the raw baseline rate (using the average fraction correct without considering the individual generation) is hard to beat; the best skill-score is around .
For line completion, the confidence measure is slightly worse than the baseline rate; calibration error is modest (). The total probability improves on the average probability, which is overconfident: the average token probability exceeds the overall success rate.
For function synthesis with raw measures, exhibits very poor calibration for Gpt-3.5 and Codex, but not for CodeGen2 on HumanEval, while the best intrinsic measure for MBPP is for Gpt-3.5 and Codex. The intrinsic measures are inconsistent; with average probability showing indicators of better calibration for Gpt-3.5 and Codex, but not for CodeGen2.
For program repair, intrinsic measures are consistently below the base rate for both models and are as such, poorly calibrated. There are several caveats here. First, Defects4J is a small dataset, so findings may not generalize. Second, CodeGen2 performs poorly on Defects4J. Since CodeGen2 is a smaller model without instruction tuning and relatively more limited reasoning capabilities it gets “distracted” by the buggy version shown in the prompt: it often just repeats the buggy lines. With very few correct outputs, the estimation of the confidence measure becomes unreliable. Therefore, we have removed the CodeGen2 results from Table III. A final caveat is that SStubs uses only exact-match as a correctness measure, which is quite different from a test passing measure.
| Line Completion | Function Synthesis | Program Repair | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DyPyBench | HumanEval | MBPP | Defects4J | SStubs | ||||||||||||
| Model | Metric | |||||||||||||||
| GPT-3.5 | Total Prob | 0.21 | +0.07 | 0.03 | 0.20 | +0.15 | 0.09 | 0.19 | +0.07 | 0.05 | 0.16 | -0.05 | 0.16 | +0.03 | ||
| Avg Prob | 0.20 | +0.08 | 0.04 | 0.23 | -0.02 | 0.20 | 0.00 | 0.16 | -0.03 | 0.16 | +0.02 | |||||
| Ask T/F | 0.22 | 0.00 | 0.20 | +0.12 | 0.11 | 0.18 | +0.09 | 0.06 | 0.15 | +0.05 | 0.16 | 0.00 | ||||
| Ask T/F N | 0.22 | 0.00 | 0.20 | +0.14 | 0.07 | 0.18 | +0.11 | 0.04 | 0.15 | +0.04 | 0.16 | +0.01 | ||||
| Verbalize | 0.22 | 0.00 | 0.24 | -0.05 | 0.20 | +0.02 | 0.17 | -0.09 | 0.16 | 0.00 | ||||||
| Length | 0.22 | 0.00 | 0.24 | -0.03 | 0.20 | +0.01 | 0.16 | -0.06 | 0.16 | 0.00 | ||||||
| Unskilled | 0.22 | 0.00 | 0.23 | 0.00 | 0.20 | 0.00 | 0.16 | 0.00 | 0.16 | 0.00 | ||||||
| [dashed] Codex | Total Prob | 0.20 | +0.09 | 0.03 | 0.22 | +0.11 | 0.08 | 0.22 | +0.06 | 0.04 | 0.18 | -0.01 | 0.19 | +0.05 | 0.02 | |
| Avg Prob | 0.20 | +0.09 | 0.04 | 0.22 | +0.14 | 0.07 | 0.21 | +0.12 | 0.06 | 0.18 | -0.02 | 0.19 | +0.05 | 0.02 | ||
| Ask T/F | 0.22 | 0.00 | 0.24 | +0.03 | 0.24 | 0.00 | 0.18 | 0.00 | 0.19 | +0.04 | ||||||
| Ask T/F N | 0.22 | 0.00 | 0.24 | +0.03 | 0.24 | 0.00 | 0.18 | -0.01 | 0.20 | +0.02 | ||||||
| Verbalize | 0.22 | 0.00 | 0.26 | -0.02 | 0.24 | -0.01 | 0.18 | 0.00 | 0.20 | 0.00 | ||||||
| Length | 0.22 | +0.01 | 0.26 | -0.03 | 0.24 | -0.01 | 0.20 | -0.10 | 0.20 | 0.00 | ||||||
| Unskilled | 0.22 | 0.00 | 0.25 | 0.00 | 0.24 | 0.00 | 0.18 | 0.00 | 0.20 | 0.00 | ||||||
| [dashed] CodeGen2 | Total Prob | 0.19 | +0.08 | 0.04 | 0.18 | 0.00 | 0.21 | 0.00 | - | - | - | - | ||||
| Avg Prob | 0.19 | +0.07 | 0.02 | 0.17 | +0.03 | 0.21 | 0.00 | - | - | - | - | |||||
| Ask T/F | 0.21 | 0.00 | 0.18 | -0.01 | 0.20 | +0.01 | - | - | - | - | ||||||
| Ask T/F N | 0.21 | 0.00 | 0.17 | +0.04 | 0.21 | 0.00 | - | - | - | - | ||||||
| Verbalize | 0.21 | 0.00 | 0.18 | -0.01 | 0.21 | 0.00 | - | - | - | - | ||||||
| Length | 0.21 | 0.00 | 0.18 | -0.02 | 0.21 | 0.00 | - | - | - | - | ||||||
| Unskilled | 0.21 | 0.00 | 0.18 | 0.00 | 0.21 | 0.00 | - | - | - | - |
IV-B RQ 2: Can alignment between LLM confidence in generated code, and its correctness, be improved by confidence rescaling?
Table IV shows the results after applying Platt scaling to all measures (See § III-D). 2(a) shows a reliability plot before rescaling, and its equivalent after rescaling in 2(b). Rescaling can improve calibration. Considering all values, improves from an average of 0.32 to 0.03. For just those measures with a post-scaling of at least 0.05, improves from 0.38 to 0.05.


Understanding “Bucket Collapse”
Platt scaling can lead to deceptively low . If a confidence measure is poorly aligned with correctness, Platt-scaling can rescale (squash) all the confidence values to the baseline rate; this places all samples in a single confidence value bucket where probability exactly matches the baseline rate of correctness, resulting in an near 0. This indicates the problem of only considering . and Brier, on the other hand, would reveal the poor utility of the confidence measure. Thus when applying rescaling, it is important to consider Skill Score, rather than only Brier and .
Results
After rescaling, only the intrinsic measures show skill improvement over the baseline rate for line completion. and are similarly calibrated. The calibration and skill appears roughly consistent between all three models in this case. Rescaling improves calibration results for function synthesis. The measure reaches a of 0.15 for HumanEval. Rescaling useful improvement for reflective prompts as well bringing and to similar values (discussed further in Section IV-C). For program repair, rescaling doesn’t improve skill score, for any measure.
Is Rescaling a Panacea for Calibration?
Rescaling typically improves calibration; it has been used in settings other than generative models of code, with other notions of correctness [22, 45, 25, 46, 47, 48, 49]. However, there are disadvantages. First, “bucket collapse” (see § IV-B) can mislead with deceptively low . Second, some correctness data is needed to fit rescaling parameters. When sweeping through various sized bootstrapped subsets of the data, we find that it can take over 64 data points for the rescaling to result in positive skill and lower , with improvements continuing into 100s of data points (see Figure A8 for bootstrapping analysis). When using the full data, the rescaling between tasks can vary dramatically.101010As seen in Figure A6, which shows the curves learned between measure-task pairs. Ideally, we want confidence measures which are reliable and allow trustworthy auditing even when applying language models to new software engineering tasks. To study how close we are to this, we fit rescaling parameters to one task, and then apply it to the other tasks (see Figure A7). We find it is viable to use rescaling between tasks of the same domain with similar base rates, such as within the program synthesis tasks. For example, for Gpt-3.5 when fitting (results in next section) rescaling to each of two function synthesis tasks, and then applying it to the other, we observe an average drop of from 0.14 0.12, and average drop of from 0.07 0.05. However, applying the rescaling fit on DyPyBench to the function synthesis tasks, results in an average change of 0.12 -1.28 and change of 0.08 0.54, indicating a lack of robustness. These reasons suggest one must be careful when analyzing and reporting calibration results based on rescaling, and highlights the need for further work on confidence measures that might be more directly calibrated.
Without rescaling, total probability shows hints of calibration. With rescaling, there is a possible 10-20% improvement over baseline rates and good calibration, but it is inconsistent as skill is poor for CodeGen2 on Function Synthesis.
IV-C RQ 3: Is confidence obtained by reflection better aligned with correctness?
The two logit-based reflective measures & are usually strongly positively correlated with one another, since they are calculated from similar numbers. The reflective verbalized self-ask confidence measure , and the two logit-based reflective confidence measures have no consistent relationships.
For function synthesis with raw measures, shows best calibration for Gpt-3.5, slightly better than Unskilled, for HumanEval. For program repair, we observe the strongest best-case performance with regards to the metrics. Both Gpt-3.5 and Codex show positive and low for , but they are inconsistent after normalization (). These metrics suggest with reflection, these models’ confidence is calibrated regarding repair correctness; however, further analysis (see Figure A3) does not indicate good calibration on this task, from any confidence measure. We find that in general, the intrinsic vs. reflective measure values have no consistent relationship, even for a given model, dataset and task.
This lack of relationship may not necessarily be negative: e.g., perhaps the model’s reflective, prompted confidence may be better calibrated, as suggested by prior work [50, 20]. Without rescaling or few-shot prompting, reflective results are inconsistent. In some cases, such as Gpt-3.5 HumanEval and Defects4J, there are signs of calibration with slightly positive values and values less than 0.2. Normalizing the T/F values induces some difference; but there are inconsistencies vis-à-vis tasks and models. For nonscaled Gpt-3.5 results, improves calibration in line completion and function synthesis by an average of -0.34 and 0.19 , but not for program repair or for CodeGen2. Rescaling generally removes any sign of a normalization trend. For the alternative reflective approach of verbalization, the probability is not well calibrated for these models on the studied SE tasks.
In some cases, the reflective approaches are best calibrated without rescaling (see Table III), and show signs of being more robust when reusing learned rescaling parameters on unseen tasks (see Figure A7).
IV-D RQ 4: Can we use few-shot techniques to achieve better calibrated confidence for code completion, using an instruction-tuned model with in-context learning?
We investigated the impact of few-shotting viz. providing a model completion and correctness as part of the prompt, on calibration [18]. To effectively perform few-shotting, we need a model that is instruction tuned and sufficiently large, which is best matched by Gpt-3.5. We explore few-shotting for the widely-used line completion task.
We perform the experiment with 5-shots consisting of prior completions from the same experiments presented in Table IV, the reflective question, and the ground truth True/False. We try two variants of this experiment, one where the examples are randomly selected, and one where they are chosen based on the similarity to the unanswered prompt. In both cases, we exclude the ground truth result for the unanswered prompt. We focus on Line Completion for this experiment as it represents widespread use and has a large number of examples available.
| Confidence Measure | |||
|---|---|---|---|
| 0-Shot Reflect | 0.25 | -0.15 | 0.15 |
| 0-Shot Reflect (Rescaled) | 0.22 | 0.00 | |
| FS Random | 0.29 | -0.29 | 0.21 |
| FS Random (Rescaled) | 0.22 | 0.0 | |
| FS BM25 | 0.20 | 0.08 | 0.10 |
| FS BM25 (Rescaled) | 0.19 | 0.15 | 0.02 |
For line completion, the non-scaled results using random examples did not result in improved calibration over the baseline , however using BM25 [6] to select similar examples yielded a positive of 0.08, which could be improved further by rescaling, up to 0.15. This result notably exceeds any other measure for DyPyBench, and significantly improves over the baseline of 0.
While random few-shotting requires limited extra data, BM25 is more similar to rescaling, in that it is dependent on a larger set of ground truths. This could be actualized by logging user completions, and building up ground truths (on if the completion was correct) based off the test case runs or acceptance of completions.
V Discussion
Language models are now widely-integrated into Software Engineering practice, via tools like Copilot [32] and Didact111111blog.research.google/2023/05/large-sequence-models-for-software.html. We raise here the importance of calibration when integrating generative LLMs in coding practice. We evaluate the calibration of generative LLM use (especially code completion) with large samples of realistic data (DyPyBench, SStubs), using widely adopted models, as well as some more academic datasets (HumanEval, MBPP).
Using a well-calibrated model–beyond simple defect prediction
To clarify how a well-calibrated model enables more well-grounded decision-making concerning generated outputs, as compared to as compared to a traditional process choosing a binary decision point—we consider Gpt-3.5 working on code completion, where correctness is determined by test-passing, and confidence is assigned by few-shotting, average token probability. The base correctness (test-passing) rate of completions is about 33%. With few-shotting, we get a very high skill score of 0.15 (Section IV-D, Table V).

If we didn’t have a well-calibrated model, we might very cautiously accept only those completions that are generated at a very high-confidence threshold; here, the FP rate could be low (of course TP rate would be low as well). While this may lower the risk of bad code, it also regrettably reduces the available help from the LLM. However, a well-calibrated confidence measure allows a more rational, graduated set of decisions. Such a well-calibrated measure is visualized in Figure 3. In this setting, for much of the confidence scale, a user could look at the confidence level, and get a very good idea of how likely the code is to be correct, and make a well-reasoned, situation-specific set of decisions to manage risk, and allocate reviewing resources, based on the model’s confidence. This provides an illustration of the greater benefit provided a well-calibrated measure (high Skill level, low ECE) over one that is just providing good precision-recall trade-off (or, ROC curve); the latter does not allow such graduated deployment of quality-control effort. However, developers would need to learn to use calibrated probabilities in decision-making.
Beyond simple “correctness”
In addition to the above uses, which considered a single notion of “correctness”, one could consider a multi-class correctness prediction task, where the model could indicate the confidence in correctness (the absence of defects) from multiple perspectives: severity of possible defect, the kind of defect (relating to security, integrity, privacy, fairness, etc.) and defect complexity (indicating the cost or schedule impact of repairs). Drawing an analogy to classical forecasting, this is analogous to not just the probability it will rain, but probability it will be a drizzle or be a drenching thunderstorm.
Why calibration now?
We’ve always had bugs; poor-quality code isn’t new. Our push for calibration, however, arises from the increasing amount of code generated by LLM. GitHub claims that up to 61% of code121212github.blog/2023-02-14-github-copilot-now-has-a-better-ai-model-and-new-capabilities in some systems is generated by LLMs. It is also known that LLMs make a lot of mistakes. A recent paper has reported [1] that LLMs, even when trained on properly fixed code, tends to recapitulate the the old unfixed, buggy code when prompted in context. However, LLMs do have very high capacity, and a demonstrated ability to usefully reflect [52, 50] on their generated text. Thus, we have both a high risk (of buggy code), and a chance to improve productivity. We believe that improved calibration could lead to better management of the risk-benefit of LLM-generated code. The studied correctness calibration is a stepping stone for more complex notions of confidence (like severity and localized confidence). Additionally, by studying code LLMs, we might make progress on the general safe deployment of capable generative models [10].
Summarizing per-token probabilities
To produce a summary confidence for generated token sequences in Tables III and IV, in Tables III & IV, we used (arithmetic mean) average & product to summarize the per-token probabilities. In this setting, it might be more reasonable to use geometric mean (as in [53]) to get a product value normalized for length; indeed, when we tried that, we found that Brier and skill scores improved marginally, but consistently so; future research could indicate whether these findings generalize.
VI Threats to Validity
Sample Size & Generalizability
While three of our datasets contain more than 800+ samples each, HumanEval and Defects4J datasets consist of only 164 and 120 samples, respectively. Results on these datasets may not generalize. However, we note that our study has a large and natural dataset for the line-level code completion task, which has current practical importance. Given the noise and variance we observe, we recommend future work push towards larger and more natural datasets, in particular for Function Synthesis & Repair.
While some of our treatments (e.g., few-shotting) suggest substantial improvements in skill score (Table V), in other cases such as the different approaches to summarize per-token confidence differences, the differences are less clear. In future work, these differences could be judged more robustly using bootstrapped p-values and effect sizes.
Artificial vs. real world data
For function synthesis, we used the popular HumanEval and MBPP function synthesis datasets. These datasets contain small-ish Python programs that may not represent real-world software development functions. However, our other datasets, such as DyPyBench and SStubs are more representative of real-world, open-source GitHub projects.
Model Selection
Results might not generalize to all models, especially those with greatly differing training/finetuning or different architectures.
Experimental Design
Our exploration is not exhaustive; other SE tasks and datasets also could benefit from calibration studies. Additionally, the specific prompts we used for this paper surely played a role in our findings. Other prompts or problem phrasings (such as different forms of context for line-level code completion) may yield different results. Regarding test flakiness: the test “flake” rate of DyPyBench is not zero, but is quite low and not unrealistic [14].
Despite these caveats, our study, which includes three tasks and five datasets, provides a good starting point for further studies.
VII Related Work
LLMs for code are extensively studied [54, 55]. While calibration has a long history in modeling [8, 56], it is not a frequently studied topic in the SE community. Early work moving into modern machine learning studied the calibration of smaller neural models performing classification tasks on text and images; while these early models were poorly calibrated per se, their performance could be improved by simple scaling [22] of their output probabilities. As models became larger, calibration was found to improve [57]. Pre-training was also found to improve calibration [58, 25]; however, these findings have been disputed [47].
More recent works evaluated LLM calibration on a wide variety of settings [18, 7, 25, 59]. [25] studied non-code (natural language) tasks such as inference or paraphrasing, with only intrinsic measures using older-generation models (BERT and RoBERTA). [7] studied calibration for natural language question-answering using just intrinsic measures. In contrast, we study calibration for three coding-related tasks, using both artificial and natural code datasets, and both intrinsic and reflective confidence measures, to evaluate calibration in the SE domain.
Other prior work has investigated tokens that might be edited. [60] discusses code model uncertainty for function-synthesis-style problems, and ran human evaluation of the usefullness of colored highlighting of uncertain tokens. They found highlighting a human-derived ground-truth of which tokens might be edited was helpful, and more useful than raw token probabilities from the model. [61] developed method of highlighting likely edit tokens via a utility optimization algorithm comparing different file completions. We find exploring more on calibrated uncertainty for local areas be a interesting area for additional work.
[49] investigate the calibration of Computer vision (CV) models from an operational perspective i.e., the shift between training input and production inputs, presenting it as a software quality problem that can be addressed using Bayesian approaches. [45] evaluate the calibration of at the time, state of the art CV models and find improved calibration with more recent models, notably those not using convolutions. [46] study the effect of the mixup technique [62] on calibration in a natural language understanding (NLU) setting using older generation models (BERT and RoBERTa). [47] investigate the calibration of pretrained language models on various NLP tasks, also using older generation models (RoBERTa and T5). [48] introduce the HELM benchmark, which includes calibration as one of its seven metrics to evaluate language models in a natural language context. [63] explored LM uncertainty with a range of techniques and tasks, including both NLP and function synthesis tasks. They evaluated using correlation measures, rather than focusing on calibration. They explore interesting sample-based and perturbation techniques which could be explored more for calibration on diverse SE tasks. Other work [64] has explored training an ML model that sees code and execution results to estimate correctness probabilities for solution reranking. For natural language question answering tasks, work has explored improving calibration by training a model to adjust token logits [53], and training a model from LLM hidden states specifically around the metric [65].
When suitably prompted, [18] found that LLMs can output well-calibrated scores on whether their own answers are correct or not, viz., larger models “know what they know”. While this work did investigate some function synthesis tasks (HumanEval & an unpublished Python function dataset), they did so using only their private models, and ultimately focused on natural language tasks. [59] developed an approach that given a natural language problem description, produces a confidence score for a sampled candidate solution based on generated specifications, allowing them to judge whether the LLM can solve the problem at all. Their metrics include calibration. Recent work has also explored calibration of software topics such as root cause analysis [66].
VIII Conclusion
In this paper, we begin with the observation that while LLMs are often helpful (for example producing code-completions for developers) they often produce buggy code. We argue that a well-calibrated confidence score, could provide a reliable indication of whether the generated code was correct, and help more rational, graduated quality-control of of LLM-generated code We studied the calibration of intrinsic and reflective confidence measures in several practical settings (completion and repair) and a widely-used competitive setting (synthesis), across several LLMs. We find that LLMs are generally poorly calibrated out of the box, across a variety of confidence measures (both intrinsic and reflective) We then found that Platt scaling generally results in somewhat better calibrated confidence measures.
Finally, we focused in on a) coding task where LLMs are most widely-deployed, viz. code completion, and b) a very widely used instruction-tuned model, viz. Gpt-3.5, and investigated whether a reflective, in-context learning approach (few-shotting) could provide better calibrated confidence measures. In this setting, we found that calibration improves substantially, reaching a skill score of , particularly with retrieval augmented few-shotting.
To our knowledge, our paper is the first to consider the problem of calibration in a real-world code generation setting. We do find that most models, both out-of-the-box and with simple reflection, don’t provide reliable confidence measures. However, our results with retrieval-augmented few-shotting are very encouraging, and point towards a future where Language Models could provide developers with guidance on how to quality-control the code they generate.
IX Acknowledgments
We acknowledge partial support for this work by the Intelligence Advanced Research Projects Agency (IARPA) under contract W911NF20C0038, the National Science Foundation under CISE SHF MEDIUM 2107592, the European Research Council (ERC grant agreement 851895), and the German Research Foundation (ConcSys, DeMoCo, and QPTest projects). Devanbu was supported by a Humboldt Research Award131313https://www.humboldt-foundation.de/en/connect/explore-the-humboldt-network/singleview/1226147/prof-dr-premkumar-t-devanbu. Our conclusions do not necessarily reflect the position or the policy of our sponsors and no official endorsement should be inferred.
References
- [1] Kevin Jesse, Toufique Ahmed, Premkumar T. Devanbu and Emily Morgan “Large Language Models and Simple, Stupid Bugs” In 2023 IEEE/ACM 20th International Conference on Mining Software Repositories (MSR), 2023, pp. 563–575
- [2] Owura Asare, Meiyappan Nagappan and N. Asokan “Is GitHub’s Copilot as Bad as Humans at Introducing Vulnerabilities in Code?” In Empirical Software Engineering 28.6, 2023, pp. 129
- [3] Roei Schuster, Congzheng Song, Eran Tromer and Vitaly Shmatikov “You Autocomplete Me: Poisoning Vulnerabilities in Neural Code Completion”, 2021, pp. 1559–1575
- [4] David Lo “Trustworthy and Synergistic Artificial Intelligence for Software Engineering: Vision and Roadmaps”, 2023 arXiv:2309.04142 [cs]
- [5] Zhenhao Zhou, Chaofeng Sha and Xin Peng “On Calibration of Pre-trained Code Models” In 2024 IEEE/ACM 46th International Conference on Software Engineering (ICSE), 2024, pp. 861–861 IEEE Computer Society
- [6] Noor Nashid, Mifta Sintaha and Ali Mesbah “Retrieval-Based Prompt Selection for Code-Related Few-Shot Learning” In 2023 IEEE/ACM 45th International Conference on Software Engineering (ICSE), 2023, pp. 2450–2462 DOI: 10.1109/ICSE48619.2023.00205
- [7] Zhengbao Jiang, Jun Araki, Haibo Ding and Graham Neubig “How Can We Know When Language Models Know? On the Calibration of Language Models for Question Answering” In Transactions of the Association for Computational Linguistics 9, 2021, pp. 962–977
- [8] Glenn W. Brier “Verification of Forecasts Expressed in Terms of Probability” In Monthly Weather Review 78.1 American Meteorological Society, 1950, pp. 1–3
- [9] Mahdi Pakdaman Naeini, Gregory Cooper and Milos Hauskrecht “Obtaining Well Calibrated Probabilities Using Bayesian Binning” In Proceedings of the AAAI Conference on Artificial Intelligence 29.1, 2015
- [10] David Gros, Prem Devanbu and Zhou Yu “AI Safety Subproblems for Software Engineering Researchers”, 2023 arXiv:2304.14597 [cs]
- [11] David M. Nierman, Clyde B. Schechter, Lisa M. Cannon and Diane E. Meier “Outcome Prediction Model for Very Elderly Critically Ill Patients” In Critical Care Medicine 29.10, 2001, pp. 1853
- [12] Johanna Schwarz and Dominik Heider “GUESS: Projecting Machine Learning Scores to Well-Calibrated Probability Estimates for Clinical Decision-Making” In Bioinformatics 35.14, 2019, pp. 2458–2465
- [13] Jiawei Liu, Chunqiu Steven Xia, Yuyao Wang and Lingming Zhang “Is Your Code Generated by ChatGPT Really Correct? Rigorous Evaluation of Large Language Models for Code Generation” In Advances in Neural Information Processing Systems 36, 2023, pp. 21558–21572
- [14] Qingzhou Luo, Farah Hariri, Lamyaa Eloussi and Darko Marinov “An Empirical Analysis of Flaky Tests” In Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering, FSE 2014 New York, NY, USA: Association for Computing Machinery, 2014, pp. 643–653
- [15] Stephanie Lin, Jacob Hilton and Owain Evans “Teaching Models to Express Their Uncertainty in Words” In Transactions on Machine Learning Research, 2022
- [16] Kaitlyn Zhou, Dan Jurafsky and Tatsunori Hashimoto “Navigating the Grey Area: How Expressions of Uncertainty and Overconfidence Affect Language Models” In EMNLP’23 Singapore: Association for Computational Linguistics, 2023, pp. 5506–5524
- [17] Katherine Tian et al. “Just Ask for Calibration” In Proceedings of the 2023 Conference on Empirical Methods in Natural Language Processing Singapore: Association for Computational Linguistics, 2023, pp. 5433–5442
- [18] Saurav Kadavath et al. “Language Models (Mostly) Know What They Know”, 2022 arXiv:2207.05221 [cs]
- [19] Mark Chen et al. “Evaluating Large Language Models Trained on Code”, 2021 arXiv:2107.03374 [cs]
- [20] Jacob Austin et al. “Program Synthesis with Large Language Models”, 2021 arXiv:2108.07732 [cs]
- [21] Nan Jiang, Kevin Liu, Thibaud Lutellier and Lin Tan “Impact of Code Language Models on Automated Program Repair” In ICSE’23’, 2023, pp. 1430–1442
- [22] Chuan Guo, Geoff Pleiss, Yu Sun and Kilian Q. Weinberger “On Calibration of Modern Neural Networks” In Proceedings of the 34th International Conference on Machine Learning PMLR, 2017, pp. 1321–1330
- [23] Jeremy Nixon et al. “Measuring Calibration in Deep Learning”, 2019, pp. 38–41
- [24] John Platt “Probabilistic Outputs for Support Vector Machines and Comparisons to Regularized Likelihood Methods” In Advances in large margin classifiers 10.3 Cambridge, MA, 1999, pp. 61–74
- [25] Shrey Desai and Greg Durrett “Calibration of Pre-trained Transformers” In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP) Online: Association for Computational Linguistics, 2020, pp. 295–302
- [26] Bianca Zadrozny and Charles Elkan “Obtaining Calibrated Probability Estimates from Decision Trees and Naive Bayesian Classifiers” In ICML’01 Morgan Kaufmann, 2001, pp. 609–616
- [27] Bianca Zadrozny and Charles Elkan “Transforming Classifier Scores into Accurate Multiclass Probability Estimates” In KDD ’02 New York, NY, USA: Association for Computing Machinery, 2002, pp. 694–699
- [28] Meelis Kull et al. “Beyond Temperature Scaling: Obtaining Well-Calibrated Multi-Class Probabilities with Dirichlet Calibration” In Advances in Neural Information Processing Systems 32 Curran Associates, Inc., 2019
- [29] Maliheh Izadi, Roberta Gismondi and Georgios Gousios “CodeFill: Multi-Token Code Completion by Jointly Learning from Structure and Naming Sequences” In ICSE’22, ICSE ’22 New York, NY, USA: Association for Computing Machinery, 2022, pp. 401–412
- [30] Seohyun Kim, Jinman Zhao, Yuchi Tian and Satish Chandra “Code Prediction by Feeding Trees to Transformers” In ICSE’21, 2021, pp. 150–162
- [31] Shuai Lu et al. “CodeXGLUE: A Machine Learning Benchmark Dataset for Code Understanding and Generation” In NeurIPS 1, 2021
- [32] Albert Ziegler et al. “Productivity Assessment of Neural Code Completion” In MAPS 2022 New York, NY, USA: Association for Computing Machinery, 2022, pp. 21–29
- [33] Tom Brown et al. “Language Models Are Few-Shot Learners” In Advances in Neural Information Processing Systems 33 Curran Associates, Inc., 2020, pp. 1877–1901
- [34] Miltiadis Allamanis and Charles Sutton “Mining Source Code Repositories at Massive Scale Using Language Modeling” In 2013 10th Working Conference on Mining Software Repositories (MSR), 2013, pp. 207–216
- [35] Veselin Raychev, Pavol Bielik and Martin Vechev “Probabilistic Model for Code with Decision Trees” In OOPSLA 2016 New York, NY, USA: Association for Computing Machinery, 2016, pp. 731–747
- [36] Islem Bouzenia, Bajaj Piyush Krishan and Michael Pradel “DyPyBench: A Benchmark of Executable Python Software” In Foundations of Software Engineering FSE, 2024
- [37] Hamel Husain et al. “CodeSearchNet Challenge: Evaluating the State of Semantic Code Search”, 2020 arXiv:1909.09436
- [38] Claire Le Goues, Michael Pradel and Abhik Roychoudhury “Automated Program Repair” In Communications of the ACM 62.12, 2019, pp. 56–65
- [39] Zhiyu Fan et al. “Automated Repair of Programs from Large Language Models” In 2023 IEEE/ACM 45th International Conference on Software Engineering (ICSE), 2023, pp. 1469–1481
- [40] Toufique Ahmed and Premkumar Devanbu “Better Patching Using LLM Prompting, via Self-Consistency” In 2023 38th IEEE/ACM International Conference on Automated Software Engineering (ASE), 2023, pp. 1742–1746
- [41] René Just, Darioush Jalali and Michael D. Ernst “Defects4J: A Database of Existing Faults to Enable Controlled Testing Studies for Java Programs” In ISSTA 2014 New York, NY, USA: Association for Computing Machinery, 2014, pp. 437–440
- [42] Rafael-Michael Karampatsis and Charles Sutton “How Often Do Single-Statement Bugs Occur? The ManySStuBs4J Dataset” In MSR ’20 New York, NY, USA: Association for Computing Machinery, 2020, pp. 573–577
- [43] Erik Nijkamp et al. “CodeGen2: Lessons for Training LLMs on Programming and Natural Languages”, 2023 arXiv:2305.02309 [cs]
- [44] Shraddha Barke, Michael B. James and Nadia Polikarpova “Grounded Copilot: How Programmers Interact with Code-Generating Models” In Proceedings of the ACM on Programming Languages 7, 2023, pp. 78:85–78:111
- [45] Matthias Minderer et al. “Revisiting the Calibration of Modern Neural Networks” In NeurIPS 34 Curran Associates, Inc., 2021, pp. 15682–15694
- [46] Seo Yeon Park and Cornelia Caragea “On the Calibration of Pre-trained Language Models Using Mixup Guided by Area Under the Margin and Saliency” In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers) Dublin, Ireland: Association for Computational Linguistics, 2022, pp. 5364–5374
- [47] Yangyi Chen et al. “A Close Look into the Calibration of Pre-trained Language Models” In ACL 2023 Toronto, Canada: Association for Computational Linguistics, 2023, pp. 1343–1367
- [48] Rishi Bommasani, Percy Liang and Tony Lee “Holistic Evaluation of Language Models” In Annals of the New York Academy of Sciences 1525.1, 2023, pp. 140–146
- [49] Zenan Li et al. “Operational Calibration: Debugging Confidence Errors for DNNs in the Field” In Proceedings of the 28th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, ESEC/FSE 2020 New York, NY, USA: Association for Computing Machinery, 2020, pp. 901–913
- [50] Yuntao Bai et al. “Constitutional AI: Harmlessness from AI Feedback”, 2022 arXiv:2212.08073 [cs]
- [51] Jason Wei et al. “Chain-of-Thought Prompting Elicits Reasoning in Large Language Models” In Advances in Neural Information Processing Systems 35, 2022, pp. 24824–24837
- [52] Noah Shinn et al. “Reflexion: Language Agents with Verbal Reinforcement Learning”, 2023 arXiv:2303.11366 [cs]
- [53] Xin Liu “LitCab: Lightweight Language Model Calibration over Short- and Long-form Responses” In ICML, 2023
- [54] Quanjun Zhang et al. “A Survey of Learning-based Automated Program Repair” In ACM Transactions on Software Engineering and Methodology 33.2, 2023, pp. 55:1–55:69
- [55] Zibin Zheng et al. “A Survey of Large Language Models for Code: Evolution, Benchmarking, and Future Trends”, 2024 arXiv:2311.10372 [cs]
- [56] Ewout W. Steyerberg et al. “Assessing the Performance of Prediction Models: A Framework for Some Traditional and Novel Measures” In Epidemiology (Cambridge, Mass.) 21.1, 2010, pp. 128–138 PMID: 20010215
- [57] Aarohi Srivastava et al. “Beyond the Imitation Game: Quantifying and Extrapolating the Capabilities of Language Models”, 2023 arXiv:2206.04615 [cs, stat]
- [58] Dan Hendrycks, Kimin Lee and Mantas Mazeika “Using Pre-Training Can Improve Model Robustness and Uncertainty” In Proceedings of the 36th International Conference on Machine Learning PMLR, 2019, pp. 2712–2721
- [59] Darren Key, Wen-Ding Li and Kevin Ellis “Toward Trustworthy Neural Program Synthesis”, 2023 arXiv:2210.00848 [cs]
- [60] Helena Vasconcelos et al. “Generation Probabilities are Not Enough: Improving Error Highlighting for AI Code Suggestions” In NeurIPS Workshop on Human-Centered AI, 2022 URL: https://www.microsoft.com/en-us/research/publication/generation-probabilities-are-not-enough-improving-error-highlighting-for-ai-code-suggestions/
- [61] Daniel D. Johnson, Daniel Tarlow and Christian Walder “R-U-SURE? uncertainty-aware code suggestions by maximizing utility across random user intents” In Proceedings of the 40th International Conference on Machine Learning, ICML’23 Honolulu, Hawaii, USA: JMLR.org, 2023
- [62] Hongyi Zhang, Moustapha Cisse, Yann N. Dauphin and David Lopez-Paz “Mixup: Beyond Empirical Risk Minimization”, 2018
- [63] Yuheng Huang et al. “Look Before You Leap: An Exploratory Study of Uncertainty Measurement for Large Language Models”, 2023 arXiv:2307.10236 [cs.SE]
- [64] Ansong Ni et al. “LEVER: learning to verify language-to-code generation with execution” In Proceedings of the 40th International Conference on Machine Learning, ICML’23 Honolulu, Hawaii, USA: JMLR.org, 2023
- [65] Xin Liu “Enhancing Language Model Factuality via Activation-Based Confidence Calibration and Guided Decoding” In ArXiv abs/2406.13230, 2024
- [66] Dylan Zhang et al. “PACE-LM: Prompting and Augmentation for Calibrated Confidence Estimation with GPT-4 in Cloud Incident Root Cause Analysis”, 2023 arXiv:2309.05833 [cs]
| Line Completion | Program Repair | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DyPyBench | Defects4J | SStubs | ||||||||
| Model | Metric | |||||||||
| GPT-3.5 | Total Prob | 0.11 | +0.38 | 0.03 | 0.13 | +0.01 | 0.16 | +0.03 | ||
| Avg Prob | 0.13 | +0.31 | 0.03 | 0.13 | +0.01 | 0.16 | +0.02 | |||
| Ask T/F | 0.18 | 0.00 | 0.12 | +0.05 | 0.16 | 0.00 | ||||
| Ask T/F N | 0.18 | 0.00 | 0.13 | +0.02 | 0.16 | +0.01 | ||||
| Verbalize | 0.18 | 0.00 | 0.13 | -0.03 | 0.16 | 0.00 | ||||
| Length | 0.17 | +0.06 | 0.03 | 0.14 | -0.06 | 0.16 | 0.00 | |||
| Unskilled | 0.18 | 0.00 | 0.13 | 0.00 | 0.16 | 0.00 | ||||
| [dashed] Codex | Total Prob | 0.10 | +0.43 | 0.02 | 0.15 | +0.01 | 0.19 | +0.05 | 0.02 | |
| Avg Prob | 0.12 | +0.34 | 0.02 | 0.16 | -0.01 | 0.19 | +0.05 | 0.02 | ||
| Ask T/F | 0.18 | +0.01 | 0.16 | -0.01 | 0.19 | +0.04 | ||||
| Ask T/F N | 0.18 | +0.02 | 0.16 | -0.01 | 0.20 | +0.02 | ||||
| Verbalize | 0.18 | 0.00 | 0.16 | -0.01 | 0.20 | 0.00 | ||||
| Length | 0.16 | +0.09 | 0.02 | 0.17 | -0.11 | 0.20 | 0.00 | |||
| Unskilled | 0.18 | 0.00 | 0.16 | 0.00 | 0.20 | 0.00 | ||||
| [dashed] CodeGen2 | Total Prob | 0.09 | +0.41 | 0.01 | - | - | - | - | ||
| Avg Prob | 0.11 | +0.30 | 0.01 | - | - | - | - | |||
| Ask T/F | 0.16 | 0.00 | - | - | - | - | ||||
| Ask T/F N | 0.16 | 0.00 | - | - | - | - | ||||
| Verbalize | 0.16 | 0.00 | - | - | - | - | ||||
| Length | 0.15 | +0.06 | 0.03 | - | - | - | - | |||
| Unskilled | 0.16 | 0.00 | - | - | - | - |
| Line Completion | Function Synthesis | Program Repair | ||||
|---|---|---|---|---|---|---|
| Model | Metric | DyPyBench | HumanEval | MBPP | Defects4J | SStubs |
| GPT-3.5 | Total Prob | 0.67 | 0.77 | 0.70 | 0.54 | 0.61 |
| Avg Prob | 0.68 | 0.61 | 0.56 | 0.57 | 0.60 | |
| Ask T/F | 0.54 | 0.73 | 0.71 | 0.67 | 0.54 | |
| Ask T/F N | 0.53 | 0.74 | 0.73 | 0.67 | 0.57 | |
| Verbalize | 0.53 | 0.54 | 0.60 | 0.43 | 0.51 | |
| Length | 0.53 | 0.64 | 0.61 | 0.48 | 0.53 | |
| Unskilled | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | |
| [dashed] Codex | Total Prob | 0.68 | 0.70 | 0.66 | 0.52 | 0.66 |
| Avg Prob | 0.68 | 0.71 | 0.69 | 0.57 | 0.65 | |
| Ask T/F | 0.49 | 0.65 | 0.56 | 0.62 | 0.61 | |
| Ask T/F N | 0.49 | 0.61 | 0.53 | 0.54 | 0.59 | |
| Verbalize | 0.52 | 0.46 | 0.50 | 0.45 | 0.49 | |
| Length | 0.55 | 0.51 | 0.50 | 0.43 | 0.49 | |
| Unskilled | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | |
| [dashed] CodeGen2 | Total Prob | 0.68 | 0.44 | 0.52 | - | - |
| Avg Prob | 0.66 | 0.67 | 0.52 | - | - | |
| Ask T/F | 0.52 | 0.39 | 0.59 | - | - | |
| Ask T/F N | 0.54 | 0.34 | 0.57 | - | - | |
| Verbalize | 0.51 | 0.49 | 0.51 | - | - | |
| Length | 0.55 | 0.39 | 0.47 | - | - | |
| Unskilled | 0.50 | 0.50 | 0.50 | - | - |











Understanding effects of verbalized retry failures
Our implementation for verbalized confidence prompts the model to output the probability its generation is correct at temperature 1.0. If it does not contain a probability, then we resample up to 3 times. If that loop fails, then a confidence of 0.5 is returned.
This implementation seemed reasonable at the time (if the model won’t tell you its confidence, just go with the maximum uncertainty of 50-50), but after collecting the data and analyzing results we reconsidered, as 50% values might be overrepresented in the data.
To try to estimate how this might have influenced our results and conclusions, we searched for instances where the verbalized confidence was 50% (this provides a upper bound on how often this happens. There can also be cases where the model actually verbalizes a 50% confidence). This is relatively rare for GPT-3.5 (with the mean dataset having 0.04 of instances as 50%, range 0.02-0.08). It is more common for Codex (mean 0.14, range 0.09-0.17) and for CodeGen2 (mean 0.10, range 0.09-0.12). This evidence of how the instruction tuned models are more likely to actually perform the prompted task.
We reran our analysis excluding all these instances. We do not believe a different handling of these fail-retry values would have greatly changed our conclusions. In the scaled case, the Skill Score on average did not change (mean diff of 0.00) with extreme change of -0.04 when already low skill. In the nonscaled case there were some drops in calibration (mean change of -0.11 and mean change of 0.02). The more extreme changes areas of already poor calibration.
It is not clear what is the best default is in the situation where the model fails to verbalize a probability. It is not particularly valid to exclude these instance. More exploration is needed on this and the effects.
| HumanEval | MBPP | |||||
|---|---|---|---|---|---|---|
| Confidence Measure | ||||||
| 0-Shot Reflect | 0.23 | 0.01 | 0.19 | 0.22 | -0.11 | 0.16 |
| 0-Shot Reflect (Scaled) | 0.20 | 0.14 | 0.07 | 0.18 | 0.11 | 0.04 |
| FS Random | 0.20 | 0.12 | 0.11 | 0.20 | -0.03 | 0.15 |
| FS Random (Scaled) | 0.19 | 0.16 | 0.04 | 0.16 | 0.16 | 0.04 |
| FS BM25 | 0.19 | 0.19 | 0.08 | 0.19 | 0.00 | 0.11 |
| FS BM25 (Scaled) | 0.19 | 0.18 | 0.04 | 0.17 | 0.14 | 0.04 |