Calabi-Yau type theorem for complete manifolds with nonnegative scalar curvature

By enlarging the region $K$ we may assume it to be a smooth connected and bounded region such that every component of $M\setminus K$ is unbounded. In the following, we just focus on one fixed component of $M\setminus K$, denoted by $E$. Two things need to be handled in the search of a bounded and weakly mean-concave region $\hat{\Omega}$ containing $K$ using variational method, including the obstacle issue caused by the existence of inner boundary $\partial E$ and a possible loss of compactness due to the non-compactness of $E$.

The obstacle issue is overcome by inserting a separation band $V$, from which we determine certain geometric quantities for later use in setting the $\mu$-bubble problem. Fix a bounded open neighborhood $U\subset M$ of $K$ and we take the separation band $V$ to be $(\overline{U}\setminus K)\cap E$. For convenience, we make the illustration of the separation band $V$ in Figure 1, where the boundary $\partial V$ can be divided into two parts $\partial E$ and $\partial U$ respectively. To clarify we point out that both $\partial E$ and $\partial U$ can be disconnected in its worst case.

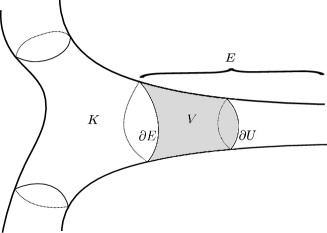
Let us introduce two positive constants associated to the separation band $V$. The first constant is designed to describe the infimum area that an arbitrary homologically non-trivial hypersurface can have. For the definition we denote $\mathcal{C}_{V}$ to be the collection

$$\left\{\begin{array}[]{c}\mbox{integer multiplicity rectifiable $(n-1)$-currents $T$ with $\operatorname{spt}T\subset V$}\\ \mbox{and $\partial T=0$ such that $T$ is homologically non-trivial}\end{array}\right\}$$

and take

$$c_{gap}=\inf\left\{\mathbb{M}_{g}(T):T\in\mathcal{C}_{V}\right\}.$$

Here we recommend the audience to consult the book [Leo83] for the precise definitions for current $T$ and mass $\mathbb{M}_{g}(T)$. For our purpose, it is enough to consider currents as oriented hypersurfaces and mass as their areas. The second constant is used to measure the height of $V$ in the sense of area, which is defined by

$$c_{height}=\inf\left\{\mathcal{H}^{n-1}_{g}(\Sigma)\left|\begin{array}[]{c}\mbox{$\Sigma\subset V$ is a connected minimal hypersurface}\\ \mbox{with $\partial\Sigma\subset\partial V$ intersecting both $\partial E$ and $\partial U$}\end{array}\right.\right\}.$$

Now let us verify the positivity of the constants $c_{gap}$ and $c_{height}$ as claimed. To see that $c_{1}$ is positive, we take a conformal metric $\check{g}$ of $g$ such that

• •

  $c^{-2}g\leq\check{g}\leq c^{2}g$ for some positive constant $c$;

• •

  and $(V,\check{g})$ is a compact Riemannian manifold with convex boundary.

From geometric measure theory we can find a smooth hypersurface $\check{\Sigma}$ which attains the least $\check{g}$-area among all the currents in $\mathcal{C}_{V}$. In particular, we have

$$c_{gap}\geq c^{1-n}\cdot\mathcal{H}_{\check{g}}^{n-1}(\check{\Sigma})>0.$$

For the positivity of $c_{2}$ we take a smooth hypersurface $\Sigma_{sep}$ separating $\partial E$ and $\partial U$. Let $\Sigma\subset V$ be any connected minimal hypersurface with $\partial\Sigma\subset\partial V$ intersecting both $\partial E$ and $\partial U$. Clearly, $\Sigma$ must have non-empty intersection with $\Sigma_{sep}$ and so it follows from the monotonicity formula that

$$\mathcal{H}_{g}^{n-1}(\Sigma)\geq c_{0}(V,g,\operatorname{dist}(\Sigma_{sep},\partial V))>0,$$

which yields $c_{height}>0$.

At this stage we are ready to set the $\mu$-bubble problem to overcome the non-compactness issue and to find the desired bounded and weakly mean-concve region $\hat{\Omega}$. Recall that $(M,g)$ has sublinear volume growth. By definition we can find a sequence of positive constants $r_{i}\to+\infty$ such that for some point $p$ we have

$$\frac{\operatorname{vol}_{g}(B_{r_{i}}(p))}{r_{i}}\to 0\mbox{ as }i\to\infty.$$

Fix a smooth and proper function $\rho:E\to[0,+\infty)$ with $\rho^{-1}(0)=\partial E$ and $\operatorname{Lip}\rho\leq 2$ as well as $|\rho(\cdot)-\operatorname{dist}(\cdot,\partial E)|\leq 1$. Then it is not difficult to verify

$$r_{i}^{-1}\operatorname{vol}_{g}\left(\rho^{-1}\left(\left[0,\frac{r_{i}}{2}\right]\right)\right)\to 0\mbox{ as }i\to\infty.$$

From the co-area formula we have

$$\int_{\frac{r_{i}}{4}}^{\frac{r_{i}}{2}}\mathcal{H}_{g}^{n-1}(\{\rho=\tau\})\,\mathrm{d}\tau=\int_{\{r_{i}/4\leq\rho\leq r_{i}/2\}}|\mathrm{d}\rho|_{g}\,\mathrm{d}\mathcal{H}^{n}_{g}\to 0\mbox{ as }i\to\infty.$$

Then it follows that for each $i$ we can find a regular value $r_{i}/4<t_{i}<r_{i}/2$ of $\rho$ such that $\mathcal{H}^{n-1}_{g}(\{\rho=t_{i}\})\to 0\mbox{ as }i\to\infty.$ In particular, we can fix $t_{i}$ large enough such that $V\subset\{\rho<t_{i}\}$ and

$$\mathcal{H}^{n-1}_{g}(\{\rho=t_{i}\})<\min\{c_{gap},c_{height}\}.$$

Just take another regular value $s_{i}>t_{i}$ of $\rho$ casually and denote $W$ to be $\rho^{-1}([0,s_{i}])$. In the following, we take $\eta:[0,s_{i})\to(-\infty,0]$ to be a smooth function such that $\eta\leq 0$ everywhere, $\eta\equiv 0$ in $[0,t_{i}]$ and $\eta(s)\to-\infty$ as $s\to s_{i}$. The prescribed mean curvature function is now defined by $h=\eta\circ\rho$.

Consider the class

$$\mathcal{C}=\left\{\begin{array}[]{c}\mbox{Caccioppoli sets $\Omega\subset M$ such that}\\ \mbox{$E^{c}\subset\Omega$ and $\Omega\setminus E^{c}\Subset W$}\end{array}\right\}$$

and the functional

$$\mathcal{A}^{h}(\Omega)=\mathcal{H}^{n-1}_{g}(\partial^{*}\Omega)-\int_{\Omega\setminus E^{c}}h\,\mathrm{d}\mathcal{H}^{n}_{g},$$

where $\partial^{*}\Omega$ is denoted to be the reduced boundary from [Giu77, Definition 3.3]. Through a standard argument from geometric measure theory we can find a minimizer $\Omega^{*}\in\mathcal{C}$ such that

$$A^{h}(\Omega^{*})=\inf_{\Omega\in\mathcal{C}}\mathcal{A}^{h}(\Omega)$$

and that $\Omega^{*}\cap\mathring{E}$ is a region in $\mathring{E}$ with smooth boundary $\partial\Omega^{*}\cap\mathring{E}$, where $\mathring{E}$ is denoted to be the interior of $E$. Denote $U^{*}_{1},\ldots,U^{*}_{k}$ to be the unbounded components of $M\setminus\Omega^{*}$ and $\hat{\Omega}_{E}$ to be the unique unbounded component of $M\setminus\left(\cup_{i}U^{*}_{i}\right)$ (the uniqueness comes from the connectedness of $K$). It is not difficult to verify $M\setminus\hat{\Omega}_{E}\subset E$. We claim that $\partial\hat{\Omega}_{E}$ is smooth and weakly mean-concave with respect to the outer unit normal as the boundary of $\hat{\Omega}_{E}$. Let $\hat{\Sigma}$ be an arbitrary component of $\partial\hat{\Omega}_{E}$. Notice that $\hat{\Sigma}$ is a common boundary of two unbounded connected regions $\hat{\Omega}_{E}$ and some $U^{*}_{i}$, then it has to be homologically non-trivial since we can construct a line intersecting $\hat{\Sigma}$ only once. Notice that the set $E^{c}\cup\rho^{-1}([0,t_{i}])$ also belongs to the class $\mathcal{C}$ and it follows from a direct comparison that

$$\mathcal{H}^{n-1}_{g}(\hat{\Sigma})\leq\mathcal{A}^{h}(\Omega^{*})\leq\mathcal{H}^{n-1}_{g}(\{\rho=t_{i}\})<\min\{c_{gap},c_{height}\}.$$

(2.1)

In particular, by definition of $c_{gap}$ we conclude that $\hat{\Sigma}\cap(E\setminus V)$ is non-empty. From the first variation formula of $\mathcal{A}^{h}$ it follows that $\hat{\Sigma}\cap\mathring{E}$ as the boundary of $\Omega^{*}$ has mean curvature $h|_{\hat{\Sigma}\cap\mathring{E}}$ with respect to the outer unit normal. In particular, $\hat{\Sigma}\cap V$ is a minimal hypersurface. If $\hat{\Sigma}$ intersects with $\partial E$, then we can find a connected minimal hypersurface $\hat{\Sigma}_{0}$ among components of $\hat{\Sigma}\cap V$ satisfying $\partial\hat{\Sigma}_{0}\subset\partial V$ and that $\hat{\Sigma}$ intersects both $\partial_{-}$ and $\partial_{+}$. This implies $\mathcal{H}^{n-1}_{g}(\hat{\Sigma})\geq\mathcal{H}^{n-1}_{g}(\hat{\Sigma}_{0})\geq c_{height}$, which contradicts to (2.1). Therefore, $\hat{\Sigma}$ does not touch $\partial E$ and so it is smooth everywhere. The mean-concavity of $\hat{\Sigma}$ comes directly from the non-positivity of the function $h$ after realizing that the outer unit normals of $\hat{\Sigma}$ with respect to $\Omega^{*}$ and $\hat{\Omega}$ coincide.

Finally let us take all unbounded components of $M\setminus K$ into consideration. After labeling them as $E_{1},E_{2},\ldots,E_{l}$ we can find regions $\hat{\Omega}_{E_{1}},\ldots,\hat{\Omega}_{E_{l}}$ with smooth weakly mean-concave boundary from above discussion. The desired bounded region is given by

$$\hat{\Omega}=\bigcap_{i=1}^{l}\hat{\Omega}_{i},$$

which is obviously a bounded region containing $K$ with weakly mean-concave boundary. ∎

Denote $K$ to be a smooth compact subset such that $(M,g)$ has nonnegative Ricci curvature outside $K$. Suppose that $(M,g)$ is non-compact but has sublinear volume growth. Then it follows from Lemma 1.2 that there is a bounded smooth region $\hat{\Omega}$ containing $K$ with weakly mean-concave boundary. Notice that $\partial\hat{\Omega}$ is weakly mean-convex as the boundary of $M\setminus\hat{\Omega}$ with respect to the corresponding outer unit normal. Since $M$ is non-compact, there is at least one unbounded component of $M\setminus\hat{\Omega}$ denoted by $E$. After applying [CK92, Theorem 2] to the end $E$ we conclude that $E$ must be isometric to the Riemannian product $(\partial E,g|_{\partial E})\times[0,+\infty)$, which obviously has linear volume growth. This leads to a contradiction! ∎

Here we take a similar argument from the author’s previous work [Zhu23b] based on Gromov’s $\mu$-bubble. Let $\rho:M_{\infty}\to[0,+\infty)$ be a smooth proper function satisfying $\rho^{-1}(0)=\partial M_{\infty}$ and $\operatorname{Lip}\rho<1$. From [Zhu23b, Lemma 2.3] we can construct a smooth function $h_{\epsilon}:[0,\frac{1}{n\epsilon})\to(-\infty,0]$ for any $0<\epsilon<1$ such that

• •

  $h_{\epsilon}$ satisfies

  $$\frac{n}{n-1}h_{\epsilon}^{2}+2h_{\epsilon}^{\prime}=n(n-1)\epsilon^{2}\mbox{ on }\left[\frac{1}{2n},\frac{1}{n\epsilon}\right)$$

  and there is a universal constant $C=C(n)$ such that

  $$\left|\frac{n}{n-1}h_{\epsilon}^{2}+2h_{\epsilon}\right|_{L^{\infty}}\leq C\epsilon^{2}.$$

• •

  $h_{\epsilon}<0$ and

  $$\lim_{t\to\frac{1}{n\epsilon}}h_{\epsilon}(t)=-\infty.$$

• •

  as $\epsilon\to 0$, $h_{\epsilon}$ converges smoothly to the zero function on any closed interval.

Now we are ready to set appropriate $\mu$-bubble problems. Take $\epsilon$ such that $\frac{1}{n\epsilon}$ appears to be a regular value of $\rho$ and denote $V_{\epsilon}=\rho^{-1}([0,\frac{1}{n\epsilon}])$. Consider the class

$$\mathcal{C}_{\epsilon}=\{\mbox{Caccioppoli sets $\Omega$ such that $M_{\infty}\setminus\Omega\Subset V_{\epsilon}$}\}$$

and the functional

$$\mathcal{A}_{\epsilon}(\Omega)=\mathcal{H}^{n-1}_{g}(\partial^{*}\Omega)-\int_{M_{\infty}\setminus\Omega}h_{\epsilon}\circ\rho\,\mathrm{d}\mathcal{H}^{n}_{g}.$$

It follows from [Zhu21, Proposition 2.1] or [CL20⁺, Proposition 12] that we can find a smooth minimizer $\Omega^{*}_{\epsilon}$ of the functional $\mathcal{A}_{\epsilon}$ among the class $\mathcal{C}_{\epsilon}$. From a direct comparison we see

$$\mathcal{H}^{n-1}_{g}(\partial\Omega^{*}_{\epsilon})\leq\mathcal{H}^{n-1}_{g}(\partial\Omega^{*}_{\epsilon})-\int_{M_{\infty}\setminus\Omega^{*}_{\epsilon}}h_{\epsilon}\circ\rho\,\mathrm{d}\mathcal{H}^{n}_{g}\leq\mathcal{H}^{n-1}_{g}(\partial M_{\infty}).$$

The first variation formula of $\mathcal{A}_{\epsilon}$ yields that the mean curvature of $\partial\Omega^{*}_{\epsilon}$ as the boundary of $\Omega^{*}_{\epsilon}$ with respect to the unit outer normal $\nu^{*}$ is

$$H_{\partial\Omega^{*}_{\epsilon}}=-(h_{\epsilon}\circ\rho)|_{\partial\Omega^{*}_{\epsilon}}.$$

From the second variation formula of $\mathcal{A}_{\epsilon}$ we have

$$\begin{split}\int_{\partial\Omega^{*}_{\epsilon}}|\nabla\phi|^{2}-\frac{1}{2}&\Big{(}R(g)-R(g|_{\partial\Omega^{*}_{\epsilon}})+|A|^{2}\\ &\qquad\qquad+H^{2}-2\partial_{\nu^{*}}(h_{\epsilon}\circ\rho)\Big{)}\phi^{2}\,\mathrm{d}\mathcal{H}^{n-1}_{g}\geq 0\end{split}$$

(2.2)

for every $\phi$ in $C_{0}^{\infty}(\partial\Omega^{*}_{\epsilon})$. Using the facts $R(g)\geq 0$ and

$$|A|^{2}+H^{2}\geq\frac{n}{n-1}(h_{\epsilon}\circ\rho)^{2}$$

as well as $\partial_{\nu^{*}}(h_{\epsilon}\circ\rho)\leq|\mathrm{d}h_{\epsilon}|\circ\rho$, we can write (2.2) as

$$\begin{split}\int_{\partial\Omega^{*}_{\epsilon}}|\nabla\phi|^{2}+&\frac{1}{2}R(g|_{\partial\Omega^{*}})\phi^{2}\,\mathrm{d}\mathcal{H}^{n-1}_{g}\\ &\geq\int_{\partial\Omega^{*}_{\epsilon}}\left.\left(\left(\frac{n}{n-1}h_{\epsilon}^{2}+2h_{\epsilon}^{\prime}\right)\circ\rho\right)\right|_{\partial\Omega^{*}_{\epsilon}}\phi^{2}\,\mathrm{d}\mathcal{H}^{n-1}_{g}.\end{split}$$

(2.3)

We claim that there is at least one component $\Sigma^{*}_{\epsilon}$ of $\partial\Omega_{\epsilon}^{*}$ having non-empty intersection with the compact subset $K_{o}:=\rho^{-1}([0,\frac{1}{2n}])$. Otherwise, $\Omega^{*}_{\epsilon}$ has to be disjoint with $K_{o}$ and in particular we can take $V$ to be the component of $M_{\infty}\setminus\Omega^{*}_{\epsilon}$ containing $K_{o}$. Let $\Sigma^{*}_{\epsilon}$ be some common boundary component of $\Omega^{*}_{\epsilon}$ and $V$. It is easy to construct a ray $\gamma:\big{(}[0,+\infty),0\big{)}\to(M_{\infty},\partial M_{\infty})$ intersecting only once with $\Sigma^{*}_{\epsilon}$, which implies that $\Sigma^{*}_{\epsilon}$ represents a non-trivial $\mathbb{Q}$-homology class. From our assumption $\Sigma^{*}_{\epsilon}$ cannot admit any metric with positive scalar curvature. On the other hand, since $\Sigma^{*}_{\epsilon}$ as part of $\partial\Omega^{*}_{\epsilon}$ is disjoint from $K_{o}$, we conclude

$$\int_{\Sigma^{*}_{\epsilon}}|\nabla\phi|^{2}+\frac{1}{2}R(g|_{\partial\Omega^{*}})\phi^{2}\,\mathrm{d}\mathcal{H}^{n-1}_{g}>0\mbox{ for any non-zero }\phi\in C_{0}^{\infty}(\hat{\Sigma}^{*}_{\epsilon}).$$

In particular, the first eigenvalue of the conformal Laplacian of $\Sigma^{*}_{\epsilon}$ is positive and we can construct a conformal metric of $\Sigma^{*}_{\epsilon}$ with positive scalar curvature, which leads to a contradiction.

Now we analyze the limiting behavior of $\Omega^{*}_{\epsilon}$ as $\epsilon\to 0$. Notice that the functional $\mathcal{A}_{\epsilon}$ converges to the area functional $\mathcal{A}$ as $\epsilon\to 0$. From geometric measure theory up to a subsequence $\Omega^{*}_{\epsilon}$ converges to a (possibly empty) Caccioppoli set $\Omega^{*}_{0}$ whose boundary is locally area-minimizing. On the other hand, all the hypersurfaces $\Sigma^{*}_{\epsilon}$ intersect with a fixed compact subset $K_{o}$ and they have a uniform area bound

$$\mathcal{H}^{n-1}_{g}(\Sigma^{*}_{\epsilon})\leq\mathcal{H}^{n-1}_{g}(\partial\Omega^{*}_{\epsilon})\leq H^{n-1}_{g}(\partial M_{\infty}).$$

Fixed a point $q^{*}_{\epsilon}$ in $\Sigma^{*}_{\epsilon}\cap K_{o}$, the curvature estimate [ZZ20, Theorem 3.6] yields that the pointed hypersurface $(\Sigma^{*}_{\epsilon},q^{*}_{\epsilon})$ converges smoothly to a pointed minimal hypersurface $(\Sigma^{*}_{0},q^{*}_{0})$ up to a subsequence, which is part of the boundary $\partial\Omega^{*}_{0}$. It follows from [Zhu23b, Proposition 3.2] (with the original condition having non-zero degree to $T^{n}$ replaced by non-existence of positive scalar curvature) that the limit hypersurface $\Sigma^{*}_{0}$ must have vanishing Ricci curvature. With the uniform area bound passing to the limit we see $\mathcal{H}^{n-1}_{g}(\Sigma^{*}_{0})\leq\mathcal{H}^{n-1}_{g}(\partial M_{\infty})$. Combined with the Calabi-Yau theorem (see Theorem 2.1 above) we conclude that the limit hypersurface $\hat{\Sigma}^{*}_{0}$ must be compact. As a consequence, $\Sigma^{*}_{0}$ represents a non-zero $\mathbb{Q}$-homology class and it is area-minimizing as a boundary component of $\Omega^{*}_{0}$. Now it follows from the foliation argument as in [Zhu20, Proposition 3.4] that $(M_{\infty},g)$ splits into the Riemannian product $(\partial M_{\infty},g|_{\partial M_{\infty}})\times[0,+\infty)$. ∎

The theorem follows immediately from the Calabi-Yau theorem in dimension two, and so we only need to deal with the case when $3\leq n\leq 4$. In these cases we are going to deduce some contradiction by assuming that $(M,g)$ is non-compact but has sublinear volume growth.

First let us find the bounded region to use Lemma 1.2. Recall that $M$ has nonnegative scalar curvature outside a compact subset $K_{0}$. Without loss of generality we can assume $K_{0}$ to be connected. Since $M$ is aspherical at infinity, we are able to find smooth compact sets $K_{n-2}\supset\cdots\supset K_{1}\supset K_{0}$ such that

$$(\pi_{i}(M\setminus K_{n-i})\to\pi_{i}(M\setminus K_{n-i-1}))=0\mbox{ for all }2\leq i\leq n-1.$$

In the same way we just assume all $K_{i}$ to be connected.

By our assumption in the beginning, $(M,g)$ has sublinear volume growth. Applying Lemma 1.2 to the compact set $K_{n-2}$ we can find a larger bounded region $\Omega\supset K_{n-2}$ with weakly mean-concave boundary $\partial\Omega$ with respect to the outer unit normal. By adding bounded components of $M\setminus\Omega$ and then passing to the component of $U$ containing $K_{n-2}$, we can further assume $U$ to be connected.

In order to apply Proposition B.2 we set $X_{i}=M\setminus K_{n-i}$ for $3\leq i\leq n$ and set $X_{2}=M\setminus\overline{\Omega}$. Now we need to verify the conditions listed in Proposition B.2. From our construction it is clear that $\pi_{i}(X_{i})\to\pi_{i}(X_{i+1})$ is the zero map for all $2\leq i\leq n-1$, so it remains to show the injectivity of $H_{n-1}(X_{2},\mathbb{Q})\to H_{n-1}(X_{n},\mathbb{Q})$ and we consider the exact sequence

$$H_{n}(X_{n},X_{2},\mathbb{Q})\to H_{n-1}(X_{2},\mathbb{Q})\to H_{n-1}(X_{n},\mathbb{Q}).$$

It suffices to show $H_{n}(X_{n},X_{2},\mathbb{Q})=0$. To see this we notice that $\overline{U}\setminus K_{0}$ consists of non-compact manifolds with boundary, which satisfies the well-known fact $H_{n}(\overline{U}\setminus K_{0},\partial U)=0$. From the excision we have

$$H_{n}(X_{n},X_{2})=H_{n}(M\setminus K_{0},M\setminus\overline{U})=H_{n}(\overline{U}\setminus K_{0},\partial U)=0.$$

In particular, we have $H_{n}(X_{n},X_{2},\mathbb{Q})=0$.

Now denote $M_{\infty}$ to be $M\setminus\Omega$ and it follows from Proposition B.2 that any embedded hypersurface representing a non-zero $\mathbb{Q}$-homology class cannot admit any metric with positive scalar curvature. Then it follows from Proposition 1.3 that $(M_{\infty},g)$ splits into the Riemannian product

$$(\partial M_{\infty},g|_{\partial M_{\infty}})\times[0,+\infty),$$

which leads to a contradiction to the fact that $(M,g)$ has sublinear volume growth. ∎

To show that $M$ is homeomorphic to $\mathbb{R}^{3}$ it suffices to prove that $M$ is simply-connected at infinity (see [Sta72] for instance). That is, for any compact subset $K$ we can find a larger compact subset $\tilde{K}$ such that the inclusion map $i_{*}:\pi_{1}(M\setminus\tilde{K})\to\pi_{1}(M\setminus K)$ is the zero map. Let us argue by contradiction and suppose that there is a compact subset $K$ such that any disk bounded by a loop $\gamma$ outside $K$ intersects $K$.

The strategy is to show that we can find arbitrarily large bounded region which has spherical boundary. From the contractibility of $M$ we see that $M$ is non-compact. Since $(M,g)$ has sublinear volume growth, from Lemma 1.2 we can find a bounded smooth region $\Omega$ containing $K$ whose boundary is weakly mean-concave. Denote $E_{1},\,E_{2},\ldots,E_{l}$ to be the unbounded components of $M\setminus\Omega$. Set the $\mu$-bubble problem on each $E_{i}$ in the same way as in the proof of Proposition 1.3. Since $(E_{i},g)$ has positive scalar curvature, for $\epsilon$ small enough we can find a smooth region $E_{i,\infty}$ from the $\mu$-bubble problem such that $E_{i}\setminus E_{i,\infty}$ is bounded and that all $\partial E_{i,\infty}$ satisfies

$$\int_{\partial E_{i,\infty}}|\nabla\phi|^{2}+\frac{1}{2}R(g|_{\partial E_{i,\infty}})\phi^{2}\,\mathrm{d}\mathcal{H}^{2}_{g}>0$$

for any non-zero $\phi\in C_{0}^{\infty}(\hat{\Sigma}^{*}_{\epsilon})$. Taking the test function $\phi\equiv 1$ on each component of $\partial E_{i,\infty}$ and using the Gauss-Bonnet formula we conclude that $\partial E_{i,\infty}$ consists of $2$-spheres. Now we take $\tilde{K}$ to be $M\setminus\cup_{i}E_{i,\infty}$.

We claim that any loop $\gamma$ in $M\setminus\tilde{K}$ can shrink to a point in $M\setminus K$. Recall that $M$ is contractible. So the loop $\gamma$ bounds a disk $D$ in $M$. After perturbation we may assume that $D$ is transversal to $\partial\tilde{K}$. Let us take the component $\Sigma$ of $D\setminus\tilde{K}$ containing $\gamma$. Then $\Sigma$ is simply the disk $D$ with finitely many disjoint sub-disks $D_{j}$ removed. Since $\partial D_{j}$ is contained in the spherical boundary $\partial\tilde{K}$, we can find disks $D_{j}^{*}\subset\partial\tilde{K}$ with $\partial D_{j}^{*}=\partial D_{j}$. As a consequence, the set

$$\Sigma\cup\left(\bigcup_{j}D_{j}^{*}\right)$$

provides a disk outside $K$ with boundary $\gamma$, which leads to a contradiction to our assumption in the beginning. ∎