Brownian dynamics of Dirac fermions in twisted bilayer graphene

We consider a hexagonal-lattice model that reflects the symmetry properties and number of subbands of the flat band in twisted bilayer graphene (TBG). Taking into account the nearest neighbor hopping, the tight-binding Hamiltonian within the continuum model approach can be expressed as [43]

$\displaystyle\mathcal{H}_{0}\left({\bf{k}}\right)$

$\displaystyle=\left(\begin{array}[]{cc}0&h_{\bf{k}}\\ h^{\ast}_{\bf{k}}&0\end{array}\right),$

(3)

with

$\displaystyle h_{\bf{k}}=\frac{W}{3}\sum_{\pmb{\delta}_{l}}e^{i{\bf{k}}\cdot\pmb{\delta}_{l}},$

(4)

where $W/3$ represents the hopping matrix element to nearest neighbours at positions $\pmb{\delta}_{l}=\left(\cos\left(2\pi l/3\right),\sin\left(2\pi l/3\right)\right)L_{M}/\sqrt{3}$, where $l=0,1,2$ and $L_{M}$ is the moiré superlattice periodicity, realized in twisted bilayer graphene. It is illustrated that $W$ represents the bandwidth measured from Dirac point, and the nearest neighbour distance $L_{M}/\sqrt{3}$ is chosen such that the lattice period of the hexagonal model mimics the moiré superlattice period. Following the analysis of Lewandowski and Levitov [43], we choose the energy and length scales such as the width of a single band $W$ and the hexagonal lattice period $L_{M}$ to be identical to the parameters in TBG: $W=3.75\textrm{meV}$ and $L_{M}=a/2\sin\left(\theta/2\right)$ is the moiré superlattice period, yielding $L_{M}=13.4\textrm{nm}$ for the magic angle $\theta=1.05^{\circ}$ and lattice constant of graphene, $a=0.246\textrm{nm}$. The relativistic energy dispersion of the Dirac fermions is

$\displaystyle E_{\lambda}\left(\bf{k}\right)=\lambda|h_{\bf{k}}|,$

(5)

where $\lambda=\pm$ is the band index and $|h_{\bf{k}}|=\frac{W}{3}\sqrt{1+4\cos\left(\frac{L_{M}}{2}k_{y}\right)\cos\left(\frac{\sqrt{3}L_{M}}{2}k_{x}\right)+4\cos^{2}\left(\frac{L_{M}}{2}k_{y}\right)}$. In the following analysis, we use Eq. (5) with $\lambda=+$.

We consider a sample of twisted bilayer graphene (TBG) on a substrate with a periodic potential $V(x)$. TBG is driven by two orthogonal harmonic drives $E_{x}(t)$ and $E_{y}(t)$ with commensurate frequencies, inducing rectification that leads to a direct current. The ratchet substrate in one dimension is modeled by the double-sine potential as [32, 44, 45, 46]

$\displaystyle V\left(x\right)=V_{0}\left[\sin\left(\frac{2\pi x}{L}\right)+\mu\sin\left(\frac{4\pi x}{L}\right)\right],$

(6)

where $V_{0}$ is the strength, $L$ is the period of the potential, and $\mu=1/4$ is a constant. The Brownian motion of Dirac fermions in TBG can be described by a set of coupled relativistic Langevin equations for the components of 2D momentum, ${\bf{k}}=\left(k_{x},k_{y}\right)$, subjected to the relativistic dispersion relation given in Eq. (5). These equations are determined by the condition that the chosen particle-reservoir coupling must lead to the same equilibrium momentum distribution as predicted by the fully microscopic theory. We follow the procedure of Dunkel et al. [47] and Pototsky et al. [44] for deriving the coupled relativistic Langevin equations. For describing the random dynamics, charge carriers in TBG require high energies for their distribution to be appropriately approximated by the relativistic Jüttner distribution,

$\displaystyle f\left(\bf{k}\right)\sim\exp\left[-E\left(\bf{k}\right)/k_{B}T\right].$

(7)

For a technical discussion on validity of the relativistic Jüttner distribution, the relevant approximations and detailed derivations of the coupled relativistic Langevin equations, the reader is referred to Refs. [47, 44]. Here we emphasize that the Jüttner distribution can be regarded as a semiclassical approximation of the Fermi-Dirac distribution for relativistic particles with rest energy on the order of, or smaller than $k_{B}T$. Such a condition is valid for charge carriers in TBG in the vicinity of Dirac points. In cartesian coordinates, a convenient [44] but not unique [47] set of semiclassical coupled relativistic Langevin equations consistent with the above 2D relativistic Jüttner distribution is

$\displaystyle\dot{x}=\frac{1}{\hbar}\frac{\partial|h_{\bf{k}}|}{\partial k_{x}},$

(8)

$\displaystyle\dot{y}=\frac{1}{\hbar}\frac{\partial|h_{\bf{k}}|}{\partial k_{y}},$

(9)

$\displaystyle\dot{k}_{x}=-\frac{\eta}{\hbar^{2}}\frac{\partial|h_{\bf{k}}|}{\partial k_{x}}-\frac{1}{\hbar}\frac{dV(x)}{dx}+\frac{e}{\hbar}E_{x}\left(t\right)+\frac{1}{\hbar}\sqrt{2\eta k_{B}T}\zeta_{x}\left(t\right),$

(10)

$\displaystyle\dot{k}_{y}=-\frac{\eta}{\hbar^{2}}\frac{\partial|h_{\bf{k}}|}{\partial k_{y}}+\frac{e}{\hbar}E_{y}\left(t\right)+\frac{1}{\hbar}\sqrt{2\eta k_{B}T}\zeta_{y}\left(t\right),$

(11)

where $\eta$ is the damping constant, $E_{x}\left(t\right)$ and $E_{y}\left(t\right)$ are the driving ac electric fields in the $x$- and $y$-directions, respectively, whereas

	$\displaystyle\frac{\partial|h_{\bf{k}}|}{\partial k_{x}}$	$\displaystyle=-\frac{WL_{M}}{\sqrt{3}}\times$
		$\displaystyle\frac{\cos\left(\frac{L_{M}}{2}k_{y}\right)\sin\left(\frac{\sqrt{3}L_{M}}{2}k_{x}\right)}{\sqrt{1+4\cos\left(\frac{L_{M}}{2}k_{y}\right)\cos\left(\frac{\sqrt{3}L_{M}}{2}k_{x}\right)+4\cos^{2}\left(\frac{L_{M}}{2}k_{y}\right)}},$		(12)

and

	$\displaystyle\frac{\partial|h_{\bf{k}}|}{\partial k_{y}}$	$\displaystyle=-\frac{WL_{M}}{3\hbar}\times$
		$\displaystyle\frac{\left[\cos\left(\frac{\sqrt{3}L_{M}}{2}k_{x}\right)\sin\left(\frac{L_{M}}{2}k_{y}\right)+\sin\left(L_{M}k_{y}\right)\right]}{\sqrt{1+4\cos\left(\frac{L_{M}}{2}k_{y}\right)\cos\left(\frac{\sqrt{3}L_{M}}{2}k_{x}\right)+4\cos^{2}\left(\frac{L_{M}}{2}k_{y}\right)}}.$		(13)

The random forces $\zeta_{x}\left(t\right)$ and $\zeta_{y}\left(t\right)$ in Eqs. (10) and (11) are two white Gaussian noises with vanishing mean, $\braket{\xi_{m}\left(t\right)}=0$, satisfying the fluctuation-dissipation relation, $\braket{\zeta_{m}\left(t\right)\zeta_{n}\left(t_{0}\right)}=\delta_{mn}\delta\left(t-t_{0}\right)$, with $m,n=x,y$, which ensures proper thermalization at temperature $T$. The damping coefficient $\gamma$ contains contributions from all possible collision mechanisms including phonon scattering, a charge carrier may undergo when moving on the surface of a TI attached to SMO. In order to take into account microscopic collision mechanisms requires a detailed quantum kinetic theory, for instance, see [48], which is beyond the scope of our semi-classical approach considered in this paper. Note that white Gaussian noise works appropriately only for sufficiently high temperatures. Analysis of Eqs. (8)- (11) reveals that the orthogonal ac-drive components $E_{x}(t)$ and $E_{y}(t)$ are nonlinearly coupled through the relativistic energy dispersion, leading to significant rectification induced by the periodic ratchet potential $V(x)$. The above mentioned equations describe the dynamics of a particle under the influence of driving forces and potential of a substrate which include effective parameters containing $\hbar$. Moreover, in these dynamical equations, $x$ and $y$ are real-space variables, whereas $k_{x}$ and $k_{y}$ are the $x$- and $y$- components, respectively, of the crystal momentum which can also be regarded as expectation values of their respective operators. It has been shown that two harmonic drives with commensurate frequencies can induce rectification, leading to direct current in the non-relativistic regime when both are applied along the same direction [49, 50, 51]. Remarkably, in the relativistic Langevin equations in Eqs. (8)- (11), coupling between the $x$ and $y$ degrees of freedom generates an unusual harmonic mixing, where rectification of current occurs even if the two harmonic drives are orthogonal to each other. Moreover, the damping coefficient $\eta$ takes into account contributions from all possible collision mechanisms a charge carrier may undergo when moving through a twisted bilayer graphene sheet. Furthermore, the noisy environment in TBG can be provided by external noise sources such as current or voltage fluctuations. As a consequence, the interaction of a single charge carrier with such an environment generates damping effects, which are included in relativistic Langevin equations. The appropriate form of the damping and the fluctuating terms can be determined by the fluctuation-dissipation theorem.

In this section, we consider charge carrier dynamics in the presence of rectification of non-equilibrium perturbations on a substrate with periodic ratchet potential $V(x)$.

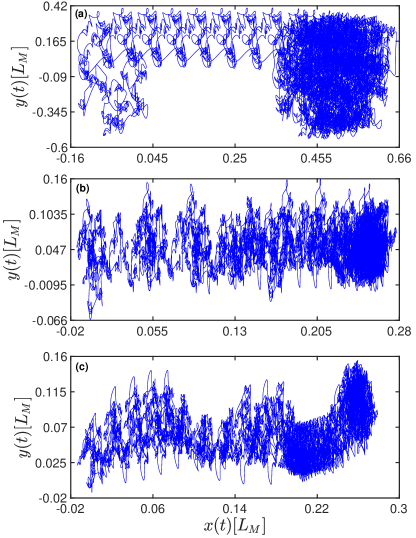
Here, we consider the driving electric field as ${\bf{E}}\left(t\right)=\left(E_{x}\cos\left(\omega_{x}t\right),E_{y}\cos\left(\omega_{y}t\right)\right)$, where $E_{x}$ and $E_{y}$ are the amplitudes, $\omega_{x}$ and $\omega_{y}$ are the oscillation frequencies of the $x$- and $y$-components of the field. It has been shown that in the non-relativistic regime, ratcheting takes place only in the $x$-direction, induced by the periodic driving field, $E_{x}(t)$ oriented along $x$-axis. The rectification weakens if $\textbf{E}(t)$ is rotated at an angle with the $x$-axis, until it drops to zero for ac drives parallel to the substrate valleys. In this process, the component $E_{y}(t)$ of the ac-field keeps the system out of equilibrium, however, it cannot be rectified, as the substrate potential is uniform in the $y$ direction. Hence, the $x$ and $y$ dynamics remain decoupled. In the relativistic Langevin equations, see Eqs. (8)- (11), instead, the orthogonal ac-drive components, $E_{x}(t)$ and $E_{y}(t)$, are nonlinearly coupled through the relativistic dispersion relation, see Eq. (5), so that both can be rectified by the periodic ratchet potential $V(x)$. In order to understand the diffusion mechanism in twisted bilayer graphene, we analyze the real space trajectories of the driven Brownian dynamics. In Fig. 1, the real-space trajectories of the mentioned dynamics have been shown for different values of the twist angle. Comparison of panels (a), (b), and (c) reveals that the Brownian dynamics changes significantly with the change of twist angle. In particular, the trajectories of Brownian particle for twist angle, $\theta=1.03^{\circ}$ are significantly different from those plotted for $\theta=1.05^{\circ}$ and $\theta=1.06^{\circ}$, showing that the dynamics in TBG strongly depends on the twist angle and the randomness is more prominent for $0<\theta<1.05^{\circ}$. Moreover, comparison of the blue and red curves shows that the $x$- and $y$-components of Brownian dynamics exhibit different dynamical behavior. In Fig. 2, the real-space trajectories of Brownian particle have been shown for different values of the twist angle in the $xy$-plane. This figure also shows that the trajectories of Brownian particle exhibit irregular behavior. The characteristic feature of Brownian dynamics in TBG stems from the fact that the trajectories fall in the experimentally accessible regime that can be measured using the recently developed experimental techniques [53, 54]. Such trajectories have also been investigated in various systems [55, 56]. However, the amplitudes of trajectories in TGB are an order of magnitude larger than these systems. Analysis of Figs. 1 and 2 reflects random behavior of the particle dynamics, hallmark of Brownian dynamics. For further analysis and understanding the dynamics, we analyze the diffusion coefficient and net current in the following sections.