Broadband-laser-diode pumped PPKTP-Sagnac polarization-entangled photon source
Abstract
We experimentally demonstrate a polarization-entangled photon source at 810 nm using a type-II phase-matched PPKTP crystal pumped by a low-cost, broadband laser diode with a central wavelength of 405 nm and a typical bandwidth of 0.53 nm. The PPKTP crystal is placed in a Sagnac-loop to realize the compact size and high stability. The downconverted biphotons, the signal and the idler, have typical bandwidths of 5.57 nm and 7.32 nm. We prepare two Bell states and with the fidelities of 0.9480.004 and 0.9630.002. In polarization correlation measurement, the visibilities are all higher than 96.2%, and in the Bell inequality test, the S value can achieve 2.780.01. This high-quality and low-cost entangled photon source may have many practical applications in quantum information processing.
I Introduction
Quantum entanglement, which represents a non-classical correlation among several quantum subsystems, is a critical feature of quantum information science. High-quality entangled photon pairs play an important role in many quantum information technologies, such as quantum communication Vaziri et al. (2002); Boileau et al. (2004), quantum computation Browne and Rudolph (2005); Walther et al. (2005), and quantum measurement Maccone and Ren (2020). A photon has many degrees of freedom, e.g., time, frequency, polarization, position, momentum, and each degree of freedom can be entangled Kuzucu et al. (2005); Oohata et al. (2007); Howell et al. (2004); Romero et al. (2012). Polarization-entangled photons, which are relatively easy to generate and characterize, have been widely investigated. As early as 1988, Shih et al. Shih and Alley (1988) and Ou et al. Ou and Mandel (1988) demonstrated the polarization-entangled photons using Type-I phase-matched spontaneous parametric down-conversion (SPDC) scheme by pumping potassium dihydrogen phosphate (KDP) crystals with monochromatic continuous-wave (CW) lasers. In 1995, Kwiat et al. showed a new entangled photon source by pumping a -barium borate (BBO) crystal under type-II phase-matching condition using argon-ion laser Kwiat et al. (1995). From then on, many schemes of entangled photon sources have been demonstrated with different pump lasers (monochromatic CW laser Grice and Walmsley (1997); Li et al. (2015) or ultra-fast pulsed laser Keller and Rubin (1997); Kim et al. (2019)), different nonlinear crystals (Periodically polarized potassium titania phosphate (PPKTP) Weston et al. (2016), BBO Kwiat et al. (1999), or periodically poled lithium niobate (PPLN) König et al. (2005)), different phase-matching types (Type-0 Chen et al. (2018); Terashima et al. (2018), Type-I Rangarajan et al. (2009); Villar et al. (2018), or Type II Martin et al. (2010); Horn and Jennewein (2019); Lee et al. (2016)), or different wavelengths (e.g., 810 nm or 1550 nm). See a recent review article on entangled photon sources in Anwar et al. (2021).
It can be noticed from the above works that the pump lasers used in the previous entangled sources are almost monochromatic CW lasers or ultrafast pulsed lasers. However, the low-cost broadband multi-mode (longitudinal mode) laser is not widely used. Recently, quantum optical technologies are spreading out from laboratory to industrialization. In practical use, the low-cost and high stability entangled photon sources are indispensable. With the rapid development of blue laser technologies, the inexpensive high-power blue laser diode (LD) can easily provide high power of over 100 mW at 405 nm. Therefore, it is necessary to investigate the multi-mode laser, especially to apply it to the field of quantum optics, e.g., for the preparation of an entangled photon source. Recently, Jeong et al. adopted the method of “universal Bell-state synthesizer” Kim et al. (2003) to prepare an entangled photon source by pumping a type-II phase-matched PPKTP with a broadband multi-mode LD Jeong et al. (2016). Lohrmann et al. prepared an entangled photon-pair source using the configuration of “linear beam displacement interferometer” using broadband LD and type-0 phase-matched PPKTP Lohrmann et al. (2020).
Compared with the above two schemes, there are other optical path configurations, such as the Sagnac-loop structure, which has the merits of compact design and high stability. The first polarization-entangled photon pair using a Sagnac interferometer was demonstrated by Shi et al. Shi and Tomita (2004) with a BBO crystal in 2004. Later, Kim et al. optimized the scheme by using a type-II phase-matched PPKTP crystal for higher brightness and stability Kim et al. (2006). Subsequently, the Sagnac-PPKTP scheme has been widely used in the research of quantum entangled sources at around 800 nm wavelength. For example, a bright entangled photon source was realized by using a mode-locked pulse pumping Kuzucu and Wong (2008); a wavelength-tunable and narrow-band entangled photon source was demonstrated by using a CW pumping Fedrizzi et al. (2007); a non-collinear PPKTP-Sagnac scheme was demonstrated using a type-0 phase-matched PPKTP Jabir and Samanta (2017). Especially, a high-quality satellite-based entangled source adopted the configuration of the PPKTP-Sagnac scheme and pumped by single-longitudinal-mode LD Yin et al. (2017); Zhou et al. (2015). The PPKTP-Sagnac entangled photon source was also demonstrated at telecom wavelengths and pumped by pico-second laser Jin et al. (2014), femto-second laser Weston et al. (2016), or CW lasers Li et al. (2015). The PPKTP-Sagnac scheme at the telecom wavelengths has extra merit of high spectral purity Jin et al. (2013). In this work, we further develop the PPKTP-Sagnac scheme to be pumped by a broadband multi-mode LD. This new polarization-entangled photon source has the merits of low-cost, high brightness, and high stability.
II Experiment


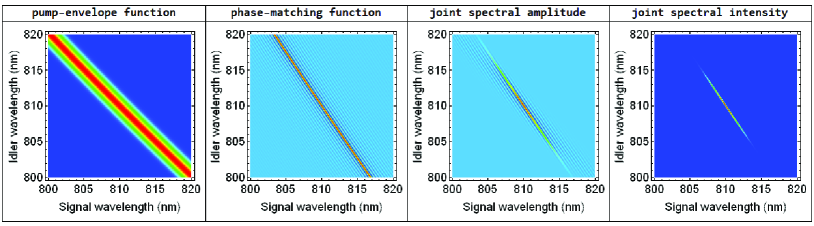
The experimental setup is shown in Fig. 1. A broadband multi-mode LD was utilized as the pump laser. A typical spectrum of the LD is shown in Fig. 2(a), with a central wavelength of 405.1 nm and a full-width-at-half-maximum (FWHM) of 0.53 nm, which was measured by a spectrometer of Princeton Instruments SP2300. The pump laser was coupled into a single-mode fiber (SMF) to filter the spatial mode, and the SMF with an FC/APC-type connector also functioned as an isolator to block the back-reflected pump laser from the Sagnac loop. After passing through a QWP (quarter-wave plate), an HWP (half-wave plate), an SPF (short-wavelength pass filter), and a lens (L1), the pump photons were sent into a triangle-shape Sagnac loop, which had a compact size of about 9 cm + 12.7 cm + 9 cm. In the Sagnac loop, the DPBS (dual-wavelength polarization beam splitter) and the DHWP (dual-wavelength HWP) worked for both 405 and 810 nm wavelengths. The PPKTP crystal was type-II phase-matched (yy+z) with a poling period of 9.825 m. The downconverted biphotons, i.e., the signal (y-polarized) and the idler (z-polarized), had a degenerate wavelength of around 810 nm at the temperature of 92.5 ∘C, and their FWHMs were measured to be 5.57 nm and 7.32 nm, respectively, as shown in Fig. 2(b-c). We also theoretically simulated their joint spectral intensity (JSI), as shown in Fig. 2(d) (Also see Fig. A1 in the Appendix). The simulated JSI explained the experimental phenomenon that the signal has a narrower bandwidth than the idler. For simplicity, in this simulation, we assumed the PPKTP crystal was 10 mm long, and the spectrum of the pump laser had a Gaussian distribution with a center wavelength of 405 nm and a bandwidth of 0.45 nm. Under this condition, the simulated FWHMs of the signal and idler are 5.25 nm and 7.78 nm, which are in good agreement with the experimental results. The biphotons generated from the clock-wise pump and the counter-clock-wise pump were separated by a DPBS, collimated by two lenses (L2 and L3 ), filtered by two LPF (long pass filters), adjusted by two polarizers, and finally coupled into two SMFs, which was connected to single-photon detectors (SPCM-AQRH-10-FC, Excelitas) and a coincidence counter (Picoharp 300, PicoQuant). For quantum correlation measurement, each polarizer was composed of an HWP and a PBS.


As theoretically analyzed in Ref. Kim et al. (2006), the output state from the PPKTP-Sagac scheme is
| (1) |
where and are the relative phase and pump ratio between the clock-wise path and counter-clock-wise path. By rotating HWP, QWP and by finely adjusting the position of PPKTP, we can prepare the Bell states and . Figure 3 shows the polarization correlation measurement result for states. For state, the maximal coincidence was around 7 kcps with a pump power a 7 mW at each projection base. The corresponding overall brightness was 2 kcps/mW. Without any background subtraction, the visibilities of 0∘, 45∘, 90∘, and 135∘ were 99.5%, 96.4%, 99.6%, 96.2%, respectively. For state, the corresponding visibilities were 99.4%, 96.2%, 99.0% and 96.6%, respectively. All the fringe visibilities in Fig. 3 were higher than 71%, the bound required to violate the Bell’s inequality. We also measured the Bell parameter S, which directly indicated the violation of Bell’s inequality. The S values measured were 2.780.01 and 2.740.01 for and , respectively, which were higher than the classical bound of 2.
We also performed the quantum state tomography of the polarization-entangled state. Polarizers 1 and 2 in Fig. 1 were replaced by combinations of HWP, QWP, and PBS. The density matrix was reconstructed with a maximum likelihood estimation method, as shown in Fig. 4. For states and , the fidelities of the reconstructed density matrix were 0.9480.004 and 0.9630.002, respectively. These values indicated that the states were highly entangled.
III Discussion
We compare this work with the previous single-mode LD pumped Sagnac-PPKTP scheme used for satellite application Yin et al. (2017), the multi-mode laser pumped “universal Bell-state synthesizer” scheme Jeong et al. (2016), and the multi-mode laser pumped “linear beam displacement interferometer” scheme Lohrmann et al. (2020) in Tab. 1. It is noteworthy that the type-0 phase-matched crystal has the highest brightness because the nonlinear coefficient of is much higher than the value of in type-II phase-matched condition. However, the spectral widths of the biphotons in type-0 phase-matched case are much broader. The Sagnac-PPKTP scheme can achieve comparable performance as the “universal Bell-state synthesizer” Kim et al. (2003) scheme in stability and brightness, but the configuration is more compact. The single-mode LD laser pumped Sagnac-PPKTP scheme can also achieve high performance, but the pump laser has a higher cost.
| Parameter | Yin2017 Yin et al. (2017) | Jeong2016 Jeong et al. (2016) | Lohrmann2020 Lohrmann et al. (2020) | This work | ||||||||||
| Configuration | Sagnac loop |
|
|
Sagnac loop | ||||||||||
|
|
|
|
|
||||||||||
| PPKTP |
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||
|
|
|
560 | 2 | ||||||||||
| Visibility | over 91% |
|
over 96.4% | over 96.2% | ||||||||||
| Fidelity |
|
|
– |
|
The models and characteristics of the components used in this work are listed in Tab. A1 in the Appendix. It can be noticed that the entangled source used in this experiment can still be optimized by improving the collection efficiency of the whole system, especially the coupling efficiency to the SMF, the transmission efficiency of the LPFs. For example, we can optimize the beam waist of the pump laser by using a proper focusing lens and choose LPF with higher transmission efficiency. Nevertheless, we have shown that it is possible to prepare a highly entangled photon source using multi-mode LD pumped PPKTP-Sagnac configuration.
For future applications this highly entangled photon source is applicable not only for foundational tests of quantum physics but also for quantum networks, e.g., entanglement-based quantum key distribution networks Liu et al. (2020). As shown in Fig. 2(d), the signal and idler photon are also entangled in frequency, so this source has the potential to be a hyper-entangled photon source Ramelow et al. (2009); Chen et al. (2020). Further, the feature of low-cost makes it applicable for educational use. But this source is not useful for Hong-Ou-Mandel (HOM)-interference-based applications, e.g., teleportation or entanglement swapping, because the HOM interference visibility is very low due to the low spectral exchanging symmetry.
IV Conclusion
In summary, we have demonstrated the combination of a broadband LD, a PPKTP, and a Sagnac loop to generate polarization-entangled photons. In polarization correlation measurement, the visibilities are all over 96%, and the S value of the Bell’s inequality reached 2.780.01. In a quantum state tomography measurement, the fidelity achieved 0.9630.002. This entangled source has the merits of being cost-effective, compact, high-brightness, and high stability and may provide a good option for practical applications in quantum information processing.
Acknowledgement
This work is supported by the National Natural Science Foundations of China (Grant Nos.12074299, 91836102, 11704290) and by the Guangdong Provincial Key Laboratory (Grant No. GKLQSE202102).
References
- Vaziri et al. (2002) Alipasha Vaziri, Gregor Weihs, and Anton Zeilinger, “Experimental two-photon, three-dimensional entanglement for quantum communication,” Phys. Rev. Lett. 89, 240401 (2002).
- Boileau et al. (2004) J.-C. Boileau, R. Laflamme, M. Laforest, and C. R. Myers, “Robust quantum communication using a polarization-entangled photon pair,” Phys. Rev. Lett. 93, 220501 (2004).
- Browne and Rudolph (2005) Daniel E. Browne and Terry Rudolph, “Resource-efficient linear optical quantum computation,” Phys. Rev. Lett. 95, 010501 (2005).
- Walther et al. (2005) P. Walther, K. J. Resch, T. Rudolph, E. Schenck, H. Weinfurter, V. Vedral, M. Aspelmeyer, and A. Zeilinger, “Experimental one-way quantum computing,” Nature 434, 169–176 (2005).
- Maccone and Ren (2020) Lorenzo Maccone and Changliang Ren, “Quantum radar,” Phys. Rev. Lett. 124, 200503 (2020).
- Kuzucu et al. (2005) Onur Kuzucu, Marco Fiorentino, Marius A. Albota, Franco N. C. Wong, and Franz X. Kärtner, “Two-photon coincident-frequency entanglement via extended phase matching,” Phys. Rev. Lett. 94, 083601 (2005).
- Oohata et al. (2007) Goro Oohata, Ryosuke Shimizu, and Keiichi Edamatsu, “Photon polarization entanglement induced by biexciton: Experimental evidence for violation of bell’s inequality,” Phys. Rev. Lett. 98, 140503 (2007).
- Howell et al. (2004) John C. Howell, Ryan S. Bennink, Sean J. Bentley, and R. W. Boyd, “Realization of the Einstein-Podolsky-Rosen paradox using momentum- and position-entangled photons from spontaneous parametric down conversion,” Phys. Rev. Lett. 92, 210403 (2004).
- Romero et al. (2012) J. Romero, D. Giovannini, S. Franke-Arnold, S. M. Barnett, and M. J. Padgett, “Increasing the dimension in high-dimensional two-photon orbital angular momentum entanglement,” Phys. Rev. A 86, 012334 (2012).
- Shih and Alley (1988) Y. H. Shih and C. O. Alley, “New type of Einstein-Podolsky-Rosen-Bohm experiment using pairs of light quanta produced by optical parametric down conversion,” Phys. Rev. Lett. 61, 2921–2924 (1988).
- Ou and Mandel (1988) Z. Y. Ou and L. Mandel, “Violation of Bell’s inequality and classical probability in a two-photon correlation experiment,” Phys. Rev. Lett. 61, 50–53 (1988).
- Kwiat et al. (1995) Paul G. Kwiat, Klaus Mattle, Harald Weinfurter, Anton Zeilinger, Alexander V. Sergienko, and Yanhua Shih, “New high-intensity source of polarization-entangled photon pairs,” Phys. Rev. Lett. 75, 4337–4341 (1995).
- Grice and Walmsley (1997) W. P. Grice and I. A. Walmsley, “Spectral information and distinguishability in type-II down-conversion with a broadband pump,” Phys. Rev. A 56, 1627–1634 (1997).
- Li et al. (2015) Yan Li, Zhi-Yuan Zhou, Dong-Sheng Ding, and Bao-Sen Shi, “CW-pumped telecom band polarization entangled photon pair generation in a Sagnac interferometer,” Opt. Express 23, 28792–28800 (2015).
- Keller and Rubin (1997) Timothy E. Keller and Morton H. Rubin, “Theory of two-photon entanglement for spontaneous parametric down-conversion driven by a narrow pump pulse,” Phys. Rev. A 56, 1534–1541 (1997).
- Kim et al. (2019) Heonoh Kim, Osung Kwon, and Han Seb Moon, “Pulsed Sagnac source of polarization-entangled photon pairs in telecommunication band,” Sci. Rep. 9 (2019).
- Weston et al. (2016) Morgan M. Weston, Helen M. Chrzanowski, Sabine Wollmann, Allen Boston, Joseph Ho, Lynden K. Shalm, Varun B. Verma, Michael S. Allman, Sae Woo Nam, Raj B. Patel, Sergei Slussarenko, and Geoff J. Pryde, “Efficient and pure femtosecond-pulse-length source of polarization-entangled photons,” Opt. Express 24, 10869–10879 (2016).
- Kwiat et al. (1999) Paul G. Kwiat, Edo Waks, Andrew G. White, Ian Appelbaum, and Philippe H. Eberhard, “Ultrabright source of polarization-entangled photons,” Phys. Rev. A 60, R773–R776 (1999).
- König et al. (2005) Friedrich König, Elliott J. Mason, Franco N. C. Wong, and Marius A. Albota, “Efficient and spectrally bright source of polarization-entangled photons,” Phys. Rev. A 71, 033805 (2005).
- Chen et al. (2018) Yuanyuan Chen, Sebastian Ecker, Sören Wengerowsky, Lukas Bulla, Siddarth Koduru Joshi, Fabian Steinlechner, and Rupert Ursin, “Polarization entanglement by time-reversed Hong-Ou-Mandel interference,” Phys. Rev. Lett. 121, 200502 (2018).
- Terashima et al. (2018) Haruka Terashima, Satoshi Kobayashi, Takaho Tsubakiyama, and Kaoru Sanaka, “Quantum interferometric generation of polarization entangled photons,” Sci. Rep. 8, 15733 (2018).
- Rangarajan et al. (2009) Radhika Rangarajan, Michael Goggin, and Paul Kwiat, “Optimizing type-I polarization-entangled photons,” Opt. Express 17, 18920–18933 (2009).
- Villar et al. (2018) Aitor Villar, Alexander Lohrmann, and Alexander Ling, “Experimental entangled photon pair generation using crystals with parallel optical axes,” Opt. Express 26, 12396–12402 (2018).
- Martin et al. (2010) A Martin, A Issautier, H Herrmann, W Sohler, D B Ostrowsky, O Alibart, and S Tanzilli, “A polarization entangled photon-pair source based on a type-II PPLN waveguide emitting at a telecom wavelength,” New J. Phys. 12, 103005 (2010).
- Horn and Jennewein (2019) Rolf Horn and Thomas Jennewein, “Auto-balancing and robust interferometer designs for polarization entangled photon sources,” Opt. Express 27, 17369–17376 (2019).
- Lee et al. (2016) Sang Min Lee, Heonoh Kim, Myoungsik Cha, and Han Seb Moon, “Polarization-entangled photon-pair source obtained via type-II non-collinear SPDC process with PPKTP crystal,” Opt. Express 24, 2941–2953 (2016).
- Anwar et al. (2021) Ali Anwar, Chithrabhanu Perumangatt, Fabian Steinlechner, Thomas Jennewein, and Alexander Ling, “Entangled photon-pair sources based on three-wave mixing in bulk crystals,” Rev. Sci. Instrum. 92, 041101 (2021).
- Kim et al. (2003) Yoon-Ho Kim, Sergei P. Kulik, Maria V. Chekhova, Warren P. Grice, and Yanhua Shih, “Experimental entanglement concentration and universal Bell-state synthesizer,” Phys. Rev. A 67, 010301(R) (2003).
- Jeong et al. (2016) Youn-Chang Jeong, Kang-Hee Hong, and Yoon-Ho Kim, “Bright source of polarization-entangled photons using a PPKTP pumped by a broadband multi-mode diode laser,” Opt. Express 24, 1165 (2016).
- Lohrmann et al. (2020) Alexander Lohrmann, Chithrabhanu Perumangatt, Aitor Villar, and Alexander Ling, “Broadband pumped polarization entangled photon-pair source in a linear beam displacement interferometer,” Appl. Phys. Lett. 116, 021101 (2020).
- Shi and Tomita (2004) Bao-Sen Shi and Akihisa Tomita, “Generation of a pulsed polarization entangled photon pair using a Sagnac interferometer,” Phys. Rev. A 69, 013803 (2004).
- Kim et al. (2006) Taehyun Kim, Marco Fiorentino, and Franco N. C. Wong, “Phase-stable source of polarization-entangled photons using a polarization Sagnac interferometer,” Phys. Rev. A 73, 012316 (2006).
- Kuzucu and Wong (2008) Onur Kuzucu and Franco N. C. Wong, “Pulsed Sagnac source of narrow-band polarization-entangled photons,” Phys. Rev. A 77, 032314 (2008).
- Fedrizzi et al. (2007) Alessandro Fedrizzi, Thomas Herbst, Andreas Poppe, Thomas Jennewein, and Anton Zeilinger, “A wavelength-tunable fiber-coupled source of narrowband entangled photons,” Opt. Express 15, 15377–15386 (2007).
- Jabir and Samanta (2017) M. V. Jabir and G. K. Samanta, “Robust, high brightness, degenerate entangled photon source at room temperature,” Sci. Rep. 7, 12613 (2017).
- Yin et al. (2017) Juan Yin, Yuan Cao, Yu-Huai Li, Sheng-Kai Liao, Liang Zhang, Ji-Gang Ren, Wen-Qi Cai, Wei-Yue Liu, Bo Li, Hui Dai, Guang-Bing Li, Qi-Ming Lu, Yun-Hong Gong, Yu Xu, Shuang-Lin Li, Feng-Zhi Li, Ya-Yun Yin, Zi-Qing Jiang, Ming Li, Jian-Jun Jia, Ge Ren, Dong He, Yi-Lin Zhou, Xiao-Xiang Zhang, Na Wang, Xiang Chang, Zhen-Cai Zhu, Nai-Le Liu, Yu-Ao Chen, Chao-Yang Lu, Rong Shu, Cheng-Zhi Peng, Jian-Yu Wang, and Jian-Wei Pan, “Satellite-based entanglement distribution over 1200 kilometers,” Science 356, 1140–1144 (2017).
- Zhou et al. (2015) Fei Zhou, Yuan Cao, Juan Yin, Ji-Gang Ren, and Cheng-Zhi Peng, “Integrated and portable entanglement source used for quantum communication over 100 kilometers,” J. Infrared Millim. Waves 34, 224–229 (2015).
- Jin et al. (2014) Rui-Bo Jin, Ryosuke Shimizu, Kentaro Wakui, Mikio Fujiwara, Taro Yamashita, Shigehito Miki, Hirotaka Terai, Zhen Wang, and Masahide Sasaki, “Pulsed Sagnac polarization-entangled photon source with a PPKTP crystal at telecom wavelength,” Opt. Express 22, 11498–11507 (2014).
- Jin et al. (2013) Rui-Bo Jin, Ryosuke Shimizu, Kentaro Wakui, Hugo Benichi, and Masahide Sasaki, “Widely tunable single photon source with high purity at telecom wavelength,” Opt. Express 21, 10659–10666 (2013).
- Liu et al. (2020) Xu Liu, Xin Yao, Rong Xue, Heqing Wang, Hao Li, Zhen Wang, Lixing You, Xue Feng, Fang Liu, Kaiyu Cui, Yidong Huang, and Wei Zhang, “An entanglement-based quantum network based on symmetric dispersive optics quantum key distribution,” APL Photon. 5, 076104 (2020).
- Ramelow et al. (2009) S. Ramelow, L. Ratschbacher, A. Fedrizzi, N. K. Langford, and A. Zeilinger, “Discrete tunable color entanglement,” Phys. Rev. Lett. 103, 253601 (2009).
- Chen et al. (2020) Yuanyuan Chen, Sebastian Ecker, Jessica Bavaresco, Thomas Scheidl, Lixiang Chen, Fabian Steinlechner, Marcus Huber, and Rupert Ursin, “Verification of high-dimensional entanglement generated in quantum interference,” Phys. Rev. A 101, 032302 (2020).
Appendix
Figure A1 shows how the JSI in Fig. 2(d) was simulated.
The models and performance of the experimental components in this work are shown in Tab. A1.
A photograph of the setup is shown in Fig. A2.
| Name | Type | Characteristics |
|---|---|---|
| Laser | LR-BSP-405nm/100mw (LR laser Co.) | =405.1 nm, FWHM=0.53 nm |
| Fiber coupler | GCX-L005-FC (Daheng Co.) | =52.6% |
| SMF (405 nm) | PM-S405-XP (Thorlabs) | with FC/APC connector |
| Mirror (405 nm) | LLM0025-45-397-405 (Union Optics Co.) | =99.2% |
| QWP (405 nm) | WPZ4420-405 (Union Optics Co.) | =100% |
| HWP (405 nm) | WPZ2420-405 (Union Optics Co.) | =100% |
| PBS (405 nm) | PBS0120-397-405 (Union Optics Co.) | extinction ratio=1000:1 |
| Lens 1 (405 nm) | PCX1809-300-500 (Union Optics Co.) | f=200 mm, =100%; fused silica |
| Lens 2/3 (810nm) | PCX0810-780-810 (Union Optics Co.) | f=200 mm, =100%; K9 glass |
| Mirror (810 nm) | GCC-102202 (Daheng Co.) | protected silver with =98.2% |
| QWP (810 nm) | GCL-060704 (Daheng Co.) | zero order QWP |
| HWP (810 nm) | GCL-060714 (Daheng Co.) | zero order HWP |
| SPF | GCC-211002 (Daheng Co.) | =96.7% for 400-630 nm |
| LPF1(DM) | DIM-K9-25.4-3 (Union Optics Co.) | =96%(810 nm),=94%(405 nm) |
| LPF2 | RG-715 (Edmund Co.) | =89.7%(810 nm) |
| DHWP | DHWP (Union Optics Co.) | HWP for 405 nm and 810 nm |
| DPBS | DPBS (Union Optics Co.) | 405nm: =93.1%, =97.4% |
| 810nm: =96.2%, =96.7% | ||
| SMF (810 nm) | GCX-XSM-4/125-FC/PC (Daheng Co.) | SMF at 810 nm |
| PPKTP | PPKTP (Raicol Co.) | size=1210 mm, =9.825 m |
| Oven | TC038-PC (HC Photonics Co.) | resolution=0.1∘C, range=0-200∘ |
| Rotator | OSMS-60YAW (Sigma Koki Co. ) | controlled by LabVIEW software |
| Si-APD | SPCM-AQRH-10-FC (Excelitas Co. ) | 60% at 810 nm |
