Bridging the Usability Gap: Theoretical and Methodological Advances for Spectral Learning of Hidden Markov Models
Abstract
The Baum-Welch (B-W) algorithm is the most widely accepted method for inferring hidden Markov models (HMM). However, it is prone to getting stuck in local optima, and can be too slow for many real-time applications. Spectral learning of HMMs (SHMM), based on the method of moments (MOM) has been proposed in the literature to overcome these obstacles. Despite its promise, SHMM has lacked a comprehensive asymptotic theory. Additionally, its long-run performance can degrade due to unchecked error propagation. In this paper, we (1) provide an asymptotic distribution for the approximate error of the likelihood estimated by SHMM, (2) propose a novel algorithm called projected SHMM (PSHMM) that mitigates the problem of error propagation, and (3) describe online learning variants of both SHMM and PSHMM that accommodate potential nonstationarity. We compare the performance of SHMM with PSHMM and estimation through the B-W algorithm on both simulated data and data from real world applications, and find that PSHMM not only retains the computational advantages of SHMM, but also provides more robust estimation and forecasting.
Keywords: hidden Markov models (HMM), spectral estimation, projection-onto-simplex, online learning, time series forecasting
1 Introduction
The hidden Markov model (HMM), introduced by Baum and Petrie, (1966), has found widespread applications across diverse fields. These include finance (Hassan and Nath,, 2005; Mamon and Elliott,, 2014), natural language processing (Zhou and Su,, 2001; Stratos et al.,, 2016), and medicine (Shirley et al.,, 2010; Scott et al.,, 2005). An HMM is a stochastic probabilistic model for sequential or time series data that assumes that the underlying dynamics of the data are governed by a Markov chain. (Knoll et al.,, 2016).
A widely adopted method for inferring HMM parameters is the Baum-Welch algorithm (Baum et al.,, 1970). This algorithm is a special case of the expectation maximization (EM) algorithm (Dempster et al.,, 1977), grounded in maximum likelihood estimation (MLE). However, the E-M algorithm can require a large number of iterations until the parameter estimates converge–which has a large computational cost, especially for large-scale time series data–and can easily get trapped in local optima. To address these issues, particularly for large, high-dimensional time series, Hsu et al., (2012) proposed a spectral learning algorithm for HMMs (SHMM). This algorithm, based on the method of moments (MOM), offers attractive theoretical properties. However, the asymptotic error distribution of the algorithm was not well characterized. Later, Rodu, (2014) improved and extended the spectral estimation algorithm to HMMs with high-dimensional, continuously distributed output, but again did not address the asymptotic error distribution. In this manuscript, we provide a theoretical discussion of the asymptotic error behavior of SHMM algorithms.
In addition to investigating the asymptotic error distribution, we provide a novel improvement to the SHMM family of algorithms. Our improvement is motivated from an extensive simulation study of the methods proposed in Hsu et al., (2012) and Rodu, (2014). We found that spectral estimation does not provide stable results under the low signal-noise ratio setting. We propose a new spectral estimation method, the projected SHMM (PSHMM), that leverages a novel regularization technique that we call ‘projection-onto-simplex’ regularization. The PSHMM largely retains the computational advantages of SHMM methods without sacrificing accuracy.
Finally, we show how to adapt spectral estimation (including all SHMM and PSHMM approaches) to allow for online learning. We examine two approaches – the first speeds up computational time required for learning a model in large data settings, and the second incorporates “forgetfulness,” which allows for adapting to changing dynamics of the data. This speed and flexibility is crucial, for instance, in high-frequency trading, and we show the effectiveness of the PSHMM on real data in this setting.
The structure of this paper is as follows: In the rest of this section, we will introduce existing models. In Section 2, we provide theorems for the asymptotic properties of SHMMs. Section 3 introduces our new method, PSHMM. In Section 4, we extend the spectral estimation to online learning for both SHMM and PSHMM. Then, Section 5 shows results from simulation studies and Section 6 shows the application on high-frequency trading. We provide extensive discussion in Section 7.
1.1 The hidden Markov model
The standard HMM (Baum and Petrie,, 1966) is defined by a set of hidden categorical states that evolve according to a Markov chain. Let denote the hidden state at time . The Markov chain is defined by two key components:
-
1.
an initial probability where , and
-
2.
a transition matrix where for .
At each time point , an observation is emitted from a distribution conditional on the value of the current hidden state, where is the emission distribution when the hidden state . Figure 1 is a graphical representation of the standard HMM. When the emission distribution is Gaussian for all states, the model is often called a Gaussian HMM (GHMM).

1.2 Spectral learning of HMM

Figure 2 illustrates the model proposed by Rodu, (2014). As in the standard HMM, denotes the hidden state at time , and the emitted observation. To estimate the model, observations are projected onto a lower-dimensional space of dimensionality . We denote these lower-dimensional projected observations as , where . We address the selection of dimension and the method for projecting observations in Section 3.3.
The spectral estimation framework builds upon the observable operator model (Jaeger,, 2000). In this model, the likelihood of a sequence of observations is expressed as:
with and is a vector with elements . Note that this formulation of still requires inferring and . To address this, the spectral estimation framework employs a similarity transformation of . This transformed version can be learned directly from the data using the MOM.
Under the spectral estimation framework of Hsu et al., (2012), the likelihood can be written as
where with and column vector . Letting , Rodu, (2014) shows that, the likelihood can be expressed as
| (1) |
where
These quantities can be empirically estimated as:
| (2) |
where
| (3) |
Prediction of is computed recursively by:
| (4) |
Observation can be recovered as:
| (5) |
In the above exposition of spectral likelihood estimation, moment estimation, and recursive forecasting we assume a discrete output HMM. For a continuous output HMM, the spectral estimation of likelihood is slightly different. We need some kernel function to calculate , so .
provides a link between the observations and their conditional probabilities in the continuous output scenario. Let be the probability vector associated with being in a particular state at time , commonly called a belief state. Then . Therefore,
Bayes formula gives
Letting , this implies that
Then we get
Finally
Using this definition of we have
Note from above that this is exactly what we want, up to a scaling constant that depends on (for more on see Rodu,, 2014). In this paper, we will use a linear kernel for simplicity. The moment estimation and recursive forecasting for the continuous case are identical to the discrete case. See Rodu et al., (2013) for detailed derivations and mathematical proofs of these results.
In the following, the theoretical properties discussed in Section 2 are based on the likelihood (Eq 1 - Eq 3), and improvements to prediction in Section 3 are based on Eq 4. Note that deriving the prediction function from the likelihood is straightforward. See Rodu, (2014) and Hsu et al., (2012) a detailed derivation.
2 Theoretical Properties of SHMM
2.1 Assumptions for SHMMs
The SHMM framework, (illustrated in Figure 2) relies on three primary assumptions:
-
•
Markovian hidden states: The sequence of underlying hidden states follows a Markov process.
-
•
Conditional independence: The observations are mutually independent, given the hidden states.
-
•
Invertibility condition: The matrix is invertible.
The first two assumptions are standard assumptions for the HMM. The third assumption places constraints on the separability of the conditional distributions given the hidden states. It also requires that the underlying transition matrix for the HMM is full rank. While the full-rank condition is crucial for the standard SHMM we address in this paper, it is worth noting that some scenarios may involve non-full rank HMMs. For such cases, relaxations of this assumption have been explored in the literature (e.g. Siddiqi et al.,, 2009).
2.2 Asymptotic framework for SHMMs
SHMM relies on the MOM to estimate the likelihood, offering a computationally efficient approach. However, the asymptotic behavior of the SHMM has not been thoroughly explored in previous literature. Prior work by Hsu et al., (2012) and Rodu et al., (2013) established conditions for convergence of the spectral estimator to the true likelihood almost surely, for discrete and continuous HMM respectively. Specifically, they showed:
| (6) |
Here, and are estimated using independent and identically distributed (i.i.d) triples , as defined in Eq 3. It is important to note that the use of i.i.d. triples is primarily a theoretical tool, used by both Hsu et al., (2012) and Rodu et al., (2013) to facilitate study of the theoretical properties of the SHMM. In practice, quantities should be estimated using the full sequence of observations, which introduces dependencies between the triplets (see section 3). The relationship between the effective sample size for estimation and the actual sample size is governed by the mixing rate of the underlying Markov chain.
In this paper, we extend these results by investigating the asymptotic distribution of the estimation error, . Theorem 1 presents a CLT type bound for this approximation error. We first identify the sources of error for the SHMM in Lemma 1, which makes use of what we refer to as the ‘’ terms, defined through the following equations: , , .
Lemma 1.
where
We provide a detailed proof of this lemma in the supplementary material. The basic strategy is to fully expand after rewriting the estimated quantities as a sum of the true quantity plus an error term. We then categorize each summand based on how many ‘’ terms it has. There are three categories: terms with zero ‘’ terms (i.e. the true likelihood ), terms with only one ‘’ (i.e. ), and all remaining terms, which involve at least two ‘’ quantities, and can be relegated to .
Lemma 1 shows how the estimated error propagates to the likelihood approximation. We can leverage the fact that our moment estimators have a central limit theorem (CLT) property to obtain the desired results in Theroem 1.
We denote the outer product as , and define a “flattening” operator for both matrices and 3-way tensors. For matrix ,
For tensor ,
We now state and prove our main theorem.
Theorem 1.
Proof (Theorem 1).
We flatten and as
Rewriting and in Eq 1 as
we have
Since the CLT applies seperately to , then
Therefore,
∎
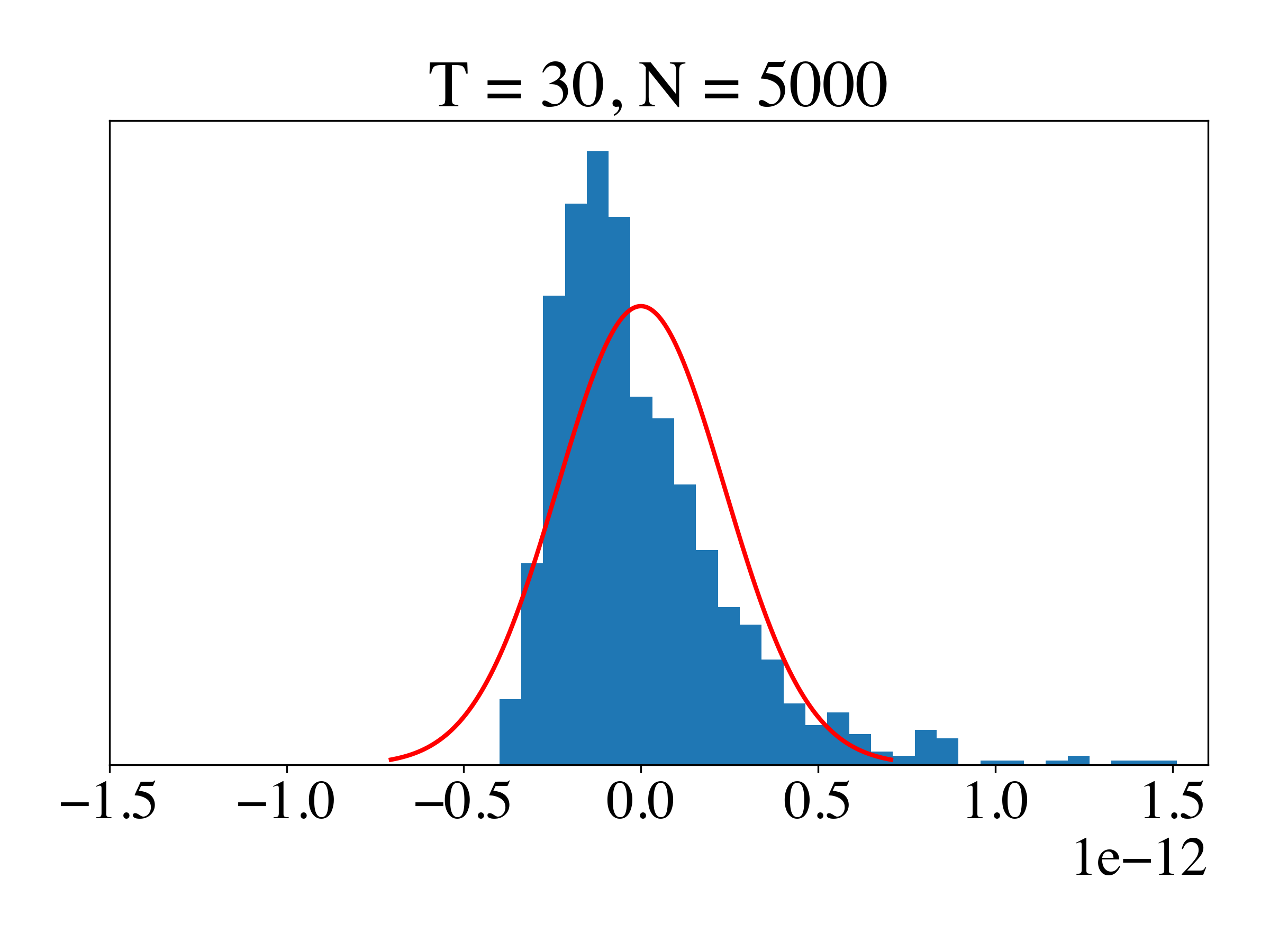







2.3 Experimental Validation of Theorem 1.
We conducted a series of experiments to validate theorem 1. We simulated a target series with and using a 3-state GHMM, where the initial probabilities and sticky transition probabilities are as described in Section 5.1.1. We set the discrete emission probability matrix to . We estimated parameters , and using training samples generated from the same model as the target series. Specifically, i.i.d. samples were used to estimate , i.i.d. samples of to estimate , and i.i.d. samples of to estimate . We used training sets of size , replicating the experiment 1000 times for each . For each replication , we estimated and constructed a histogram of the estimation errors . We compared this histogram to the theoretical probability density function (pdf), which by Theorem 1 should converge to a normal distribution as increases.
In Figure 3 we see that, as increases, the distribution of the estimated likelihood converges to the normal distribution, and with a shorter length , the error converges faster. We also analyzed the asymptotic behavior of the first-order estimation errors separately for the first moment, , second moment, , and third moment, (see Figure 4). We found that the third moment estimation error has the largest effect, as shown in Table 1. We further analyzed the asymptotic distribution of the Frobenius norm of the first, second and third moment estimation error. Figure 5 shows the empirical histogram and its corresponding theoretical pdf.






We note two sources of error in estimating the likelihood. The first is the typical CLT-type error in parameter estimation, which decreases as increases. The second the propagation of estimation errors during forward recursion. To achieve a stable normal distribution given the second issue, must be much greater than . In our simulation with , we observe reasonable evidence of asymptotic normality at , but not at . When or is only slightly larger, the distribution is heavy-tailed, suggesting that regularization could be beneficial.
For simplicity of presentation, we derive Theorem 1 under the assumption that the output distribution is discrete. For continuous output, the CLT still holds with a proper kernel function as mentioned in section 1.2.
| Error source | Mathematical expression | Theoretical std | Variance explained ratio |
|---|---|---|---|
| 1st moment estimation | |||
| 2nd moment estimation | |||
| 3rd moment estimation |
| Error source | Mathematical expression | Theoretical std | Variance explained ratio |
|---|---|---|---|
| 1st moment estimation | |||
| 2nd moment estimation | |||
| 3rd moment estimation |
3 Projected SHMM
3.1 Motivation for Adding Projection
The Baum-Welch algorithm (Baum et al.,, 1970) predicts belief probabilities, or weights, for each underlying hidden state. Let denote the predicted weight vector at time . The prediction can be expressed as a weighted combination of cluster means: where . In the Baum-Welch algorithm, these weights are explicitly guaranteed to be non-negative and sum to 1 during forward propagation, which is consistent with their interpretation as probabilities.
However, SHMM does not directly estimate the belief probabilities, and these constraints are not explicitly enforced in spectral estimation. Consequently, SHMM can sometimes produce predictions that are far from the polyhedron spanned by the cluster means. To address this issue, we propose the projected SHMM, where projection serves to regularize the predictions, constraining them within a reasonable range.
This is particularly important when is not sufficiently large, and extreme deviations of the estimated likelihood from the true likelihood can occur when error is propagated over time. Regularization can help stabilize the performance of estimation of the likelihood by limiting this propagation of error.
3.2 Projection Methods for SHMM
We propose two projection methods for SHMM: projection-onto-polyhedron and projection-onto-simplex. Projection-onto-polyhedron directly addresses the motivation for using projections in SHMM but is computationally expensive. As a computationally efficient alternative, we propose projection-onto-simplex.
3.2.1 Projection-onto-Polyhedron
Projection-onto-polyhedron SHMM first generates prediction through the standard SHMM and then projects it onto the polyhedron with vertices . Mathematically, we replace the recursive forecasting in Eq 4 with
| (7) |
where is a distance function (e.g., Euclidean distance), and
is the polyhedron with vertices . This results in a convex optimization problem if the distance is convex. While solvable using standard methods such as the Newton-Raphson algorithm (Boyd et al.,, 2004) with log-barrier methods (Frisch,, 1955), to the best of our knowledge finding an efficient solution for projection-onto-polyhedron is challenging. The optimization must be performed at every time step, creating a trade-off between accuracy and computational speed. Because speed over the Baum-Welch algorithm is one of the distinct advantages of SHMM, any modification should not result in a substantial increase in computational time.
3.2.2 Projection-onto-Simplex
To improve computational efficiency, we propose projection-onto-simplex. To avoid projection onto a polyhedron, we leverage the fact that and optimize over on the simplex:
| (8) |
This allows us to calculate the projection with time complexity (Wang and Carreira-Perpinán,, 2013). This approach, while not equivalent to the solution from the projection-onto-polyhedron– in general–ensures predictions are constrained to the same polyhedron. Importantly, it can be solved using a closed-form solution (Algorithm 1), avoiding iterative optimization and yielding faster estimation. Figure 6 illustrates the projection-onto-polyhedron and projection-onto-simplex methods.
The full projected SHMM algorithm is shown in Algorithm 2. In Algorithm 2, Steps 1-3 are identical to the standard SHMM. Steps 4-5 estimate by Gaussian Mixture Models (GMM) (McLachlan and Basford,, 1988), calculate the weight processes , and apply SHMM on the weight process. Step 6 applies projection-onto-simplex on the recursive forecasting. Step 7 projects the data back into the original space.


3.2.3 Bias-variance tradeoff
In PSHMM, we leverage GMM to provide projection boundaries, which would introduce bias, since the hidden state means estimated by GMM are biased when we ignore time dependency information. In addition, either projection method– ’projection-onto-polyhedron’ or ’projection-onto-simplex’– can introduce bias since they are not necessarily an orthogonal projection due to optimization constraints. However, adding such a projection will largely reduce the variance. That is, there is a bias-variance tradeoff.
3.3 Considerations for PSHMM Implementation
This section addresses two key aspects of PSHMM implementation: choosing the dimensionality of the projection space and computing the projection matrix .
3.3.1 Choice of projection space dimensionality
The hyperparameter determines the dimensionality of the projection space. Theoretically, should equal the number of states in the HMM. Our simulations confirm that when matches the true number of underlying states, estimation and prediction performance improves. However, in practice, the number of hidden states is often unknown. We recommend either choosing based on prior knowledge or tuning it empirically when strong prior beliefs are absent.
3.3.2 Computation of projection matrix
The projection matrix is typically constructed using the first left singular vectors from the singular value decomposition (SVD) (Eckart and Young,, 1936) of the bigram covariance matrix . This approach encodes transition information while eliminating in-cluster covariance structure. Alternatively, could be estimated through an SVD of , which would incorporate both covariance structure and cluster mean information. We generally recommend using the bigram matrix approach.
For extremely high-dimensional data, we propose a fast approximation algorithm based on randomized SVD (Halko et al.,, 2011). This method avoids computing the full covariance matrix , reducing time complexity from to for , where and are the sample size and data dimensionality, respectively. The algorithm proceeds as follows:
-
1.
Noting that , where and , perform a randomized SVD of and separately to obtain two rank- decompositions with : , .
Now , where has dimension .
-
2.
Perform an SVD on to get .
-
3.
We can reconstruct .
and are orthonormal matrices and is a diagonal matrix, so this is the rank- SVD of . The first vectors of are an estimate of the matrix we compute in Step 1 and 2 in Algorithm 2
4 Online Learning
Online learning is a natural extension for SHMMs, given their computational efficiency advantages. This section introduces online learning approaches for both SHMM and PSHMM, addressing scenarios where traditional batch learning may be unsuitable. For example, in quantitative trading, markets often exhibit a regime-switching phenomenon. Thus, it is likely that the observed returns for some financial products are nonstationary. In high frequency trading, especially in second-level or minute-level trading, the delay from frequent offline re-training of the statistical model could impact the strategy and trading speed (Lahmiri and Bekiros,, 2021).
4.1 Online Learning of SHMM and PSHMM
We illustrate an online learning strategy that allows for adaptive parameter estimation. Let , and , be the estimated moments based on data points. Upon receiving new data , we update our moments recursively:
| (9) |
The update strategy applies to both SHMM and PSHMM. Algorithm 3 provides pseudo-code for online learning in PSHMM.
Updating the GMM used in PSHMM
For PSHMM, updating the Gaussian Mixture Model (GMM) requires careful consideration. We recommend updating the GMM without changing cluster membership. For example, classify a new input into a particular cluster and update that cluster’s mean and covariance. We advise against re-estimating the GMM, which could add or remove clusters, as this would alter the relationship between ’s dimensionality and the number of hidden states. In practice, we find PSHMM performs well even without GMM updates.
4.2 Online Learning of SHMM Class with Forgetfulness
To handle nonstationary data, we introduce a forgetting mechanism in online parameter estimation. This approach requires specifying a decay factor , which determines the rate at which old information is discarded. The updating rule becomes:
| (10) |
Here serves as an effective sample size. This strategy is equivalent to calculating the exponentially weighted moving average for each parameter:
| (11) |
5 Simulations
This section presents simulation studies to evaluate the performance of SHMM and PSHMM under various conditions. We assess robustness to different signal-to-noise ratios, misspecified models, and heavy-tailed data. We also test the effectiveness of the forgetfulness mechanism and compare computational efficiency.
5.1 Tests of Robustness under Different Signal-Noise Ratio, Mis-specified Models and Heavy-Tailed Data
5.1.1 Experiment setting
We simulated -dimensional data with training points and test points using various GHMM configurations. Each simulation was repeated times. We compared SHMM, three variants of PSHMM (projection onto polyhedron, projection onto simplex, and online learning with projection onto simplex), and the E-M algorithm. Prediction performance was evaluated using the average over all repetitions. The online learning variant of PSHMM used training samples for the initial estimate (warm-up), and incorporated the remaining training samples using online updates. We also calculated an oracle , assuming knowledge of all HMM parameters but not the specific hidden states.
In our simulations, online training for PSHMM differs from offline training for two reasons. First, the estimation of and are based only on the warm-up set for online learning (as is the case for the online version of SHMM), and the entire training set for offline learning. Second, during the training period, for PSHMM, the updated moments are based on the recursive predictions of , which are themselves based on the weights . In contrast, for the offline learning of PSHMM, the weights used to calculate the moments are based on the GMM estimates from the entire training dataset.
For each state, we made two assumptions about the emission distribution. First, it has a one-hot mean vector in which the -th state is , where is the indicator function. Second, it has a diagonal covariance matrix. We tested the SHMM, PSHMM methods, and the E-M algorithm under two types of transition matrix, five different signal-noise ratios and different emission distributions as below:
-
•
Transition matrix:
-
–
Sticky: diagonal elements are , off-diagonal elements are , where is the number of states that generated the data;
-
–
Non-sticky: diagonal elements are , off-diagonal elements are .
-
–
-
•
Signal-noise ratio: Covariance specified by , where .
-
•
Emission distributions:
-
–
Gaussian distribution, generated according to mean vector and covariance matrix;
-
–
distribution: generated a standard a random vector of , , and distribution, then multiplied by the covariance matrix and shifted by the mean vector.
-
–
5.1.2 Simulation Results



Figure 7 shows that the performance of PSHMM is competitive with the E-M algorithm. While both methods achieve similar values in most scenarios, PSHMM outperforms E-M under conditions of high noise or heavy-tailed distributions. Note that our E-M implementation employs multiple initializations to mitigate local optima issues, which comes at the cost of increased computational time.
Our simulations used -dimensional observed data (), which we found approached the practical limits of the E-M algorithm. In higher-dimensional scenarios ( or ), E-M failed, whereas SHMM continued to perform effectively. To ensure a fair comparison, we present results for throughout this section.
The last point is important. In Figure 7, in order to include the E-M algorithm in our simulations, we restrict our investigation to settings where E-M is designed to succeed, and show comparable performance with our methodology. Many real-world scenarios exist in a space where E-M is a nonstarter. This highlights PSHMM’s robustness and scalability advantages over traditional E-M approaches, particularly for high-dimensional data.
In Figure 7, we can also see that adding projections to SHMM greatly improved , achieving near oracle-level performance in some settings. The top row shows that, under both high- and low-signal-to-noise scenarios, PSHMM works well. The middle row shows that PSHMM is robust and outperforms SHMM when the model is mis-specified, for example, when the underlying data contains 5 states but we choose to reduce the dimensions to or . The last row shows that PSHMM is more robust and has a better than SHMM with heavy-tailed data such as data generated by a t distribution. In all figures, when , we threshold to for plotting purpose. See supplementary tables for detailed results. Negative occurs only for the standard SHMM, and implies that it is not stable. Since we simulated trials for each setting, in addition to computing the mean we also calculated the variance of the metric. We provide the variance of the in the appendix, but note here that the variance of under PSHMM was smaller than that of the SHMM. Overall, while SHMM often performs well, it is not robust, and PSHMM provides a suitable solution.
Finally, in all simulation settings, we see that the standard SHMM tends to give poor predictions except in non-sticky and high signal-to-noise ratio settings. PSHMM is more robust against noise and mis-specified models. Among the PSHMM variants, projection-onto-simplex outperforms projection-onto-polyhedron. The reason is that the projection-onto-simplex has a dedicated optimization algorithm that guarantees the optimal solution in the projection step. In contrast, projection-onto-polyhedron uses the log-barrier method, which is a general purpose optimization algorithm and does not guarantee the optimality of the solution. Since projection-onto-polyhedron also has a higher computational time, we recommend using projection-onto-simplex. Additionally, for projection-onto-simplex, we see that online and offline estimation perform similarly in most settings, suggesting that online learning does not lose too much power compared with offline learning.
5.2 Testing the effectiveness of forgetfulness
Experimental setting.
Similarly to Section 5.1.1, we simulated 100-dimensional, 5-state GHMM data with and of length where the first steps are for training and the last steps are for testing. The transition matrix is no longer time-constant but differ in the training and testing period as follows:
-
•
training period (diagonal-0.8): ;
-
•
testing period (antidiagonal-0.8): .
We tested different methods on the last 100 time steps, including the standard SHMM, projection-onto-simplex SHMM, online learning projection-onto-simplex SHMM, online learning projection-onto-simplex SHMM with decay factor , E-M, and the oracle as defined above. For online learning methods, we used the first steps in the training set for warm-up and incorporated the remaining samples using online updates.

Simulation results.
Figure 8 shows the simulation results. Since the underlying data generation process is no longer stationary, most methods failed including the E-M algorithm, with the exception of the online learning projection-onto-simplex SHMM with decay factor . Adding the decay factor was critical for accommodating non-stationarity. As increases even PSHMM performs poorly– the oracle shows that this degredation in performance is hard to overcome.
5.3 Testing Computational Time
Experimental setting
We used a similar experimental setting from Section 5.1.1. We simulated 100-dimensional, 3-state GHMM data with and length 2000. We used the first half for warm-up and tested computational time on the last 1000 time steps. We tested both E-M algorithm and SHMM (all variants). For the SHMM family of algorithms, we tested under both online and offline learning regimes. We computed the total running time in seconds. The implementation is done in python with packages Numpy (Harris et al.,, 2020), Scipy (Virtanen et al.,, 2020) and scikit-learn (Pedregosa et al.,, 2011) without multithreading. Note that in contrast to our previous simulations, the entire process is repeated only 30 times. The computational time is the average over the 30 runs.
Simulation results
Table 2 shows the computational times for each method. First, online learning substantially reduced the computational cost. For the offline learning methods, projection-onto-simplex SHMM performed similarly to SHMM, and projection-onto-polyhedron was much slower. In fact, the offline version of projection-onto-polyhedron was slow even compared to the the E-M algorithm. However, the online learning variant of projection-onto-polyhedron was much faster than the Baum-Welch algorithm. Taking both the computational time and prediction accuracy into consideration, we conclude that online and offline projection-onto-simplex SHMM are the best choices among these methods.
| Method | Offline/online | Computational time (sec) |
|---|---|---|
| E-M (Baum-Welch) | - | 2134 |
| SHMM | offline | 304 |
| SHMM | online | 0.5 |
| PSHMM (simplex) | offline | 521 |
| PSHMM (simplex) | online | 0.7 |
| PSHMM (polyhedron) | offline | 10178 |
| PSHMM (polyhedron) | online | 14 |
6 Application: Backtesting on High Frequency Crypto-Currency Data
6.1 Data Description & Experiment Setting
To evaluate our algorithm’s performance on real-world data, we utilized a cryptocurrency trading dataset from Binance (https://data.binance.vision), one of the world’s largest Bitcoin exchanges. We focused on minute-level data for five major cryptocurrencies: Bitcoin, Ethereum, XRP, Cardano, and Polygon. Our analysis used log returns for each minute as input for our models.
We used the period from July 1, 2022, to December 31, 2022, as our test set. For each day in this test set, we employed a 30-day rolling window of historical data for model training. After training, we generated consecutive-minute recursive predictions for the entire test day without updating the model parameters intra-day.
Our study compared three models: the HMM with EM (HMM-EM), the SHMM, and the PSHMM with simplex projection. For all models, we assumed 4 latent states, motivated by the typical patterns observed in log returns, which often fall into combinations of large/small gains/losses.
To assess the practical implications of our models’ predictions, we implemented a straightforward trading strategy. This strategy generated buy signals for positive forecasted returns and short-sell signals for negative forecasted returns. We simulated trading a fixed dollar amount for each cryptocurrency, holding positions for one minute, and executing trades at every minute of the day.
We evaluated the performance of our trading strategy using several standard financial metrics. The daily return was calculated as the average return across all five cryptocurrencies, weighted by our model’s predictions:
where is the return for minute of day for currency , is its prediction, and is if is positive, if is negative, and if . From these daily returns, we computed the annualized return
to measure overall profitability. To assess risk-adjusted performance, we calculated the Sharpe ratio (Sharpe,, 1966)
where and are the sample mean and standard deviation of the daily returns. The Sharpe ratio provides insight into the return earned per unit of risk. Lastly, we determined the maximum drawdown (Grossman and Zhou,, 1993)
which quantifies the largest peak-to-trough decline as a percentage. Since the financial data is leptokurtic, the maximum drawdown shows the outlier effect better than the Sharpe ratio which is purely based on the first and second order moments. A smaller maximum drawdown indicates that the method is less risky.
6.2 Results
| Method | Sharpe Ratio | Annualized Return | Maximum drawdown |
|---|---|---|---|
| PSHMM | |||
| SHMM | |||
| HMM-EM |
From Table 3, we see that PSHMM outperforms all other benchmarks with the highest Sharpe ratio and annualized return, and the lowest maximum drawdown. PSHMM outperforms SHMM and SHMM outperforms HMM-EM. SHMM outperforms HMM-EM because spectral learning does not suffer from the local minima problem of the E-M algorithm. PSHMM outperforms SHMM because projection-onto-simplex provides regularization.

The accumulated daily return is shown in Figure 9. PSHMM outperformed the other methods. The maximum drawdown of PSHMM is . Considering the high volatility of the crypto-currency market during the second half of 2022, this maximum drawdown is acceptable. For computational purposes, the drawdown is allowed to be larger than because we always use a fixed amount of money to buy or sell, so we are effectively assuming an infinite pool of cash. Between PSHMM and SHMM, the only difference is the projection-onto-simplex. We see that the maximum drawdown of PSHMM is only about half that of SHMM, showing that PSHMM takes a relatively small risk, especially given that PSHMM has a much higher return than SHMM.
7 Discussion
Spectral estimation avoids being trapped in local optima.
E-M (i.e. the B-W algorithm) optimizes the likelihood function and is prone to local optima since the likelihood function is highly non-convex, whereas spectral estimation uses the MOM directly on the observations. Although multiple initializations can mitigate the local optima problem with E-M, it, there is no guarantee that it will convergence to the true global optimum. Spectral estimation provides a framework for estimation which not only avoids non-convex optimization, but also has nice theoretical properties. The approximate error bound tells us that when the number of observations goes to infinity, the approximation error will go to zero. In this manuscript, we also provide the asymptotic distribution for this error.
Projection-onto-simplex serves as regularization.
The standard SHMM can give poor predictions due to the accumulation and propagation of errors. Projection-onto-simplex pulls the prediction back to a reasonable range. This regularization is our primary methodological innovation, and importantly makes the SHMM well-suited for practical use. Although the simplex, estimated by the means from a GMM, can be biased, this simplex provides the most natural and reasonable choice for a projection space. This regularization introduces a bias-variance trade-off. When the data size is small, it accepts some bias in order to reduce variance.
Online learning can adapt to dynamic patterns and provide faster learning.
Finally, we provide an online learning strategy that allows the estimated moments to adapt over time, which is critical in several applications that can exhibit nonstationarity. Our online learning framework can be applied to both the standard SHMM and PSHMM. Importantly, online learning substantially reduces the computational costs compared to re-training the entire model prior to each new prediction.
SUPPLEMENTAL MATERIALS
Appendix A Proof for Lemma 1
Proof (Lemma 1).
First, we expand the estimated likelihood by decomposing it into the underlying truth plus the error terms. We have
Consider the matrix perturbation , Here the matrix norm can be any norm since all matrix norms have equivalent orders. Also note that all items with are . is the number of triple for estimating . Note that and are not related, and that we work in the regime where is fixed but . For example, . Similar analyses apply to and can be similarly. So
where is the dimension of . One application is .
According to the previous two expansions, we can rewrite Eq LABEL:eqn:ErrorTermExpansion as
In the above, we first substitute with , then distribute all multiplications. After distribution, we can categorize the resulting terms into 3 categories according to different orders of convergence. The first category is the deterministic term without any randomness or estimation error. There is only one term in this category, which is , i.e. . The second category is the part that converges with order . This category involves all terms with one ‘’ term, i.e. one , or . These terms comprise the sum . To be useful for the main Theorem, we simplify each term by representing the collection of “true” quantities that exist in each term with as defined in the lemma. Note that each collection contains only terms that fall either to the left or to the right of the ‘’ term. The third category contains all remaining terms. These terms converge faster than– or on the order of– . These terms are all finite, and thus their summation is also .
∎
Appendix B Detailed Results for Simulations
Table 4 shows the detailed simulation results. The first columns represents the emission distribution. The second column shows the type of the transition matrix, which we describe in the simulation settings of the paper. Here we show two types of oracle: “limited oracle” is the oracle described in the paper (and is the most commonly used oracle). Limited oracle assumes we know all parameters but don’t know the true hidden states. The “strong oracle” assumes knowledge of every parameter, as well as the particular hidden state at each time point. From the table below, we can see that these oracles nearly overlapped, and that PSHMM with projection-onto-simplex is very close to the oracle in most cases.
| E | T | #Cluster | Limited | Strong | SHMM | PSHMM | PSHMM | PSHMM | |
|---|---|---|---|---|---|---|---|---|---|
| inferred | oracle | oracle | simplex | polyhedron | simplex | ||||
| online | |||||||||
| sticky | |||||||||
| sticky | |||||||||
| sticky | |||||||||
| sticky | |||||||||
| nonsticky | |||||||||
| nonsticky | |||||||||
| nonsticky | |||||||||
| nonsticky | |||||||||
| sticky | |||||||||
| sticky | |||||||||
| nonsticky | |||||||||
| nonsticky | |||||||||
| sticky | |||||||||
| nonsticky | |||||||||
| sticky | |||||||||
| nonsticky | |||||||||
| sticky | |||||||||
| sticky | |||||||||
| sticky | |||||||||
| nonsticky | |||||||||
| nonsticky | |||||||||
| nonsticky |
References
- Baum and Petrie, (1966) Baum, L. E. and Petrie, T. (1966). Statistical inference for probabilistic functions of finite state markov chains. The annals of mathematical statistics, 37(6):1554–1563.
- Baum et al., (1970) Baum, L. E., Petrie, T., Soules, G., and Weiss, N. (1970). A maximization technique occurring in the statistical analysis of probabilistic functions of markov chains. The annals of mathematical statistics, 41(1):164–171.
- Boyd et al., (2004) Boyd, S., Boyd, S. P., and Vandenberghe, L. (2004). Convex optimization. Cambridge university press.
- Dempster et al., (1977) Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Series B Stat. Methodol., 39(1):1–22.
- Eckart and Young, (1936) Eckart, C. and Young, G. (1936). The approximation of one matrix by another of lower rank. Psychometrika, 1(3):211–218.
- Frisch, (1955) Frisch, K. (1955). The logarithmic potential method of convex programming. Memorandum, University Institute of Economics, Oslo, 5(6).
- Grossman and Zhou, (1993) Grossman, S. J. and Zhou, Z. (1993). Optimal investment strategies for controlling drawdowns. Mathematical finance, 3(3):241–276.
- Halko et al., (2011) Halko, N., Martinsson, P.-G., and Tropp, J. A. (2011). Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions. SIAM review, 53(2):217–288.
- Harris et al., (2020) Harris, C. R., Millman, K. J., van der Walt, S. J., Gommers, R., Virtanen, P., Cournapeau, D., Wieser, E., Taylor, J., Berg, S., Smith, N. J., Kern, R., Picus, M., Hoyer, S., van Kerkwijk, M. H., Brett, M., Haldane, A., del Río, J. F., Wiebe, M., Peterson, P., Gérard-Marchant, P., Sheppard, K., Reddy, T., Weckesser, W., Abbasi, H., Gohlke, C., and Oliphant, T. E. (2020). Array programming with NumPy. Nature, 585(7825):357–362.
- Hassan and Nath, (2005) Hassan, M. R. and Nath, B. (2005). Stock market forecasting using hidden markov model: a new approach. In 5th International Conference on Intelligent Systems Design and Applications (ISDA’05), pages 192–196. IEEE.
- Hsu et al., (2012) Hsu, D., Kakade, S. M., and Zhang, T. (2012). A spectral algorithm for learning hidden markov models. Journal of Computer and System Sciences, 78(5):1460–1480.
- Jaeger, (2000) Jaeger, H. (2000). Observable Operator Models for Discrete Stochastic Time Series. Neural Comput., 12(6):1371–1398.
- Knoll et al., (2016) Knoll, B. C., Melton, G. B., Liu, H., Xu, H., and Pakhomov, S. V. (2016). Using synthetic clinical data to train an hmm-based pos tagger. In 2016 IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI), pages 252–255. IEEE.
- Lahmiri and Bekiros, (2021) Lahmiri, S. and Bekiros, S. (2021). Deep learning forecasting in cryptocurrency high-frequency trading. Cognitive Computation, 13:485–487.
- Mamon and Elliott, (2014) Mamon, R. S. and Elliott, R. J. (2014). Hidden Markov models in finance: Further developments and applications, volume II. International series in operations research & management science. Springer, New York, NY, 2014 edition.
- McLachlan and Basford, (1988) McLachlan, G. J. and Basford, K. E. (1988). Mixture models: Inference and applications to clustering, volume 38. M. Dekker New York.
- Pedregosa et al., (2011) Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., and Duchesnay, E. (2011). Scikit-learn: Machine learning in Python. Journal of Machine Learning Research, 12:2825–2830.
- Rodu, (2014) Rodu, J. (2014). Spectral estimation of hidden Markov models. University of Pennsylvania.
- Rodu et al., (2013) Rodu, J., Foster, D. P., Wu, W., and Ungar, L. H. (2013). Using regression for spectral estimation of hmms. In International Conference on Statistical Language and Speech Processing, pages 212–223. Springer.
- Scott et al., (2005) Scott, S. L., James, G. M., and Sugar, C. A. (2005). Hidden markov models for longitudinal comparisons. J. Am. Stat. Assoc., 100(470):359–369.
- Sharpe, (1966) Sharpe, W. F. (1966). Mutual fund performance. The Journal of business, 39(1):119–138.
- Shirley et al., (2010) Shirley, K. E., Small, D. S., Lynch, K. G., Maisto, S. A., and Oslin, D. W. (2010). Hidden markov models for alcoholism treatment trial data. aoas, 4(1):366–395.
- Siddiqi et al., (2009) Siddiqi, S., Boots, B., and Gordon, G. J. (2009). Reduced-rank hidden markov models. AISTATS, 9:741–748.
- Stratos et al., (2016) Stratos, K., Collins, M., and Hsu, D. (2016). Unsupervised part-of-speech tagging with anchor hidden markov models. Trans. Assoc. Comput. Linguist., 4:245–257.
- Virtanen et al., (2020) Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S. J., Brett, M., Wilson, J., Millman, K. J., Mayorov, N., Nelson, A. R. J., Jones, E., Kern, R., Larson, E., Carey, C. J., Polat, İ., Feng, Y., Moore, E. W., VanderPlas, J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen, I., Quintero, E. A., Harris, C. R., Archibald, A. M., Ribeiro, A. H., Pedregosa, F., van Mulbregt, P., and SciPy 1.0 Contributors (2020). SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods, 17:261–272.
- Wang and Carreira-Perpinán, (2013) Wang, W. and Carreira-Perpinán, M. A. (2013). Projection onto the probability simplex: An efficient algorithm with a simple proof, and an application. arXiv preprint arXiv:1309.1541.
- Zhou and Su, (2001) Zhou, G. and Su, J. (2001). Named entity recognition using an HMM-based chunk tagger. In Proceedings of the 40th Annual Meeting on Association for Computational Linguistics - ACL ’02, Morristown, NJ, USA. Association for Computational Linguistics.