Benemérita Universidad Autónoma de Puebla,
C.P. 72570, Puebla, Pue., Mexico 22institutetext: Ingeniería en Mecatrónica,
Universidad Politécnica de Puebla,
Tercer Carril del Ejido Serrano s/n, San Mateo Cuanalá, Juan C. Bonilla,
Puebla, Puebla, México
Bounds on the absorptive parts of the chromomagnetic and chromoelectric dipole moments of the top quark from LHC data
Abstract
Bounds on the absorptive (imaginary) parts of the top quark chromomagnetic and chromoelectric dipole moments are obtained by reinterpreting the most recent LHC data in top quark pair production. It is found that both limits are of the order of , which are consistent with the standard model prediction of . The effects of the absorptive parts of the top quark dipole moments are also studied via some kinematic distributions of production, though no significant deviation from the standard model leading order contribution is observed. Our bounds can be useful to constrain the parameter space of standard model extensions.
1 Introduction
Quite recently, the study of the chromomagnetic dipole moment (CMDM) of the top quark has become a topic of great interest both theoretically and experimentally. On the theoretical side, a new evaluation of the lowest order contributions to within the framework of the standard model (SM) was presented in Refs. Hernandez-Juarez:2020drn ; Aranda:2020tox , which has settled some ambiguities found in previous evaluations: in contrast to what was claimed before Martinez:2007qf , it has become clear that the CMDM is infrared divergent, with the divergent part arising from the non-abelian term of the gluon field tensor Hernandez-Juarez:2020drn ; Aranda:2020tox . Therefore, the study of the static CMDM has no sense in perturbative QCD. Nevertheless, the off-shell CMDM is finite and gauge independent in the SM Hernandez-Juarez:2020drn , and therefore it can be a valid observable quantity. In addition several non SM contributions to the CMDM have been calculated up to the one-loop level in the framework of extension theories such as two Higgs doublet models (THDM) Gaitan:2015aia , fourth-generation THDMs Hernandez-Juarez:2018uow , 331 models Hernandez-Juarez:2020xon , models with an extra gauge boson Aranda:2018zis , etc. As far as the top quark chromoelectric dipole moment (CEDM) is concerned, it is induced up to the three-loop level in the SM Czarnecki:1997bu and thus could give a clear signal of violation. The top quark CEDM has also been a topic of interest the literature as it can arise at one-loop level in some beyond the SM (BSM) theories Hernandez-Juarez:2018uow ; Hernandez-Juarez:2020xon , thereby opening the possibility of a considerable enhancement. In general, both the off-shell CMDM and CEMD can have non-zero imaginary parts, whose effects remain almost unexplored.
On the experimental side, the leading order corrections to the cross section of top quark pair production induced by the top quark CMDM and CEDM have been studied in Atwood:1994vm ; Simmons:1995hb ; Haberl:1995ek ; Cheung:1995nt ; Choi:1997ie ; Hikasa:1998wx ; Czakon:2008ii ; Antipin:2008zx ; Gupta:2009eq ; Zhang:2010dr ; Degrande:2010kt ; Baumgart:2012ay ; Englert:2012by ; Hayreter:2013kba ; Bernreuther:2013aga ; Fabbrichesi:2014wva ; Aguilar-Saavedra:2014iga ; Bernreuther:2015yna ; Cao:2015doa ; Barducci:2017ddn ; Malekhosseini:2018fgp , and the next-to-leading order corrections have also been calculated more recently Englert:2014oea ; Franzosi:2015osa ; AguilarSaavedra:2018nen , whereas the effects of the dipole moments have been analyzed in some processes Kane:1991bg ; Atwood:1992vj ; Grzadkowski:1997yi ; Lampe:1997sj ; Yang:1997iv ; Tsuno:2005qb ; Hioki:2009hm ; Gupta:2009wu ; Hioki:2010zu ; HIOKI:2011xx ; Kamenik:2011dk ; Hioki:2012vn ; Hioki:2013hva ; MammenAbraham:2021ssc . The CMS collaboration has imposed the following current bounds on the top quark CMDM and CEDM: and CMS:2018jcg , which where obtained via two opposite sign leptons (, , ) in the final state. Furthermore, the CMS collaboration also set the limits and Sirunyan:2019eyu obtained by the analysis of lepton+jets events in the final state. These bounds were extracted from experimental data by assuming that the top quark CMDM and CEDM are real quantities.
An appropriate approach to study the anomalous couplings and their effects on observable processes in a model-independent way is provided by the effective Lagrangian approach, where a gauge-invariant effective Lagrangian is introduced to parametrize the effects of physics BSM. Such an effective Lagrangian contains the SM Lagrangian plus a tower of effective operators () constructed out of the SM fields
| (1) |
where the coupling constants parametrizes our ignorance of the new physics and is the new physics scale. In particular, non-standard top-gluon interactions arise from a dimension-six operator Arzt:1994gp ; Aguilar-Saavedra:2009ygx , which after electroweak symmetry breaking gives rise to the the following Lagrangian
| (2) |
where are the color generators, are the gluon fields, is the gluon field tensor, whereas and are constant coefficients that parametrizes the anomalous contributions to the coupling arising from new physics. It must be noted however that the above Lagrangian does not yield the most general interaction, which in fact can be written in terms of four independent form factors Nowakowski:2004cv .
The above Lagrangian also describes the interaction between an off-shell gluon and two on-shell quarks Davydychev:2000rt . Since the off-shell CMDM and CEDM of the top quark are complex in general, they will be written as
| (3) | ||||
| (4) |
As far as the SM predictions are concerned, the real and imaginary parts of the off-shell CMDM of the top quark are of the order of Hernandez-Juarez:2020drn , whereas the predictions for the off-shell CEDM are not available yet. Nevertheless, in BSM theories both real and imaginary parts of the off-shell top quark CEDM are of the order of Hernandez-Juarez:2020xon . On the other hand, the effects of the absorptive parts of the CMDM and CEDM at LHC were first studied in Bernreuther:2013aga but to our knowledge, there is no update on such analysis, which we believe is in the order given the current experimental bounds on these observables.
We would like to note that although the off-shell dipole form factors are dependent on the gluon transfer momentum, we will follow the authors of Ref. Bernreuther:2013aga and consider in our analysis below that both the real and absorptive parts of the dipole form factors are constant, which is valid as long as unitarity is not spoiled. This approach has also been used for instance to obtain bounds on the trilinear neutral gauge boson couplings () Baur:1992cd , which due to Bose statistics and angular momentum conservation are non-vanishing only for off-shell . In fact, over a large interval of , the SM contribution to the top quark CMDM shows little variation Hernandez-Juarez:2020drn , and the same is true for both the CMDM and CEDM in some BSM theories (see for instance Hernandez-Juarez:2020xon ; Aranda:2018zis ). Our main goal is to obtain bounds on and using the data for top quark pair production at the LHC run 2, which in turn can be useful to constraint the parameter space of some BSM theories.
Our work is organized as follows. In Sec. 2 we discuss the framework for the study of the CMDM and CEDM absorptive parts. Section 3 we present a novel calculation of the parton cross-sections of production for complex CMDM and CEDM, which to our knowledge has not been reported before. In Sec. 4 a numerical simulation is presented for top quark pair production at the LHC via MadGraph5, where the effective Lagrangian of Eq. (2) was implemented with the help of the FeynRules package. The results for the cross section as a function of the real and imaginary parts of and are then used to obtain bounds on their absorptive parts. The possibility that kinematic distributions could be helpful to disentangle the top quark CMDM and CEDM absorptive parts is examined in Section 5. Finally, in Sec. 6 we present our conclusions.
2 Remarks on the absorptive parts of the CMDM in the SM
In the SM, the CMDM of quarks arises at the one-loop level through the Feynman diagrams of Figs. 1 (QCD contribution) and 2 (electroweak contribution). The off-shell CMDM can develop an absorptive (imaginary) part when the gluon transfer four-momentum crosses the threshold , with the mass of the virtual particles attached to the off-shell gluon. In such region these particles are allowed to be pair produced, which is true for all energies of the external gluon in Feynman diagram (b) of Fig. 1, whereas the threshold is for Feynman diagrams 1(a), 2(a) and 2(c), and in Feynman diagram 2(b). The absorptive contributions to the CMDM can also be extracted by the Cutkosky rules Cutkosky_1960 , which yield the same results obtained via the usual techniques for Feynman diagram calculation Zhou:2004gm . It is also important to emphasize that the the SM contribution to the off-shell dipole moment is finite and gauge independent for arbitrary .
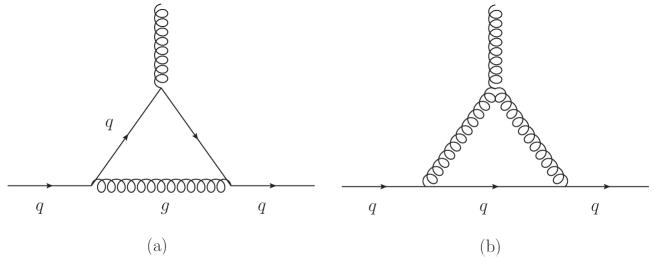
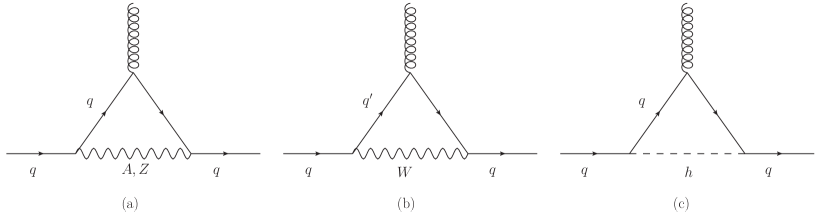
For the top quark CMDM, the contribution from the diagram (b) of Fig. 2 develops an absorptive part at , whereas that from the diagram (b) of Fig. 1 is complex for any value. The remaining contributions become complex at . Moreover, the corresponding contributions to the top quark CEDM would also become complex at the same energy thresholds. It is thus interesting to obtain a bound on the absorptive part of the top quark CMDM and CEDM consistent with the CMS limits. Such a bound can be interpreted as a limit on the new physics effects inducing new contributions to the CMDM and CEDM of the top quark. To assess the order of magnitude of the absorptive part of the CMDM at the LHC energies, we have performed a numerical evaluation of the analytical expressions of Ref. Hernandez-Juarez:2020drn to find the energy interval of the transfer momentum of the gluon where the real part of the top quark CMDM predicted by the SM matches the CMS bounds CMS:2018jcg ; Sirunyan:2019eyu . We obtain that the value reported in Ref Sirunyan:2019eyu corresponds to the 57 GeV 59 GeV interval, where the respective absorptive part value is . As far as the bound reported in Ref. CMS:2018jcg , it is consistent with energies above GeV, in this case, the absorptive part can be one order of magnitude smaller than in the previous one: for values around GeV, , whereas at higher energies the corresponding value is of the order of and remains almost constant as the energy increases.
3 Contributions of CMDM and CEDM to production
Top pair production can receive contributions from the anomalous coupling Haberl:1995ek ; Cheung:1995nt of Eq. (2) but also from the non-SM vertex arising from the non-abelian part of the gluon field strength tensor. The corresponding Feynman rules follow straightforwardly and are shown in Fig. 3. As already mentioned, in a strict sense, the top quark dipole form factors are functions of the gluon transfer momentum , with such functions being model dependent. Furthermore, when working with off-shell green functions one must address the problem of gauge dependence. Along this line, methods such as the pinch technique have been used in the past to remove any gauge-dependent terms by considering additional Feynman diagrams contributing to the physical process under study. However, as argued in Ref. Hernandez-Juarez:2020drn the off-shell CMDM of the top quark is gauge-independent in the SM and the same is true for both the CMDM and CEDM in electroweak extension models. Also, as shown in Refs. Hernandez-Juarez:2020xon ; Aranda:2018zis there is little dependence of the top quark dipole form factors on over a large energy interval in the SM and some BSM theories. We will thus assume that both the real and absorptive parts of the CMDM and CEDM are constant and obtain bounds on the absorptive parts from the data on top quark production at the LHC.


The most recent analyses on top quark production assume that both CMDM and CEDM are purely real CMS:2018jcg ; Sirunyan:2019eyu . In this work, we are interested in the study of the contributions of the absorptive parts of these dipole moments. Therefore we consider that and are complex and calculate the following parton cross-sections:
| (5) |
which apart from the SM contribution receive a new one from the Feynman diagrams of Fig. 4, where the large dot represents the anomalous CMDM and CEDM contributions.






After some algebra we obtain the respective differential cross sections for general complex CMDM and CEDM:
| (6) |
and
| (7) |
where , and are the usual parton Mandelstam variables and we introduced the definitions
| (8) | ||||
| (9) |
In the center of mass frame, the parameter , is related to the angle between the momentum of the outgoing top quark and that of the incoming parton as
| (10) |
with .
For the above cross sections reduce to the known SM results Gluck:1977zm as expected. We also have verified that in the scenario with purely real CMDM and CEDM, Eq. (3) reproduces the result reported in Ref. Haberl:1995ek ; Cheung:1995nt . Nevertheless, in the same scenario we do not find agreement with our result for Eq. (3) and the one previously reported Haberl:1995ek ; Cheung:1995nt , which apparently is incomplete as there is no agreement in the coefficients of and .
4 Bounds on absorptive parts of the CMDM and CEDM of the top quark
We now turn to constrain the absorptive parts and via the LHC data on top quark pair production CMS:2018jcg ; Aad:2020tmz ; Sirunyan:2019eyu . We follow a similar approach to that discussed in Hayreter:2013kba and use a Monte Carlo simulation to obtain the theory predictions for the leading order contribution to the cross section. In order to compute the corresponding contributions from the top quark CMDM and CEDM, we use MadGraph5 Alwall:2014hca , where the anomalous interactions of Eq. (2) were implemented with the help of FeynRules Alloul:2013bka .
We will consider the most recent LHC results for top quark pair production at center-of-mass energy 13 TeV. Therefore we use the ATLAS cross section in the lepton plus jets channel Aad:2020tmz
| (11) |
whereas for the theoretical SM prediction we use Zyla:2020zbs ; Czakon:2008ii
| (12) |
wherein both cases the errors have been added in quadrature. We will assume that the small deviation in from the theoretical leading order SM prediction is due to the real and absorptive parts of the top quark CMDM and CEDM. While 90% (85%) of arises dominantly from the partonic process at TeV (=7 TeV), the contribution of vertex has not been considered in the computation of (12) as it is a non-SM interaction. However, as observed in Eqs. (3) and (3), the dipole moments induce a deviation in . Thus, the top quark CMDM and CEDM may explain slight deviations from the SM prediction to production.
The ratio between the measured and predicted cross sections is
| (13) |
Following Ref. Hayreter:2013kba , we will interpret the error of Eq. (13) as a window to BSM effects in top quark pair production and use it to set constraints on the absorptive parts of and . As already mentioned, in the analysis of the CMS collaboration the CMDM and CEDM of the top quark were assumed to be real quantities. In Ref. CMS:2018jcg all the measurements are analyzed under a linearized approximation of the anomalous couplings Bernreuther:2015yna , which parametrizes the non-SM interactions and include the vertex, though the dipole moments are not interpreted as complex quantities and thus the absorptive parts are not considered in the differential cross section used to study BSM effects. Also, in Ref. Sirunyan:2019eyu the kinematic distribution used to obtain constraints on and were defined via Eqs. (3) and (3), though once again it was assumed that both the top quark CMDM and CEDM are real quantities. Thus, the effects of the absorptive parts have never been studied by the CMS collaboration, however, such consequences has a negligible effect on their analysis as the kinematic distributions measured at the LHC Bernreuther:2015yna ; Baumgart:2012ay are strongly constrained Fabbrichesi:2014wva ; Cao:2015doa . Below we will consider a similar approach to that followed in Refs. Hayreter:2013kba ; Sirunyan:2019eyu to obtain bounds on the absorptive parts of and by reinterpreting the LHC data. We will also show explicitly that the relevant kinematic distributions of production are not sensitive to the imaginary parts of the dipole moments, as already pointed out in Refs. Bernreuther:2013aga ; Bernreuther:2015yna ; Baumgart:2012ay .
To study the absorptive part of the top quark CMDM and CEDM we proceed as follows: We first set and obtain the SM cross section , afterwards we generate the new physics contribution for non-zero , whereas all the remaining parameters are set to zero. This procedure is repeated for each one of the , and parameters. All our event samples for the cross section are generated at 14 TeV.
We show in Fig. 5 the ratio as a function of the real and absorptive parts of the CMDM (left plot) and CEDM (right plot), where the MadGraph5 estimated error is included. We plot the best fit curves.

To fit the data of Fig. 5, we have not considered the interference terms of the real and absorptive parts of and . Such an approach has been used in the past to study the implications of the top quark CMDM and CEDM in production Hayreter:2013kba ; Malekhosseini:2018fgp ; Englert:2014oea . Thus, from Eqs. (3) and (3) we observe that the ratio is a fourth-order polynomial of the real and imaginary parts of and , though there are only even powers of the absorptive parts. The expression obtained from the fit of Fig. 5 reads
| (14) |
We observe that the contributions of , and are of the same order and similar size, which is actually in accordance with Eq. (3). Moreover, shows a similar dependence on the absorptive parts and , which makes it possible to obtain bounds on and following Refs. Hayreter:2013kba ; Sirunyan:2019eyu , where limits on the real part of are obtained using Eqs. (3), (3) and (4). We also note that the leading contribution to arises from the linear term of as the other dipole terms contribute quadratically at the lowest order and are thus more suppressed. The values predicted for the off-shell top quark CMDM are of the order of in the SM Hernandez-Juarez:2020drn , whereas the typical values predicted for the CEDM in some BSM theories are of the order of Hernandez-Juarez:2020xon . Thus. the effects of the top quark dipole moments would hardly induce a significant deviation to the top quark production cross section.
To analyze the effects of the absorptive parts of the top quark dipole moments we will proceed as follows. We fix the corresponding real parts using the CMS limits CMS:2018jcg ; Sirunyan:2019eyu , which allow us to constrain the absorptive parts and via Eqs. (4) and (13), with the error being attributed to the anomalous contributions. In other words, we fix and to their current constraints and find the allowed area of and values. With this aim we assume the following three scenarios:
-
•
Scenario I: we use the lower bounds and reported in CMS:2018jcg .
-
•
Scenario II: we use the upper bounds and reported in CMS:2018jcg .
-
•
Scenario III: we use the value and the upper bound reported in Sirunyan:2019eyu .
We do not consider the scenario where is set to its lower (negative) bound Sirunyan:2019eyu as it yields similar bounds to those obtained in scenario III as is an even function of . A similar situation arises for other possible scenarios, which yield bounds of a similar order of magnitude.
The allowed areas in the plane at the 95% C.L. are the concentric ellipses shown in Fig. 6 for the three scenarios discussed above. The corresponding bounds are: and in scenario I (blue solid lines); and in scenario III (green dot-dashed lines); and and in scenario II (orange dashed line). The latter scenario yields the intersected area allowed by the three scenarios, which means that the corresponding bounds are consistent with both CMS limits. Note that in both cases the bounds on the absorptive parts of and are quite similar, of the order of at the 95% C.L.
For completeness, we revisit the case where the gluon transfer four-momentum () dependence is considered for , which is possible using the expressions for reported in Ref. Hernandez-Juarez:2020drn . The real part of the CEDM is set as since there are not any analytic results for . In Fig. 7, the allowed areas in the plane at the 95% C.L. for three different energies of are shown. We note that at low energies ( GeV) the bounds are slightly larger than scenario III but they are still of the same order, whereas from the limits are similar to those found in Fig. 6. Thus, the bounds obtained by taking the real parts as constants are compatible with those where their dependence on is considered. Especially, for energies above the boson mass both constraints are almost identical.
It is worth comparing our limits with the theoretical predictions of the SM and some BSM theories. In particular, for a transfer momentum in the interval 30 GeV 1000 GeV, the SM prediction for the absorptive part of can be as large as Hernandez-Juarez:2020drn , which is close to our bounds. On the other hand, several BSM theories predict values for the absorptive part of of the order of , which is far away from our bound.
We have also made the same analysis but including the interference terms of Eq. (3). Nonetheless, the obtained fit is still consistent with Eq. (4) and the bounds are similar to those of Fig. 6. Thus, the interference terms can be neglected as their contribution is not relevant.


5 Kinematic distributions
The effects of and on top quark pair production have been analyzed in the past as some kinematic distributions can be sensitive to such parameters Atwood:1994vm ; Cheung:1995nt ; Franzosi:2015osa ; Barducci:2017ddn . On the other hand, to our knowledge the possible effects of the absorptive parts and have only been explored in Ref. Bernreuther:2013aga through the longitudinal and polarizations. Therefore, for completeness we will examine the possibility that the differential cross sections for top quark pair production could be sensitive to the absorptive parts of the top quark CMDM and CEDM, such implications are supposed to be unobservable Bernreuther:2015yna ; Baumgart:2012ay , nonetheless it has been never shown explicitly. To this end, we use the CMS constraints on the real parts of the top quark dipole form factors ( and ) and analyze any possible deviation in the kinematic distributions of top quark production when both dipole moments develop an absorptive part. We consider the following three cases for and :
-
i)
.
-
ii)
.
-
iii)
and .
We consider such values as they are consistent with the SM prediction for the CMDM and the constraints of Sec. 4. Scenarios i) and ii) allow us to explore the possibility that the kinematic distributions can be sensitive to small changes in the absorptive terms, whereas scenario iii) allows us to test the effect of a flip of sign. For the graphical analysis, we use MADANALYSIS 5 Conte:2012fm .
In Figs. 8 and 8 we show the kinematic distributions of the invariant mass and the top quark transverse momentum in the scenarios discussed above. It is observed that there is no considerable distinction between the kinematic distributions obtained in the general case with complex top quark dipole form factors and those obtained in the scenario in which they are purely real. This was also observed in the case where the contributions of the real part of the top quark dipole moments are compared with the SM leading order contribution Degrande:2010kt ; Barducci:2017ddn . A similar situation occurs for the kinematic distribution of the rapidity , which is shown in Fig. 8.


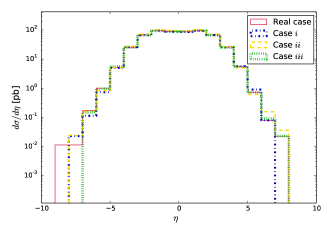
We have also examined the sensitivity of the forward-backward (FB) asymmetry to the CMDM and CEDM in top quark pair production at the LHC, which is possible at the leading order in some models Dorsner:2009mq ; Degrande:2010kt , whereas in the SM there is only a significant deviation up to next-to-leading order Dorsner:2009mq . Unfortunately, Eqs. (3) and (3) cannot be expressed as a linear combination of via Eq. (10). Thus, a deviation to the FB asymmetry at the leading order is not possible Frampton:2009rk . However, other asymmetries could be sensitive to the CMDM and CEDM of the top quark, as shown in Ref. Bernreuther:2013aga ; Hayreter:2013kba . In summary, all the kinematic distributions studied here show no significant deviation from leading order contribution to top quark pair production arising from the real and absorptive parts of the top quark dipole form factors.
6 Conclusions
The off-shell CMDM and CEDM of quarks have become a topic of interest recently Hernandez-Juarez:2020drn ; Aranda:2020tox . However, the study of their absorptive (imaginary) parts remains almost unexplored. In this work, we have obtained bounds on the new physics contributions to the absorptive parts of the off-shell top quark CMDM and CEDM via the experimental data of top quark pair production at the LHC, which to our knowledge are the first limits of this kind. We present explicit expressions for the corresponding differential parton cross-sections considering complex CMDM and CEDM, which have also been calculated for the first time. We point out that there is a disagreement between our result for the differential cross section and the expression previously reported in the scenario where only the real part of the top quark dipole form factors are considered Haberl:1995ek ; Cheung:1995nt . Our bounds for the absorptive parts were obtained using the most recent data for the top quark CMDM and CEDM reported by the CMS collaboration CMS:2018jcg ; Sirunyan:2019eyu . It was found that the upper bound on the absorptive parts of both dipole moments are of order . In particular, values of order are consistent with all the CMS results. We also note that our bound on is consistent with the SM prediction for the absorptive part of , which is of order Hernandez-Juarez:2020drn ; Aranda:2020tox . On the other hand, in some BSM theories the absorptive part of the CEDM is of the order of Hernandez-Juarez:2020xon , which seems well beyond the experimental reach. Our limits could be useful to constrain the parameter space of BSM theories and are consistent with the case where the gluon transfer four-momentum () dependence is considered for the real part of the top quark CMDM.
We also explored the possibility that several kinematic distributions for top quark pair production at the LHC can be sensitive to the absorptive parts of the CMDM and CEDM, but we find that there are no significant deviation from the scenario where the CMDM and CEDM are purely real. In fact, even in the case of real CMDM and CEDM, there is no significant deviation from the leading order SM contribution as discussed previously Degrande:2010kt ; Barducci:2017ddn .
7 acknowledgements
We acknowledge support from Consejo Nacional de Ciencia y Tecnología and Sistema Nacional de Investigadores. Partial support from Vicerrectoría de Investigación y Estudios de Posgrado de la Benémerita Universidad Autónoma de Puebla is also acknowledged. We also thank to M. A. Arroyo-Ureña for discussions to implement our model in MadGraph5.
Data Availability Statement
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
- [1] A. I. Hernández-Juárez, A. Moyotl, and G. Tavares-Velasco. New estimate of the chromomagnetic dipole moment of quarks in the standard model. Eur. Phys. J. Plus, 136(2):262, 2021.
- [2] J. I. Aranda, T. Cisneros-Pérez, J. Montaño, B. Quezadas-Vivian, F. Ramírez-Zavaleta, and E. S. Tututi. Revisiting the top quark chromomagnetic dipole moment in the SM. Eur. Phys. J. Plus, 136(2):164, 2021.
- [3] R. Martinez, M. A. Perez, and N. Poveda. Chromomagnetic Dipole Moment of the Top Quark Revisited. Eur. Phys. J. C, 53:221–230, 2008.
- [4] R. Gaitan, E.A. Garces, J. H. Montes de Oca, and R. Martinez. Top quark Chromoelectric and Chromomagnetic Dipole Moments in a Two Higgs Doublet Model with CP violation. Phys. Rev. D, 92(9):094025, 2015.
- [5] A.I. Hernández-Juárez, A. Moyotl, and G. Tavares-Velasco. Chromomagnetic and chromoelectric dipole moments of the top quark in the fourth-generation THDM. Phys. Rev. D, 98(3):035040, 2018.
- [6] A. I. Hernández-Juárez, A. Moyotl, and G. Tavares-Velasco. Chromomagnetic and chromoelectric dipole moments of quarks in the reduced 331 model. Chinese Physics C, 12 2021.
- [7] J.I. Aranda, D. Espinosa-Gómez, J. Montaño, B. Quezadas-Vivian, F. Ramírez-Zavaleta, and E.S. Tututi. Flavor violation in chromo- and electromagnetic dipole moments induced by Z’ gauge bosons and a brief revisit of the Standard Model. Phys. Rev. D, 98(11):116003, 2018.
- [8] Andrzej Czarnecki and Bernd Krause. Neutron electric dipole moment in the standard model: Valence quark contributions. Phys. Rev. Lett., 78:4339–4342, 1997.
- [9] D. Atwood, A. Kagan, and T.G. Rizzo. Constraining anomalous top quark couplings at the Tevatron. Phys. Rev. D, 52:6264–6270, 1995.
- [10] Elizabeth H. Simmons and Peter L. Cho. Anomalous gluon self-interactions and production. AIP Conf. Proc., 350:323–334, 1995.
- [11] P. Haberl, O. Nachtmann, and A. Wilch. Top production in hadron hadron collisions and anomalous top - gluon couplings. Phys. Rev. D, 53:4875–4885, 1996.
- [12] King-man Cheung. Probing the chromoelectric and chromomagnetic dipole moments of the top quark at hadronic colliders. Phys. Rev. D, 53:3604–3615, 1996.
- [13] S. Y. Choi, C. S. Kim, and Jake Lee. odd gluon - top quark effective couplings at the CERN large hadron collider. Phys. Lett. B, 415:67–74, 1997.
- [14] Ken-ichi Hikasa, K. Whisnant, Jin Min Yang, and Bing-Lin Young. Probing anomalous top quark interactions at the Fermilab Tevatron collider. Phys. Rev. D, 58:114003, 1998.
- [15] M. Czakon and A. Mitov. Inclusive Heavy Flavor Hadroproduction in NLO QCD: The Exact Analytic Result. Nucl. Phys. B, 824:111–135, 2010.
- [16] Oleg Antipin and G. Valencia. T-odd correlations from CP violating anomalous top-quark couplings revisited. Phys. Rev. D, 79:013013, 2009.
- [17] Sudhir Kumar Gupta and G. Valencia. CP-odd correlations using jet momenta from events at the Tevatron. Phys. Rev. D, 81:034013, 2010.
- [18] Cen Zhang and Scott Willenbrock. Effective-Field-Theory Approach to Top-Quark Production and Decay. Phys. Rev. D, 83:034006, 2011.
- [19] Celine Degrande, Jean-Marc Gerard, Christophe Grojean, Fabio Maltoni, and Geraldine Servant. Non-resonant New Physics in Top Pair Production at Hadron Colliders. JHEP, 03:125, 2011.
- [20] Matthew Baumgart and Brock Tweedie. A New Twist on Top Quark Spin Correlations. JHEP, 03:117, 2013.
- [21] Christoph Englert, Ayres Freitas, Michael Spira, and Peter M. Zerwas. Constraining the Intrinsic Structure of Top-Quarks. Phys. Lett. B, 721:261–268, 2013.
- [22] Alper Hayreter and German Valencia. Constraints on anomalous color dipole operators from Higgs boson production at the LHC. Phys. Rev. D, 88:034033, 2013.
- [23] Werner Bernreuther and Zong-Guo Si. Top quark spin correlations and polarization at the LHC: standard model predictions and effects of anomalous top chromo moments. Phys. Lett. B, 725:115–122, 2013. [Erratum: Phys.Lett.B 744, 413–413 (2015)].
- [24] M. Fabbrichesi, M. Pinamonti, and A. Tonero. Limits on anomalous top quark gauge couplings from Tevatron and LHC data. Eur. Phys. J. C, 74(12):3193, 2014.
- [25] Juan A. Aguilar-Saavedra, Benjamin Fuks, and Michelangelo L. Mangano. Pinning down top dipole moments with ultra-boosted tops. Phys. Rev. D, 91:094021, 2015.
- [26] Werner Bernreuther, Dennis Heisler, and Zong-Guo Si. A set of top quark spin correlation and polarization observables for the LHC: Standard Model predictions and new physics contributions. JHEP, 12:026, 2015.
- [27] Qing-Hong Cao, Bin Yan, Jiang-Hao Yu, and Chen Zhang. A General Analysis of Wtb anomalous Couplings. Chin. Phys. C, 41(6):063101, 2017.
- [28] D. Barducci, M. Fabbrichesi, and A. Tonero. Constraints on top quark nonstandard interactions from Higgs and production cross sections. Phys. Rev. D, 96(7):075022, 2017.
- [29] Malihe Malekhosseini, Mehrdad Ghominejad, Hamzeh Khanpour, and Mojtaba Mohammadi Najafabadi. Constraining top quark flavor violation and dipole moments through three and four-top quark productions at the LHC. Phys. Rev. D, 98(9):095001, 2018.
- [30] Christoph Englert, Dorival Goncalves, and Michael Spannowsky. Nonstandard top substructure. Phys. Rev. D, 89(7):074038, 2014.
- [31] Diogo Buarque Franzosi and Cen Zhang. Probing the top-quark chromomagnetic dipole moment at next-to-leading order in QCD. Phys. Rev. D, 91(11):114010, 2015.
- [32] D. Barducci et al. Interpreting top-quark LHC measurements in the standard-model effective field theory. 2 2018.
- [33] Gordon L. Kane, G. A. Ladinsky, and C. P. Yuan. Using the Top Quark for Testing Standard Model Polarization and CP Predictions. Phys. Rev. D, 45:124–141, 1992.
- [34] D. Atwood, A. Aeppli, and A. Soni. Extracting anomalous gluon - top effective couplings at the supercolliders. Phys. Rev. Lett., 69:2754–2757, 1992.
- [35] B. Grzadkowski, B. Lampe, and K. J. Abraham. CP violation, top quarks and the Tevatron upgrade. Phys. Lett. B, 415:193–199, 1997.
- [36] Bodo Lampe. New interactions in top quark production and decay at the Tevatron upgrade. Phys. Lett. B, 415:63–66, 1997.
- [37] Jin Min Yang and Bing-Lin Young. Dimension-six CP violating operators of the third family quarks and their effects at colliders. Phys. Rev. D, 56:5907–5918, 1997.
- [38] S. Tsuno, I. Nakano, Y. Sumino, and R. Tanaka. Search for anomalous couplings in top decay at hadron colliders. Phys. Rev. D, 73:054011, 2006.
- [39] Zenro Hioki and Kazumasa Ohkuma. Search for anomalous top-gluon couplings at LHC revisited. Eur. Phys. J. C, 65:127–135, 2010.
- [40] Sudhir Kumar Gupta, Alaettin Serhan Mete, and G. Valencia. CP violating anomalous top-quark couplings at the LHC. Phys. Rev. D, 80:034013, 2009.
- [41] Zenro Hioki and Kazumasa Ohkuma. Addendum to: Search for anomalous top-gluon couplings at LHC revisited. Eur. Phys. J. C, 71:1535, 2011.
- [42] Zenro HIOKI and Kazumasa OHKUMA. Exploring anomalous top interactions via the final lepton in productions/decays at hadron colliders. Phys. Rev. D, 83:114045, 2011.
- [43] Jernej F. Kamenik, Michele Papucci, and Andreas Weiler. Constraining the dipole moments of the top quark. Phys. Rev. D, 85:071501, 2012. [Erratum: Phys.Rev.D 88, 039903 (2013)].
- [44] Zenro Hioki and Kazumasa Ohkuma. Optimal-observable Analysis of Possible Non-standard Top-quark Couplings in . Phys. Lett. B, 716:310–315, 2012.
- [45] Zenrō Hioki and Kazumasa Ohkuma. Latest constraint on nonstandard top-gluon couplings at hadron colliders and its future prospect. Phys. Rev. D, 88:017503, 2013.
- [46] Roshan Mammen Abraham, Dorival Gonçalves, Tao Han, Sze Ching Iris Leung, and Han Qin. Directly probing the Higgs-top coupling at high scales. Phys. Lett. B, 825:136839, 2022.
- [47] Albert M Sirunyan et al. Measurement of the top quark polarization and spin correlations using dilepton final states in proton-proton collisions at 13 TeV. Phys. Rev. D, 100(7):072002, 2019.
- [48] Albert M Sirunyan et al. Measurement of the top quark forward-backward production asymmetry and the anomalous chromoelectric and chromomagnetic moments in pp collisions at = 13 TeV. JHEP, 06:146, 2020.
- [49] C. Arzt, M. B. Einhorn, and J. Wudka. Patterns of deviation from the standard model. Nucl. Phys. B, 433:41–66, 1995.
- [50] J. A. Aguilar-Saavedra. A Minimal set of top-Higgs anomalous couplings. Nucl. Phys. B, 821:215–227, 2009.
- [51] Marek Nowakowski, E.A. Paschos, and J.M. Rodriguez. All electromagnetic form-factors. Eur. J. Phys., 26:545–560, 2005.
- [52] Andrei I. Davydychev, P. Osland, and L. Saks. Quark gluon vertex in arbitrary gauge and dimension. Phys. Rev. D, 63:014022, 2001.
- [53] U. Baur and Edmond L. Berger. Probing the weak boson sector in production at hadron colliders. Phys. Rev. D, 47:4889–4904, 1993.
- [54] R. E. Cutkosky. Singularities and discontinuities of feynman amplitudes. Journal of Mathematical Physics, 1(5):429–433, sep 1960.
- [55] Yong Zhou. Imaginary part of Feynman amplitude, cutting rules and optical theorem. 12 2004.
- [56] M. Gluck, J. F. Owens, and E. Reya. Gluon Contribution to Hadronic J/psi Production. Phys. Rev. D, 17:2324, 1978.
- [57] Georges Aad et al. Measurement of the production cross-section in the lepton+jets channel at TeV with the ATLAS experiment. Phys. Lett. B, 810:135797, 2020.
- [58] J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer, H. S. Shao, T. Stelzer, P. Torrielli, and M. Zaro. The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP, 07:079, 2014.
- [59] Adam Alloul, Neil D. Christensen, Céline Degrande, Claude Duhr, and Benjamin Fuks. FeynRules 2.0 - A complete toolbox for tree-level phenomenology. Comput. Phys. Commun., 185:2250–2300, 2014.
- [60] P. A. Zyla et al. Review of Particle Physics. PTEP, 2020(8):083C01, 2020.
- [61] Eric Conte, Benjamin Fuks, and Guillaume Serret. MadAnalysis 5, A User-Friendly Framework for Collider Phenomenology. Comput. Phys. Commun., 184:222–256, 2013.
- [62] Ilja Dorsner, Svjetlana Fajfer, Jernej F. Kamenik, and Nejc Kosnik. Light colored scalars from grand unification and the forward-backward asymmetry in t t-bar production. Phys. Rev. D, 81:055009, 2010.
- [63] Paul H. Frampton, Jing Shu, and Kai Wang. Axigluon as Possible Explanation for p anti-p — t anti-t Forward-Backward Asymmetry. Phys. Lett. B, 683:294–297, 2010.