Bipartite Leggett-Garg and macroscopic Bell inequality violations using cat states: distinguishing weak and deterministic macroscopic realism

The Leggett-Garg inequalities were derived for the situation where one considers succcessive measurements on a single system, at times $t_{i}$. Here, following macro-bell-lg ; weak-hybrid and different to the original treatment legggarg-1 , we consider two systems $A$ and $B$ (Figure 2). Measurements $\hat{M_{i}}^{(A)}$ and $\hat{M}_{j}^{(B)}$ are made on systems $A$ and $B$ at times $t_{i}$ and $t_{j}$ respectively. The measurements give two outcomes, $+1$ and $-1$, corresponding to two macroscopically distinguishable states. However, here there is no choice of measurement setting at a given time: Rather, the unitary rotation stage $U_{A}$ (or $U_{B}$) of the measurement is considered to be part of the dynamics. In the examples we consider in this paper, the measurements $\hat{M_{i}}^{(A)}$ and $\hat{M}_{j}^{(B)}$ that occur at the times $t_{i}$ and $t_{j}$ are analogous to the pointer measurements, $\hat{M}^{(A)}$ and $\hat{M}^{(B)}$, of Figure 1.

The Leggett-Garg inequalities are derived based on the assumption of macroscopic realism legggarg-1 . Hence one may identify specific macroscopic hidden variables $\lambda_{i}^{(A)}$ and $\lambda_{i}^{(B)}$ to describe the states immediately prior to the pointer measurements $\hat{M_{i}^{(A)}}$ and $\hat{M}_{j}^{(B)}$. Different to the Bell derivation of Section II.A.1 however, one does not ascribe to the system simultaneously at a time $t_{i}$ predetermined results $\lambda_{i}^{(A)}$ and $\lambda_{j}^{(A)}$ for both future measurements, $\hat{M}_{i}^{(A)}$ and $\hat{M}_{j}^{(A)}$. What was the local unitary interaction ($U_{A}$ or $U_{B}$) with the measurement device in the Bell test is now the local trajectory. One therefore assumes macroscopic realism for a measurement with just a single setting, at the time $t_{i}$. This means that the Leggett-Garg-Bell inequalities for the systems of interest may be derived based on the assumption of weak macroscopic realism (wMR): that for a system $A$ prepared in a superposition of macroscopically distinct pointer states, the system can be described by a single hidden variable $\lambda_{i}$ at that time $t_{i}$ (and this is not affected by a space-like separated measurement event at the different site $B$).

The traditional Leggett-Garg test invokes a second assumption, that it is in principle possible to determine which of the two macrosopically distinct states the system is in at any given time, by performing a noninvasive measurement that has a negligible effect on the subsequent dynamics legggarg-1 . This assumption is necessary because the traditional Leggett-Garg tests involve measurements at different times performed on the same system, and there is the possibility of direct disturbance of the system due to measurement. In this paper, we follow macro-bell-lg , and consider two systems (Figure 2). One assumes validity of (weak) macroscopic realism, but the additional assumption of noninvasive measureability is replaced by the assumption of locality. Specifically, for measurements at $A$ and $B$ that are spacelike separated events, one assumes the hidden variable value $\lambda_{i}^{(A)}$ is not changed by whether the measurement at $B$ takes place or not, and similarly for $\lambda_{j}^{(B)}$.

We consider measurements made at times $t_{1}$ and $t_{3}$ at site $A$, and at times $t_{2}$ and $t_{4}$ at site $B$, where $t_{1}<t_{2}<t_{3}<t_{4}$. Let us denote the spin outcome $S_{A}$ at $A$ for the measurement made at time $t_{i}$ by $S_{i}^{(A)}$. The spin $S_{j}^{(B)}$ is defined similarly, for site $B$. With the assumptions of macroscopic realism and noninvasive measurability (locality), the Leggett-Garg-Bell inequality

	$\displaystyle-2$	$\displaystyle\leq$	$\displaystyle E(t_{1},t_{2})-E(t_{1},t_{4})+E(t_{2},t_{3})+E(t_{3},t_{4})\leq 2$
					(3)

where $E(t_{i},t_{j})=\langle S_{i}^{(A)}S_{j}^{(B)}\rangle$ can be shown to hold legggarg-1 . This inequality was derived as a Leggett-Garg inequality in Ref. legggarg-1 , and as a Leggett-Garg-Bell inequality, in Refs. macro-bell-lg ; weak-hybrid . Since the expectation values $E(t_{i},t_{j})$ of the inequality involve measurements made at diffferent sites, the inequality follows based on the assumption of locality, which justifies that $E(t_{i},t_{j})=\langle S_{i}^{(A)}S_{j}^{(B)}\rangle=\langle\lambda_{i}^{(A)}\lambda_{j}^{(B)}\rangle$. We note that while we assume the time order $t_{1}<t_{2}<t_{3}<t_{4}$, in fact because we have two localised sites, we need only take $t_{1}<t_{3}$ and $t_{2}<t_{4}$.

A three-time Leggett-Garg-Bell inequality

$\displaystyle-3$

$\displaystyle\leq$

$\displaystyle E(t_{1},t_{2})-E(t_{1},t_{3})+E(t_{2},t_{3})\leq 1,$

(4)

where $E(t_{i},t_{j})=\langle S_{i}^{(B)}S_{j}^{(A)}\rangle$ is also useful. This is based on the original three-time Leggett-Garg inequality, derived for the single-system set-up, in Refs. weak-solid-state-qubits ; jordan_kickedqndlg2-1 . Here, one assumes however that a measurement at time $t_{1}$ at site $A$ does not affect the outcome at the later time $t_{3}$ at the same site, which raises the issue of a disturbance due to the measurement at $t_{1}$. However, for correlated initial states, one may use that the result for $S_{1}^{(B)}$ can be inferred from a measurement of $S_{1}^{(A)}$. Thus, assuming locality, one may deduce macro-bell-lg :

$$E(t_{1},t_{3})=\langle S_{1}^{(A)}S_{3}^{(A)}\rangle=-\langle S_{1}^{(B)}S_{3}^{(A)}\rangle$$

(5)

We note that the no-signalling-in-time (NSIT) equality has been shown to give a stronger test of Leggett-Garg’s macrorealism NSTmunro-1 ; nst . However, it is more challenging to use this equality for a bipartite test.

Since we are to show violation of the macroscopic Bell and Leggett-Garg-Bell inequalities, it is important to summarise what is the weakest (i.e. minimal) assumption needed to derive the inequalities. The Bell inequalities (2) can be derived from the minimal assumption of macroscopic local causality (MLC), as in Section 1.A.2. In this paper, however, we use the terms macroscopic local realism (MLR) and macroscopic local causality (MLC) interchangeably. The Leggett-Garg-Bell inequalities (3) and (4) on the other hand are derived assuming weak macroscopic realism, combined with macroscopic noninvasiveness (NIM) of the measurement, which for two sites is justified by macroscopic locality (ML).

At locations $A$ and $B$, we assume local unitary transformations $U_{A}(t_{a})$ and $U_{B}(t_{b})$ take place, as in Figure 1. States $|\pm\rangle_{a}$ and $|\pm\rangle_{b}$ are transformed after a time $t_{a}$ and $t_{b}$ according to (at site $A$)

	$\displaystyle U_{A}(t{}_{a})|+\rangle_{a}$	$\displaystyle=$	$\displaystyle a|+\rangle_{a}+i\sqrt{1-a^{2}}|-\rangle_{a}$
	$\displaystyle U_{A}(t{}_{a})|-\rangle_{a}$	$\displaystyle=$	$\displaystyle a|-\rangle_{a}+i\sqrt{1-a^{2}}|+\rangle_{a}$		(8)

and (at site $B$)

	$\displaystyle U_{B}(t{}_{b})|+\rangle_{b}$	$\displaystyle=$	$\displaystyle b|+\rangle_{b}+i\sqrt{1-b^{2}}|-\rangle_{b}$
	$\displaystyle U_{B}(t{}_{b})|-\rangle_{b}$	$\displaystyle=$	$\displaystyle b|-\rangle_{b}+i\sqrt{1-b^{2}}|+\rangle_{b}$		(9)

For a system prepared in the superposition $|\psi_{Bell}\rangle$ of eqn. (7), the system will evolve into the final state

	$\displaystyle|\psi_{f}\rangle$	$\displaystyle=\frac{1}{\sqrt{2}}(U_{A}|+\rangle_{a}U_{B}|-\rangle_{b}-U_{A}|-\rangle_{a}U_{B}|+\rangle_{b})$
		$\displaystyle=\frac{1}{\sqrt{2}}\{(ab+\bar{a}\bar{b})(|+\rangle_{a}|-\rangle_{b}-|-\rangle_{a}|+\rangle_{b})$
		$\displaystyle\thinspace\thinspace{\color[rgb]{0,0,1}{\normalcolor+}}i(\bar{a}b-a\bar{b})(|+\rangle_{a}|+\rangle_{b}-|-\rangle_{a}|-\rangle_{b})\}$		(10)

where we have abbreviated $\bar{a}=\sqrt{1-a^{2}}$ and $\bar{b}=\sqrt{1-b^{2}}.$ Using that the states $|\pm\rangle$ are orthogonal, and defining the measurement $\hat{S}$ which measures the sign $S$ (which we label as its “spin”), according to $\hat{S}^{(A)}|\pm\rangle_{a}=\pm|\pm\rangle_{a}$ and $\hat{S}^{(B)}|\pm\rangle_{b}=\pm|\pm\rangle_{b}$, we find that the expectation value $E(t_{a},t_{b})$ of the spin product $\hat{S}^{(A)}\hat{S}^{(B)}$ is

$$E(t_{a},t_{b})=|\bar{a}b-a\bar{b}|^{2}-|ab+\bar{a}\bar{b}|^{2}$$

(11)

For the traditional Bell experiment where the transformation is achieved using a polarising beam splitter, we have $a=\cos\theta$ and $b=\cos\phi$, and

$$E(\theta,\phi)=-\cos 2(\theta-\phi)$$

(12)

It is known that the choice of angles $\theta=0$, $\phi=\pi/8$, $\theta^{\prime}=\pi/4$ and $\phi^{\prime}=3\pi/8$ in the Bell inequality (1) will lead to $B=-2\sqrt{2}$ which violates the inequality.

Now we consider how to realise the transformations (8) and (9). We seek a unitary transformation $U_{\theta}^{(A)}\equiv U_{A}(\theta)$ such that at site $A$ the transformation

	$\displaystyle U_{A}(\theta)|\alpha\rangle$	$\displaystyle=$	$\displaystyle\cos\theta|\alpha\rangle+i\sin\theta|-\alpha\rangle$
	$\displaystyle U_{A}(\theta)|-\alpha\rangle$	$\displaystyle=$	$\displaystyle\cos\theta|-\alpha\rangle+i\sin\theta|\alpha\rangle$		(13)

holds, for the particular angle choices $\theta=0$ and $\theta=\pi/4$. At site $B$, we seek a transformation such that

	$\displaystyle U_{B}(\phi)|\beta\rangle$	$\displaystyle=$	$\displaystyle\cos\phi|\beta\rangle+i\sin\phi|-\beta\rangle$
	$\displaystyle U_{B}(\phi)|-\beta\rangle$	$\displaystyle=$	$\displaystyle\cos\phi|-\beta\rangle+i\sin\phi|\beta\rangle$		(14)

for the angle choices $\phi=\pi/8$, and $\phi=3\pi/8$. We drop subscripts $a$ and $b$, where the meaning is clear.

These transformations can be achieved by interacting each single mode system with a nonlinear medium at the given site, where the interaction Hamiltonian is $H_{NL}=\Omega\hat{n}^{k}$ ($k>2$ and $k$ even) manushan-cat-lg ; yurke-stoler-1 ; wrigth-walls-gar-1 ; macro-bell-lg . Here $\hat{n}$ is the mode number operator and $\Omega$ is the nonlinear coefficient. We choose units such that $\hbar=1$. The interaction takes place independently for each mode $a$ and $b$, and we denote the respective Hamiltonians as $H_{NL}^{(A)}$ and $H_{NL}^{(B)}$. Thus we define local interactions at each site

$$H_{NL}^{(A)}=\Omega\hat{n}_{a}^{k},\ \ H_{Nl}^{(B)}=\Omega\hat{n}_{b}^{k}$$

(15)

The boson destruction mode operators for modes $a$ and $b$ are denoted by $\hat{a}$ and $\hat{b}$, respectively, and the number operators are $\hat{n}_{a}=\hat{a}^{\dagger}\hat{a}$ and $\hat{n}_{b}=\hat{b}^{\dagger}\hat{b}$.

One may solve for the dynamics given by $H_{NL}$. If the system $A$ is prepared in a coherent state $|\alpha\rangle_{a}$, the state after time $t$ is yurke-stoler-1

	$\displaystyle\left|\alpha,t_{a}\right\rangle$	$\displaystyle=$	$\displaystyle U_{A}(t_{a})|\alpha\rangle_{a}$		(16)
		$\displaystyle=$	$\displaystyle\exp[-\frac{\left|\alpha\right|^{2}}{2}]\underset{n=0}{\sum^{\infty}}\frac{\alpha^{n}\exp(-i\phi_{n})}{\sqrt{n!}}\left|n\right\rangle_{a}$

where $U_{A}(t_{a})=e^{-iH_{NL}^{(A)}t_{a}/\hbar}$ and $\phi_{n}=\varOmega t_{a}n^{k}$. For an initial coherent state $|\beta\rangle_{b}$ at $B$, the state after a time $t$ is given similarly, as $\left|\beta,t_{b}\right\rangle=U_{B}(t_{b})|\beta\rangle_{b}$ where $U_{B}(t_{b})=e^{-iH_{NL}^{(B)}t_{b}/\hbar}$. These solutions are well known manushan-cat-lg ; yurke-stoler-1 and are depicted graphically in Figures 3 and 4 in terms of the $Q$ function, defined as $Q(x_{A},p_{A})=\frac{1}{\pi}\langle\alpha_{0}|\rho|\alpha_{0}\rangle$ Husimi-Q-1 . Here $\alpha_{0}=x_{A}+ip_{A}$ and $|\alpha_{0}\rangle$ is a coherent state. At certain intervals of time, the system evolves into a superposition of the macroscopically distinct coherent states $|-\alpha\rangle$ and $|\alpha\rangle$ (Figure 4).

Suppose at time $t_{a}=t_{b}=0$, the systems are in the initial states $|\alpha\rangle$ and $|\beta\rangle$. After a time $t_{b}=\pi/4\Omega$, the system at $B$ is in the state $U_{B}(\pi/4\Omega)|\beta\rangle$ (second picture of Figure 3). This gives the transformation of eq. (14) with $\phi=\pi/8$ manushan-cat-lg . We write the state at this time as

$\displaystyle U_{\pi/8}^{(B)}|\beta\rangle$

$\displaystyle=$

$\displaystyle e^{-i\pi/8}\{(\cos\pi/8|\beta\rangle+i\sin\pi/8|-\beta\rangle\}$

After a time $t_{a}=\pi/2\Omega$, the state is $U_{A}(\pi/2\Omega)|\alpha\rangle$ which corresponds to the transformation eq. (13) with $\theta=\pi/4$. We write the state at $t_{a}=\pi/2\Omega$ as manushan-cat-lg

$\displaystyle U_{\pi/4}^{(A)}|\alpha\rangle$

$\displaystyle=$

$\displaystyle\frac{e^{-i\pi/4}}{\sqrt{2}}\{|\alpha\rangle+e^{i\pi/2}|-\alpha\rangle\}$

(18)

To obtain the transformation (14) with $\phi=3\pi/8$, we consider the state at time $t_{b}=3\pi/4\Omega$ manushan-cat-lg , which is given by $U_{B}(3\pi/4\Omega)|\beta\rangle$. The state at the time $t_{b}=3\pi/4\Omega$ is

$\displaystyle U_{3\pi/8}^{(B)}|\beta\rangle$

$\displaystyle=$

$\displaystyle e^{i\pi/8}\{(\cos 3\pi/8|\beta\rangle+i\sin 3\pi/8|-\beta\rangle\}$

These transformations are shown graphically in Figure 3. The transformations at each site $A$ and $B$ are summarised as

$$U_{A}(t_{a})=e^{-iH_{NL}^{(A)}t_{a}/\hbar},\ \ U_{B}(t_{b})=e^{-iH_{NL}^{(B)}t_{b}/\hbar}$$

(20)

where $t_{a}=0$, $t_{b}=\pi/4\Omega$, $t^{\prime}_{a}=\pi/2\Omega$ and $t_{b}^{\prime}=3\pi/4\Omega$. Noting from above, $U_{B}(\pi/4\Omega)=U_{\pi/8}^{(B)}$, $U_{A}(\pi/2\Omega)=U_{\pi/4}^{(A)}$ and $U_{B}(3\pi/4\Omega)=U_{3\pi/8}^{(B)}$.

The Bell test of Section III.A requires a measurement of the spin $\hat{S}$ for the states after the unitary rotations. As we have seen above, the unitary parts of the measurements $\hat{M}_{\theta}^{(A)}$ and $\hat{M}_{\phi}^{(B)}$ are to be made by interacting with the nonlinear medium at each site. This creates the superpositions (LABEL:eq:state3-20) of the coherent states $|-\alpha\rangle$ and $|\alpha\rangle$ ($|-\beta\rangle$ and $|\beta\rangle$) which are rotated relative to the initial state $|\alpha\rangle$ ($|\beta\rangle$). The initial states determine the orientiation of real axis (i.e. the phase direction). The coherent states $|-\alpha\rangle$ and $|\alpha\rangle$ ($|-\beta\rangle$ and $|\beta\rangle$) are hence the basis states for a particular pointer measurement, $\hat{M}^{(A)}$ ($\hat{M}^{(B)}$) that determines the sign of the coherent amplitude i.e. the value of the macroscopic qubit. The pointer measurements are hence measurements of the quadrature phase amplitudes yurke-stoler-1

$$\hat{X}_{A}={\color[rgb]{1,0,0}{\color[rgb]{0,0,1}{\color[rgb]{0,0,0}\frac{1}{\sqrt{2}}}}}(\hat{a}+\hat{a}^{\dagger}),\ \ \hat{X}_{B}=\frac{1}{\sqrt{2}}(\hat{b}+\hat{b}^{\dagger})$$

(21)

on the evolved states at each site. The orientation of the axis that defines quadratures is aligned with the orientation of the initial coherent states $|\alpha\rangle$ ($|\beta\rangle$) in phase space. This is set in the experiment by a local oscillator. Finally, such a measurement involves a coupling to detectors. Let us denote the results of the pointer measurements $\hat{X}_{A}$ and $\hat{X}_{B}$ by $X_{A}$ and $X_{B}$ respectively. The final spin outcome of the measurement $\hat{M}_{\theta}^{(A)}$ is taken to be $S_{A}=+1$ if $X_{A}>0$, and $-1$ otherwise. Similarly, the outcome of the measurement $\hat{M}_{\phi}^{(B)}$ is $S_{B}=+1$ if $X_{B}>0$, and $-1$ otherwise.

At each site $A$ and $B$, the system of Figure 1 prepared in the cat state (6) undergoes unitary transformations $U_{A}$ and $U_{B}$, given by (20). There is the choice of two rotation angles, corresponding to two different times, at each site. These give transformations of the form (13) and (14).

A violation of the Bell inequality (1) is obtained if we select angles $\theta=0$ and $\theta=\pi/4$ at site $A$, and $\phi=\pi/8$ and $\phi=3\pi/8$ at site $B$ (Figure 1). Therefore, in order to violate the Bell inequality (2), we select $t_{a}=0$ (which gives rotation $\theta=0$) and $t^{\prime}_{a}=\pi/2\Omega$ (which gives rotation $\theta=\pi/4$). Similarly at site B, we select $t_{b}=\pi/4\Omega$ (rotation $\phi=\pi/8$) and $t^{\prime}_{b}=3\pi/(4\Omega)$ (rotation $\phi=3\pi/8$). Using the prediction $E(t_{a},t_{b})=E(\theta,\phi)$ given by (12) for orthogonal states undergoing the unitary transformations (8) and (9), we see that this choice of time-settings will give a violation of the Bell inequality (2).

To account for the nonorthogonality due to finite amplitudes $\alpha$ and $\beta$, we evaluate the distributions $P(X_{A},X_{B})$ for the outcomes of the joint measurement of the amplitudes $\hat{X}_{A}$ and $\hat{X}_{B}$ (eqn (21), for each of the time-settings. This constitutes the prediction for the final pointer measurements. The final state after the unitary transformations is

$\displaystyle|\psi_{f}\rangle$

$\displaystyle=$

$\displaystyle\mathcal{N}\thinspace U_{A}(t_{a})U_{B}(t_{b})\Bigr{(}|\alpha\rangle|-\beta\rangle-|-\alpha\rangle|\beta\rangle\Bigl{)}$

where the unitary operators are given by (20) and $\mathcal{N}$ is the normalisation constant. The probability is

$$P(X_{A},X_{B})=|\langle X_{A}|\langle X_{B}|\psi_{f}\rangle|^{2}$$

(23)

where $|X_{A}\rangle$, $|X_{B}\rangle$ are eigenstates of $X_{A}$ and $X_{B}$ respectively. Details of calculation are given in the Appendix. Integrating gives the results needed for the evaluation of the Bell inequality term, $B$, of eqn (2). We use $E(t_{a},t_{b})=P_{++}+P_{--}-P_{+-}-P_{-+}$ where

$\displaystyle P_{++}$

$\displaystyle=$

$\displaystyle\int_{0}^{\infty}\int_{0}^{\infty}P(X_{A},X_{B})dX_{A}dX_{B}$

(24)

and $P_{--}$, $P_{-+}$ and $P_{+-}$ are defined similarly for the remaining three quadrants.

The results for the four choices of time settings are shown in Figures 5 and 6. For $\alpha,\beta\geq 1.5$, the overlap of the coherent states $|\alpha\rangle$ and $|-\alpha\rangle$ (and $|\beta\rangle$ and $|-\beta\rangle$) is small and there is agreement with the calculations based on the assumption of orthogonality of the states. For each time setting, the results of the measurements $S^{(A)}$ and $S^{(B)}$ have two possible values, $+1$ and $-1$, and there are four joint outcomes. In Figure 5, the plots of $P(X_{A},X_{B})$ show four distinct Gaussian peaks corresponding to the probabilities of these joint outcomes, the peaks becomes macroscopically separated for large $\alpha$ and $\beta$. We thus verify that maximal violations of the Bell inequality (2) ($|B|=2\sqrt{2}$) are indeed predicted for the macroscopic qubits, where measurements distinguish macroscopically distinct states, as $\alpha$, $\beta\rightarrow\infty$.

In the set-up of Figure 1, two spacelike separated systems display failure of macroscopic local realism. As the measurements take place, the systems evolve dynamically over an interval of time. This is a realistic model because the analyser measurements involve interactions over a finite time duration. In order to gain insight into how the macroscopic Bell violations arise over the course of the dynamics, we present plots in terms of the Q function.

The Husimi Q function is defined uniquely as a positive function for a two-mode quantum state $\rho$ by $Q(\alpha_{0},\beta_{0})=\frac{1}{\pi^{2}}\langle\alpha_{0}|\langle\beta_{0}|\rho|\beta_{0}\rangle|\alpha_{0}\rangle$ where $|\alpha_{0}\rangle$ and $|\beta_{0}\rangle$ are coherent states for the modes Husimi-Q-1 . It is a function of four real variables $x_{A}$, $p_{A}$, $x_{B}$ and $p_{B}$, where $\alpha_{0}=x_{A}+ip_{A}$ and $\beta_{0}=x_{B}+ip_{B}$. The Q function is a quasi-probability distribution, corresponding to an anti-normal ordering of moments, and therefore (different to a positive Wigner function) does not provide a probability distribution for the actual outcomes $X_{A}$, $P_{A},$ $X_{B}$, $P_{B}$ of the measurements $\hat{X}_{A}={\color[rgb]{1,0,0}{\color[rgb]{0,0,1}{\color[rgb]{0,0,0}\frac{1}{\sqrt{2}}}}}(\hat{a}+\hat{a}^{\dagger}),\hat{X}_{B}={\color[rgb]{1,0,0}{\color[rgb]{0,0,1}{\color[rgb]{0,0,0}\frac{1}{\sqrt{2}}}}}(\hat{b}+\hat{b}^{\dagger})$, $\hat{P}_{A}={\color[rgb]{1,0,0}{\color[rgb]{0,0,1}{\color[rgb]{0,0,0}\frac{1}{i\sqrt{2}}}}}(\hat{a}-\hat{a}^{\dagger}),\hat{P}_{B}={\color[rgb]{1,0,0}{\color[rgb]{0,0,1}{\color[rgb]{0,0,0}\frac{1}{i\sqrt{2}}}}}(\hat{b}-\hat{b}^{\dagger})$. However, the $Q$ function provides at any given time the correct probability distribution for the outcomes of the macroscopically separated spins $S_{j}^{(B)}$ and $S_{i}^{(A)}$, as we confirm below.

Assuming the system is prepared in the cat state (6), the state of the system after interaction times $t_{a}$ at site $A$ and $t_{b}$ at site $B$ is given by eq. (LABEL:eq:234-1-1-1). The Q function at the time $t_{a}$ and $t_{b}$ is $Q(x_{A},x_{B},p_{A},p_{B})=\frac{1}{\pi^{2}}|\langle\beta_{0}|\langle\alpha_{0}|\psi_{f}\rangle|^{2}$. The marginal for the two $X$ quadratures, given by

$\displaystyle Q(x_{A},x_{B})$

$\displaystyle=$

$\displaystyle\int dp_{A}dp_{B}Q(x_{A},x_{B},p_{A},p_{B})$

(25)

One can also evaluate the marginals for each system e.g. $Q(x_{A},p_{A}$) by integrating over $x_{B}$ and $p_{B}$.

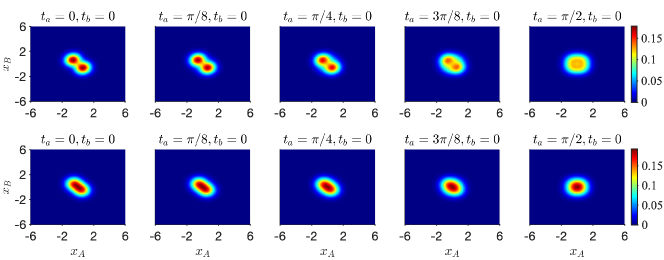
In Figures 7 and 8, we plot the marginals $Q(x_{A},x_{B})$ and $Q(x_{A},p_{A})$ corresponding to the states created after the interaction times $t_{a}$ and $t_{b}$, as in Figure 5, where there is a violation of the Bell inequality (2). As expected, there is similarity in the macroscopic limit of the Q function $Q(x_{A},x_{B})$ with the actual distributions $P(X_{A},X_{B})$, of Figure 5. The additional noise of order $\hbar$ (scaled to order $\sim 1$ in the plots) which is characteristic of the Q function does not change the probabilities for the macroscopically distinct outcomes, $S_{A}$ and $S_{B}$.

To investigate the dynamics leading to the violation of macroscopic local realism (MLR), we give a comparison with the predictions if the system is initially prepared in the non-entangled mixed state

$\displaystyle\rho_{mix}$

$\displaystyle=$

$\displaystyle\frac{1}{2}(|\alpha\rangle|-\beta\rangle\langle\alpha|\langle-\beta|+|-\alpha\rangle|\beta\rangle\langle-\alpha|\langle\beta|)$

The mixture evolves to

$\displaystyle\rho_{mix}(t_{a},t_{b})$

$\displaystyle=$

$\displaystyle U_{B}(t_{b})U_{A}(t_{a})\rho_{mix}U_{A}^{\dagger}(t_{a})U_{B}^{\dagger}(t_{b})$

We plot the Q function of the mixed state $\rho_{mix}$, eqn. (LABEL:eq:mixunit), in Figure 7 (lower) for the choice of time-settings that for the state $|\psi_{Bell}\rangle$ lead to a violation of the Bell inequality (top). The mixed state has the interpretation that the system is in one or other of the quantum states with a definite outcome for $S_{A}$ and $S_{B}$ at a time $t=0$, as $\alpha$, $\beta\rightarrow\infty$. Consistent with that interpretation, the dynamics does not lead to a violation of the Bell inequality. We see that the Q functions for the initial states ($|\psi_{Bell}\rangle$ and $\rho_{mix}$) at $t=0$ are indistinguishable. In fact, calculation shows that there is a microscopic difference $\mathcal{C}$, of order $e^{-|\alpha|^{2}-|\beta|^{2}}$, between these two Q functions. We also see that the Q functions arising from initial states ($|\psi_{Bell}\rangle$ and $\rho_{mix}$) are indistinguishable if either $t_{a}$ or $t_{b}$ is zero. However, for the time settings where there is evolution (rotation) at both the sites, the final outcomes are macroscopically different.

The timescales of the dynamics leading to the violation of macroscopic local realism (MLR) can be visualised if we calculate the full dynamics associated with the unitary measurements (rotations) (Figures 9 and 10). The predictions for the joint distributions $P(X_{A},X_{B})$ depend only on the absolute value of the times $t_{a}$ and $t_{b}$ of interaction with the measurement apparatus at each site. The same violation of the Bell inequalities can thus be achieved in different ways relative to a shared clock. For example, one may measure system $A$ first, and subsequently measure system $B$; or vice versa. Alternatively, one may measure by evolving the systems simultaneously. In Figures 9 and 10, we choose to evolve sequentially, with $B$ first. On comparing the sequences of Q functions for the entangled state and for the mixture $\rho_{mix}$ in Figures 9 and 10, we observe the transition from indistinguishable Q functions at $t_{a}=t_{b}=0$ though to a small but noticable difference at times $t_{a}=\pi/8\Omega$ and $t_{b}=\pi/4\Omega$. Finally, at times $t_{a}=\pi/2\Omega$ and $t_{b}=\pi/4\Omega$, the difference has become macroscopic.