Fudan University
BerDiff: Conditional Bernoulli Diffusion Model for Medical Image Segmentation
Abstract
Medical image segmentation is a challenging task with inherent ambiguity and high uncertainty, attributed to factors such as unclear tumor boundaries and multiple plausible annotations. The accuracy and diversity of segmentation masks are both crucial for providing valuable references to radiologists in clinical practice. While existing diffusion models have shown strong capacities in various visual generation tasks, it is still challenging to deal with discrete masks in segmentation. To achieve accurate and diverse medical image segmentation masks, we propose a novel conditional Bernoulli Diffusion model for medical image segmentation (BerDiff). Instead of using the Gaussian noise, we first propose to use the Bernoulli noise as the diffusion kernel to enhance the capacity of the diffusion model for binary segmentation tasks, resulting in more accurate segmentation masks. Second, by leveraging the stochastic nature of the diffusion model, our BerDiff randomly samples the initial Bernoulli noise and intermediate latent variables multiple times to produce a range of diverse segmentation masks, which can highlight salient regions of interest that can serve as valuable references for radiologists. In addition, our BerDiff can efficiently sample sub-sequences from the overall trajectory of the reverse diffusion, thereby speeding up the segmentation process. Extensive experimental results on two medical image segmentation datasets with different modalities demonstrate that our BerDiff outperforms other recently published state-of-the-art methods. Our results suggest diffusion models could serve as a strong backbone for medical image segmentation.
Keywords:
Conditional diffusion Bernoulli noise Medical image segmentation.1 Introduction
Medical image segmentation plays a crucial role in enabling better diagnosis, surgical planning, and image-guided surgery [8]. The inherent ambiguity and high uncertainty of medical images pose significant challenges [5] for accurate segmentation, attributed to factors such as unclear tumor boundaries in brain Magnetic resonance imaging (MRI) images and multiple plausible annotations in lung nodule Computed Tomography (CT) images. Existing medical image segmentation works typically provide a single, deterministic, most likely hypothesis mask, which may lead to misdiagnosis or sub-optimal treatment. Therefore, providing accurate and diverse segmentation masks as valuable references [16] for radiologists is crucial in clinical practice.
Recently, diffusion models [10] have shown strong capacities in various visual generation tasks [19, 20]. However, how to better integrate with discrete segmentation tasks needs further consideration. Although many researches [1, 24] have combined diffusion model with segmentation tasks and made some modifications, these methods do not take full account of the discrete characteristic of segmentation task and still use Gaussian noise as their diffusion kernel. To achieve accurate and diverse segmentation, we propose a novel Conditional Bernoulli Diffusion model for medical image segmentation (BerDiff). Instead of using the Gaussian noise, we first propose to use the Bernoulli noise as the diffusion kernel to enhance the capacity of the diffusion model for segmentation, resulting in more accurate segmentation masks. Moreover, by leveraging the stochastic nature of the diffusion model, our BerDiff randomly samples the initial Bernoulli noise and intermediate latent variables multiple times to produce a range of diverse segmentation masks, which can highlight salient regions of interest (ROI) that can serve as a valuable reference for radiologists. In addition, our BerDiff can efficiently sample sub-sequences from the overall trajectory of the reverse diffusion based on the rationale behind the Denoising Diffusion Implicit Models (DDIM) [23], thereby speeding up the segmentation process.
The contributions of this work are summarized as follows. 1) Instead of using the Gaussian noise, we propose a novel conditional diffusion model based on the Bernoulli noise for discrete binary segmentation tasks, achieving accurate and diverse medical image segmentation masks. 2) Our BerDiff can efficiently sample sub-sequences from the overall trajectory of the reverse diffusion, thereby speeding up the segmentation process. 3) Experimental results on two medical images, CT and MRI, specifically the LIDC-IDRI and BRATS 2021 datasets, demonstrate that our BerDiff outperforms other state-of-the-art methods.
2 Methodology
In this section, we first describe the problem definitions, then demonstrate the Bernoulli forward and diverse reverse processes of our BerDiff, as shown in Fig. 1. Finally, we provide an overview of the training and sampling procedures.
2.1 Problem definition

Let us assume that denotes the input medical image with a spatial resolution of and number of channels. The ground-truth mask is represented as , where represents background while ROI. Inspired by diffusion-based models such as denoising diffusion probabilistic model (DDPM) and DDIM, we propose a novel conditional Bernoulli diffusion model, which can be represented as , where are latent variables of the same size as the mask . For medical binary segmentation tasks, the diverse reverse process of our BerDiff starts from the initial Bernoulli noise and progresses through intermediate latent variables constrained by the input medical image to produce segmentation masks, where denotes an all-ones matrix of the size .
2.2 Bernoulli forward process
In previous generation-related diffusion models, Gaussian noise is progressively added with increasing timestep . However, for segmentation tasks, the ground-truth masks are represented by discrete values. To address this, our BerDiff gradually adds more Bernoulli noise using a noise schedule , as shown in Fig. 1. The Bernoulli forward process of our BerDiff is a Markov chain, which can be represented as:
| (1) | ||||
| (2) |
where denotes the Bernoulli distribution with the probability parameters . Using the notation and , we can efficiently sample at an arbitrary timestep as follows:
| (3) |
To ensure that the objective function described in Sec. 2.4 is tractable and easy to compute, we use the sampled Bernoulli noise to reparameterize of Eq. (3) as , where denotes the logical operation of “exclusive or (XOR)”. Additionally, let denote elementwise product, and denote normalizing the input data along the channel dimension and then returning the second channel. The concrete Bernoulli posterior can be represented as:
| (4) |
where .
2.3 Diverse reverse process
The diverse reverse process can be also viewed as a Markov chain that starts from the Bernoulli noise and progresses through intermediate latent variables constrained by the input medical image to produce diverse segmentation masks, as shown in Fig. 1. The concrete diverse reverse process of our BerDiff can be represented as:
| (5) | ||||
| (6) |
Specifically, we utilize the estimated Bernoulli noise of to parameterize via a calibration function , as follows:
| (7) |
where denotes the absolute value operation.
2.4 Detailed procedure
Here, we provide an overview of the training and sampling procedure in Algorithms 1 and 2. During the training phase, given an image and mask data pair , we sample a random timestep from a uniform distribution , which is used to sample the Bernoulli noise .
We then use to sample from , which allows us to obtain the Bernoulli posterior . We pass the estimated Bernoulli noise through the calibration function to parameterize . Based on the variational upper bound on the negative log-likelihood in previous diffusion models [3], we adopt Kullback-Leibler (KL) divergence and binary cross-entropy (BCE) loss to optimize our BerDiff as follows:
| (8) | ||||
| (9) |
Finally, the overall objective function is presented as:
| (10) |
where is set to in our experiments.
During the sampling phase, our BerDiff first samples the initial latent variable , followed by iterative calculation of the probability parameters of for different . In Algorithm 2, we present two different sampling strategies from DDPM and DDIM for the latent variable . Finally, our BerDiff is capable of producing diverse segmentation masks. By taking the mean of these masks, we can further obtain a saliency segmentation mask to highlight salient ROI that can serve as a valuable reference for radiologists. Note that our BerDiff proposes a novel parameterization technology, calibration function, to estimate the Bernoulli noise of , which is different from previous discrete state diffusion-based models [3, 11, 22].
3 Experiment
3.1 Experimental setup
Dataset and preprocessing The data used in this experiment are obtained from LIDC-IDRI [2, 7] and BRATS 2021 [4] datasets. LIDC-IDRI contains 1,018 lung CT scans with plausible segmentation masks annotated by four radiologists. We adopt a standard preprocessing pipeline for lung CT scans and the train-validation-test partition as in previous work [5, 14, 21]. BRATS 2021 consists of four different sequence (T1, T2, FlAIR, T1CE) MRI images for each patient. All 3D scans are sliced into axial slices and discarded the bottom 80 and top 26 slices. Note that we treat the original four types of brain tumors as one type following previous work [23], converting the multi-target segmentation problem into binary. Our training set includes 55,174 2D images scanned from 1,126 patients, and the test set comprises 3,991 2D images scanned from 125 patients. Finally, the images from LIDC-IDRI and BRAST 2021 are resized to and , respectively.
| Loss | Estimation | GED | HM-IoU | |||
| Target | 16 | 8 | 4 | 1 | 16 | |
| Bernoulli noise | 0.332 | 0.365 | 0.430 | 0.825 | 0.517 | |
| Bernoulli noise | 0.251 | 0.287 | 0.359 | 0.785 | 0.566 | |
| Bernoulli noise | 0.249 | 0.287 | 0.358 | 0.775 | 0.575 | |
| Ground-truth mask | 0.277 | 0.317 | 0.396 | 0.866 | 0.509 | |
| Training | Diffusion | GED | HM-IoU | |||
| Iteration | Kernel | 16 | 8 | 4 | 1 | 16 |
| 21,000 | Gaussian | 0.671 | 0.732 | 0.852 | 1.573 | 0.020 |
| Bernoulli | 0.252 | 0.287 | 0.358 | 0.775 | 0.575 | |
| 86,500 | Gaussian | 0.251 | 0.282 | 0.345 | 0.719 | 0.587 |
| Bernoulli | 0.238 | 0.271 | 0.340 | 0.748 | 0.596 | |
Implementation Details We implement all the methods with the PyTorch library and train the models on NVIDIA V100 GPUs. All the networks are trained using the AdamW [17] optimizer with a batch size of 32. The initial learning rate is set to for BRATS 2021 and for LIDC-IDRI. The Bernoulli noise estimation U-net network in Fig. 1 of our BerDiff is the same as previous diffusion-based models [18]. We employ a linear noise schedule for timesteps for all the diffusion models. And we use the sub-sequence sampling strategy of DDIM to accelerate the segmentation process. During mini-batch training of LIDC-IDRI, our BerDiff learn diverse expertise by randomly sampling one from four annotated segmentation masks for each image. Three metrics are used for performance evaluation, including Generalized Energy Distance (GED), Hungarian-matched Intersection over Union (HM-IoU), and Dice coefficient. We compute GED using a varying number of segmentation samples (1, 4, 8, and 16), HM-IoU using 16 samples.
3.2 Ablation study
We start by conducting ablation experiments to demonstrate the effectiveness of different losses and estimation targets, as shown in Table 1. All experiments are trained for 21,000 training iterations on LIDC-IDRI. We first conduct the ablation study of different losses while estimating Bernoulli noise in the top three rows. We find that the combination of KL divergence and BCE loss can achieve the best performance. Then, we conduct an ablation study of selecting estimation target in the bottom two rows. We observe that estimating Bernoulli noise, instead of directly estimating the ground-truth mask, is more suitable for our binary segmentation task. All of these findings are consistent with previous works [3, 10]. Please refer to Appendix 0.A for extra ablation studies on the sampling strategy and sampled timesteps.
| Methods |
|
|
||||
| Prob.U-net [14] | 0.3200.03 | 0.5000.03 | ||||
| Hprob.U-net [15] | 0.2700.01 | 0.5300.01 | ||||
| CAR [13] | 0.2640.00 | 0.5920.01 | ||||
| JPro.U-net [26] | 0.2600.00 | 0.5850.00 | ||||
| PixelSeg [25] | 0.2600.00 | 0.5870.01 | ||||
| SegDiff [1] | 0.2480.01 | 0.5850.00 | ||||
| MedSegDiff [24] | 0.4200.03 | 0.4130.03 | ||||
| BerDiff (ours) | 0.2380.01 | 0.5960.00 |

Here, we conduct ablation experiments on our BerDiff with Gaussian or Bernoulli noise, and the results are shown in Table 2. For discrete segmentation tasks, we find that using Bernoulli noise can produce favorable results when training iterations are limited (e.g. 21,000 iterations), and even outperform using Gaussian noise when training iterations are sufficient (e.g. 86,500 iterations). We also provide a more detailed performance comparison between Bernoulli- and Gaussian-based diffusion models over training iterations in Appendix 0.B. In addition, we present a toy example to demonstrate the superiority of Bernoulli diffusion over Gaussian diffusion in Appendix 0.C.
3.3 Comparison to other state-of-the-art methods

Results on LIDC-IDRI Here, we present the quantitative comparison results of LIDC-IDRI in Table 3.2, and find that our BerDiff perform well for discrete segmentation tasks. Probabilistic U-net (Prob.U-net), Hierarchical Prob.U-net (Hprob.U-net), and Joint Prob.U-net (JPro.U-net) use conditional variational autoencoder (cVAE) to accomplish segmentation tasks. Calibrated Adversarial Refinement (CAR) employs generative adversarial networks (GAN) to refine segmentation. PixelSeg is based on autoregressive models, while SegDiff and MedSegDiff are diffusion-based models. We have the following two observations: 1) diffusion-based methods have demonstrated significant superiority over traditional approaches based on VAE, GAN, and autoregression models for discrete segmentation tasks; and 2) our BerDiff has outperformed other diffusion-based models that use Gaussian noise as the diffusion kernel. At the same time, we present comparison segmentation results in Fig. 2. Compared to other models, our BerDiff can effectively learn diverse expertise, resulting in more diverse and accurate segmentation masks. Especially for small nodules that can create ambiguity, such as the lung nodule on the left, our BerDiff approach produces segmentation masks that are more in line with the ground-truth masks.
Results on BRATS 2021 Here, we present the quantitative and qualitative comparison results of BRATS 2021 in Table 3.2 and Fig. 3, respectively. We conducted a comparative analysis of our BerDiff with other models such as nnU-net, transformer-based models like TransU-net and Swin UNETR, as well as diffusion-based methods like SegDiff. First, we find that diffusion-based methods have shown superior performance compared to traditional U-net and transformer-based approaches. Besides, the high performance achieved by U-net, which shares the same architecture as our noise estimation network, highlights the effectiveness of the backbone design in diffusion-based models. Moreover, our proposed BerDiff surpasses other diffusion-based models that use Gaussian noise as the diffusion kernel. Finally, from Fig. 3, we find that our BerDiff segments more accurately on parts that are difficult to recognize by the human eye, such as the tumor in the rd row. At the same time, we can also generate diverse plausible segmentation masks to produce a saliency segmentation mask. We note that some of these masks may be false positives as shown in the st row, but they can be filtered out due to low saliency. Please refer to Appendix 0.D for more examples of diverse segmentation masks generated by our BerDiff.
4 Conclusion
We first propose to use the Bernoulli noise as the diffusion kernel to enhance the capacity of the diffusion model for binary segmentation tasks, achieving accurate and diverse medical image segmentation results. Our BerDiff only focuses on binary segmentation tasks and takes much time during the iterative sampling process as other diffusion-based models; e.g. our BerDiff takes 0.4s to segment one medical image, which is ten times of traditional U-net. In the future, we will extend our BerDiff to the multi-target segmentation problem and implement additional strategies for speeding up the segmentation process.
References
- [1] Amit, T., Nachmani, E., Shaharbany, T., Wolf, L.: SegDiff: Image segmentation with diffusion probabilistic models. arXiv:2112.00390 (2021)
- [2] Armato III, S.G., McLennan, G., Bidaut, L., McNitt-Gray, M.F., Meyer, C.R., Reeves, A.P., Zhao, B., Aberle, D.R., Henschke, C.I., Hoffman, E.A., et al.: The lung image database consortium (LIDC) and image database resource initiative (IDRI): a completed reference database of lung nodules on CT scans. Medical physics 38(2), 915–931 (2011)
- [3] Austin, J., Johnson, D.D., Ho, J., Tarlow, D., van den Berg, R.: Structured denoising diffusion models in discrete state-spaces. Advances in Neural Information Processing Systems 34, 17981–17993 (2021)
- [4] Baid, U., Ghodasara, S., Mohan, S., Bilello, M., Calabrese, E., Colak, E., Farahani, K., Kalpathy-Cramer, J., Kitamura, F.C., Pati, S., et al.: The RSNA-ASNR-MICCAI BraTS 2021 benchmark on brain tumor segmentation and radiogenomic classification. arXiv:2107.02314 (2021)
- [5] Baumgartner, C.F., Tezcan, K.C., Chaitanya, K., Hötker, A.M., Muehlematter, U.J., Schawkat, K., Becker, A.S., Donati, O., Konukoglu, E.: PHISeg: Capturing uncertainty in medical image segmentation. In: Medical Image Computing and Computer Assisted Intervention, 2019, Proceedings, Part II 22. pp. 119–127. Springer (2019)
- [6] Chen, J., Lu, Y., Yu, Q., Luo, X., Adeli, E., Wang, Y., Lu, L., Yuille, A.L., Zhou, Y.: TransUNet: Transformers make strong encoders for medical image segmentation. arXiv:2102.04306 (2021)
- [7] Clark, K., Vendt, B., Smith, K., Freymann, J., Kirby, J., Koppel, P., Moore, S., Phillips, S., Maffitt, D., Pringle, M., et al.: The cancer imaging archive (TCIA): maintaining and operating a public information repository. Journal of digital imaging 26(6), 1045–1057 (2013)
- [8] Haque, I.R.I., Neubert, J.: Deep learning approaches to biomedical image segmentation. Informatics in Medicine Unlocked 18, 100297 (2020)
- [9] Hatamizadeh, A., Nath, V., Tang, Y., Yang, D., Roth, H.R., Xu, D.: Swin UNETR: Swin transformers for semantic segmentation of brain tumors in MRI images. In: Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Part I. pp. 272–284. Springer (2022)
- [10] Ho, J., Jain, A., Abbeel, P.: Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems 33, 6840–6851 (2020)
- [11] Hoogeboom, E., Nielsen, D., Jaini, P., Forré, P., Welling, M.: Argmax flows and multinomial diffusion: Learning categorical distributions. Advances in Neural Information Processing Systems 34, 12454–12465 (2021)
- [12] Isensee, F., Jaeger, P.F., Kohl, S.A., Petersen, J., Maier-Hein, K.H.: nnU-Net: a self-configuring method for deep learning-based biomedical image segmentation. Nature methods 18(2), 203–211 (2021)
- [13] Kassapis, E., Dikov, G., Gupta, D.K., Nugteren, C.: Calibrated adversarial refinement for stochastic semantic segmentation. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 7057–7067 (2021)
- [14] Kohl, S., Romera-Paredes, B., Meyer, C., De Fauw, J., Ledsam, J.R., Maier-Hein, K., Eslami, S., Jimenez Rezende, D., Ronneberger, O.: A probabilistic U-Net for segmentation of ambiguous images. Advances in neural information processing systems 31 (2018)
- [15] Kohl, S.A., Romera-Paredes, B., Maier-Hein, K.H., Rezende, D.J., Eslami, S., Kohli, P., Zisserman, A., Ronneberger, O.: A hierarchical probabilistic u-net for modeling multi-scale ambiguities. arXiv preprint arXiv:1905.13077 (2019)
- [16] Lenchik, L., Heacock, L., Weaver, A.A., Boutin, R.D., Cook, T.S., Itri, J., Filippi, C.G., Gullapalli, R.P., Lee, J., Zagurovskaya, M., et al.: Automated segmentation of tissues using CT and MRI: a systematic review. Academic radiology 26(12), 1695–1706 (2019)
- [17] Loshchilov, I., Hutter, F.: Decoupled weight decay regularization. arXiv preprint arXiv:1711.05101 (2017)
- [18] Nichol, A.Q., Dhariwal, P.: Improved denoising diffusion probabilistic models. In: International Conference on Machine Learning. pp. 8162–8171. PMLR (2021)
- [19] Ramesh, A., Dhariwal, P., Nichol, A., Chu, C., Chen, M.: Hierarchical text-conditional image generation with clip latents. arXiv:2204.06125 (2022)
- [20] Saharia, C., Chan, W., Saxena, S., Li, L., Whang, J., Denton, E., Ghasemipour, S.K.S., Ayan, B.K., Mahdavi, S.S., Lopes, R.G., et al.: Photorealistic text-to-image diffusion models with deep language understanding. arXiv:2205.11487 (2022)
- [21] Selvan, R., Faye, F., Middleton, J., Pai, A.: Uncertainty quantification in medical image segmentation with normalizing flows. In: Machine Learning in Medical Imaging. pp. 80–90. Springer (2020)
- [22] Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N., Ganguli, S.: Deep unsupervised learning using nonequilibrium thermodynamics. In: International Conference on Machine Learning. pp. 2256–2265. PMLR (2015)
- [23] Wolleb, J., Sandkühler, R., Bieder, F., Valmaggia, P., Cattin, P.C.: Diffusion models for implicit image segmentation ensembles. arXiv:2112.03145 (2021)
- [24] Wu, J., Fang, H., Zhang, Y., Yang, Y., Xu, Y.: MedSegDiff: Medical image segmentation with diffusion probabilistic model. arXiv preprint arXiv:2211.00611 (2022)
- [25] Zhang, W., Zhang, X., Huang, S., Lu, Y., Wang, K.: PixelSeg: Pixel-by-pixel stochastic semantic segmentation for ambiguous medical images. In: Proceedings of the -th ACM International Conference on Multimedia. pp. 4742–4750 (2022)
- [26] Zhang, W., Zhang, X., Huang, S., Lu, Y., Wang, K.: A probabilistic model for controlling diversity and accuracy of ambiguous medical image segmentation. In: Proceedings of the -th ACM International Conference on Multimedia. pp. 4751–4759 (2022)
Appendix
Appendix 0.A Ablation study on sampling strategy and timestep
Our BerDiff is compatible with various sampling strategies, and here, we compare the performance of BerDiff using DDPM’s and DDIM’s sampling strategies. The concrete sampling algorithms can be found in Algorithm 2. Our results in Table A1 indicate that for binary segmentation tasks, BerDiff using DDIM’s sampling strategy achieves better performance compared to using DDPM’s. Furthermore, to attain satisfactory performance with limited computational resources, we uniformly sample 10 timesteps from the complete trajectory in all other experiments.
| Configuration | Sampled | GED | HM-IoU | |||
| Timestep | 16 | 8 | 4 | 1 | 16 | |
| BerDiff + DDPM’s sampling strategy | 2 | 0.441 | 0.483 | 0.568 | 1.076 | 0.303 |
| 10 | 0.266 | 0.302 | 0.377 | 0.824 | 0.533 | |
| 100 | 0.258 | 0.296 | 0.372 | 0.829 | 0.539 | |
| 1000 | 0.254 | 0.293 | 0.369 | 0.832 | 0.539 | |
| BerDiff + DDIM’s sampling strategy | 2 | 0.432 | 0.481 | 0.579 | 1.167 | 0.341 |
| 10 | 0.252 | 0.287 | 0.358 | 0.775 | 0.575 | |
| 100 | 0.250 | 0.284 | 0.351 | 0.759 | 0.582 | |
| 1000 | 0.247 | 0.280 | 0.348 | 0.758 | 0.585 | |

Appendix 0.B Performance curves
Here we present a detailed performance comparison between Bernoulli- and Gaussian-based diffusion models over training iterations in Fig. A1. Results show that employing Bernoulli noise leads to faster convergence and higher performance in contrast to Gaussian noise.
Appendix 0.C Toy example
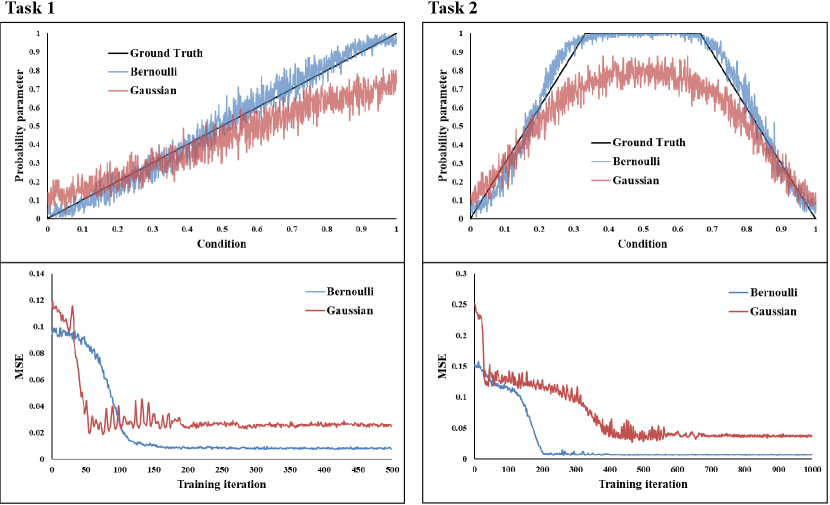
We provide intuitive insight into why Bernoulli diffusion outperforms Gaussian diffusion by designing and conducting experiments on two simple one-dimensional binary classification tasks. To create the datasets, we apply a predefined conditional probability function, as shown in the first row of Fig. A2, to map an input to an output , which serves as the Ground Truth. For each data configuration, we use a 4-layer MLP for the noise estimation network. We train all runs using a learning rate of 1e-3. During inference, we uniformly sample 1000 points from and generate 100 samples using the diffusion model for each point. We take the mean of the 100 samples as the estimated probability parameter and evaluate performance using mean-squared error (MSE) between the estimated and ground truth probability parameters. Fig. A2 shows that Bernoulli diffusion offers superior training stability, faster convergence, and better fitting of the conditional distribution compared to Gaussian diffusion.
Appendix 0.D More examples of diverse segmentation masks
In this section, we provide additional examples of diverse segmentation masks generated by our BerDiff for LIDC-IDRI and BRATS 2021, as shown in Figs. A3 and A4, respectively.

