Bell nonlocality and entanglement in $e^{+}e^{-}\rightarrow Y\bar{Y}$ at BESIII

Before our investigation of Bell nonlocality, it is convenient to transform the two-qubit state in Eqs. (1) and (3) to the $X$ state. First, we swap the $\hat{\mathbf{y}}$ and $\hat{\mathbf{z}}$ axes in $Y$ and $\bar{Y}$’s rest frame. Then we diagonalize $C_{ij}$ for $Y$ and $\bar{Y}$. The transformed spin density operator can be written in terms of Pauli matrices as

	$\displaystyle\rho_{Y\bar{Y}}^{X}=$	$\displaystyle\frac{1}{4}\biggl{(}\mathds{1}\otimes\mathds{1}+a\sigma_{z}\otimes\mathds{1}+\mathds{1}\otimes a\sigma_{z}$
		$\displaystyle+\sum_{i}t_{i}\sigma_{i}\otimes\sigma_{i}\biggr{)},$		(7)

which is in the standard form of a symmetric two-qubit $X$ state [37]. Thus we place the superscript “$X$” to $\rho_{Y\bar{Y}}$. The corresponding $\Theta_{\mu\nu}$ becomes

$$\Theta_{\mu\nu}^{X}=\left[\begin{array}[]{c|ccc}1&0&0&a\\ \hline\cr 0&t_{1}&0&0\\ 0&0&t_{2}&0\\ a&0&0&t_{3}\end{array}\right],$$

(8)

where the elements $a$ and $t_{i}$ ($i=1,2,3$) are given by

	$\displaystyle a$	$\displaystyle=\frac{\beta_{\psi}\sin\vartheta\cos\vartheta}{1+\alpha_{\psi}\cos^{2}\vartheta},$
	$\displaystyle t_{1,2}$	$\displaystyle=\frac{1+\alpha_{\psi}\pm\sqrt{\left(1+\alpha_{\psi}\cos 2\vartheta\right)^{2}-\beta_{\psi}^{2}\sin^{2}2\vartheta}}{2(1+\alpha_{\psi}\cos^{2}\vartheta)},$
	$\displaystyle t_{3}$	$\displaystyle=\frac{-\alpha_{\psi}\sin^{2}\vartheta}{1+\alpha_{\psi}\cos^{2}\vartheta}.$		(9)

We note that $a=P_{y}^{\pm}$ , $t_{3}=C_{yy}$, and $t_{1,2}$ come from diagonalizing the block matrix of $C_{ij}$ with $i,j=x,z$ in $\Theta_{\mu\nu}$.

We note that the swapping of $\hat{\mathbf{y}}$ and $\hat{\mathbf{z}}$ axes and diagonalizing $C_{ij}$ can be obtained by a local unitary transformation:

$$\rho_{Y\bar{Y}}^{X}=(U_{Y}\otimes U_{\bar{Y}})\rho_{Y\bar{Y}}(U_{Y}\otimes U_{\bar{Y}})^{\dagger},$$

(10)

where $U_{Y}$ and $U_{\bar{Y}}$ are two unitary operators acting independently in $Y$ and $\bar{Y}$’s Hilbert space respectively [38]. The states described by $\rho_{Y\bar{Y}}$ and $\rho_{Y\bar{Y}}^{X}$ are said to be local unitary equivalent in the sense that they have same quantum correlation properties such as Bell nonlocality and entanglement [39]. In the remainder of this paper, all analyses are based on the $X$ state in Eqs. (8) and (7).

The nonlocal property in a quantum entangled system can be tested by the violation of Bell inequality [1]. The most widely used Bell-type inequality is the CHSH inequality [40]

$$\left|\left\langle A_{1}\otimes B_{1}\right\rangle+\left\langle A_{1}\otimes B_{2}\right\rangle+\left\langle A_{2}\otimes B_{1}\right\rangle-\left\langle A_{2}\otimes B_{2}\right\rangle\right|\leq 2,$$

(11)

where $A_{i}=\mathbf{a}_{i}\cdot\boldsymbol{\sigma}$, $B_{i}=\mathbf{b}_{i}\cdot\boldsymbol{\sigma}$, and $\langle A_{i}\otimes B_{j}\rangle\equiv\mathrm{Tr}\left[\rho(\mathbf{a}_{i}\cdot\boldsymbol{\sigma}\otimes\mathbf{b}_{j}\cdot\boldsymbol{\sigma})\right]$ with $i,j=1,2$. Here $\mathbf{a}_{1}$, $\mathbf{a}_{2}$, $\mathbf{b}_{1}$ and $\mathbf{b}_{2}$ are four directions (unit vectors) along which the spin polarization is measured. Then the inequality can be rewritten in a simpler form

$$\left|\mathbf{a}_{1}^{\mathrm{T}}C\left(\mathbf{b}_{1}+\mathbf{b}_{2}\right)+\mathbf{a}_{2}^{\mathrm{T}}C\left(\mathbf{b}_{1}-\mathbf{b}_{2}\right)\right|\leq 2,$$

(12)

with $C$ being the correlation matrix $C_{ij}$ in Eq. (1). Those quantum states that violate the CHSH inequality are called Bell nonlocal states. The maximum of the left-hand side of Eq. (12) can be obtained by tuning $\mathbf{a}_{1}$, $\mathbf{a}_{2}$, $\mathbf{b}_{1}$ and $\mathbf{b}_{2}$ as

	$\displaystyle\mathcal{B}\left[\rho\right]$	$\displaystyle\equiv\max_{\mathbf{a}_{1},\mathbf{a}_{2},\mathbf{b}_{1},\mathbf{b}_{2}}\left|\mathbf{a}_{1}^{\mathrm{T}}C\left(\mathbf{b}_{1}+\mathbf{b}_{2}\right)+\mathbf{a}_{2}^{\mathrm{T}}C\left(\mathbf{b}_{1}-\mathbf{b}_{2}\right)\right|$
		$\displaystyle=2\sqrt{m_{1}+m_{2}},$		(13)

where $m_{1}$ and $m_{2}$ are two largest eigenvalues of $C^{\mathrm{T}}C$ [41]. Therefore, the CHSH inequality can be violated iff (if and only if) $m_{1}+m_{2}>1$, and the maximum possible violation of the CHSH inequality is the upper bound value $2\sqrt{2}$. For convenience, we define a function of two-qubit density operator $\mathfrak{m}_{12}[\rho]\equiv m_{1}+m_{2}\in[0,2]$ to be a measure of the Bell nonlocality [16, 18].

Since we have put the density operator into the $X$ form in (8), the correlation matrix is diagonal: $\mathbf{t}=\mathrm{diag}\{t_{1},t_{2},t_{3}\}$. The three eigenvalues of $C^{\mathrm{T}}C$ or $\mathbf{t}^{\mathrm{T}}\mathbf{t}$ are $t_{1}^{2}$, $t_{2}^{2}$ and $t_{3}^{2}$. Then, according to Eq. (13), one needs to select the largest two values among them.

As we can see from Eq. (9) that $t_{1,2,3}$ are functions of three parameters $\alpha_{\psi}$, $\Delta\Phi$ and $\vartheta$. Since $t_{1}^{2}\geq t_{2}^{2}$ always holds for any values of $\alpha_{\psi}$, $\Delta\Phi$ and $\vartheta$, $t_{1}^{2}$ should note be the smallest one. Then, one needs to compare $t_{2}^{2}$ and $t_{3}^{2}$. If $\alpha_{\psi}\geq 0$, we aways have $t_{2}^{2}\geq t_{3}^{2}$. Therefore, the measure of nonlocality becomes $\mathfrak{m}_{12}[\rho_{Y\bar{Y}}^{X}]=t_{1}^{2}+t_{2}^{2}$. However, for $\alpha_{\psi}<0$, one can not judge which is larger $t_{2}^{2}$ or $t_{3}^{2}$, since it depends on the specific values of three parameters. In this case the measure of nonlocality can be expressed as $\mathfrak{m}_{12}[\rho_{Y\bar{Y}}^{X}]=\max\left\{t_{1}^{2}+t_{2}^{2},t_{1}^{2}+t_{3}^{2}\right\}$. In summary, the measure of the Bell nonlocality reads

$$\mathfrak{m}_{12}\left[\rho_{Y\bar{Y}}^{X}\right]=\begin{cases}t_{1}^{2}+t_{2}^{2},&\alpha_{\psi}\geq 0\\ \max\left\{t_{1}^{2}+t_{2}^{2},t_{1}^{2}+t_{3}^{2}\right\},&\alpha_{\psi}<0\end{cases}$$

(14)

where $t_{1}^{2}+t_{2}^{2}$ and $t_{1}^{2}+t_{3}^{2}$ are given by

$$t_{1}^{2}+t_{2}^{2}=1+\left(\frac{\alpha_{\psi}\sin^{2}\vartheta}{1+\alpha_{\psi}\cos^{2}\vartheta}\right)^{2}-2\left(\frac{\beta_{\psi}\sin\vartheta\cos\vartheta}{1+\alpha_{\psi}\cos^{2}\vartheta}\right)^{2},$$

(15)

	$\displaystyle t_{1}^{2}+t_{3}^{2}=$	$\displaystyle\left(\frac{1+\alpha_{\psi}+\sqrt{(1+\alpha_{\psi}\cos 2\vartheta)^{2}-\beta_{\psi}^{2}\sin^{2}2\vartheta}}{2(1+\alpha_{\psi}\cos^{2}\vartheta)}\right)^{2}$
		$\displaystyle+\frac{\alpha_{\psi}^{2}(1-\cos 2\vartheta)^{2}}{4(1+\alpha_{\psi}\cos^{2}\vartheta)^{2}}.$		(16)

In Table 1 are listed the values of $\alpha_{\psi}$ and $\Delta\Phi$ for $J/\psi$’s decays into a pair of octet hyperons in electron-positron annihilation. According to these parameters, we plot $\mathfrak{m}_{12}$ as a function of the scattering angle $\vartheta$ in Fig. 2 for different decay channels. From Fig. 2, we find that $\mathfrak{m}_{12}$ is a symmetric function of $\vartheta$ relative to $\vartheta=\pi/2$ in the range $\vartheta\in[0,\pi]$, and it reaches the maximum value $1+\alpha_{\psi}^{2}$ at $\vartheta=\pi/2$. Thus we obtain

$$\max_{\vartheta}\,\mathcal{B}\left[\rho_{Y\bar{Y}}^{X}\right]=2\sqrt{1+\alpha_{\psi}^{2}}.$$

(17)

By solving $\mathfrak{m}_{12}>1$ in Eq. (14) with fixed $\alpha_{\psi}$ and $\Delta\Phi$, we obtain the nonlocality range of the scattering angle as $\left(\vartheta^{*},\pi-\vartheta^{*}\right)$. For $\alpha_{\psi}\geq 0$, we can have an analytical expression for the critical angle $\vartheta^{*}$

$$\vartheta^{*}=\arctan\left|\sqrt{2-2\alpha_{\psi}^{2}}\frac{\sin\Delta\Phi}{\alpha_{\psi}}\right|,\ \ \mathrm{for}\ \alpha_{\psi}\geq 0.$$

(18)

The maximum violation in Eq. (17) and critical angles in different decay channels are listed in Table 2.

For a bipartite quantum system living in the combined Hilbert space $\rho_{AB}\in\mathscr{H}_{A}\otimes\mathscr{H}_{B}$, the state is said to be separable iff the following decomposition holds

$$\rho_{AB}=\sum_{k}p_{k}\rho_{A}^{k}\otimes\rho_{B}^{k},$$

(19)

where $p_{k}\geq 0$ and $\sum_{k}p_{k}=1$, and $\rho_{A}^{k}$ and $\rho_{B}^{k}$ are the density operator of the corresponding subsystem $A$ and $B$, respectively. Moreover, the state cannot be decomposed into the above form is called non-separable or entangled.

For two-qubit and qubit-qutrit systems ($2\times 2$ and $2\times 3$ respectively), the Peres-Horodecki criterion provides a sufficient and necessary condition for separability [48, 49]: a state $\rho_{AB}$ is separable iff its partial transpose $\rho_{AB}^{\mathrm{T}_{B}}$ with respect to the second subsystem is positive semi-definite. The Peres-Horodecki criterion is also called Positive Partial Transpose (PPT) criterion.

The concurrence is an entanglement monotone, and it has a direct relationship with entanglement of formation [50]. In this work, we utilize the concurrence as a measure of the entanglement. In Ref. [51], Wootters derived the two-qubit concurrence as

$$\mathcal{C}[\rho]\equiv\max\left\{0,\mu_{1}-\mu_{2}-\mu_{3}-\mu_{4}\right\},$$

(20)

where $\mu_{i}$ with $i=1,2,3,4$ are the eigenvalues of the Hermitain matrix $\sqrt{\sqrt{\rho}\tilde{\rho}\sqrt{\rho}}$ with $\tilde{\rho}=(\sigma_{y}\otimes\sigma_{y})\rho^{*}(\sigma_{y}\otimes\sigma_{y})$ in the decreasing order, and $\rho^{*}$ denotes the complex conjugate of $\rho$ in the spin basis of $\sigma_{z}$. Wootters’ concurrence is a function in the range $[0,1]$. A state is separable for $\mathcal{C}[\rho]=0$ and is entangled for $\mathcal{C}[\rho]>0$. When $\mathcal{C}[\rho]=1$, the state is said to be maximally entangled.

We rewrite the spin density operator for the hyperon-antihyperon system in the $\sigma_{z}$ basis

$$\rho_{Y\bar{Y}}^{X}=\frac{1}{4}\begin{bmatrix}1+2a+t_{3}&0&0&t_{1}-t_{2}\\ 0&1-t_{3}&t_{1}+t_{2}&0\\ 0&t_{1}+t_{2}&1-t_{3}&0\\ t_{1}-t_{2}&0&0&1-2a+t_{3}\end{bmatrix},$$

(21)

where $a$ and $t_{1,2,3}$ are defined in Eq. (9). The above expression can be directly obtained by expanding Pauli operators in Eq. (7) into a $2\times 2$ matrix form. The name $X$ state comes from its resemblance to the letter $X$.

The Peres-Horodecki criterion for a general $X$ state claims that the state is entangled iff either $\rho_{22}^{X}\rho_{33}^{X}<|\rho_{14}^{X}|^{2}$ or $\rho_{11}^{X}\rho_{44}^{X}<|\rho_{23}^{X}|^{2}$ holds [52], but both conditions cannot be satisfied simultaneously [53]. The Wootters’ concurrence for the $X$ state is given by [37]

$$\mathcal{C}\left[\rho^{X}\right]=2\max\left\{0,|\rho_{14}^{X}|-\sqrt{\rho_{22}^{X}\rho_{33}^{X}},|\rho_{23}^{X}|-\sqrt{\rho_{11}^{X}\rho_{44}^{X}}\right\},$$

(22)

with $\rho_{ij}^{X}$ being given in (21). We see that the Peres-Horodecki criterion for the $X$ state is compatible with the concurrence.

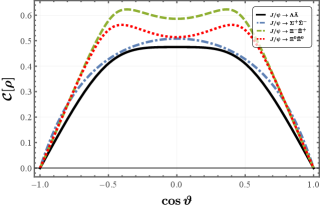
With Eqs. (21) and (22), we derive the concurrence for the hyperon-antihyperon system as

	$\displaystyle\mathcal{C}\left[\rho_{Y\bar{Y}}^{X}\right]=\left|t_{2}\right|$
	$\displaystyle=\frac{\left|1+\alpha_{\psi}-\sqrt{\left(1+\alpha_{\psi}\cos 2\vartheta\right)^{2}-\beta_{\psi}^{2}\sin^{2}2\vartheta}\right|}{2(1+\alpha_{\psi}\cos^{2}\vartheta)}.$		(23)

The results for the concurrence as functions of $\vartheta$ for octet hyperons listed in Table 1 are shown in Fig. 3. We see that the entanglement of $Y\bar{Y}$ pairs exists in the whole range of the scattering angle $\vartheta$ except at two collinear limits $\vartheta=0$ or $\pi$. However, unlike the Bell nonlocality, the maximum value of the concurrence (or maximum entanglement) does not necessarily take place at $\vartheta=\pi/2$. Instead, it can occur at other angles such as the ones for $\Xi^{-}\bar{\Xi}^{+}$ and $\Xi^{0}\bar{\Xi}^{0}$ shown in Table 3.

In summary, the outgoing hyperon-antihyperon pairs are entangled in the full range of the scattering angle except at two boundaries.

Given that both Bell nonlocality and quantum entanglement characterize quantum properties of a system, we try to look for the relationship between them.

For a two-qubit density operator $\rho$ with Wootters’ concurrence $\mathcal{C}[\rho]$, the maximum violation of the CHSH inequality $\mathcal{B}[\rho]$ has an upper bound [54]

$$\mathcal{B}[\rho]\leq 2\sqrt{1+\mathcal{C}^{2}[\rho]},$$

(24)

with $\mathcal{B}[\rho]\equiv 2\sqrt{\mathfrak{m}_{12}}$ defined in Eq. (13). In Fig. 4 we plot $\mathcal{B}$ and $2\sqrt{1+\mathcal{C}^{2}}$ as functions of $\cos\vartheta$. We see in Fig. 4 that the inequality (24) is always satisfied and the equality $\mathcal{B}=2\sqrt{1+\mathcal{C}^{2}}$ (or equivalently $\mathfrak{m}_{12}=1+\mathcal{C}^{2}$) holds at $\vartheta=\pi/2$. At this transverse scattering angle, $Y$’s and $\bar{Y}$’s polarizations vanish from Eq. (5), then the spin density operator $\rho_{Y\bar{Y}}^{X}$ reduces to a very special subclass of the $X$ state: $T$ state or Bell Diagonal State (BDS). The upper bound of $\mathcal{B}$ in (24) is attained for rank-2 BDSs [54].

From Fig. 4, both measures for the Bell nonlocality and entanglement are symmetric with respect to $\vartheta=\pi/2$. However, even if hyperon-antihyperon pairs are entangled in the full range of scattering angle except at $\vartheta=0$ or $\pi$, the Bell nonlocality only appears in the range $\vartheta\in(\vartheta^{*},\pi-\vartheta^{*})$. This corresponds to the range where orange dot-dashed lines lie above the black line in Fig. 4. This indicates the relation between the Bell nonlocality and entanglement in the hierarchy of quantumness

$$\textrm{Bell nonlocality}\subset\textrm{entanglement}.$$

(25)

Any nonlocal state must be entangled, but not all entangled states can have nonlocal correlation [55].

Another interesting behavior of the entanglement and nonlocality appears in the panels (c) and (d) in Fig. 4 for $\Xi^{-}\bar{\Xi}^{+}$ and $\Xi^{0}\bar{\Xi}^{0}$: the entanglement in the range from the maximum concurrence angle $\vartheta_{\max}$ (see Table 3) to $\pi/2$ shows a decreasing trend while the Bell nonlocality is still increasing. This phenomenon, where less entanglement corresponds to more nonlocality, sometimes referred to as an anomaly of nonlocality [56]. It can be explained by the quantum resource theory that the entanglement and nonlocality may be inequivalent resources [57]. The subtle relationship between the entanglement and nonlocality is still an active topic in this field [58].

Any two-qubit density operator can be decomposed as $\rho=\sum_{i=1}^{4}\lambda_{i}|\lambda_{i}\rangle\langle\lambda_{i}|$, with $\lambda_{i}$ being the eigenvalue and $|\lambda_{i}\rangle$ the corresponding eigenstate. According to Eq. (21), the spin density operator has only two non-zero eigenvalues

$$\lambda_{1,2}=\frac{1}{2}\left(1\mp\frac{\alpha_{\psi}\sin^{2}\vartheta}{1+\alpha_{\psi}\cos^{2}\vartheta}\right),$$

(26)

for the corresponding eigenstates

	$\displaystyle\left|\lambda_{1}\right\rangle$	$\displaystyle=\sqrt{\frac{1+\alpha_{\psi}\cos 2\vartheta+\beta_{\psi}\sin 2\vartheta}{2(1+\alpha_{\psi}\cos 2\vartheta)}}\left|00\right\rangle$
		$\displaystyle\ +\sqrt{\frac{1+\alpha_{\psi}\cos 2\vartheta-\beta_{\psi}\sin 2\vartheta}{2(1+\alpha_{\psi}\cos 2\vartheta)}}\left|11\right\rangle,$
	$\displaystyle\left|\lambda_{2}\right\rangle$	$\displaystyle=\frac{1}{\sqrt{2}}\left(\left|01\right\rangle+\left|10\right\rangle\right),$		(27)

where we adopt the notation for spin states: $|0\rangle\equiv|\uparrow_{z}\rangle$, $|1\rangle\equiv|\downarrow_{z}\rangle$. Through the eigenvalue decomposition, the spin configuration can be clearly shown in Eqs. (26) and (27) that $\rho_{Y\bar{Y}}^{X}$ can be treated as an ensemble of two pure states $\{|\lambda_{1}\rangle,|\lambda_{2}\rangle\}$ with probabilities $\{\lambda_{1},\lambda_{2}\}$.

The eigenstate $|\lambda_{1}\rangle$ is a superposition of two spin triplet states: $|00\rangle=|S=1,S_{z}=1\rangle$ and $|11\rangle=|S=1,S_{z}=-1\rangle$, and $|\lambda_{2}\rangle$ is another spin triplet state: $|S=1,S_{z}=0\rangle$. We see that there is no spin singlet component in the $Y\bar{Y}$ system. This is the result of the angular momentum conversation in $J/\psi$’s decay, and it coincides with the partial wave analysis that the outgoing $Y\bar{Y}$ only has contributions from ${}^{3}S_{1}$ and ${}^{3}D_{1}$ waves [59].

The lack of spin singlet component can also be seen by imposing the spin projection operator $F_{S}=(1-\boldsymbol{\sigma}\cdot\boldsymbol{\sigma})/4$ on the spin density matrix [60] as

$$\mathrm{Tr}\left\{\rho_{Y\bar{Y}}^{X}F_{S}\right\}=\mathrm{Tr}\,\mathbf{t}=\mathrm{Tr}\,C=0,$$

(28)

with $\mathbf{t}$ and $C$ being the correlation matrix in Eqs. (7) and (3) respectively.

In this subsection, we will look into the time-like electromagnetic form factors (EMFFs) in $e^{+}e^{-}\rightarrow Y\bar{Y}$ and investigate their effects on nonlocality and entanglement.

The electromagnetic current of the spin-1/2 hyperon can be expressed in terms of the Dirac form factor $F_{1}$ and Pauli form factor $F_{2}$ as [36]

$$\Gamma^{\mu}=\gamma^{\mu}F_{1}(q^{2})+i\frac{\sigma^{\mu\nu}q_{\nu}}{2M}F_{2}(q^{2}),$$

(29)

where $q=p_{1}+p_{2}$ with $p_{1}$ and $p_{2}$ being the four-momentum of the hyperon and antihyperon respectively, and $M$ is the hyperon mass. With $s=q^{2}$, the electric and magnetic form factors $G_{E}$ and $G_{M}$ are related to $F_{1}$ and $F_{2}$ by

$$G_{E}(s)=F_{1}+\frac{s}{4M^{2}}F_{2},\ \ G_{M}(s)=F_{1}+F_{2}.$$

(30)

Two parameters $\alpha_{\psi}$ and $\Delta\Phi$ in the process $e^{+}e^{-}\rightarrow Y\bar{Y}$ are related to $G_{E}$ and $G_{M}$ by

	$\displaystyle\alpha_{\psi}$	$\displaystyle=$	$\displaystyle\frac{s-4M^{2}\left|G_{E}/G_{M}\right|^{2}}{s+4M^{2}\left|G_{E}/G_{M}\right|^{2}}\in[-1,1],$
	$\displaystyle\Delta\Phi$	$\displaystyle=$	$\displaystyle\arg\left\{G_{E}/G_{M}\right\}\in(-\pi,\pi].$		(31)

From Eq. (5), nonvanishing polarizations of $Y$ and $\bar{Y}$ produced in annihilation of unpolarized electron and positron require $\Delta\Phi\neq 0$ and $\pi$. At the limit $\Delta\Phi=0$ or $\pi$, however, there is only the spin correlation part in $\rho_{Y\bar{Y}}^{X}$ and without polarizations part from Eq. (7). This indicates that $\rho_{Y\bar{Y}}$ is reduced to a BDS form as

$$\rho_{Y\bar{Y}}^{\mathrm{BDS}}=\frac{1}{4}\biggl{(}\mathds{1}\otimes\mathds{1}+\sum_{i}t_{i}\sigma_{i}\otimes\sigma_{i}\biggr{)},$$

(32)

where $t_{2}^{2}=t_{3}^{2}$. We note that a BDS is also a $X$ state but without polarization.

Following Eqs. (14) and (15), the measure of the Bell nonlocality becomes

$$\mathfrak{m}_{12}\left[\rho_{Y\bar{Y}}^{\mathrm{BDS}}\right]=1+\left(\frac{\alpha_{\psi}\sin^{2}\vartheta}{1+\alpha_{\psi}\cos^{2}\vartheta}\right)^{2}\geq 1.$$

(33)

We see in this circumstance the violation of the CHSH inequality occurs in the full range of the scattering angle $\vartheta\in(0,\pi)$ for any $\alpha_{\psi}\neq 0$. This result is different from what we discussed in Sec. III, where the Bell nonlocality is violated in a restricted angle range $(\vartheta^{*},\pi-\vartheta^{*})$. However, the maximal violation of the CHSH inequality also takes place at $\vartheta=\pi/2$ with the value in (17).

The concurrence in Eq. (23) for a BDS is reduced to

$$\mathcal{C}\left[\rho_{Y\bar{Y}}^{\mathrm{BDS}}\right]=\frac{|\alpha_{\psi}|\sin^{2}\vartheta}{1+\alpha_{\psi}\cos^{2}\vartheta}.$$

(34)

Comparing Eq. (33) and (34), one can see that the inequality in Eq. (24) becomes an equality $\mathcal{B}=2\sqrt{1+\mathcal{C}^{2}}$ (or equivalently $\mathfrak{m}_{12}=1+\mathcal{C}^{2}$) in the whole range of the scattering angle (not only at $\vartheta=\pi/2$). It is not a surprise since the property $\mathcal{B}=2\sqrt{1+\mathcal{C}^{2}}$ (or equivalently $\mathfrak{m}_{12}=1+\mathcal{C}^{2}$) is valid for any rank-$2$ BDS [54] with the fact that both $|\lambda_{1}\rangle$ and $|\lambda_{2}\rangle$ become two Bell states $(|00\rangle+|11\rangle)/\sqrt{2}$ and $(|01\rangle+|10\rangle)/\sqrt{2}$ with $\beta_{\psi}=0$.

From Eq. (31) we see that $\Delta\Phi$ is the relative phase between $G_{E}$ and $G_{M}$. Let us take an example for the limit case $\Delta\Phi=0,\pi$ by assuming $G_{E}=\pm G_{M}$. As a consequence, the measures for the nonlocality and Wootters’ concurrence are given by

	$\displaystyle\mathfrak{m}_{12}$	$\displaystyle=$	$\displaystyle 1+\left[\frac{\left(s-4M^{2}\right)\sin^{2}\vartheta}{4M^{2}\sin^{2}\vartheta+s\left(\cos^{2}\vartheta+1\right)}\right]^{2},$
	$\displaystyle\mathcal{C}$	$\displaystyle=$	$\displaystyle\frac{\left(s-4M^{2}\right)\sin^{2}\vartheta}{4M^{2}\sin^{2}\vartheta+s\left(\cos^{2}\vartheta+1\right)}.$		(35)

The above expressions coincide with Eqs. (3.4) and (3.7) in Ref. [18] for $e^{+}e^{-}\rightarrow\tau^{+}\tau^{-}$. This is reasonable since the vertex Eq. (29) in $e^{+}e^{-}\rightarrow\tau^{+}\tau^{-}$ is simply $\gamma^{\mu}$ indicating $G_{E}=G_{M}$.

In the process $e^{+}e^{-}\rightarrow Y\bar{Y}$, the existence of EMFFs manifests in a polarized final state, even if the colliding beams are unpolarized [61]. And this polarization effect leads to the $Y\bar{Y}$ spin correlation different from that in processes $e^{+}e^{-}\rightarrow\tau^{+}\tau^{-}$ and $pp\rightarrow t\bar{t}$ pairs [18, 13, 15].