BD+30549: young helium-weak silicon star in NGC 1333 star-forming region
Abstract
We present results of the spectroscopic study of the chemically peculiar star BD+30549 which is bona-fide member of young NGC 1333 star forming region. We found that the star possesses negligible rotation and helium-weak spectroscopic pattern with strongly enhanced Si ii and Si iii lines. The fundamental parameters of the star =13100 K and =2.1 indicate its age of about 2.7 Myr and position on the Hertzsprung-Russell diagram at the end of the Pre-Main Sequence evolutionary track, close to the Zero Age Main Sequence. Abundance analysis reveals the modest deficit of almost all elements with exception of Si , Fe , Ca and P which are overabundant. We performed the non-LTE calculations for Si ii/Si iii, Mg ii and Ca ii in order to check the influence of departures from LTE on line formation. Non-LTE calculations lead to much better reproduction of individual silicon line profiles, but does not completely remove the abundance discrepancy between Si ii and Si iii lines. We also investigate the effects of possible chemical stratification in BD+30549. We suspect that the "Si ii/Si iii anomaly" observed in BD+30549 spectrum arises under the combined action of the vertical and horizontal abundance gradients and non-LTE effects. We suppose that evolutionary status and phenomena observed in BD+30549 indicate that conditions favorable for the selective diffusion and formation of the surface chemical composition peculiarities (slow rotation and stabilization of the atmosphere) can be built up already at the Pre-Main Sequence phase.
keywords:
stars:pre-main-sequence – stars: chemically peculiar – stars:individual: BD+30549 – stars: fundamental parameters – stars: abundances – stars: rotation1 Introduction
About 15-20 of stars on the upper Main sequence (MS) represent peculiar spectra which are indicative for the severe anomalies in surface chemical composition (see Smith, 1996; Romanyuk, 2007, for review). The subgroup of the helium-peculiar stars with the weakened or vice versa enhanced helium lines are considered as an extension of the sequence of magnetic Ap/Bp stars in the region of higher temperatures. The helium-peculiar stars are encountered among the spectral classes B3-B8 and many of them also host the large-scale magnetic fields with the intensity G strength. It is believed that the vertical abundance gradients in atmospheres of magnetic chemically peculiar (CP) stars and, hence, inhomogeneities of their surface elemental composition are developed by the atomic diffusion processes (Michaud, 1970; Michaud et al., 2015). It is clear that the diffusion can be sufficiently efficient and leads to the build-up of observable strong abundance inhomogeneities only in absence of the macroscopic mixing caused by convection, turbulence or meridional circulation due to axial rotation of the star.
The exact evolutionary stage when atmospheric stabilization and formation of the vertical abundance gradients occurs is still unknown. The vast majority of CP stars are the MS objects (Kochukhov & Bagnulo, 2006). However, there are number of evidence from the evolutionary trend in abundances (Bailey et al., 2014), frequency of CP stars in clusters of different ages (Netopil et al., 2015) as well as from the theoretical expectations that the surface chemical inhomogeneities could be developed before the star reached the Zero Age MS (ZAMS). The special searches of CP stars were conducted by Folsom et al. (2012) among Herbig Ae/Be stars which are still contracting Pre-MS (PMS) progenitors of the MS intermediate mass stars. They found several stars with Boo peculiarity and only one star with weak Ap/Bp pattern - V380 Ori. Recently the weak magnetic field and Ap spectral pattern were discovered in the secondary component of the PMS binary AK Sco (Castelli et al., 2020). Except these two PMS objects the present sample of very young CP stars is still very limited and contains few members of young clusters which are believed to settle on the ZAMS very recently (e.g. Bagnulo et al., 2004; Netopil et al., 2014). The expansion of this sample is essential for better understanding of the timescale and mechanisms which lead to stabilization and formation of the abundance gradients in the atmospheres of early type stars.
One possibility for increasing the sample is based on the data stored in the literature and spectral archives. In discussion on the problem of young CP stars Herbig & Dahm (2006) pointed out few poorly investigated stars as possible candidates, including BD+30549 which is the subject of the present study. The star BD+30549 locates in the northern part of NGC 1333 star forming region and illuminates the eponymous reflection nebula also known as VdB 17 (van den Bergh, 1966). The designation of NGC 1333 star forming region refers to the young stellar cluster associated with complex reflection nebula and dark cloud B255 (or L1450). NGC 1333 lies on the western edge of Perseus molecular cloud at average distance 29322 pc (Ortiz-León et al., 2018). It is the most active site of the ongoing low- to intermediate mass star formation within Perseus cloud (Bally et al., 2008; Walawender et al., 2008) with an age of its stellar population ranged from to yr Aspin (2003). The high fraction of embedded protostars and disk-bearing stars, Herbig-Haro objects and molecular outflows in this region is consistent with the more recent estimate of the cluster’s median age as 1 Myr (Luhman et al., 2016). At this age the stars later than B5 should be still PMS or early MS objects.
In early studies BD+30549 was classified as B9-8Vp star (Hubble, 1922; Racine, 1968). However, no indication of the type of peculiarity and any description of its spectrum was given in these papers. Later BD+30549 was often included in samples of Herbig Ae/Be stars, satisfying the fundamental criteria for early spectral type and association with the reflection nebula. Though the presence of emission lines in the spectrum which are indicators of the ongoing mass accretion from the circumstellar disk, and hence definite attribution BD+30549 to Herbig Ae/Be group, remains confusing. The index appeared after the spectral classification of BD+30549 in the list of Cep R1 members in Racine (1968), but was omitted in his Table II. To the best of our knowledge the only high-resolution spectrum of BD+30549 in modern era was obtained by G. Herbig, but remained unpublished. According to the characteristics given above, the star is a promising candidate for PMS chemically peculiar star. The aim of the present study is to determine the parameters of BD+30549 atmosphere, age and evolutionary status, and also to quantitatively characterize its chemical composition.
2 Observations and data reduction
To our analysis we used the high resolution optical spectrum of BD+30549 retrieved from Keck Observatory archive111https://www2.keck.hawaii.edu/koa/public/koa.php. The star was observed with the Keck I telescope and High Resolution Echelle Spectrometer (HIRES) on 2 Feb. 2000 (PI: G.Herbig). The observations were carried out with the 0.86 projected slit width that resulted in nominal resolving power about . The 4240-6710 Å range was covered by spectrogram with some interorder gaps in the red. The signal-to-noise ratio was estimated in the region near as S/N130 (per pixel). The raw data were processed with the MAKEE222https://sites.astro.caltech.edu/~tb/makee/ (MAuna Kea Echelle Extraction) pipeline written by T. Barlow. The data processing workflow included the bias subtraction and flatfielding of the science frames as well as wavelength calibration using reference spectrum of Th-Ar hollow cathode lamp. After this calibration the 1D spectrum extraction was performed. The accuracy of the localization of spectral orders in the 2D image, boundaries of object and background extraction were manually controlled.
A well-known difficulty in processing the echelle spectra of the early type stars is the normalization of the orders containing broad hydrogen lines to the continuum level. We used the method of interpolating a continuum from the neighboring orders traced with low-degree cubic spline. Thanks to the relatively smoothness of HIRES blaze function application of this method resulted in reasonably accurate normalization of the wings of hydrogen lines. The only exception was the very broad and weak depression in the red wing of H centered roughly at 4880 Å which is presumably of interstellar origin. Indeed this feature coincide in wavelength with the very broad and shallow diffuse interstellar band (DIB) at 4882 Å (Herbig, 1995; Galazutdinov et al., 2020). In any case, this region was excluded from the further spectroscopic analysis.
3 Results
3.1 Stellar parameters, distance, extinction
The absorption line-spectrum of BD+30549 generally corresponds to the mid- to late B photosphere. No hydrogen or metallic lines emissions indicative for the accretion activity were detected. Hence BD+30549 cannot be classified as typical Herbig Ae/Be star at least on the base of the spectrogram at our disposal. Its comparison with the spectra333High resolution (=42000) spectra were retrieved from the ELODIE archive (Moultaka et al., 2004) of two late-B MK standards (Gray & Corbally, 2009), namely HR1029 (sp:B7V) and 134 Tau (sp:B9IV) revealed the striking absence of the He i lines, even the strongest ones at 4471 and 5876 Å . The strong Mg ii 4481 Å line visible in spectrum of of BD+30549 seems to be somewhat shallow comparing to that in 134 Tau spectrum. At the same time the Si ii lines at 4621, 5041, 5055, 5466, 6347, 6371 Å are abnormally enhanced. The Si iii triplet at 4552, 4567, 4574 Å which is almost absent in the spectra of standards clearly seen in the spectrum of BD+30549. The notable sharpness of the absorption lines of different metals indicates very slow rotation. Qualitatively it is possible to classify BD+30549 as helium-weak Bp star with silicon peculiarity.
Rich interstellar spectrum which contains both atomic and molecular features as well as numerous DIBs is superimposed on the photospheric ones. Measurements of the radial velocity of the CH at 4300 Å , Na i D interstellar features and few most symmetric DIBs including those at 5780, 5797, 6380, 6614 Å provide average value +14 km s-1 which is close to the heliocentric radial velocity =+16.45 km s-1of BD+30549 measured by cross-correlation of the photospheric absorption lines with the template spectrum in several spectral windows.
The Gaia EDR3 (Gaia Collaboration et al., 2021) provides the parallax for BD+30549 with Renormalised Unit Weight Error parameter . This value of RUWE is well below the recommended 1.4 upper threshold444https://dms.cosmos.esa.int/COSMOS/doc_fetch.php?id=3757412 and indicates the "good behaved" astrometric solution. The parallax of the star can be converted into distance pc which is in the perfect agreement with the average distance to the NGC 1333 cluster. Both the spatial position and coincidence of the radial velocity of the star with the mean velocity of molecular material in NGC 1333 region kms-1 determined from the 13CO (3-2) and C18O (3-2) transitions (Curtis et al., 2010) confirms that location of BD+30549 inside the reflection nebula is not due to the projection effect. The star is bona fide member of NGC 1333 star forming region and still intimately connected with its parental molecular material.
Embeddedness inside the reflection nebula implies the non-negligible effects of interstellar reddening which affect the observed photometry of BD+30549. The variations of the ratio of total to selective absorption within NGC 1333 was investigated by Cernis (1990) who found that in direction toward BD+30549 it deviates significantly from the interstellar one and equals to . In order to determine the value of the interstellar extinction we used the color excess calculated from the observed color index =+0.48m (Henden et al., 2016) and the intrinsic colors interpolated from the Pecaut & Mamajek (2013) tables for our best-fit effective temperature =13100 K (Sect. 3.3). As a result we obtained visual extinction . The observed spectrophotometry of BD+30549 was dereddened using this value and Fitzpatrick et al. (2019) extinction curve. The bolometric absolute magnitude was found for BD+30549 adopting 287 pc distance and using this extinction value as well as the bolometric correction (Pecaut & Mamajek, 2013). Finally, the absolute magnitude was converted to luminosity: .
With the obtained values of luminosity and effective temperature the star was placed on HR diagram (Fig. 1). Comparison with the evolutionary tracks and isochrones from the PARSEC model grid (Bressan et al., 2012) calculated for solar metallicity revealed that BD+30549 lies near the end of the PMS track, close to ZAMS. The stellar radius inferred from the model track is . The age of the star was determined from the closest theoretical isochrone as 2.7 Myr.

3.2 Spectrophotometric properties and variability of BD+30549
3.2.1 Spectral energy distribution
The spectral energy distribution (SED) of BD+30549 was constructed in the 0.2-24 wavelength range (from ultraviolet (UV) to mid-infrared (mid-IR)) using the photometric data from XMM-OM survey (Page et al., 2012), APASS-9 (Henden et al., 2016), 2MASS (Skrutskie et al., 2006), WISE (Wright et al., 2010) catalogs and Spitzer photometry (Evans et al., 2003). Comparison of the photospheric flux calculated with our final set of atmospheric parameters (Sect. 3.3) and dilluted for the given distance pc with dereddened observations is shown in Fig. 2. Previously, BD+30549 was classified as -type source that implies the presence of near-IR (NIR) excess due to thermal radiation of circumstellar dust (Guzmán-Díaz et al., 2021). With a newly adopted and specific reddening our SED fitting resulted in excellent match between the theoretical flux and observed photometry in the optical and NIR regions within 0.23-8 range. However, the observed SED definitely shows the UV excess in the XMM-OM , bands as well as mid-IR excess at 12 in the and MPIS 24 bands. While the UV excess could be caused by the anomalous temperature structure of the BD+30549 atmosphere (Sect. 3.6), the mid-IR excess is reasonably well fitted by the 200 K blackbody radiation, as one can see from Fig. 2. The peak temperature of the excess is about an order of magnitude higher than the typical K dust temperature in the reflection nebulae (e.g. Gibson & Nordsieck, 2003). Thus the observed mid-IR excess traces the radiation of the warm dust located closer to the star in the circumstellar disk surrounding BD+30549. At the same time, the lack of NIR excess in the JHK bands and absence of the spectroscopic signatures of accretion indicates that gas and dust are depleted in the immediate vicinity of the star. Such a radial distribution of the circumstellar material is characteristic for the rather evolved disks: transitional or debris ones (Williams & Cieza, 2011)
A noteworthy detail in the mid-IR part of the SED of BD+30549 is the step difference in flux between two nearby and MPIS 24 points. The differences of about order of magnitude exceed the errors of both WISE and Spitzer photometry, thus most probably it reflects the real variability of flux. We have inspected the WISE multiepoch photometry of BD+30549 obtained on a few dates within a 6-month interval in 2010, but were not able to detect any variability exceeding 0.2m. However, the Spitzer data we used were obtained in the course of original Cores-to-Disks (c2d) Legacy program (Evans et al., 2003). Thus, variations in 24 flux occurred on a decadal timescale. A possible explanation of this mid-IR variability is the appearance of a large amount of dust in the disk at some point between the Spitzer and WISE observations. As simulations show (Kenyon & Bromley, 2005), the amount of dust which can significantly affects the observed excess at 24 could arise from the collision of 1000-km size bodies: planetesimals or planetary embryos during the late stages of planet formation. Indeed such catastrophic events resulting in temporary rise of mid-IR excess are sometimes observed in young stars with planet-forming disks (e.g. Melis et al., 2012; Su et al., 2022).


3.2.2 Photometric variability
In order to investigate the long-term photometric behavior of BD+30549, we retrieved its light curve from the database of All-Sky Automated Survey for Supernovae (ASAS-SN) (Kochanek et al., 2017). Observations in Sloan filter covering six observational seasons from 2017 to 2022 were analyzed. Even at the first glance, the periodic changes in the stellar brightness with an amplitude were manifested in the lightcurve. The frequency analysis yielded several peaks on the Lomb-Scargle periodogram, the most powerful of which correspond to 123d.3 period (Fig. 3, panel a). The phase curve folded using the ephemeris is also shown in Fig. 3 (panel b). One can see the smooth quasi-sinusoidal light changes with the prolonged minimum and somewhat sharper maximum.
Similar variability is common within the Ap/Bp stars with elemental spots on their surface. For example, well studied Ap-Si star CU Vir shows quasi-sinusoidal light changes with an amplitude up to in filter (Pyper et al., 1998). The brightness maximum of CU Vir coincides with the maximum of absorption in the Si ii lines. If we assume that the photometric variability of BD+30549 is also rotationally-modulated and caused by the chemical spots with an altered temperature structure, the date of spectral observation falling on the phase should also corresponds to the line absorption maximum. It is essential to obtain additional spectroscopic observations near the phase (corresponding to the minimum light) to test this hypothesis.
Except the main peak at the stellar rotational period we identified its first harmonic and few aliases at 73d.7, 91d.5 and 1d. After subtraction rotationally-modulated signal corresponding to the main peak, aliases at 73d.7 and 91d.5 became insignificant, however periodogram still contained meaningful peaks corresponding to the first harmonic of rotational period and diurnal alias (Fig. 3, panel c). Further subtraction of the latter two signals from the data resulted in the 3- scatter of residuals around the mean of about (Fig. 3, panel d). This is typical accuracy of the ground-based patrol photometry. However, it is worth noting that BD+30549 lies in the temperature domain of the Slowly Pulsating B (SPB) stars with periods typically ranged from to 4d (Waelkens, 1991; Kurtz, 2022). Whether BD+30549 possesses such type of variability or not could be clarified with high-precision space photometry.
3.3 Atmospheric parameters and average abundances

The atmospheric parameters of BD+30549 were determined using the self-consistent iterative procedure based on spectral synthesis technique. As an initial guess, we used the effective temperature and surface gravity of a B8 star from the MK system calibrations (Gray & Corbally, 2009; Schmidt-Kaler, 1982). In the next step, the grid of the helium-weak atmospheric models with hydrogen abundance was calculated using the LLmodels code (Shulyak et al., 2004), which accurately accounts the influence of anomalies in chemical composition on the opacity distribution in the atmosphere. Hereafter, we use the models with the temperature structure calculated for the homogeneous abundance distribution as the best approximation to date (see Sect. 3.6 for discussion). Using these model atmospheres and atomic data extracted from the VALD3 database (Piskunov et al., 1995; Ryabchikova et al., 2015; Pakhomov et al., 2019) the synthetic spectra were calculated with the Synth3 code (Kochukhov, 2007). The , parameters had been refining by the comparison of the synthetic spectrum with the observed one in the region of the wings of hydrogen H, H and H lines. Since in late-B stars the hydrogen lines are both temperature- and gravity-sensitive we used the observed SED as the independent temperature constraint. The observed spectrophotomery was dereddened using Fitzpatrick et al. (2019) extinction curve adopting . The dereddened SED was compared with the synthetic fluxes computed on each iteration with LLmodels code for a given model atmosphere. The theoretical fluxes were dilluted assuming the 287 pc distance and the stellar radius . The microturbulent velocity was determined by the classical method of minimizing the slope of the dependence of the elemental abundance on the equivalent widths. We used a set of unblended Fe ii/ iii lines further employed for stratification analysis (see Sect. 3.5 and Tab. 4). The calculations were performed with a version of the Kurucz’s Width code modified by V. Tsymbal (priv.com.). The procedure of spectrum and SED fitting was repeated in a few iterations. The uncertainties of derived parameters were estimated from the dispersion of few last iterations around the best-fit solution.
As a result the following set of parameters was determined: the effective temperature =13100100 K, the surface gravity =4.2, the microturbulent velocity =0 km s-1. The stellar parameters are also summarised in Table 1. The comparison of the observed and synthetic Balmer lines profiles calculated with this final set of parameters is shown in Fig. 4. One can see the reasonable agreement between synthetic spectrum and observations for H and H lines. The prominent discrepancy between the observations and synthetic spectrum in the core of the H line is caused by unaccounted non-LTE effects, while a little mismatch in the red wing could be due to the spectrum reduction faults. At the same time, the theoretical SED reproduces well the magnitude of the Balmer discontinuity and the slope of the Paschen continuum (Fig. 2), that confirms the reliability of our effective temperature determination.
The macroscopic broadening parameters: rotational broadening and macroturbulence were found by fitting the metallic lines profiles in several spectral windows (e.g. 4590-4650 Å , 5045-5115 Å ) with the BinMag6 tool (Kochukhov, 2018). In agreement with the visual impression of the lines sharpness, neither rotational nor macroturbulence broadening was detected. Given the spectral resolution and instrumental profile width we can set the upper limit for rotational velocity as 1-2 km s-1 .
Despite the sharpness of absorption lines and the evidence for highly stabilized atmosphere no sign of Zeeman splitting or sufficient magnetic intensification was detected in the magnetically-sensitive spectral lines like Fe ii 4303, 4385, 4520, 6149 Å . Within the measurement error we also were unable to detect the differential magnetic intensification in the Fe ii 6147/6149 Å pair of lines which often is considered as an indication of the magnetic field presence (Mathys &
Lanz, 1992; Kochukhov
et al., 2013). These lines have identical intensity in normal stars without magnetic fields but possess a different Zeeman spitting that produces a difference in the observed equivalent widths when the magnetic field is presented.
We estimate the normalized equivalent width difference of these lines as . Unfortunately, there is no accurate experimental transition probabilities for these lines. Non-magnetic spectrum synthesis results in =0.026 with the theoretical transition probabilities from Raassen &
Uylings (1998) while =0.003 with the theoretical transition probabilities from Kurucz’s 2013 line list555http://kurucz.harvard.edu/atoms/2601/gfemq2601.pos. Magnetic spectrum syntesis of this pair with the help of SYNMAST code (Kochukhov, 2007) showed that a global magnetic field 1 kG produced too wide synthetic line profiles. Therefore, we set an upper limit on the strength of the mean magnetic field as 1 kG. Although based on single-epoch spectroscopy, we cannot rule out the possible existence of a stronger magnetic field in BD+30549, which could be detected in another rotational phase, or, more confidently, with the spectropolarimetric observations.
| Parameter | Value |
|---|---|
| 13100100 K | |
| 4.20.1 dex | |
| 0.00.2 km s-1 | |
| 0.01.5 km s-1 | |
| <2.0 km s-1 | |
| kGs | |
| 2.8m | |
| 2.130.05 | |
| 3.2 | |
| 2.2 | |
| Age | 2.7 Myr |
Line identification in BD+30549 spectrum was performed using a synthetic spectrum calculated in the entire range 4240-6710 Å covered by the spectrogram at our disposal, we also used the line lists from Fossati et al. (2009) for guidance. Due to relatively high effective temperature most of the elements in BD+30549 spectrum are presented by the moderate number of lines of the first ions. Only iron and silicon possess lines originated from two different ionization stages. The negligible rotational broadening simplified the task of lines selection. We were able to select a reasonable number of lines for abundance analysis, although for some light elements e.g. C and O the sampling was incomplete due to the limited spectral coverage and decrease of S/N ratio in the blue spectral region. The atomic data for abundance analysis were taken from the VALD3 database. For the light elements Mg and Si the oscillator strengths , excitation energies and damping constants retrieved from the VALD were checked against critically selected data from Alexeeva et al. (2018); Mashonkina (2020) and if necessary replaced by the latter values. We compiled a list of Fe ii/ iii with excitation energies ranged from 2.8 to 18.2 eV for the abundance determination and subsequent stratification analysis (see Tab. 4). Hyperfine splitting was taken into account for Al ii and Ti ii using the facilities of VALD3 database (Pakhomov et al., 2019).
Abundances, , were determined under LTE assumption as the mean of measurements of several lines of a given element . Individual abundances were deduced from the fitting of observed line profiles by synthetic one with BinMag6 tool. The error in abundance determinations was estimated as a standard deviation of individual measurement from the mean.

We derived LTE abundances of 13 elements. The results of the abundance analysis are summarised in Table 2 and are also shown in Fig. 5. In the latter plot we compare the derived abundances with the solar ones as [X/H]=. The reference solar abundances were taken from Scott et al. (2015a); Scott et al. (2015b) for elements from Na to Ni while the rest were adopted from Asplund et al. (2009). Most of the studied elements in BD+30549 show depletion up to dex with respect to the solar atmosphere. We were unable to detect any traces of absorption due to He i at 4471, 5015, 5876 Å and hence put the upper limit for helium abundance as dex, which is 2.4 dex lower than the solar value. Contrary, Si , Ca , P and Fe display the overabundance. For silicon and iron, we found substantial abundance differences of 0.8 dex and 1.2 dex, respectively, between the lines of the first and second ions. Also for the strongest lines of Si ii (5055/5056, 6347, 6371 Å) and Mg ii 4481 Å, their wings and cores cannot be fitted with a single value of abundance. In such cases, the element abundance that fits the entire profile in the best way was adopted as a final value. The found discrepancies inspired us to check an influence of the departures from LTE on line formation for Si ii-iii, Mg ii, and Ca ii and to determine the non-local thermodynamic equilibrium (non-LTE) abundances (Sect. 3.4).
Despite the mild phosphorus overabundance in BD+30549 atmosphere, we were unable to detect any gallium lines which could be also enhanced in spectra of the phosphorus-gallium subgroup of the helium-weak stars. We also did not find any strontium lines, because the strongest of them, Sr ii 4077Å and 4215 Å, were not covered by our spectrogram.
| Ion | |||
|---|---|---|---|
| He i | … | -1.07 | |
| C ii | 2 | -4.67 | -3.57 |
| O i | 3 | -4.21 | -3.31 |
| Mg ii | 6 | -5.48 | -4.41 |
| Al ii | 4 | -6.16 | -5.57 |
| Si ii | 7 | -3.15 | -4.49 |
| Si iii | 3 | -2.33 | -4.49 |
| P ii | 6 | -6.20 | -6.59 |
| S ii | 6 | -6.29 | -4.88 |
| Ca ii | 5 | -5.04 | -5.68 |
| Ti ii | 6 | -7.77 | -7.07 |
| Cr ii | 8 | -6.70 | -6.38 |
| Fe ii | 20 | -4.61 | -4.53 |
| Fe iii | 7 | -3.44 | -4.53 |
| Ni ii | 5 | -6.15 | -5.80 |
3.4 Non-LTE effects on lines of Si ii– iii, Ca ii, and Mg ii

Lines of Si ii and Si iii in BD+30549 reveal the largest deviations from the classical line-formation scenario that is based on the assumptions of LTE and a chemical homogeneity of the atmosphere. In this section, we check an influence of the departures from LTE on the statistical equilibrium (SE) of silicon and the element abundances derived from different Si lines. The non-LTE calculations were performed with the model atom treated by Mashonkina (2020). It includes levels of the first three ionization stages (Si i, Si ii, and Si iii) and the ground state of Si iv and implements the most up-to-date atomic data on transition probabilities, photoionization cross-sections, and electron-impact excitation rates. One of the stars studied by Mashonkina (2020), namely, HD 17081 ( Cet), has atmospheric parameters ( = 12800 K and log = 3.75) close to that of our star. The LTE analysis of Cet found an abundance difference of 0.23 dex between the two ionization stages, Si ii and Si iii, while consistent within 0.03 dex abundances were obtained in the non-LTE calculations. Compared with Cet, BD+30549 reveals substantially larger LTE abundance discrepancies between Si ii and Si iii and high Si abundance, which exceeds the solar one by more than 1.3 dex. In the atmosphere enhanced with silicon, the Si line-formation depths shift to the upper atmospheric layers that can result in the stronger non-LTE effects compared with those for Cet.
The coupled radiative transfer and statistical equilibrium equations were solved with the code detail (Giddings, 1981; Butler, 1984), where the opacity package was updated as presented by Mashonkina et al. (2011). Figure 6 displays the departure coefficients, b, of the selected levels of Si ii and Si iii involved in the transitions, where the Si ii 5041, 5055, 5056 Å ( – ) and Si iii 4552 Å ( – ) lines arise. Here, and are the SE and thermal (Saha-Boltzmann) number densities, respectively. Si ii is subject to overionization in the line-formation layers, above log = 0, resulting in depleted populations of the ground state and the excited levels up to ( = 10.1 eV). The upper level of the Si ii – transition is depopulated to a lesser extent than is the lower level in the atmospheric layers up to log and, in contrary, to a greater extent in the higher layers. Such a behavior of is explained by a competition of the pumping UV transition from the ground state and spontaneous transitions to the levels below . As a result, the Si ii 5041 Å line, which forms downwards log , is weakened compared with its LTE strength (Fig. 7, middle panel) due to b() and the line source function, , greater than the Planck function, . The core of Si ii 5055.98 Å forms around log , where , and this prevails over b() , resulting in strengthened line core (Fig. 7, top panel). The wings of Si ii 5055.98 Å form in deeper layers and are weakened compared with the LTE case. Note that, in Fig. 7, the non-LTE profile of Si ii 5055.98 Å was computed with a higher Si abundance than that for the LTE profile.
The Si iii levels have enhanced populations in the line-formation layers, resulting in strengthened Si iii lines compared with their LTE strengths, as shown in Fig. 7 for Si iii 4552 Å.

| Ion | , Å | Comment | , eV | ||||
|---|---|---|---|---|---|---|---|
| LTE | non-LTE | (line center) | |||||
| Si ii | 4621.42 | 12.53 | -0.610 | -3.09 | -2.97 | -1.69 | |
| Si ii | 4621.70 | blend | 12.53 | -1.750 | -3.09 | -3.07 | -1.83 |
| Si ii | 4621.72 | blend | 12.53 | -0.450 | -3.09 | -3.07 | -1.83 |
| Si ii | 5041.02 | 10.07 | 0.030 | -3.15 | -2.97 | -3.23 | |
| Si ii | 5055.98 | 10.07 | 0.520 | -3.20 | -3.10 | -3.56 | |
| Si ii | 5466.85 | blend | 12.52 | -1.380 | -3.20 | -2.99 | -2.26 |
| Si ii | 5466.89 | blend | 12.52 | -0.080 | -3.20 | -2.99 | -2.26 |
| Si ii | 6371.37 | 8.12 | -0.080 | -3.18 | -3.18 | -4.07 | |
| mean | -3.150.05 | -3.040.08 | |||||
| Si iii | 4552.62 | 19.02 | 0.290 | -2.28 | -2.52 | -0.78 | |
| Si iii | 4567.84 | 19.02 | -0.070 | -2.20 | -2.38 | -0.66 | |
| Si iii | 4574.76 | 19.02 | -0.410 | -2.51 | -2.62 | -0.56 | |
| mean | -2.330.16 | -2.510.12 | |||||
| Ca ii | 5001.48 | 7.51 | -0.507 | -4.94 | -4.48 | -0.76 | |
| Ca ii | 5019.97 | 7.51 | -0.247 | -5.20 | -4.73 | -0.76 | |
| Ca ii | 5307.22 | 7.51 | -0.848 | -4.99 | -4.53 | -0.37 | |
| Ca ii | 5339.19 | 8.44 | -0.079 | -5.01 | -4.55 | -0.51 | |
| mean | -5.040.11 | -4.570.11 | |||||
The LTE and non-LTE synthetic spectra were calculated with the SynthV_NLTE code (Tsymbal et al., 2019), which implements the pre-computed departure coefficients from the DETAIL code. The best fit to the observed spectrum was obtained automatically using the IDL BinMag6 tool. In the fitting procedure, = 0, = 0, and = 48 000 were fixed, while the Si abundance and macroturbulent velocity were allowed to vary.
We found that profiles of the Si ii 4621.4, 4621.7, 5041.0, 5466.8 Å lines are well fitted in non-LTE (see Fig. 7 for Si ii 5041 Å) and the obtained non-LTE abundances are higher than the LTE ones, by 0.12 to 0.21 dex (Tab. 3). For the Si ii 5056 Å blend, the non-LTE profile reproduces the observed one better than the LTE profile, however, fails to fit to the observed line core (Fig. 7). The non-LTE abundance obtained from the line wings beyond the relative flux of is only about 0.1 dex lower compared with that for the well-fitted Si ii lines. The strongest Si ii 6347.1 and 6371.3 Å lines, with their cores formed in the uppermost atmospheric layers (log ), can only be fitted in their outer wings ().
The Si iii line profiles in BD+30549 are well fitted in the non-LTE calculations. Their non-LTE abundance corrections, , are negative and amount to dex to dex (Tab. 3). Thus, non-LTE reduces an abundance discrepancy between Si iii and Si ii, however, it is still substantial, (Si iii – Si ii) = 0.53 dex. The non-LTE calculations confirm a strong enhancement of silicon in the atmosphere of BD+30549, with [Si/H] = 1.45 and 1.98 from lines of Si ii and Si iii, respectively.
Our spectrum of BD+30549 covers only weak Ca ii lines listed in Table 3. They all form in deep atmospheric layers and, in the LTE analysis, indicate an enhanced Ca abundance. We performed the non-LTE calculations using the model atom treated by Mashonkina et al. (2007). It was successfully applied by Sitnova et al. (2018) to achieve the Ca i/Ca ii ionization equilibrium in the sample of A-B type stars, including the star Cet with and log close to the corresponding parameters of BD+30549.
We obtained that, in the line-formation layers of BD+30549, Ca ii is subject to overionization, resulting in depleted level populations, weakened spectral lines, and positive non-LTE abundance corrections. The lines under investigation have very similar = 0.46 and 0.47 dex (Tab. 3). Thus, the derived Ca abundance is pushed up to [Ca/H] = 1.11.
The non-LTE calculations were also performed for Mg i-Mg ii using the non-LTE method treated by Alexeeva et al. (2018). In contrast to Si and Ca, Mg is underabundant in the atmosphere of BD+30549, with [Mg/H] from the LTE analysis. Therefore, compared with the Si ii lines of similar excitation energy and -value, the Mg ii lines form deeper in the atmosphere, and the non-LTE effects are expected to be smaller. The core of the strongest of the used lines, Mg ii 4481 Å, forms around log and the remaining Mg ii lines listed in Table 4 form close to log . Similarly to Si ii and Ca ii, Mg ii is subject to overionization in the atmosphere of BD+30549. The non-LTE effects are minor, with 0.01 dex, for all the Mg ii lines except Mg ii 4481 Å. For the latter, non-LTE leads to the strengthened line core, but the weakened line wings and dex.
In summary, accounting for the non-LTE effects leads to much better representation of those silicon lines, which are formed at intermediate optical depths (log ), but fails to reproduce profiles of the strongest Si ii 5056, 6347, 6371 Å lines. Non-LTE reduces, but does not remove the abundance discrepancy between Si ii and Si iii. The obtained results lead us to suspect a presence of a vertical abundance gradient for silicon, with increasing abundance towards deeper layers. We consider the chemical stratification in the next section.
3.5 Vertical abundance stratification in BD+30549 atmosphere
Abundance analysis of BD+30549 under assumption of a chemically homogeneous atmosphere led to the following discrepancies, which are canonical signatures of a vertical abundance gradients (Ryabchikova et al., 2003):
-
•
Strong Si and Mg lines require different abundances to fit their wings and cores.
-
•
The abundances obtained from the lines of the same ion, e.g. Fe ii show a dependence on the excitation energies. The strong Fe ii lines which are formed in the upper layers indicate a lower abundance than the weaker ones, forming deeper in the atmosphere.
-
•
The lines of the second ions Fe iii and Si iii are abnormally strong and could not be fitted with the same abundances as for the first ions of iron and silicon.
Therefore we performed the stratification analysis using the approximation of the vertical abundance distribution in the atmosphere by the step-like function (see e.g Ryabchikova et al., 2005; Kochukhov et al., 2006, for validation of the method). Stratification calculations were made for three elements Fe , Si and Mg with DDAFit code (Kochukhov et al., 2006). The automatic procedure is based on the least-square fitting of the observed line profiles varying the four parameters which characterize the stratification profile: lower and upper abundances, position and width of the abundance jump in the scale. Selection of spectral lines and atomic data for analysis is of critical importance for reliable reconstruction of stratification profile. The employed linelist should include lines with different excitation energy of the lower level, , and formed at different optical depths, which are uniformly distributed through the atmospheric layers contributing to the line absorption.

The linelist with atomic parameters used in our calculations is presented in Table 4. Thanks to the large number of observed lines, including those from the second ionization stage, these line selection criteria are easily fulfilled for the iron. For iron we performed calculations with two sets of atomic data. First was based on Kurucz’s 2010 and 2013 lists for Fe iii and Fe ii respectively, while in second one we used primarily Raassen & Uylings (1998) data for Fe ii. Both datasets resulted in the fairly close parameters of the stratification profile, but linelist based entirely on the Kurucz’s data made it possible to fit the observed line profiles more accurately. The silicon lines we used also originate from the two ionization states and are more or less evenly distributed in the 8-19 eV energy range. In contrast, most of the available magnesium transitions are in the narrow range of excitation energies. However, the strong Mg ii 4481Å line is formed over a wide range of optical depths and allows to account for the contribution of different atmospheric layers.
| Ion | Wavelength, Å | , eV | Ref. | ||
|---|---|---|---|---|---|
| Fe ii | 4508.280 | 2.85 | -2.420 | -6.530 | K13, WS() |
| Fe ii | 5018.436 | 2.89 | -1.399 | -6.583 | K13 |
| Fe ii | 5022.418 | 10.35 | -0.054 | -5.567 | K13 |
| Fe ii | 5022.789 | 10.35 | -0.005 | -5.367 | K13 |
| Fe ii | 5030.632 | 10.29 | 0.381 | -5.891 | K13 |
| Fe ii | 5045.106 | 10.31 | -0.151 | -4.984 | K13 |
| Fe ii | 5127.961 | 5.57 | -2.397 | -6.520 | K13 |
| Fe ii | 5169.028 | 2.89 | -1.300 | -6.590 | K13 |
| Fe ii | 5278.939 | 5.91 | -2.520 | -6.696 | K13 |
| Fe ii | 5291.661 | 10.48 | 0.561 | -5.468 | K13 |
| Fe ii | 5303.393 | 8.18 | -1.625 | -5.822 | K13 |
| Fe ii | 5325.552 | 3.22 | -3.185 | -6.603 | K13 |
| Fe ii | 5549.000 | 10.52 | -0.186 | -5.330 | K13 |
| Fe ii | 5567.831 | 6.73 | -1.866 | -6.578 | K13 |
| Fe ii | 6149.246 | 3.89 | -2.732 | -6.588 | K13 |
| Fe iii | 4395.751 | 8.26 | -2.586 | -6.680 | K10 |
| Fe iii | 4419.596 | 8.24 | -1.690 | -6.680 | K10 |
| Fe iii | 5063.467 | 8.65 | -2.922 | -6.680 | K10 |
| Fe iii | 5086.706 | 8.66 | -2.563 | -6.680 | K10 |
| Fe iii | 5114.606 | 8.65 | -3.235 | -6.680 | K10 |
| Fe iii | 5156.111 | 8.64 | -1.922 | -6.680 | K10 |
| Fe iii | 5276.476 | 18.26 | -0.067 | -6.350 | K10 |
| Fe iii | 5282.297 | 18.26 | 0.044 | -6.350 | K10 |
| Mg ii | 4384.637 | 9.99 | -0.790 | -4.07 | NIST |
| Mg ii | 4390.514 | 9.99 | -1.490 | -4.07 | NIST |
| Mg ii | 4390.572 | 9.99 | -0.530 | -4.07 | NIST |
| Mg ii | 4427.994 | 9.99 | -1.208 | -4.40 | NIST |
| Mg ii | 4433.988 | 9.99 | -0.910 | -4.40 | KP |
| Mg ii | 4481.126 | 8.86 | 0.749 | -4.70 | NIST |
| Mg ii | 4481.150 | 8.86 | -0.560 | -4.70 | NIST |
| Mg ii | 4481.325 | 8.86 | 0.590 | -4.70 | NIST |
| Mg ii | 6545.942 | 11.63 | 0.040 | -2.98 | KP |
| Mg ii | 6545.994 | 11.63 | 0.150 | -2.98 | KP |
| Si ii | 4621.418 | 12.52 | -0.610 | -3.86 | M95 |
| Si ii | 4621.696 | 12.52 | -1.750 | -3.86 | M95 |
| Si ii | 4621.722 | 12.52 | -0.450 | -3.86 | M95 |
| Si ii | 5041.024 | 10.07 | 0.030 | -4.80 | M01 |
| Si ii | 5055.984 | 10.07 | 0.520 | -4.76 | M01 |
| Si ii | 5056.317 | 10.07 | -0.490 | -4.76 | M01 |
| Si ii | 5056.317 | 10.07 | -0.490 | -4.76 | M01 |
| Si ii | 5462.144 | 12.88 | -1.107 | -4.04 | K14 |
| Si ii | 5466.460 | 12.52 | -0.080 | -4.20 | M95 |
| Si ii | 5466.849 | 12.52 | -1.380 | -4.20 | M95 |
| Si ii | 5466.894 | 12.52 | -0.080 | -4.20 | M95 |
| Si ii | 5469.451 | 12.88 | -0.762 | -4.06 | M95 |
| Si ii | 5469.233 | 16.73 | -1.100 | -4.06 | M95 |
| Si ii | 6371.371 | 8.12 | -0.080 | -5.08 | M01 |
| Si iii | 4552.622 | 19.02 | 0.290 | 0.00 | NIST |
| Si iii | 4567.840 | 19.02 | -0.070 | 0.00 | NIST |
| Si iii | 4574.757 | 19.02 | -0.410 | 0.00 | NIST |
The resulting abundance stratification for Mg and Fe are shown in Fig. 8. The iron and magnesium possess the step abundance gradient in the narrow range of optical depths near . Both elements show tendency to increase abundance in the deeper atmosphere. Iron is mildly depleted in the upper atmosphere and increased its concentration with depth up to dex excess relative to the Sun. Magnesium is significantly underabundant by 1.9 dex in the upper atmospheric layers, reaches the solar value at and experiences a mild overabundance in the deepest layers contributing to line absorption. Comparison between observed lines profiles and synthetic ones calculated with stratified abundances shows a reasonable agreement in case of Fe and Mg . Compared with the homogeneous distribution, accounting for stratification allows to adequately reproduce the line core depths for Fe lines arising from both ionization stages (Fig. 9), as well as the profiles of magnesium lines including wings of the Mg ii 4481Å line (Fig. 10).
In contrast, the jump of stratification profile for silicon turned out to be very gradual, distributed over the wide range of optical depths. Resulting fit of the observed lines profiles is poor and can reproduce neither the enhanced absorption in the Si iii lines, nor the wings of the strong Si ii lines.


Qualitatively, depth-dependence of iron and magnesium abundance as well as the depletion of helium in the upper atmosphere of BD+30549, is consistent with the results of theoretical calculations (LeBlanc et al., 2009) and points to selective diffusion as the reason for the vertical stratification of these elements. However, exact position and magnitude of the abundance jumps in the BD+30549 atmosphere deviates from the model predictions. First, these parameters depend on the physical conditions in a given atmosphere, and, second, the calculations represent the equilibrium solution while equilibrium could not yet be reached in the young BD+30549 atmosphere. It is interesting to note that the results of the LeBlanc et al. (2009) calculations show a flattening of the stratification profiles as the rises from 8000 K to 12000 K. The latter value is the maximum effective temperature used in their calculations, and the resulting abundance gradients are overplotted in our Fig. 8. It is evident that the stratification profiles in the hotter atmosphere of BD+30549 are steeper, in contrast to the theoretical predictions. This can be due to the star’s young age and non-equilibrium diffusion processes.
3.6 Impact of the Si overabundance on the atmospheric structure
Our abundance analysis revealed that both silicon and iron are substantially overabundant in BD+30549 atmosphere (Sect. 3.3) and also these elements possess both vertical and probably lateral abundance gradients (Sect. 3.5; 3.2.2). These metals play the important role in the opacity distribution throughout the atmosphere due to bound-free transitions and consequently affect its thermal balance (e.g. Khan & Shulyak, 2007). Indeed, as far back as Strom & Strom (1969) it was shown that 1.5 dex silicon enhancement affects the structure of the atmosphere in the same way as a 1000 K increase in and also causes a flux redistribution in the UV.
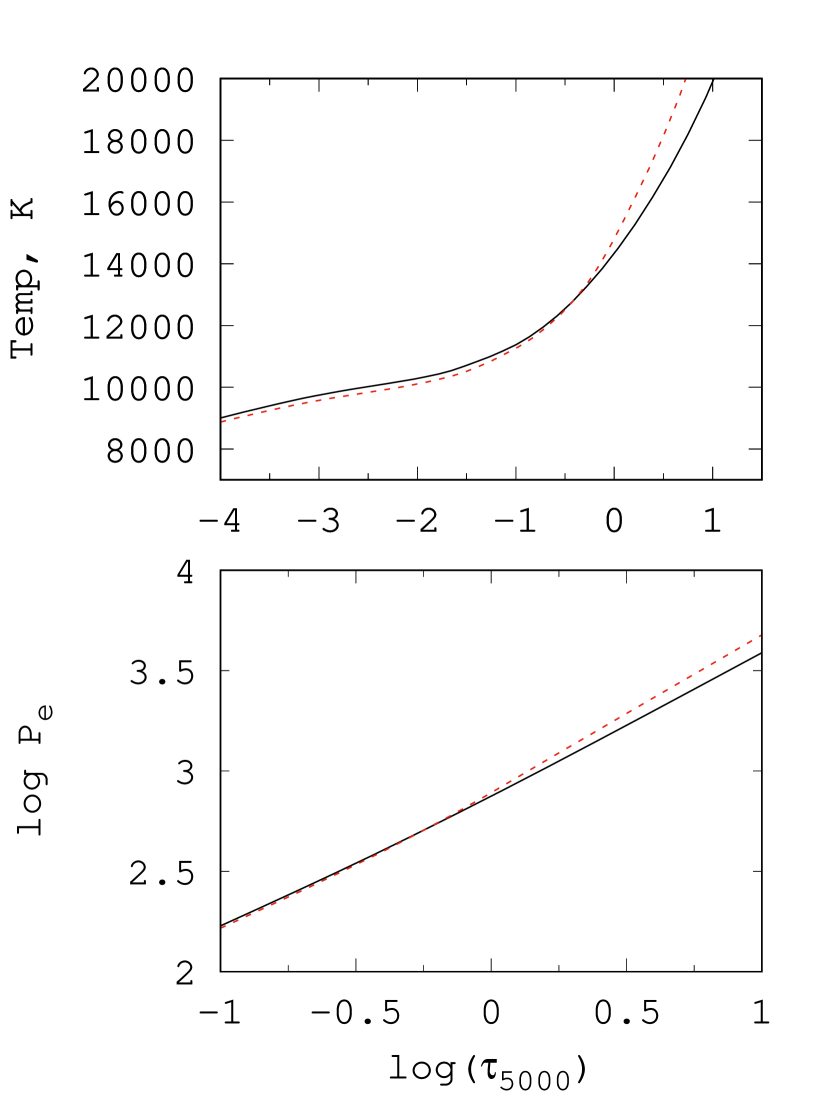
We performed a preliminary series of calculations to check how the vertical and horizontal stratification of the silicon affects the atmospheric model structure and emergent spectrum in case of BD+30549. First, we calculated with LLmodel code the atmospheric model taking into account the individual abundances determined in BD+30549 atmosphere as well as the vertical stratification for Si , Fe and Mg . For iron and magnesium we applied stratification profiles derived from our analysis (see Fig. 8). For silicon profile was set manually. The abundance dex deduced from the LTE determination using Si iii lines was adopted for the deep atmospheric layers, while as the upper limit we took dex obtained from our fitting procedure with DDAFit. The location of the abundance jump was set at the same optical depths as for iron. Results of calculations are shown in Fig. 11. One can see that the temperature structure of the model changed noticeably both in the regions of lines and continuum formation. In the line forming region, we obtained a trend of decreasing temperature with depth compared to the homogeneous model (also helium-weak and silicon-rich). The difference reaches 3 at . The change in the electron pressure was less pronounced and occured predominantly in the deep atmospheric layers with . The joint effect of these changes on the SED and line profiles appeared to be significant. The stratified model provides the larger Balmer discontinuity and steeper Balmer continuum in UV. The latter resulted in better fit of the observed fluxes in the XMM-OM and filters than in case of homogeneous model (see Fig. 2). The magnitude of the Balmer jump produced with stratified model is less consistent with the observations, but this can be compensated by small variations in extinction and increasing within 300 K. Nevertheless, in the synthetic spectrum calculated with the stratified model, the Balmer lines became much broader. Fitting the theoretical profiles to the observed ones requires significant temperature correction, conflicting with the SED fitting. We conclude that current calculations with the homogeneous provide better simultaneous representation of the SED and line absorption spectrum of BD+30549.
Although our spectrum allowed to put only an upper limit on the strength of the magnetic field of BD+30549 at the date of observation, generally helium-weak silicon stars belongs to the magnetic sequence of CP stars (Romanyuk, 2007). Therefore, if BD+30549 hosts a large-scale magnetic field, it could also lead to the patchy horizontal distribution of elements, i.e. existence of elemental spots with an altered temperature structure. The detected photometric variability of BD+30549 preliminary confirms this assumption.
To take into account the influence of the silicon spot on the emergent spectrum, we used approach similar to that applied for another silicon star CU Vir (Krivoseina et al., 1980). A grid of simple models in which 50% of the stellar surface is occupied by a spot with enhanced silicon abundance and the rest of the surface being with the solar abundance has been computed. The temperature structure of the spot was recomputed with the LLmodel code, taking into account the opacity due to the increased silicon abundance. Varying the spot area and silicon abundance within reasonable limits, we were able to reproduce the profiles of individual silicon lines. However, the attempt to simultaneously reproduce Si ii and Si iii lines with the same abundance in the spot also failed. A simple estimate also shows that presence of such a spot with [Si /H]=+1.8 dex leads to rotational brightness modulation with an amplitude up to magnitude in the filter. This value is less than the observed amplitude, but it should be taken into account that in reality the temperature structure of the spot could be modified by opacity due to other elements as well as by effects of vertical stratification. Thus, in order to reproduce the emergent spectrum, one needs to know both the distribution of spots on the stellar surface and the elemental abundances within each of them. Such information can be obtained from a subsequent spectroscopic monitoring of BD+30549.
4 Discussion
4.1 Stellar parameters, chemical abundances and stratification
Our spectroscopic analysis of BD+30549 atmosphere yields the following parameters: =13100100 K and = 4.20.1. According to the modern temperature calibrations of MKK system (Gray & Corbally, 2009; Pecaut & Mamajek, 2013) such an effective temperature, as well as the bolometric absolute magnitude , are in the reasonable agreement with the historical spectral classification of the star as B8. Our analysis revealed the significant depletion of helium in the atmosphere of BD+30549 with dex. Other elements on average are also depleted, with the exception of Ca , P , Si and Fe which possess mild- to strong overabundance. The helium-weak stars constitute a rather heterogeneous group of hot CP stars and reveal a diversity of the element abundance patterns (see e.g. Ghazaryan et al., 2019). With the obtained element abundance pattern, BD+30549 is not an outlier in this group. We attribute BD+30549 with a caution to the silicon subgroup of helium-weak stars because of strikingly enhanced lines of Si ii and Si iii in its spectrum.
Except the general enrichment of silicon in BD+30549 atmosphere which exceeds more than 1.3 dex with respect to the solar value, the lines corresponding to the two ionization stages yield an abundance difference of about 0.8 dex. In fact, such a discrepancy in abundances deduced from the Si ii and Si iii lines is known for B-type stars (see Bailey & Landstreet, 2013, and references therein). The latter authors studied this "Si ii/ iii-anomaly" on the representative sample containing normal B-type stars as well as magnetic Bp and HgMn stars. It was shown that both magnetic and non-magnetic stars exhibit (Si iii – Si ii) difference, but in case of normal B stars it is less pronounced reaching dex. The non-LTE effects and abundance stratification were proposed as possible reasons for this "Si ii/ iii-anomaly" . Indeed the non-LTE calculations by Mashonkina (2020) resulted in agreement between Si iii and Si ii based abundances for normal B7 and B3 stars, i.e. eliminated the difference in LTE abundances of 0.23 and 0.7 dex.
However, in case of BD+30549 even after accounting for the non-LTE effects the 0.5 dex difference still persists between abundances deduced from the Si ii and Si iii lines. Intuitively, the discrepancy in the silicon lines after accounting for the non-LTE effects suggest its depletion in the upper atmosphere with increasing abundance in the deepest layers. Indeed, we found clear observational evidence of vertical abundance stratification in BD+30549 manifested in the lines of some other elements, e.g. Fe and Mg . However, in our analysis we were unable to construct such a stratification profile to equalize the abundances determined from the silicon lines forming at significantly different optical depths. Although at present state we cannot fully explain the "Si ii/ iii-anomaly" observed in BD+30549 spectrum, our results clearly indicate that combination of the effects of abundance stratification as well as departures from LTE in the silicon’s line formation region contributes to its appearance, in agreement with suggestion by Bailey & Landstreet (2013).
Another important factor which have to be accounted is inhomogeneous lateral distribution of elements over the stellar surface (chemical spots), which is typical for Ap/Bp stars. In the case of BD+30549, the spots manifest in the rotationally-modulated period, detected in photometric variability of the star. Our preliminary calculations have shown that both silicon overabundance and vertical gradient of its abundance also affects significantly the temperature structure of the atmosphere. Thus, we reinforce the conclusion by Kochukhov & Ryabchikova (2018) that sophisticated interpretation of the observed spectra of CP stars generally requires taking into account the 3D distribution of abundances and subsequent recalculation of the atmospheric structure.
4.2 Evolutionary status and conditions for early development of chemical peculiarity
CP helium stars are abundant among the young stellar population in OB associations and Galactic star forming regions. For a long time numerous helium-weak stars are known in young Orion and Scorpius-Centaurus OB associations (see review in Smith, 1996). The existence of helium-weak stars in Ori OB1c ( Myr old, Bally (2008)) subgroup (Romanyuk et al., 2013), as well as recent finding of the helium-weak silicon star in the Orion’s Trapezium region (Costero et al., 2021) (although without unambiguous attribution to Myr old Trapezium cluster) indicate that the onset of this type of peculiarity is either a very rapid process, or it can be triggered long before star’s settling on the ZAMS, during the PMS phase. The target of the present study, BD+30549, is the member of active NGC 1333 star forming region and still embedded in the reflection nebula. Its isochronal age Myr is slightly larger than the median cluster age Myr (Luhman et al., 2016) but is well within age dispersion found by Aspin (2003). In the HR diagram, BD+30549 lies at the end of its PMS track, very close to the ZAMS.
Results of modern time-dependent diffusion calculations show that the diffusion timescale in the typical Ap/Bp atmosphere is of order yr (Alecian et al., 2011; Alecian & Stift, 2019), and hence development of the surface chemical inhomogeneities can occurs rapidly when the favorable conditions for an effective atomic diffusion have been achieved. Basically, such conditions are set up by slow axial rotation and hence ineffective meridional circulation as well as by suppressing of the microturbulence.
Indeed, our spectroscopic analysis revealed zero turbulence in the atmosphere of BD+30549 and undetectable rotational broadening of the absorption lines with the upper limit on projected rotational velocity kms-1. Is BD+30549 a really slow rotator or it is observed pole-on? If the photometric variability of the star is rotationally-modulated, then the 123d.3 period corresponds to the equatorial rotation velocity kms-1, adopting the stellar radius . This velocity is in good agreement with our spectroscopic determination and implies that the star is observed close to equator-on. If we assume that during the PMS phase, BD+30549 followed the evolutionary path of a typical Herbig Ae/Be star, then after the main protostellar mass-accretion phase it should gained the angular momentum resulted in typical equatorial rotational velocity of order 150 kms-1 (corresponding rotational period for ). Comparing this value with the present day rotational period we conclude that that BD+30549 has lost (or not gained) a significant fraction of its angular momentum during the PMS phase.
The main agent in various macroscopic mechanisms of rotational braking (see Bouvier, 2013, for review) is believed to be the magnetic field, which is also effectively suppresses the turbulence and various types of circulation in the outer layers of the atmosphere (Mestel & Moss, 1977). Another possibility sometimes invoked to explain the loss of the angular momentum by Ap/Bp stars is synchronization in a binary system. Below we will examine both of these scenarios to see if they can explain an increase the rotational period of BD+30549 from to about during the lifetime of the star, i.e Myr.
4.2.1 Synchronization in binary system
The structure of the SED of BD+30549 shows the absence of the NIR emission above the photospheric level within 1.2-8 range, indicative for the inner cavity in the disk. At the same time, the mid-IR excess peaked at 24 is approximated by K blackbody radiation and traces warm dust on the inner edge of the disk. Assuming 200 K as the equilibrium temperature of the dust, we can estimate its radial distance from the relation . Substituting the stellar parameters =13100 K and we obtain the inner cavity radius 50 au. Such a radial distribution of dust is typical for evolved transitional or debris disks (Williams & Cieza, 2011). Recent interferometric observations showed that such large cavities in disks around Herbig Ae/Be stars are widespread (e.g. van der Plas et al., 2017a, b) and could be opened by both accretion and photoevaporation processes, as well as by the orbital motion of the secondary companion.
If we assume that the radius of the circular orbit of the putative secondary companion coincides with the inner boundary of the disk, then corresponding Keplerian period at this distance will be 196 yr for the given stellar parameters. However, the variability of the mid-IR excess indicates the existence of the population of 1000-km size bodies at this distance rather than single massive companion (see Sect. 3.2). Obviously, such bodies cannot play a role in tidal slowdown of the host star.
Moreover, synchronization for such a long period is fundamentally doubtful. Both the observational studies (Abt & Snowden, 1973; Gerbaldi et al., 1985) and theoretical consideration (Zahn, 1977) suggest that synchronization usually occurs for the short orbital periods , and statistically the number of synchronized systems among Ap/Bp stars is low. Thus, we have to assume the existence of a closer and more massive companion inside the central cavity in the disk in order to explain the braking of BD+30549 rotation due to synchronization. Currently neither the photometric behavior of the star, nor the structure of its disk, indicates existence of such a companion. However, we cannot completely rule out its existence and observations with high-angular resolution could be beneficial.
4.2.2 Magnetic braking
Another explanation for slowing down the rotation of the BD+30549 is magnetic braking. The evolution of the angular momentum of the disk-bearing PMS star can be generally expressed as:
| (1) |
In the right hand part of the equation the terms with specific lower indexes correspond to the torques due to accretion, disk locking and magnetized wind. Generally the accretion term provides the angular momentum inflow and leads to spin up of the star. The remaining terms and describe the braking due to the magnetic coupling with the disk (e.g. Rosen et al., 2012) and carrying away the angular momentum via the magnetized wind (Weber & Davis, 1967). For the simplified estimation of the braking timescale of BD+30549 during its PMS phase let us consider the action of only braking terms neglecting spin up due to accretion. Before a special comment have to be given on the origin of the wind which we will consider below. The fully radiative early type stars do not host solar-type winds powered by dynamo-generated magnetic field originally employed in Weber&Davis mechanism. Also the radiatively-driven wind is insufficient within late-B stars temperature domain (Babel, 1996) with the mass-loss rates of order yr-1. However during the phase of active accretion there are few types of accretion-driven winds, e.g. "X-wind" or "stellar wind" which propagate via the open lines of stellar magnetic field (see Ferreira, 2013, for review). These winds carrying away the substantial mass up to yr-1 and thus could have the sufficient impact on the angular momentum evolution of young star. However, their operational time is limited by the period of active accretion.
Let us assume that during the significant fraction of its PMS evolution BD+30549 followed the typical path of accreting Herbig Ae/Be star. First we consider the disk locking, which should lead to spin down of the stellar rotational rate to the angular velocity at the inner boundary of the Keplerian disk located at distance from the central star. It is usually assumed that the inner boundary of the full accretion disk is determined by the Alfven radius (), i.e radius of magnetosphere. The latter can be calculated using the expression (Lamb et al., 1973):
| (2) |
Where is the strength of dipole component of stellar magnetic field, and - mass accretion rate. Assuming the typical accretion rate yr-1, G field which is characteristic for the magnetic Herbig star (Alecian et al., 2013) and substituting the mass and radius of the star into the Eq.2, we obtain that BD+30549 has a very compact magnetosphere . If the field strength matches those of magnetic Ap/Bp stars with kG, then . Keplerian periods of and days correspond to these radii. Thus, in the first case, the coupling with the disk should lead to the spin up of the star, while in the second case the deceleration turns out to be insignificant to achieve the present day rotational rate of BD+30549.
On the other hand the timescale of the angular momentum loss due to the magnetically-driven mass loss with the rate can be found from the equation:
| (3) |
Using for clarity the largest value , and adopting the relatively high mass-loss rate and parameterized gyration radius we finally obtained from Eq.3 the estimation of the braking time of the star from the initial equatorial velocity kms-1 as Myr. Obviously this value is of order magnitude larger than the duration of PMS evolution of star and indicate that magnetic wind-braking in its simplest form is not enough efficient to explain the present slow rotation of BD+30549. Moreover, the obtained is the low limit since it was implicitly assumed that the mass-loss rate remained constant throughout the whole considered time span. In fact, in addition to the decrease of the accretion rate with time, dissipation of the inner disk in BD+30549 (see Sect. 3.2) and the corresponding termination of the accretion/outflow processes indicate that the action of this mechanism also halted before it could lead to a significant deceleration of the star.
Our simplified estimations are in agreement with those of Spruit (2018) and with results of more sophisticated numerical calculations by Rosen et al. (2012) who showed that the spin down of the intermediate mass stars as well as formation of the long-period-tail in rotational period distribution of the Ap/Bp stars is unlikely directed by the mechanisms of disk locking and wind braking considered above. Alternatively, Spruit (2018) proposed an idea that in rare cases the initial phases of protostellar mass accretion can occur without acquiring of angular momentum. For this scenario of "magnetically dominated accretion" , it is important that the connection between the magnetic field of the disk and the field inside the parental cloud is preserved. Application of this model to BD+30549 suggests that its long lasting association with reflection nebula could be an essential factor. Indeed the survey of NGC 1333 with James Clerk Maxwell Telescope (JCMT) (Doi et al., 2020) revealed the presence of dust polarized emission in the BD+30549 region which is indicative for the particles alignment by the global interstellar (IS) magnetic field. This IS field itself is aligned in NW-SE direction, which is roughly coincidental with orientation of the reflection nebula in the optical images. The IS field may be the anchor that initially prevented the star from gaining large angular momentum at the stage of protostellar collapse. Detection of the proper magnetic field of BD+30549 with the spectropolarimetric observations is essential to proof this magnetic braking scenario.
5 Conclusions
We summarise our main findings as follows:
-
1.
BD+30549 is 2.7 Myr old PMS or early-ZAMS member of NGC 1333 star forming region with pronounced chemical peculiarity of helium-weak silicon type. With the spectral synthesis technique we found the following parameters of its atmosphere =13100100 K, =4.20.1 and also detected the evidence for the highly stabilized atmosphere with negligible axial rotation and zero turbulence.
-
2.
The average chemical composition indicates a deficit of almost all of the investigated elements, except Si , Fe , Ca and P . The Si is overabundant up to 2.2 dex, with significant difference in abundance determined with the lines of the first and second ions (so-called "Si ii/ iii anomaly" ). We also found additional observational signatures of vertical abundance stratification in BD+30549 atmosphere.
-
3.
Non-LTE calculations resulted in minor- to moderate corrections for Mg and Ca abundances respectively. Also NLTE approach leads to much better reproduction of individual silicon line profiles, but does not completely remove the abundance discrepancy between Si ii and iii.
-
4.
We determined stratification profiles for iron and magnesium, which show depletion of these elements in the upper atmosphere and increased concentrations with depth. We were unable to reconstruct the reliable stratification profile for the silicon.
-
5.
Currently neither the non-LTE effects nor the vertical abundance gradient exclusively explain the "Si ii/ iii anomaly" observed in BD+30549 spectrum. The observed difference in abundances probably could be reduced by accounting also for the non-uniform lateral distribution of the silicon, i.e. its concentration in the spots with an altered temperature structure. The existence of such a spots is suspected on the basis of the period found in low-amplitude photometric variability of BD+30549.
-
6.
The vertical distribution of elements in BD+30549 atmosphere is qualitatively consistent with results of theoretical diffusion calculations and points to atomic diffusion as mechanism of their formation.
-
7.
The star with an age 2.7 Myr lies close to the ZAMS. Nevertheless, the conditions favorable for development of the peculiar chemical composition under the action of the diffusion processes apparently arose at the PMS phase. One of the mechanisms responsible for the slow rotation and rapid stabilization of the atmosphere could be the sustained magnetic linkage of the stellar field lines with interstellar magnetic field in the parental cloud.
-
8.
The detection of the mid-IR excess indicates that BD+30549 hosts circumstellar disk with developed inner cavity. Tentatively discovered variability of the flux at 24 on the decadal timescale is likely indicative for the ongoing collisions in planetesimal belt producing significant amount of secondary generated dust.
Acknowledgements
This research was funded by the grant of Russian Science Foundation №21-72-00022, https://rscf.ru/en/project/21-72-00022/.
This research has made use of the Keck Observatory Archive (KOA), which is operated by the W. M. Keck Observatory and the NASA Exoplanet Science Institute (NExScI), under contract with the National Aeronautics and Space Administration.
We thank Vladimir Grinin for a discussion on the possible variability of the star’s mid-IR flux. We also thank the anonymous referee for the thorough reading of the manuscript and the comments which helped to improve it.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
References
- Abt & Snowden (1973) Abt H. A., Snowden M. S., 1973, ApJS, 25, 137
- Alecian & Stift (2019) Alecian G., Stift M. J., 2019, MNRAS, 482, 4519
- Alecian et al. (2011) Alecian G., Stift M. J., Dorfi E. A., 2011, MNRAS, 418, 986
- Alecian et al. (2013) Alecian E., et al., 2013, MNRAS, 429, 1001
- Alexeeva et al. (2018) Alexeeva S., Ryabchikova T., Mashonkina L., Hu S., 2018, ApJ, 866, 153
- Aspin (2003) Aspin C., 2003, AJ, 125, 1480
- Asplund et al. (2009) Asplund M., Grevesse N., Sauval A. J., Scott P., 2009, ARA&A, 47, 481
- Babel (1996) Babel J., 1996, A&A, 309, 867
- Bagnulo et al. (2004) Bagnulo S., Hensberge H., Landstreet J. D., Szeifert T., Wade G. A., 2004, A&A, 416, 1149
- Bailey & Landstreet (2013) Bailey J. D., Landstreet J. D., 2013, A&A, 551, A30
- Bailey et al. (2014) Bailey J. D., Landstreet J. D., Bagnulo S., 2014, A&A, 561, A147
- Bally (2008) Bally J., 2008, in Reipurth B., ed., , Vol. 4, Handbook of Star Forming Regions, Volume I. p. 459
- Bally et al. (2008) Bally J., Walawender J., Johnstone D., Kirk H., Goodman A., 2008, The Perseus Cloud. p. 308
- Bouvier (2013) Bouvier J., 2013, in Hennebelle P., Charbonnel C., eds, EAS Publications Series Vol. 62, EAS Publications Series. pp 143–168 (arXiv:1307.2891), doi:10.1051/eas/1362005
- Bressan et al. (2012) Bressan A., Marigo P., Girardi L., Salasnich B., Dal Cero C., Rubele S., Nanni A., 2012, MNRAS, 427, 127
- Butler (1984) Butler K., 1984, Ph.D. Thesis, University of London
- Castelli et al. (2020) Castelli F., Hubrig S., Järvinen S. P., Schöller M., 2020, MNRAS, 491, 2010
- Cernis (1990) Cernis K., 1990, Ap&SS, 166, 315
- Costero et al. (2021) Costero R., Allen C., Ruelas-Mayorga A., Sánchez L., Ramírez Vélez J., Echevarría J., Melgoza G. C., 2021, MNRAS, 507, 3400
- Curtis et al. (2010) Curtis E. I., Richer J. S., Buckle J. V., 2010, MNRAS, 401, 455
- Den Hartog et al. (2014) Den Hartog E. A., Ruffoni M. P., Lawler J. E., Pickering J. C., Lind K., Brewer N. R., 2014, ApJS, 215, 23
- Doi et al. (2020) Doi Y., et al., 2020, ApJ, 899, 28
- Evans et al. (2003) Evans Neal J. I., et al., 2003, PASP, 115, 965
- Ferreira (2013) Ferreira J., 2013, in Hennebelle P., Charbonnel C., eds, EAS Publications Series Vol. 62, EAS Publications Series. pp 169–225, doi:10.1051/eas/1362006
- Fitzpatrick et al. (2019) Fitzpatrick E. L., Massa D., Gordon K. D., Bohlin R., Clayton G. C., 2019, ApJ, 886, 108
- Folsom et al. (2012) Folsom C. P., Bagnulo S., Wade G. A., Alecian E., Landstreet J. D., Marsden S. C., Waite I. A., 2012, MNRAS, 422, 2072
- Fossati et al. (2009) Fossati L., Ryabchikova T., Bagnulo S., Alecian E., Grunhut J., Kochukhov O., Wade G., 2009, A&A, 503, 945
- Foster et al. (2015) Foster J. B., et al., 2015, ApJ, 799, 136
- Gaia Collaboration et al. (2021) Gaia Collaboration et al., 2021, A&A, 649, A1
- Galazutdinov et al. (2020) Galazutdinov G., Bondar A., Lee B.-C., Hakalla R., Szajna W., Krełowski J., 2020, AJ, 159, 113
- Gerbaldi et al. (1985) Gerbaldi M., Floquet M., Hauck B., 1985, A&A, 146, 341
- Ghazaryan et al. (2019) Ghazaryan S., Alecian G., Hakobyan A. A., 2019, MNRAS, 487, 5922
- Gibson & Nordsieck (2003) Gibson S. J., Nordsieck K. H., 2003, ApJ, 589, 347
- Giddings (1981) Giddings J., 1981, Ph.D. Thesis, University of London
- Gray & Corbally (2009) Gray R. O., Corbally Christopher J., 2009, Stellar Spectral Classification
- Guzmán-Díaz et al. (2021) Guzmán-Díaz J., et al., 2021, A&A, 650, A182
- Henden et al. (2016) Henden A. A., Templeton M., Terrell D., Smith T. C., Levine S., Welch D., 2016, VizieR Online Data Catalog, p. II/336
- Herbig (1995) Herbig G. H., 1995, ARA&A, 33, 19
- Herbig & Dahm (2006) Herbig G. H., Dahm S. E., 2006, AJ, 131, 1530
- Hubble (1922) Hubble E. P., 1922, ApJ, 56, 400
- Kenyon & Bromley (2005) Kenyon S. J., Bromley B. C., 2005, AJ, 130, 269
- Khan & Shulyak (2007) Khan S. A., Shulyak D. V., 2007, A&A, 469, 1083
- Kochanek et al. (2017) Kochanek C. S., et al., 2017, PASP, 129, 104502
- Kochukhov (2007) Kochukhov O. P., 2007, in Romanyuk I. I., Kudryavtsev D. O., Neizvestnaya O. M., Shapoval V. M., eds, Physics of Magnetic Stars. pp 109–118 (arXiv:astro-ph/0701084)
- Kochukhov (2018) Kochukhov O., 2018, BinMag: Widget for comparing stellar observed with theoretical spectra, Astrophysics Source Code Library, record ascl:1805.015 (ascl:1805.015)
- Kochukhov & Bagnulo (2006) Kochukhov O., Bagnulo S., 2006, A&A, 450, 763
- Kochukhov & Ryabchikova (2018) Kochukhov O., Ryabchikova T. A., 2018, MNRAS, 474, 2787
- Kochukhov et al. (2006) Kochukhov O., Tsymbal V., Ryabchikova T., Makaganyk V., Bagnulo S., 2006, A&A, 460, 831
- Kochukhov et al. (2013) Kochukhov O., et al., 2013, A&A, 554, A61
- Kramida et al. (2021) Kramida A., Yu. Ralchenko Reader J., and NIST ASD Team 2021, NIST Atomic Spectra Database (ver. 5.9), [Online]. Available: https://physics.nist.gov/asd [2017, April 9]. National Institute of Standards and Technology, Gaithersburg, MD.
- Krivoseina et al. (1980) Krivoseina A. A., Ryabchikova T. A., Khokhlova V. L., 1980, Nauchnye Informatsii, 43, 70
- Kurtz (2022) Kurtz D. W., 2022, ARA&A, 60, 31
- Kurucz & Peytremann (1975) Kurucz R. L., Peytremann E., 1975, SAO Special Report,
- Lamb et al. (1973) Lamb F. K., Pethick C. J., Pines D., 1973, ApJ, 184, 271
- LeBlanc et al. (2009) LeBlanc F., Monin D., Hui-Bon-Hoa A., Hauschildt P. H., 2009, A&A, 495, 937
- Luhman et al. (2016) Luhman K. L., Esplin T. L., Loutrel N. P., 2016, ApJ, 827, 52
- Mashonkina (2020) Mashonkina L., 2020, MNRAS, 493, 6095
- Mashonkina et al. (2007) Mashonkina L., Korn A. J., Przybilla N., 2007, A&A, 461, 261
- Mashonkina et al. (2011) Mashonkina L., Gehren T., Shi J.-R., Korn A. J., Grupp F., 2011, A&A, 528, A87
- Matheron et al. (2001) Matheron P., Escarguel A., Redon R., Lesage A., Richou J., 2001, Journal of Quantitative Spectroscopy and Radiative Transfer, 69, 535
- Mathys & Lanz (1992) Mathys G., Lanz T., 1992, A&A, 256, 169
- Melis et al. (2012) Melis C., Zuckerman B., Rhee J. H., Song I., Murphy S. J., Bessell M. S., 2012, Nature, 487, 74
- Mendoza et al. (1995) Mendoza C., Eissner W., Dourneuf M. L., Zeippen C. J., 1995, Journal of Physics B: Atomic, Molecular and Optical Physics, 28, 3485
- Mestel & Moss (1977) Mestel L., Moss D. L., 1977, MNRAS, 178, 27
- Michaud (1970) Michaud G., 1970, ApJ, 160, 641
- Michaud et al. (2015) Michaud G., Alecian G., Richer J., 2015, Atomic Diffusion in Stars, doi:10.1007/978-3-319-19854-5.
- Moultaka et al. (2004) Moultaka J., Ilovaisky S. A., Prugniel P., Soubiran C., 2004, PASP, 116, 693
- Netopil et al. (2014) Netopil M., Fossati L., Paunzen E., Zwintz K., Pintado O. I., Bagnulo S., 2014, MNRAS, 442, 3761
- Netopil et al. (2015) Netopil M., Fossati L., Zwintz K., Paunzen E., Bagnulo S., Pintado O. I., 2015, in Balega Y. Y., Romanyuk I. I., Kudryavtsev D. O., eds, Astronomical Society of the Pacific Conference Series Vol. 494, Physics and Evolution of Magnetic and Related Stars. p. 148
- Ortiz-León et al. (2018) Ortiz-León G. N., et al., 2018, ApJ, 865, 73
- Page et al. (2012) Page M. J., et al., 2012, MNRAS, 426, 903
- Pakhomov et al. (2019) Pakhomov Y. V., Ryabchikova T. A., Piskunov N. E., 2019, Astronomy Reports, 63, 1010
- Pecaut & Mamajek (2013) Pecaut M. J., Mamajek E. E., 2013, ApJS, 208, 9
- Piskunov et al. (1995) Piskunov N. E., Kupka F., Ryabchikova T. A., Weiss W. W., Jeffery C. S., 1995, A&AS, 112, 525
- Pyper et al. (1998) Pyper D. M., Ryabchikova T., Malanushenko V., Kuschnig R., Plachinda S., Savanov I., 1998, A&A, 339, 822
- Raassen & Uylings (1998) Raassen A. J. J., Uylings P. H. M., 1998, A&A, 340, 300
- Racine (1968) Racine R., 1968, AJ, 73, 233
- Romanyuk (2007) Romanyuk I. I., 2007, Astrophysical Bulletin, 62, 62
- Romanyuk et al. (2013) Romanyuk I. I., Semenko E. A., Yakunin I. A., Kudryavtsev D. O., 2013, Astrophysical Bulletin, 68, 300
- Rosen et al. (2012) Rosen A. L., Krumholz M. R., Ramirez-Ruiz E., 2012, ApJ, 748, 97
- Ryabchikova et al. (2003) Ryabchikova T., Wade G. A., LeBlanc F., 2003, in Piskunov N., Weiss W. W., Gray D. F., eds, Vol. 210, Modelling of Stellar Atmospheres. p. 301
- Ryabchikova et al. (2005) Ryabchikova T., Leone F., Kochukhov O., 2005, A&A, 438, 973
- Ryabchikova et al. (2015) Ryabchikova T., Piskunov N., Kurucz R. L., Stempels H. C., Heiter U., Pakhomov Y., Barklem P. S., 2015, Phys. Scr., 90, 054005
- Schmidt-Kaler (1982) Schmidt-Kaler T., 1982, Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology—New Series “Gruppe/Group 6 Astronomy and Astrophysics” Vol. 2 Schaifers/Voigt: Astronomy and Astrophysics/Astronomie und Astrophysik “Stars and Star Clusters/Sterne und Sternhaufen. Springer
- Scott et al. (2015a) Scott P., et al., 2015a, A&A, 573, A25
- Scott et al. (2015b) Scott P., Asplund M., Grevesse N., Bergemann M., Sauval A. J., 2015b, A&A, 573, A26
- Shulyak et al. (2004) Shulyak D., Tsymbal V., Ryabchikova T., Stütz C., Weiss W. W., 2004, A&A, 428, 993
- Sitnova et al. (2018) Sitnova T. M., Mashonkina L. I., Ryabchikova T. A., 2018, MNRAS, 477, 3343
- Skrutskie et al. (2006) Skrutskie M. F., et al., 2006, AJ, 131, 1163
- Smith (1996) Smith K. C., 1996, Ap&SS, 237, 77
- Spruit (2018) Spruit H. C., 2018, arXiv e-prints, p. arXiv:1810.06106
- Strom & Strom (1969) Strom S. E., Strom K. M., 1969, ApJ, 155, 17
- Su et al. (2022) Su K. Y. L., Kennedy G. M., Schlawin E., Jackson A. P., Rieke G. H., 2022, ApJ, 927, 135
- Tsymbal et al. (2019) Tsymbal V., Ryabchikova T., Sitnova T., 2019, in Kudryavtsev D. O., Romanyuk I. I., Yakunin I. A., eds, Astronomical Society of the Pacific Conference Series Vol. 518, Physics of Magnetic Stars. pp 247–252
- Waelkens (1991) Waelkens C., 1991, A&A, 246, 453
- Walawender et al. (2008) Walawender J., Bally J., Francesco J. D., Jørgensen J., Getman K. ., 2008, NGC 1333: A Nearby Burst of Star Formation. p. 346
- Weber & Davis (1967) Weber E. J., Davis Leverett J., 1967, ApJ, 148, 217
- Williams & Cieza (2011) Williams J. P., Cieza L. A., 2011, ARA&A, 49, 67
- Wright et al. (2010) Wright E. L., et al., 2010, AJ, 140, 1868
- Zahn (1977) Zahn J. P., 1977, A&A, 57, 383
- van den Bergh (1966) van den Bergh S., 1966, AJ, 71, 990
- van der Plas et al. (2017a) van der Plas G., et al., 2017a, A&A, 597, A32
- van der Plas et al. (2017b) van der Plas G., Ménard F., Canovas H., Avenhaus H., Casassus S., Pinte C., Caceres C., Cieza L., 2017b, A&A, 607, A55