Baxter permuton and Liouville quantum gravity
Abstract
The Baxter permuton is a random probability measure on the unit square which describes the scaling limit of uniform Baxter permutations. We determine an explicit formula for the density of the expectation of the Baxter permuton. This answers a question of Dokos and Pak (2014). We also prove that all pattern densities of the Baxter permuton are strictly positive, distinguishing it from other permutons arising as scaling limits of pattern-avoiding permutations. Our proofs rely on a recent connection between the Baxter permuton and Liouville quantum gravity (LQG) coupled with the Schramm-Loewner evolution (SLE). The method works equally well for a two-parameter generalization of the Baxter permuton recently introduced by the first author, except that the density is not as explicit. This new family of permutons, called skew Brownian permuton, describes the scaling limit of a number of random constrained permutations. We finally observe that in the LQG/SLE framework, the expected proportion of inversions in a skew Brownian permuton equals where is the so-called imaginary geometry angle between a certain pair of SLE curves.
1 Introduction
Baxter permutations were introduced by Glen Baxter in 1964 [Bax64] while studying fixed points of commuting functions. They are classical examples of pattern-avoiding permutations, which have been intensively studied both in the probabilistic and combinatorial literature (see e.g. [Boy67, CGHK78, Mal79, BM03, Can10, FFNO11, BGRR18]). They are known to be connected with various other interesting combinatorial structures, such as bipolar orientations [BBMF10], walks in cones [KMSW19], certain pairs of binary trees and a family of triples of non-intersecting lattice paths[FFNO11], and domino tilings of Aztec diamonds [Can10].
In recent years there has been an increasing interest in studying limits of random pattern-avoiding permutations. One approach is to look at the convergence of relevant statistics, such as the number of cycles, the number of inversions, or the length of the longest increasing subsequence. For a brief overview of this approach see e.g. [Bor21a, Section 1.4]. The more recent approach is to directly determine the scaling limits of permutation diagrams. Here given a permutation of size , its diagram is a table with points at position for all . (See Figure 12, p. 12, for an example.) Their scaling limits are called permutons. See e.g. [Bor21a, Section 2.1] for an overview of this approach; and Section 1.1.2 and Appendix A for an introduction to permutation pattern terminology.
Dokos and Pak [DP14] studied the expected limiting permuton of the so-called doubly alternating Baxter permutations. The authors raised the question of proving the existence of the Baxter permuton as the scaling limit of uniform Baxter permutations, and determine its expected density. The existence of the Baxter permuton was established in [BM22] based on the bijection between Baxter permutations and bipolar orientations. In [Bor21b], a two-parameter family of permutons called the skew Brownian permuton was introduced. This family includes the Baxter permuton and a well-studied one-parameter family of permutons, called the biased Brownian separable permuton ([BBF+18, BBF+20]), as special cases.
By [KMSW19, GHS16], the scaling limit of random planar maps decorated with bipolar orientations is described by Liouville quantum gravity (LQG) decorated with two Schramm-Loewner evolution (SLE) curves. In [Bor21b], the author built a direct connection between the skew Brownian permuton (including the Baxter permuton) and SLE/LQG (see also [BGS22] for further developments). The main goal of the present paper is to use this connection to derive some properties of these permutons. In particular, we find an explicit formula for the density of the intensity measure of the Baxter permuton (see Section 1.1.1 for definitions), which answers the aforementioned question of Dokos and Pak. We also prove that all (standard) pattern densities of the Baxter permuton are strictly positive. The second result extends to the skew Brownian permuton except in one case where it is not true, namely for the biased Brownian separable permuton.
In the rest of the introduction, we first state our main results on the Baxter permuton in Section 1.1. Then, in Section 1.2, we recall the construction of the skew Brownian permuton and state the corresponding results. Finally, in Section 1.3 we review the connection with LQG/SLE and explain our proof techniques.
1.1 Main results on the Baxter permuton
A Baxter permutation is a permutation which satisfies the following pattern avoidance property.
Definition 1.1.
A permutation is a Baxter permutation if it is not possible to find such that or .
Note that there are finitely many Baxter permutations of size . Therefore it makes sense to consider a uniform Baxter permutation of size .
A Borel probability measure on the unit square is a permuton if both of its marginals are uniform, i.e., for any . A permutation can be viewed as a permuton by uniformly distributing mass to the squares More precisely,
where is a Borel measurable set of .
For a deterministic sequence of permutations , we say that converge in the permuton sense to a limiting permuton , if the permutons induced by converge weakly to . The set of permutons equipped with the topology of weak convergence of measures can be viewed as a compact metric space.
Theorem 1.2 ([BM22, Theorem 1.9]).
Let be a uniform Baxter permutation of size . The following convergence w.r.t. the permuton topology holds: where is a random permuton called the Baxter permuton.
We present our main results on the Baxter permuton in the next section.
1.1.1 The intensity measure of the Baxter permuton
The Baxter permuton is a random probability measure on the unit square (with uniform marginals). Our first result is an explicit expression of its intensity measure, defined by , which answers [DP14, Question 6.7].
Theorem 1.3.
Consider the Baxter permuton . Define the function
| (1.1) |
Then the intensity measure is absolutely continuous with respect to the Lebesgue measure on . Moreover, it has the following density function
| (1.2) |
where is a normalizing constant.
Remark 1.4.
As discussed in Section 3.3.3, further computation of the integral (1.2) is tricky, as it involves integrating a four-dimensional Gaussian in the first quadrant. Nevertheless, this integral in can be expressed as the volume function (and its derivatives) of a three-dimensional spherical tetrahedron as given in [Mur12, AM14].
We highlight that the intensity measure of other universal random limiting permutons has been investigated in the literature. For instance, the intensity measure of the biased Brownian separable permuton, was determined by Maazoun in [Maa20]. We recall that the biased Brownian separable permuton , defined for all , is a one-parameter universal family of limiting permutons arising form pattern-avoiding permutations (see Section 1.2 for more explanations). In [Maa20, Theorem 1.7], it was proved that for all , the intensity measure of the biased Brownian separable permuton is absolutely continuous with respect to the Lebesgue measure on . Furthermore, has the following density function
The proof of [Maa20, Theorem 1.7] relies on an explicit construction of the biased Brownian separable permuton from a one-dimensional Brownian excursion decorated with i.i.d. plus and minus signs. To the best of our knowledge this proof cannot be easily extended to the Baxter permuton case. See the figures below for some plots of and using numerical approximations of the integrals.







1.1.2 Positivity of pattern densities for the Baxter permuton
Our second result is Theorem 1.7 states that the Baxter permuton a.s. contains a positive density of every possible (standard) pattern. To state our result, we first define the permutation induced by points in the square . Recall that .
Definition 1.5.
Let be a sequence of points in with distinct and coordinates. The -reordering of , denoted by , is the unique reordering of the sequence such that . The values are then in the same relative order as the values of a unique permutation of size , called the permutation induced by and denoted by .
We now define the random permutation of size induced by a deterministic permuton.
Definition 1.6.
Let be a deterministic permuton and . Let be an i.i.d. sequence with distribution . We denote by the random permutation induced by .
We will also consider random permutations induced by random permutons . In order to do that, we need to construct a sequence , where the points are independent with common distribution conditionally on . This is possible up to considering a new probability space where the joint distribution of is determined as follows: for every positive measurable functional ,
We now recall some standard notation related to permutation patterns; see Appendix A for more details. Let be the set of permutations of size and be the set of permutations of finite size. Fix and . Given a subset of cardinality of the indices of , the pattern induced by in , denoted , is the permutation corresponding to the diagram obtained by rescaling the points in a table (keeping the relative position of the points). If we will say that is an occurrence of in . We denote by the number of occurrences of a pattern in a permutation . Moreover, we denote by the proportion of occurrences of in that is,
We finally recall an important fact about permuton convergence. Suppose is a sequence of random permutations converging in distribution in the permuton sense to a limiting random permuton , i.e. . Then, from [BBF+20, Theorem 2.5], it holds that converges in distribution in the product topology as to the random vector , where the random variables are defined for all as follows
| (1.3) |
Theorem 1.7.
For all patterns , it holds that
Our result is quenched in the sense that for almost every realization of the Baxter permuton , it contains a strictly positive proportion of every pattern . Since pattern densities of random permutations converge to pattern densities of the corresponding limiting random permuton, we have the following corollary of Theorems 1.2 and 1.7.
Corollary 1.8.
Let be a uniform Baxter permutation of size . Then, for all , we have that
1.2 Positivity of pattern densities for the skew Brownian permuton
Permuton limits have been investigated for various models of random permutations. For many models, the permuton limits are deterministic, for instance, Erdös-Szekeres permutations [Rom06], Mallows permutations [Sta09], random sorting networks [Dau22], almost square permutations [BS20, BDS21], and permutations sorted with the runsort algorithm [ADK22]. For random constrained permutations which have a scaling limit, the limiting permutons appear to be random in many cases. In [Bor21b] a two-parameter family of permutons, called the skew Brownian permuton, was introduced to cover most of the known examples.
The skew Brownian permuton is indexed by and , and coincides with Baxter permuton. We now recall the construction of the skew Brownian permuton for and . This is only for completeness since at the technical level we will use an alternative definition coming from SLE/LQG which has proven to be equivalent to Definition 1.9 below; see Section 1.3. We do not recall the case as our theorem only concerns .
For , let be a two-dimensional Brownian motion of correlation . This is a continuous two-dimensional Gaussian process such that the components and are standard one-dimensional Brownian motions, and . Let be a two-dimensional Brownian loop of correlation . Namely, it is a two-dimensional Brownian motion of correlation conditioned to stay in the non-negative quadrant and to end at the origin, i.e. . For , consider the solutions of the following family of stochastic differential equations (SDEs) indexed by and driven by :
| (1.4) |
where is the symmetric local-time process at zero of , i.e.
The solutions to the SDEs (1.4) exist and are unique thanks to [Bor21b, Theorem 1.7]. The collection of stochastic processes is called the continuous coalescent-walk process driven by . Here is defined in the following sense: for a.e. is a solution for almost every . For more explanations see the discussion below [Bor21b, Theorem 1.7]. Let
Definition 1.9.
Fix and . The skew Brownian permuton of parameters , denoted , is the push-forward of the Lebesgue measure on via the mapping , that is
We mention that it is also possible to generalize the previous construction when . Then the permuton coincides with the biased Brownian separable permuton of parameter mentioned before; see [Bor21b, Section 1.4 and Theorem 1.12] for further explanations.
We now summarize the list of known random permutations which have the skew Brownian permuton as scaling limit. Uniform separable permutations [BBF+18] converge to . Uniform permutations in proper substitution-closed classes [BBF+20, BBFS20] or classes having a finite combinatorial specification for the substitution decomposition [BBF+22] converge (under some technical assumptions) to , where the parameter depends on the chosen class. Uniform Baxter permutations converge to , namely the Baxter permuton. Uniform semi-Baxter permutations [Bor22], converge to , where and . Uniform strong-Baxter permutations [Bor22], converge to , where is the unique real solution of the polynomial and is the unique real solution of the polynomial .
We will not give the detailed definitions of all random constrained permutations mentioned above but emphasize an important division. On the one hand, models converging to with are similar to Baxter permutations in the following sense: their constraints are not defined by avoiding certain patterns completely, but only avoiding them when the index locations satisfy certain additional conditions; see e.g. Definition 1.1. We say that such permutations avoid generalized patterns. On the other hand, models converging towards the biased Brownian separable permuton , they avoid a certain set of patterns completely. For example, separable permutations avoid the patterns and . We say that such permutations avoid (standard) patterns. (Here the word standard is added to distinguish from generalized patterns.)
Our next theorem, which generalizes Theorem 1.7, shows that in the scaling limit, the division between and becomes the following. On the one hand, for , the permuton almost surely admits a positive density of any (standard) pattern. On the other hand, the biased Brownian separable permuton presents a zero density of some (standard) patterns. For instance, almost surely avoids all the (standard) patterns that are not separable; see [BBF+20, Definition 5.1].
Theorem 1.10.
For all and all (standard) patterns , it holds that
Note that the latter theorem answers [Bor21b, Conjecture 1.20]. By Theorem 1.10, if a sequence of random permutations avoiding (standard) patterns converges to a skew Brownian permuton then it has to be the biased Brownian separable permuton. Namely, we have the following result.
Corollary 1.11.
Let be a family of permutations avoiding (standard) patterns. Let be a random permutation of size in . Assume that for some it holds that . Then .
1.3 Relation with SLE and LQG
We now review the connection between the skew Brownian permuton and SLE/LQG established in [Bor21b, Theorem 1.17]. Then we explain our proof techniques. Precise definitions and more background on various SLE/LQG related objects will be given in Section 2.
1.3.1 The skew Brownian permuton and the SLE-decorated quantum sphere
Fix and some angle . In what follows we consider:
-
•
a unit-area -Liouville quantum sphere with two marked points at 0 and and associated -LQG area measure (see Definition 2.1);
-
•
an independent whole-plane GFF (see Section 2.1.1);
-
•
two space-filling SLE counterflow lines of in with angle and constructed from angle and flow lines with (see Section 2.1.3). We denote these two space-filling SLE curves from to by and .
We emphasize the independence of the counterflow lines and the quantum sphere. In addition, we assume that the curves and are parametrized so that and for . We have the following result.
Theorem 1.12 ([Bor21b, Theorem 1.17]).
Fix and . Let and be the unit-area -Liouville quantum sphere and the pair of space-filling SLE introduced above. For , let denote the first time111We recall that space-filling SLE curves have multiple points. Nevertheless, for each , a.s. is not a multiple point of , i.e., hits exactly once. Since is independent from and and are parametrized by -mass, a.s. the set of times such that is a multiple point of has zero Lebesgue measure. at which hits the point . Then the random permuton
is a skew Brownian permuton of parameter and .
For every fixed , the function
is a decreasing homeomorphism and therefore has an inverse function . Finally, for all and all , it holds that . In particular, for all . The Baxter permuton corresponds to and .
1.3.2 Proof techniques for the main results
To prove Theorem 1.3, we first extend Theorem 1.12 to give a more explicit description of the skew Brownian permuton measure in terms of a unit-area quantum sphere and two space-filling SLEs, i.e. we prove the following.
Proposition 1.13.
Fix and . Let and be the unit-area -Liouville quantum sphere and the pair of space-filling SLE introduced above. Let also and be such that and , and consider the skew Brownian permuton constructed as in Theorem 1.12. Then, almost surely, for every and ,
Using Proposition 1.13, we express the intensity measure in terms of a quantum sphere decorated by certain flow lines of a Gaussian free field, which are simple SLEκ curves with . This is proved in Proposition 3.7 using the rerooting invariance of marked points for quantum spheres ([DMS21]; see also Proposition 3.6 below) and the fact that the outer boundaries of the SLE16/κ-type curves and are simple SLEκ curves. Using conformal welding results and scaling properties of quantum disks and spheres ([AHS20]; see also Section 3.1), this leads to a simpler expression for via the density function of the area of quantum disks with given quantum boundary lengths and (see Theorem 3.8). When , the density is the same as the density of the duration of a Brownian excursion in a cone of angle (as argued in [AHS20, Section 7]; see also Proposition 3.3). The latter can be computed using standard heat equation argument as done in Section 3.3 via [Iye85]. We finally briefly explain the relation between the integrals in (1.2) and spherical tetrahedra (see Section 3.3.3).
To prove Theorem 1.10, we begin by observing that the occurrence of a fixed (standard) pattern in can be reformulated in terms of a specific condition on the crossing and merging order of some collection of flow lines of a Gaussian free field (see Lemma 4.1 and Figure 7 for a precise statement). Then building on the key result from [MS17, Lemma 3.8], which roughly speaking states that a simple SLEκ curve can approximate any continuous simple curves with positive probability, we prove that this crossing and merging condition holds with positive probability (the main difficulty here is that we need to look at several flow lines of different angles together). Finally, by the scaling invariance of the whole-plane GFF and a tail triviality argument, we conclude the proof of Theorem 1.10.
We conclude the introduction with three observations. First, qualitatively, our method works equally well for with any . But quantitatively, the Baxter permuton corresponds to a special case where the function is significantly simpler than the general case; see Remark 3.14. This is why Theorem 1.3 is restricted to the Baxter case while Theorem 1.10 is for the general case.
Second, the angle in Theorem 1.12 has a simple permutation interpretation.
Proposition 1.14.
For all , let be related to by the relation given in Theorem 1.12 with such that . Then
| (1.5) |
The third and fourth named authors of this paper are working on deriving an exact formula for with Ang. For the Baxter permuton by symmetry, which is consistent with . In fact, we can express for any pattern in terms of SLE and LQG, but for we do not find any exact information as enlightening as (1.5); see the end of Section 3. Note that Proposition 1.14 answers [Bor21b, Conjecture 1.22], which conjectures that the expected proportion of inversions in is an increasing function of (recall that is a decreasing function of ).
Finally, our work falls into the line of work proving integrability results (i.e., exact formulas) via SLE and/or LQG techniques. Integrability results for SLE and LQG can be proven via a variety of methods, see e.g. [Sch01, Law05a, Dub06, GTF06, SSW09, SZ10, SW11, HS11, BI12, AKL12, BJV13, LV19, ALS22] for SLE results and [KRV20, Rem20] for LQG results. As a particular class of methods, couplings between SLE and LQG [She16, DMS21] allows to exploit the interplay between SLE and LQG to prove new results about both objects. For example, the KPZ formula [KPZ88] has been used to predict exponents of statistical mechanics models and dimensions of SLE curves via combinatorics on planar maps; see e.g. [GHM20] for rigorous computations in this spirit. Chen, Curien and Maillard [CCM20] give a heuristic derivation of the conformal radius formula in [SSW09] by using the coupling with LQG; see also [HL22] for a proof via LQG techniques. A number of integrability results based on the SLE and LQG coupling have been established by subsets of the coauthors of this paper [AHS20, AHS21, ARS21, AS21], and our Theorem 1.3 can be viewed as a part of this ongoing endeavor.
Acknowledgments. N.H. was supported by grant 175505 of the Swiss National Science Foundation. X.S. was supported by the NSF grant DMS-2027986 and the Career grant 2046514. P.Y. was supported by the NSF grant DMS-1712862. We thank two anonymous referees for all their precious and useful comments.
2 Permuton-LQG/SLE correspondence
This section collects the background needed for later sections. We review in Section 2.1 some definitions related to the Gaussian free field, quantum surfaces and SLE curves. Then, in Section 2.2 we prove Proposition 1.13.
Notation. In this paper we will often work with non-probability measures. We extend the terminology of ordinary probability to this setting: For a (possibly infinite but -finite) measure space , we say is a random variable if is an -measurable function with its law defined via the push-forward measure . In this case, we say is sampled from and write for . By conditioning on some event with , we are referring to the probability measure over the space with . Finally, for a finite measure we let be its total mass and be its normalized version.
2.1 Gaussian free fields, quantum surfaces and SLE curves
We assume throughout the rest of the paper that , unless otherwise stated. We introduce the following additional parameters defined in terms of
2.1.1 Gaussian free fields
Recall that the Gaussian free field (GFF) with free boundary conditions (resp. zero boundary conditions) on a planar domain is defined by taking an orthonormal basis of (resp. ), the Hilbert space completion of the set of smooth functions on with finite Dirichlet energy (resp. finite Dirichlet energy and compact support) with respect to the Dirichlet inner product, an i.i.d. sequence of standard normal random variables, and considering the sum . This series converges in an appropriate Sobolev space and hence in the space of distributions; see for instance [BP21, Theorem 1.24]. In the case of the free boundary GFF, we view as a distribution modulo a global additive constant (see also [BP21, Definition 5.2]).
The whole-plane Gaussian free field , viewed as a distribution on modulo a global additive constant, is defined in a similar manner as the free boundary GFF, but with (see for instance [BP21, Section 5.4]). Sometimes we will fix this additive constant or view the whole-plane GFF as a distribution modulo a global additive integer multiple of some other fixed constant; if this is done, it will be always specified in the paper. We refer to [She07, WP20, BP21] for more background on the GFF.
2.1.2 Quantum surfaces
Consider the space of pairs , where is a planar domain and is a distribution on (often some variant of the GFF). Define the equivalence relation , where if there is a conformal map such that
| (2.1) |
A quantum surface is an equivalence class of pairs under the relation , and we say is an embedding of if . In this paper, the domain shall be either the upper half plane , the Riemann sphere , or a planar domain cut out by curves. We will often abuse notation and identify the pair with its equivalence class, e.g. we may refer to as a quantum surface (rather than a representative of a quantum surface).
A quantum surface with marked points is an equivalence class of elements of the form , where is a quantum surface, the points , and with the further requirement that marked points (and their ordering) are preserved by the conformal map in (2.1).
A curve-decorated quantum surface is an equivalence class of tuples , where is a quantum surface, are curves in , and with the further requirement that is preserved by the conformal map in (2.1). Similarly, we can define a curve-decorated quantum surface with marked points. Throughout this paper, the curves are type curves (which have conformal invariance properties) sampled independently of the surface .
Given some variant of the GFF, one can make sense of the bulk measure , where , by considering the circle average of on the circle and taking the weak limit of as ; see for instance [Kah85, RV11, DS11]. The measure is then called the -Liouville quantum gravity area measure. Similarly, one can define a length measure , called the -Liouville quantum gravity length measure, on certain curves in the closure of . Notice that and depend on the parameter , but we skip from the notation since the value of will always be implicitly understood from the context. The two measures satisfy natural scaling properties, namely and for an arbitrary constant. See [DS11] for more details on these bulk and boundary Liouville quantum gravity measures. A self-contained introduction to GFF, Liouville quantum gravity measures, and quantum surfaces, can be also found in [GHS19, Section 3.2-3] or in the lecture notes [BP21].
Now we formally introduce quantum spheres and quantum disks, which are the main types of quantum surfaces considered in this paper and are defined in terms of some natural variants of the GFF. The reader can find intuitive explanations of the next definitions at the end of this section. We also highlight that it is not strictly necessary to understand the technical details involved in the following definitions in order to then follow our proofs in the consecutive sections.
As argued in [DMS21, Section 4.1], when (resp. ), we have the decomposition (resp. ), where (resp. ) is the subspace of radially symmetric functions, and (resp. ) is the subspace of functions having mean 0 on all circles (resp. semicircles ). For a whole-plane GFF , we can decompose , where and are independent distributions given by the projection of onto and , respectively. We remark that is defined modulo an additive constant while is not. The same result applies for the upper half plane .
Since a quantum surface is an equivalence class of pairs (or, more generally, an equivalence class of tuples with ), in order to describe the law of a quantum sphere, we will start by describing the law of its random field .
Definition 2.1 (Quantum sphere).
Fix and let and be independent standard one-dimensional Brownian motions. Fix a weight parameter and set . Let be sampled from the infinite measure on independently from and . Let
conditioned on and for all . Let be a whole-plane GFF on independent of with projection onto given by . We consider the random distribution
Let be the infinite measure describing the law of . We call a sample from a quantum sphere of weight with two marked points.
A unit-area -quantum sphere with two marked points is the quantum sphere of weight with two marked points conditioned on having total -LQG area measure equal to one.
It is explained in [DMS21, Sections 4.2 and 4.5] that the considered conditioning on and , along with the conditioning on the quantum area of a weight quantum sphere, can be made rigorous via a limiting procedure, although we are conditioning on probability zero events.
We remark that the weight here is “typical” because in this case the two marked points (which currently correspond to 0 and ) can be realized as independent samples from the -LQG area measure (see Proposition 3.6 below for a precise statement). This important rerooting invariance property shall later be used in Section 3.3 in order to compute the density of the Baxter permuton via quantum surfaces.
We now turn to the definition of quantum disks, which is splitted in two different cases: thick quantum disks and thin quantum disks.
Definition 2.2 (Thick quantum disk).
Fix and let and be independent standard one-dimensional Brownian motions. Fix a weight parameter and let . Let be sampled from the infinite measure on independently from and . Let
conditioned on and for all . Let be a free boundary GFF on independent of with projection onto given by . Consider the random distribution
Let be the infinite measure describing the law of . We call a sample from a quantum disk of weight with two marked points.
We call and the left and right boundary quantum length of the quantum disk .
When , we define the thin quantum disk as the concatenation of weight thick disks with two marked points as in [AHS20, Section 2].
Definition 2.3 (Thin quantum disk).
Fix . For , the infinite measure is defined as follows. First sample a random variable from the infinite measure ; then sample a Poisson point process from the intensity measure ; and finally consider the ordered (according to the order induced by ) collection of doubly-marked thick quantum disks , called a thin quantum disk of weight .
Let be the infinite measure describing the law of this ordered collection of doubly-marked quantum disks . The left and right boundary length of a sample from is set to be equal to the sum of the left and right boundary lengths of the quantum disks .
We give a heuristic interpretation of the last definition. Note that one can interpret the ordered collection of doubly-marked quantum disks as if we are concatenating the surfaces by “gluing” them at their marked points, as shown in Figure 3. These collections of doubly-marked quantum surfaces are sometime called beaded surfaces.

Remark 2.4.
The quantum spheres and disks introduced in this section can also be equivalently constructed via methods in Liouville conformal field theory (LCFT); see e.g. [DKRV16, HRV18] for these constructions and see [AHS17, Cer21, AHS20] for proofs of equivalence with the surfaces defined above. Fundamental properties of the surfaces such as structure constants and correlation functions have also been established via methods in LCFT [KRV20, GKRV20, GRV19], confirming predictions from the physics literature [BPZ84, ZZ96, DO94]. The quantum spheres and disks also arise as the scaling limit of certain random planar maps. For example, when , is the law of the LQG realization of the Brownian disk with two marked boundary points with free area and free boundary length [MS20, MS21], where we recall that the Brownian disk is the scaling limit of triangulations or quadrangulations with disk topology sampled from the critical Boltzmann measure [BM17, GM19].
We conclude this section by briefly explaining some intuitions behind the definitions of quantum spheres and quantum disks. We remark that these explanations are not needed to follow the rest of the paper.
Following [DMS21, Section 1.2], we explain why the weight parameter encodes in some sense how “thick/thin” the surface is. In Definition 2.1 (resp. Definition 2.2), the process (resp. ) encodes the average of the field on (resp. on ) over the circle (resp. semicircle) of radius centered at 0, and can be defined by taking the logarithm of Bessel excursions of dimensions and , respectively; see [DMS21, Section 4]. Note that the dimension of the Bessel process increases as increases.
Since the processes and (and so also the corresponding Bessel excursions) are sampled from infinite measures, the measures for quantum spheres and quantum disks are infinite. Moreover, the random constant appearing in the two definitions encodes the largest value of the processes and , which is attained by definition at (equivalently, the random constant encodes the largest value attained during the corresponding Bessel excursions). The process (resp. ) encodes some other field average process when the quantum sphere (resp. the quantum disk) is embedded onto the cylinder instead of , where stands for the equivalence relation if (resp. onto the strip instead of ). The term in these processes comes from the change of coordinates formula in (2.1). As a consequence, the random constant reflects the largest value of these field average processes under these other embeddings. Note that “tends” to be larger when increases.
The two marked points on each quantum surface are related to the starting and the ending points of the corresponding Bessel excursion, and near these marked points the field looks like (if the surface is embedded in with the relevant marked point at 0), where for quantum spheres and is a whole-plane GFF, while for quantum disks and is a free boundary GFF on . That is, near these marked points, the field looks like a GFF plus a -log-singularity, and such singularity is smaller when increases, decreasing the amount of mass in the neighborhood of the two marked points. In fact, for readers familiar with the Liouville CFT approach, as proved in [AHS21], a weight quantum sphere with two marked points can be understood as the uniform embedding of the Liouville field with insertion points , while a weight quantum disk with two marked points can be realized as the uniform embedding of the Liouville field with insertion points . Moreover, as shown in [DMS21, AHS20, ASY22], the weight is additive under the operation of conformal welding, which shall be further discussed in Section 3.1.
2.1.3 SLE curves and imaginary geometry
Now we briefly recall the construction of the Schramm–Loewner evolution () curves with parameter , which were introduced by Schramm [Sch00] and arise as scaling limits of many statistical physics models, see e.g. [Smi06, Law05b, Sch11]. Roughly speaking, on the upper half plane , the curve can be described via the Loewner equation
where is the conformal map from to with and is times a standard Brownian motion. This curve starts at , ends at , and travels on the upper half plane [RS05]. Moreover, it has conformal invariance properties and therefore the definition can be extended to other domains (with other starting and ending points) via conformal maps. When the curve is simple, while for the curve is self hitting (later on, when we denote by for , being consistent with [MS16, MS17]). We refer the reader to the lecture note [BN14] for more background on SLEs.
It is also possible to define a variant of the on from 0 to known as the on from 0 to , where . For the curve is still simple but a.s. hits (countably) infinitely many times the left (resp. right) boundary of when (resp. ), and it does not hit at all the left (resp. right) boundary of when (resp. ). Also in this case, the definition can be extended to other domains (with other starting and ending points) via conformal maps. See [MS16, Section 2] for more details.
We shall also consider the whole-plane for , which is a random curve in from a starting point to . For the curve hits itself (countably) infinitely many times when , but does not hit itself at all when . See [MS17, Section 2.1] for more details.
Given a whole-plane GFF viewed modulo a global additive integer multiple of (see [MS17, Section 2.2] for further details) and , one can construct the -angle flow lines of (or more precisely of ) from to as shown in [MS16, MS17]. The marginal law of is that of a whole-plane SLE curve from to . We remark that we measure angles in counter-clockwise order, where zero angle corresponds to the north direction.
For distinct , the flow lines and cannot cross , but they may hit and bounce off when . See Figure 4 for an illustration. Additionally, flow lines of with the same angle started at different points of merge into each other when intersecting and form a tree [MS17, Theorem 1.9]. This gives an ordering of , where whenever the -angle flow line from merges into the -angle flow line from on the left side. Equivalently, if and only if lies in a connected component of which lies to the left of and to the right of . One can construct a unique Peano curve which visits points of with respect to this ordering [MS17, Theorem 1.16]. We call this curve the space-filling SLE counterflow line of in with angle and we denote this curve by . It follows from the construction that a.s. for any fixed , the flow lines and are the left and right boundaries of stopped upon hitting . We highlight that any pair of counterflow lines of with different angles or different starting points are not independent and their coupling is encoded via the whole-plane GFF .

2.2 LQG description of the skew Brownian permuton
In this section, we prove Proposition 1.13 by directly applying Theorem 1.12 (we invite the reader to review the statement of these theorem now that all the objects have been properly introduced). Fix and an angle . In what follows we consider:
-
•
a unit-area -Liouville quantum sphere with two marked points at 0 and ;
-
•
the associated -LQG area measure (which is in particular a random, non-atomic, Borel probability measure on which assigns positive mass to every open subset of );
-
•
an independent whole-plane GFF (viewed modulo a global additive integer multiple of );
-
•
two space-filling SLE counterflow lines of in with angles and , denoted by and and started from at time and ending at at ;
-
•
the skew Brownian permuton with and as constructed in Theorem 1.12 from .
Also recall that is the first time when hits , and that the curves and are parametrized so that for .
Proof of Proposition 1.13.
By [Bor21b, Theorem 1.11], the random measure is almost surely a permuton, i.e., almost surely its marginals are uniform. We first prove that for fixed and , is a.s. equal to the quantum area of . By Theorem 1.12, we know that a.s.
| (2.2) |
Using the fact that the set of multiple points for and a.s. has zero quantum area (see e.g. [DMS21, Section B.5]), and since we are parameterizing by quantum area, it follows that a.s. for almost every , if and only if . This implies that a.s.
| (2.3) |
Again since we are parameterizing using quantum area, by (2.2) and (2.3) it follows that a.s.
| (2.4) |
for fixed and . Now we fix and let vary. By Fubini’s theorem, there exists a set with Lebesgue measure zero, such that (2.4) holds for any . Since both sides of (2.4) are monotone in , and the right-hand side of (2.4) is a.s. continuous in (this follows because -LQG measure a.s. has no atoms), we see that a.s. for fixed and all , (2.4) holds. We can continue this argument by fixing and and letting both of and vary, and then only fixing , and finally letting vary. Therefore we arrive at the conclusion that a.s. (2.4) holds for all and . ∎
3 Density of the Baxter permuton
In this section, building on Proposition 1.13, we study the expectation of the skew Brownian permuton and express it in terms of the law of the areas of certain quantum disks. In the special case and , i.e. when is the Baxter permuton, we compute this area law by considering the random duration of certain Brownian excursions and derive Theorem 1.3. The main tools are the rerooting invariance for marked points of quantum spheres and the conformal welding of quantum disks.
This section is organized as follows. In Sections 3.1 and 3.2, we review the input from conformal welding and the rerooting invariance, respectively. Then, in Section 3.3, we give an expression for the intensity measure of the skew Brownian permuton and in particular we prove Theorem 1.3. Finally, in Section 3.4 we will show that the expected occurrence linearly depends on , proving Proposition 1.14.
Throughout this section we fix and , except that in Section 3.3.2 we restrict to the Baxter case where .
3.1 Conformal welding of quantum disks
We start by reviewing in Section 3.1.1 the disintegration and the scaling properties of quantum disks and spheres, and then in Section 3.1.2 we recall the notion of conformal welding of quantum disks from [AHS20].
3.1.1 Properties of quantum disks and quantum spheres
We recap the disintegration of measures on quantum surfaces as in [AHS20, Section 2.6]. For the infinite measure , one has the following disintegration for the quantum boundary length:
| (3.1) |
where are -finite measures supported on doubly boundary-marked quantum surfaces with left and right boundary arcs having quantum length and , respectively. See for instance [AHS20, Definition 2.22 and Proposition 2.23]. We remark that the exact meaning of the identity in (3.1) is that for all measurable sets . The measure is finite when (see e.g. [AHS20, Lemmas 2.16 and 2.18]); the measure is also finite for certain larger (e.g. ) but the range is sufficient for us (see the proof of Lemma 3.4).
Using precisely the same argument, we can disintegrate the measure over the quantum area . In particular, we have
| (3.2) |
where for all the measures are -finite (and finite if and only if [RV10]) supported on doubly marked quantum surfaces with quantum area .
We also remark that if is a sample from or from , then is a random field on (more precisely, a random distribution on ) and in particular not a random field modulo additive constant.
The next input is a scaling property of quantum disks. Recall our definition of sampling given at the beginning of Section 2.
Lemma 3.1 (Lemma 2.24 of [AHS20]).
Fix . The following two random variables sampled as follows have the same law for all :
-
1.
Sample a quantum disk from ;
-
2.
Sample a quantum disk from and add to its field.
Similarly we have the following scaling property for quantum spheres, which can be proved in the same manner as [AHS20, Lemma 2.24].
Lemma 3.2.
Fix . The following two random variables sampled as follows have the same law for all :
-
1.
Sample a quantum sphere from ;
-
2.
Sample a quantum sphere from and add to its field.
We end this subsection with two results on the measures . Before stating them, let us recall the definition of the Brownian excursion in a cone with non-fixed duration as constructed in [LW04, Section 3]. (We highlight that here we are considering non-fixed time interval excursions. This is a key difference with the Brownian loops introduced in Section 1.2, where the time interval was fixed and equal to .) Fix an angle and let be the cone . Let be the collection of continuous planar curves in defined for time , where is the duration of the curve. Then can be seen as a metric space with
where ranges from all the possible increasing homeomorphisms from to . For and , let be the law of the standard planar Brownian motion starting from and conditioned on exiting at (see [LW04, Section 3.1.2] for further details on this conditioning). This is a Borel probability measure on , and for all the following limit exists for the Prohorov metric
| (3.3) |
We denote the limiting measure by and call it the law of the Brownian excursion in the cone from to with non-fixed duration.
The next result describes the area of a disk sampled from when . We remark that this result holds only in the special case . Recall also from the beginning of Section 2 that for a finite measure we let be its total mass and we let denote its normalized version.
Proposition 3.3 (Proposition 7.7 of [AHS20]).
Fix and . There exists a constant such that for all ,
| (3.4) |
Moreover, the quantum area of a sample from has the same law as the duration of a sample from .
The next result holds for arbitrary . The upper bound guarantees that the measure is finite, as explained after (3.1).
Lemma 3.4.
For any and the quantum area of a sample from is absolutely continuous with respect to Lebesgue measure.
Proof.
For the result follows from Proposition 3.3. For we get the result from [AHS20, Theorem 2.2]222The inexperienced reader might consider to skip this part of the proof at a first read and come back to this proof after reading Section 3.1.2 where a counterpart of [AHS20, Theorem 2.2] for quantum spheres (i.e. Theorem 3.5 below) will be presented in detail. with and , along with the fact that the sum of two independent random variables has a density function if at least one of the summands has a density. Note that the statement of [AHS20, Theorem 2.2] involves the measures and we are using the fact that these measures are finite when as explained after (3.1).
Finally, we get the result for by using that we know the lemma for thick quantum disks with weights in and that a thin quantum disk of weight can be described as an ordered collection of doubly-marked thick quantum disks of weight , as done in Definition 2.3. ∎
3.1.2 Conformal welding of quantum disks
In this section we review one of the main results of [AHS20], which is stated as Theorem 3.5 below and will be a key input in the proof of Theorem 1.3. We first give the formal statement of the theorem and then we explain the interpretation of the theorem as a conformal welding of quantum surfaces.

Recall that and whole-plane were introduced in Section 2.1.3. In particular, recall that from to in a domain hit (countably) infinitely many times the left (resp. right) boundary if and only if (resp. ), and whole-plane SLE curves from to hit themselves (countably) infinitely many times if and only if .
Fix , , and let . Let be a proper simply connected domain contained in with two points and lying on the boundary of . We inductively define some probability measures on non-crossing curves in joining and for all . When , define the measure to be an SLE in ; when , the measure on non-crossing curves is defined recursively by first sampling from SLE on and then the tuple as concatenation of samples from in each connected component of lying to the left of (where and are the first and the last point on the boundary visited by ; see also Fig. 5). We remark that when there are (countably) infinitely many connected components , while when there is only one component .
Note that using conformal invariance of SLE, the definition above can be extended to all proper simply connected domains of with two boundary points and .
We also analogously define the probability measure on -tuple of curves in from to as follows. First sample a whole-plane SLE curve from 0 to in and then the tuple as concatenation of samples from in each connected component of . We remark that when when there are (countably) infinitely many connected components, while when there is only one component.
Given a measure on quantum surfaces with marked points and a conformally invariant measure on curves, let be the measure on the curve-decorated surfaces with marked points constructed by first sampling a surface from and then drawing independent curves on sampled from the measure . Note that we require that the measure on curves is conformally invariant (which is satisfied in the above case of -type curves) so that this notation is compatible with the coordinate change (2.1). Sometimes the curves are required to start and/or end at given marked points of the surface; this will either be stated explicitly or be clear from the context.
Now we are ready to state one of the main results of [AHS20].
Theorem 3.5 (Theorem 2.4 of [AHS20]).
Fix and . Let . Then there exists a constant depending only on and , such that
We refer to this type of results as conformal welding of quantum surfaces. We now give a more informal interpretation of the above result in order to help the reader to develop some intuition on the statement of Theorem 3.5. The right-hand side of the indented equation in the theorem can be interpreted as the “conformal welding” of the quantum disks sampled from the measures into a quantum sphere with law decorated with SLEκ-type curves with joint law . More precisely, one can first conformally weld the first pair of quantum disks sampled from along their length boundary arcs, yielding a new quantum disk with two marked boundary points, a SLEκ-type curve joining them, and two boundary arcs of quantum lengths and . Then one can iterate this procedure by conformally welding this new curve-decorated quantum disk with the next quantum disks sampled from for all (), obtaining in the end another quantum disk with two marked boundary points, SLEκ-type curves joining them, and two boundary arcs of equal quantum lengths . Welding together the left and the right boundary of this final quantum disk, yield to a quantum sphere decorated by SLEκ-type curves. Theorem 3.5 states that the law of this curve-decorated quantum-sphere is . We refer the curious reader to the original paper [AHS20] for further details.
3.2 Rerooting invariance of quantum spheres and its consequences on the skew Brownian permuton
In this section we review the rerooting invariance of the marked points on a unit-area quantum sphere and give an alternative expression for the intensity measure of the skew Brownian permuton. The following result is [DMS21, Proposition A.13] and is the base point of our arguments.
Proposition 3.6 (Rerooting invariance of quantum spheres).
Let . Suppose is a unit-area quantum sphere of weight . Then conditional on the surface , the points which corresponds to and are distributed independently and uniformly from the quantum area measure . That is, if in are chosen uniformly from and is a conformal map with and , then has the same law as when viewed as doubly marked quantum surfaces.
In particular, if we condition on in the statement of Proposition 3.6 and resample according to the quantum area measure , then the quantum surface has the same law as .
Before proving the main result of this section, we introduce some more notation. Let be a whole-plane GFF (viewed modulo a global additive integer multiple of ). For , we denote by the flow lines of issued from with corresponding angles (defined at the end of Section 2.1.3). Recall that from [MS17, Theorem 1.7] flow lines from the same point with different angles might bounce off each other but can never cross or merge. We denote by the areas of the four regions cut out by the four flow lines , labeled as in Figure 6. When , we simply write for and for . In this case, it can be argued using the imaginary geometry coupling in [MS16, Theorem 1.1] and [MS17, Theorem 1.1] that the joint law of the four flow lines can be viewed as with determined by
| (3.5) |
See [DMS21, Tables 1.1 and 1.2] for the complete correspondence between imaginary geometry angles and quantum surface weights.

Proposition 3.7.
Let . Let be a unit-area quantum sphere of weight , and let . Let be a whole-plane GFF (viewed modulo a global additive integer multiple of ) independent of and consider the corresponding four areas defined above (see also Figure 6). Set and such that and and consider the skew Brownian permuton . Then for all rectangles ,
where are given in (3.5).
Proof.
Given the unit-area quantum sphere , we uniformly sample a point according to the -LQG area measure . Consider the flow lines of the whole-plane GFF starting from and going to infinity. Also assume that the skew Brownian permuton is coupled with and under the same probability measure as in Proposition 1.13. On the one hand, by Proposition 1.13, is the probability of falling into the random set . On the other hand, is a.s. not a double point for neither nor ; and by the definition of space-filling SLE curves given at the end of Section 2.1.3, the flow lines and (resp. and ) are a.s. left and right boundaries of (resp. ) stopped upon hitting . From this and the fact that we are parametrizing the curves and using , we see that a.s. falls into if and only if and , which implies that
Now we treat and as the two marked points of the quantum sphere, and consider the shift . Let be the corresponding doubly marked surface, where . We also set . It is clear that given and the quantum sphere , the field has the law as a whole-plane GFF (modulo a global additive integer multiple of ), and the four flow lines are mapped by the shift to corresponding flow lines of issued from 0. Moreover, by the rerooting invariance stated in Proposition 3.6, has the same law as the unit-area quantum sphere and it is independent of the whole-plane GFF . Since, as discussed above, the joint law of the four flow lines is where are given in (3.5), and the law of a unit-area quantum sphere is by Definition 2.1 and (3.2), it follows that
which justifies the proposition. ∎
3.3 Density of the Baxter permuton
In this section we conclude the proof of Theorem 1.3. First we derive in Section 3.3.1 a formula for the density of the skew Brownian permuton which holds for all and (Theorem 3.8), and in Section 3.3.2 we simplify this formula in the special case of the Baxter permuton. Finally, in Section 3.3.3 we sketch how the formula can be made yet more explicit for the Baxter permuton via known formulas for the volume of spherical tetrahedra.
3.3.1 Density of the skew Brownian permuton in terms of quantum disks
Recall from Lemma 3.4 that for any and the quantum area of a sample from is absolutely continuous with respect to Lebesgue measure. Let denote the density of , that is, for any non-negative measurable function , we have
| (3.6) |
where is an embedding of a sample from (recall the definition of embedding from Section 2.1.2). The aim of this section is to prove the following.
Theorem 3.8.
Consider the skew Brownian permuton of parameters and . Let and be defined by and . Set as in (3.5) and denote by the density of the quantum area of a sample from in the sense of (3.6). Then the intensity measure is absolutely continuous with respect to the Lebesgue measure on and has the following density function
where is a normalizing constant.
We start the proof by recalling that the joint law of the four flow lines can be viewed as with determined by (3.5). Then, in order to prove Theorem 3.8, we first use the scaling property of quantum disks and quantum spheres to remove the conditioning on having total quantum area one (see Proposition 3.9), and then we conclude the proof by applying Theorem 3.5.
Proposition 3.9.
Let . Let be a quantum sphere of weight (here we do not condition on the area of the quantum sphere to be 1), and let . Let be a whole-plane GFF (viewed modulo a global additive integer multiple of ) independent of and consider the corresponding four areas defined above (see also Figure 6). Set and such that and and consider the skew Brownian permuton .
Let be a non-zero function on with . There exists a universal constant depending only on , and (and so only on , and ), such that for all and , it holds that
| (3.7) |
where denotes the area of a quantum sphere sampled from , and the weights are given by (3.5).
Remark 3.10.
We remark that the function purely serves as a test function and scaling factor, which shall be eliminated later once we apply the scaling property of quantum disks. The condition is made to assure that the integral on the right hand side of (3.7) is finite.
Proof of Proposition 3.9.
We disintegrate the right-hand side of (3.7) in terms of quantum area. By Lemma 3.2, we have the following relation for any fixed
| (3.8) |
Recall that denotes the area of the quantum sphere sampled from . By multiplying both sides of (3.8) by and integrate over , we get
where on the last equality we used the disintegration formula (3.2) and the fact that a sample from has quantum area .
The conclusion follows from Proposition 3.7 with ∎
We can now apply the conformal welding result stated in Theorem 3.5 to the right-hand side of (3.7). To simplify the expressions, we first need the following scaling property of quantum disks.
Lemma 3.11.
For any , the density defined in (3.6) satisfies the scaling property
Proof.
We now complete the proof of Theorem 3.8.
Proof of Theorem 3.8.
Recall that . By Theorem 3.5 and the definition given in (3.6), we can write the right-hand side of (3.7) as
| (3.9) |
where . Applying the change of variables
then one can compute that . Then (3.9) is equal to
| (3.10) |
If we further apply the change of variables , then from Lemma 3.11 and the fact that from (3.5), we get that (3.10) is the same as
which concludes the proof. ∎
3.3.2 The explicit formula for the density of the Baxter permuton
In this section we restrict to the case when and . Then, as remarked below Theorem 1.12, we have that . In addition, from (3.5), we also have that
We refer the reader to Remark 3.14 for a discussion on the difficulties to address the general case and . From Proposition 3.3, if then the quantum area of a sample from has the same law as the duration of a sample from with (where we recall that denotes the law of the Brownian excursion in the cone from to with non-fixed time duration). In our specific case and .
Building on this, we prove in the next proposition that the density of the area of a quantum disk sampled from introduced in (3.6) is a constant times the function given by (1.1). This will conclude the proof of Theorem 1.3.
Proposition 3.12.
For , the duration of a sample from has density
Proof.
Let be the standard basis for . For , let be the reflection on about line , and . Also for , let be its reflection about . Then for a standard Brownian motion started at killed upon leaving (the corresponding probability measure is denoted by ), following [Iye85, Equation 16], its duration and the hitting point has joint law
| (3.11) |
where the dot represents the usual inner product in . Note that , , , , , . Then the right-hand side of (3.11) can be written as
On the other hand, using the conformal mapping and the conformal invariance of planar Brownian motion, together with standard planar Brownian exit probability calculations on , one has
and it follows that .
Remark 3.13.
We can now complete the proof of Theorem 1.3.
Proof of Theorem 1.3.
Remark 3.14.
We remark that for general and , Theorem 3.8 gives a description of the skew Brownian permuton in terms of the density of quantum disks. For , an explicit description of the law of the quantum area under will be given in a forthcoming work [ARSZ22] of Ang, Remy, Zhu and the third author of this paper. This and other results from [ARSZ22] will then be used to give a formula for by Ang and the third and the fourth authors of this paper. The law of the quantum area is much more involved than its counterpart when , but preliminary calculations suggest that the formula for is rather simple.
3.3.3 Relations between the density of the Baxter permuton and spherical tetrahedrons
In this subsection, we comment on the relation between the density given by (1.2) and the area function of spherical tetrahedrons in .
Recall the function in (1.1), that is
Let
From Propositions 3.3 and 3.12 we know that is the joint law of the quantum areas of the four weight quantum disks obtained by welding a weight quantum sphere (as in the statement of Theorem 3.5) for . On the other hand, the density of the intensity measure of the Baxter permuton satisfies, as stated in (1.2),
For fixed , the function can be written as a linear combination of integrals
| (3.14) |
where , , and is a non-negative definite matrix depending only on .
There are two cases: (i) is non-singular (implying that is positive definite) and (ii) is singular. We will only consider case (i) below, but remark that (3.14) for singular can be approximated arbitrarily well by (3.14) for non-singular, so the discussion below is also relevant for case (ii) as we can consider an approximating sequence of non-singular matrices .
For , we write if all the entries of are non-negative. Consider the function
defined on the space , which in particular contains the set of positive definite symmetric matrices. Then it is clear that is a smooth function in this domain. Since we assume is positive definite, we have
Using polar coordinates and letting
| (3.15) |
we get
Hence the integral in (3.14) can be expressed in terms of the function defined in (3.15) as follows
where is viewed as element of .
The function can be described in terms of volume of spherical tetrahedron. The region can be thought as points on the sphere staying on the positive side of the hyperplanes passing through the origin induced by rows of . Then it follows that the six dihedral angles are given by where is the -th row of , while the Gram matrix has entries . is precisely given by the volume of the spherical tetrahedron with dihedral angles for , , , , which can be traced from [Mur12, Theorem 1.1] and also the Sforza’s formula as listed in [AM14, Theorem 2.7]. Therefore the value of can be described as a linear combination of dilogarithm functions.
3.4 Expected proportion of inversions in the skew Brownian permuton
In this section we prove Proposition 1.14. We start with the following description for sampling a point in the unit square from the skew Brownian permuton . Recall the notation for the quantum areas introduced before Proposition 3.7 (see Figure 6).
Lemma 3.15.
With probability 1, given an instance of the unit-area quantum sphere and a whole-plane GFF (viewed modulo a global additive integer multiple of ) with associated space-filling counterflow lines and , the following two sampling procedures agree:
-
1.
Let be the skew Brownian permuton constructed from the tuple as in Theorem 1.12. Sample from .
-
2.
First sample a point from the quantum area measure . Output .
Proof.
We have the following expression for (recall its definition from (1.3)).
Lemma 3.16.
Let be a unit-area quantum sphere and an independent whole-plane GFF (viewed modulo a global additive integer multiple of ) with associated space-filling counterflow lines and . Let be the skew Brownian permuton constructed from the tuple as in Theorem 1.12. For a point sampled from the quantum area measure , it a.s. holds that
Proof.
By symmetry and the definition given in (1.3),
| (3.16) |
Therefore applying Lemma 3.15, if we first independently sample from the quantum area measure , then the right-hand side of (3.16) is the same as
| (3.17) |
Using again the definition of space-filling SLE curves given at the end of Section 2.1.3 (recall also Figure 6), we observe that
if and only if hits the point after hitting , and hits before hitting . This implies that falls into the region between and (i.e. the region with quantum area ). Therefore we conclude the proof by integrating (3.17) over . ∎
Proof of Proposition 1.14.
By Lemma 3.16, it suffices to show that . By the +rerooting invariance stated in Proposition 3.6, the quantum area has the same distribution as . It remains to prove that
| (3.18) |
First assume that where are integers. By Theorem 3.5, the flow lines , …, of , with angle , cut the whole sphere into quantum disks each of weight . We denote the quantum area of the region between and by , for (with the convention that ). Since the total area is 1, by symmetry . Then from linearity of expectation, we see that
which verifies (3.18) for . Now for general , we observe that by flow line monotonicity (see [MS16, Theorem 1.5] and [MS17, Theorem 1.9]) the flow lines starting from the same point with different angles will not cross each other, and it follows that the expression is decreasing in . Then it is clear that (3.18) holds for any , which concludes the proof. ∎
Remark 3.17.
Although the quantity appearing in Lemma 3.16 is generally tractable using the rerooting invariance for marked points of quantum spheres, its conditional expectation given would be more tricky. In particular, the rerooting invariance is a key technical step in the proof.
Remark 3.18.
The proof of Lemma 3.16 does not only give the expectation of as done in Proposition 1.14; it also gives a description of the law of this random variable in terms of formulas for LQG surfaces. The law can be expressed in terms of the function , the function from Section 3.3.1, and counterparts of Proposition 3.3 for disks of other weights.
Remark 3.19.
Also for other choices of can be expressed in terms of the LQG area of certain domains cut out by flow lines started from a fixed number of points sampled from the LQG area measure. However, for general patterns , the expectation of the relevant LQG area is not as straightforward to compute, and the intersection pattern of the flow lines is more involved. We therefore do not pursue more general formulas. However, we do prove in Section 4 that we have a.s. positivity of for all (standard) patterns .
4 Positivity of pattern densities of the skew Brownian permuton
The goal of this section is to prove Theorem 1.10. Our proof will use the theory of imaginary geometry from [MS16, MS17] (see also [Dub09]). Following these papers, let
Recall from Section 2.1.3 that if is a whole-plane GFF (defined modulo a global additive integer multiple of ), and , then we can define the flow line of from to of angle , which is an SLE curve. We refer to flow lines of angle (resp. ) as north-going (resp. west-going). As explained in [MS16, MS17], one can also define flow lines if one has a GFF in a subset , including flow lines which start from a point on the domain boundary for appropriate boundary conditions.
Let , , and be as in the previous paragraph, and let be a stopping time for . Conditioned on , the conditional law of is given by a zero boundary GFF in , plus the function which is harmonic in this domain and has boundary conditions along given by times the winding of the curve plus (resp. ) on the left (resp. right) side, where the winding is relative to a segment of the curve going straight upwards. We refer to [MS17, Section 1] for the precise description of this conditional law and in particular to [MS17, Figures 1.9 and 1.10] for more details on boundary conditions and the concept of winding. The analogous statement holds if we consider flow lines of a GFF in a subset .
As mentioned above, the whole-plane GFF is typically only defined modulo a global additive integer multiple of in the setting of imaginary geometry. Throughout the remainder of this section we will fix this additive constant by requiring that the average of the GFF on the unit circle is between 0 and . Fixing the additive constant is convenient when considering the height difference between two interacting flow lines and when we want to describe the absolute boundary values along each flow line.
To simplify notation we will focus on the case of Theorem 1.10 throughout the section, and then afterwards explain the necessary (very minor) modification which is needed for general . The key input to the proof of Theorem 1.10 is the following lemma. See Figure 7 for an illustration.

Lemma 4.1.
Let and let be a (standard) pattern of size . For let and let (resp. ) be the time at which (resp. ) merges into (resp. ) for . Then there is a such that with strictly positive probability the following events occur for all , .
-
(i)
merges into on its left side if and only if ; these two flow lines merge before leaving the ball ; and .
-
(ii)
merges into on its left side if and only if ; these two flow lines merge before leaving the ball ; and .
-
(iii)
For all the flow line (resp. ) merges into (resp. ) before leaving the square .
Before proceeding to the proof of Lemma 4.1, we give the proof of Theorem 1.10 conditioned on this result.
Proof of Theorem 1.10 for given Lemma 4.1.
For and a whole-plane GFF as above, let be the event (i)-(ii)-(iii) of Lemma 4.1, but with all points scaled by , i.e., we consider the setting of the lemma under the image of the map (equivalently, (i)-(ii)-(iii) occur for the field ). By Lemma 4.1 we have , and by scale invariance of the GFF we have for all . Since the occurrence of is determined by , we get by tail triviality of (see e.g. [HS18, Lemma 2.2]) that occurs for infinitely many a.s. In particular, we can a.s. find some (random) such that occurs.
Recall that and denotes the angle 0 and the angle space-filling SLE16/κ counterflow lines constructed from . By the definition of space-filling SLE16/κ counterflow line as given at the end of Section 2.1.3 (see also Figure 7), if (i) (resp. (ii)) occurs then the ordering in which the points are visited by (resp. ) is (resp. ). Furthermore, by the same argument, if (i) (resp. (ii)) occurs in the setting where points are rescaled by then the ordering in which the points are visited by (resp. ) is (resp. ).
Finally, also by the definition of space-filling SLE16/κ, if (iii) occurs in addition to (i) and (ii), then every points and are visited in the same relative ordering as and for both and . Indeed, for and , if (i) and (iii) occur, we have that merges into on its left side if and only if merges into on its left side, and the corresponding statements hold with (ii) and W instead of (i) and N, respectively.
We now consider a unit-area quantum sphere independent of and the skew Brownian permuton constructed form the tuple as in Theorem 1.12. Note that by (1.3) and Theorem 1.12, a.s.
where is the -LQG area measure associated with . Hence, if (i), (ii), and (iii) occur (in the setting where all points are rescaled by ) then it a.s. holds
| (4.1) |
The latter bound concludes the proof since the balls for a.s. have positive Liouville quantum area measure. ∎
Proof of Theorem 1.10 for general .
All steps of the proof carry through precisely as in the case , except that we consider instead of throughout the proof for such that . ∎
The rest of this section is devoted to the proof of Lemma 4.1. We will in fact instead prove Lemma 4.3 below, which immediately implies Lemma 4.1. In order to state Lemma 4.3, we first need the following definition.
Definition 4.2.
Let be a set of the form for and , denote its top (resp. bottom, left, right) boundary arc by (resp. ), and let . We say that crosses nicely in north direction if the following criteria are satisfied, where is the first time at which hits .
-
(i)
and .
-
(ii)
Let be a path which agrees with until time and which parametrizes a vertical line segment in during . Let be the function which is harmonic in , is equal to (resp. ) on the left (resp. right) side of the vertical segment , and which otherwise along changes by times the winding of . We require that the boundary conditions of along are as given by .
-
(iii)
does not have any top-bottom crossings, i.e., if then and .
We say that crosses nicely in west direction if the following criteria are satisfied, where is the first time at which hits .
-
(i’)
and .
-
(ii’)
Let be a path which agrees with until time and which parametrizes a horizontal line segment in during . Let be the function which is harmonic in , is equal to (resp. ) on the bottom (resp. top) side of the horizontal segment , and which otherwise along changes by times the winding of . We require that the boundary conditions of along are as given by .
Notice that the requirements in (ii) and (ii’) above are automatically satisfied if we are only interested in the boundary conditions of the curve modulo a global additive integer multiple of , but that these requirements are non-trivial in our setting (since we fixed the additive constant of the field) and depend on the winding of the flow lines about their starting point. For example, suppose would make an additional counterclockwise loop around before entering ; then its boundary conditions when crossing would increase by , and we need to keep track of these multiples of when checking whether (ii) occurs. It is important to keep track of these multiples of when studying the interaction of two flow lines, e.g. in Lemmas 4.5 and 4.6 below.
Also notice that we do not require the counterpart of (iii) for west-going flow lines. This is due to the specific argument we use below where we first sample north-going flow lines and then sample the west-going flow lines conditioned on the realization of the north-going flow lines, and property (iii) is introduced in order to guarantee that it is possible to sample well-behaved west-going flow lines conditioned on the realization of the north-going flow lines.

Lemma 4.3.
Let and let be a (standard) pattern of size . For let and make the following definitions (see Figure 8):
Also let (resp. ) be the time at which (resp. ) merges into (resp. ) for . Then there is a such that with strictly positive probability the following events occur for all , .
-
(i)
The flow line stays inside until time , and crosses nicely in north direction for .
-
(ii)
The flow line stays inside until time , and crosses nicely in west direction for .
-
(iii)
merges into on its left side if and only if , and .
-
(iv)
merges into on its left side if and only if , and .
-
(v)
For all the flow line (resp. ) merges into (resp. ) before leaving the square .
The next two lemmas say, roughly speaking, that a flow line stays close to any given curve with positive probability. In the first lemma we consider the flow line until it hits a given curve in the bulk of the domain, while in the second lemma we consider the flow line until it hits the domain boundary. Closely related results are proved in [MS17]. These two results will be stated for flow lines of general angle since they will be applied both to north-going and west-going flow lines, and the result for a general angle is no harder to prove that the result for any fixed angle. See Figure 9 for an illustration of the following result.

Lemma 4.4 (Bulk case).
Let be a GFF in a domain . Let , , and be the flow line of of angle started from . Let be the trace of a simple curve in . Let also be an almost surely strictly positive and finite stopping time for such that , , and and are in the same connected component of almost surely.333If we require in particular that the boundary conditions of in close to are such that the flow line and an appropriate stopping time exists. Given , let be a simple path satisfying , , and . For fixed , let denote the -neighborhood of , and define
Then .
Proof.
Our proof is very similar to that of [MS17, Lemma 3.8] and we will therefore only explain the difference as compared to that proof. The reader should consult that proof for the definition of and below. There are two differences between our lemma and [MS17, Lemma 3.8]. First, the latter lemma requires , while we consider general domains and allow . Second, we define to be the hitting time of the set instead of letting it be the time that gets within distance of . The proof carries through just as before with the first change. For the second change, the proof also carries through just as before except that (in the notation of the proof of [MS17, Lemma 3.8]) we pick the point in the proof such that any path in connecting and must intersect . ∎
The following lemma is [MS17, Lemma 3.9], except that we have stated it for flow lines of a general angle . We first introduce some terminology appearing in the next lemma. It is recalled below the statement of the lemma in [MS17] that the admissible range of height differences for hitting is (resp. ) if the flow line is hitting on the right (resp. left) side, where we refer to [MS17, Figure 1.13] for the definition of the height difference between two flow lines when they intersect. Flow line boundary conditions means that the boundary conditions for the GGF determining the flow line change by times the winding of the curve.
Lemma 4.5 (Boundary case).
Suppose that is a GFF on a proper subdomain whose boundary consists of a finite disjoint union of continuous paths, each with flow line boundary conditions of a given angle (which can change from path to path). Fix and and let be the flow line of of angle started from . Fix any almost surely positive and finite stopping time for such that and almost surely. Given , let be any simple path in starting from such that is contained in the unbounded connected component of , , and . Moreover, assume that if we extended the boundary conditions of the conditional law of given along as if it were a flow line then the height difference of and upon intersecting at time is in the admissible range of height differences for hitting. Fix , let be the -neighborhood of in , and let
Then .
The following result is a restatement of (part of) [MS17, Theorem 1.7] and gives a criterion to determine when two flow lines cross or merge when they hit each other.
Lemma 4.6 (Criterion for crossing/merging).
Let be GFF with arbitrary boundary conditions on . For and let be a stopping time for given and work on the event that hits on its right side at time . Let denote the height difference between and upon intersecting at . Then the following hold.
-
(i)
If then crosses at time and does not subsequently cross back.
-
(ii)
If then merges with at time and does not subsequently separate from .
The following lemma will be used to argue that the north-going flow lines in Lemma 4.3 behave according to condition (i) with positive probability.

Lemma 4.7 (Condition (i) in Lemma 4.3).
Let , let , and let be the time at which exits the rectangle . Then it holds with positive probability that and that crosses nicely in north direction for .
Proof.
See Figure 10 for an illustration. The lemma follows by repeated applications of Lemma 4.4. Throughout the proof we assume that in the statement of Lemma 4.4 is sufficiently small. First, we apply Lemma 4.4 to make sure conditions (i) and (ii) in Definition 4.2 are satisfied for the square with positive probability. Letting be some neighborhood of which is compactly contained in , we apply Lemma 4.4 with , and a path in which winds around appropriately many times such that condition (ii) of Definition 4.2 is satisfied for . We then apply Lemma 4.4 another time with equal to in the previous application of the lemma, , and with such that condition (iii) of Definition 4.2 is satisfied for if and the flow line does not reenter after time in the second application of the lemma.
We iteratively apply Lemma 4.4 for each square with in order to guarantee that all the requirements of the lemma are satisfied. Note in particular that we need to stop the flow line at least once in each square in order to guarantee that (iii) in Definition 4.2 is satisfied since Lemma 4.4 itself only guarantees that the flow line stays close to some reference path and does not rule out that the flow line oscillates many times back and forth along the reference path. ∎
The following lemma will be used to argue that the west-going flow lines in Lemma 4.3 behave according to condition (ii) with positive probability.
Lemma 4.8 (Condition (ii) in Lemma 4.3).
Let , , , for . Suppose that for the flow line crosses nicely in north direction. Let be the time at which exits the rectangle . Then it holds with positive probability that and that crosses each box for nicely in west direction.
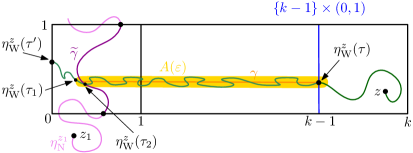
Proof.
For concreteness we consider the case but the general case can be treated similarly. See Figure 11 for an illustration. First apply Lemma 4.4 with similarly in the proof of Lemma 4.7 to make sure conditions (i’) and (ii’) in Definition 4.2 are satisfied for the square with positive probability. Let be the segment of corresponding to the (unique, by condition (ii) of Definition 4.2) up-crossing of , i.e., it is a path which starts (resp. ends) on the lower (resp. upper) boundary of . Apply Lemma 4.5 with equal to the hitting time of , equal to the infinite connected component of the complement of , and equal to a path starting at and ending at an interior point of , such that does not cross ; it is possible to find an appropriate by condition (iii) of Definition 4.2. When applying this lemma we note that by Definition 4.2, the boundary conditions of the two flow lines is such that their height difference is in the admissible range for hitting. By the first assertion of Lemma 4.6, will cross without coming back immediately after hitting . We now conclude the proof by applying Lemma 4.4 again. ∎
Combining the lemmas above, we can now conclude the proof of Lemma 4.3.
Proof of Lemma 4.3.
We will first argue that (i)-(iv) occur with positive probability. Condition (i) occurs with positive probability by Lemma 4.7, where we can apply the latter lemma iteratively for all the flow lines since the law of the field restricted to conditioned on the realization of a subset of the other flow lines is absolutely continuous with respect to the unconditional law of the field, conditioned on the event that none of the other flow lines intersect . Conditioned on (i), we get that (iii) occurs with positive probability by Lemma 4.5 and the second assertion of Lemma 4.6, where we apply Lemma 4.5 with and the flow lines are in the admissible range for merging (i.e., ) due to condition (ii) of Definition 4.2. Note that in order to also guarantee that , one can use a similar argument as in the proofs of Lemmas 4.7 and 4.8.
Similarly, condition (ii) occurs with positive conditional probability given occurrence of (i) and (iii) by Lemma 4.8, and finally condition (iv) occurs with positive conditional probability given (i)-(iii) by Lemma 4.5 and the second assertion of Lemma 4.6. We conclude that (i)-(iv) occur with positive probability, and we denote this probability by .
To prove the full lemma, it is sufficient to argue that we a.s. can find a (random) such that the event in (v) occurs. Indeed, this implies that with probability at least the event in (v) occurs for some sufficiently small fixed , which concludes the proof by the result of the previous paragraph and a union bound. We will now argue the a.s. existence of such a . It is sufficient to consider only the north-going flow line starting from . By continuity of the space-filling SLE generated by the north-going flow lines we can a.s. find an open interval such that is contained in and is contained in Furthermore, since is a.s. not a double point of and so must be contained in the interior of , there is a.s. a (random) such that is contained in . This satisfies our requirement since for all the flow line merges into before leaving . ∎
Appendix A Permutation patterns
Recall that denotes the set of permutations of size and denotes the set of permutations of finite size. We write permutations using the one-line notation, that is, if is a permutation of size then we write . Given a permutation of size , its diagram is a table with points at position for all (see the left-hand side of Figure 12). Given a subset of the indexes of , i.e. , recall that the pattern induced by in , denoted , is the permutation corresponding to the diagram obtained by rescaling the points in a table (keeping the relative position of the points). Later, whenever , we will also say that is an occurrence of in . An example will be given in Example A.1 and Figure 12 below.
A (standard) pattern of size is just a permutation of size . A permutation avoids a (standard) pattern if it is not possible to find a subset of the indexes of such that . The collection of all permutations (of any size) avoiding a set of (standard) patterns is often called a permutation class.
A generalized pattern of size , sometime also called vincular pattern, is a permutation , where some of its consecutive values are underlined. For instance, the permutation is a generalized pattern. A permutation avoids a generalized pattern , if it is not possible to find a subset of the indexes of such that and has consecutive elements corresponding to the underlined values of . We clarify the latter definition in the following example.
Example A.1.
We consider the permutation . Its diagram is plotted on the right-hand side of Figure 12. Given the set of indices , the pattern induced by in is the permutation , plotted in the middle of Figure 12. Therefore the permutation does not avoid the standard pattern , but for instance it avoids the standard pattern because it is not possible to find 4 points in the diagram of that are in decreasing order.
We also note that the permutation avoids the generalized pattern . Indeed it is not possible to find four indices such that and .
We remark that Baxter permutations, introduced in Definition 1.1, can be described as permutations avoiding the generalized patterns and .

Data availability statement: Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Conflict of interest: The authors have no competing interests to declare that are relevant to the content of this article.
References
- [ADK22] Noga Alon, Colin Defant, and Noah Kravitz. The runsort permuton. Adv. in Appl. Math., 139:Paper No. 102361, 18, 2022.
- [AHS17] Juhan Aru, Yichao Huang, and Xin Sun. Two perspectives of the 2D unit area quantum sphere and their equivalence. Comm. Math. Phys., 356(1):261–283, 2017.
- [AHS20] Morris Ang, Nina Holden, and Xin Sun. Conformal welding of quantum disks. arXiv preprint:2009.08389, 2020.
- [AHS21] Morris Ang, Nina Holden, and Xin Sun. Integrability of SLE via conformal welding of random surfaces. arXiv preprint:2104.09477, 2021.
- [AKL12] Tom Alberts, Michael J. Kozdron, and Gregory F. Lawler. The Green function for the radial Schramm-Loewner evolution. J. Phys. A, 45(49):494015, 17, 2012.
- [ALS22] Juhan Aru, Titus Lupu, and Avelio Sepúlveda. Extremal distance and conformal radius of a loop. Ann. Probab., 50(2):509–558, 2022.
- [AM14] Nikolay Abrosimov and Alexander Mednykh. Volumes of polytopes in spaces of constant curvature. In Rigidity and Symmetry, pages 1–26. Springer, 2014.
- [ARS21] Morris Ang, Guillaume Remy, and Xin Sun. FZZ formula of boundary Liouville CFT via conformal welding. arXiv preprint:2104.09478, 2021.
- [ARSZ22] Morris Ang, Guillaume Remy, Xin Sun, and Tunan Zhu. Integrability of bulk-boundary coupling in Liouville CFT. In preparation, 2022+.
- [AS21] Morris Ang and Xin Sun. Integrability of the conformal loop ensemble. arXiv preprint: 2107.01788, 2021.
- [ASY22] Morris Ang, Xin Sun, and Pu Yu. Quantum triangles and imaginary geometry flow lines. arXiv preprint: 2211.04580, 2022.
- [Bax64] Glen Baxter. On fixed points of the composite of commuting functions. Proceedings of the American Mathematical Society, 15(6):851–855, 1964.
- [BBF+18] Frédérique Bassino, Mathilde Bouvel, Valentin Féray, Lucas Gerin, and Adeline Pierrot. The Brownian limit of separable permutations. Ann. Probab., 46(4):2134–2189, 2018.
- [BBF+20] Frédérique Bassino, Mathilde Bouvel, Valentin Féray, Lucas Gerin, Mickaël Maazoun, and Adeline Pierrot. Universal limits of substitution-closed permutation classes. J. Eur. Math. Soc. (JEMS), 22(11):3565–3639, 2020.
- [BBF+22] Frédérique Bassino, Mathilde Bouvel, Valentin Féray, Lucas Gerin, Mickaël Maazoun, and Adeline Pierrot. Scaling limits of permutation classes with a finite specification: a dichotomy. Adv. Math., 405:Paper No. 108513, 84, 2022.
- [BBFS20] Jacopo Borga, Mathilde Bouvel, Valentin Féray, and Benedikt Stufler. A decorated tree approach to random permutations in substitution-closed classes. Electron. J. Probab., 25:Paper No. 67, 52, 2020.
- [BBMF10] Nicolas Bonichon, Mireille Bousquet-Mélou, and Éric Fusy. Baxter permutations and plane bipolar orientations. Séminaire Lotharingien de Combinatoire, 61:B61Ah, 2010.
- [BDS21] Jacopo Borga, Enrica Duchi, and Erik Slivken. Almost square permutations are typically square. Annales de l’Institut Henri Poincare, Probabilites et Statistiques, 57(4):1834–1856, 2021.
- [BGRR18] Mathilde Bouvel, Veronica Guerrini, Andrew Rechnitzer, and Simone Rinaldi. Semi-Baxter and strong-Baxter: two relatives of the Baxter sequence. SIAM J. Discrete Math., 32(4):2795–2819, 2018.
- [BGS22] Jacopo Borga, Ewain Gwynne, and Xin Sun. Permutons, meanders, and SLE-decorated Liouville quantum gravity. arXiv preprint:2207.02319, 2022.
- [BI12] Dmitri Beliaev and Konstantin Izyurov. A proof of factorization formula for critical percolation. Comm. Math. Phys., 310(3):611–623, 2012.
- [BJV13] Dmitry Beliaev and Fredrik Johansson Viklund. Some remarks on SLE bubbles and Schramm’s two-point observable. Comm. Math. Phys., 320(2):379–394, 2013.
- [BM03] M. Bousquet-Mélou. Four classes of pattern-avoiding permutations under one roof: generating trees with two labels. Electron. J. Combin., 9(2):Research paper 19, 31, 2002/03. Permutation patterns (Otago, 2003).
- [BM17] Jérémie Bettinelli and Grégory Miermont. Compact Brownian surfaces I: Brownian disks. Probab. Theory Related Fields, 167(3-4):555–614, 2017.
- [BM22] Jacopo Borga and Mickaël Maazoun. Scaling and local limits of Baxter permutations and bipolar orientations through coalescent-walk processes. Ann. Probab., 50(4):1359–1417, 2022.
- [BN14] Nathanaël Berestycki and James Norris. Lectures on Schramm–Loewner Evolution. Available at https://homepage.univie.ac.at/nathanael.berestycki/wp-content/uploads/2022/05/sle.pdf, 2014.
- [Bor21a] Jacopo Borga. Random permutations – a geometric point of view. arXiv preprint:2107.09699 (Ph.D. Thesis), 2021.
- [Bor21b] Jacopo Borga. The skew Brownian permuton: a new universality class for random constrained permutations. arXiv preprint:2112.00156, 2021.
- [Bor22] Jacopo Borga. The permuton limit of strong-Baxter and semi-Baxter permutations is the skew Brownian permuton. Electron. J. Probab., 27:–, 2022.
- [Boy67] William M. Boyce. Generation of a class of permutations associated with commuting functions. Math. Algorithms 2 (1967), 19–26; addendum, ibid., 3:25–26, 1967.
- [BP21] Nathana l Berestycki and Ellen Powell. Gaussian free field, Liouville quantum gravity and Gaussian multiplicative chaos. Lecture notes available at https://homepage.univie.ac.at/nathanael.berestycki/Articles/master.pdf, 2021.
- [BPZ84] A. A. Belavin, A. M. Polyakov, and A. B. Zamolodchikov. Infinite conformal symmetry in two-dimensional quantum field theory. Nuclear Phys. B, 241(2):333–380, 1984.
- [BS20] Jacopo Borga and Erik Slivken. Square permutations are typically rectangular. Ann. Appl. Probab., 30(5):2196–2233, 2020.
- [Can10] Hal Canary. Aztec diamonds and Baxter permutations. Electron. J. Combin., 17(1):Research Paper 105, 12, 2010.
- [CCM20] Linxiao Chen, Nicolas Curien, and Pascal Maillard. The perimeter cascade in critical boltzmann quadrangulations decorated by an loop model. Annales de l’Institut Henri Poincare D, 7(4):535–584, 2020.
- [Cer21] Baptiste Cerclé. Unit boundary length quantum disk: a study of two different perspectives and their equivalence. ESAIM Probab. Stat., 25:433–459, 2021.
- [CGHK78] Fan-Rong K. Chung, Ronald L. Graham, Verner Emil Hoggatt, Jr., and Mark Kleiman. The number of Baxter permutations. J. Combin. Theory Ser. A, 24(3):382–394, 1978.
- [Dau22] Duncan Dauvergne. The Archimedean limit of random sorting networks. J. Amer. Math. Soc., 35(4):1215–1267, 2022.
- [DKRV16] François David, Antti Kupiainen, Rémi Rhodes, and Vincent Vargas. Liouville quantum gravity on the Riemann sphere. Communications in Mathematical Physics, 342(3):869–907, 2016.
- [DMS21] Bertrand Duplantier, Jason Miller, and Scott Sheffield. Liouville quantum gravity as a mating of trees. Astérisque, 427, 2021.
- [DO94] H. Dorn and H.-J. Otto. Two- and three-point functions in Liouville theory. Nuclear Physics B, 429:375–388, October 1994.
- [DP14] Theodore Dokos and Igor Pak. The expected shape of random doubly alternating Baxter permutations. Online J. Anal. Comb., 9:12, 2014.
- [DS11] Bertrand Duplantier and Scott Sheffield. Liouville quantum gravity and KPZ. Inventiones mathematicae, 185(2):333–393, 2011.
- [Dub06] Julien Dubédat. Excursion decompositions for SLE and Watts’ crossing formula. Probab. Theory Related Fields, 134(3):453–488, 2006.
- [Dub09] Julien Dubédat. SLE and the free field: partition functions and couplings. Journal of the American Mathematical Society, 22(4):995–1054, 2009.
- [FFNO11] Stefan Felsner, Éric Fusy, Marc Noy, and David Orden. Bijections for Baxter families and related objects. J. Combin. Theory Ser. A, 118(3):993–1020, 2011.
- [GHM20] Ewain Gwynne, Nina Holden, and Jason Miller. An almost sure KPZ relation for SLE and Brownian motion. Ann. Probab., 48(2):527–573, 2020.
- [GHS16] Ewain Gwynne, Nina Holden, and Xin Sun. Joint scaling limit of a bipolar-oriented triangulation and its dual in the peanosphere sense. arXiv preprint:1603.01194, 2016.
- [GHS19] Ewain Gwynne, Nina Holden, and Xin Sun. Mating of trees for random planar maps and Liouville quantum gravity: a survey. arXiv preprint:1910.04713, 2019.
- [GKRV20] Colin Guillarmou, Antti Kupiainen, Rémi Rhodes, and Vincent Vargas. Conformal bootstrap in Liouville theory. arXiv preprint:2005.11530, 2020.
- [GM19] Ewain Gwynne and Jason Miller. Convergence of the free Boltzmann quadrangulation with simple boundary to the Brownian disk. Ann. Inst. Henri Poincaré Probab. Stat., 55(1):551–589, 2019.
- [GRV19] Colin Guillarmou, Rémi Rhodes, and Vincent Vargas. Polyakov’s formulation of bosonic string theory. Publ. Math. Inst. Hautes Études Sci., 130:111–185, 2019.
- [GTF06] Christophe Garban and José A. Trujillo Ferreras. The expected area of the filled planar Brownian loop is . Comm. Math. Phys., 264(3):797–810, 2006.
- [HL22] Nina Holden and Matthis Lehmkuehler. Liouville quantum gravity weighted by conformal loop ensemble nesting statistics. arXiv preprint:2204.09905, 2022.
- [HRV18] Yichao Huang, Rémi Rhodes, and Vincent Vargas. Liouville quantum gravity on the unit disk. Ann. Inst. Henri Poincaré Probab. Stat., 54(3):1694–1730, 2018.
- [HS11] Clément Hongler and Stanislav Smirnov. Critical percolation: the expected number of clusters in a rectangle. Probab. Theory Related Fields, 151(3-4):735–756, 2011.
- [HS18] Nina Holden and Xin Sun. SLE as a mating of trees in Euclidean geometry. Communications in Mathematical Physics, 364(1):171–201, 2018.
- [Iye85] Satish Iyengar. Hitting lines with two-dimensional brownian motion. SIAM Journal on Applied Mathematics, 1985.
- [Kah85] Jean-Pierre Kahane. Sur le chaos multiplicatif. Ann. Sci. Math. Québec, 9(2):105–150, 1985.
- [KMSW19] Richard Kenyon, Jason Miller, Scott Sheffield, and David B Wilson. Bipolar orientations on planar maps and SLE12. The Annals of Probability, 47(3):1240–1269, 2019.
- [KPZ88] V.G. Knizhnik, A.M. Polyakov, and A.B. Zamolodchikov. Fractal structure of 2D-quantum gravity. Modern Phys. Lett A, 3(8):819–826, 1988.
- [KRV20] Antti Kupiainen, Rémi Rhodes, and Vincent Vargas. Integrability of Liouville theory: proof of the DOZZ formula. Ann. of Math. (2), 191(1):81–166, 2020.
- [Law05a] Gregory F. Lawler. Conformally invariant processes in the plane, volume 114 of Mathematical Surveys and Monographs. American Mathematical Society, Providence, RI, 2005.
- [Law05b] Gregory F. Lawler. Conformally invariant processes in the plane, volume 114 of Mathematical Surveys and Monographs. American Mathematical Society, Providence, RI, 2005.
- [LV19] Jonatan Lenells and Fredrik Viklund. Schramm’s formula and the Green’s function for multiple SLE. J. Stat. Phys., 176(4):873–931, 2019.
- [LW04] Gregory Lawler and Wendelin Werner. The brownian loop soup. Probability theory and related fields, 128(4):565–588, 2004.
- [Maa20] Mickaël Maazoun. On the Brownian separable permuton. Combin. Probab. Comput., 29(2):241–266, 2020.
- [Mal79] Colin L. Mallows. Baxter permutations rise again. J. Combin. Theory Ser. A, 27(3):394–396, 1979.
- [MS16] Jason Miller and Scott Sheffield. Imaginary Geometry I: Interacting SLEs. Probability Theory and Related Fields, 164(3-4):553–705, 2016.
- [MS17] Jason Miller and Scott Sheffield. Imaginary geometry IV: interior rays, whole-plane reversibility, and space-filling trees. Probability Theory and Related Fields, 169(3):729–869, 2017.
- [MS20] Jason Miller and Scott Sheffield. Liouville quantum gravity and the Brownian map I: the metric. Invent. Math., 219(1):75–152, 2020.
- [MS21] Jason Miller and Scott Sheffield. Liouville quantum gravity and the Brownian map II: Geodesics and continuity of the embedding. Ann. Probab., 49(6):2732–2829, 2021.
- [Mur12] Jun Murakami. Volume formulas for a spherical tetrahedron. Proceedings of the American Mathematical Society, 140(9):3289–3295, 2012.
- [Rem20] Guillaume Remy. The Fyodorov-Bouchaud formula and Liouville conformal field theory. Duke Math. J., 169(1):177–211, 2020.
- [Rom06] Dan Romik. Permutations with short monotone subsequences. Adv. in Appl. Math., 37(4):501–510, 2006.
- [RS05] S. Rohde and O. Schramm. Basic properties of SLE. Ann. of Math., 161(2), 2005.
- [RV10] Raoul Robert and Vincent Vargas. Gaussian multiplicative chaos revisited. The Annals of Probability, 38(2):605–631, 2010.
- [RV11] Rémi Rhodes and Vincent Vargas. KPZ formula for log-infinitely divisible multifractal random measures. ESAIM Probab. Stat., 15:358–371, 2011.
- [Sch00] Oded Schramm. Scaling limits of loop-erased random walks and uniform spanning trees. Israel Journal of Mathematics, 118(1):221–288, 2000.
- [Sch01] Oded Schramm. A percolation formula. Electronic Communications in Probability, 6:115–120, 2001.
- [Sch11] Oded Schramm. Conformally invariant scaling limits: an overview and a collection of problems. In Selected works of Oded Schramm. Volume 1, 2, Sel. Works Probab. Stat., pages 1161–1191. Springer, New York, 2011.
- [She07] Scott Sheffield. Gaussian free fields for mathematicians. Probab. Theory Related Fields, 139, 2007.
- [She16] Scott Sheffield. Conformal weldings of random surfaces: SLE and the quantum gravity zipper. Ann. Probab., 44(5):3474–3545, 2016.
- [Smi06] Stanislav Smirnov. Towards conformal invariance of 2D lattice models. In International Congress of Mathematicians. Vol. II, pages 1421–1451. Eur. Math. Soc., Zürich, 2006.
- [SSW09] Oded Schramm, Scott Sheffield, and David B. Wilson. Conformal radii for conformal loop ensembles. Comm. Math. Phys., 288(1):43–53, 2009.
- [Sta09] Shannon Starr. Thermodynamic limit for the Mallows model on . J. Math. Phys., 50(9):095208, 15, 2009.
- [SW11] Scott Sheffield and David B. Wilson. Schramm’s proof of Watts’ formula. Ann. Probab., 39(5):1844–1863, 2011.
- [SZ10] Oded Schramm and Wang Zhou. Boundary proximity of SLE. Probab. Theory Related Fields, 146(3-4):435–450, 2010.
- [WP20] Wendelin Werner and Ellen Powell. Lecture notes on the Gaussian Free Field. arXiv preprint: 2004.04720, April 2020.
- [ZZ96] A. Zamolodchikov and A. Zamolodchikov. Conformal bootstrap in Liouville field theory. Nuclear Physics B, 477:577–605, February 1996.