Batch Multivalid Conformal Prediction

We design, analyze, and empirically evaluate two algorithms: one for giving group conditional guarantees for an arbitrary collection of groups $\mathcal{G}$, and the other for giving full multivalid coverage guarantees for an arbitrary collection of groups $\mathcal{G}$. We give PAC-style guarantees (Park et al., 2019), which means that with high probability over the draw of the calibration set, our deployed prediction sets have their desired coverage properties on the underlying distribution. Thus our algorithms also offer “training-conditional coverage” in the sense of Bian and Barber (2022). We prove our generalization theorems under the assumption that the data is drawn i.i.d. from some distribution, but note that De Finetti’s theorem (Ressel, 1985) implies that our analysis carries over to data drawn from any exchangeable distribution (see Remark B.1).

Conformal prediction (see Shafer and Vovk (2008); Angelopoulos and Bates (2021) for excellent surveys) has seen a surge of activity in recent years. One large category of recent work has been the development of sophisticated non-conformity scores that yield compelling empirical coverage in various settings when paired with split conformal prediction (Papadopoulos et al., 2002; Lei et al., 2018). This includes Romano et al. (2019) who give a nonconformity score based on quantile regression, Angelopoulos et al. (2020) and Romano et al. (2020b) who give nonconformity scores designed for classification, and Hoff (2021) who gives a nonconformity score that leads to Bayes optimal coverage when data is drawn from the assumed prior distribution. This line of work is complementary to ours: we give algorithms that can be used as drop-in replacements for split conformal prediction, and can make use of any of these nonconformity scores.

Another line of work has focused on giving group conditional guarantees. Romano et al. (2020a) note the need for group-conditional guarantees with respect to demographic groups when fairness is a concern, and propose separately calibrating on each group in settings in which the groups are disjoint. Foygel Barber et al. (2020) consider the case of intersecting groups, and give an algorithm that separately calibrates on each group, and then uses the most conservative group-wise threshold when faced with examples that are members of multiple groups — the result is that this method systematically over-covers. The kind of “multivalid” prediction sets that we study here were first proposed by Jung et al. (2021) in the special case of prediction intervals: but the algorithm given by Jung et al. (2021), based on calibrating to moments of the label distribution and using Chebyshev’s inequality, also generally leads to over-coverage. Gupta et al. (2022) gave a theoretical derivation of an algorithm to obtain tight multivalid prediction intervals in the sequential adversarial setting, and Bastani et al. (2022) gave a practical algorithm to obtain tight multivalid coverage using prediction sets generated from any non-conformity score, also in the sequential adversarial setting. Although the sequential setting is more difficult in the sense that it makes no distributional assumptions, it also requires that labels be available after predictions are made at test time, in contrast to the batch setting that we study, in which labels are not available. Gupta et al. (2022) give an online-to-batch reduction that requires running the sequential algorithm on a large calibration set, saving the algorithm’s internal state at each iteration, and then deploying a randomized predictor that randomizes over the internal state of the algorithm across all rounds of training. This is generally impractical; in contrast we give a direct, simple, deterministic predictor in the batch setting.

Our algorithms can be viewed as learning quantile multiaccurate predictors and quantile multicalibrated predictors respectively — by analogy to multiaccuracy Kim et al. (2019) and multicalibration Hébert-Johnson et al. (2018b) which are defined with respect to means instead of quantiles. Their analysis is similar, but with pinball loss playing the role played by squared error in (mean) multicalibration. This requires analyzing the evolution of pinball loss under Lipschitzness assumptions on the underlying distribution, which is a complication that does not arise for means. More generally, our goals for obtaining group conditional guarantees for intersecting groups emerge from the literature on “multigroup” fairness — see e.g. (Kearns et al., 2018; Hébert-Johnson et al., 2018b; Kearns et al., 2019; Rothblum and Yona, 2021; Dwork et al., 2019; Globus-Harris et al., 2022)

In this section we establish lemmas that will be key to the analysis of both of the algorithms we give. Both of our algorithms will rely on analyzing pinball loss as a potential function. All proofs can be found in the Appendix.

It is well known that pinball loss is minimized by the function that predicts for each $x$ the target quantile $q$ of a conditional score distribution given $x$, but we will need a more refined set of statements. First we define a model’s marginal quantile consistency error:

Informally, we will need the pinball loss to have both a progress and an “anti-progress” property:

1. 1.

   If a model $f$ is far from satisfying marginal quantile consistency, then linearly shifting it so that it satisfies marginal quantile consistency will reduce pinball loss substantially, and

2. 2.

   If a model does satisfy marginal quantile consistency, then perturbing it slightly won’t increase pinball loss substantially.

The next lemma establishes these, under the assumption that the underlying distribution is Lipschitz.

We now define what will be a basic building block of our iterative algorithm for obtaining multivalid coverage, and of the analysis of our algorithm for obtaining group conditional coverage. It is a simple “patch” operation on a model, that shifts the model’s predictions by a constant term $\Delta$ only on those examples $x$ that lie in some subset $B$ of the feature space:

We next show that if we have a model $f$, and we can identify a large region $B$ on which it is far from satisfying marginal quantile consistency, then “patching” the model so that it satisfies marginal quantile consistency on $S|B$ substantially improves its pinball loss.

We now give an extremely simple algorithm BatchGCP (Batch Group-Conditional Predictor) that obtains group conditional (but not threshold calibrated) prediction sets. BatchGCP only needs to solve a single closed-form convex optimization problem. Specifically, Algorithm 1 takes as input an arbitrary threshold model $f$ and collection of groups $\mathcal{G}$, and then simply minimizes pinball loss over all linear combinations of $f$ and the group indicator functions $g\in\mathcal{G}$. This is a quantile-analogue of a similar algorithm that obtains group conditional mean consistency (Gopalan et al., 2022b).

The analysis is simple: if the optimal model $\hat{f}(x,\lambda^{*})$ did not satisfy marginal quantile consistency on some $g\in\mathcal{G}$, then by Lemma 3.2, a patch operation on the set $B(g)=\{x:g(x)=1\}$ would further reduce its pinball loss. By definition, this patch would just shift the model parameter $\lambda^{*}_{g}$ and yield a model $\hat{f}(x,\lambda^{\prime})$ for $\lambda^{\prime}\neq\lambda^{*}$, falsifying the optimality of $\hat{f}(x,\lambda^{*})$ among such models.

In this section, we give a simple iterative algorithm BatchMVP (Batch Multivalid Predictor) that trains a threshold model $f$ that provides full multivalid coverage — i.e. that produces prediction sets $\mathcal{T}^{f}(x)$ that are both group conditionally valid and threshold calibrated. To do this, we start by defining quantile multicalibration, a quantile prediction analogue of (mean) multicalibration defined in Hébert-Johnson et al. (2018b); Gopalan et al. (2022a) and a variant of the quantile multicalibration definition given in Gupta et al. (2022)⁴⁴4Informally, Hébert-Johnson et al. (2018b) defines an $\ell_{\infty}$ notion of multicalibration (that takes the maximum rather than expectation over levelsets $v$) that Gupta et al. (2022) generalizes to quantiles. Gopalan et al. (2022a) define an $\ell_{1}$ notion of calibration for means. Here we give an $\ell_{2}$ variant of calibration generalized from means to quantiles..

Conditional on membership in each group $g$, the quantile multicalibration error gives a bound on the expected coverage error when conditioning both on membership in $g$ and on a predicted threshold of $f(x)=v$, in expectation over $v$. In particular, it implies (and is stronger than) the following simple worst-case (over $g$ and $v$) bound on coverage error conditional on both $g(x)=1$ and $f(x)=v$:

This claim follows by fixing any group $g$ and threshold value $v$, and dropping all the (nonnegative) terms in $Q(f,g)$ except the one corresponding to $g$ and $v$ (see the Appendix).

Algorithm 2 is simple: Given an initial threshold model $f$, collection of groups $\mathcal{G}$, and target quantile $q$, it repeatedly checks whether its current model $f_{t}$ satisfies $\alpha$-approximate quantile multicalibration. If not, it finds a group $g_{t}$ and a threshold $v_{t}$ such that $f_{t}$ predicts a substantially incorrect quantile conditional on both membership of $x$ in $g_{t}$ and on $f_{t}(x)=v_{t}$ — such a pair is guaranteed to exist if $f_{t}$ is not approximately quantile multicalibrated. It then fixes this inconsistency and produces a new model $f_{t+1}$ with a patch operation up to a target discretization parameter $m$ which ensures that the range of $f_{t+1}$ does not grow too large. Under the assumption that the non-conformity score distribution is Lipschitz, each patch operation substantially reduces the pinball loss of the current predictor, which ensures fast convergence to quantile multicalibration.

We first consider a linear regression problem on synthetic data drawn from a feature domain of 10 binary features and 90 continuous features, with each binary feature drawn uniformly at random, and each continuous feature drawn from a normal distribution $\mathcal{N}(0,\sigma^{2}_{x})$. The 10 binary features are used to define 20 intersecting groups, each depending on the value of a single binary feature. An input’s label is specified by an ordinary least squares model with group-dependent noise as:

where each term $\sigma^{2}_{i}$ is associated with one binary feature. We set $\sigma^{2}_{i}=i$ for all $i\in[10]$. So the more groups an input $x$ is a member of, the more label noise it has, with larger index groups contributing larger amounts of label noise.

We generate a dataset $\{(x_{i},y_{i})\}$ of size 40000 using the above-described model, and split it evenly into training and test data. The training data is further split into training data of size 5000 (with which to train a least squares regression model $f$) and calibration data of size 15000 (with which to calibrate our various conformal prediction methods). Given the trained predictor $f$, we use non-conformity score $s(x,y)=|f(x)-y|$. Next, we define the set of groups $\mathcal{G}=\{g_{1},g_{2},\cdots,g_{20}\}$ where for each $j\in[20]$, $g_{j}=\{x\in\mathcal{X}\mid x_{\lfloor(j+1)/2\rfloor}\equiv_{2}j+1\}$. We run Algorithm 1 (BatchGCP) and Algorithm 2 (BatchMVP with $m=100$ buckets) to achieve group-conditional and full multivalid coverage guarantees respectively, with respect to $\mathcal{G}$ with target coverage $q=0.9$. We compare the performance of these methods to naive split-conformal prediction (which, without knowledge of $\mathcal{G}$, uses the calibration data to predict a single threshold) and the method of Foygel Barber et al. (2020) which predicts a threshold for each group in $\mathcal{G}$ that an input $x$ is part of, and chooses the most conservative one.

Figures 1 and 2 present results over 50 runs of this experiment. Notice that both BatchGCP and BatchMVP achieve close to the desired group coverage across all groups—with BatchGCP achieving nearly perfect coverage and BatchMVP sometimes deviating from the target coverage rate by as much as 1%. In contrast, the method of Foygel Barber et al. (2020) significantly overcovers on nearly all groups, particularly low-noise groups, and naive split-conformal starts undercovering and overcovering on high-noise and low-noise groups respectively as the expected label-noise increases. Group-wise calibration error is high across all groups but the last using the method of Foygel Barber et al. (2020), and naive split-conformal has low calibration error on groups where inclusion/exclusion reflects less fluctuation in noise, and higher calibration error in groups where there is much higher fluctuation in noise based on inclusion. Both BatchGCP and BatchMVP have lower group calibration errors — interestingly, BatchGCP appears to do nearly as well as BatchMVP in this regard despite having no theoretical guarantee on threshold calibration error. A quantile multicalibrated predictor must have low coverage error conditional on groups $g$ and thresholds $\tau_{i}$ that appear frequently, and may have high coverage error for pairs that appear infrequently—behavior that we see in BatchMVP in Figure 2. On the other hand, for both naive split conformal prediction and the method of Foygel Barber et al. (2020), we see high mis-coverage error even for pairs $(g,\tau_{i})$ containing a large fraction of the probability mass.

We fix the upper-limit of allowed iterations $T$ for BatchMVP to 1000, but typically the algorithm converges and halts in many fewer iterations. Across the 50 runs of this experiment, the average number of iterations $T$ taken to converge was $45.54\pm 14.77$.

We also compare our methods to naive split conformal prediction and the method of Foygel Barber et al. (2020) on real data from the 2018 Census American Community Survey Public Use Microdata, compiled by the Folktables package (Ding et al., 2021). This dataset records information about individuals including race, gender and income. In this experiment, we generate prediction sets for a person’s income while aiming for valid coverage on intersecting groups defined by race and gender.

The Folktables package provides datasets for all 50 US states. We run experiments on state-wide datasets: for each state, we split it into 60% training data $\mathcal{D}_{train}$ for the income-predictor, 20% calibration data $\mathcal{D}_{calib}$ to calibrate the conformal predictors, and 20% test data $\mathcal{D}_{test}$. After training the income-predictor $f$ on $\mathcal{D}_{train}$, we use the non-conformity score $s(x,y)=|f(x)-y|$. There are 9 provided codes for race⁵⁵51. White alone, 2. Black or African American alone, 3. American Indian alone, 4. Alaska Native alone, 5. American Indian and Alaska Native tribes specified; or American Indian or Alaska Native, not specified and no other races, 6. Asian alone, 7. Native Hawaiian and other Pacific Islander alone, 8. Some Other Race alone, 9. Two or More Races. and 2 codes for sex (1. Male, 2. Female) in the Folktables data. We define groups for five out of nine race codes (disregarding the four with the least amount of data) and both sex codes. We run all four algorithms (naive split-conformal, the method of Foygel Barber et al. (2020), BatchGCP, and BatchMVP with $m=300$ buckets) with target coverage $q=0.9$.

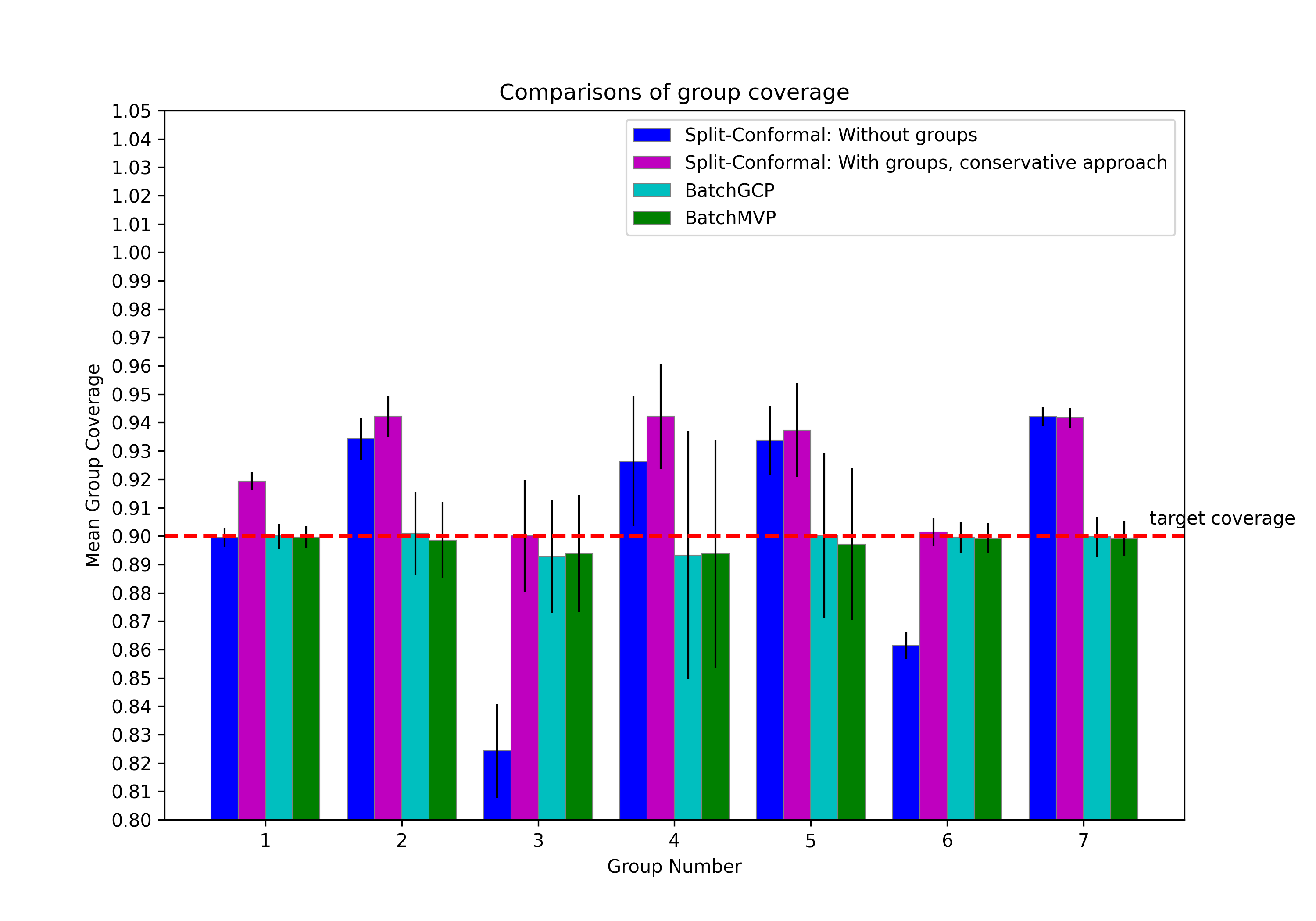
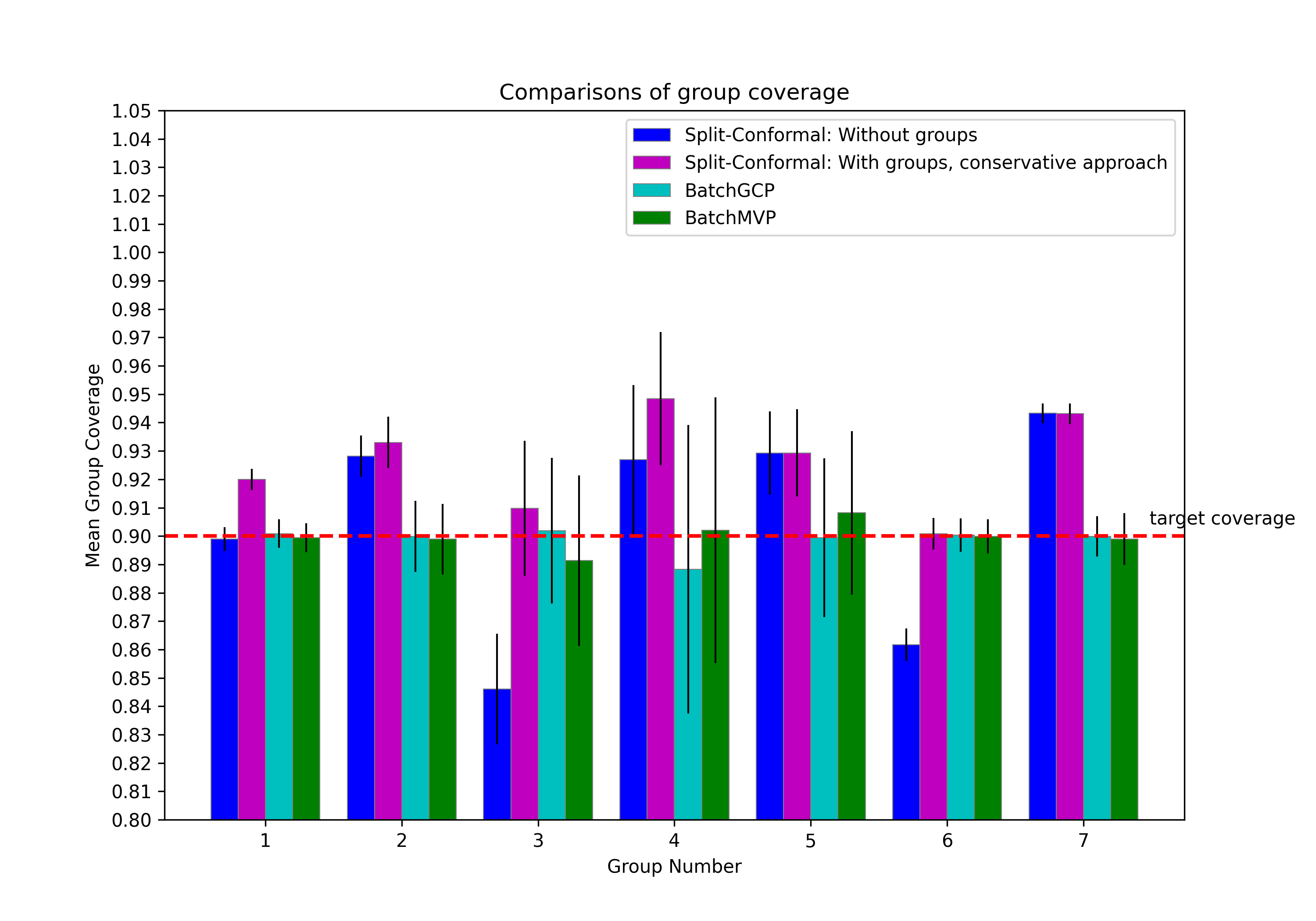
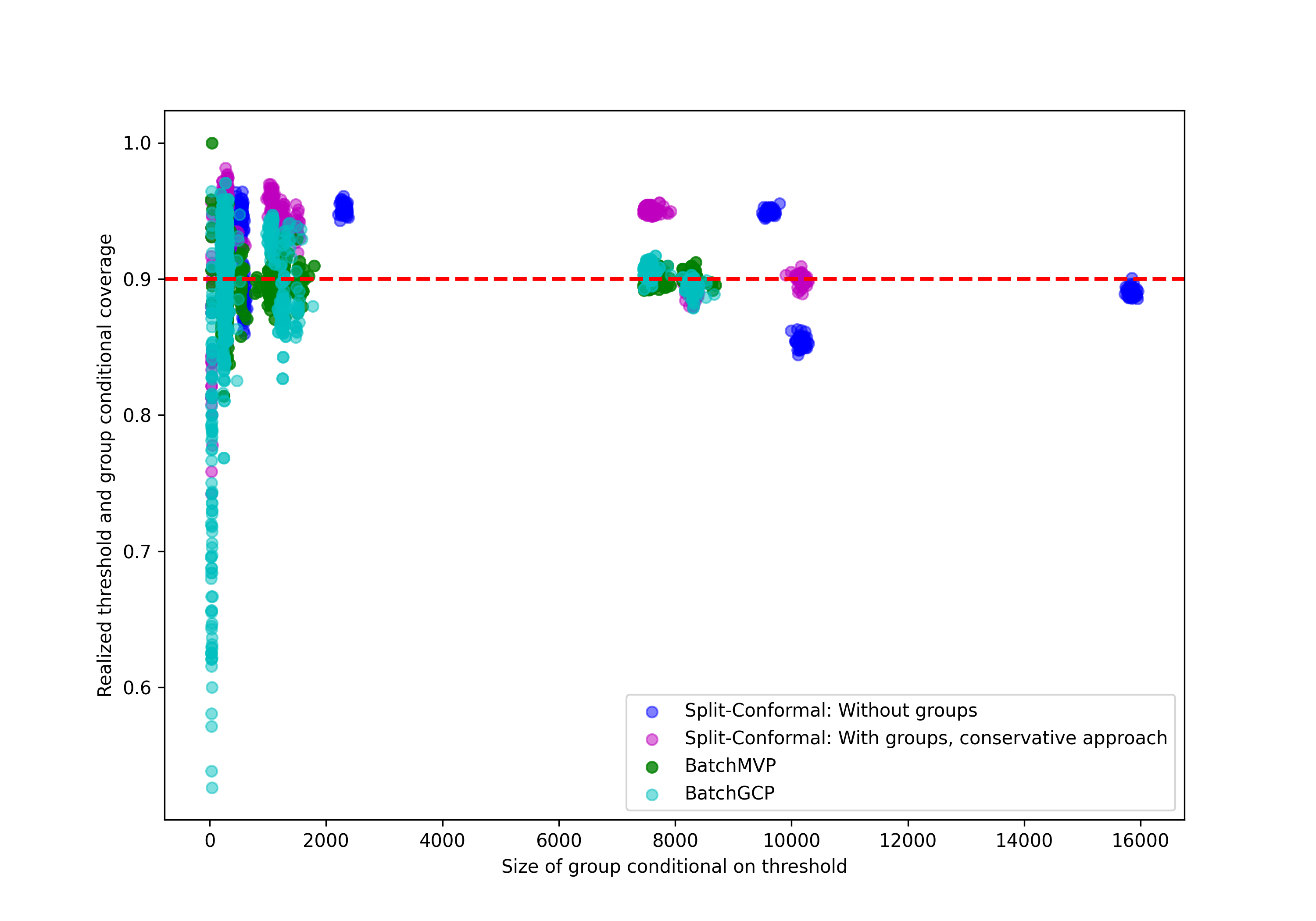
We ran this experiment on the 10 largest states. Figure 3 and Figure 4 present comparisons of the performance of all four algorithms on data taken from California, averaged over 50 different runs. Results on all remaining states are presented in Appendix C.2.

Just as in the synthetic experiments, both BatchGCP and BatchMVP achieve excellent coverage across all groups—in fact now, we see nearly perfect coverage for both BatchGCP and BatchMVP, with BatchGCP still obtaining slightly better group conditional coverage. In contrast, naive split-conformal prediction undercovers on certain groups and overcovers on others, and the method of Foygel Barber et al. (2020) significantly overcovers on some groups (here, group 4 and 7). The conservative approach also generally yields prediction sets of much larger size. We see also that BatchMVP achieves very low rates of calibration error across all groups, outperforming BatchGCP in this regard. Calibration error is quite irregular across groups for both naive split-conformal prediction and for the method of Foygel Barber et al. (2020), being essentially zero in certain groups and comparatively much larger in others. The average number of iterations $T$ BatchMVP converged in was $10.64\pm 1.12$.