Baryons Shaping Dark Matter Haloes
Abstract
In this work we aim at investigating the effects of baryons on the dark matter (DM) haloes structure, focusing on the correlation between the presence and importance of stellar discs and the halo shapes. We study the properties of a subsample of DM haloes from Fenix and eagle cosmological simulations. We inspect the central regions of haloes in the mass range at , comparing the hydrodynamic runs and their dark matter only (DMo) counterparts. Our results indicate that baryons have a significant impact on the shape of the inner halo, mainly within 20 percent of the virial radius. We find haloes to be more spherical when hosting baryons. While the impact of baryons depends on the mass of the haloes, we also find a trend with morphology which suggests that the way baryons are assembled is also relevant in agreement with previous works. Our findings also indicate that disc galaxies preferentially form in haloes whose DMo counterparts were originally more spherical and with stronger velocity anisotropy. The presence of baryons alter the orbital structure of the DM particles of the haloes, which show a decrease in their velocity anisotropy, towards more tangentially biased orbits. This relative decrease is weaker in the case of disc-dominated galaxies. Our results point out to a cosmological connection between the final morphology of galaxies and the intrinsic properties of their DM haloes, which gets reinforce by the growth of the discs.
keywords:
galaxies: disc – galaxies: formation – galaxies: haloes – dark matter.1 Introduction
Dark matter (DM) haloes are the building blocks in the concordance cosmological scenario of the Universe. The accurate determination of their properties in the presence of baryons has been a crucial task in the studies of galaxy formation (Knebe et al., 2004; Moore et al., 2004; Faltenbacher et al., 2005; Avila-Reese et al., 2005; Bailin & Steinmetz, 2005; Patiri et al., 2006; Vera-Ciro et al., 2011). Additionally, cosmological simulations have been a forceful tool to investigate them. Even though, through the last decade several studies have provided robust insights of the DM haloes characteristics, many problems remain to be fully understood, such as the "cusp-core" problem (Moore et al., 2004; Walker & Peñarrubia, 2011; Oh et al., 2015) or the "missing satellite problem" (Diemand et al., 2007; Guo et al., 2010; Bullock & Boylan-Kolchin, 2017).
The outcomes of dark matter only (DMo) simulations showed that CDM haloes are triaxial (e.g. Dubinski & Carlberg, 1991; Allgood, 2005). However, the condensation of baryons within the central regions during the assembly of galaxies modifies their internal structure (e.g. Tissera & Dominguez-Tenreiro, 1998; Kazantzidis et al., 2010; Butsky et al., 2016).
DM haloes respond by contracting or, in some cases, expanding to the assembly of baryons in the inner regions as shown by comparative studies of the DM profiles in hydrodynamical simulations and those of their DMo counterparts (Pedrosa et al., 2010; Tissera et al., 2010; Duffy et al., 2010; Dutton et al., 2016; Chua et al., 2019). Baryonic processes such as supernova feedback (SN) contribute to regulate the presence of baryons in the most inner parts of the galaxy (Navarro et al., 1996; Governato et al., 2012). As a byproduct, SN could also help to transform cuspy into core profiles by triggering cycles of inflows and outflows which can contribute in reshaping the inner regions of haloes (Dutton et al., 2016; Benítez-Llambay et al., 2019).
The close-connected evolution between the central galaxy and its host halo has been analysed by several studies from different point of views (e.g. Barnes & White, 1984; Tissera & Dominguez-Tenreiro, 1998; Gnedin et al., 2004; Debattista et al., 2008; Romano-Díaz et al., 2008; Valluri et al., 2010). In particular, Pedrosa et al. (2010), Zavala et al. (2016) and Teklu et al. (2017) studied the exchange of angular momentum between the galaxy and the inner and outer parts of the DM halo. Zavala et al. (2016) found a correlation between the evolution of the specific stellar angular momentum of the galaxy and the one of the inner DM halo. Teklu et al. (2017) reported that disc galaxies are hosted preferentially by haloes that have central angular momentum aligned with the total angular momentum of the halo. More recently Zhu et al. (2017) found that when baryons are included, DM particle orbits go mainly from box to tube types. These authors also proposed a link between the angular momentum of the baryonic discs and the DM haloes so that for the changes in orbits to be irreversible, angular momentum exchange between baryons and DM is required (e.g. Pedrosa et al., 2010).
It has been extensively established that baryons also produce an impact on the DM halo shapes. Haloes from hydrodynamical simulations appear to be less triaxials than their DMo counterpart (Tissera & Dominguez-Tenreiro, 1998; Dubinski & Carlberg, 1991; Chabrier, 2003; Debattista et al., 2008; Kazantzidis et al., 2010; Tissera et al., 2010). The shapes of DM haloes are related to the orbital structure of the DM particles that form them (Barnes & Hernquist, 1996). The sphericalization detected in the presence of baryons is related with the modification of the DM particles orbits. Using hydrodynamical simulations, Debattista et al. (2008) and Valluri et al. (2010) found that box orbits that support triaxial haloes become rounder due to the presence of baryons, causing the shape to change. Vera-Ciro et al. (2014) analysed the Aquarius simulation haloes with peak circular velocity in the range of and found a relation between the triaxiality and the mass of the halo: smallest haloes are between 40 and 50 percent rounder than Milky Way-type ones, at the radius where circular velocity peaks. Additionally Butsky et al. (2016), using the NIHAO zoom-in simulations, found a strong mass dependence of the inner halo shape between DMo and Hydro simulations.
Tissera et al. (2010) found that baryons modify the velocity dispersion structure in a rather complicated way, with very different behaviours between haloes of the Aquarius Project (Scannapieco et al., 2009). The relation between DM halo shape and velocity anisotropy was also studied by Sparre & Hansen (2012) for a wide range of DMo simulations finding a correlation between them. It is interesting to point out that the presence of a baryonic disc structure disc-like DM structures. Schaller et al. (2016) showed that for a set of 24 simulated Milky Way like galaxies of the apostle and eagle projects, 23 of these haloes showed no evidence for a dark disc and the only case found resulted from a recent satellite merger.
Using the Illustris and Illustris-Dark simulations, Chua et al. (2019) reported that baryonic physics has a significant impact on the halo shape, sphericalizing haloes, with stronger effects in the inner region. In agreement with Pedrosa et al. (2010) and Tissera et al. (2010), they found that the presence of baryons altered the DM velocity dispersion and decreased the velocity anisotropy along all radii and masses, their orbits becoming more tangentially biased.
Kazantzidis et al. (2010) investigated the effect of the growth of a central disc galaxy on the shape of a triaxial DM halo in a DMo simulation and reported clear sphericalization of the DM haloes by the galaxy discs. Interestingly, Thob et al. (2019) studied the morphology and kinematics of galaxies in the eagle suite, finding a link among several kinematic indicators of baryon morphology. Their results also suggested that there might be an intrinsic correlation between the flatness of the hosted galaxies and their haloes.
These strong numerical predictions for the three-dimensional shapes of DM haloes (and in particular the Milky Way DM halo) is poorly constrained by current observational data (Bovy et al., 2016). Lately, Law & Majewski (2010); Bovy et al. (2016); Malhan & Ibata (2019) established stronger observational constrains of the Milky Way halo shape within the galactocentric radial interval (20 kpc < r < 60 kpc), using the effect of Sagittarius stream and the analysis of the observed phase-space of Pal 5 and GD-1, finding that the potential gleaned from the tracks of these streams are precise measurements of the shape of the gravitational potential at the location of the streams, with weaker constraints on the radial and vertical accelerations separately.
In this paper, we extend the analysis done in previous works by studying in detail the connection between galaxy morphology, quantified by the relevance of the disc component, and the properties of the inner regions of DM haloes. We also investigate how this relation changes within the measuring radius and galaxy stellar mass. We explore the possible preexisting correlation between galaxy morphology and their corresponding DMo haloes. This correlation could be implemented as a "predictor" in semianalytical models of galaxy formation. We use the disc-to-total stellar mass fraction, , to quantify galaxy morphology with this purpose. The analysis is based on one-to-one comparison between the properties of the DM haloes in the fully hydrodynamical runs eagle and Fenix, and their DMo counterparts. Analysing samples from two numerical experiments, which implemented different subgrid physics models, allows us to asses that the trends found do not depend on the particular feedback implementation.
This work is organized as follows.Section 2 summarizes the main properties of the simulations. Section 3 presents the results of the DM and baryon distribution in the inner regions. The DM shape dependence on galaxy morphology is investigated in Section 4. Finally, we present the conclusions in Section 5.
2 Numerical simulations
For this study we analyse two simulations performed with different versions of gadget code (Springel & Hernquist, 2003; Springel, 2005) and different feedback implementations. In this section we describe their main features.
2.1 eagle simulations
We analyse galaxies selected from the 100 Mpc sized box reference run of the eagle Project, a suite of hydrodynamical simulation that follows the structure formation in cosmological representative volume. All of them are consistent with the current favoured -CDM cosmology (Crain et al., 2015; Schaye et al., 2015). These simulations include: radiative heating and cooling (Wiersma et al., 2009), stochastic star formation (Schaye & Dalla Vecchia, 2008), stochastic stellar feedback (Dalla Vecchia & Schaye, 2012) and AGN feedback (Rosas-Guevara et al., 2015). The AGN feedback is particularly important for the evolution of SF activity in massive early-type galaxies (ETGs). An Initial Mass Function (IMF) of Chabrier (2003) is used. A more detailed description of the code and the simulation can be seen in Crain et al. (2015) and Schaye et al. (2015).
The adopted cosmological parameters are , , , , with (Planck Collaboration et al., 2014). The 100 Mpc sized box reference simulation, so called L100N1504, is represented by dark matter particles and the same initial number of gas particles, with an initial mass of and , respectively. The maximum gravitational softening of is adopted.
The energy injected into the gas corresponds to erg per supernovae event times a dimensionless factor, , that depends on the local gas metallicity and density. For haloes with more than 1500 DM particles (approximately ), black hole sink particles are placed at the center of the halos. Feedback due to AGN activity is implemented in a similar way to the feedback from star formation. For haloes, at , with masses higher than the stellar feedback becomes less effective but AGN feedback can still expel baryons (Schaller et al., 2015a).
The halo catalogue 111We use the publicly available data by McAlpine et al. (2016) http://icc.dur.ac.uk/Eagle/database.php was constructed by using a Friends-of-Friends algorithm, while the substructures were identified using the SUBFIND algorithm (Springel et al., 2001). For the eagle simulations the match of the haloes in the Hydro and DMo simulations was done following Schaller et al. (2015b).
2.2 Fenix simulations
We use the cosmological simulation S230D from the Fenix Project suite. Several properties of galaxies in this simulation have been thoroughly studied such as the morphological properties (Pedrosa et al., 2014), the size-mass relation and the angular momentum evolution (Pedrosa & Tissera, 2015), the stellar and gaseous metallicity gradients of the disc components (Tissera et al., 2016a; Tissera et al., 2016b; Tissera et al., 2017), the chemical abundance of the circumgalactic medium (Machado et al., 2018) and the fundamental properties of the elliptical galaxies, such as Faber-Jackson relations and the Fundamental Plane (Rosito et al., 2018).
This simulation is consistent with a -CDM universe with , and , with , and a normalization of the power spectrum of . The simulated box is a side. The initial conditions have total particles and a mass resolution of and for the DM particle and initial gas particle, respectively. The maximum gravitational softening is . The initial condition has been chosen to correspond to a typical region of the Universe with no massive group present (the largest haloes have virial masses smaller than ). We acknowledge the fact that the initial conditions (ICs) represent a small volume of the Universe. Nevertheless, De Rossi et al. (2013) showed that the growth of the simulated haloes are well-described in these simulations by confronting them with those from the Millenium Simulation (Fakhouri et al., 2010).
These simulations were run using gadget-3, an update version of gadget-2 (Springel & Hernquist, 2003; Springel, 2005), optimised for massive parallel simulations of highly inhomogeneous systems. It includes treatments for metal-dependent radiative cooling, stochastic star formation, chemical and energetic supernovae (SN) feedback (Scannapieco et al., 2005, 2006). This feedback model is able to reproduce galactic mass-loaded winds without introducing any mass-dependent scaling parameter. It also includes a multiphase model for the ISM that allows the coexistence of the hot, diffuse phase and the cold, dense gas phase (Scannapieco et al., 2006, 2008), where star formation takes place. Part of the stars ends their lives as Type II and Type Ia Supernovae, injecting energy and chemical elements into the ISM. Each SN event releases erg, which are distributed equally between the cold and hot phases surrounding the stellar progenitor. The adopted code uses the chemical evolution model developed by Mosconi et al. (2001) and adapted to gadget-3 by Scannapieco et al. (2005). This model considers the enrichment by SNII and SNIa adopting the yield prescriptions of Woosley & Weaver (1995) and Iwamoto et al. (1999), respectively and the Initial Mass Function (IMF) of Salpeter (1955). The synthesised chemical elements are distributed between the cold and hot phase ( and , respectively). The lifetimes for SNIa are randomly selected within the range [0.1, 1] Gyr. Albeit simple, this model reproduces well the mean chemical patterns obtained by adopting the single degenerated model (Jiménez et al., 2015). This combination of star formation and feedback parameters produced systems which can reproduce the angular momentum and the mass-size relation of the discs and bulges of galaxies in agreement with the observational trends (Pedrosa & Tissera, 2015).
The halo catalog was constructed by using a Friends-of-Friends algorithm, while the substructures were identified using the SUBFIND algorithm (Springel et al., 2001). As a result 317 galaxies were identified, resolved with more than DM particles. The virial masses of the haloes () were defined as the mass within a sphere of radius () containing times the cosmic critical matter density at the corresponding redshift. The hydrodynamic simulation has a DMo run counterpart. We refer to them as "Hydro" and "DMo", respectively. The Hydro and DMo simulations start from identical ICs. The shrinking sphere method proposed by Power et al. (2003) is applied to find the coordinates of the centre of mass of the haloes in each simulation. Haloes are matched between the Hydro and DMo runs by one-by-one as performed for the EAGLE set.
3 Properties of DM Haloes
In order to minimize numerical artifacts, we select objects resolved with more than baryonic particles within the optical radius (222The optical radius, , is defined as the radius that encloses 80 percent of the baryonic mass (gas and stars) of the galaxy.). This threshold yields a subsample of 38 objects for the Fenix Project simulation, with masses in the range . While for eagle simulation, the subsample comprises 1696 objects from the original sample selected by Tissera et al. (2019), with masses in the range . The DM haloes were re-scaled in order to take into account the baryonic fraction , where , when comparing Hydro and DMo runs.
The Fenix haloes have radial density profiles that are well described by an Einasto (1965) and Navarro-Frenk-White (NFW) (Navarro et al., 1996, 1997) profiles for Hydro and DMo runs respectively. In the case of the eagle sample, Schaye et al. (2015) find that they are well-fitted by a sum of a NFW profile in the outer regions and an NFW-like profile but with a sharper bend, that takes into account the effect of the accumulation of stars in the inner regions.
3.1 Baryons distribution in the inner regions
The modification of the potential well due to the gathering of baryons in the inner regions to form a galaxy, induces changes in the mass distribution of the DM haloes. Several studies have addressed this issue adopting different radius to evaluate the effects (Butsky et al., 2016; Zavala et al., 2016; Thob et al., 2019; Chua et al., 2019). In order to estimate the radius that maximizes the signal, we inspect three possible selections defined by the radii that enclose 5, 10 and 20 percent of M200 (hereafter measuring radius).
This redistribution can be appreciated in Fig. 1 where we show the ratio between the DM masses measured at the three defined measuring radii in the Hydro and DMo runs, = MHydro/M, as a function of the stellar-to-halo mass ratio . The label denotes the measuring radii defined to enclose 5, 10, and 20 percent of M200.

The results in Fig. 1 show that, for the inner regions, haloes in eagle can contract or expand (i.e. higher or lower DM masses in the Hydro run compared to the DM only). This type of behaviour has also been detected by Dutton et al. (2016) using 100 hydrodynamical cosmological zoom-in simulations of the NIHAO Project. While the contraction is the response to the increase of the potential well due to the accumulation of baryons, the expansion is claimed to be the result of stellar feedback.
An important fraction of the eagle haloes expand when comparing Hydro and DMo runs, while Fenix haloes contract in almost all cases and radii. The expansion in eagle haloes in the central regions has been thoroughly analysed by Schaller et al. (2015a) and is the result of a more effective stellar feedback and a greater loss of baryons (Sawala et al., 2013). Also it can be noticed in Fig. 1 that for higher masses, the contraction is more important as a result of a less effective feedback action. As can be seen, in the case of Fenix simulation, the subsample of haloes studied always contracts when baryons are present within the mass range obtained with this experiment.
We also estimate the galaxy compactness factor, (Dutton et al., 2016), defined as the ratio between the galactic half-mass radius333The half-mass radius, , is defined as the one that enclosed 50 percent of the baryons., , and the virial radius, i.e. . For convenience it is expressed as a percentage. The colours in Fig. 1 map . In the most inner regions, within 5 percent of , haloes hosting more compact galaxies tend to be more concentrated as can be seen in the top panel of Fig. 1. When these ratios are measured at () and (), this trend gradually disappears. This is expected since the larger effects on baryons in the density distribution will be in the very central region where they are located. The concentration of the most inner regions of the haloes depends not on the global baryonic mass gathered in the very centre of haloes but also on their degree of compactness (e.g. Pedrosa et al., 2010; Tissera et al., 2010; Dutton et al., 2016).
The change of the DM concentration in the inner regions can be also quantified through the contraction/expansion parameter , defined as the ratio of the mean DM density to the critical density within the radius at which the DM reaches half of its maximum circular rotational velocity, .
This parameter was previously implemented in Pedrosa et al. (2010) in the study of the halo contraction evolution with the redshift and originally introduced by Alam et al. (2002). By using the radius "half way up", , the rising part of the rotation curve, Alam et al. (2002) focus on the region where conflicts between predicted and observed DM halo densities are more severe (and where the observations are still typically robust against resolution uncertainties).


In Fig. 2 we compare the concentration parameters from the Hydro and DMo runs as a function of and the stellar-to-virial-mass ratio. Haloes with higher contraction (i.e., ) are populated with more compact galaxies (i.e., lower ). The compactness of galaxies appears as a key parameter to trace the degree of concentration of the dark matter haloes. When haloes expand (i.e., ), they tend to host more extended galaxies. In the top panel it can be seen that compact galaxies are hosted by haloes with shorter , indicating that the DM maximum rotational velocity moves to the inner part of the halo with respect to their DMo counterparts. The lower panel shows that both Fenix and eagle subsamples present a slight correlation (Spearman rank coefficient ) with , in the sense that more massive galaxies with respect to halo mass tend to gather also larger DM masses within the very inner regions when baryons are present.
These results confirm the discussed above findings, showing that less concentrated galaxies are located in haloes with expanded central regions with respect to their DMo counterparts. This is clear for the eagle halo sample, which in turn spans on a wide range of stellar-to-dark-matter ratio.
3.2 Baryons shaping haloes
Our main interest is to dig into the interdependence of halo shape and galaxy morphology and try to quantitatively correlate them.
We describe the shapes using the semi-axes of the triaxial ellipsoids, , where , and are the major, intermediate and minor axis respectively of the (e.g. Bailin & Steinmetz, 2005; Zemp et al., 2011). An iterative method is used, starting with particles selected in a spherical shell (i.e. Dubinski & Carlberg, 1991; Curir et al., 1993).
In order to obtain these ratios and , we diagonalize the reduce inertia tensor to compute the eingervectors and eigenvalues, as described in Tissera & Dominguez-Tenreiro (1998). Traditionally the shape parameter has been used as a measure of halo sphericity (e.g. Allgood, 2005; Vera-Ciro et al., 2014; Chua et al., 2019).
We adopt the triaxiality parameter, defined as , which quantifies the degree of prolatness or oblatness: describes a completely prolate halo () while describes a completely oblate halo (). Haloes with are considered prolate and haloes with oblates, while those with are considered triaxials (Allgood, 2005; Artale et al., 2019).
In the next sections we inspect the shape parameters of the haloes in relation with the measuring radius of the inner region, the D/T fraction and the stellar mass of the hosted galaxy.
3.2.1 Shape dependence on radius
To characterize galaxy morphology we use the ratio, calculated for the eagle galaxies in Rosito et al. (2018). These authors adopted the criteria of Tissera et al. (2012). This implementation used the circularity parameter defined as , the ratio between the angular momentum of each stellar particle and , the maximum over all particles at a given binding energy, E. A star on a prograde circular orbit in the disc plane has . The disc component is associated with those particles with and the rest of the particles are associated with the spheroidal component. The same procedure is applied to Fenix galaxies. This implementation allows us to define the morphology of a galaxy by using the stellar disc-to-total mass ratio, D/T.



Fig. 3 shows the shape parameters , and median values as a function of radius normalized by the virial one, , for Hydro (light green) and DMo (black) runs. Three D/T intervals are evaluated for both Fenix and eagle simulations, , and . The shaded areas enclose the and central quartiles. It can be seen that near the virial radius the effects of baryons on T diminish, recovering the triaxiality typical of the outer regions, in agreement with previous studies of Allgood (2005) and Butsky et al. (2016). In the lower sub-panels, the relative change of the halo shape with respect to the DMo counterpart is quantified by defining (in the case of the s shape parameter, it means ), for the eagle haloes. The signal appears to maximize around independently of the predominance of stellar disc. For Fenix haloes subsample we do not detect a clear strengthening of the signal for a particular radius. The relative change of the median values of the shape parameters in Fenix haloes are greater than in eagle haloes.
Shape changes have been shown to be related with the modification of the orbital structure of the DM particles (Zhu et al., 2017). Hence the region that maximizes the effects of the shape changes could be located outside the main galaxy, shifted with respect to the most inner region where haloes concentration changes are stronger.
In a previous study using the NIHAO zoom-in simulations, Butsky et al. (2016) choose as the characteristic radius, based on the findings of Ibata et al. (2001) of the Sagittarius stream location within 20-60 kpc. Thob et al. (2019), using a similar subsample of eagle haloes, use a fixed aperture of for the whole sample. As it comes out from Fig. 3, the strength of the effects of the baryons on the DM haloes is sensitive to the regions where it is measured. Our results indicate that the effects on the shape are stronger in the range of 20–40 percent of the virial radius.
Another way to visualize the modifications of the shape for the different radii can be appreciated in Fig. 4 where we show histograms comparing the shape parameters for Hydro and DMo haloes for the eagle simulation at the four selected radii: , , and the virial one 444for the Fenix haloes see Fig. A1 in the Appendix, Section A. In the outer regions the , and parameters are almost identical for both runs as changes in halo shape are less significant near the virial radius. The dispersion for and is greater at this radii. In the inner regions, the largest deviation from the identity is detected at and is consistent with more triaxials haloes in the DMo run.These trends are in good agreement with the results found by Chua et al. (2019) analysing the Illustris haloes. Our results indicate that the impact on the shapes are stronger close to .


3.2.2 Shape dependence on mass
We also explore the mass dependence of the shape parameters. We inspect this with respect to both, the stellar mass fraction and at 20 percent of . Fig. 5 shows the shape parameters as a function of the virial mass and the ratio . For both Hydro and DMo runs, more massive haloes tend to be more triaxials. On the other hand, when considering the dependence on , the triaxiality gets lower for larger stellar mass as expected (Butsky et al., 2016; Chua et al., 2019).



To better visualize these trends, Fig. 6 shows, for the eagle haloes, the axial ratios as a function of within for different intervals of . In this plane, haloes close to the top right corner are more spherical (, , ) as described in Trayford et al. (2019).

There is a rather statistically weak trend for more prolate halo shapes to be found hosting more massive stellar objects. Butsky et al. (2016) found a strong mass dependence for the NIHAO zoom-ins: low mass haloes tend to retain their original triaxiality while for higher mass haloes, the inner regions become more spherical.
Fig. 6 also shows observational constrains for the DM halo shape of the Milky Way at different radius, spanning between kpc. Our results show good agreement with Bovy et al. (2016) and Malhan & Ibata (2019). The value found by Law & Majewski (2010) is higher than ours, and are significantly different between each other. The best fitting Law & Majewski (2010) model has an oblate halo, with axes ratios, and .
Fenix and eagle cover different stellar mass ranges mainly due to the limited size of the Fenix simulation box. Despite the different feedback implementation both trends present a general agreement, within the same mass range. On the other hand, haloes from eagle simulation have a wider stellar mass range and morphology because of the small volume which includes a rich variety of environments: field, groups and clusters (Fenix represents a field region only).
4 Shape Dependence on morphology
Previous numerical studies find that haloes become rounder when they host baryons in their centres, and more recent ones suggest that it might exist a correlation with the shape of the galaxy (see Tissera & Dominguez-Tenreiro 1998, for an earlier comment on this aspect).
Recently, Thob et al. (2019) found that the morphology of eagle galaxies present a slight correlation with the morphology of its host halo. Furthermore, they suggest that this correlation could have an intrinsic rather than induced origin. In order to further inspect this, in Fig. 7 we show the semi-axis ratios as a function of the ratio, for the Hydro haloes (left panel) and their DMo counterparts (right panel) at (for the same plot estimated at 5 and 10 percent of see Fig. A2 and Fig.A3 in Appendix, Section A).
There is a trend for haloes at to be globally more oblate for higher ratios in both eagle and Fenix simulations (although in the last one, only two intervals could be defined due to the smaller sample). Our results are in good agreement with Kazantzidis et al. (2010). A clear intrinsic trend in the DMo shapes with the fraction can be appreciated.


The presence of baryons alters the DM haloes by making them less triaxials. Some authors suggest that this effect is enhanced when the baryons are organized in disc structures (Kazantzidis et al., 2010). However, the trend that can be seen in Fig. 7 for the DMo runs also suggest that extended disc galaxies preferentially form in haloes that are intrinsically more spherical (i.e. the DMo counterparts are more spherical).
The connection between the inner DM halo and the characteristics of the galaxy it can host was previously mentioned by Zavala et al. (2016) by studying the angular momentum evolution of the galaxies in relation with their DM haloes and by Thob et al. (2019) who analyse the galaxy flattening in comparison the flattening on the DM haloes. Both works used the eagle simulation for this purpose. We made a step forward and measured the degree of sphericalization for different morphologies and quantify with the fraction in relation with the DMo shapes.
Our results show that the combination of the DMo halo masses, used as an input in semianalytical models, and shapes could be use to predict the probability that a halo hosts a galaxy with a specific morphology.


In order to better display this trend, in Fig 8 we show the DM halo shape parameters , , , measured at the 20 percent of the virial radius, as a function of the . For the Fenix haloes the D/T ratios cover a shorter range (), as previously mentioned, while for the eagle haloes larger D/T ratios are found ( ).
| Spearman (p-value) | |||
|---|---|---|---|
| Pearson r (p-value) | |||
| Spearman (p-value) | |||
| Pearson r (p-value) | |||
In the left panels of Fig 8, it can be appreciated clearly that haloes are rounder and less triaxials for larger . However, when this relation is normalized by their correspondent DMo counterpart, the correlations strongly weakens as shown on the right panel. We estimate the Spearman and Pearson correlation coefficients in Table 1. The p-values of Fenix sample show a greater deviation from 0 what impact negatively in the reliability for the strength of the correlation. This is to be expected since the small size of the sample impact on the p-values.
This supports a cosmological origin for the link between DM haloes and the morphology of their central galaxies, which can be also affected by other processes during its assembly history, producing a large dispersion in the relation.
Recall that there is a dependence of the shape parameters on and . The relations shown in this figure consider all haloes regardless of their stellar content. We note that Fenix haloes cover the lower range of stellar masses of eagle and hence, they tend to be rounder compared to the overall median values.
4.1 DM velocity structure
The velocity anisotropy of individual haloes presents a variety of behaviours depending on their particular formation history (see e.g., Tissera et al., 2010). In this section we analyse the change in velocity anisotropy of the DM haloes as a function of radius and the morphology of the hosted galaxy. The velocity structure of the DM particles are closely related with the resulting shapes of the haloes. Additionally, it has important implications for the predicted scattering rates in direct detection experiments (Kuhlen et al., 2010).
We inspect the velocity anisotropy parameter defined as:
| (1) |
where and are the radial and tangential velocity dispersions averaged over concentric spherical shells. This anisotropy parameter provides some indication of the velocity distribution of the haloes. Isotropic distributions have whereas those that more radially biased have .
In Fig. 9 we show the median distributions of as a function of the radius normalized by the virial one, , for galaxies grouped according to their morphology: , , , , and , for the Fenix (left panel) and eagle (right panel) haloes. Both eagle and Fenix simulations show a noticeable trend for radius smaller than approximately : haloes hosting almost bulgeless galaxies present higher values of . The velocity structure within the central regions of DM haloes hosting the highest D/T fraction depart from isotropy. For radius larger than this trend disappear.
When the DMo is inspected (lower panels), show a slight trend in the same sense albeit weaker. As we have found for the shapes, there is an intrinsic behaviour indicating that haloes that host important stellar disc structures tend to have a distinct, slightly less isotropic, DM velocity pattern. To better quantify this behaviour, we estimate as a function of for both the Hydro and DMo runs for galaxies with different morphologies.
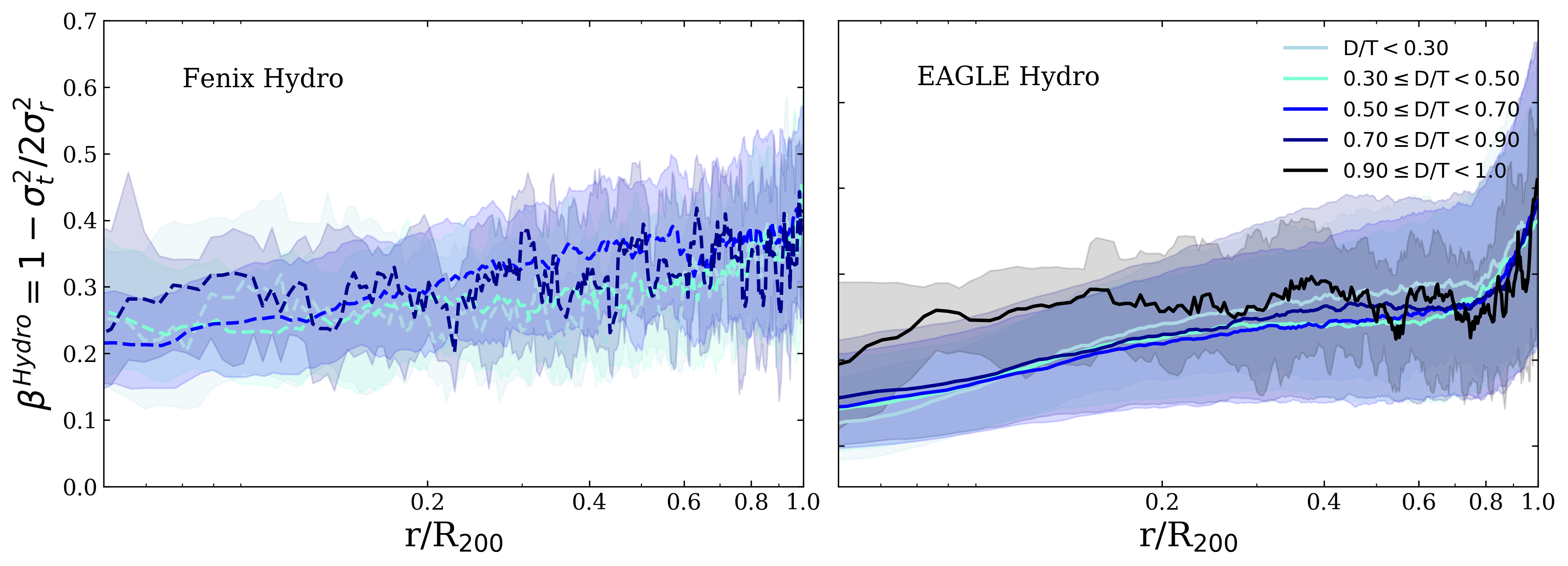


Fig. 10 show the relative change of with respect to the median relations (i.e ) for both Fenix (panels a,b) and eagle (panels c, d) haloes as a function of . , panels b and d, show a slight trend in the same sense albeit weaker. As we have found for the shapes, there is an intrinsic behaviour indicating that haloes that host more important stellar disc structures tend to have a distinct, slightly less isotropic, DM velocity pattern. The error regions were computed by using a bootstrap method with a resampling of 200 for each D/T interval. As can be seen, the larger velocity anisotropies are found in haloes with almost bulgeness galaxies within . The correspondent DMo counterpart haloes show similar estimations but using the .
A greater velocity anisotropy could be related with modification in the orbit structure of DM velocity. We have also looked for DM discs in the central regions of the selected Fenix haloes without any detection. Schaller et al. (2016) concludes that the presence of a dark disc is unlikely in the eagle haloes. The DM configuration could be related to more tube-type orbits, as found by Zhu et al. (2017). So this change in orbit configuration towards higher central velocity anisotropies together with intrinsic DMo haloes shapes could foster preferentially the formation of stellar discs.
The presence of a similar excess in the same radial range is consistent with the claim of an intrinsic characteristics of the haloes that might contribute to the formation of the disc-dominated galaxies.
5 Conclusions
We investigate the relation between the properties of the DM haloes and the morphologies of the hosted galaxies. For this purpose we analysed two simulations with different subgrid physics implementation: a subsample from from the largest volume run of the eagle Project (L100N1504) and haloes from the Fenix Project. We investigate the effects on the halo shape in the central regions. Our main findings can be summarized as follow:
-
1.
We find that haloes hosting galaxies with higher D/T fractions are rounder and less triaxials. Remarkably this trend is already present in the DMo haloes as shown in the right panel of Fig. 7. This suggests that discs will form preferentially in haloes that are already more spherical showing that galaxy morphology is interlinked with the intrinsic structure of DM haloes (without baryonic physics). This could allow us to roughly statistically predict the morphology a galaxy will have if it were to form in a halo of a given shape. This could be important for semi-analytical models.
-
2.
More massive haloes tend to be more triaxials. When considering the dependence on , the triaxiality gets lower for larger stellar mass as expected.
-
3.
We find that the impact of baryons on the DM halo structure maximizes when measured within . While more compact galaxies are located in more concentrated DM haloes, the effects of galaxy assembly are clearer when measured within . As expected, baryonic physics affects halo shape mainly in the inner regions. Haloes hosting baryons become less triaxials, in agreement with previous studies (see Fig. 3 and Fig. 4).
-
4.
The analysis of the velocity structure of haloes using the anisotropy parameter shows a trend in the sense that almost bulgeless galaxies are associated with greater deviations from isotropy in the velocity distribution. This trend seems also to be intrinsic in the sense that it is also detected when using the velocity anisotropies of the DMo counterparts albeit weaker.
Our results shows that DM halo shapes, measured within , are correlated with galaxy morphology. This correlations appears to be intrinsic as we detect that the same trend is already present in the DMo haloes. Hence, there is an indication that more important disc preferentially form in more rounder haloes. This intrinsic trend is reinforced by the growth of the disc galaxies, which strengths its cosmological origin. These results could potentially provide a statistical predictor of the morphology the galaxy would have if it were to form in a halo of a given shape.
Acknowledgements
We would like to thank the anonymous referee for the thorough revision of our manuscript. The authors thank Matthieu Schaller for assistance with the DMo EAGLE data. PBT acknowledges partial support from Fondecyt Regular 1200703 and CONICYT project Basal AFB-170002(Chile). This project has received funding from the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie grant agreement No 734374 and the GALNET Network (ANID, Chile). Also this project was supported through PIP CONICET 11220170100638CO; SP acknowledges partial support by the Ministerio de Ciencia, Innovación y Universidades (MICIU/FEDER) under research grant PGC2018-094975-C21. MCA acknowledges financial support from the Austrian National Science Foundation through FWF stand-alone grant P31154-N27. This work used the DiRAC Data Centric system at Durham University, operated by the Institute for Computational Cosmology on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk). This equipment was funded by BIS National E-infrastructure capital grant ST/K00042X/1, STFC capital grants ST/H008519/1 and ST/K00087X/1, STFC DiRAC Operations grant ST/K003267/1 and Durham University. DiRAC is part of the National E-Infrastructure.
Data Availability
The data underlying this article will be shared on reasonable request to the corresponding authors.
References
- Alam et al. (2002) Alam S. M. K., Bullock J. S., Weinberg D. H., 2002, ApJ, 572, 34
- Allgood (2005) Allgood B. A., 2005, PhD thesis, University of California, nta Cruz, California, USA
- Artale et al. (2019) Artale M. C., Pedrosa S. E., Tissera P. B., Cataldi P., Di Cintio A., 2019, A&A, 622, A197
- Avila-Reese et al. (2005) Avila-Reese V., Colín P., Gottlöber S., Firmani C., Maulbetsch C., 2005, ApJ, 634, 51
- Bailin & Steinmetz (2005) Bailin J., Steinmetz M., 2005, ApJ, 627, 647
- Barnes & Hernquist (1996) Barnes J. E., Hernquist L., 1996, ApJ, 471, 115
- Barnes & White (1984) Barnes J., White S. D. M., 1984, MNRAS, 211, 753
- Benítez-Llambay et al. (2019) Benítez-Llambay A., Frenk C. S., Ludlow A. D., Navarro J. F., 2019, MNRAS, 488, 2387
- Bovy et al. (2016) Bovy J., Bahmanyar A., Fritz T. K., Kallivayalil N., 2016, ApJ, 833, 31
- Bullock & Boylan-Kolchin (2017) Bullock J. S., Boylan-Kolchin M., 2017, ARA&A, 55, 343
- Butsky et al. (2016) Butsky I., et al., 2016, MNRAS, 462, 663
- Chabrier (2003) Chabrier G., 2003, PASP, 115, 763
- Chua et al. (2019) Chua K. T. E., Pillepich A., Vogelsberger M., Hernquist L., 2019, MNRAS, 484, 476
- Crain et al. (2015) Crain R. A., et al., 2015, MNRAS, 450, 1937
- Curir et al. (1993) Curir A., Diaferio A., de Felice F., 1993, ApJ, 413, 70
- Dalla Vecchia & Schaye (2012) Dalla Vecchia C., Schaye J., 2012, MNRAS, 426, 140
- De Rossi et al. (2013) De Rossi M. E., Avila-Reese V., Tissera P. B., González-Samaniego A., Pedrosa S. E., 2013, MNRAS, 435, 2736
- Debattista et al. (2008) Debattista V. P., Moore B., Quinn T., Kazantzidis S., Maas R., Mayer L., Read J., Stadel J., 2008, ApJ, 681, 1076
- Diemand et al. (2007) Diemand J., Kuhlen M., Madau P., 2007, ApJ, 657, 262
- Dubinski & Carlberg (1991) Dubinski J., Carlberg R. G., 1991, ApJ, 378, 496
- Duffy et al. (2010) Duffy A. R., Schaye J., Kay S. T., Dalla Vecchia C., Battye R. A., Booth C. M., 2010, MNRAS, 405, 2161
- Dutton et al. (2016) Dutton A. A., et al., 2016, MNRAS, 461, 2658
- Einasto (1965) Einasto J., 1965, Trudy Astrofizicheskogo Instituta Alma-Ata, 5, 87
- Fakhouri et al. (2010) Fakhouri O., Ma C.-P., Boylan-Kolchin M., 2010, MNRAS, 406, 2267
- Faltenbacher et al. (2005) Faltenbacher A., Allgood B., Gottlöber S., Yepes G., Hoffman Y., 2005, MNRAS, 362, 1099
- Gnedin et al. (2004) Gnedin O. Y., Kravtsov A. V., Klypin A. A., Nagai D., 2004, ApJ, 616, 16
- Governato et al. (2012) Governato F., et al., 2012, MNRAS, 422, 1231
- Guo et al. (2010) Guo Q., White S., Li C., Boylan-Kolchin M., 2010, MNRAS, 404, 1111
- Ibata et al. (2001) Ibata R., Irwin M., Lewis G. F., Stolte A., 2001, ApJ, 547, L133
- Iwamoto et al. (1999) Iwamoto K., Brachwitz F., Nomoto K., Kishimoto N., Umeda H., Hix W. R., Thielemann F.-K., 1999, ApJS, 125, 439
- Jiménez et al. (2015) Jiménez N., Tissera P. B., Matteucci F., 2015, ApJ, 810, 137
- Kazantzidis et al. (2010) Kazantzidis S., Abadi M. G., Navarro J. F., 2010, ApJ, 720, L62
- Knebe et al. (2004) Knebe A., Gill S. P. D., Gibson B. K., Lewis G. F., Ibata R. A., Dopita M. A., 2004, ApJ, 603, 7
- Kuhlen et al. (2010) Kuhlen M., Weiner N., Diemand J., Madau P., Moore B., Potter D., Stadel J., Zemp M., 2010, J. Cosmology Astropart. Phys., 2010, 030
- Law & Majewski (2010) Law D. R., Majewski S. R., 2010, ApJ, 714, 229
- Machado et al. (2018) Machado R. E. G., Tissera P. B., Lima Neto G. B., Sodré L., 2018, A&A, 609, A66
- Malhan & Ibata (2019) Malhan K., Ibata R. A., 2019, MNRAS, 486, 2995
- McAlpine et al. (2016) McAlpine S., et al., 2016, Astronomy and Computing, 15, 72
- Moore et al. (2004) Moore B., Kazantzidis S., Diemand J., Stadel J., 2004, MNRAS, 354, 522
- Mosconi et al. (2001) Mosconi M. B., Tissera P. B., Lambas D. G., Cora S. A., 2001, MNRAS, 325, 34
- Navarro et al. (1996) Navarro J. F., Frenk C. S., White S. D. M., 1996, ApJ, 462, 563
- Navarro et al. (1997) Navarro J. F., Frenk C. S., White S. D. M., 1997, ApJ, 490, 493
- Oh et al. (2015) Oh S.-H., et al., 2015, AJ, 149, 180
- Patiri et al. (2006) Patiri S. G., Cuesta A. J., Prada F., Betancort-Rijo J., Klypin A., 2006, ApJ, 652, L75
- Pedrosa & Tissera (2015) Pedrosa S. E., Tissera P. B., 2015, A&A, 584, A43
- Pedrosa et al. (2010) Pedrosa S., Tissera P. B., Scannapieco C., 2010, MNRAS, 402, 776
- Pedrosa et al. (2014) Pedrosa S. E., Tissera P. B., De Rossi M. E., 2014, A&A, 567, A47
- Planck Collaboration et al. (2014) Planck Collaboration et al., 2014, A&A, 571, A1
- Power et al. (2003) Power C., Navarro J. F., Jenkins A., Frenk C. S., White S. D. M., Springel V., Stadel J., Quinn T., 2003, MNRAS, 338, 14
- Romano-Díaz et al. (2008) Romano-Díaz E., Shlosman I., Heller C., Hoffman Y., 2008, ApJ, 687, L13
- Rosas-Guevara et al. (2015) Rosas-Guevara Y. M., et al., 2015, MNRAS, 454, 1038
- Rosito et al. (2018) Rosito M. S., Pedrosa S. E., Tissera P. B., Avila-Reese V., Lacerna I., Bignone L. A., Ibarra-Medel H. J., Varela S., 2018, preprint, (arXiv:1803.00034)
- Salpeter (1955) Salpeter E. E., 1955, ApJ, 121, 161
- Sawala et al. (2013) Sawala T., Frenk C. S., Crain R. A., Jenkins A., Schaye J., Theuns T., Zavala J., 2013, MNRAS, 431, 1366
- Scannapieco et al. (2005) Scannapieco C., Tissera P. B., White S. D. M., Springel V., 2005, MNRAS, 364, 552
- Scannapieco et al. (2006) Scannapieco C., Tissera P. B., White S. D. M., Springel V., 2006, MNRAS, 371, 1125
- Scannapieco et al. (2008) Scannapieco C., Tissera P. B., White S. D. M., Springel V., 2008, MNRAS, 389, 1137
- Scannapieco et al. (2009) Scannapieco C., White S. D. M., Springel V., Tissera P. B., 2009, MNRAS, 396, 696
- Schaller et al. (2015a) Schaller M., et al., 2015a, MNRAS, 451, 1247
- Schaller et al. (2015b) Schaller M., Dalla Vecchia C., Schaye J., Bower R. G., Theuns T., Crain R. A., Furlong M., McCarthy I. G., 2015b, MNRAS, 454, 2277
- Schaller et al. (2016) Schaller M., Frenk C. S., Fattahi A., Navarro J. F., Oman K. A., Sawala T., 2016, MNRAS, 461, L56
- Schaye & Dalla Vecchia (2008) Schaye J., Dalla Vecchia C., 2008, MNRAS, 383, 1210
- Schaye et al. (2015) Schaye J., et al., 2015, MNRAS, 446, 521
- Sparre & Hansen (2012) Sparre M., Hansen S. H., 2012, Journal of Cosmology and Astroparticle Physics, 2012, 049–049
- Springel (2005) Springel V., 2005, MNRAS, 364, 1105
- Springel & Hernquist (2003) Springel V., Hernquist L., 2003, MNRAS, 339, 289
- Springel et al. (2001) Springel V., Yoshida N., White S. D. M., 2001, New Astron., 6, 79
- Teklu et al. (2017) Teklu A. F., Remus R.-S., Dolag K., Burkert A., 2017, MNRAS, 472, 4769
- Thob et al. (2019) Thob A. C. R., et al., 2019, MNRAS, 485, 972
- Tissera & Dominguez-Tenreiro (1998) Tissera P. B., Dominguez-Tenreiro R., 1998, MNRAS, 297, 177
- Tissera et al. (2010) Tissera P. B., White S. D. M., Pedrosa S., Scannapieco C., 2010, MNRAS, 406, 922
- Tissera et al. (2012) Tissera P. B., White S. D. M., Scannapieco C., 2012, MNRAS, 420, 255
- Tissera et al. (2016a) Tissera P. B., Pedrosa S. E., Sillero E., Vilchez J. M., 2016a, MNRAS, 456, 2982
- Tissera et al. (2016b) Tissera P. B., Machado R. E. G., Sanchez-Blazquez P., Pedrosa S. E., Sánchez S. F., Snaith O., Vilchez J., 2016b, A&A, 592, A93
- Tissera et al. (2017) Tissera P. B., Machado R. E. G., Vilchez J. M., Pedrosa S. E., Sanchez-Blazquez P., Varela S., 2017, A&A, 604, A118
- Tissera et al. (2019) Tissera P. B., Rosas-Guevara Y., Bower R. G., Crain R. A., del P Lagos C., Schaller M., Schaye J., Theuns T., 2019, MNRAS, 482, 2208
- Trayford et al. (2019) Trayford J. W., Frenk C. S., Theuns T., Schaye J., Correa C., 2019, MNRAS, 483, 744
- Valluri et al. (2010) Valluri M., Debattista V. P., Quinn T., Moore B., 2010, MNRAS, 403, 525
- Vera-Ciro et al. (2011) Vera-Ciro C. A., Sales L. V., Helmi A., Frenk C. S., Navarro J. F., Springel V., Vogelsberger M., White S. D. M., 2011, MNRAS, 416, 1377
- Vera-Ciro et al. (2014) Vera-Ciro C. A., Sales L. V., Helmi A., Navarro J. F., 2014, MNRAS, 439, 2863
- Walker & Peñarrubia (2011) Walker M. G., Peñarrubia J., 2011, ApJ, 742, 20
- Wiersma et al. (2009) Wiersma R. P. C., Schaye J., Smith B. D., 2009, MNRAS, 393, 99
- Woosley & Weaver (1995) Woosley S. E., Weaver T. A., 1995, ApJS, 101, 181
- Zavala et al. (2016) Zavala J., et al., 2016, MNRAS, 460, 4466
- Zemp et al. (2011) Zemp M., Gnedin O. Y., Gnedin N. Y., Kravtsov A. V., 2011, ApJS, 197, 30
- Zhu et al. (2017) Zhu Q., Hernquist L., Marinacci F., Springel V., Li Y., 2017, MNRAS, 466, 3876
Appendix A Extended analysis of halo shape
We present in Fig. A1 the histograms comparing the shape parameters for Hydro and DMo haloes for the Fenix simulation at the three selected radii: , , and the virial radius . As well as eagle haloes, in the inner regions, the largest deviation of Hydro haloes shape haloes from DMo ones is detected at .


We also extend the analysis presented in Section 4, by showing the distribution of the inner axial ratios for eagle and Fenix haloes at (Fig. A2) and (Fig. A3).



