(eccv) Package eccv Warning: Package ‘hyperref’ is loaded with option ‘pagebackref’, which is *not* recommended for camera-ready version
https://talegqz.github.io/BAGS/
33email: [email protected], {gaoqingzhe97,weiyuli.cn}@gmail.com, {libin.liu, baoquan}@pku.edu.cn
BAGS: Building Animatable Gaussian Splatting from a Monocular Video with Diffusion Priors
Abstract
Animatable 3D reconstruction has significant applications across various fields, primarily relying on artists’ handcraft creation. Recently, some studies have successfully constructed animatable 3D models from monocular videos. However, these approaches require sufficient view coverage of the object within the input video and typically necessitate significant time and computational costs for training and rendering. This limitation restricts the practical applications. In this work, we propose a method to build animatable 3D Gaussian Splatting from monocular video with diffusion priors. The 3D Gaussian representations significantly accelerate the training and rendering process, and the diffusion priors allow the method to learn 3D models with limited viewpoints. We also present the rigid regularization to enhance the utilization of the priors. We perform an extensive evaluation across various real-world videos, demonstrating its superior performance compared to the current state-of-the-art methods.
Keywords:
Gaussian Splatting Animation Diffusion models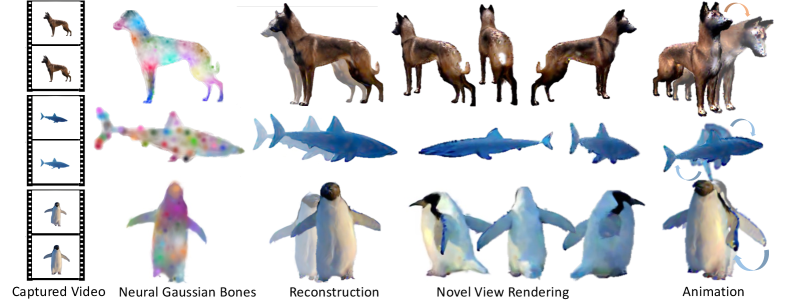
1 Introduction
Animatable 3D models play an important role in diverse fields such as augmented and virtual reality (AR/VR), gaming, and digital content creation, offering advanced motion control and flexibility for various applications. However, the process of acquiring these models poses significant challenges. Traditional methods are not only time-consuming and costly but also heavily reliant on the expertise of artists, which can result in models that often fall short of achieving realistic accuracy.
An alternative approach involves directly reconstructing articulated objects from real-world data. By employing template-based parametric models [64, 28, 19, 24], some works[63, 1] have successfully reconstructed animatable models from videos, even with a limited number of images. However, these parametric models depend on extensive registered 3D scans of humans or animals. This dependence presents great challenges when 3D scan data is unavailable.
Alternatively, videos can provide motion information, facilitating the learning of some aspects of motion and structure [41, 7]. Utilizing videos, some studies [51, 18, 55, 13, 45] learned to reconstruct animatable objects. Among these approaches, some works still depend on category-level information [45] to aid in reconstruction, such as key points [18]. Recently, BANMo [55] achieved state-of-the-art results in reconstructing non-rigid, animatable 3D models from single-object videos without relying on template shape priors and category-level information. However, BANMo suffers from slow training and rendering time due to its use of NeRF [26]. Moreover, an individual video may not always contain sufficient information to accurately reconstruct a given object. Consequently, BANMo incorporates several videos of the same objects, such as filming a family member or a pet over several months or years. Nonetheless, access to such extensive video collections may not be feasible for all objects.
To address these challenges, we introduce BAGS, designed to Build Anima-table 3D Gaussian Splatting with diffusion priors. We propose animatable Gaussian Splitting driven by neural bone, enabling rapid training and rendering. To address the challenge posed by insufficient view coverage, we incorporate the diffusion priors as supervision for our model. However, a naïve application of the priors may lead to the emergence of artifacts, as the diffusion model may not guarantee accuracy and consistency across all time. Consequently, we introduce a rigid regularization technique aimed at optimizing the utilization of the priors.
In experiments, we demonstrate that our approach surpasses the state-of-the-art methods in terms of geometry, appearance, and animation quality with in-the-wild videos. In summary, our contributions are:
-
•
We present BAGS, a framework for constructing animatable 3D Gaussian Splatting incorporating diffusion priors, which achieves state-of-the-art performance, alongside rapid training and real-time rendering.
-
•
We integrate diffusion priors to compensate for the unseen view information in casual videos. Furthermore, we introduce a rigid regularization technique to enhance the utilization of the priors.
-
•
We collect a dataset from in-the-wild videos to evaluate our method. Both qualitative and quantitative results demonstrate that BAGS achieves superior performance compared to baseline models.
2 Related work
2.1 Animatable model reconstruction
As parametric models [19, 64, 28, 24] develop, some research [1, 2, 16, 8, 17, 63, 38, 62] can recover 3D shapes and motions for the human body, face, and animals, even with a few or a single image as input. However, these parametric models are built from large volumes of ground-truth 3D data. It is challenging to apply them to arbitrary categories where 3D data of scan is unavailable. Alternatively, videos can provide temporal information that aids in understanding motion [41, 7], and some research [4, 9, 10, 14, 15, 40, 42, 53, 54] relies on video to recover shape and motion. Nevertheless, these approaches may still result in blurry geometry and unrealistic articulations. Inspired by the promising outcomes of dynamic neural representations [21, 6, 23, 27, 26, 31], some research [51, 55, 56, 18, 56, 45, 54] has demonstrated the ability to reconstruct appearances with enhanced quality. However, these methods require the input video to cover all views of the object comprehensively. Among these, Banmo is the most relevant to our method. In addition to the above problem, BANMo [55] relies on NeRF [26], which results in expensive training and rendering times. Our method, in contrast, leverages 3D Gaussian Splatting [12] based on video input, enabling quick training and real-time rendering. Additionally, we employ a diffusion model to address the lack of viewpoint information.
2.2 Reconstruction with Priors
Leveraging category-level priors, several methods [11, 47, 58, 13, 57, 9] have been proposed for creating animatable 3D models without the use of templates, by reconstructing shapes and poses from 2D image datasets. These approaches employ weak supervision techniques, including key points [18] and object silhouettes, obtained from offthe-shelf models or through human annotations. However, these approaches still necessitate category-level information and exhibit limitations in scenarios with sparse data inputs.
Diffusion models [34, 37, 39, 44, 59] have demonstrated remarkable capabilities in generating realistic images beyond category level. Recent studies [33, 20, 25, 30, 35, 36, 43, 48, 22] have explored utilizing 2D diffusion models to create 3D assets from text prompts or input images. Moreover, some methods [50, 52, 61, 22] reconstruct static scenes from sparse image inputs. Our method not only employs diffusion priors but also integrates motion information from videos to reconstruct animatable models.
Concurrent work
DreaMo [46] similarly utilizes diffusion priors and video information to reconstruct animatable models. Unlike DreaMo, which employs NeRF [26], our method incorporates 3DGS[12], achieving superior training efficiency and rendering speed. Additionally, while DreaMo primarily uses diffusion for geometric supervision, our approach uses it to enhance appearance in uncovered viewpoints.
3 Method
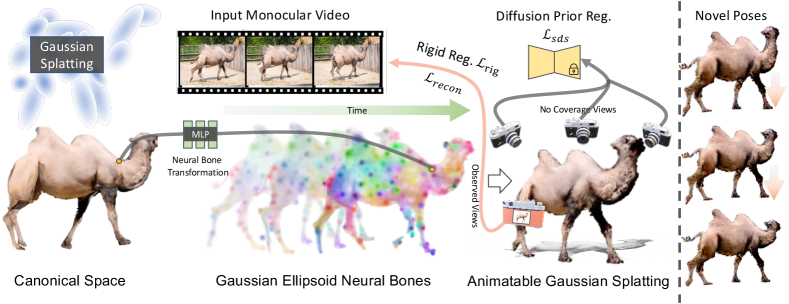
Given a single video of a moving object, our method aims to construct an animatable 3D model of this object. We outline the necessary preliminaries in Section 3.1. Subsequently, we introduce our novel neural bone and LBS structure, detailing its utilization for animating the Gaussian Splatting in Section 3.2. Finally, we describe the diffusion priors to compensate for the unseen views of the object and apply additional regularization techniques to improve the training procedure in Section 3.3. The pipeline of our approach is illustrated in Figure 2.
3.1 Preliminaries
3.1.1 Gaussian Splatting
3D Gaussian Splatting [12] is a scene representation that allows high-quality real-time rendering. The representation is parameterized by a set of static 3D Gaussians. The Gaussian, denoted as , is defined by a translation , a rotation , a per-axis scale, represented by a diagonal matrix , an opacity , and a color . The spatial extent of each Gaussian is defined in 3D by its covariance matrix
For rendering these 3D Gaussians, the method [35] first transforms them from the world to the camera space and then projects them onto a 2D screen plane. This projection employs the covariance matrix , where denotes the Jacobian of an affine approximation of the projective transformation, and is the viewing transformation matrix. The color of a pixel is determined through alpha blending of the ordered Gaussians contributing to that pixel, as:
| (1) |
The term is derived using the 2D covariance matrix and calculated by the per-Gaussian opacity .
3.1.2 Linear Blender Skinning
Given a 3D point , we can transform the point by the Linear Blend Skinning (LBS) function, which is defined as:
| (2) |
where are the rigid bone transformations, and represents the skinning weight of point with respect to bone .
3.2 Neural Bone and Skinning Weight
The bone transformation mentioned can be estimated using parametric model parameters, such as SMPL [24] and SMAL [64]. Building on this, numerous work [1, 2, 17] successfully constructed animatable 3D models. The key idea of these methods involves constructing a canonical space and utilizing the parametric model to drive this canonical space to the target pose. In contrast to these studies, our paper does not depend on such priors knowledge. Inspired by BANMo [55], we develop the neural bone and skinning weight approach.
The set of neural bones, denoted by , is defined using Gaussian ellipsoids, where each bone is represented by center , diagonal scale matrices and rotation . In practice, for each time point , the MLPs is employed to predict the bone parameters based on the positional embedding, :
| (3) |
Without loss of generality, the bone information in canonical space can be determined through a learnable embedding.
The transformation of each bone is determined by its rotation and position, whereas its influence is determined by the scale matrix. More specifically, akin to the approach in LASR [53], the weight of given point the relationship between a given point and a bone can be calculated using the Mahalanobis distance:
| (4) |
We then apply the softmax function to normalize the weight, resulting in the final skinning weights:
| (5) |
Thanks to the explicit modeling provided by Gaussian splatting, we can directly apply Linear Blend Skinning (LBS) as described in Equation (2) to drive the model in canonical space to the target pose. For a given target pose in time , we can readily obtain , which transforms the 3D Gaussian in canonical space,as follows:
| (6) |
where the LBS weight can be estimated using Equations (3) and (4). Moreover, the bone transformations can be derived from the rotations and translations between bones in the canonical space and the target pose.
Subsequently, the rotation and scale of can be obtained through the changes in the covariance matrix:
| (7) |
The color and opacity of the Gaussian are assumed to remain constant. Consequently, we can utilize Equation (1) to render the final color of pixel at time .
In summary, given a time and arbitrary camera parameters , we can render the corresponding image with our model. We denote this process by , where represents our model, and denotes the model’s parameters.
3.3 Diffusion Priors
The primary challenge in constructing an animatable object from a video lies in the insufficiency of the input video to cover the object comprehensively. If the video does not encompass enough perspectives, it lacks the necessary information for an accurate reconstruction of the subject. BANMo [55] addresses this issue by utilizing casually collected videos. However, collecting suitable videos can be challenging, therefore, we employ the diffusion priors to address this issue.
Conditioned on the input image, we employ ImageDream [49] to synthesize novel view images and utilize Score Distillation Sampling (SDS) to supervise our model. Given a time , and the input image , our model randomly generates multiple views. The SDS loss can be expressed as follows:
| (8) |
Where the represents random noise, denotes the noise predicted by the diffusion model, and is the random camera viewpoint. represents the step of the diffusion model, distinct from the input video time index .
However, naively using this priors can result in artifacts. While the diffusion priors offers information for unseen views, its accuracy and consistency are not guaranteed across all time. Although the Gaussian Splatting process largely preserves temporal consistency due to fixed color and opacity, incorrect transformations may still occur. To address this issue, drawing inspiration from traditional methods [3] in physical simulations, we propose the rigid regularization to constrain the transformation:
| (9) |
Where and are the unitary matrices resulting from the Singular Value Decomposition (SVD) of .
can be considered the most similar rotation matrix to , and this rigid regularization aims to approximate the transformation as closely as possible to a rigid transformation. We also discover that this regularization can mitigate the adverse effects caused by inconsistencies, which arise from imperfect foreground segmentation.
3.4 Training objective
Besides and , we also employ reconstruction loss to compare the input with the rendered results using a combination the L1 loss , the mask loss and the perceptual loss [60] .
In summary, the final loss can be written:
| (10) |
where is the weight of each loss.


4 Experiment
4.1 Implementation Details
During the experiment, it was discovered that training all Gaussians and the neural network-based bones simultaneously resulted in converging toward a noisy canonical space. Consequently, a random frame of the input video was selected as a reference for the preliminary warm-up training of the canonical space. After warming up, we start the joint training of all the frames. We employ operations similar to those described by [12]—specifically, split, clone, and prune—to manipulate the Gaussians and enhance rendering quality. These controls are only applied during the warm-up stage.
During the Training, we find out that training all frames together immediately after warming up may cause mistakes. When a target frame is too far from the chosen frame for warming up, the losses may drive the bones to a completely wrong position, since there’s a huge difference between the target pose and the current pose. On considering this problem, we adopt a strategy to limit the training frames: At first, only the chosen frame and the other 6 frames nearby are added to the training set. During the training progress, we gradually add all frames to the joint training, making full use of the temporal continuity of motions between adjacent frames.
Throughout the experiments, the weights of our loss terms , , , and are , , , and , respectively. For the SDS loss, during the warm-up stage, we linearly decrease the from to . In the joint training stage, the warm-up phase ensures a good initialization, allowing to be linearly reduced from to . We run all experiments on a single 40 GB A100 GPU. Further details are available in the supplementary material.
4.2 Dataset
To evaluate our method both qualitatively and quantitatively, we collect 40 videos from the Internet and DAVIS [29] featuring a variety of animal species exhibiting natural behaviors. To specifically assess our method’s capability in reconstructing unseen parts of animals, we opt for videos with lower view coverage. For foreground segmentation, we utilize SAM-Track [5], which is effective across a broad range of object categories.
4.3 Quantitative Results
We select BANMo [55], which closely matches our setup and is open-source, as the baseline. Due to the absence of ground truth for novel view and keypoint information, we utilize CLIP [32] for evaluation. Initially, for each frame of the input video, the input image served as the reference image, and we generate a novel view image at this time index. Subsequently, we compute the CLIP image embedding for both the novel view images and the reference images, employing their cosine similarity as the evaluation metric. Consistency was further assess by calculating the cosine similarity between pairs of novel view images. Additionally, we compare both the training time and rendering time between our method and the baseline.
The results are presented in Table 1. Our method achieves higher similarity to the reference images and better consistency in novel view images. Additionally, it significantly reduced the optimization time from hours to minutes, enabling real-time rendering. It is important to note that while BANMo training requires 2 GPUs, our method operates with just a single GPU.
| CLIP-reference | CLIP-novel | Training | rendering | |
|---|---|---|---|---|
| BANMo | 0.8337 | 0.8795 | 12h (2 GPUs) | 0.1 FPS |
| Ours | 0.9023 | 0.9292 | 40min (1 GPU) | 61 FPS |

4.4 Qualitative Results
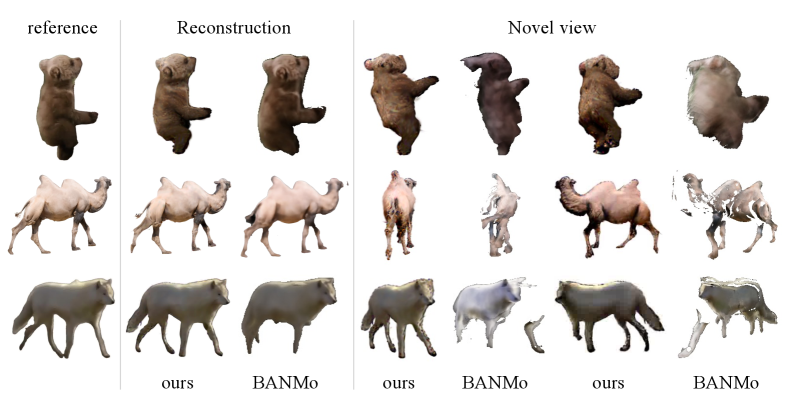
We present qualitative results in Figure 3 and Figure 5, illustrating the outcomes rendered across different time steps and camera views. Our approach is compared with BANMo, demonstrating that our method achieves enhanced detail in both geometry and texture. Furthermore, our approach demonstrates superior performance in novel view synthesis, where BANMo struggles to produce accurate 3D shapes, often resulting in the reconstruction of merely a 2D plane that overfits the input video. Additionally, animation results showcased in Figure 4 illustrate the results of manual manipulation of the 3D models. More results can be found in the supplementary material.
4.5 Ablation Study
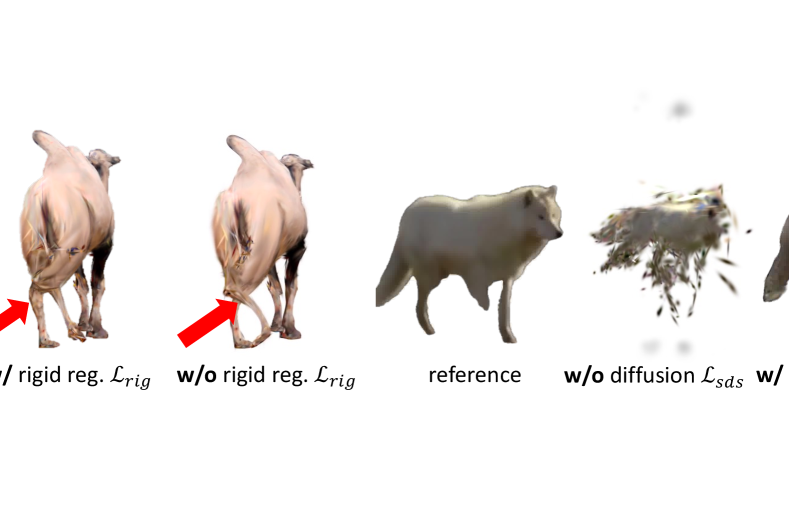
The primary contribution of our paper is the utilization of diffusion priors combined with rigid regularization to enhance the application of diffusion priors. As illustrated in Figure 6, without diffusion priors, the model can not obtain reasonable results. In the absence of rigid regularization, the transformation results in artifacts, such as a tortuous leg. Even when the reference image possesses an incorrect foreground segmentation, our method, with rigid regularization, still manages to achieve reasonable results.
5 Limitation
Although our method can achieve notably positive results, it is not without limitations. Firstly, while our method utilizes diffusion to compensate for unseen view information, the motion information is still dependent on the input video. Therefore, if the objects in the video do not exhibit sufficient motion, our method may not accurately learn the animatable ability. The motion diffusion model can potentially be integrated into the pipeline to address this issue. Secondly, the generation of unseen views relies on a diffusion model. Although this model has capabilities beyond the category level, it sometimes produces artifacts, as shown in Figure 7. While the rigid loss can occasionally mitigate these issues, artifacts remain a concern. We aim to address them in future work.
6 Conclusion
In conclusion, this study introduces BAGS, an innovative approach for creating animatable 3D models from monocular videos through Gaussian Splatting with diffusion priors, marking an advancement in 3D reconstruction technology. Unlike previous methods that depend heavily on extensive view coverage and incur high computational costs, our method significantly enhances efficiency in training and rendering processes. The integration of diffusion priors enables the learning of 3D models from limited viewpoints, while rigid regularization further optimizes the utilization of these priors. Comparative evaluations with various real-world videos underscore our method’s superior performance against existing state-of-the-art techniques.
References
- [1] Badger, M., Wang, Y., Modh, A., Perkes, A., Kolotouros, N., Pfrommer, B.G., Schmidt, M.F., Daniilidis, K.: 3d bird reconstruction: a dataset, model, and shape recovery from a single view. In: European Conference on Computer Vision. pp. 1–17. Springer (2020)
- [2] Biggs, B., Boyne, O., Charles, J., Fitzgibbon, A., Cipolla, R.: Who left the dogs out? 3d animal reconstruction with expectation maximization in the loop. In: Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part XI 16. pp. 195–211. Springer (2020)
- [3] Bouaziz, S., Martin, S., Liu, T., Kavan, L., Pauly, M.: Projective dynamics: Fusing constraint projections for fast simulation. In: Seminal Graphics Papers: Pushing the Boundaries, Volume 2, pp. 787–797 (2023)
- [4] Bregler, C., Hertzmann, A., Biermann, H.: Recovering non-rigid 3d shape from image streams. In: Proceedings IEEE Conference on Computer Vision and Pattern Recognition. CVPR 2000 (Cat. No. PR00662). vol. 2, pp. 690–696. IEEE (2000)
- [5] Cheng, Y., Li, L., Xu, Y., Li, X., Yang, Z., Wang, W., Yang, Y.: Segment and track anything. arXiv preprint arXiv:2305.06558 (2023)
- [6] Gao, C., Saraf, A., Kopf, J., Huang, J.B.: Dynamic view synthesis from dynamic monocular video. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 5712–5721 (2021)
- [7] Gao, Q., Wang, B., Liu, L., Chen, B.: Unsupervised co-part segmentation through assembly. In: International Conference on Machine Learning. pp. 3576–3586. PMLR (2021)
- [8] Gao, Q., Wang, Y., Liu, L., Liu, L., Theobalt, C., Chen, B.: Neural novel actor: Learning a generalized animatable neural representation for human actors. IEEE Transactions on Visualization and Computer Graphics (2023)
- [9] Goel, S., Kanazawa, A., Malik, J.: Shape and viewpoint without keypoints. In: Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part XV 16. pp. 88–104. Springer (2020)
- [10] Gotardo, P.F., Martinez, A.M.: Non-rigid structure from motion with complementary rank-3 spaces. In: CVPR 2011. pp. 3065–3072. IEEE (2011)
- [11] Kanazawa, A., Tulsiani, S., Efros, A.A., Malik, J.: Learning category-specific mesh reconstruction from image collections. In: Proceedings of the European Conference on Computer Vision (ECCV). pp. 371–386 (2018)
- [12] Kerbl, B., Kopanas, G., Leimkühler, T., Drettakis, G.: 3d gaussian splatting for real-time radiance field rendering. ACM Transactions on Graphics 42(4) (2023)
- [13] Kokkinos, F., Kokkinos, I.: To the point: Correspondence-driven monocular 3d category reconstruction. Advances in Neural Information Processing Systems 34, 7760–7772 (2021)
- [14] Kong, C., Lucey, S.: Deep non-rigid structure from motion. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 1558–1567 (2019)
- [15] Kumar, S.: Non-rigid structure from motion: Prior-free factorization method revisited. In: Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision. pp. 51–60 (2020)
- [16] Lei, B., Ren, J., Feng, M., Cui, M., Xie, X.: A hierarchical representation network for accurate and detailed face reconstruction from in-the-wild images. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 394–403 (2023)
- [17] Lei, J., Wang, Y., Pavlakos, G., Liu, L., Daniilidis, K.: Gart: Gaussian articulated template models. arXiv preprint arXiv:2311.16099 (2023)
- [18] Li, R., Tanke, J., Vo, M., Zollhöfer, M., Gall, J., Kanazawa, A., Lassner, C.: Tava: Template-free animatable volumetric actors. In: European Conference on Computer Vision. pp. 419–436. Springer (2022)
- [19] Li, T., Bolkart, T., Black, M.J., Li, H., Romero, J.: Learning a model of facial shape and expression from 4d scans. ACM Trans. Graph. 36(6), 194–1 (2017)
- [20] Lin, C.H., Gao, J., Tang, L., Takikawa, T., Zeng, X., Huang, X., Kreis, K., Fidler, S., Liu, M.Y., Lin, T.Y.: Magic3d: High-resolution text-to-3d content creation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 300–309 (2023)
- [21] Lin, C.H., Ma, W.C., Torralba, A., Lucey, S.: Barf: Bundle-adjusting neural radiance fields. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 5741–5751 (2021)
- [22] Liu, R., Wu, R., Van Hoorick, B., Tokmakov, P., Zakharov, S., Vondrick, C.: Zero-1-to-3: Zero-shot one image to 3d object. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 9298–9309 (2023)
- [23] Liu, Y.L., Gao, C., Meuleman, A., Tseng, H.Y., Saraf, A., Kim, C., Chuang, Y.Y., Kopf, J., Huang, J.B.: Robust dynamic radiance fields. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 13–23 (2023)
- [24] Loper, M., Mahmood, N., Romero, J., Pons-Moll, G., Black, M.J.: Smpl: A skinned multi-person linear model. In: Seminal Graphics Papers: Pushing the Boundaries, Volume 2, pp. 851–866 (2023)
- [25] Metzer, G., Richardson, E., Patashnik, O., Giryes, R., Cohen-Or, D.: Latent-nerf for shape-guided generation of 3d shapes and textures. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 12663–12673 (2023)
- [26] Mildenhall, B., Srinivasan, P.P., Tancik, M., Barron, J.T., Ramamoorthi, R., Ng, R.: Nerf: Representing scenes as neural radiance fields for view synthesis. Communications of the ACM 65(1), 99–106 (2021)
- [27] Park, K., Sinha, U., Barron, J.T., Bouaziz, S., Goldman, D.B., Seitz, S.M., Martin-Brualla, R.: Nerfies: Deformable neural radiance fields. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 5865–5874 (2021)
- [28] Pavlakos, G., Choutas, V., Ghorbani, N., Bolkart, T., Osman, A.A., Tzionas, D., Black, M.J.: Expressive body capture: 3d hands, face, and body from a single image. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. pp. 10975–10985 (2019)
- [29] Perazzi, F., Pont-Tuset, J., McWilliams, B., Van Gool, L., Gross, M., Sorkine-Hornung, A.: A benchmark dataset and evaluation methodology for video object segmentation. In: Computer Vision and Pattern Recognition (2016)
- [30] Poole, B., Jain, A., Barron, J.T., Mildenhall, B.: Dreamfusion: Text-to-3d using 2d diffusion. arXiv preprint arXiv:2209.14988 (2022)
- [31] Pumarola, A., Corona, E., Pons-Moll, G., Moreno-Noguer, F.: D-nerf: Neural radiance fields for dynamic scenes. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 10318–10327 (2021)
- [32] Radford, A., Kim, J.W., Hallacy, C., Ramesh, A., Goh, G., Agarwal, S., Sastry, G., Askell, A., Mishkin, P., Clark, J., et al.: Learning transferable visual models from natural language supervision. In: International conference on machine learning. pp. 8748–8763. PMLR (2021)
- [33] Raj, A., Kaza, S., Poole, B., Niemeyer, M., Ruiz, N., Mildenhall, B., Zada, S., Aberman, K., Rubinstein, M., Barron, J., et al.: Dreambooth3d: Subject-driven text-to-3d generation. arXiv preprint arXiv:2303.13508 (2023)
- [34] Ramesh, A., Pavlov, M., Goh, G., Gray, S., Voss, C., Radford, A., Chen, M., Sutskever, I.: Zero-shot text-to-image generation. In: International Conference on Machine Learning. pp. 8821–8831. PMLR (2021)
- [35] Ren, J., Pan, L., Tang, J., Zhang, C., Cao, A., Zeng, G., Liu, Z.: Dreamgaussian4d: Generative 4d gaussian splatting. arXiv preprint arXiv:2312.17142 (2023)
- [36] Richardson, E., Metzer, G., Alaluf, Y., Giryes, R., Cohen-Or, D.: Texture: Text-guided texturing of 3d shapes. arXiv preprint arXiv:2302.01721 (2023)
- [37] Rombach, R., Blattmann, A., Lorenz, D., Esser, P., Ommer, B.: High-resolution image synthesis with latent diffusion models. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. pp. 10684–10695 (2022)
- [38] Rueegg, N., Zuffi, S., Schindler, K., Black, M.J.: Barc: Learning to regress 3d dog shape from images by exploiting breed information. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 3876–3884 (2022)
- [39] Saharia, C., Chan, W., Saxena, S., Li, L., Whang, J., Denton, E., Ghasemipour, S.K.S., Ayan, B.K., Mahdavi, S.S., Lopes, R.G., et al.: Photorealistic text-to-image diffusion models with deep language understanding, 2022. URL https://arxiv. org/abs/2205.11487 4
- [40] Sand, P., Teller, S.: Particle video: Long-range motion estimation using point trajectories. International journal of computer vision 80, 72–91 (2008)
- [41] Siarohin, A., Roy, S., Lathuilière, S., Tulyakov, S., Ricci, E., Sebe, N.: Motion-supervised co-part segmentation. In: 2020 25th International Conference on Pattern Recognition (ICPR). pp. 9650–9657. IEEE (2021)
- [42] Sidhu, V., Tretschk, E., Golyanik, V., Agudo, A., Theobalt, C.: Neural dense non-rigid structure from motion with latent space constraints. In: Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part XVI 16. pp. 204–222. Springer (2020)
- [43] Singer, U., Sheynin, S., Polyak, A., Ashual, O., Makarov, I., Kokkinos, F., Goyal, N., Vedaldi, A., Parikh, D., Johnson, J., et al.: Text-to-4d dynamic scene generation. arXiv preprint arXiv:2301.11280 (2023)
- [44] Song, Y., Sohl-Dickstein, J., Kingma, D.P., Kumar, A., Ermon, S., Poole, B.: Score-based generative modeling through stochastic differential equations. arXiv preprint arXiv:2011.13456 (2020)
- [45] Tan, J., Yang, G., Ramanan, D.: Distilling neural fields for real-time articulated shape reconstruction. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 4692–4701 (2023)
- [46] Tu, T., Li, M.F., Lin, C.H., Cheng, Y.C., Sun, M., Yang, M.H.: Dreamo: Articulated 3d reconstruction from a single casual video. arXiv preprint arXiv:2312.02617 (2023)
- [47] Tulsiani, S., Kulkarni, N., Gupta, A.: Implicit mesh reconstruction from unannotated image collections. arXiv preprint arXiv:2007.08504 (2020)
- [48] Wang, H., Du, X., Li, J., Yeh, R.A., Shakhnarovich, G.: Score jacobian chaining: Lifting pretrained 2d diffusion models for 3d generation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 12619–12629 (2023)
- [49] Wang, P., Shi, Y.: Imagedream: Image-prompt multi-view diffusion for 3d generation. arXiv preprint arXiv:2312.02201 (2023)
- [50] Wu, R., Mildenhall, B., Henzler, P., Park, K., Gao, R., Watson, D., Srinivasan, P.P., Verbin, D., Barron, J.T., Poole, B., et al.: Reconfusion: 3d reconstruction with diffusion priors. arXiv preprint arXiv:2312.02981 (2023)
- [51] Wu, S., Jakab, T., Rupprecht, C., Vedaldi, A.: Dove: Learning deformable 3d objects by watching videos. International Journal of Computer Vision pp. 1–12 (2023)
- [52] Wynn, J., Turmukhambetov, D.: Diffusionerf: Regularizing neural radiance fields with denoising diffusion models. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 4180–4189 (2023)
- [53] Yang, G., Sun, D., Jampani, V., Vlasic, D., Cole, F., Chang, H., Ramanan, D., Freeman, W.T., Liu, C.: Lasr: Learning articulated shape reconstruction from a monocular video. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 15980–15989 (2021)
- [54] Yang, G., Sun, D., Jampani, V., Vlasic, D., Cole, F., Liu, C., Ramanan, D.: Viser: Video-specific surface embeddings for articulated 3d shape reconstruction. Advances in Neural Information Processing Systems 34, 19326–19338 (2021)
- [55] Yang, G., Vo, M., Neverova, N., Ramanan, D., Vedaldi, A., Joo, H.: Banmo: Building animatable 3d neural models from many casual videos. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 2863–2873 (2022)
- [56] Yang, G., Yang, S., Zhang, J.Z., Manchester, Z., Ramanan, D.: Ppr: Physically plausible reconstruction from monocular videos. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 3914–3924 (2023)
- [57] Yao, C.H., Hung, W.C., Li, Y., Rubinstein, M., Yang, M.H., Jampani, V.: Lassie: Learning articulated shapes from sparse image ensemble via 3d part discovery. Advances in Neural Information Processing Systems 35, 15296–15308 (2022)
- [58] Yao, C.H., Raj, A., Hung, W.C., Rubinstein, M., Li, Y., Yang, M.H., Jampani, V.: Artic3d: Learning robust articulated 3d shapes from noisy web image collections. Advances in Neural Information Processing Systems 36 (2024)
- [59] Zhang, L., Rao, A., Agrawala, M.: Adding conditional control to text-to-image diffusion models. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 3836–3847 (2023)
- [60] Zhang, R., Isola, P., Efros, A.A., Shechtman, E., Wang, O.: The unreasonable effectiveness of deep features as a perceptual metric. In: CVPR (2018)
- [61] Zhou, Z., Tulsiani, S.: Sparsefusion: Distilling view-conditioned diffusion for 3d reconstruction. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 12588–12597 (2023)
- [62] Zuffi, S., Kanazawa, A., Berger-Wolf, T., Black, M.J.: Three-d safari: Learning to estimate zebra pose, shape, and texture from images" in the wild". In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 5359–5368 (2019)
- [63] Zuffi, S., Kanazawa, A., Black, M.J.: Lions and tigers and bears: Capturing non-rigid, 3d, articulated shape from images. In: Proceedings of the IEEE conference on Computer Vision and Pattern Recognition. pp. 3955–3963 (2018)
- [64] Zuffi, S., Kanazawa, A., Jacobs, D.W., Black, M.J.: 3d menagerie: Modeling the 3d shape and pose of animals. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 6365–6373 (2017)