Automorphisms of a family of surfaces with $p_{g}=q=2$ and $K^{2}=7$

The classification of general type surfaces with low numerical invariants is unanimously considered a very difficult problem to tackle. It is already difficult to construct new surfaces with low numerical invariants. Therefore, as soon as new examples are found, it is natural to test the famous conjectures on them. This short note stems from the question whether it is possible to verify the Mumford-Tate conjecture for surfaces $S$ of general type with $p_{g}=q=2$ and $K^{2}=7$ first constructed by Rito in [Rit18] and later studied by the authors in [PePi20].

These surfaces $S$ are obtained as a generically finite double covering of an abelian surface $A$, which turns out to be the Albanese variety of $S$, branched along a curve with a singular point of type $(3,3)$ and no other singularities. These surfaces give rise to three disjoint open subsets in the Gieseker moduli space $\mathcal{M}^{\mathrm{can}}_{2,\,2,\,7}$ which are all irreducible, generically smooth of dimension 2, that we shall denote by $\mathcal{M}_{1}$, $\mathcal{M}_{2}$ and $\mathcal{M}_{4}$.

The Mumford-Tate conjecture for surfaces is still an open problem and only in very few examples it has been verified as true, see for example [Moo17a]. A strategy to prove the conjecture for surfaces with $p_{g}=q=2$ and of maximal Albanese dimension is outlined in the article [CoPe20]. The strategy reduces to finding geometric quotients $X$ of $S$ that are K3 surfaces whose weight 2 Hodge structure is a sub-Hodge structure of the weight 2 Hodge structure of $S$ orthogonal to the the sub-Hodge structure coming from the Albanese surface of $S$. This strategy proved to be very successful in many cases, see [CoPe20]. The first question toward exploiting the strategy is to calculate the automorphism of the surfaces $S$ and then classify all possible quotients. This is the content of the main theorem of this note.

The second step of the strategy is to identify the quotients. We have at once

This corollary tells us that in order to prove the Mumford-Tate conjecture for these surfaces a new strategy is needed.

Now, let us explain the way in which this paper is organized.

In the second section we recall the construction of the surfaces $S$ with the calculation of the invariants. The third section is devoted to the proof of the Main Theorem. The section four contains the calculation of the invariants of the quotient surfaces. Finally we include a section five where it is explained the strategy to prove the conjecture for surfaces with $p_{g}=q=2$ and of maximal Albanese dimension.

Acknowledgments. The first author was partially supported by GNSAGA-INdAM, by PRIN 2020KKWT53 003 - Progetto: Curves, Ricci flat Varieties and their Interactions and by the DIMA - Dipartimento di Eccellenza 2023-2027. The second author was partially supported by supported by the ”National Group for Algebraic and Geometric Structures, and their Applications” (GNSAGA - INdAM) and by the European Union under NextGenerationEU, PRIN 2022 Prot. n. 20223B5S8L.

Notation and conventions. We work over the field $\mathbb{C}$ of complex numbers. By surface we mean a projective, non-singular surface $S$, and for such a surface $K_{S}$ denotes the canonical class, $p_{g}(S)=h^{0}(S,\,K_{S})$ is the geometric genus, $q(S)=h^{1}(S,\,K_{S})$ is the irregularity and $\chi(\mathcal{O}_{S})=1-q(S)+p_{g}(S)$ is the Euler-Poincaré characteristic.

In this section we report, for the convenience of the reader, the construction of the families of surfaces under consideration. We use the notation of [PePi20], the main result in this direction is the following one.

In [Rit18] and later in [PePi20] the existence of the abelian surface $A$, that has the properties as in Proposition 2.1, is proved. In particular, it is also shown that the double cover coincides with the Albanese map, hence $A$ is the Albanese variety associated to $S$, we denote it by

We can be more precise, $A$ is isogenous to a product of two elliptic curves $T_{1}$ and $T_{2}$. We denote by

the isogeny, which is of degree 2. Clearly, $A$ carries a (1,2)-polarization $L$ which is a pull-back of a (product) principal polarization via the isogeny $\iota$. In addition, on $A$ we have two elliptic fibrations $f_{j}\colon A\rightarrow T_{j}$ with fibres $\Lambda_{i}$ with $\Lambda_{i}$ isogenous to $T_{i}$ by a degree two isogeny for $i,j\in\{1,2\}$. Notice that the isogeny is given by the restriction of $\iota$ to the fibres.

The branching locus of $\alpha$ is an effective divisor with two irreducible components

where $C_{1}=f_{2}^{-1}(b_{1})$ is an element of $|\Lambda_{2}|$, with $b_{1}\in T_{2}$. While, $t$ is a curve of geometric genus $3$ with a tacnode tangent to $C_{1}$ at a point $p$. The situation is exemplified in the following Figure 1.

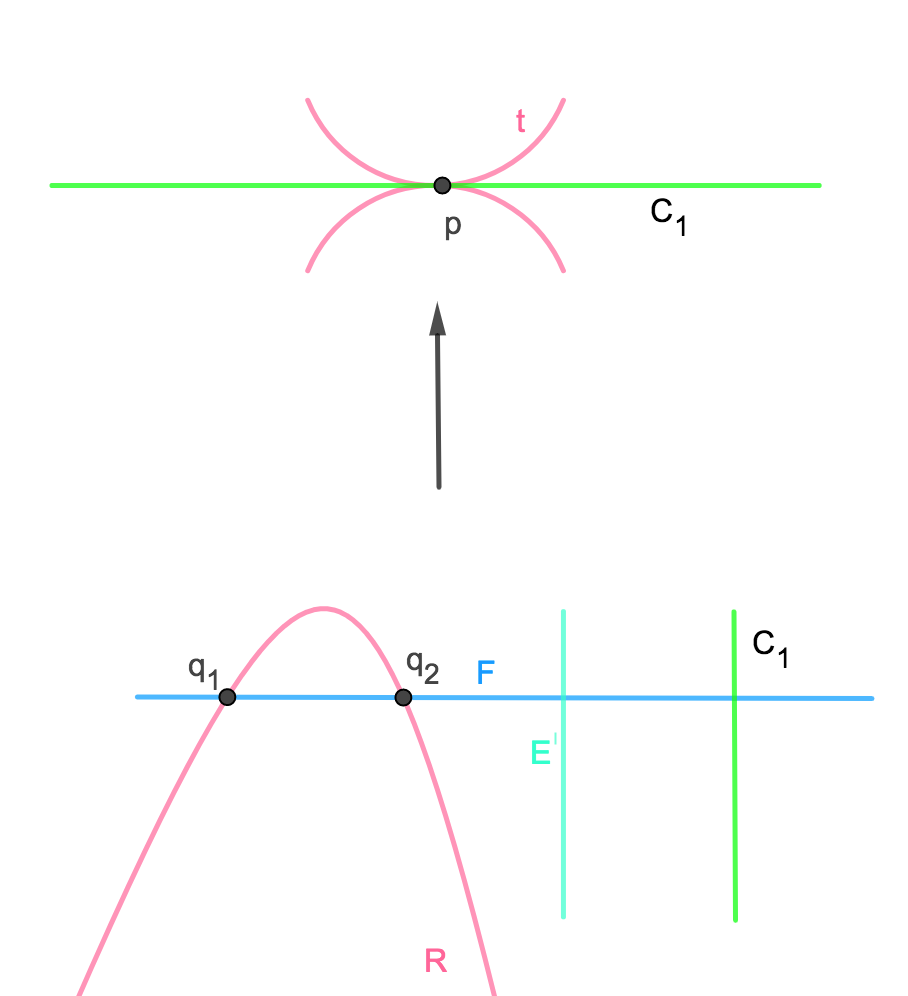
We deduce that

notice that $(C_{1}+t)^{2}=16$.

Notice that the branch locus is singular in $p$. Therefore, to get a smooth surface $S$ as a generically finite double cover of $A$ branched along $C_{1}+t$ we have to blow up the point $p$ (see Figure 1) first.

1. 2.0.1.

   First, we resolve the singularity in $p$. To do that, we need to blow up $A$ twice, first in $p$ and then in a point infinitely near to $p$. Let us denote these two blow ups by

   $$B^{\prime}\stackrel{{\scriptstyle\sigma_{4}}}{{\longrightarrow}}B\stackrel{{\scriptstyle\sigma_{3}}}{{\longrightarrow}}A.$$

   On $B^{\prime}$, let us denote by $F$ the exceptional divisor relative to $\sigma_{4}$, by $E^{\prime}$ the strict transform of the exceptional divisor $E$ relative to $\sigma_{3}$, by $C_{1}$ the strict transform of $C_{1}$ and, finally, by $R$ the strict transform of $t$ (see Figure 1).

   In addition, one gathers the following information: $E^{\prime}\cong{\mathbb{P}}^{1}$ and $(E^{\prime})^{2}=-2$, $F\cong{\mathbb{P}}^{1}$ and $F^{2}=-1$, $g(C_{1})=1$ and $C_{1}^{2}=-2$.

2. 2.0.2.

   Second, we consider a double cover of $\beta\colon S^{\prime}\longrightarrow B^{\prime}$ ramified over $R+C_{1}+E^{\prime}$ (this is even since $t+C_{1}$ is even on $A$). The surface $S^{\prime}$ is a surface of general type, not minimal. Indeed, it contains a $-1$-curve, which is $\hat{E}=\beta^{-1}(E^{\prime})$. The ramification divisor is denoted $\hat{R}+\hat{C_{1}}+\hat{E}$. Notice that $\hat{C_{1}}$ has genus $1$ and $\hat{C_{1}}^{2}=-1$.

3. 2.0.3.

   Finally, to get $S$ we contract the $-1$-curve $\hat{E}$.

We can summarize the construction of $S$ with the following diagram.

Moreover, the point $p$ is a [3,3] point, which is not a negligible singularities. A [3,3] point is a pair $(x_{1},\,x_{2})$ such that $x_{1}$ belongs to the first infinitesimal neighborhood of $x_{2}$ and both are triple points for the curve. Thus, we may calculate the invariants of $S$ by using the formulae in [BHPV03, p. 237]. In those formulas $x_{2}$ counts as a triple point (so $m_{2}=1$) and $x_{1}$ as a quadruple point (so $m_{1}=2$). Then

Finally, once we contract the $-1$-curve on $S^{\prime}$, we obtain hence $K_{S}^{2}=7$ and $\chi(S)=1$.

Considering the Abelian varieties $A,T_{1},T_{2},T_{1}\times T_{2}$ we choose the following points as neutral elements:

With this particular choice $\iota,f_{1},f_{2}$ are homomorphism of groups too.

The remaining $2$-torsion points on each elliptic curve $T_{j}$ will be denoted by

This yields $\iota_{*}{\mathcal{O}}_{A}^{-}\cong{\mathcal{O}}_{T_{1}}(a_{4}-a_{3})\boxtimes{\mathcal{O}}_{T_{2}}(b_{2}-b_{1})$ , where $\iota_{*}{\mathcal{O}}_{A}^{-}$ is the anti-invariant part of $\iota_{*}{\mathcal{O}}_{A}$, see [PePi20, Lemma 3.4] for a detailed proof.

Consider the abelian variety $A$. We know that there is an isogeny of degree $2$ onto a product of elliptic curves $T_{1}\times T_{2}$.

By taking the universal covers, we can write $T_{j}:={\mathbb{C}}/\lambda_{j}$ where the $\lambda_{j}\cong{\mathbb{Z}}^{2}$ are lattices so that the origin maps to $a_{3}$ respectively $b_{1}$. We choose generators $\bar{e}_{1},\bar{e}_{2}$ of $\lambda_{1}$, $\bar{e}_{3},\bar{e}_{4}$ of $\lambda_{2}$ so that $\frac{\bar{e}_{1}}{2}$ maps to $a_{1}$, $\frac{\bar{e}_{2}}{2}$ maps to $a_{2}$, $\frac{\bar{e}_{3}}{2}$ maps to $b_{3}$, $\frac{\bar{e}_{4}}{2}$ maps to $b_{4}$.

So, in ${\mathbb{C}}^{2}$ -coordinates we have

Since the universal cover of $T_{1}\times T_{2}$ factors through the isogeny $\iota$, we obtain $A={\mathbb{C}}^{2}/\lambda$ where $\lambda$ is a sublattice of index $2$ of the lattice

We will need the following general result for an abelian surface with a $(1,2)$-polarization, the proof of which can be found in [Bar87, Section 1.2].

Since the Albanese morphism $\alpha\colon S\longrightarrow A$ has degree $2$, it determines an involution $\sigma\colon S\rightarrow S$ that is central in $\text{\rm Aut}\ S$ and an exact sequence

where $G$ is the group of the self-biholomorphisms $\varphi\colon A\rightarrow A$ such that

1. 3.0.1.

   $\varphi^{*}L=L$;

2. 3.0.2.

   $\varphi(C_{1}+t)=C_{1}+t$, equivalently $\varphi(C_{1})=C_{1}$, $\varphi(t)=t$, $\varphi(p)=p$.

We have written an isomorphism $A\cong{\mathbb{C}}^{2}/\lambda$ where the point $p$ is the image of the origin of ${\mathbb{C}}^{2}$. From $\varphi(p)=p$ it follows that the elements of $G$ are automorphisms of $A$ as a group with the group structure induced by ${\mathbb{C}}^{2}$. Now, we can see that one of the above assumption is not necessary, indeed we have the following lemma.

The action of $G$ on $A$ may be uniquely lifted to an action on ${\mathbb{C}}^{2}$ fixing the origin, so representing $G$ as a finite subgroup of the linear group $GL_{2}({\mathbb{C}})$ of the matrices preserving the lattice $\lambda$. We will then write $\varphi$ as a matrix

In particular $\varphi$ is given by two roots of the unity $\varphi_{jj}\in{\mathbb{C}}$ giving automorphisms of the two elliptic curves: each $\varphi_{jj}$ gives an automorphism of $T_{j}$.

We will now need the following well known facts on automorphisms of elliptic curves see for instance [Sil08, Section III.10].

With these facts in mind we can prove

Then we can compute $\text{\rm Aut}(S)$.

In this brief section we shall prove Corollary 1.2. By Proposition 3.7 $\text{\rm Aut}(S)=\langle\sigma\rangle\times G$ let us consider $H\leq\text{\rm Aut}(S)$, then we have the following diagram

A natural question to address is the classification of quotient surfaces $S/H$.

A first step in studying the quotient surfaces is to determine their numerical invariants. To this end we study the induced action of the group $H$ on the cohomology groups of $S$. Recall that the the global sections of $H^{1,0}(S)$ comes from the one forms on $A$ that we denote by $dx,dy$. Moreover, one of the two generators of the global sections of $H^{2,0}(S)$ can be identified with $dx\wedge dy$, and of course being $p_{g}(S)=2$ we have a global 2-forms $\omega$ not coming from $A$. To summarize this we can write

Let us denote by $g$ the generator of the cyclic group $G$, which has order $2$ or $4$ according to the three cases of Proposition 3.6. The same proposition describes completely the induced action on the generators of the cohomology groups in each case. In particular, we have

If $H$ is trivial or $H\cong<\sigma>$ then we know that the quotients are respectively $S$ or birational to $A$. Else $H\cap G\neq\{1\}$ and this yields at once that $q(X)=1$. More precisely, $H^{1}(X)\cong<dy>$, and thus we have proved Corollary 1.2. We can remark already that no quotient $X$ can be a K3 surface. Moreover, we have

Therefore we have that $p_{g}(X)$ is either $0$ or $1$ according to the $H$-invariance of $\omega$ .

This section is devoted to explain the strategy used up to know for proving the Mumford Tate conjecture for surfaces with $p_{g}(S)=q(S)=2$ and of maximal Albanese dimension.

Let $S$ be a smooth projective complex surface with invariants $p_{g}(S)=q(S)=2$, and assume that the Albanese morphism $\alpha\colon S\to A$ is surjective. We can make the following general observations (see also [CoPe20]). It holds:

1. 5.0.1.

   The induced map on cohomology $\alpha^{*}\colon H^{*}(A,{\mathbb{Z}})\to H^{*}(S,{\mathbb{Z}})$ is injective. The orthogonal complement $H^{2}_{\textnormal{new}}=H^{*}(A,{\mathbb{Z}})^{\perp}\subset H^{*}(S,{\mathbb{Z}})$ is a Hodge structure of weight $2$ with Hodge numbers $(1,n,1)$, where $n=h^{1,1}(S)-4$. Such a Hodge structure is said to be of K3 type.

2. 5.0.2.

   Let $S^{\prime}$ be a smooth projective complex surface with invariant $p_{g}(S^{\prime})=1$. Then Morrison [Mor87] showed that there exists a K3 surface $X^{\prime}$ together with an isomorphism $\iota^{\prime}\colon H^{2}(S^{\prime},{\mathbb{Q}})^{\textnormal{tra}}\to H^{2}(X^{\prime},{\mathbb{Q}})^{\textnormal{tra}}$ that preserves the Hodge structure, the integral structure, and the intersection pairing. (Here $(\_)^{\textnormal{tra}}$ denotes the transcendental part of the Hodge structure, that is, the orthogonal complement of the Hodge classes.)

We now look closely to our surfaces $S$ with $p_{g}(S)=q(S)=2$, for which we know that the Albanese map is a generically finite cover.

Then we have

This is a direct consequence of [Mor87]. Notice that the surface $X$ is related only Hodge theoretically to $S$. Therefore, this is not enough to prove the conjecture, to this end we have to address the following question:

Let us briefly explain and recall some facts on categories of motives, and for the reader convenience we state the motivic Mumford–Tate conjecture, for a more detailed introduction on the subject see [Moo17b, Moo17a]. First we recall some facts about Chow motives and André motives of surfaces. We do not need full generality, so let $K$ be a subfield of ${\mathbb{C}}$.

Given smooth and projective varieties $X$ and $Y$ over a field $K$ (i.e., objects in the category $\textnormal{SmPr}_{/K}$) of dimension $d_{X}$ and $d_{Y}$ respectively, a correspondence of degree $k$ from $X$ to $Y$ is an element $\gamma$ of $A^{d_{X}+k}(X\times Y)$. Then $\gamma$ induces a map $A^{\cdot}(X)\rightarrow A^{\cdot+k}(Y)$ by the formula

where $\pi_{1}\colon X\times Y\rightarrow X$ and $\pi_{2}\colon X\times Y\rightarrow Y$ denote the projections. The category $\mathcal{M}_{\textnormal{rat}}$ of Chow motives (with rational coefficients) over $K$ is defined as follows:

• »

  the objects of $\mathcal{M}_{\textnormal{rat}}$ are triples $(X,p,n)$ such that $X\in\textnormal{SmPr}_{K},\,p\in A^{d_{X}}(X\times X)$ is an idempotent correspondence (i.e. $p_{*}\circ p_{*}=p_{*}$) and $n$ is an integer;

• »

  the morphisms in $\mathcal{M}_{\textnormal{rat}}$ from $(X,p,n)$ to $(Y,q,m)$ are correspondences $f\colon X\rightarrow Y$ of degree $n-m$, such that $f\circ p=f=q\circ f$.

We recall that $\mathcal{M}_{\textnormal{rat}}$ is an additive, ${\mathbb{Q}}$-linear, pseudoabelian category, see [Sch91, Theorem 1.6].

We consider from here only the cases in which we are interested hence let us suppose $K={\mathbb{C}}$, There exists a functor

from the opposite category of smooth projective varieties over ${\mathbb{C}}$ to the category of Chow motives.

We denote also with $A^{i}(M)$ the $i$-th Chow group of a motive $M\in\mathcal{M}_{\textnormal{rat}}$. In general, it is not known whether the Künneth projectors $\pi_{i}$ are algebraic, so it does not (yet) make sense to speak of the summand $h^{i}(X)\subset h(X)$ for an arbitrary smooth projective variety $X/{\mathbb{C}}$. However, a so-called Chow–Künneth decomposition does exist for curves [Man68], for surfaces [Mur90], and for abelian varieties [DeMu91]. For algebraic surfaces there is in fact the following theorem, which strengthens the decomposition of the Chow motive. Statement is copied from [Lat19, Theorem 2.2].