Automata-based constraints for language model decoding

A finite-state automaton ${\cal A}$ is a tuple $(\Sigma,Q,I,F,E)$ where $\Sigma$ is a set of input symbols, $Q$ is a finite set of states, $I\in Q$ and $F\subseteq Q$ are initial and final states, and $E\subseteq Q\times\Sigma_{\epsilon}\times Q$, where $\Sigma_{\epsilon}=\Sigma\cup\{\epsilon\}$, is a set of edges (Hopcroft et al., 2001; Riley et al., 2009). Each edge $e\in E$ is a tuple $(\smash{e^{s}},\smash{e^{\sigma}},\smash{e^{t}})$ of source state $\smash{e^{s}}$, input label $\smash{e^{\sigma}}$ or $\epsilon$ if none, and target state $\smash{e^{t}}$. See Figure 1.

An FSA ${\cal A}$ accepts $w\in\Sigma^{*}$ if there exist $e_{1},...,e_{n}\in E$ such that $w=\smash{e^{\sigma}_{1}}\parbox[b][4.49997pt][c]{8.99994pt}{ \raggedright\parbox{2.5pt}{$\cdot$}\parbox{2.5pt}{$\cdot$}\parbox{2.5pt}{$\cdot$} \@add@raggedright}\smash{e^{\sigma}_{n}}$, $\smash{e^{s}_{1}}=I$, $\smash{e^{t}_{n}}\in F$, and $\smash{e^{s}_{i}}=\smash{e^{t}_{i-1}}$ for $i>1$; note that $n>|w|$ iff $\exists i,\,\smash{e^{\sigma}_{i}}=\epsilon$. To express the functional behavior of FSAs, we overload notation and define ${\cal A}(w)$ as a predicate that is true iff ${\cal A}$ accepts $w$. For any FSA ${\cal A}$, we define its language $L_{{\cal A}}=\{w\in\Sigma^{*}:{\cal A}(w)\}$ as the set of strings it accepts. More generally, the regular languages can be defined as $\{L_{{\cal A}}:\textrm{${\cal A}$ is an FSA}\}$ (Chomsky, 1956).

Conveniently, the regular languages can also be defined by regular expressions¹¹1 In this paper we use the mathematical definition of regular expressions. Many tools extend regular expressions with non-regular features like backreferences—at the cost of exponential runtime. , which are equivalent to FSAs (Kleene, 1951). Common tools like UNIX grep compile regular expressions into FSAs with $\Sigma=\textrm{Unicode}$, which are then used as predicates on text (McNaughton & Yamada, 1960; Thompson, 1968). See Figure 2 (left).

An FSA is deterministic if $\forall e\in E,\,\,\smash{e^{\sigma}}\neq\epsilon$ and $\forall q\in Q,a\in\Sigma,\,\,|\{e\in E:\smash{e^{s}}=q\land\smash{e^{\sigma}}=a\}|\leq 1$. Intuitively, outbound edges have unique inputs so executing the FSA is trivial: track the current state and traverse the edge matching the next input. Surprisingly, non-deterministic and deterministic FSAs are equivalent. In particular, given an arbitrary FSA ${\cal A}$ one can build a deterministic FSA ${\cal A^{\prime}}$ such that $L_{{\cal A}}=L_{{\cal A^{\prime}}}$ (Rabin & Scott, 1959). See Figure 2.

A finite-state transducer is an FSA that generates output. Formally, an FST ${\cal T}$ is a tuple $(\Sigma,\Delta,Q,I,F,E)$ where $\Sigma$, $Q$, $I$, and $F$ are as defined for FSAs, $\Delta$ is a set of output symbols, and $E\subseteq Q\times\Sigma_{\epsilon}\times\Delta_{\epsilon}\times Q$ is a set of edges (Mohri, 1997; 2004; Riley et al., 2009). Each edge $e\in E$ is a tuple $(\smash{e^{s}},\smash{e^{\sigma}},\smash{e^{\delta}},\smash{e^{t}})$ where $e^{s}$, $e^{\sigma}$, and $e^{t}$ are as defined for FSAs and $e^{\delta}$ is its output label, or $\epsilon$ if none. See Figure 3.

An FST ${\cal T}$ transduces $w\in\Sigma^{*}$ into $v\in\Delta^{*}$ if there exist $e_{1},...,e_{n}\in E$ such that $w=\smash{e^{\sigma}_{1}}\parbox[b][4.49997pt][c]{8.99994pt}{ \raggedright\parbox{2.5pt}{$\cdot$}\parbox{2.5pt}{$\cdot$}\parbox{2.5pt}{$\cdot$} \@add@raggedright}\smash{e^{\sigma}_{n}}$, $v=\smash{e^{\delta}_{1}}\parbox[b][4.49997pt][c]{8.99994pt}{ \raggedright\parbox{2.5pt}{$\cdot$}\parbox{2.5pt}{$\cdot$}\parbox{2.5pt}{$\cdot$} \@add@raggedright}\smash{e^{\delta}_{n}}$, $\smash{e^{s}_{1}}=I$, $\smash{e^{t}_{n}}\in F$, and $\smash{e^{s}_{i}}=\smash{e^{t}_{i-1}}$ for $i>1$. Similar to FSAs, we write²²2 ${\cal T}(w)$ should be a set because a non-deterministic FST can transduce the same input to different outputs. In this paper, the FSTs we define satisfy $|{\cal T}(w)|=1$ so we simply write $v={\cal T}(w)$. $v={\cal T}(w)$ if ${\cal T}$ transduces $w$ to $v$. Critically, the output of one FST can be fed as the input of another FST or FSA (Riley et al., 2009). Given FSTs ${\cal T}_{1}$ and ${\cal T}_{2}$ where $\Delta_{1}=\Sigma_{2}$, we can compose them into a new FST ${\cal T^{\prime}}={\cal T}_{2}\circ{\cal T}_{1}$ where $\Sigma^{\prime}=\Sigma_{1}$, $\Delta^{\prime}=\Delta_{2}$, and ${\cal T^{\prime}}(w)={\cal T}_{2}({\cal T}_{1}(w))$. Similarly, given an FST ${\cal T}_{1}$ and FSA ${\cal A}_{2}$ where $\Delta_{1}=\Sigma_{2}$, we can compose them into a new FSA ${\cal A^{\prime}}={\cal A}_{2}\circ{\cal T}_{1}$ where $\Sigma^{\prime}=\Sigma_{1}$ and ${\cal A^{\prime}}(w)={\cal A}_{2}({\cal T}_{1}(w))$.

Our first contribution is a reformulation of detokenization (i.e., the process of converting token sequences back into text) as an FST, using the following construction:

For compactness, common prefixes of the chains can be merged to form a trie-like structure, as in Figure 4; see Appendix B.1 for a proof of correctness.

Our next contribution is a generic method for adapting any FSA from characters to tokens. Specifically, given a token vocabulary $V$ and an FSA ${\cal A}$ that accepts character sequences, ${\cal A^{\prime}}={\cal A}\circ{\cal T}_{V}$ accepts essentially the same language as ${\cal A}$, but in token form. More precisely, for each token sequence $w\in L_{{\cal A^{\prime}}}$, the detokenization of $w$ is in $L_{{\cal A}}$.

Note that the converse does not hold: $w\in L_{{\cal A}}$ has a counterpart in $L_{{\cal A^{\prime}}}$ only if $w$ can be segmented into tokens from $V$. For example, suppose ${\cal A}$ accepts any number in hexadecimal format, but the tokens in $V$ only cover the digits 0-9. Nevertheless, to the extent that $L_{{\cal A}}$ can be tokenized by $V$, strings in $L_{{\cal A}}$ are represented in $L_{{\cal A^{\prime}}}$. Indeed, due to tokenization ambiguity, there may be multiple token sequences in $L_{{\cal A^{\prime}}}$ that are equivalent to the same string in $L_{{\cal A}}$. See Figure 5.

We now present our method for constraining an LM to a regular language:

Note that ${\cal A}_{R\circ V}$ is a closed-form solution: it expresses $R$ using all relevant tokens from $V$ and can be executed independently from both. See Appendix B.2 for a proof of correctness.

The required operations are indexing, slicing, and basic arithmetic, which are efficient and simple enough to execute directly on an accelerator with minimal latency overhead. One pleasing aspect of this solution is how neatly it separates concerns amongst the two halves:

• •

  ${\cal T}_{V}$ is vocabulary-specific and, while large, can easily be pre-computed for each LM.

• •

  ${\cal A}_{R}$ is vocabulary-agnostic, easily specified, and portable across different LMs.

This clean decomposition is only possible because FST-FSA composition provides a fast, automatic, and general method for joining the two halves.

For example, alternative detokenization automata (see Section 4.3) can be slotted into ${\cal T}_{V}$ without changing the rest of the system. Similarly, alternative constraint automata (see Section 3.1) can be substituted for ${\cal A}_{R}$ and FST composition still works.

Our last contribution in this section is a set of regular expression extensions, written as specially-named capturing groups, that greatly increase the efficiency and expressiveness of the system. We describe some illustrative examples below and list others in Table 1.

A push-down automaton can be viewed as an FSA equipped with a stack. Formally, a PDA ${\cal P}$ is a tuple $(\Sigma,\Pi,S,Q,I,F,E)$ where $\Sigma$, $Q$, $I$, and $F$ are as defined for FSAs, $\Pi$ is a set of stack symbols, $S\in\Pi$ is a unique initial stack symbol, and $E\subseteq Q\times\Sigma_{\epsilon}\times\Pi^{*}\times Q\times\Pi^{*}$ is a set of edges (Hopcroft et al., 2001). Each edge $e\in E$ is a tuple $(\smash{e^{s}},\smash{e^{\sigma}},\smash{e^{\scaleobj{0.75}{\uparrow}}},\smash{e^{t}},\smash{e^{\scaleobj{0.75}{\downarrow}}})$ where $e^{s}$, $e^{\sigma}$, and $e^{t}$ are as defined for FSAs, and $e^{\scaleobj{0.75}{\uparrow}}$ and $e^{\scaleobj{0.75}{\downarrow}}$ are popped and pushed stack symbols. See Figure 6.

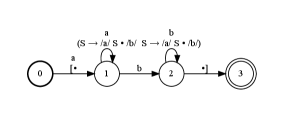${\cal P}$ accepts $w\in\Sigma^{*}$ if there exist $e_{1},...,e_{n}\in E$ such that $w=\smash{e^{\sigma}_{1}}\parbox[b][4.49997pt][c]{8.99994pt}{ \raggedright\parbox{2.5pt}{$\cdot$}\parbox{2.5pt}{$\cdot$}\parbox{2.5pt}{$\cdot$} \@add@raggedright}\smash{e^{\sigma}_{n}}$, $\smash{e^{s}_{1}}=I$, $\smash{e^{t}_{n}}\in F$, $\smash{e^{s}_{i}}=\smash{e^{t}_{i-1}}$ for $i>1$, and $\smash{e^{\scaleobj{0.75}{\uparrow}}_{i}}$ and $\smash{e^{\scaleobj{0.75}{\downarrow}}_{i}}$ form a coherent sequence of stack edits. Formally, let $s^{i}$ be the stack before $e_{i}$ where $\smash{s^{1}}=S$, $n_{i}=|\smash{s^{i}}|$, $m_{i}=n_{i}-|\smash{e^{\scaleobj{0.75}{\uparrow}}_{i}}|$, and $\smash{s^{i+1}}=s^{i}_{1:m_{i}}\smash{e^{\scaleobj{0.75}{\downarrow}}_{i}}$, then $\smash{e^{\scaleobj{0.75}{\uparrow}}_{i}}=s^{i}_{m_{i}+1:n_{i}}$ must hold. In other words, at each step $e^{\scaleobj{0.75}{\uparrow}}_{i}$ must match the suffix of $s_{i}$, and we update the stack by popping $e^{\scaleobj{0.75}{\uparrow}}_{i}$ off and pushing $e^{\scaleobj{0.75}{\downarrow}}_{i}$ on. As above, we write ${\cal P}(w)$ to indicate that ${\cal P}$ accepts $w$.

Unlike FSAs, non-deterministic and deterministic PDAs are not equivalent: the former accept the context-free languages, which are also defined by context-free grammars (Chomsky, 1956; Hopcroft et al., 2001), while the latter accept a strict subset, the deterministic context-free languages (Ginsburg & Greibach, 1966). This subset nevertheless includes all regular languages and the LL($k$) and LR($k$) languages (Knuth, 1965), covering the syntax of most programming languages. As a result of this non-equivalence, there is no general algorithm to determinize an arbitrary PDA, as we had for FSAs. Instead, as LL($k$) and LR($k$) parsers do, our system detects non-deterministic grammars and signals an error, leaving it to the author of the grammar to rewrite the grammar in a deterministic manner.

Although PDAs are more expressive than FSAs, they behave similarly in many ways and, crucically, FSTs and PDAs are composable (Allauzen & Riley, 2012). Formally, given an FST ${\cal T}_{1}$ and PDA ${\cal P}_{2}$ where $\Delta_{1}=\Sigma_{2}$, we can compose them into a new PDA ${\cal P^{\prime}}={\cal P}_{2}\circ{\cal T}_{1}$ where $\Sigma^{\prime}=\Sigma_{1}$ and ${\cal P^{\prime}}(w)={\cal P}_{2}({\cal T}_{1}(w))$. As with FSAs, composition with the detokenizing FST ${\cal T}_{V}$ adapts a character-based PDA into one that accepts tokens in $V$. See Figure 7.

This allows us to reuse Algorithm 2 with minimal modification (see Appendix B.3 for proof):

It’s worth re-emphasizing the benefits of formulating detokenization as an FST. By representing the entire task in terms of automata, our approach easily generalizes from regular expressions to grammars while preserving many desirable features. For example, just as FST-FSA composition enables tokens to cross sub-expression boundaries in the regular expression (see Figure 5), FST-PDA composition enables tokens to cross (non-)terminal boundaries in the grammar (see Figure 7).

Automata have been used to constrain learned sequence models for some time. Below, we mention a few representative examples from the literature.

Sproat & Jaitly (2017) and Zhang et al. (2019), among others in this line of work, examine text normalization for TTS applications. Certain phrases are difficult to verbalize (e.g., ”4/5” to ”four fifths” or ”April fifth” or ”four out of five [stars]”), and neural models are prone to hallucinations (e.g., ”60” to ”six”). The authors build FSTs that translate from written forms to possible verbalizations, and use those to guide the deep model similarly to this work. Our approach allows a wider range of constraints, supporting any regular or deterministic context-free language, and also addresses the token-mismatch issues endemic to current LM tokenizers (see Appendix A).

Deutsch et al. (2019) use (intersections of) FSAs and PDAs to constrain the output of a sequential model to some formal language. This work predates the rise of general-purpose LMs, and thus does not address the problems created by mismatches between the LM’s tokenization and the targeted formal language. Both Outlines (Willard & Louf, 2023) and this work address those mismatches, but by different means.

The most relevant work is Outlines (Willard & Louf, 2023), which is based on a bespoke ”indexing” operation that builds a token-based overlay on an FSA or PDA. Unfortunately, when applied to PDAs their algorithm is over-constrained w.r.t. tokenization³³3 https://github.com/outlines-dev/outlines/issues/684 (see Appendix A.1), whereas our approach naturally generalizes to PDAs while preserving tokenization freedom (see Section 3.2). Our approach also easily generalizes to different tokenization schemes (see Section 4.3), which does not seem possible for Outlines and likely requires a rewrite of their indexing algorithm. Finally, their approach is ~7,000x slower to compile than ours (see Section 6.1), so it is only practical when the constraint can be pre-compiled. Our core innovation allows us to recast the entire process in automata-theoretic terms, making our solution extensible (via decomposition into FST and FSA/PDA modules), correct (via basic properties of FSTs), and fast (via access to highly-optimized algorithms). For clarity, Figure 8 illustrates which parts of our system are similar to or different from Outlines.

Building on Outlines, Yin et al. (2024) extended the package with the ability to ”compress” runs of text into prefills. This technique is of significant practical interest and could be adapted to our approach as our techniques appear to be largely orthogonal.

SynCode (Ugare et al., 2024) is a more recent system that also exploits FSAs, but handles grammars using LALR(1) and LR(1) parsers rather than PDAs. Like Outlines, their approach relies on a bespoke algorithm; in this case, they speculatively unroll future lexer tokens to allow LM tokens to cross multiple lexer tokens. This introduces significant complexity relative to our purely automata-theoretic approach, and deciding how many lexer tokens to unroll is a trade-off between computational cost and completeness.

Some less closely-related approaches still constrain by masking logits, but dynamically match the vocabulary on each step instead of devising a method to statically pre-compute these matches, as we and the systems above do. For example, Synchromesh (Poesia et al., 2022) iterates the entire LM vocabulary on every decoding step, making it impractical with current LMs. Guidance (Microsoft, 2023) improves upon this with a cached trie, and grammar-constrained decoding (Geng et al., 2023) adds expressive power beyond context-free. While these latter two are more flexible than our approach, they are less efficient and harder to deploy at scale.

Finally, some other approaches no longer predictively mask logits, but instead sample unconstrained continuations and reject invalid ones post-hoc. For example, PICARD (Scholak et al., 2021) converts the top-$k$ tokens to text and performs various levels of validation. Lew et al. (2023) do sequential Monte-Carlo sampling that, in the case of hard constraints, reduces to something like rejection sampling with rescoring. These approaches are quite flexible, but may have issues when the constraints require the LM to select a low-probability token. In addition, note that post-hoc filtering is orthogonal to predictive masking, so our approaches could be merged.

Concurrently with review, Berglund et al. (2024) presented a finite-state machine that only accepts ”correct” BPE tokenizations. Unlike the simple detokenizing FST presented in Section 2.3, their FSA is unambiguous: for any character sequence $w$, it only accepts the correct BPE tokenization of $w$. As they mention in their conclusion, their construction can be straightforwardly generalized into an FST.

From there, we could compose their FST with any regex-derived FSA or grammar-derived PDA, yielding an automaton that accepts only correct BPE tokenizations that also obey the constraint. In essence, any tokenization policy that can be expressed in finite-state form can be dropped into our approach, demonstrating its modularity and generality.

JSON (Pezoa et al., 2016) is a widely-used structured data format that LMs are often expected to generate. We study the problem of generating JSON that conforms to a schema, which is a mapping from field name to type. Field types range from simple primitives like booleans, numbers, and strings, to sub-objects based on sub-schemas, and arrays or unions of other types. Field values can be nullable, meaning that they can be substituted with null, and fields can be marked optional, meaning that both the field name and value may be omitted.

Although the set of all JSON expressions of any kind is a context-free language, somewhat surprisingly the set of JSON expressions conforming to a particular schema is a regular language, as the schema limits recursion. It is difficult to manually write the regular expression corresponding to a particular schema: while leaf-level matchers like /(true|false)/ are simple enough, complexity grows quickly as they are composed into objects, arrays, and unions. For user convenience, we have implemented tools that automatically translate schemas into regular expressions.

We have also explored schema-free JSON, which as mentioned above is context-free. A simple approach is to impose constant limits $k_{O}$ and $k_{A}$ on object and array nesting, which reduces from context-free to regular, and we have implemented tools to generate regular expressions for this form of depth-truncated JSON. Naturally, one can also directly convert the JSON grammar into a PDA-based constraint.

Another case study is constraining LMs to output Python dataclasses (Van Rossum & Drake, 2009). Like the JSON schemas described above, a Python dataclass defines a mapping from field names to types, and we have implemented similar tooling that reflects on a dataclass to automatically build a regular expression matching constructor calls. This enables a particularly convenient API where one can use a dataclass type T to build a constraint, and then parse the constrained LM response back into an instance of T.

Speculative decoding (Leviathan et al., 2023) is a method for speeding up LM inference via speculative execution. Short runs of tokens are sampled from a faster approximation model, and then verified with a more accurate target model that accepts some prefix of the sampled tokens. Although the system now runs two LMs instead of one, significant latency reductions can still be achieved due to batching and parallelization of the target model. The speedup is largely determined by the acceptance rate, which is the proportion of speculatively-sampled tokens that pass verification.

The approximation model is typically a smaller LM that has disproportionately greater difficulties following formal syntax, so a natural application is to constrain the approximation model and increase its acceptance rate on formal language outputs. There are several complications to address. For one, the constraint must be ”rewindable” because the target model can reject some of the speculated tokens, forcing the approximation model to restart at an earlier point. This can be accomplished by tracking a full history of states instead of just one. In addition, the logits of the target model must also be penalized, or the divergence between the two will reduce the acceptance rate and may even allow the target model to resample invalid tokens. To avoid re-evaluating the constraints, we devised a method for sharing the penalties with the target model.

We measured our system and Outlines (Willard & Louf, 2023) on the following tasks:

1. 1.

   Constraint compilation: Time to convert a regular expression into an automaton that can consume decoder tokens. See Appendix C.2 for details.

2. 2.

   Per-step overhead: Time to apply constraints on each decoding step. See Appendix C.3 for details.

We used Gemma (Team et al., 2024), executed both systems on the same workstation, and averaged over 10 runs to reduce noise. Both systems were timed on several regexes reflecting different usage regimes and applications. Since runtime can vary based on platform, instead of giving precise latencies we report scaling factors relative to Outlines; see Table 2.

To help ground the comparison, here are some rough latency ranges. For constraint compilation, Outlines takes 10s of seconds on JSON and a few seconds elsewhere, while our system takes a few milliseconds on JSON and 100s of microseconds elsewhere. For per-step overhead, Outlines takes 10s of microseconds and our system takes a few microseconds.

While our system has less per-step overhead, in practice both systems have negligible latency so the speedup is not very impactful. The compilation speedup, on the other hand, is a qualitative difference that lowers the barriers to entry for applying constraints and enables new usage patterns—for example, pre-compilation is no longer required.

The primary reason for the large compilation speedup is that we use OpenFST’s highly-optimized⁴⁴4 Even further optimization is possible, too. For example, Argueta & Chiang (2018) claim a 4.5x improvement over OpenFST by applying GPUs. implementations of FST operations (Riley et al., 2009). Critically, this is only possible because we reformulated the whole problem in terms of automata. As an analogy, imagine two programs for some scientific computing task. The first is entirely written by hand, while the second reduces the problem to linear algebra and uses NumPy (Harris et al., 2020). The latter is likely to be much faster, due to the sheer volume of effort that has gone into optimizing NumPy.

We exercise output formatting correctness with Gemma on GPQA (Rein et al., 2023); see Table 3 for results and Appendix D for additional details. The Gemma models have issues following the schema without constraints, but achieve perfect conformance with constraints.