Augmented physics informed extreme learning machine to solve the biharmonic equations via Fourier expansions
Abstract
To address the sensitivity of parameters and limited precision for physics-informed extreme learning machines (PIELM) with common activation functions, such as sigmoid, tangent, and Gaussian, in solving high-order partial differential equations (PDEs) relevant to scientific computation and engineering applications, this work develops a Fourier-induced PIELM (FPIELM) method. This approach aims to approximate solutions for a class of fourth-order biharmonic equations with two boundary conditions on both unitized and non-unitized domains. By carefully calculating the differential and boundary operators of the biharmonic equation on discretized collections, the solution for this high-order equation is reformulated as a linear least squares minimization problem. We further evaluate the FPIELM with varying hidden nodes and scaling factors for uniform distribution initialization, and then determine the optimal range for these two hyperparameters. Numerical experiments and comparative analyses demonstrate that the proposed FPIELM method is more stable, robust, precise, and efficient than other PIELM approaches in solving biharmonic equations across both regular and irregular domains.
AMS subject classifications 35J58 65N35 68T07
keywords:
FPIELM; Activation function; Boundary; Non-unitized domain; Linear system1 Introduction
Partial differential equations (PDEs), which have their roots in science and engineering, have been instrumental in advancing the fields of physics, chemistry, biology, image processing, and more. In general, the analytical solutions of PDEs are often elusive, necessitating the reliance on numerical methods and approximation techniques for their resolution. This paper focuses on the numerical solution of the following biharmonic equation:
| (1) |
where is a polygonal or polyhedral domain of dimension in Euclidean space, with a piecewise Lipschitz boundary satisfying an interior cone condition. Here, is a prescribed function, and denotes the standard Laplace operator. The expression of the biharmonic operator is given by:
In practice, the solution of equation (1) can be uniquely and precisely determined by the one of the following two boundary conditions:
-
1.
Dirichlet boundary conditions:
(2) -
2.
Navier boundary conditions:
(3)
where denotes the boundary of , and is the outward normal vector on . The functions , , and describe the boundary behavior of the solution and are assumed to be sufficiently smooth.
The biharmonic equation, a high-order PDE, frequently occurs in fields such as elasticity and fluid mechanics. Its application ranges from scattered data fitting with thin plate splines [1] to the simulation of fluid mechanics [2, 3] and linear elasticity [4, 5]. Solving it is challenging due to the fourth-order derivative terms, particularly in complex geometries. Various traditional numerical methods for solving (1) can be broadly classified into direct (uncoupled) methods and coupled (splitting, mixed) methods.
In the direct approach, methodologies include finite difference methods(FDM) [6, 7, 8, 9], finite volume techniques [10, 11, 12], and finite element methods (FEM) based on the variational formulation, such as non-conforming FEM [13, 14, 15] and conforming FEM [16, 17]. In the coupled approach, the biharmonic equation is decomposed into two interrelated Poisson equations, solvable by methods like FDM, FEM, and mixed element methods [18, 19, 20, 21, 22]. Additional methods include the collocation method [23, 24, 25] and the radial basis functions (RBF) method [26, 27, 28].
Conventional methods, however, encounter challenges with irregular domains and high dimensions, often referred to as the curse of dimensionality. Machine learning, especially artificial neural networks (ANNs), has shown promise in approximating the solutions of PDEs, potentially overcoming the limitations of traditional numerical techniques. Various ANN approaches, such as extreme learning machines (ELM) and deep neural networks (DNN), have been developed to solve PDEs, including (1). Physics-informed neural network methods have also been proposed, minimizing loss and incorporating residuals and boundary conditions [29, 30, 31]. Despite their potential, these methods may suffer from limited accuracy, uncertain convergence, and slow training. Recently, a physics-informed extreme learning machine (PIELM) approach was introduced, combining physical laws with ELM to address various linear or nonlinear PDEs [32, 33, 34, 35, 36, 37]. This method retains the advantages of ELM, including mesh-free operation, rapid learning, and parallel architecture compatibility, while effectively handling complex PDEs.
The choice of activation function is critical for ELM networks. For regression and classification, the sigmoid and Gaussian functions are often effective [38, 39]. For solving PDEs, experiments have shown that sigmoid, Gaussian, and hyperbolic tangent functions are ideal, producing high-precision solutions [32, 40, 41, 34]. However, these functions may impede information transmission in high-order problems with large-scale inputs, as their high-order derivatives are complex. Fourier-type functions, such as , have been suggested as alternative to mitigate these issues [42, 43, 44]. Moreover, initializing ELM’s internal weights and biases uniformly within with has been shown to enhance performance [45, 46, 47].
This work addresses the biharmonic equations (1) with Dirichlet and Navier boundary conditions by combining the Fourier spectral theorem with PIELM, resulting in a Fourier-induced PIELM model (FPIELM). Various hidden node configurations and uniform initialization scale factors are tested to optimize hyperparameters. We further compare the performance of FPIELM against that of the PIELM model with sigmoid, tangent, and Gaussian activation functions. Numerical results indicate that FPIELM achieves exceptional performance and robustness for solving (1) on both unitized and non-unitized domains.
2 Preliminary for ELM
This section provides a concise overview of essential concepts and the mathematical formulation of the ELM model. ELM falls within the category of single hidden layer fully connected neural networks (SHFNN) in artificial neural networks and is designed to establish a mapping : . A key characteristic of ELM is the random assignment of weights and biases in the input layer, while the output weights are determined analytically [48, 49]. Mathematically, the ELM mapping with input and output is defined as:
| (4) |
For convenience, we denote , where represents the weight of the -th hidden unit in ELM, and is the corresponding bias vector. The activation function operates element-wise. The matrix , where , represents the weights connecting the hidden units to the outputs. A schematic of the ELM with hidden units is shown in Fig. 1.
Incorporating physical laws into the ELM model introduces a novel approach called PIELM. PIELM optimizes its loss function, which integrates information from governing terms as well as enforced boundary or initial conditions, by analytically calculating the weights of the outer layer. Unlike PINN, which are commonly used for solving PDEs, PIELM addresses several limitations associated with PINN, such as restricted accuracy, uncertain convergence, and tremendous computational demand that can lead to slow training speeds. Similar to previous ELM applications in classification and fitting tasks, PIELM is data-adaptive, fast convergent, and outperforms the gradient descent-based methods. Additionally, PIELM preserves the core advantages of ELM as a universal approximator for any continuous function; Huang et al. [50] rigorously proved that for any infinitely differentiable activation function, SLFNs with hidden nodes can exactly learn distinct samples. This implies that if a learning error () is permissible, SLFNs require fewer than hidden nodes.
3 Fourier induced PIELM architecture for biharmonic equations
In this section, the unified architecture of FPIELM is proposed to solve the biharmonic equation (1) with boundaries (2) or (3) by embracing the vanilla PIELM method with Fourier theorem.
3.1 Vanilla PIELM framework to solve biharmonic equations
This section provides a detailed introduction to the PIELM method for solving the biharmonic equation (1) with boundaries (2) or (3). To obtain an ideal solution to the biharmonic equation, one can seek the solution in trial function space spanned by the ELM model with a high-order smooth activation function. Then, an ansatz expressed by ELM is designed to approximate the solutions of (1), it is:
Substituting into the equation of (1) for , we can obtain the following equation
| (5) |
with being the linear output for hidden unit of ELM and is the number of hidden unit. Additionally, still holds on the prescribed boundaries (2) or (3), we then have the following formulation
| (6) |
or
| (7) |
For solving the biharmonic equations by the aforementioned PIELM method, a collection of collocation points is sampled from both the interior and boundaries of the domain. At these collocation points, the governed function (5) and the (6) or (7) exhibit coerciveness. Let denote the number of random collocation points in the interior of and denote by , and denote the number of random collocation points on hyperface of and denote by . Feeding the above collocation points into the pipeline of PIELM, we have the following residual terms for Dirichlet boundaries:
| (8) |
and the last term in (8) will be replaced by
| (9) |
for Navier boundaries.
To approximate the functions well, we need to adjust the output weights of the PIELM model to make each residual of (8) to near-zero or minimize the error of the following system of linear equations:
| (10) |
Here with
and
Additionally, the matrices , and are given by
with
and
In the above expressions, and are the second and fourth-order derivatives of activation function , respectively, and stands for the Hadamard product operator. In addition, , , and .
When the weights and biases of the hidden layer for the PIELM model are randomly initialized and fixed, the matrix is determined for given input data, then the output weights of PIELM model are obtained by solving the linear systems (10). The system equation is solvable and meets the following several cases:
-
1.
If the coefficient matrix is square and invertible, then
(11) -
2.
If the coefficient matrix is rectangular and full rank, then
(12) where is the pseudo inverse of defned by .
- 3.
According to the above discussions, the detailed procedures involved in the PIELM algorithm to address the biharmonic equation (1) within finite-dimensional spaces are described in the following.
-
1)
Generating the points set includes interior points with and boundary points with . Here, we draw the random points and from with positive probability density , such as uniform distribution.
-
2)
Selecting a shallow neural network and randomly initialize weights and biases of the hidden layer, then fixing the parameters of the hidden layer.
-
3)
Embedding the input data into the implicit feature space by a linear transformation, then activating nonlinearly the results and casting them into the output layer.
-
4)
Combining linearly the all output features of the hidden layer and output this results.
-
5)
Computing the derivation about the input variable for the output of the FELM model and constructing the linear system (10).
-
6)
Learning the output layer weights by the least-squares method.
3.2 The option of activation function
In terms of function approximation, the hidden nodes governed by a given activation function in the ELM model can be considered a set of basis functions, and then the ELM model produces its output through a linear aggregation of these fundamental functions. Similar to other artificial neural network (ANN) architectures, the choice of activation function is critical for the ELM model’s performance. Since the biharmonic equations (1) studied here is a high-order PDE, activation functions with strong regularity are preferred. Previous studies, including Fabiani et al. [40], Calabrò et al. [41], and Ma et al. [52], have investigated the influence of sigmoidal functions and radial basis functions in the ELM model for solving both linear and nonlinear PDEs. These studies indicate that ELM models with sigmoid, Gaussian, and tangent activation functions achieve commendable numerical accuracy.
Remark 1.
(Lipschitz continuity) If a function is continuous (i.e., ) and satisfies the following boundedness condition:
for any . Then, we have
for any .
The sigmoid, gaussian, and tangent functions all fulfill the Lipschitz continuity and exhibit robust regularity, they ensure the boundedness of the output for hidden units in ELM. In terms of the high-order PDEs, the high-order derivate of activation is required. Then, the first, second, and fourth-order derivatives for the sigmoidal function , Gaussian function and hyperbolic tangent function are given by
| (14) |
| (15) |
and
| (16) |
respectively. Figs. 2 – 4 illustrate the curves of the sigmoid, Gaussian, and tangent functions and their corresponding first-order, second-order and fourth-order derivatives, respectively.











This visualization shows that the derivatives of the sigmoid, Gaussian, and tanh functions are bounded and tend to saturate for narrow-range inputs. However, their performance may degrade with large-range inputs. Inspired by the Fourier-based spectral method, a global basis function can generate responses, along with its derivatives, for both narrow- and large-range inputs. Furthermore, approximations based on such basis functions can handle data across various scales. The sine function serves as an ideal global Fourier basis function (with sine and cosine being fundamentally equivalent). In this study, we adopt the sine function as the activation function in the PIELM method, referring to this modified approach as FPIELM.
4 Numerical experiments
4.1 Experimental setup
In this section, we apply the proposed FPIELM method to solve the two- and three-dimensional biharmonic equation (1) in both unitized and non-unitized domains. Additionally, PIELM models using Sigmoid, Gaussian, and Tanh as activation functions are established as baselines for solving (1) and are referred to as SPIELM, GPIELM, and TPIELM, respectively. Following the results in Dong and Yang [46], the weight matrices and bias vectors for the hidden layers of each model are initialized uniformly within the interval .
A criterion is provided to evaluate the performance of the four aforementioned methods, given by
where and denote the approximate solution obtained by numerical methods and the exact solution, respectively, for the collection set , with being the number of collection points.
All experiments are implemented in Numpy (version 1.21.0) on a workstation equipped with 256 GB RAM and a single NVIDIA GeForce RTX 4090 Ti GPU with 24 GB of memory.
4.2 Numerical examples for Dirichlet boundary
Example 4.1.
To start, we aim to approximate the solution to the biharmonic equation (1) with Dirichlet boundary in the regular domain . An exact solution is given by
such that
The boundary functions and can be obtained easily by direct computation.
First, we approximate the solution of (1) using the four methods on 16,384 equidistant grid points distributed across regular domains: , , , and . In addition to the grid points, the training set includes 10,000 random points within and 4,000 random points on . The number of hidden nodes for each of the four PIELM methods is set to 1,000.
Figure 5 shows the point-wise absolute error of the four PIELM models on the domain . Table 1 presents the optimal value of , the REL, and the runtime for each PIELM method across the different domains.
Next, we examine the impact of the scale factor and the number of hidden nodes on the FPIELM model in the domain , with results illustrated in Fig. 6. Finally, comparison curves for REL as a function of the scale factor for the four PIELM methods on the domains and are shown in Fig. 7.





| Domain | SPIELM | GPIELM | TPIELM | FPIELM | |
|---|---|---|---|---|---|
| 6.0 | 1.5 | 1.4 | 8.0 | ||
| REL | |||||
| Time(s) | 8.203 | 3.939 | 3.265 | 2.875 | |
| 2.0 | 0.8 | 1.4 | 5.0 | ||
| REL | |||||
| Time(s) | 6.676 | 3.081 | 3.129 | 2.152 | |
| 0.5 | 0.3 | 0.2 | 1.0 | ||
| REL | |||||
| Time(s) | 8.077 | 4.046 | 3.328 | 3.031 | |
| 0.1 | 0.2 | 0.12 | 0.8 | ||
| REL | |||||
| Time(s) | 8.138 | 3.891 | 3.251 | 2.843 |





Based on the point-wise absolute error distribution shown in Figures 5(b) – 5(e) and the data in Table 1, it can be concluded that the FPIELM method outperforms other types of PIELM methods. As observed in the curves in Figure 6(a), the relative error does not decrease with an increasing number of hidden units, indicating that the performance of the FPIELM model stabilizes as the number of hidden neurons grows. The time-neuron curve in Figure 6(b) demonstrates a superlinear increase in runtime with the addition of hidden neurons, though this increase is gradual. Furthermore, Figure 6(c) illustrates that the FPIELM model remains stable and robust across variations in the scale factor on the domain . The REL curves in Figure 7 confirm that FPIELM maintains stability and allows for a broader range of scale factor values across both unitized and non-unitized domains. In summary, our FPIELM method not only achieves high accuracy but also demonstrates efficiency and robustness. Additionally, it is noteworthy that the coefficient matrix in the final linear system is full rank, given that the number of samples exceeds the number of hidden nodes.
For comparison, we employ the finite difference method (FDM) with a five-point central difference scheme to solve the coupled scheme of (1) on the domain . The FDM is implemented in MATLAB (version 12.0.0.341360, R2019a). For the FPIELM model, the number of hidden nodes is set to 1,000, and the scale factor for initializing weights and biases is set to 5.0. The numerical results in Table 2 indicate that the proposed FPIELM method maintains stability across various mesh grid sizes and significantly outperforms FDM in terms of accuracy, particularly on sparse grids.
| number of mesh grid | ||||||
|---|---|---|---|---|---|---|
| FDM | REL | |||||
| Time(s) | 0.028 | 0.037 | 0.127 | 0.485 | 2.05 | |
| FPIELM | REL | |||||
| Time(s) | 2.09 |
Example 4.2.
We consider the biharmonic equation (1) with Dirichlet boundary conditions in two-dimensional space and obtain its numerical solution within two hexagram-shaped domains, , derived from and , respectively. An analytical solution is given by
such that
The boundary constraint functions and on can be obtained by direct computation, but are omitted here for brevity.
In this example, the setup for the four PIELM methods is identical to that in Example 4.1. An approximate solution to (1) is derived by applying the four methods on 19,214 collection points located within the hexagram domains . Numerical results are presented in Table 3 for the two scenarios, and the point-wise absolute error for the four PIELM methods is shown in Figure 8 over the hexagram domain derived from .
Additionally, Figure 9 illustrates the variation in relative error and runtime concerning the number of hidden nodes, as well as the variation in relative error with the scale factor for FPIELM on the hexagram domain derived from . Finally, Figure 10 plots the REL comparison curves for the four PIELM methods, showing how REL varies with the scale factor across the hexagram domains derived from and .





| Domain | SPIELM | GPIELM | TPIELM | FPIELM | |
|---|---|---|---|---|---|
| 1.2 | 1.4 | 0.6 | 8.5 | ||
| REL | |||||
| Time(s) | 6.121 | 2.794 | 2.868 | 2.095 | |
| 0.6 | 0.6 | 0.3 | 8.5 | ||
| REL | |||||
| Time(s) | 4.879 | 2.541 | 2.651 | 2.011 |



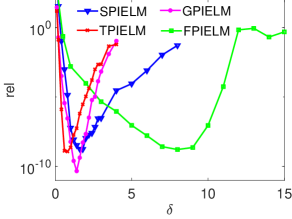

Based on the data in Table 3 and the point-wise absolute errors depicted in Figs. 8(b) – 8(e), we can infer that the FPIELM method outperforms the PIELM methods with sigmoid, tanh, and Gaussian activation functions. As observed in the curves in Fig. 16(a), the performance of the FPIELM method stabilizes as the number of hidden nodes increases. The time-neuron curve in Fig. 16(b) shows that the runtime exhibits a superlinear increase with the growing number of hidden nodes, although the increase remains gradual. Lastly, Figs. 9(c) and 10 illustrate that the FPIELM method remains stable and robust across variations in the scale factor . In summary, our FPIELM method demonstrates not only high accuracy but also efficiency and robustness.
Example 4.3.
We now approximate the solution of the biharmonic equation (1) in a three-dimensional cubic domain containing one large hole (cyan) and eight smaller holes (red and blue), as shown in Fig. 11. An analytical solution and its corresponding source term are given by
and
respectively. The boundary functions and can be directly obtained from the exact solution; however, we omit them here for brevity.


In this example, the number of hidden units for each of the four PIELM methods is set to 2,000. The testing set consists of 40,000 random points within the cut planes, excluding the holes, and includes planes parallel to the and coordinate planes. Additionally, 6,000 points randomly sampled from the six boundary surfaces are integrated into the testing set. The results are presented in Figs. 12 – 14.







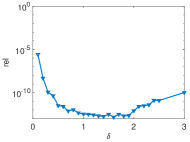

Based on the point-wise error shown in Figs. 12(b) – 12(e), our proposed FPIELM method outperforms the other three methods in solving the biharmonic equation (1) in three-dimensional space. The relative errors presented in Fig. 14 indicate that the FPIELM method remains stable across various scale factors and is superior to the other methods. Furthermore, the curves of relative error and runtime in Fig. 13 demonstrate the favorable stability and robustness of the FPIELM method as both the number of hidden nodes and the scale factor increase. It is also noteworthy that the coefficient matrix in the final linear system is full rank for this example, eliminating the need for adjustment through Tikhonov regularization.
4.3 Numerical examples for Navier boundary
Example 4.4.
In this example, our goal is to solve the biharmonic equation (1) with Navier boundary conditions in a regular rectangular domain . An exact solution is given by
which naturally leads to the essential boundary function . The function is defined as
With careful calculations, the expression for the force term is determined as
In this example, the setup for the four PIELM methods is identical to that in Example 4.1. An approximate solution of (1) is obtained by applying the four methods on 16,384 grid points within the rectangular domains and . The numerical results are listed in Table 4 for these two scenarios, and the point-wise absolute error for the four PIELM methods is shown in Fig. 15 on the domain .
Additionally, Fig. 16 illustrates the variation in relative error and runtime concerning the number of hidden nodes, as well as the variation in relative error with the scale factor for FPIELM on the domain . Finally, Fig. 17 plots the comparison curves for REL as a function of the scale factor for the four PIELM methods on the rectangular domains and , respectively.





| Domain | SPIELM | GPIELM | TPIELM | FPIELM | |
|---|---|---|---|---|---|
| 6.5 | 4.1 | 3.2 | 9.0 | ||
| REL | |||||
| Time(s) | 11.958 | 4.648 | 4.823 | 2.775 | |
| 3.0 | 1.5 | 4.0 | 11.0 | ||
| REL | |||||
| Time(s) | 6.795 | 3.133 | 3.121 | 2.178 |





Based on the point-wise errors depicted in Figs. 15(b) – 15(e) and the relative errors presented in Fig. 16, our proposed FPIELM method outperforms the other three methods for solving the biharmonic equation (1) with Navier boundary conditions in both unitized and non-unitized domains. The FPIELM method remains stable across various scale factors , and its runtime increases linearly with the number of hidden nodes. Additionally, the curves of relative error and runtime in Fig. 17 highlight the favorable stability and robustness of the FPIELM method as both the number of hidden nodes and the scale factor increase.
Example 4.5.
We consider the biharmonic equation (1) on two porous domains , derived from the two-dimensional domains and , respectively. The exact solution is given by
such that and . The boundary conditions can be easily obtained through direct calculation.
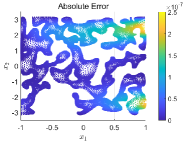
In this example, the setup for the four PIELM methods is identical to that in Example 4.4. An approximation of the solution to the biharmonic equation (1) is obtained using the four methods on 20,000 points randomly sampled from the hexagonal domain . The numerical results are presented in Figs. 18 – 20 and in Table 5.




| Domain | SPIELM | GPIELM | TPIELM | FPIELM | |
|---|---|---|---|---|---|
| 0.7 | 0.4 | 0.4 | 2.5 | ||
| REL | |||||
| Time(s) | 5.902 | 2.788 | 2.715 | 1.924 | |
| 0.6 | 0.4 | 0.3 | 1.2 | ||
| REL | |||||
| Time(s) | 6.095 | 2.748 | 2.842 | 1.941 |





Based on the results in Fig. 18 and Table 5, the FPIELM method demonstrates a remarkable ability to achieve a satisfactory approximation of the solution to (1) with Navier boundary conditions, even within an irregular domain in two-dimensional space. Its performance surpasses that of the other three methods. As shown in Figs. 19(a) and 19(b), the FPIELM method remains stable as the number of hidden nodes varies, with computational complexity increasing only linearly as hidden nodes increase. Regarding the scale factor , the FPIELM method shows insensitivity across a broad range, while the other three methods are sensitive in the unitized domain and fail to converge on the non-unitized domain. Additionally, the coefficient matrix in the final linear systems for this example is full rank.
Example 4.6.
We consider the biharmonic equation (1) in three-dimensional space and obtain its numerical solution within a closed domain , bounded by two spherical surfaces with radii and , respectively.
An exact solution is given by
which naturally determines the boundary conditions on . The second-order boundary function is given by . Through careful calculation, the source term is determined as .
In this example, we obtain the numerical solution of (1) using the CELM model with 2,000 hidden units in . The other settings of the CELM model are the same as in Example 4.4. The testing set consists of 3,000 mesh grid points on the spherical surface with radius . In addition to the mesh grid points, the training set includes 40,000 randomly sampled points from the domain and 20,000 random points equally sampled from the inner and outer spherical surfaces. The numerical results are shown in Figs. 21 – 23.










For the spherical cavity in three-dimensional space, the point-wise errors in Figs. 21(c) – 21(f) indicate that our proposed FPIELM method produces lower errors than those achieved using sigmoid, hyperbolic tangent, and Gaussian functions in solving the biharmonic equation (1). The curves for relative error and runtime in Figs. 22 and 23 demonstrate the excellent stability and robustness of the FPIELM method across varying scale factors , with a notably broad effective range for the scale factor . Furthermore, the runtime of FPIELM increases linearly as the number of hidden nodes gradually grows.
5 Conclusion
We have introduced a Fourier-induced extreme learning machine (FPIELM) to solve biharmonic problems, utilizing the Fourier expansion of a given function within a simple ELM network. Similar to other mesh-free approaches like PINN and radial basis function models, FPIELM operates independently of a mesh and does not require an initial guess. Unlike the PINN framework, FPIELM is an efficient solution for approximating (1) without needing parameter updates via iterative, gradient descent-based methods. Additionally, we examined the effects of different activation functions—tanh, Gaussian, Sigmoid, and Sine—on the performance of the PIELM model. The computational results strongly suggest that the proposed method achieves high accuracy and efficiency in solving (1) across both regular and irregular domains.
It is also worth noting that random projection neural networks have been applied not only to forward problems in steady-state and time-dependent scenarios [53, 45] but have also shown effectiveness in addressing inverse problems [54, 55]. These networks outperform traditional solvers [53] and other machine learning architectures [54], excelling in both numerical accuracy and computational efficiency. Given these advantages, future work will focus on extending our neural network models to address other PDE-related problems.
Contributions
Xi’an Li: Conceptualization, Methodology, Investigation, Validation, Software and Writing - Original Draft; Jinran Wu: Conceptualization, Methodology, Validation, Writing - review editing; Yujia Huang: Conceptualization, Investigation, Writing - review editing; Zhe Ding: Conceptualization, Writing - review editing; Xin Tai: Writing - Review & Editing, Funding acquisition and Project administration.; Liang Liu: Writing - Review & Editing and Project administration; You-Gan Wang: Writing - Review & Editing and Project administration. All authors have read and agreed to the published version of the manuscript.
Declaration of interests
All authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This study was supported by the National Key RD Program of China (No. 2023YFF0717300).
References
- Wahba [1990] G. Wahba, Spline models for observational data, SIAM, 1990.
- Greengard and Kropinski [1998] L. Greengard, M. C. Kropinski, An integral equation approach to the incompressible navier–stokes equations in two dimensions, SIAM Journal on Scientific Computing 20 (1998) 318–336.
- Ferziger and PeriC [2002] J. H. Ferziger, M. PeriC, Computational methods for fluid dynamics, Springer, 2002.
- Christiansen [1975] S. Christiansen, Integral equations without a unique solution can be made useful for solving some plane harmonic problems, IMA Journal of Applied Mathematics 16 (1975) 143–159.
- Constanda [1995] C. Constanda, The boundary integral equation method in plane elasticity, Proceedings of the American Mathematical Society 123 (1995) 3385–3396.
- Gupta and Manohar [1979] M. M. Gupta, R. P. Manohar, Direct solution of the biharmonic equation using noncoupled approach, Journal of Computational Physics 33 (1979) 236–248.
- Altas et al. [1998] I. Altas, J. Dym, M. M. Gupta, R. P. Manohar, Multigrid solution of automatically generated high-order discretizations for the biharmonic equation, SIAM Journal on Scientific Computing 19 (1998) 1575–1585.
- Ben-Artzi et al. [2008] M. Ben-Artzi, J.-P. Croisille, D. Fishelov, A fast direct solver for the biharmonic problem in a rectangular grid, SIAM Journal on Scientific Computing 31 (2008) 303–333.
- Bialecki [2012] B. Bialecki, A fourth order finite difference method for the dirichlet biharmonic problem, Numerical Algorithms 61 (2012) 351–375.
- Bi and Li [2004] C.-J. Bi, L.-K. Li, Mortar finite volume method with adini element for biharmonic problem, Journal of Computational Mathematics (2004) 475–488.
- Wang [2004] T. Wang, A mixed finite volume element method based on rectangular mesh for biharmonic equations, Journal of Computational and Applied Mathematics 172 (2004) 117–130.
- Eymard et al. [2012] R. Eymard, T. Gallouët, R. Herbin, A. Linke, Finite volume schemes for the biharmonic problem on general meshes, Mathematics of Computation 81 (2012) 2019–2048.
- Baker [1977] G. A. Baker, Finite element methods for elliptic equations using nonconforming elements, Mathematics of Computation 31 (1977) 45–59.
- Lascaux and Lesaint [1975] P. Lascaux, P. Lesaint, Some nonconforming finite elements for the plate bending problem, Revue française d’automatique, informatique, recherche opérationnelle. Analyse numérique 9 (1975) 9–53.
- Morley [1968] L. S. D. Morley, The triangular equilibrium element in the solution of plate bending problems, Aeronautical Quarterly 19 (1968) 149–169.
- Zienkiewicz et al. [2013] O. C. Zienkiewicz, R. L. Taylor, P. Nithiarasu, The finite element method for fluid dynamics, Butterworth-Heinemann, 2013.
- Ciarlet [2002] P. G. Ciarlet, The finite element method for elliptic problems, SIAM, 2002.
- Brezzi and Fortin [2012] F. Brezzi, M. Fortin, Mixed and hybrid finite element methods, volume 15, Springer Science & Business Media, 2012.
- Cheng et al. [2000] X.-l. Cheng, W. Han, H.-c. Huang, Some mixed finite element methods for biharmonic equation, Journal of computational and applied mathematics 126 (2000) 91–109.
- Davini and Pitacco [2000] C. Davini, I. Pitacco, An unconstrained mixed method for the biharmonic problem, SIAM Journal on Numerical Analysis 38 (2000) 820–836.
- Lamichhane [2011] B. P. Lamichhane, A stabilized mixed finite element method for the biharmonic equation based on biorthogonal systems, Journal of Computational and Applied Mathematics 235 (2011) 5188–5197.
- Stein et al. [2019] O. Stein, E. Grinspun, A. Jacobson, M. Wardetzky, A mixed finite element method with piecewise linear elements for the biharmonic equation on surfaces, arXiv preprint arXiv:1911.08029 (2019).
- Mai-Duy et al. [2009] N. Mai-Duy, H. See, T. Tran-Cong, A spectral collocation technique based on integrated chebyshev polynomials for biharmonic problems in irregular domains, Applied Mathematical Modelling 33 (2009) 284–299.
- Bialecki and Karageorghis [2010] B. Bialecki, A. Karageorghis, Spectral chebyshev collocation for the poisson and biharmonic equations, SIAM Journal on Scientific Computing 32 (2010) 2995–3019.
- Bialecki et al. [2020] B. Bialecki, G. Fairweather, A. Karageorghis, J. Maack, A quadratic spline collocation method for the dirichlet biharmonic problem, Numerical Algorithms 83 (2020) 165–199.
- Mai-Duy and Tanner [2005] N. Mai-Duy, R. Tanner, An effective high order interpolation scheme in biem for biharmonic boundary value problems, Engineering Analysis with Boundary Elements 29 (2005) 210–223.
- Adibi and Es’haghi [2007] H. Adibi, J. Es’haghi, Numerical solution for biharmonic equation using multilevel radial basis functions and domain decomposition methods, Applied Mathematics and Computation 186 (2007) 246–255.
- Li et al. [2011] X. Li, J. Zhu, S. Zhang, A meshless method based on boundary integral equations and radial basis functions for biharmonic-type problems, Applied Mathematical Modelling 35 (2011) 737–751.
- Guo et al. [2019] H. Guo, X. Zhuang, T. Rabczuk, A deep collocation method for the bending analysis of kirchhoff plate, Computers, Materials & Continua 59 (2019) 433–456.
- Huang et al. [2021] Z. Huang, S. Chen, W. Chen, L. Peng, Neural network method for thin plate bending problem, Chinese Journal of Solid Mechanics 42 (2021) 10.
- Vahab et al. [2022] M. Vahab, E. Haghighat, M. Khaleghi, N. Khalili, A physics-informed neural network approach to solution and identification of biharmonic equations of elasticity, Journal of Engineering Mechanics 148 (2022) 04021154.
- Dwivedi and Srinivasan [2020a] V. Dwivedi, B. Srinivasan, Physics informed extreme learning machine (pielm)–a rapid method for the numerical solution of partial differential equations, Neurocomputing 391 (2020a) 96–118.
- Dwivedi and Srinivasan [2020b] V. Dwivedi, B. Srinivasan, Solution of biharmonic equation in complicated geometries with physics informed extreme learning machine, Journal of Computing and Information Science in Engineering 20 (2020b) 061004.
- Li et al. [2023] S. Li, G. Liu, S. Xiao, Extreme learning machine with kernels for solving elliptic partial differential equations, Cognitive Computation 15 (2023) 413–428.
- Wang and Dong [2024] Y. Wang, S. Dong, An extreme learning machine-based method for computational pdes in higher dimensions, Computer Methods in Applied Mechanics and Engineering 418 (2024) 116578.
- Joshi et al. [2024] K. Joshi, V. Snigdha, A. K. Bhattacharya, Physics informed extreme learning machines with residual variation diminishing scheme for nonlinear problems with discontinuous surfaces, IEEE Access (2024).
- Liu et al. [2023] X. Liu, W. Yao, W. Peng, W. Zhou, Bayesian physics-informed extreme learning machine for forward and inverse pde problems with noisy data, Neurocomputing 549 (2023) 126425.
- Chen et al. [2013] Z. X. Chen, H. Y. Zhu, Y. G. Wang, A modified extreme learning machine with sigmoidal activation functions, Neural Computing and Applications 22 (2013) 541–550.
- Ding et al. [2015] S. Ding, H. Zhao, Y. Zhang, X. Xu, R. Nie, Extreme learning machine: algorithm, theory and applications, Artificial Intelligence Review 44 (2015) 103–115.
- Fabiani et al. [2021] G. Fabiani, F. Calabrò, L. Russo, C. Siettos, Numerical solution and bifurcation analysis of nonlinear partial differential equations with extreme learning machines, Journal of Scientific Computing 89 (2021) 1–35.
- Calabrò et al. [2021] F. Calabrò, G. Fabiani, C. Siettos, Extreme learning machine collocation for the numerical solution of elliptic pdes with sharp gradients, Computer Methods in Applied Mechanics and Engineering 387 (2021) 114188.
- Huang et al. [2006] G.-B. Huang, L. Chen, C.-K. Siew, Universal approximation using incremental constructive feedforward networks with random hidden nodes, IEEE Transactions on Neural Networks 17 (2006) 879–892.
- Huang et al. [2015] G.-B. Huang, Z. Bai, L. L. C. Kasun, C. M. Vong, Local receptive fields based extreme learning machine, IEEE Computational Intelligence Magazine 10 (2015) 18–29.
- Rahimi and Recht [2008] A. Rahimi, B. Recht, Uniform approximation of functions with random bases, in: 2008 46th annual allerton conference on communication, control, and computing, IEEE, 2008, pp. 555–561.
- Dong and Li [2021] S. Dong, Z. Li, Local extreme learning machines and domain decomposition for solving linear and nonlinear partial differential equations, Computer Methods in Applied Mechanics and Engineering 387 (2021) 114129.
- Dong and Yang [2022] S. Dong, J. Yang, On computing the hyperparameter of extreme learning machines: Algorithm and application to computational pdes, and comparison with classical and high-order finite elements, Journal of Computational Physics 463 (2022) 111290.
- Dong and Li [2021] S. Dong, Z. Li, A modified batch intrinsic plasticity method for pre-training the random coefficients of extreme learning machines, Journal of Computational Physics 445 (2021) 110585.
- Schmidt et al. [1992] W. F. Schmidt, M. A. Kraaijveld, R. P. Duin, et al., Feed forward neural networks with random weights, in: International conference on pattern recognition, IEEE Computer Society Press, 1992, pp. 1–1.
- Igelnik and Pao [1995] B. Igelnik, Y.-H. Pao, Stochastic choice of basis functions in adaptive function approximation and the functional-link net, IEEE Transactions on Neural Networks 6 (1995) 1320–1329.
- Huang et al. [2006] G.-B. Huang, Q.-Y. Zhu, C.-K. Siew, Extreme learning machine: theory and applications, Neurocomputing 70 (2006) 489–501.
- Adriazola [2022] J. Adriazola, On the role of tikhonov regularizations in standard optimization problems, arXiv preprint arXiv:2207.01139 (2022).
- Ma et al. [2022] M. Ma, J. Yang, R. Liu, A novel structure automatic-determined fourier extreme learning machine for generalized black–scholes partial differential equation, Knowledge-Based Systems 238 (2022) 107904.
- Fabiani et al. [2023] G. Fabiani, E. Galaris, L. Russo, C. Siettos, Parsimonious physics-informed random projection neural networks for initial value problems of odes and index-1 daes, Chaos: An Interdisciplinary Journal of Nonlinear Science 33 (2023).
- Galaris et al. [2022] E. Galaris, G. Fabiani, I. Gallos, I. Kevrekidis, C. Siettos, Numerical bifurcation analysis of pdes from lattice boltzmann model simulations: a parsimonious machine learning approach, Journal of Scientific Computing 92 (2022) 34.
- Dong and Wang [2023] S. Dong, Y. Wang, A method for computing inverse parametric pde problems with random-weight neural networks, Journal of Computational Physics (2023) 112263.