Atomistic Origin of Diverse Charge Density Wave States in CsV3Sb5
Abstract
Kagome metals AV3Sb5 (A = K, Rb, or Cs) exhibit intriguing charge density wave (CDW) instabilities, which interplay with superconductivity and band topology. However, despite firm observations, the atomistic origins of the CDW phases, as well as hidden instabilities, remain elusive. Here, we adopt our newly developed symmetry-adapted cluster expansion method to construct a first-principles-based effective Hamiltonian of CsV3Sb5, which not only reproduces the established inverse star of David (ISD) phase, but also predict a series of D3h-n states under mild tensile strains. With such atomistic Hamiltonians, the microscopic origins of different CDW states are revealed as the competition of the second-nearest neighbor V-V pairs versus the first-nearest neighbor V-V and V-Sb couplings. Interestingly, the effective Hamiltonians also reveal the existence of ionic Dzyaloshinskii–Moriya interaction in the high-symmetry phase of CsV3Sb5 and drives the formation of non-collinear CDW patterns. Our work thus not only deepens the understanding of the CDW formation in AV3Sb5, but also demonstrates that the effective Hamiltonian is a suitable approach for investigating CDW mechanisms, which can be extended to various CDW systems.
The kagome lattice provides a fertile playground to explore intriguing correlated phenomena [1, 2, 3, 4]. Recently, the vanadium-based kagome metals V3Sb5 ( = K, Rb, or Cs) [5] was reported to feature charge density wave (CDW), as well as superconductivity and Z2 topology [6, 7]. The interplay between CDW and other properties triggered enormous research interests [8, 9, 10].
As an example of V3Sb5, CsV3Sb5 exhibits diverse CDW instabilities, enriching their couplings with different electronic orders [6, 7, 9, 8, 11, 12, 10, 13, 14, 15]. The high temperature pristine phase of CsV3Sb5 crystallizes in the layered structure of V-Sb sheets intercalated by Cs atoms with the space group of P6/mmm [5], as depicted in Fig.1(a, b). In the kagome layer, the V atoms form a kagome net interspersed by Sb1 atoms and sandwiched by two honeycomb Sb2 layers. CsV3Sb5 exhibits a CDW transition at TCO 94 K, corresponding to a 221 inverse star of David (ISD) pattern with point group [6, 16]. At an intermediate temperature of TSO 50-60 K, a unidirectional 4a0 or 5a0 stripe order has been observed on Sb-terminated surface, the atomic pattern of which is still elusive [8, 17, 11, 18, 19, 20]. With a slightly lower temperature of TN 40 K, a nematic state occurs, reducing the rotation symmetry from C6 to C2 [11]. Also, the 222 and 224 CDW phases have been observed, associated with the stacking of the adjacent kagome layers [22, 21]. Moreover, such CDW instabilities compete with each other and the ground state varies with doping, surfacing and pressure [23, 24, 25, 26]. Among different CDW states, the origin of ISD state was successfully explained with soft phonons in a collective manner [16]. However, it still lacks an overall understanding of the known and possible hidden CDW instabilities in CsV3Sb5, especially in an atomistic perspective.
In this work, we apply the first-principles-based effective Hamiltonian approach [27, 28], which is widely used in ferroelectric systems [29, 30], to investigate the atomic CDW instabilities in CsV3Sb5. Significantly, a series of breathing-kagome-like D3h phases are predicted with mild tensile epitaxial strain. The atomic origins for the new D3h phases and the known ISD state are comprehensively understood in terms of V-V and V-Sb pairs. Particularly, the atomic Hamiltonian reveals the existence of ionic Dzyaloshinskii–Moriya interaction (DMI), which is found to be the driving force of the formation of these nonlinear CDW patterns.
CDW transition from DFT. Phonon dispersion of the pristine phase at zero strain is displayed in Fig. 1(f). The imaginary phonon mode at M point [e.g., (1/2, 0, 0)] indicates a 211 modulation of the structure, which mainly involves the V-V in-plane movements as shown in Fig. 1(d). A linear combination of the soft modes at the three symmetry-equivalent M points give rise to the star of David (SD) or ISD [Fig. 2(a)] pattern within a 221 supercell. Note that the ISD structure exhibits inverse atomic displacements compared to the SD structure. The ISD phase is energetically favored (see Fig. S1 in Supplemental materials (SM) [27]), which is consistent with previous results [16] and will be explained in terms of the microscopic interactions discussed below. Similarly, the three L-point soft modes indicate a 222 structural reconstruction, which is manifested by the ISD + ISD stacking pattern with -phase shift (see Fig. S2 [27]), agreeing well with previous studies [16, 17]. For simplicity, we will focus on the 221 CDW orders in the following discussion unless stated otherwise.
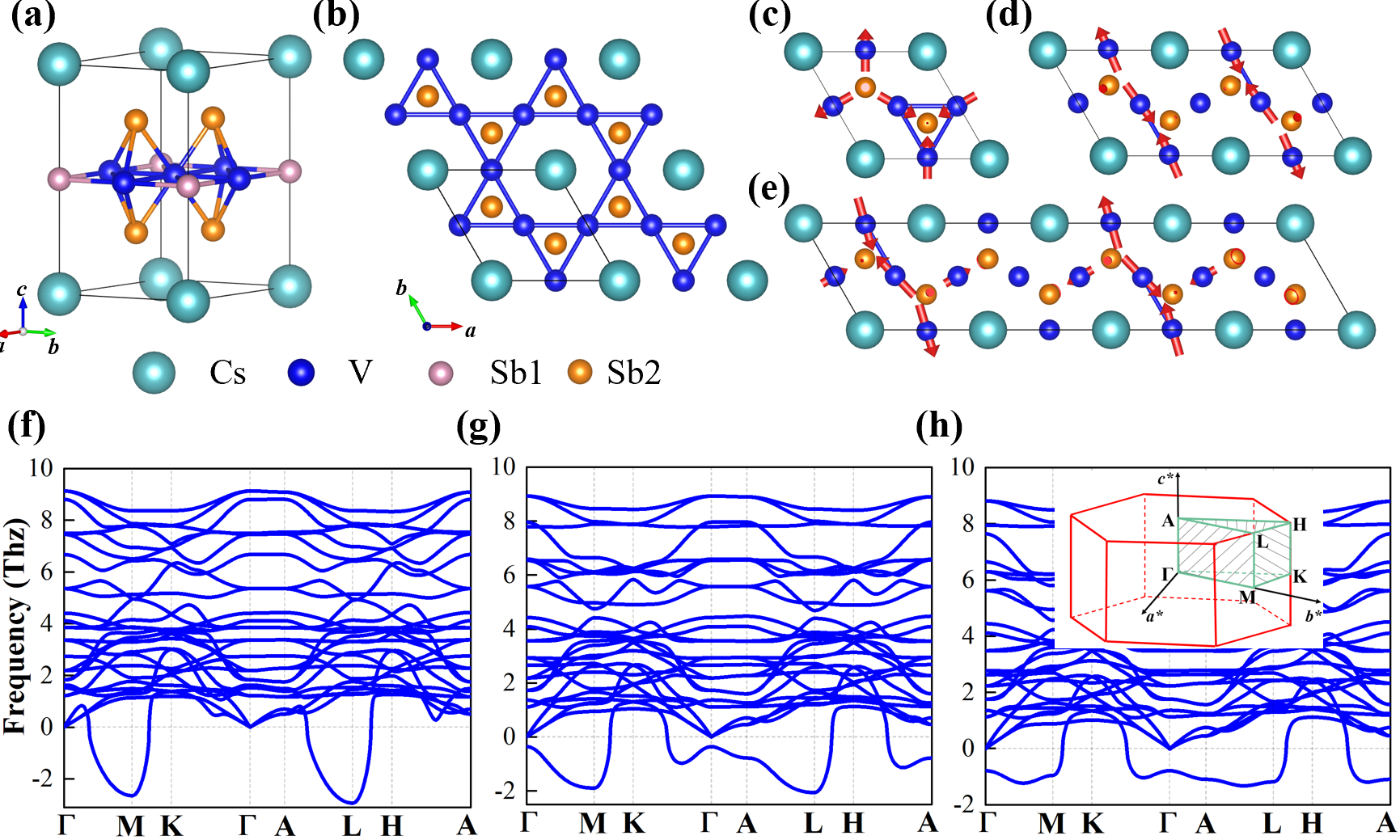
Let us then look at the strain effects. Recent experiments report different critical temperatures between bulk and nano flakes of CsV3Sb5, indicating surface strain releasing plays an important role [31, 32, 33]. We thus investigate the phonons of the CsV3Sb5 pristine phase with in-plane biaxial strain (see Method in Part I of SM [27]). As shown in Fig. 1(g, h), the phonon instability changes rapidly with increasing tensile strain. An additional imaginary phonon mode appears at point at 2% strain and is found to correspond to a breathing kagome mode, in which the V atoms move inward in one triangle and outward in the adjacent triangles [Fig. 1(c)]. Superposing this mode onto the ISD structure leads to a new 221 structural reconstruction, characterized by shrinked triangle of V atoms with surrounding V-V dimers (D3h-2 phase in Fig. 2(b), here, the supercell with D3h symmetry is denoted by D3h-n, [see Part VIII-X, XIV of SM for band structures, scanning tunneling microscopy (STM), structural information and XRD patterns of these states [27]]. In addition, the lowest imaginary frequency moves from M point under zero strain to approximately the middle of -M for 2.8 tensile strain, corresponding to the mode characterized by the V-V in-plane dimerization within a 411 supercell [Fig. 1(e)]. Such dimerization with a phase shift along axis strongly implies a new possible 4a0 stripe order [8, 17, 11, 20, 19], consistent with the observation of Ref. [8] (see Part IX for STM images [27]). Considering the multiplicity of above imaginary mode, the new D3h-4 state [Fig. 2(c)] can be constructed. Interestingly, as strain goes more tensile, it is found that the lowest frequency moves more and more toward point, indicating larger and larger supercells. For example, the D3h-6 state [Fig. 2(d)] can emerge at the strain of 3.5% (Fig. S4 [27]). Such results thus imply a continuum evolution of CDW states with increasing strain.
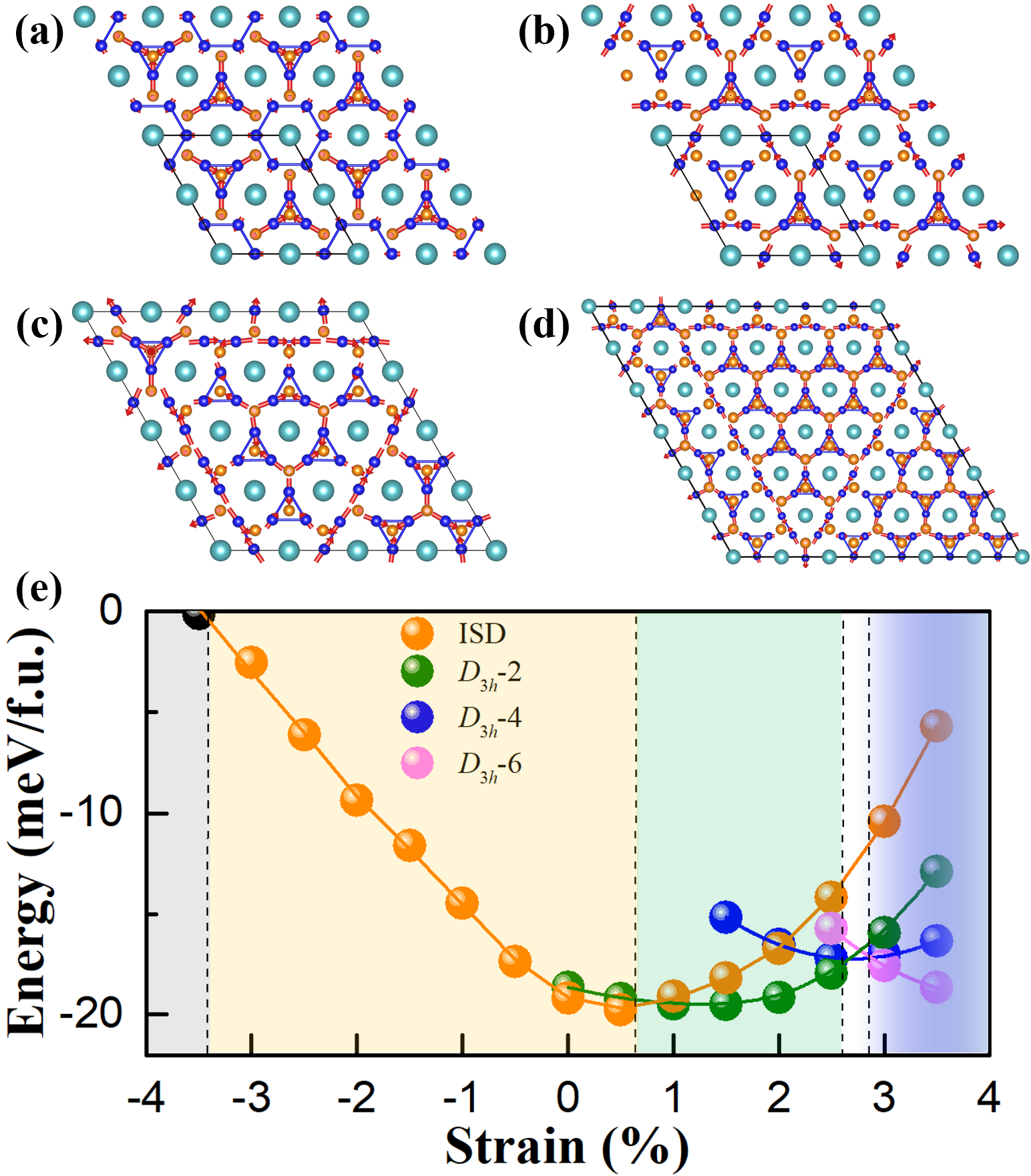
In order to determine the ground states at different strains, we perform density functional theory (DFT) calculations on various CDW configurations, which are condensated from the soft phonons (see Part V for all considered structures [27]). Figure 2(e) shows the energy-vs-strain curves of selected low-energy states. It indicates that, for the compressive strains exceeding -3.4, CsV3Sb5 prefers the pristine phase [Fig.1(a, b)], which is in line with the observation that pristine phase becomes ground state under hydrostatic pressure [20]. From -3.4 compressive strain to 0.7 tensile strain, the ISD state shown in Fig. 2(a) is energetically favorable, which is also consistent with observations [6]. Particularly, between tensile strain of 0.7 and 2.7%, the aforementioned new D3h-2 CDW state is stabilized (see Fig. S8 for phonon dispersion and XIII for the prediction of CsV3Bi5 which exhibits D3h-2 phase in the absence of any strain [27]). As the tensile strain increases, the V-V dimers form larger and larger triangle, which encircles more and more shrinked triangles of V atoms, corresponding to the D3h-4 phase [Fig. 2(c)], D3h-6 phase [Fig. 2(d)], etc. It is thus reasonable to speculate that, for even stronger tensile strain, the ground state will transform to a phase with only shrinked triangles, which is actually the breathing kagome state. Note that the D3h-n phases also prefer that adjacent kagome layers have a -shift. Such -shift further lowers the rotation symmetry from C3 to C2 (Fig. S3 [27]).
| Coefficient | Length (Å) | Invariant | 0% | 2% |
|---|---|---|---|---|
| - | u | 1201 | 883 | |
| - | u | 613 | 532 | |
| - | u | 432 | 616 | |
| - | u | 1238 | 1271 | |
| 2.75 (2.74) | u1Yu1Z | 498 | 540 | |
| 2.72 (2.77) | u1Yu2Y | 142 | 240 | |
| 4.71 (4.81) | u1Yu2Y | -150 | -160 | |
| 4.71 (4.81) | uu2Y+ u1Yu | -250 | -296 | |
| 2.72 (2.77) | (U1U2) | 158 | -39 |
Atomic driving forces from Effective Hamiltonian. In order to get more insights into the microscopic origins of the CDW states, we develop first-principles-based effective Hamiltonians for CsV3Sb5 (see Table. S5 for KV3Sb5 and RbV3Sb5). Here we adopt the symmetry-adapted cluster expansion method, as implemented in the PASP software [28]. Such method enables defining local modes (atomic displacements) and generating all possible forms of interactions, i.e., the invariants. With input energies of random structures from DFT, the coefficients of such invariants can be fitted using machine learning method for constructing Hamiltonian [34]. Note that the effect of electron-phonon coupling is implicitly included in these coefficients. For the present case of CsV3Sb5, local modes are defined as (i) in-plane displacements of V atoms and (ii) out-of-plane displacements of Sb2 atoms, while other minor movements are neglected. The initial model contains enough invariants, including the self-energy of local mode up to fourth-order and the cluster interactions up to the four-body and fourth-order. After repeated fitting and refining, it arrives at below Hamiltonian,
| (1) |
where is the single site energy and is the energy of pair interaction, which indicates that three-body and four-body interactions are not important here. Herein the two effective Hamiltonians are constructed separately for strains of 0% and 2% (see more strains in Table. S3), with the primary coefficients listed in Table 1, while a full model and details can be found in Part VII in SM [27]. The energies from DFT and effective Hamiltonians are in good consistency (see Fig. S11). Note that the forms of interactions are expressed in local basis [see Fig. 3(a-c)] for simplicity. As shown in Fig. 3(e), Monte Carlo simulations with the obtained effective Hamiltonians indicate that (i) at zero strain, ISD state forms below 100 K, which is rather close to the measured T = 94 K [6]; and (ii) at 2% strain, the D3h-2 state emerges below T = 20 K, indicating that the tensile strain largely lowers the CDW critical temperature.
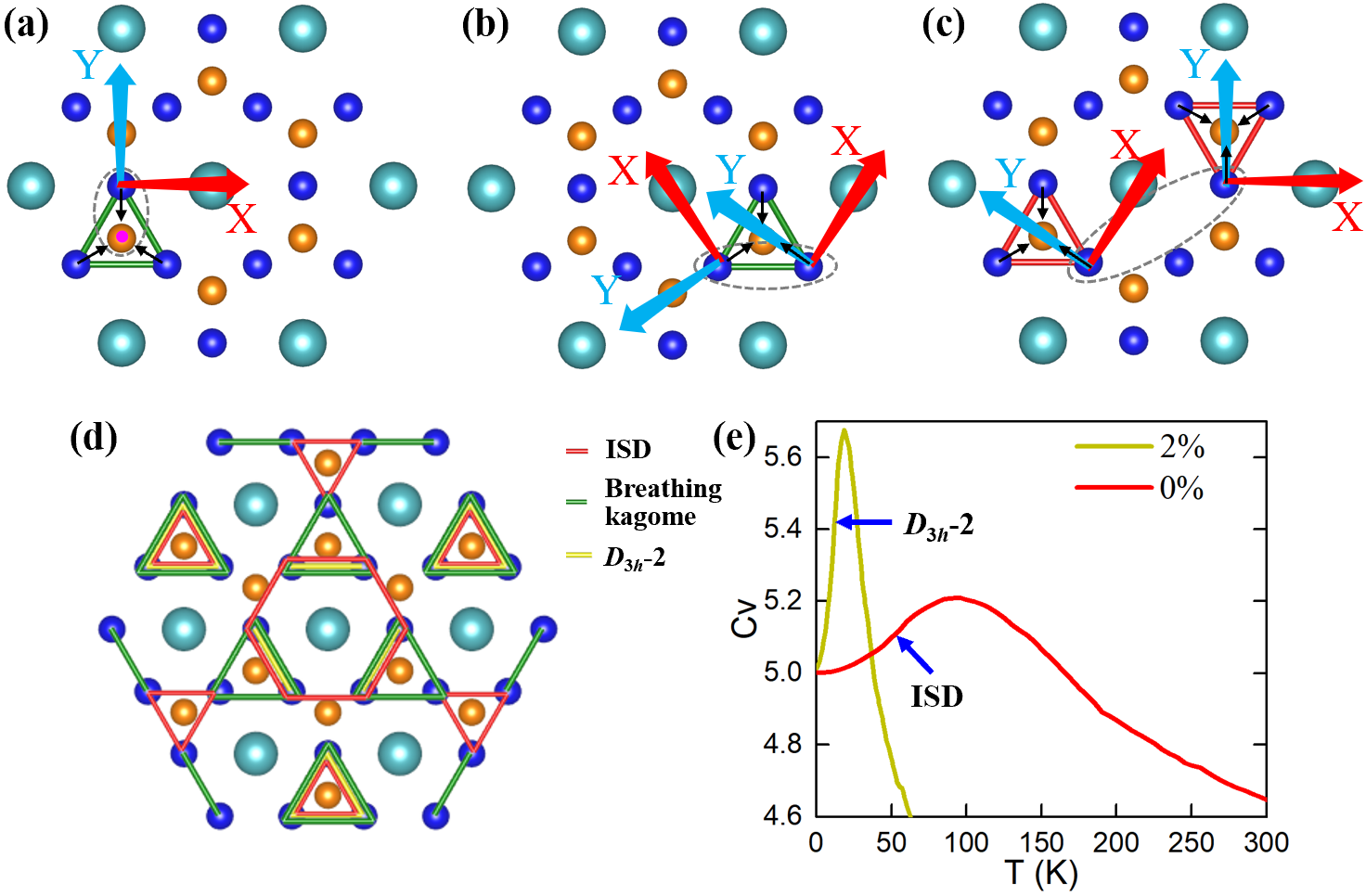
We now work on understanding the formation of ISD and D3h-2 states by analysing the invariants and their coefficients. According to the experience of Hamiltonians for ferroelectrics, the second-order interactions usually act as the driving force of the phase transition, while that the fourth-order interactions prevent too large atomic displacements [29]. Such mechanisms lead to the well-known double-well energy landscape. Here, as shown in Table 1, single site terms, either second or fourth orders, all have positive coefficients, indicating that neither ISD nor D3h-2 states are initiated by on-site instability. On the other hand, three second-order pair interactions are found to drive the deformations to CDW states (note that the local basis {XYZ} is adopted): (i) the first-nearest neighbor (1NN) V-Sb2 interaction, with the form of and a positive coefficient, drives V atoms toward in-plane trimerization (shrinked triangle) and Sb2 atoms moving toward out-of-plane direction [Fig. 3(a)]; (ii) the 1NN V-V interaction, with the form of and also a positive coefficient, also tends to form trimers of V atoms [Fig. 3(b)]; and (iii) the second-nearest neighbor (2NN) V-V interaction, with the form of and a negative coefficient, drives trimerization of V atoms at a large distance [Fig. 3(c)] (the sign of the coefficient of these pair interactions can be related to the band splitting near Fermi level, which may lower the energy relative to the band crossing at the inverse sign, see Figs. S13-14 [27]). Note that (i) and (ii) lead to trimers with the same orientation, while (iii) results in trimers with opposite orientations. Such analyses indicate that (i) and (ii) tend to stabilize breathing kagome state, while (iii) favors ISD state. Interestingly, the 2NN V-V pair has a third-order interaction of uu2Y+ u1Yu, which naturally lifts the energy degeneracy between SD and ISD, or between D3h-n and inverse D3h-n. We then look at the strain effects. At zero strain, the 2NN V-V pairs play the dominant role, which results in the ISD deformation. When a 2 tensile strain is applied, values of and 1NN are significantly enhanced (Table 1), which tends to stabilize the breathing kagome pattern. This is understandable since the larger lengths of 1NN V-V pairs under tensile strain enhance the tendency close to each other. Meanwhile, the 2NN barely changes with strain and thus still favors the formation of ISD phase. The interplay of such two strain effects is shown in Fig. 3(d), which clearly demonstrate that the D3h-2 reconstruction (yellow bonds) originates from superposing breathing kagome (green bonds) and the ISD (red bonds) deformations (see Part IV for the superposition of D3h-4 and D3h-6 states).
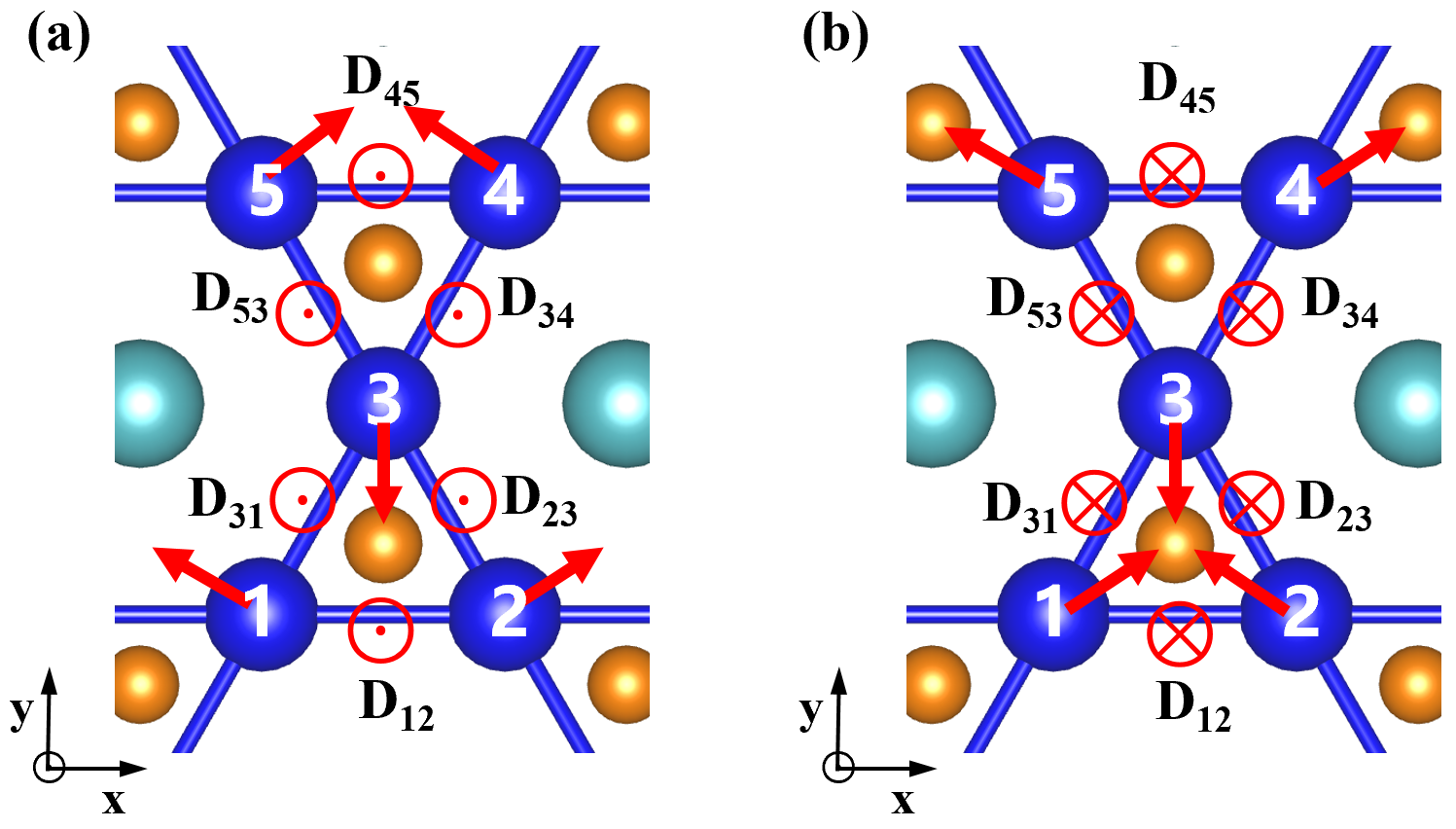
Let us now further understand the nature of V-V interactions in the global basis. As shown in Fig. 4, between 1NN V-V pairs, e.g., the pair of V1-V2, our Hamiltonians indicate an interaction in the form of U1xU2y-U1yU2x, which can be written as (U1U2), where has only component and the displacements of and possess only in-plane components. Such interaction is analogous to the magnetic DMI and is thus named as ionic DMI (i-DMI) here. As U1U2 has the same symmetry transformation properties as S1S2 (where S represents spins), the direction of the DM vector in the i-DMI case is determined by the crystal structure in the same way as the magnetic DMI case. According to Moriya’s rules [35], DM vector of V1-V2 pair is along direction, as a result of an in-plane mirror including V1-V2 pair and a mirror perpendicular to V1-V2 pair. Such i-DMI favors related displacements being perpendicular to each other with the plane, which is similar to the effects of magnetic DMI. However, it finally forms the 120∘ patterns, as shown in Fig. 4, due to the competition associated with kagome lattice (see Part XI of SM [27]). Note that the i-DMI of 2NN V-V pairs is not discussed here due to their negligible values.
From the aspect of i-DMI, we now further understand the CDW transition from ISD to D3h state. At zero strain, the i-DMIs exhibit a positive value of meV, which stabilizes a ISD-like state, as shown in Fig. 4a, with an energy gain of per V atom. For the exact ISD pattern that CsV3Sb5 displays, such i-DMI leads to an energy gain of , while the pattern shown in Fig. 4b results in an energy cost of per V atom. Note that it is assumed that all V atoms share the same amount of displacements. In contrast, with a tensile strain of 2%, the i-DMIs change their signs and render a negative value of meV, which favors the formation of breathing kagome pattern, as shown in Fig. 4b. In such case of negative , the breathing kagome pattern yields an energy gain of per V atom, while the ISD-like pattern cost energy of per V atom. It is thus clear that, above a critical point of tensile strain, the i-DM vectors flip their directions, which deforms the ISD phase and stabilizes the breathing kagome state.
The present discovery of i-DMI as a driving force to induce CDW states provides a new perspective to understand structural phase transitions. We note that the existence of i-DMI was first pointed out in the low energy distorted perovskites [36]. Here, we find that CsV3Sb5 is the first system where the i-DMI exists in the high-symmetry high temperature structure, and is responsible for the structure phase transition to the low energy structure. Considering that the kagome lattice intrinsically lacks inversion center between first nearest neighbors, the i-DMI is likely to be a common mechanism to induce structural distortions there.
In summary, combining DFT calculations, we apply the effective Hamiltonian approach to CsV3Sb5 and predict a series of D3h-n CDW phases and a possible 4a0 pattern, besides the known ISD structure. The nature of such CDW states is revealed as that the 2NN V-V pairs dominate the formation of ISD state, while that the 1NN V-V and V-Sb2 interactions tends to stabilize the D3h-n breathing kagome state. The ionic DMI is identified as a new driving force to induce structural distortions, which is expected to commonly exist in different kagome CDW systems. Experimental verification of the new atomics mechanisms and new CDW states revealed in this work is called for.
Acknowledgements.
We thank Prof. Tao Wu for useful discussions on strain effects. H.T. acknowledges Shangfei Wu for helpful discussions. We acknowledge financial support from the National Key RD Program of China (No. 2022YFA1402901), NSFC (Grants No. 11825403, No. 11991061, No. 12188101, No. 12174060, and No. 12274082), the Guangdong Major Project of the Basic and Applied basic Research (Future functional materials under extreme conditions–2021B0301030005), and Shanghai Pilot Program for Basic Research—FuDan University 21TQ1400100 (23TQ017). C. X. also acknowledges support from the Shanghai Science and Technology Committee (Grant No. 23ZR1406600). B. Z. also acknowledge the support from China Postdoctoral Science Foundation (grant No. 2022M720816).References
- [1] M. P. Shores, E. A. Nytko, B. M. Bartlett, and D. G. Nocera, “A structurally perfect S= 1/2 kagome antiferromagnet,” J. Am. Chem. Soc., vol. 127, no. 39, pp. 13 462–13 463, 2005.
- [2] E. Liu, Y. Sun, N. Kumar, L. Muechler, A. Sun, L. Jiao, S.-Y. Yang, D. Liu, A. Liang, Q. Xu, J. Kroder, V. Sü, H. Borrmann, C. Shekhar, Z. Wang, C. Xi, W. Wang, W. Schnelle, S. Wirth, Y. Chen, S. T. B. Goennenwein, and F. Claudia, “Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal,” Nat. Phys., vol. 14, no. 11, pp. 1125–1131, 2018.
- [3] S. V. Isakov, S. Wessel, R. G. Melko, K. Sengupta, and Y. B. Kim, “Hard-core bosons on the kagome lattice: Valence-bond solids and their quantum melting,” Phys. Rev. Lett., vol. 97, no. 14, p. 147202, 2006.
- [4] W.-H. Ko, P. A. Lee, and X.-G. Wen, “Doped kagome system as exotic superconductor,” Phys. Rev. B, vol. 79, no. 21, p. 214502, 2009.
- [5] B. R. Ortiz, L. C. Gomes, J. R. Morey, M. Winiarski, M. Bordelon, J. S. Mangum, I. W. H. Oswald, J. A. Rodriguez-Rivera, J. R. Neilson, S. D. Wilson, E. Ertekin, T. M. McQueen, and E. S. Toberer, “New kagome prototype materials: Discovery of KV3Sb5, RbV3Sb5, and CsV3Sb5,” Phys. Rev. Mater., vol. 3, no. 9, p. 094407, 2019.
- [6] B. R. Ortiz, S. M. L. Teicher, Y. Hu, J. L. Zuo, P. M. Sarte, E. C. Schueller, A. M. M. Abeykoon, M. J. Krogstad, S. Rosenkranz, R. Osborn, R. Seshadre, L. Balents, J. He, and S. D. Wilson, “CsV3Sb5: A Z2 topological kagome metal with a superconducting ground state,” Phys. Rev. Lett., vol. 125, no. 24, p. 247002, 2020.
- [7] B. R. Ortiz, P. M. Sarte, E. M. Kenney, M. J. Graf, S. M. L. Teicher, R. Seshadri, and S. D. Wilson, “Superconductivity in the Z2 kagome metal KV3Sb5,” Phys. Rev. Mater., vol. 5, no. 3, p. 034801, 2021.
- [8] H. Zhao, H. Li, B. R. Ortiz, S. M. Teicher, T. Park, M. Ye, Z. Wang, L. Balents, S. D. Wilson, and I. Zeljkovic, “Cascade of correlated electron states in the kagome superconductor CsV3Sb5,” Nature, vol. 599, no. 7884, pp. 216–221, 2021.
- [9] H. Chen, H. Yang, B. Hu, Z. Zhao, J. Yuan, Y. Xing, G. Qian, Z. Huang, G. Li, Y. Ye, S. Ma, S. Ni, H. Zhang, Q. Yin, C. Gong, Z. Tu, H. Lei, H. Tan, S. Zhou, C. Shen, X. Dong, B. Yan, Z. Wang, and H. Gao, “Roton pair density wave in a strong-coupling kagome superconductor,” Nature, vol. 599, no. 7884, pp. 222–228, 2021.
- [10] Y.-X. Jiang, J.-X. Yin, M. M. Denner, N. Shumiya, B. R. Ortiz, G. Xu, Z. Guguchia, J. He, M. S. Hossain, X. Liu et al., “Unconventional chiral charge order in kagome superconductor KV3Sb5,” Nat. Mater., vol. 20, no. 10, pp. 1353–1357, 2021.
- [11] L. Nie, K. Sun, W. Ma, D. Song, L. Zheng, Z. Liang, P. Wu, F. Yu, J. Li, M. Shan et al., “Charge-density-wave-driven electronic nematicity in a kagome superconductor,” Nature, vol. 604, no. 7904, pp. 59–64, 2022.
- [12] X. Feng, K. Jiang, Z. Wang, and J. Hu, “Chiral flux phase in the kagome superconductor AV3Sb5,” Sci. Bull., vol. 66, no. 14, pp. 1384–1388, 2021.
- [13] S. Wu, B. R. Ortiz, H. Tan, S. D. Wilson, B. Yan, T. Birol, and G. Blumberg, “Charge density wave order in the kagome metal AV3Sb5 (A= Rb, Cs),” Phys. Rev. B, vol. 105, no. 15, p. 155106, 2022.
- [14] A. Ptok, A. Kobiałka, M. Sternik, J. Łażewski, P. T. Jochym, A. M. Oleś, and P. Piekarz, “Dynamical study of the origin of the charge density wave in AV3Sb5 (A= K, Rb, Cs) compounds,” Phys. Rev. B, vol. 105, no. 23, p. 235134, 2022.
- [15] B. R. Ortiz, S. M. Teicher, L. Kautzsch, P. M. Sarte, N. Ratcliff, J. Harter, J. P. Ruff, R. Seshadri, and S. D. Wilson, “Fermi surface mapping and the nature of charge-density-wave order in the kagome superconductor CsV3Sb5,” Phys. Rev. X, vol. 11, no. 4, p. 041030, 2021.
- [16] H. Tan, Y. Liu, Z. Wang, and B. Yan, “Charge density waves and electronic properties of superconducting kagome metals,” Phys. Rev. Lett., vol. 127, no. 4, p. 046401, 2021.
- [17] Z. Liang, X. Hou, F. Zhang, W. Ma, P. Wu, Z. Zhang, F. Yu, J.-J. Ying, K. Jiang, L. Shan et al., “Three-dimensional charge density wave and surface-dependent vortex-core states in a kagome superconductor CsV3Sb5,” Phys. Rev. X, vol. 11, no. 3, p. 031026, 2021.
- [18] Z. Wang, Y.-X. Jiang, J.-X. Yin, Y. Li, G.-Y. Wang, H.-L. Huang, S. Shao, J. Liu, P. Zhu, N. Shumiya et al., “Electronic nature of chiral charge order in the kagome superconductor CsV3Sb5,” Phys. Rev. B, vol. 104, no. 7, p. 075148, 2021.
- [19] Z. Ye, A. Luo, J.-X. Yin, M. Z. Hasan, and G. Xu, “Structural instability and charge modulations in the kagome superconductor AV3Sb5,” Phys. Rev. B, vol. 105, no. 24, p. 245121, 2022.
- [20] L. Zheng, Z. Wu, Y. Yang, L. Nie, M. Shan, K. Sun, D. Song, F. Yu, J. Li, D. Zhao, S. Li, B. Kang, Y. Zhou, K. Liu, Z. Xiang, J. Ying, Z. Wang, T. Wu, and X. Chen, “Emergent charge order in pressurized kagome superconductor CsV3Sb5,” Nature, vol. 611, no. 7937, pp. 682–687, 2022.
- [21] L. Kautzsch, B. R. Ortiz, K. Mallayya, J. Plumb, G. Pokharel, J. P. C. Ruff, Z. Islam, E.-A. Kim, R. Seshadri, and S. D. Wilson, “Structural evolution of the kagome superconductors AV3Sb5 (A= K, Rb, and Cs) compounds through charge density wave order,” Phys. Rev. Mater., vol. 7, no. 2, p. 024806, 2023.
- [22] Q. Stahl, D. Chen, T. Ritschel, C. Shekhar, E. Sadrollahi, M. C. Rahn, O. Ivashko, M. v. Zimmermann, C. Felser, and J. Geck, “Temperature-driven reorganization of electronic order in CsV3Sb5,” Phys. Rev. B, vol. 105, no. 19, p. 195136, 2022.
- [23] F. Du, S. Luo, B. R. Ortiz, Y. Chen, W. Duan, D. Zhang, X. Lu, S. D. Wilson, Y. Song, and H. Yuan, “Pressure-induced double superconducting domes and charge instability in the kagome metal KV3Sb5,” Phys. Rev. B, vol. 103, no. 22, p. L220504, 2021.
- [24] K. Y. Chen, N. N. Wang, Q. W. Yin, Y. H. Gu, K. Jiang, Z. J. Tu, C. S. Gong, Y. Uwatoko, J. P. Sun, H. C. Lei, J. P. Hu, and J. G. Cheng, “Double superconducting dome and triple enhancement of TC in the kagome superconductor CsV3Sb5 under high pressure,” Phys. Rev. Lett., vol. 126, no. 24, p. 247001, 2021.
- [25] F. Yu, D. Ma, W. Zhuo, S. Liu, X. Wen, B. Lei, J. Ying, and X. Chen, “Unusual competition of superconductivity and charge-density-wave state in a compressed topological kagome metal,” Nat. Commun., vol. 12, no. 1, pp. 1–6, 2021.
- [26] Y. M. Oey, B. R. Ortiz, F. Kaboudvand, J. Frassineti, E. Garcia, R. Cong, S. Sanna, V. F. Mitrović, R. Seshadri, and S. D. Wilson, “Fermi level tuning and double-dome superconductivity in the kagome metal CsV3Sb5-xSnx,” Phys. Rev. Mater., vol. 6, no. 4, p. L041801, 2022.
- [27] See Supplemental Material at http://link for more information about the method, 2x2x1 CDW, 2x2x2 CDW, phonon dispersion of pristine CsV3Sb5 at 3.5% tensile strain, DFT phase diagram, dynamical and thermal stability of D3h-2 state, effective Hamiltonian calculations, band structure, STM, the distinguishable ISD, D3h-2 phase and 4a0 stripe order, the i-DMI in CsV3Sb5 AV3Sb5, CsV3Bi5, and X-ray scattering patterns for different CDW states, which includes Refs. [38, 39, 40, 41, 42, 43, 37, 13].
- [28] F. Lou, X. Li, J. Ji, H. Yu, J. Feng, X. Gong, and H. Xiang, “PASP: Property analysis and simulation package for materials,” J. Chem. Phys., vol. 154, no. 11, p. 114103, 2021.
- [29] W. Zhong, D. Vanderbilt, and K. M. Rabe, “First-principles theory of ferroelectric phase transitions for perovskites: The case of BaTiO3,” Phys. Rev. B, vol. 52, no. 9, p. 6301, 1995.
- [30] L. Bellaiche, A. García, and D. Vanderbilt, “Finite-temperature properties of Pb(Zr1-xTix)O3 alloys from first principles,” Phys. Rev. Lett., vol. 84, no. 23, p. 5427, 2000.
- [31] Y. Song, T. Ying, X. Chen, X. Han, X. Wu, A. P. Schnyder, Y. Huang, J.-g. Guo, and X. Chen, “Competition of superconductivity and charge density wave in selective oxidized CsV3Sb5 thin flakes,” Phys. Rev. Lett., vol. 127, no. 23, p. 237001, 2021.
- [32] B. Song, X. Kong, W. Xia, Q. Yin, C. Tu, C. Zhao, D. Dai, K. Meng, Z. Tao, Z. Tu et al., “Competing superconductivity and charge-density wave in kagome metal CsV3Sb5: Evidence from their evolutions with sample thickness,” arXiv:2105.09248, 2021.
- [33] W. Zhang, L. Wang, C. W. Tsang, X. Liu, J. Xie, W. C. Yu, K. T. Lai, and S. K. Goh, “Emergence of large quantum oscillation frequencies in thin flakes of a kagome superconductor CsV3Sb5,” arXiv:2202.08570, 2022.
- [34] X.-Y. Li, F. Lou, X.-G. Gong, and H. Xiang, “Constructing realistic effective spin Hamiltonians with machine learning approaches,” New J. Phy., vol. 22, no. 5, p. 053036, 2020.
- [35] T. Moriya, “New mechanism of anisotropic superexchange interaction,” Phys. Rev. Lett., vol. 4, no. 5, p. 228, 1960.
- [36] H. J. Zhao, P. Chen, S. Prosandeev, S. Artyukhin, and L. Bellaiche, “Dzyaloshinskii–moriya-like interaction in ferroelectrics and antiferroelectrics,” Nature Materials, vol. 20, no. 3, pp. 341–345, 2021.
- [37] V. Wang, N. Xu, J.-C. Liu, G. Tang, and W.-T. Geng, “VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code,” Comput. Phys. Commun., vol. 267, p. 108033, 2021.
- [38] J. P. Perdew, K. Burke, and M. Ernzerhof, “Generalized gradient approximation made simple,” Phys. Rev. Lett., vol. 77, no. 18, p. 3865, 1996.
- [39] G. Kresse and J. Furthmüller, “Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set,” Comput. Mater. Sci., vol. 6, no. 1, pp. 15–50, 1996.
- [40] G. Kresse and J. Furthmüller, “Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set,” Phys. Rev. B, vol. 54, no. 16, p. 11169, 1996.
- [41] P. E. Blöchl, “Projector augmented-wave method,” Phys. Rev. B, vol. 50, no. 24, p. 17953, 1994.
- [42] S. Grimme, J. Antony, S. Ehrlich, and H. Krieg, “A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu,” J. Chem. Phys., vol. 132, no. 15, p. 154104, 2010.
- [43] A. Togo and I. Tanaka, “First principles phonon calculations in materials science,” Scr. Mater., vol. 108, pp. 1–5, 2015.