Atomic engineering of interfacial polarization switching in van der Waals multilayers

Samples were prepared using a dry transfer method and consist of the twisted trilayer (stacked with a parallel orientation between $\mathrm{WSe_{2}}$ layers) sandwiched between thin hBN dielectric sheets (each $<15$ nm thick) and few-layer graphite electrodes (see Methods and Supplementary Section 1). The full heterostructure is thin enough for transmission of an incident electron beam, enabling TEM imaging of the device while simultaneously applying an out-of-plane electric field across the sample (Fig. 1a). Due to the presence of a rotational offset between the $\mathrm{WSe_{2}}$ layers, there is a spatial variation in the crystallographic stacking order, referred to as a moiré superlattice, throughout the trilayer; however, as a consequence of spontaneous relaxation of this superlattice,[11, 12, 13] four configurations with the lowest stacking energy comprise the majority of the moiré structure. Of these, the ABC and CBA stacking types have equal and opposite non-zero net polarization due to uncompensated charge transfer at the two stacked interfaces, while the ABA and BAB stackings have no net polarization due to mirror symmetry (Fig. 1b). The spatial arrangement of polar and non-polar domains depends on the relative rotations between the $\mathrm{WSe_{2}}$ sheets. In the A-twist-A^′ (AtA^′) polytype, the outer layers (layers 1 and 3) are nearly aligned ($0\degree<\theta_{13}<0.1\degree$) while the middle layer (layer 2) is rotated further ($\theta_{12}>\theta_{13}$). In the twist-A-B^′ (tAB^′) polytype the bottom and middle layers are nearly aligned ($0\degree<\theta_{12}<0.1\degree$) while the top layer is rotated further ($\theta_{23}>\theta_{12}$) (Fig. 1c).

To view the moiré structure in these two polytypes we use dark-field TEM (DF-TEM), which is a diffraction-based imaging technique that can be used to filter signal in multi-component structures,[14, 11] making it well-suited for the observation of buried interfaces. As shown in the DF-TEM images in Fig. 1d,e, the AtA^′ and tAB^′ polytypes produce distinct moiré patterns. In the AtA^′ polytype we observe a kagome-like pattern superimposed on a triangular superlattice. Since $\theta_{12}>\theta_{13}$, the longer lengthscale kagome structure is attributed to the moiré between the outer layers and the shorter triangular structure to the moiré between the outer layers and middle layer. In the tAB^′ polytype there are two superimposed triangular superlattices; the superlattice with the longer (shorter) periodicity comes from the bottom and middle (middle and top) layers since $\theta_{23}>\theta_{12}$. The diffraction contrast observed in the DF-TEM images arises from differences in local stacking and from the presence of a global tilt of the sample away from the zone axis (Supplementary Section 2).[15]

To identify which regions of the observed moiré structures have a net polarization, we use interferometric four-dimensional scanning transmission electron microscopy (4D-STEM, Fig. 1f,g). This imaging technique relates the intensities in interfering electron diffraction disks to the local translational offset between layers (Supplementary Section 3) and therefore can be used to map out the stacking order throughout the moiré.[16, 17, 18, 13] We first perform multislice simulations to calculate the cumulative diffraction intensity for the $\langle 1010\rangle$ and $\langle 1210\rangle$ Bragg peaks for the high-symmetry stacking orders in both polytypes (Fig. 1h,i). These computed values are then compared to the experimental 4D-STEM diffraction intensities (Supplementary Section 3) to assign the stacking order in each domain in the scan region. In the AtA^′ polytype, we find that the ABC and CBA (i.e., polar) domains are localized in the kagome-like structures, alternating in the points of each star, and on either side of elongated domain walls, the origin of which will be discussed later. Meanwhile the tAB^′ polytype is divided into large sections containing either ABC or CBA stacking domains in periodic triangular arrangements. We note that interferometric 4D-STEM is purely a structural diagnostic and therefore can not be used to measure the local polarization (P) direction (i.e., net +P versus -P); however, the polarization direction in each domain can be confirmed by observing the response to an applied electric field, which we discuss next.

The distinct arrangements of polar domains in the AtA^′ and tAB^′ trilayers suggest that these two polytypes will behave differently in an applied field. We first investigate the structural response in the AtA^′ polytype. Fig. 2a shows how one of the star structures from the sample in Fig. 1d distorts under application of an electric bias. At zero field, the ABC (-P) and CBA (+P) regions are approximately the same size because they are energetically degenerate. As a negative (positive) bias is applied, this degeneracy is lifted and the ABC (CBA) regions grow while the CBA (ABC) regions shrink (Supplementary Video 1). To quantify this change, we define an order parameter, dA, which is the normalized relative area of the ABC and CBA domains, described by Eq.1:

Previous studies have demonstrated that this order parameter can be used as a proxy for net polarization.[10] The variation in dA in the star structure is plotted as a function of field (E) in Fig. 2b, showing an approximately linear relationship with minimal structural hysteresis or remnant net polarization. In polar twisted bilayers, this behavior has been referred to as a moiré anti-ferroelectric response (MAFE)[10] and is a direct consequence of the moiré structure, wherein the topology of the moiré domain wall network precludes complete switching of polar domains.[19, 20, 21] We do not observe structural distortions in the surrounding non-polar regions (Supplementary Section 4) except as a consequence of deformation of nearby polar domains, such as in the center of the star in Fig. 2a.

It is also common for moiré structures to acquire heterostrain during sample fabrication, where one or more layers are uniaxially stretched relative to the adjacent layer(s).[22, 23, 24] Moiré structures with a large periodicity are particularly susceptible to substantial distortions even in the presence of a small atomic scale heterostrain (Supplementary Section 5).[25] A DF-TEM image of an AtA^′ sample with a very slight misalignnment between the outer layers ($\theta_{13}<0.03\degree$) and an estimated heterostrain $<0.03\%$ (Supplementary Fig. 9) is shown in Fig. 2c. This sample contains extended polar domain walls (PDWs) in the longer lengthscale moiré rather than a kagome-like pattern. Similar elongated domain walls have been observed in heterostrained twisted trilayer graphene.[13] Interestingly, in this heterostrained sample we observe two groups of PDWs with different responses to an applied field (Supplementary Videos 2–4). The first type displays a gradual response to the field (Fig. 2d,e) where the ABC and CBA domains steadily grow and shrink during biasing. However, the second type has a much sharper response where the polar domains rapidly flip between ABC and CBA stacking (Fig. 2f,g), similar to an untwisted polar heterostructure but on a much shorter lengthscale (10s rather than 100s of nm). Additionally, this second domain wall type has structural hysteresis and a remnant net polarization at zero field, a FE response. In the PDW shown in Fig. 2f,g, the coercivity is relatively small due to the small domain size; however some FE PDWs, discussed in the next section, exhibit a larger coercivity. Uniquely, the polar domains in the heterostrained twisted trilayer structures shown here are not confined by the same topology as either a twisted bilayer or a non-heterostrained twisted trilayer, enabling a true ferroelectric response in a moiré material for the first time.

To understand the origin of the different switching responses exhibited by these two groups of domain walls, we calculate the polarizability for various PDW segments with different orientations for the sample shown in Fig. 2c. Here, polarizability, the ease with which the net polarization switches, is equivalent to the slope of dA versus E ($\delta dA/\delta E$). Fig. 2c illustrates the orientation of the PDWs in the sample ($\theta_{PDW}$) and Fig. 2h relates the polarizability of a selection of these PDWs to their average orientation (additional information in Supplementary section 6). Based on this investigation, it is evident that, for this sample, PDWs oriented around 60-90$\degree$ relative to the x-axis have a polarizability that is roughly 3-4 times lower than PDWs oriented closer to 0$\degree$. Knowing that domain polarizability is affected by domain anisotropy in twisted bilayers,[26, 10] the phenomenon we observe could be attributed to uniaxial heterostrain present in the superimposed small moiré, which is oriented on average around 72$\degree$ relative to the x-axis in this sample (Supplementary Fig. 10). This heterostrain introduces global structural anisotropy in the trilayer, as seen by the distortion of the triangular moiré unit cells, which could produce a preferential sliding axis for domain switching, analogous to an easy axis for spin reorientation in magnetic systems.[27, 28] Overall, it is clear that polarization switching in the AtA^′ trilayer is influenced by the uniaxial strain fields in all three $\mathrm{WSe_{2}}$ layers collectively.

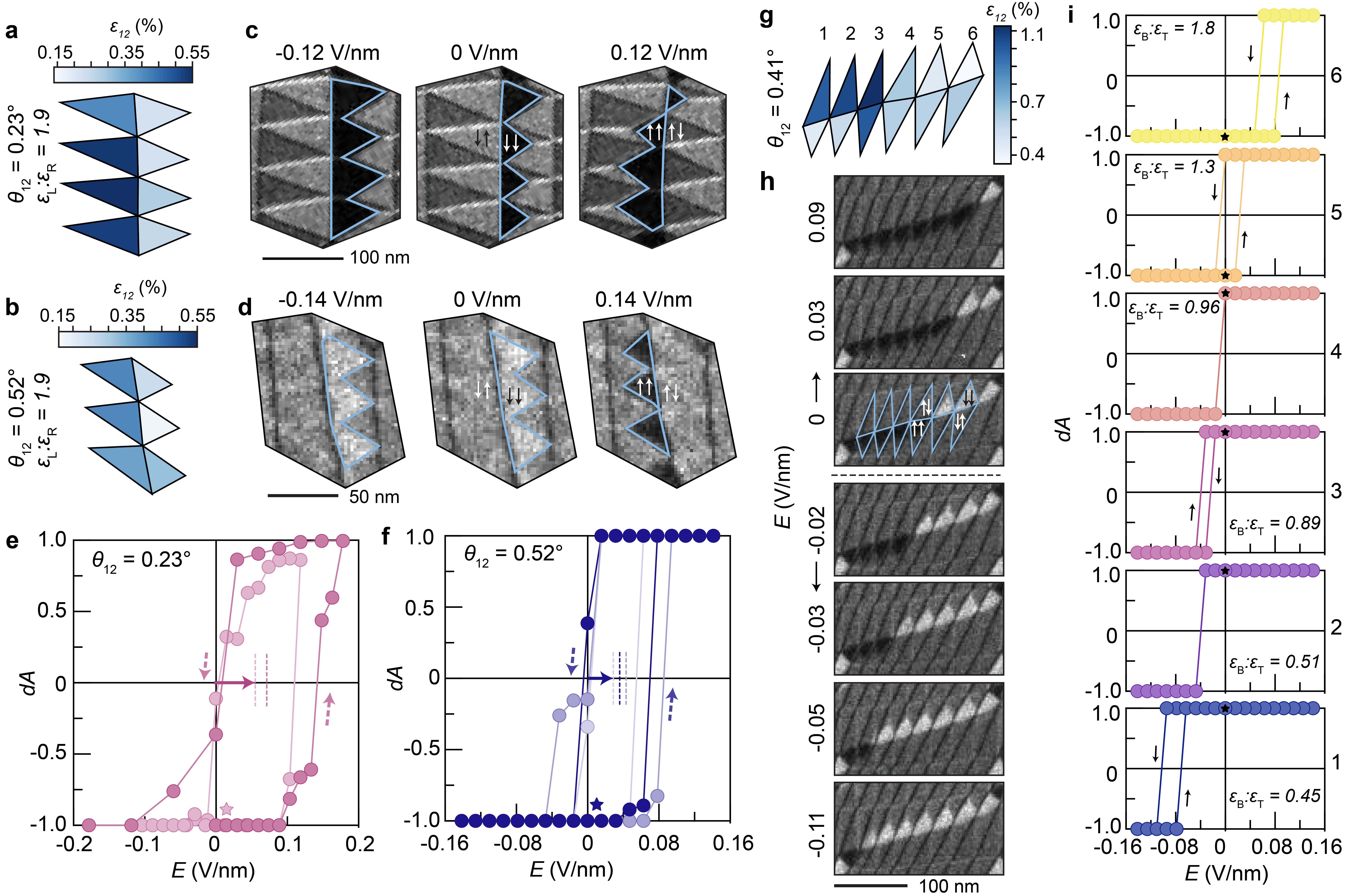
Some PDWs run through a heterostrain gradient where the small moiré is considerably more distorted on one side of the domain wall than the other. For example, in the regions shown in Fig. 3a,b, the magnitude of heterostrain between layers 1 and 2 ($\epsilon_{12}$) is approximately twice as large on the left side of the PDW compared to the right side ($\epsilon_{L}:\epsilon_{R}=1.9$). In both regions, which have different interlayer twist angles between the outer and middle layers ($\theta_{12}$), we observe that the polar domains localize on the less heterostrained half of the PDW at zero field. It has been demonstrated that the presence of anisotropic strain in multilayer graphene further increases the energy of the rhombohedral (ABC/CBA) stacking types relative to the Bernal (ABA/BAB) stacking.[29] Presuming that $\mathrm{WSe_{2}}$ behaves similarly, we rationalize that the observed preferential alignment of polar domains at zero field arises from an intrinsic thermodynamic bias generated by the appreciable difference in heterostrain between the sides of the PDW. Plotting dA versus E (Fig. 3e,f) over two or three biasing cycles, we see that this energetic preference toward one polarization state at zero field ultimately shifts the hysteresis curve along the electric field axis. We note that the enhanced coercivity of these two PDWs compared to that shown in Fig. 2g likely stems from a combination of structural factors, such as domain size, local distortions of the small moiré after polarization switching, and random variations in structural pinning sites at the ends of the domain wall segments pictured. Nevertheless, it is evident that the heterostrain gradient effectively pins the polar domains along one scan direction to produce a consistently biased FE response.

Remarkably, this asymmetry in the polarization curve can be systematically tuned down to the length scale of an individual polar domain. To demonstrate, we consider a PDW in a continuously varying heterostrain gradient. Fig. 3g illustrates that $\epsilon_{12}$ is smaller on the bottom side of the PDW than on the top for domains 1–4 and vice versa for domains 5–6. Based on this variation in the direction of the heterostrain gradient, at zero field polar domains 1–4 align on the bottom side of the PDW and polar domains 5–6 align on the top, as shown in Fig. 3h. As a field is applied, each domain responds independently in a domino-like fashion (Fig. 3h), where the field necessary for polarization switching is directly correlated to the magnitude and direction of the local heterostrain gradient (Fig. 3i). These results demonstrate that coupling strain engineering[30, 31, 32] with moiré engineering could offer a route for precise, spatially localized manipulation of interfacial polarization.

Next we discuss how the tAB^′ polytype responds to an applied field. Whereas the AtA^′ polytype had a highly localized polarization switching response, the tAB^′ structure globally deforms under application of an electric field (Fig. 4a, Supplementary Videos 5,6). The tAB^′ polytype is quite similar structurally to a twisted bilayer considering that both the large and small moiré patterns in the tAB^′ trilayer relax into triangular domains.[11, 16, 13] With this in mind, we analyze the field-dependent structural distortions in both moiré lengthscales of the tAB^′ structure and compare them to analogous twisted $\mathrm{WSe_{2}}$ bilayers in Fig. 4b (twisted bilayer images provided in Supplementary Video 7). We do not observe marked differences in behavior between the smaller moiré in the trilayer ($\theta_{23}=0.25\degree$) and a twisted bilayer with a similar interlayer rotation ($\theta=0.31\degree$). Interestingly, the larger moiré in the trilayer ($\theta_{12}<0.05\degree$), has a considerably lower polarizability than its twisted bilayer counterpart ($\theta\approx 0.03\degree$).

DF-TEM images of the tAB^′ structure show that the domain walls of the larger moiré are roughly commensurate with the domain walls in the smaller moiré, and as a field is applied, these two sets of domain walls appear to be pinned to one another (Fig. 4c). At one point, around -0.01 V/nm, the domain wall of the large moiré de-pins from that of the small moiré and jumps to an adjacent domain wall in the small moiré, leading to the S-shaped polarization curve in Fig. 4b. To quantitatively analyze this pinning effect, we track how the side lengths ($\lambda$) of the triangular domains in the small moiré (from Fig. 4c) evolve as a function of field along the length of one of the large moiré domain walls over three cycles of biasing. The results illustrate that the small moiré domains stretch anisotropically as the large moiré deforms in response to the field, particularly at positive field values (Fig. 4d). This increase in the periodicity of the small moiré could be facilitated by either a reduction in the local interlayer rotation in these domains or by a reduction in local lattice mismatch. Considering that one or more layers are sliding and stretching in response to the applied field, it is unlikely that the local lattice mismatch between layers is decreasing (we would expect the converse instead), and therefore we conclude that changes in local rotational offset between the middle and top layers ($\theta_{23}$, Fig. 4e) drive the observed deformation of the small moiré domains. Fig. 4f,g shows how the average values of $\lambda$ and $\theta_{23}$ evolve for a group of domains from the region in Fig. 4c over three biasing cycles (field profile in Fig. 4h), showing that the small moiré length increases and the local twist angle decreases by up to factor of two as a result of pinning between the domain walls across the two interfaces. Importantly, these results indicate that the interfaces in polar multilayer heterostructures are not decoupled from one another and cooperative effects can influence observed switching dynamics, such as the reduction in polarizability observed in Fig. 4b. Notably, the results in Fig. 4c–e also demonstrate an electrical route to controlling superlattice wavelength in moiré structures.

Two-dimensional vdW materials have exhibited promise as FE components in emerging technologies[33, 34] due to their robustness to depolarization at atomic thicknesses,[35, 36, 37, 38, 39, 40, 41] their compatibility with silicon-based device schemes, and their ability to be stacked into multi-component heterostructures with sought-after functionalities, such as FE field-effect transistors (FE-FETs)[42] and multiferroic devices.[43, 44] Here, we have revealed that a diverse range of polarization switching dynamics can be accessed in twisted trilayer heterostructures due to the presence of more than one moiré periodicity as well as interactions between all three layers, as summarized in Fig. 5. Namely, changing relative rotations between layers and intralayer uniaxial strain fields leads to a variety of polar domain structures with different polarizabilities, coercivities, and intrinsic thermodynamic biases. This work paves the way for engineering polarization switching and structural dynamics in polar multilayer systems, particularly as developments in 2D heterostructure fabrication and strain engineering continue to advance. For example, variations in the arrangements of polar domains in the AtA^′ versus tAB^′ structures as well as the highly localized nature of preferential polarization states in the AtA^′ polytype opens avenues for the design of structures and surfaces with deterministically patterned polarization. Even in untwisted polar vdW multilayers, manipulation of intralayer strain could afford control over consequent switching dynamics. In moiré multilayers comprised of semiconducting vdW materials, including $\mathrm{WSe_{2}}$, such variability in polar order and switching responses could also lead to the emergence of exotic, electrically-tunable moiré exciton responses, beyond those that have been previously observed in bilayer heterostructures.[45]

All dark-field TEM images supporting the findings of this study are contained within the main text and supplementary files. Raw 4D-STEM data sets will be publicly accessible on Zenodo upon publication of the manuscript.

The computer code for generation of colored stacking order maps and multislice simulations is available from the authors upon request.

This work was supported by the U.S. National Science Foundation (NSF) under award no. DMR-2238196 (D.K.B.). M.V. acknowledges support from a University of California, Berkeley Philomathia Graduate Fellowship. I.M.C. acknowledges support from a University of California, Berkeley Berkeley Fellowship and a National Defense Science and Engineering Graduate (NDSEG) Fellowship under contract FA9550-21-F-0003 sponsored by the Air Force Research Laboratory (AFRL), the Office of Naval Research (ONR) and the Army Research Office (ARO). Work at the Molecular Foundry, LBNL was supported by the Office of Science, Office of Basic Energy Sciences, the U.S. DOE under Contract no. DE-AC02-05CH11231. Other instrumentation used in this work was supported by grants from the Gordon and Betty Moore Foundation EPiQS Initiative (Award no. 10637, D.K.B.), Canadian Institute for Advanced Research (CIFAR–Azrieli Global Scholar, Award no. GS21-011, D.K.B.), and the 3M Foundation through the 3M Non-Tenured Faculty Award (no. 67507585, D.K.B.). K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the Ministry of Education, Culture, Sports, Science and Technology, Japan (grant no. JPMXP0112101001) and Japan Society for the Promotion of Science, Grants-in-Aid for Scientific Research (KAKENHI; grant nos. 19H05790, 20H00354 and 21H05233).

M.V.W. and D.K.B. conceived the study. M.V.W., N.D., and N.K. designed and fabricated the samples. M.V.W. and R.D. acquired TEM and 4D-STEM data. M.I. performed multislice simulations with input from I.M.C.. I.M.C. wrote the code used for generation of color-coded virtual dark-field images. T.T. and K.W. provided the bulk hBN crystals. M.V.W. processed and analyzed the data. M.V.W. and D.K.B. wrote the manuscript with input from all co-authors.

The authors declare no competing interests.

Correspondence and requests for materials should be emailed to D.K.B.
(email: [email protected]).