Asymptotic theory of -pseudo-cones111This paper was supported by the NSFC (No. 12371060), the Shaanxi Fundamental Science Research Project for Mathematics and Physics (No. 22JSZ012) and the Excellent Graduate Training Program of SNNU (No. LHRCCX23142).
Abstract
In this paper, we study the non-degenerated -pseudo-cones which can be uniquely decomposed into the sum of a -asymptotic set and a -starting point. Combining this with the novel work in [34], we introduce the asymptotic weighted co-volume functional of the non-degenerated -pseudo-cone , which is also a generalized function with the singular point (the origin). Using our convolution formula for , we establish a decay estimate for at infinity and present some interesting results. As applications of this asymptotic theory, we prove a weighted Brunn-Minkowski type inequality and study the solutions to the weighted Minkowski problem for pseudo-cones. Moreover, we pose an open problem regarding , which we call the asymptotic Brunn-Minkowski inequality for -pseudo-cones.
Mathematics Subject Classification 2020. 52A30, 52A39, 52A40.
Keywords. -pseudo-cone, -starting point, asymptotic weighted co-volume, Brunn-Minkowski type inequality.
1 Introduction
The polar operator on the space of convex bodies and its functional counterpart, the Legendre transform on the class of lower semi-continuous convex functions, play an important role in convex geometry, see [28] for more details. As an abstraction, an order reversing involution on certain partially ordered sets is called a duality. All dualities on and are completely characterized by the polar operator [8] and the Legendre transform [4], respectively. In [3, 5], Artstein-Avidan and Milman introduced a new duality transform that is different from the Legendre transform on the sub-class (the class of geometric convex functions) of . Naturally, a question arises: what is the geometric version corresponding to this new duality transform? In a special case, Rashkovskii [27] studied the copolarity of coconvex sets in the positive orthant of . Later, Artstein-Avidan, Sadovsky and Wyczesany [6] pointed out that all order reversing quasi-involutions can be induced by a cost function and exhibited various attractive dualities. Moreover, they systematically studied this geometric version of the new duality transform (termed dual polarity) and showed that the acting object of the dual polarity is a cone-like unbounded closed convex set. They also established the Blaschke-Santaló type inequality for the cone-like sets under the condition of essential symmetry. The cone-like set and dual polarity were further examined in [42], where the authors referred to this cone-like set as the pseudo-cone.
On the other hand, inspired by the works of Khovanskii and Timorin [19] and Milman and Rotem [25], Schneider [30] established the Brunn-Minkowski theory for -close sets, where is a pointed closed convex cone in . Similar to the dual Minkowski problem posed by Huang, Lutwak, Yang and Zhang [16] for convex bodies, Li, Ye and the fourth author [22] introduced the concept of -compatible sets and studied their copolarity to address the dual Minkowski problem for unbounded closed convex sets. Adopting terms and conventions from [33, 34], these related results have shown that dual polarity is equivalent to copolarity and that -compatible sets are the same as -pseudo-cones. Quite recently, Semenov and Zhao [37] studied some characterizations of the -asymptotic sets to solve the Minkowski problem for the -asymptotic sets given by the infinity measure. Inspired by these, our first result in this paper is a classification of -pseudo-cones. That is, a non-degenerated -pseudo-cone can be uniquely decomposed into the sum of a -asymptotic set and a point in . To state this result precisely, we gather some foundational concepts, which can be found in [6, 22, 30, 33, 34, 35, 42].
Denote by and the inner product and norm in , respectively. We write and for the unit ball and the unit sphere in , respectively. The topological boundary and the topological interior of a subset are denoted by and , respectively. Denote by a negative half-space with the outer normal vector . Let be a pointed closed convex cone in with non-empty interior, i.e., is a -dimensional closed convex cone that is line-free. The polar cone of is defined by , which is also line-free. Denote by and . Let be an unbounded closed convex set and . If has finite volume, then is called a -close set and is called a -coconvex set. Specifically, a -close set is called a -full set if is bounded. Moreover, is called a -asymptotic set if is asymptotic to at infinity, i.e.,
| (1) |
where is the distance from to . Let be a non-empty closed convex set. The recession cone of is defined by . If is unbounded, then is a closed convex cone. Let be a non-empty closed convex set, is called a pseudo-cone if there holds for any and . For an -dimensional pointed closed convex cone , if is a pseudo-cone and , then is called a -pseudo-cone.
Now, we present a asymptotic characterization for the -pseudo-cones. For the definition of the support function of -pseudo-cones, please see (3).
Theorem 1.
Let be a pointed closed convex cone in with non-empty interior and be a -pseudo-cone, then the following two statements are equivalent:
There is a point such that for all ;
can be uniquely decomposed into , where is a -asymptotic set and .
We call a -pseudo-cone satisfying or in Theorem 1 as a non-degenerated -pseudo-cone. Moreover, for a non-degenerated -pseudo-cone , we call as the -starting point of and as the asymptotic cone of . If , then Theorem 1 reduces to Theorem 2.6 in [37]. But the methods in this paper are different from [37]. There is a beautiful example of the degenerated -pseudo-cone proposed by Schneider in high dimension (), please see Figure 1 in Section 3. Furthermore, from a new perspective, the -starting point of a non-degenerated -pseudo-cone can offer insights into the conic linear bundle. As applications of this asymptotic theory of -pseudo-cones, one can establish a strengthened version of the Brunn-Minkowski inequality for -coconvex sets [30], see Section 6 for details.
Since the main behavior of a -pseudo-cone concentrates around the origin, i.e., all -pseudo-cones have almost same asymptotic behavior at infinity, the usual Lebesgue measure space is not suitable for -pseudo-cones. Following Schneider’s idea on the finiteness of the measure [34], one can endow a weight on to ensure the compactness for -pseudo-cones. Throughout this paper, we denote the weight function by , which is a -homogeneous continuous function with . A good example of such a weight function is for any .
The weighted surface area measure [34] of is given by the push-forward measure of the weighted boundary Hausdorff measure, specifically,
where is the Gauss image of and is the effective boundary of (see [22] or section 2 for more details). Schneider [34] showed that for and every -pseudo-cone , is finite. Moreover, the weighted volume and the weighted co-volume of -pseudo-cone are defined as follows:
Schneider [34] also proved that for any and every -pseudo-cone , is finite.
From the asymptotic perspective of a -pseudo-cone, we define the asymptotic weighted co-volume functional of non-degenerated -pseudo-cones as follows: Let be the -starting point of the -pseudo-cone , expressed as for some -asymptotic set . The asymptotic weighted co-volume of is defined by
We can view this asymptotic weighted co-volume as a functional of two variables. If we fix a -asymptotic set , then becomes a generalized function on . As our second result, we summarize and enhance Schneider’s finiteness theory from [34] into the following results.
Theorem 2.
Let be a -pseudo-cone and be a -asymptotic set with . Then the following table holds:
| finite | finite | finite | |||
| finite | finite | ||||
| finite | finite | finite | finite | ||
| finite or | finite or | finite or | finite or |
In the table above, the case of has been solved by Schneider [34]. Here, we focus more on the case of . The highlighted (in blue) entries indicate that there is useful and interesting information regarding the finiteness of the asymptotic weighted co-volume and the weighted co-volume of the -pseudo-cone . This suggests that as exceeds , we can gain additional insights into the structure and properties of -pseudo-cones. For example, we demonstrate that for every and any -asymptotic set , there exists a basic yet important convolution formula (see Section 4 for details):
where is the characteristic function of . Fixing a -asymptotic set , is a generalized function on . We establish a decay estimate for at infinity, and then we obtain the following interesting formula: Let and . If the weight function is -smooth, then
We believe that this imperceptible formula will be instrumental in establishing the Brunn-Minkowski inequality for .
Based on the fact that the Minkowski sum of two -pseudo-cones is also a -pseudo-cone (see Lemma 3.9 in [37]), we can derive the following Brunn-Minkowski type inequality. For , we call a -pseudo-cone as a -close set if .
Theorem 3.
Suppose that . Let and be two -close sets. Then, we have
| (2) |
Moreover, if , the equality holds in inequality (2) if and only if and are dilates of each other.
From the asymptotic perspective of -pseudo-cones, we conjecture that the following Brunn-Minkowski type inequality holds. Open problem (Asymptotic Brunn-Minkowski inequality for -pseudo-cones): Let be two non-degenerated -pseudo-cones, and let be their respective -starting points. For and , there holds
Remark 1 (Weighted theory v.s. dual theory).
Comparing the weighted Brunn-Minkowski theory for -pseudo-cones in [34] with the dual Brunn-Minkowski theory for -compatible sets in [22], we would like to note that the dual theory is a logarithmic version of the isotropic weighted theory. The weight functions , which can be isotropic or anisotropic, have two representative examples in [34]: and for and some fixed unit vector . If we consider the weight function , then the -th dual curvature measure of the -pseudo-cone in [22] is given by
The -dual volume of -pseudo-cone is defined as
Here, and denote the support function and radial function of , respectively. By applying Theorem 2, we will show that is finite for every -pseudo-cone and for any in Section 4.
Related results of the noncompact version of the classical Minkowski problem have long been studied by Pogorelov [26], Bakelman [7], and Urbas [38]. Subsequently, Chou and Wang [12] studied the smooth solutions to noncompact Minkowski problems in detail. Recently, Choi et al. [9, 10, 11] studied significant problems related to the evolution of hypersurfaces asymptotic to a cylinder. In cases where these hypersurfaces are asymptotic to a cone, Schneider [30, 34] was the first to investigate the noncompact Minkowski problem. Moreover, concerning the weighted Minkowski problem for -pseudo-cones, Schneider [34] provided an elegant result that characterizes the weighted surface area measure for . As applications of our asymptotic theory, we present solutions to the weighted Minkowski problem for as follows.
Theorem 4.
For , given a nonzero finite Borel measure on , there exists a -close set such that . Moreover, if and are -determined sets by such that , then .
The organization of this paper is as follows. In Section 2, we discuss the push-forward measure and co-area formula related to -pseudo-cones. Section 3 presents the asymptotic theory of -pseudo-cones. Section 4 summarizes results on the finiteness of the weighted co-volume and the asymptotic weighted co-volume. In Section 5, we provide integral formulas for the (asymptotic) weighted co-volume and the weighted surface area measure. Theorem 3 and the asymptotic Brunn-Minkowski inequality for -pseudo-cones are discussed in Section 6. Finally, we study the weighted Minkowski problem with subcritical exponent.
Acknowledgement. The authors would like to thank Professor Rolf Schneider for providing a crucial example of the degenerated -pseudo-cone.
2 Background: Push-forward measure and the Co-area formula
In this section, we introduce some tools related to -pseudo-cones. Let be a non-empty closed convex set. The recession cone of is defined as If is unbounded, then is a closed convex cone.
Definition 1 (see [6, 33, 34, 42]).
Let be a non-empty closed convex set. The set is called a pseudo-cone if for any and . Crucially, we have:
Moreover, if is -dimensional and line-free, then is an -dimensional pointed closed convex cone and is called a -pseudo-cone; Conversely, given an -dimensional pointed closed convex cone , if is a pseudo-cone and , then is called a -pseudo-cone.
Let be a -pseudo-cone. The support function of is defined by
| (3) |
Note that for any , we denote . The radial function of is defined by
Fixed , then for any (see e.g., [33]). Define and .
Li, Ye and the fourth author [22] introduced the following notion of -compatible set.
Definition 2 (see [22]).
Let be a non-empty set. The closed convex hull of with respect to is defined by
If , then is called a -compatible set.
Lemma 1 (see [22]).
Let , then is a -pseudo-cone if and only if it is a -compatible set.
Let be a -pseudo-cone. Some geometric mappings and sets associated with , such as the Gauss image map and the effective boundary of , as discussed in [22], are summarized as follows:
For more details, one can refer to [22, p. 2018-2019]. Let be a positive continuous function on . We consider two measures with density : the -weighted spherical Lebesgue measure, denoted by and the -weighted boundary Hausdorff measure, denoted by . The measure can be pushed forward to the -weighted surface area measure on via the Gauss image map . Specifically, for any Borel set ,
| (4) |
It is not hard to verify that is a Radon measure on . By the standard approximation theory in measure theory, (4) is equivalent to the following: for any bounded measurable function on ,
| (5) |
where is the Gauss map of defined -a.e. on .
To transform the boundary integrals and the spherical integrals, one can apply the co-area formula of Federer [13, Theorem 3.2.22] and the approximation Jacobian of the radial map. For further details, please refer to [18, p. 170], [22, p. 2022], and [34, p. 9]. To ensure rigor, we provide a simple yet important lemma:
Lemma 2.
The radial map of the -pseudo-cone is an internally closed Lipschitz homeomorphism between and . Therefore, we can conclude that the convex hypersurface is a spherical locally Lipschitz graph on .
Proof.
There exists a hyperplane such that can be represented by the epigraph of some convex function on , with . For any compact subset and any , there exists an -dimensional convex body such that
Since is a convex function on , it follows that is Lipschitz on , and we denote the Lipschitz constant by . Thus, one has
Since is compact and , there exists a constant , depending only on and , such that for all . Note that can be represented as for . Thus
Therefore, one has
which shows that is a Lipschitz mapping on , i.e., is internally closed Lipschitz on . It is clear that is Lipschitz on . ∎
Due to Lemma 2, is differentiable almost everywhere on and is differentiable almost everywhere on . Let be a regular normal vector of , and . By establishing the orthonormal frame of at , we obtain the orthogonal decomposition:
where is the covariant partial derivative of the support function with respect to the frame . Denote by Id the identity mapping on , then the tangent mapping of at is given by (noting that is differentiable -a.e. on ):
Therefore, using the Gram matrix of , we have
thus the -approximate Jacobian of at -a.e. is
Since , the -approximate Jacobian of at -a.e. is
Applying the co-area formula in [13, Theorem 3.2.22], for any integrable functions on and on , we have
| (6) |
3 Asymptotic analysis of -pseudo-cones
As an unbounded closed convex set in , the -pseudo-cone is a central research object in unbounded Brunn-Minkowski theory. In this section, we will discuss some asymptotic properties of -pseudo-cones. These properties are useful for establishing the Brunn-Minkowski theory for more general unbounded closed convex sets.
Lemma 3.
If is a -asymptotic set, then is a -pseudo-cone and
Proof.
For a -asymptotic set , its normal vectors belong to due to formula (1). Since is also a closed convex set and for any , we have
Combining this with Definition 2, we have
which shows that is a -compatible set ( is also a -pseudo-cone), and hence
Suppose there exists a point but .Let and denote the metric projection of on and , respectively. Define . Let
where is sufficiently small such that
Thus, , which implies . However,
where we used
This contradiction shows that , which implies
∎
Let be a -pseudo-cone and be the metric projection of the origin on , . Denote by the ray starting at in the direction . If for some , we define the following set
then there exists a boundary partition
Moreover, we define the function as .
Lemma 4.
Let be a -pseudo-cone, and . If , then the function is monotonically decreasing. Therefore, there exists the following limiting function
| (7) |
Moreover, the following holds
Proof.
For any , let with . Since a -pseudo-cone is the same as a -compatible set and given that , we have
Combining with , we find that the ray lies in between and . Thus,
For with , we denote by the angle between and , then . Let , and let be the geodesic curve between and on . By the formula (7), we have . Due to the continuity of the boundary of the closed convex sets and , is continuous with respect to . Similarly, is also continuous with respect to . Therefore, for any , there exists an open neighborhood of the geodesic curve in such that
| (8) |
and
| (9) |
for all and . Now, the collection forms a family of open covers of the spherical closed convex set . By the Heine-Borel finite covering theorem, there exists a finite sub-family of such that
Hence, for any , there exists an such that for some .
For the above and for every , by the formula (7), we have
Thus, there exists such that for all with , the following holds
| (10) |
Now, let . Consider and with .
Case : If for some , then by (10), we have
Case : If for some , then
Therefore, for the above , if , then
for all . This shows that as and . ∎
Definition 3 (-starting point).
Let be a -pseudo-cone and . We call as the -starting point of if and
as with .
Remark 2.
If is a -starting point of -pseudo-cone , then is unique. To do so, let and be two -starting points of . For some , we have
. By the uniqueness of limits, it follows that . Therefore, we conclude that .
Lemma 5.
Let be a -pseudo-cone and , then
Proof.
Without loss of generality, let be not a closed convex cone. Note that
we have
where can be checked easily. Since for all , one has
By Lemma 4, we have
We claim that for any . To do so, assume there exists such that . Denote by the angle between and , then the ray
is an asymptotic line of in the -dimensional plane . Thus,
By Theorem 1.3.7 in [28], the ray and the set can be separated by a hyperplane with the normal , where . Clearly, is parallel to . If , then . Since , we have
Letting , leads to the conclusion , a contradiction. Thus, we conclude that .
Next, we claim that . Suppose , then . Since and , it follows that . This gives
which is a contradiction. If , then for some . In the plane , since , the point lies on the other side satisfies , which contradicts the fact that . Thus, we conclude that .
Let satisfy . We can choose a geodesic curve connecting and on . For any , we have
Noting that , we conclude that for . By the properties of , there exists a sequence such that
| (11) |
Since is continuous with respect to , there is a small neighbourhood of such that for some and any . Consequently, by the sufficiently small neighborhood and , we have
| (12) |
Using the convexity of and the convergence (11), we have
Note that , the above results contradict with (12). Thus, we conclude that
In other words, we have . Therefore, is indeed the -starting point of .
Let be the -starting point of the -pseudo-cone , then and
| (13) |
as with . Since , one has for all . Suppose that there exists a point such that
then one has
where satisfies . Since , for all , one has
This contradicts with (13). Therefore, for all . ∎
Lemma 6.
Let and . If is a -asymptotic set, then is a -pseudo-cone and is the -starting point of . Conversely, if is a -pseudo-cone and is the -starting point of , then is a -asymptotic set.
Proof.
Suppose that is a -asymptotic set and . By Lemma 3, we have
Since is an unbounded closed convex set, by Definition 2, one has
which shows . Therefore, is a -compatible set, i.e., is a -pseudo-cone. Since is a -asymptotic set, one has
| (14) |
By Lemma 4, there holds . Suppose that for some , then there is a neighborhood of such that for all and some from the continuity of the distance function . Therefore, one has
This contradicts with (14). Thus, , i.e., is the -starting point of .
Let be a -pseudo-cone and be the -starting point of . By Definition 3, we have , i.e., and
. Thus, for any given , there exists such that if and , then for all . Hence, if and , there exists some such that
This induces
then is a -asymptotic set. ∎
Here we gave the following results as an expansion to Theorem 1.
Theorem 5.
Let be a pointed closed convex cone in with non-empty interior and be a -pseudo-cone, then the following three statements are equivalent:
There is a point such that for all ;
There is a point such that is the -starting point of ;
can be uniquely decomposed into , where is a -asymptotic set and .
Proof.
Lemma 5 shows that is equivalent to . Now, we assume that satisfies or . By Lemma 6, is a -asymptotic set. Thus, can be decomposed into
Suppose that there are two -asymptotic set and such that
then . Since is a -asymptotic set, one has
which induces
If , then the above formula contradicts with the fact that is a -asymptotic set. Thus, there are and . This shows holds.
Conversely, if holds, then for all . For -asymptotic set , we claim that for all . Otherwise, if for some , then
Note that , so the above formula contradicts with the formula 1. Thus, for all , i.e., holds. ∎
As a special case, we have the following corollary.
Corollary 1.
Let be a -pseudo-cone. Then the following statements are equivalent:
is a -asymptotic set;
The origin is the -starting point of ;
for all .
Remark 3.
Recently, the equivalence between and was also established by Semenov and Zhao [37].
Definition 4.
Remark 4.
From the perspective of the -starting point, a non-degenerated -pseudo-cone has its -starting point, but a degenerated -pseudo-cone does have the -starting point. In the plane , each -pseudo-cone all are non-degenerated. However, there are many degenerated -pseudo-cones in high dimension. For example, please see Figure 1.
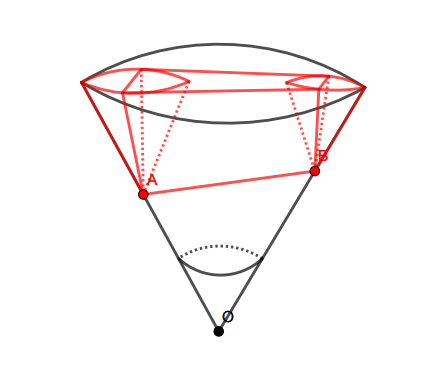
This is an example of the degenerated -pseudo-cone in and was provided by R. Schneider. In which, we place two points and on the boundary of the circular cone whose vertex is . Then the highlighted domain (in red) swept by the motion from to is a pseudo-cone, but it cannot be decomposed as Theorem 1.
Lemma 7.
Let be two -asymptotic sets. Then the Minkowski sum is also a -asymptotic set.
Proof.
By Lemma 3, we have
Clearly, and are unbounded closed convex sets contained in , so the Minkowski sum is also an unbounded closed convex sets in . For any , we have
Hence, according to the closeness and convexity of , it follows that
| (15) |
By Corollary 1, we have for . Thus,
| (16) |
Combining (15) with (16), one has
which implies that by Definition 2. Therefore, is a -compatible set. Since for all , we conclude that is a -asymptotic set by Corollary 1. ∎
Corollary 2.
The Minkowski sum of two non-degenerated -pseudo-cones and is still a non-degenerated -pseudo-cone.
Proof.
Recently, Lemma 7 was also established by Semenov and Zhao [37]. Moreover, they also established the following results.
Lemma 8 (see [37]).
The Minkowski sum of two -pseudo-cones and is still a -pseudo-cone.
4 Finiteness of the asymptotic weighted co-volume
Recall that the weight function is a -homogeneous continuous function with . By the compactness of the set , we can define two positive constants
For any , since , it follows that
| (17) |
Let and . Then, we have . Similar to [34], we define the sequence , for , and the sequences of sets
| (18) |
where the upper cylinders , lower cylinders , and convex bodies satisfy the relationship:
| (19) |
Firstly, we present the following result regrading the weighted volume of -pseudo-cones:
Lemma 9.
Let be a -pseudo-cone. If , then is finite; if , then is infinite.
Proof.
Since is continuous on and , it follows that
Then, the following integral can be divided as
. For , by (17) and (19), we have the following estimate:
which implies
According to the comparison test for -series, and since , the infinite series is convergent, so is finite.
. For , as above, we have
which also leads to
Again, by the comparison test for -series, and since , we have , so is infinite. ∎
Next, we provide the proof of a key estimate concerning the finiteness of weighted surface area measure, as discussed in [34, p. 9].
Lemma 10.
For the sets in (18), there exists a constant , independent of , such that
Proof.
Firstly, by the definitions in (18), we have
Since the surface area of convex bodies increases monotonically with respect to set inclusion, we have
thus, we have
∎
Remark 5.
Using the above estimate, Schneider [34] proved that is finite for any and every -pseudo-cone . In fact, one can also obtain the same results by using the binomial expansion and the comparison test for -series directly. When , Schneider [34] provided a counterexample to show that for some -pseudo-cone .
Counterexample 1.
For the critical case , we provide a counterexample as follows. In the plane , let and consider the weight function
Choose a fixed cone and a -pseudo-cone
then we have
Therefore, if , the weighted surface area measure of a -pseudo-cone may be infinite. However, it may also be finite, as in the case of -full sets.
The weighted co-volume of the -pseudo-cone can be divided into
It has been proven that is finite for and is finite for (see [34, Lemma 7]). Thus, is finite for . Here, we present some additional conclusions on the weighted co-volume.
Lemma 11.
If , then is infinite for every -pseudo-cone .
Proof.
According to (17) and the Cauchy-Schwarz inequality, we have
Let , then . Thus,
Since , we have
Thus, . ∎
Counterexample 2.
If , there is a counterexample that shows is infinite for some -pseudo-cone .
Proof.
In the plane , let us choose a fixed cone and consider the weight function
where . We construct a -pseudo-cone . For , we have
Since
there exists such that
for all . Thus,
For , since
there exists a constant such that for all . Thus, we have
Therefore, if , then may be infinite. However, it may also be finite. ∎
Recall the -improper integral over infinite interval:
and the -improper integral with singularities:
From the above discussion, it is clear that the weighted volume of a -pseudo-cone is the natural -dimensional generalization of the -improper integral over infinite interval, and the integral is the natural -dimensional generalization of the -improper integral with singularities. However, neither nor effectively captures the relative information about . Furthermore, the weighted co-volume calculates some invalid volumes of form the perspective of the -starting point of . Therefore, we will focus on studying the asymptotic behavior of the weighted co-volume of .
Definition 5.
Let be the -starting point of -pseudo-cone , i.e., can be decomposed into the sum of a -asymptotic set and the -starting point , then we define the asymptotic weighted co-volume of by
Remark 6.
Here we consider this asymptotic weighted co-volume as a functional of two variables. Thus, if we fix a -asymptotic set , then is precisely a generalized function on the cone .
It is evident that the weighted volume of a -pseudo-cone serves the -dimensional generalization of the -improper integral over infinite interval. However, the -dimensional generalization of the -improper integral with singularities is more intricate, involving both the weighted co-volume and the asymptotic weighted co-volume . Moreover, the properties of the asymptotic weighted co-volume are superior to those of the weighted co-volume.
Lemma 12.
Let be a -asymptotic set and . If , is finite. If , the following holds:
Thus, the origin is the unique singularity of for .
Proof.
According to the definition of the asymptotic weighted co-volume, we have
If , since is continuous on and is compact, the integral is finite. Similar to Lemma 7 in [34], using (17), we obtain
Next, using the binomial expansion:
Since , we have for , which implies that
Thus, is finite.
If , similar to [34, p. 13] and Lemma 11, for we have
For , we have
Let , then . Thus,
It is easy to check that for . Therefore,
Moreover, it is not hard to prove that is continuous, that is, as , similarly to [34, p. 14]. ∎
Counterexample 3.
Let and . Then there exists some -asymptotic set such that .
Proof.
Choose a fixed cone and consider the weight function
where . Let be a -asymptotic set, and choose a -starting point . For , we have
According to the limit
there exists such that
for all . Thus,
For , due to
there exists a constant such that for all . Thus,
Therefore, if , the asymptotic weighted co-volume may be infinite, but it can also be finite. ∎
Proof of Theorem 2.
Let be a -pseudo-cone and let be a -asymptotic set with . According to Lemma 11, the weighted co-volume is infinite for ; as stated in Remark 2, can be either finite or infinite for . The behavior of is same as . By Remark 5, the weighted surface area measure can also be finite or infinite for . From Lemma 9, the weighted volume is finite for and infinite for . According to Lemma 12 and Remark 3, is finite for , but it may be finite or infinite for . Finally, combining these results with those in [34], we can derive Theorem 2, which summarizes the behavior of the weighted co-volume, surface area measure, and asymptotic weighted co-volume.
| finite | finite | finite | |||
| finite | finite | ||||
| finite | finite | finite | finite | ||
| finite or | finite or | finite or | finite or |
In the table above, the blue color indicates that there is some useful and interesting information. ∎
5 Integral formulas and convolution formulas
In Sections 3 and 4, we discussed several notable properties of the asymptotic -pseudo-cone. Based on these properties, we can explore the relationships between , , and . Firstly, we present the following results.
Lemma 13.
Let be a -pseudo-cone and . Then, there exist integral representations of the weighted co-volume of as follows:
| (20) | ||||
| (21) |
Proof.
Remark 7.
The integral formula analogous to (21) for the volume functional in the classical case can be established using approximations of convex polytopes (see e.g., [28, p. 275-276]). The study of the push-forward measure of the radial Gauss image was first undertaken by [16], utilizing the Gauss-Green formula for finite perimeter sets and various approximation techniques. In fact, the co-area formula of Federer [13] serves as a more powerful tool for these problems (see [28, chapter. 4] and [18, p. 170]). Generally, the volume formulas for general measures with continuous density have also been derived using the co-area formula, as demonstrated in [20]. In the case of -close sets, Schneider [30] utilized the volume formula for convex bodies in conjunction with approximation methods. Here, we also present a general version of the volume formula (21) utilizing the co-area formula.
Lemma 14.
Suppose . Let be a -pseudo-cone with its decomposition for the -asymptotic set and the starting point . If , we have
| (22) | ||||
If , we have
| (23) | ||||
Proof.
If , since , we have and . Thus,
If , we have
∎
According to the definition of the -th dual volume given in [22], the formula (20) implies that is finite, as follows.
Corollary 3.
For any , the -th dual volume is finite for every -pseudo-cone .
Proof.
Lemma 15.
Let be a -pseudo-cone with its decomposition for the -asymptotic set and the starting point . If , we have the following convolution formula:
| (24) |
In particular, if , we have
| (25) |
Proof.
Suppose . For , both and are finite. Noting that
we have
where the weight function can be extended to the whole space , making the convolution well-defined.
It is easy to verify the following property from the definition of , we omit the proof.
Lemma 16.
Let be a -pseudo-cone with its decomposition , where is the -asymptotic set and . If , then for any , we have
If is -smooth function on , then we have the following variational results:
Lemma 17.
Let be a -pseudo-cone with its decomposition , where is the -asymptotic set and . If and is -smooth function on , then for any , we have
| (26) |
In particular,
Proof.
Firstly, we observe that
then
On the other hand,
Taking the derivative with respect to , we obtain
which implies
Since is a -homogeneous function on , i.e.,
Differentiating both sides of the above formula with respect to at , we obtain
which gives
Thus, we have
Let , then
∎
Given a fixed -asymptotic set , is defined as a generalized function on . We can establish the following decay estimate for as it approaches infinity.
Lemma 18 (Decay estimate of the asymptotic weighted co-volume).
Let be a -pseudo-cone with its decomposition , where is the -asymptotic set and . If , then there exists a constant , depending only on , , and , such that
for sufficiently large . Therefore,
Proof.
Let . We choose a point , and denote and . Similar to Lemma 12, we can derive the following estimate by the Fubini theorem, the formula (17) and the binomial expansion theorem:
| (27) |
Since and , the last terms of -singular integral converge to zero, i.e.,
By the L’Hopital’s rule, we have
Thus, by the Squeeze Theorem, we have
| (28) | |||
| (29) |
Using this decay estimate, we obtain the following imperceptible formula:
Theorem 6.
Let be -smooth function on with . For any , the following formula holds:
Proof.
Let be a -asymptotic set. We claim that:
Since the weight function is a -smooth and -homogeneous function, is a non-negative continuous and -homogeneous function. By Lemma 9, we have
where a non-negative integrable function does not affect this result. According to the absolute value inequality, we have
Noting that , by the dominated convergence theorem, we have
Let . By the L’Hopital’s rule, Lemma 18, and formula (26), we have
which gives
This completes the proof. ∎
Remark 8.
Noting that the directional derivative of along may be positive or negative, as in the case of , the result in Theorem 6 indicates that its integral over must be negative.
6 The Brunn-Minkowski type inequality for -pseudo-cones
Let and be two -close sets. The co-sum of two -coconvex sets and is defined by , where is the usual Minkowski sum. The closeness of the co-sum operator is guaranteed by the complemented Brunn-Minkowski inequality for -coconvex sets, which has been studied by Khovanskiĭ and Timorin [19], as well as Milman and Rotem [25]. Schneider [30] established the equality condition for this inequality. Additionally, Milman and Rotem [25, p. 895-902] also explored the complemented Brunn-Minkowski inequality for star-shaped sets and radial sum. Inspired by their work, we aims to consider the asymptotic Brunn-Minkowski inequality for -pseudo-cones in this section.
For convenience, we define the radial sum of -pseudo-cones and as follows:
where is generally not a -pseudo-cone. The radial function of a -coconvex set is defined by , which is a locally Lipschitz continuous function on by Lemma 2. The radial sum of -coconvex sets and is defined by
Regarding the radial sum and the co-sum, we have the following result:
Lemma 19.
Let and be two -pseudo-cones. Then
In particular, for -coconvex sets , we have
Proof.
For each , we have and , then
Since is a -pseudo-cone by Corollary 8, for any , we have
Thus, we can conclude that
which implies
For -coconvex sets , we have
∎
Suppose that , we call a -pseudo-cone a -close set if
If and , then a -close set is just a -close set.
Proof of Theorem 3.
By Lemma 19, we have
with equality if and only if by the properties of continuous functions. Using the polar coordinates formula, we have
Since , by the Minkowski inequality for the -norm, we obtain
Equality holds if and only if and are dilates of each other. Note that if and are dilates of each other, then . Therefore, we have
where the two equalities hold if and only if and are dilates of each other. ∎
When and , we obtain the following corollary:
Corollary 4.
Let be two -coconvex sets. Then
Both equalities hold if and only if and are dilates of each other.
This corollary strengthens the complementary Brunn-Minkowski inequality from [30] and identifies its equality condition through a different approach. It is important to note that the key to establishing the equality condition is the closeness of the Minkowski sum of -pseudo-cones, which is guaranteed by our asymptotic theory and is completely independent of the methods used in [30].
The case of is satisfactory. However, for , Schneider [34] noted that the solution to the weighted Minkowski problem lacks uniqueness, which implies that Brunn-Minkowski type inequalities may not exist in this case. In fact, according to [25, Corollary 4.4], a Borel measure with a homogeneous density of degree satisfies the -complemented Brunn-Minkowski inequality
where and
Let , then and hence . Thus, it is evident that Brunn-Minkowski type inequality may not hold in this case. Moreover, for , the weighted co-volume functional is infinite for any -pseudo-cone, as established in Theorem 2. However, utilizing our asymptotic theory, we conjecture that the following Brunn-Minkowski type inequality holds. We also believe that the convolution formula in Theorem 6 will be instrumental in establishing the inequality. Asymptotic Brunn-Minkowski inequality for -pseudo-cones: Let be two -pseudo-cones with their -starting points , and let . If , then
7 The weighted Minkowski problem for
As an application of our asymptotic theory, we will consider the solutions to the weighted Minkowski problem in this section. First, we recall some notations from [34]. Let denote the distance of the -pseudo-cone from the origin, and let represent the spherical distance of from for . For , we define . According to [30], a set is -determined by the compact set if
Denote by the set of -pseudo-cones that are -determined by . Let be a positive continuous function. The Wulff shape associated with is defined by
which belongs to (See [22, 30, 34] for more details). For , using methods similar to those in [34], we have the following Lemmas 20-22:
Lemma 20 (see [34]).
Let be a nonempty compact set, and let . Let be continuous, and let be the Wulff shape associated with . Then
| (30) |
Lemma 21 (see [34], Upper bound estimate).
There exists a constant , depending only on and , such that every -close set with satisfies .
Lemma 22 (see [34], Lower bound estimate).
There exsts a number such that
Proof of Theorem 4.
The existence of a solution to the weight Minkowski problem will be divided into two steps as follows.
Step 1: Assume that is compact and that is a nonzero finite Borel measure on . We consider the functional defined by
| (31) |
where is the Wulff shape of . Suppose there exists an such that
where due to for every . By the variational formula (30), for each , we have
where due to and . Thus, the Euler-Lagrange equation of the functional is
| (32) |
where
Applying the Riesz representation theorem to the Euler-Lagrange equation (32), we have
Therefore, we need to show that the functional has maximum. Similar to Lemmas 7 and 8 in [34], for , the functional remains a -homogeneous continuous functional, so we have
where . For any , since is a -close set, by Lemma 21, we have for some constant . Combining Lemma 22 and Schneider’s selection theorem (see [33, Lemma 1]), we conclude that attains a maximum on .
Step 2: Now we assume that is a nonzero finite Borel measure on . Choose a number such that and a sequence of compact subsets of such that
Define measures by for each and every . From step 1, there exists a sequence of such that
with
Let , then . To apply the Blaschke selection theorem for the sequence , we need upper and lower bound estimates for the distances . By Lemma 21, we have with a constant independent of . Since
it follows that
Thus, is bounded from above. Choose a number such that
and we have . Then, by [33, Lemma 9], we conclude that for some constant depending only on and . Therefore, using the Blaschke selection theorem, there exists a -pseudo-cone such that as . Following the methods in [34], we find that
Using the formula (21), we have
By the continuity of the weighted co-volume, we have , which means is a -close set.
Next, we prove the uniqueness. Let satisfy
By the weighted Brunn-Minkowski inequality (2), the function
is a negative convex function, which implies . Applying the variational formula (30), we have
Thus, we obtain
By switching the roles of and , we also find that
This shows that
Consequently, we have
which shows that the negative convex function . By the equality condition of the inequality (2) and the -homogeneity of the weighted surface area measure, we conclude that . ∎
References
- [1]
- [2] S. Artstein-Avidan, Dualities, measure concentration and transportation, Lecture Notes in Math. 2332, Springer, Cham, (2023), 159–231.
- [3] S. Artstein-Avidan, V.D. Milman, A new duality transform, Comptes Rendus Math., 346 (2008), 1143–1148.
- [4] S. Artstein-Avidan, V.D. Milman, The concept of duality in convex analysis, and the characterization of the Legendre transform, Ann. of Math., 169 (2009), 661–674.
- [5] S. Artstein-Avidan, V.D. Milman, Hidden structures in the class of convex functions and a new duality transform, J. Eur. Math. Soc., 13 (2011), 975–1004.
- [6] S. Artstein-Avidan, S. Sadovsky, K. Wyczesany, A zoo of dualities, J. Geom. Anal., 33 (2023), 1–40.
- [7] I.J. Bakelman, Variational problems and elliptic Monge-Ampère equations, J. Differ. Geom., 18 (1983), 669-699.
- [8] K. Böröczky, R. Schneider, A characterization of the duality mapping for convex bodies, Geom. Funct. Anal., 18 (2008), 657–667.
- [9] B. Choi, K. Choi, P. Daskalopoulos, Convergence of Gauss curvature flows to translating solitons, Adv. Math., 397 (2022), 30 pp.
- [10] B. Choi, K. Choi, P. Daskalopoulos, Uniqueness of ancient solutions to Gauss curvature flow asymptotic to a cylinder, J. Differ. Geom., 127 (2024), 77–104.
- [11] K. Choi, P. Daskalopoulos, L. Kim, K. A. Lee, The evolution of complete non-compact graphs by powers of Gauss curvature, J. Reine Angew. Math., 757 (2019), 131–158.
- [12] K.S. Chou, X.-J. Wang, Minkowski problems for complete noncompact convex hypersurfaces, Topol. Methods Nonlinear Anal., 6 (1995), 151–162.
- [13] H. Federer, Geometric Measure Theory, Springer, Berlin, (1969).
- [14] M. Fradelizi, D. Langharst, M. Madiman, A. Zvavitch, Weighted Brunn-Minkowski Theory \@slowromancapi@: On weighted surface area measures, J. Math. Anal. Appl., 529 (2024), 1–30.
- [15] R.J. Gardner, G. Zhang, Affine inequalities and radial mean bodies, Amer. J. Math., 120 (1998), 505–528.
- [16] Y. Huang, E. Lutwak, D. Yang, G. Zhang, Geometric measures in the dual Brunn-Minkowski theory and their associated Minkowski problems, Acta Math., 216 (2016), 325–388.
- [17] Y. Huang, J. Liu, Noncompact -Minkowski problems, Indiana Univ. Math. J., 70 (2021), 855–880.
- [18] D. Hug, W. Weil, Lectures on Convex Geometry, Springer, Cham, (2020).
- [19] A. Khovanskiĭ, V. Timorin, On the theory of coconvex bodies, Discrete Comput. Geom., 52 (2014), 806–823.
- [20] L. Kryvonos, D. Langharst, Weighted Minkowski’s existence theorem and projection bodies, Trans. Amer. Math. Soc., 376 (2023), 8447–8493.
- [21] D. Langharst, E. Putterman, M. Roysdon, D. P. Ye, On higher-order weighted projection body operator and related inequalities, (2023), arXiv: 2305.00479v1.
- [22] N. Li, D. Ye, B. Zhu, The dual Minkowski problem for unbounded closed convex sets, Math. Ann., 388 (2024), 2001–2039.
- [23] G.V. Livshyts, An extension of Minkowski’s theorem and its applications to questions about projections for measures, Adv. Math., 356 (2019), 1–40.
- [24] E. Lutwak, The Brunn-Minkowski-Firey Theory \@slowromancapi@: Mixed Volumes and the Minkowski Problem, J. Differ. Geom., 38 (1993), 131–150.
- [25] E. Milman, L. Rotem, Complemented Brunn-Minkowski inequalities and isoperimetry for homogeneous and non-homogeneous measures, Adv. Math., 262 (2014), 867–908; Corrigendum: Adv. Math., 307 (2017), 1378–1379.
- [26] A. Pogorelov, An analogue of the Minkowski problem for infinite complete convex hypersurfaces, Dokl. Akad. Nauk SSSR, 250 (1980), 553–556.
- [27] A. Rashkovskii, Copolar convexity, Ann. Pol. Math., 120 (2017), 83–95.
- [28] R. Schneider, Convex bodies: the Brunn-Minkowski theory. 2nd edn., Encyclopedia of Mathematics and Its Applications, vol. 151, Cambridge University Press, Cambridge, (2014).
- [29] R. Schneider, Convex cones–geometry and probability, Lecture Notes in Mathematics 2319, Springer, Cham, (2022).
- [30] R. Schneider, A Brunn-Minkowski theory for coconvex sets of finite volume, Adv. Math., 332 (2018), 199–234.
- [31] R. Schneider, Conic support measures, J. Math. Anal. Appl., 471 (2019), 812–825.
- [32] R. Schneider, Minkowski type theorems for convex sets in cones, Acta Math. Hungar., 164 (2021), 282–295.
- [33] R. Schneider, Pseudo-cones, Adv. Appl. Math., 155 (2024), 1–22.
- [34] R. Schneider, A weighted Minkowski theorem for pseudo-cones, Adv. Math., 450 (2024), 26pp.
- [35] R. Schneider, Weighted cone-volume measures of pseudo-cones, (2024), arXiv:2407.05095v1.
- [36] R. Schneider, The copolarity of pseudo-cones, (2024), arXiv:2407.17320v1.
- [37] V. Semenov, Y. Zhao, The growth rate of surface area measure for noncompact convex sets with prescribed asymptotic cone, (2024), arXiv:2409.18699v1.
- [38] J. Urbas, The equation of prescribed Gauss curvature without boundary conditions, J. Differ. Geom., 20 (1984), 311–327.
- [39] J. Urbas, Complete noncompact self-similar solutions of Gauss curvature flows \@slowromancapi@. Positive powers, Math. Ann., 311 (1998), 251–274.
- [40] X. Wang, B. Zhu, The decompositions of geometric measures \@slowromancapi@: the singularity of the curvature measures of convex body, (2024), preprint.
- [41] K. Wyczesany, Topics in high-dimensional geometry and optimal transport, PhD thesis, University of Cambridge, (2020), 141pp.
- [42] Y. Xu, J. Li, G. Leng, Dualities and endomorphisms of pseudo-cones, Adv. Appl. Math., 142 (2023), 1–31.
- [43] J. Yang, D. Ye, B. Zhu, On the Brunn-Minkowski theory and the Minkowski problem for -coconvex sets, Int. Math. Res. Not., 2023 (2022), 6252–6290.
- [44] N. Zhang, The Minkowski problem for the non-compact convex set with an asymptotic boundary condition, (2024), arXiv:2402.12802v1.
Xudong Wang, [email protected]
School of Mathematics and Statistics, Shaanxi Normal University
Xi’an, 710119, China
Wenxue Xu, [email protected]
School of Mathematics and Statistics, Southwest University
Chongqing, 400715, China
Jiazu Zhou, [email protected]
School of Mathematics and Statistics, Southwest University
Chongqing, 400715, China
Baocheng Zhu, [email protected]
School of Mathematics and Statistics, Shaanxi Normal University
Xi’an, 710119, China