Aslamazov Larkin Conductivity in Weyl Semimetals
Abstract
The Aslamazov-Larkin conductivity (ALC) in the Weyl semi-metals is calculated both for Type-I and Type II for different dimensionality and magnetic fields. The ALC strongly depends on the tilt parameter of the dispersion relation cone. While the 3D and 2D the Aslamazov -Larkin conductivity slightly depends on tilt parameter in Type-I phase and increases in the Type-II phase the 1D ALC decreases in Type-I phase up to zero close to border between Type-I and Type-II phases. Results are discussed in light of the resent experiments on the layered Weyl semi-metals. It is concluded the one dimensional AL conductivity well explained the experimental data.
pacs:
PACS: 74.25.Fy, 74.40.+k,74.40.-n, 74.70.-bI Introduction.
Dispersion relation near Fermi surface in recently synthesized two and three dimensional Weyl (Dirac) (WSM/DSM) semi-metals one ,two ,three is qualitatively distinct from conventional metals, semi - metals or semiconductors in which all the bands are parabolic. In type I Weyl semi-metals (WSM), the band inversion results in Weyl points in low-energy excitations being anisotropic massless ”relativistic” fermions with dispersion relation of these semimetals looks as a tilted Dirac cone. In Type I WSM/DSM the tilt angle of the cone is smaller than some critical value four while recently discovered layered transition-metal dichalcogenides is defined as type-II WSM/DSM five . six . In this latter case, the Dirac cone exhibits a strong tilt, so that it can be characterized by a nearly flat band at Fermi surface. The type-II WSM also exhibit exotic topological properties different from the type-I ones, such anti-chiral effect of the chiral Landau level and novel quantum oscillations. Graphene is a prime example of the type I WSM, while materials, like layered organic compound were long suspected to be a 2D type-II Dirac fermions. Several materials were observed to undergo the type- I to II transition while doping or pressure is changed seven ,eigth ,nine . Theoretically physics of the topological (Lifshitz) phase transitions between the type I to type II Weyl semi-metals were considered in the context of superfluid phase in , layered organic materials in 2D and 3D Weyl semi-metals ten ,elleven ,twelve . The pressure modifies the spin orbit coupling that in turn determines the topology of the Fermi surface of these novel materials 13 .
Many Weyl and Dirac materials are known to be superconducting. A detailed study of superconductivity in WSM/DSM under hydrostatic pressure revealed a curious dependence of critical temperature of the superconducting transition on pressure. In particular the critical temperature in some of these systems like show a sharp maximum as a function of pressure 14 . This contrasts with generally smooth dependence on pressure in other superconductors (not suspected to be Weyl materials) like cuprates. Magnetic properties in these topological superconductors are also very different from that in conventional superconductors. In particular the Abrikosov parameter used to distinguish between the superconductivity of the first from the second type depends on the cone tilt and may totally change magnetic properties varying from first kind superconductor (like clean metals) to the second kind. The critical fields, coherence lengths magnetic penetration depths and the Ginzburg number characterizing the strength of fluctuations strongly depend on cone tilt 15 ; 16 . It reveals an extremely important relation between the cone title and fluctuation in WSM/DSM superconductors 17 . We begin with a brief review of studies of fluctuations in superconductors. The subject was initiated in the work of Aslamazov and Larkin 18 calculated the conductivity of fluctuating Cooper pairs in zero magnetic field. Maki and Thomson 19 ; 20 ; 21 included effects of electron scattering off the fluctuations. It was found that there is another badly divergent contribution known as anomalous Maki-Thomson correction. Physically, this correction is connected with the coherent scattering of the electrons by the impurities and analogous to the weak localization correction. The divergence can be removed by introducing a pair-breaking rate. It should be noted that, the experimental results at temperature close to the critical can be described by the Aslamazov-Larkin term only. This suggests that the pair-breaking rate is relatively large in real superconductors. Later, Thomson and Maki returned to the issue and evaluated fluctuation correction to the normal conductivity in finite fields 22 , 23 . A theory of transport phenomena in the fluctuation region in the dirty, clean and super clean limits was developed by Aronov et al. 24 . Their consideration was based on the Ginzburg-Landau equations and, thus, is applicable for relatively small fields. Experimentally the broadened of the normal-to-superconductivity transition curve caused by the superconducting fluctuations was studied in a lot of WSM/DSM materials while the 2D Aslamazov Larkin conductivity was detected in 3D WSM material 25 . In the present paper we study of Aslamazov-Larkin conductivity (ALC) in Weyl/Dirac semimetals. The focus generally is on the dependence of the ALC in the cone tilt parameter and consequently on the ALC in the vicinity of the transition from type-I to type-II WSM.
II Model
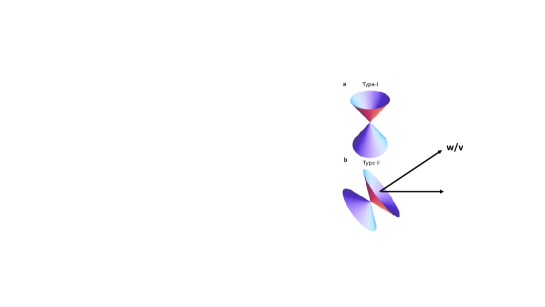
Since the Weyl material typically possesses several sublattices the effect of the topological transition on superconductivity was exemplified using the simplest possible model with just two sublattices. The band structure near the Fermi level of a 3D layered Weyl semi-metal is well captured by the non-interacting massless Weyl dispersion relation with the ”in plane” Fermi velocity (assumed to be isotropic in the plane) and conventional parabolic term on direction26 ,27 ,28 ,29 (see Fig.1) and described by the Hamiltonian
| (1) | |||||
Here is the chemical potential, , are Pauli matrices in the sublattice in the sublattice space in the WSM layers, with just two sublattices denoted by and is spin projection. The velocity vector defines the tilt of the Dirac dispersion cone. The graphene - like dispersion relation for represents the type I Weyl semi-metal, while for the velocity exceeding , the material becomes a type II Weyl semi - metal.
We restrict our self to the case of just one left handed and one right handed Dirac points, typically but not always separated in the Brillouin zone. Generalization to include the opposite chirality and several ”cones” is straightforward. We assume that different valleys are paired independently and drop the valley indices.
III Ginzburg-Landau theory.
The effective electron-electron attraction due to the electron - phonon attraction opposed by Coulomb repulsion (pseudopotential) mechanism creates pairing below . Assuming the singlet s-channel interaction with essentially local interaction in the layers one obtains the set of Gor’kov equations 27 and their microscopic Ginzburg-Landau expansion 28 , 29 for arbitrary Dirac cone tilt parameter in the form:
| (2) |
Where
The index , is the DOS for layered graphene , dimensionless constant is the electron-electron strength for zero tilt parameter We use below units with . The tunneling of the electrons moving between the superconducting layers via dielectric streak described by the effective mass of the electrons moving along the z axis. Within tight binding model the effective mass is estimated as
| (3) |
where is the mass of free electron, is the distance between layers of thickness , see Fig.1. The GL coefficients in Eq.2 have been calculated for all values of cone tilt parameter in our Ref.29 . In particular for the type I WSM, , in which the Fermi surface is a closed ellipsoid and it is given by:
| (4) |
In the type II phase, , the Fermi surface becomes open, extending over the Brillouin zone, and the corresponding expression is:
| (5) |
Here is an ultraviolet cut off parameter , where is an interatomic spacing, is the phonon frequency around the Fermi energy.
The critical temperature has the sharp spike at the border between Type-I and Type-II states at where the topology of the Fermi surface undergoes the Lifshitz 2.5 type transition 28 .
IV Aslamazov-Larkin Conductivity.
Using the standard time dependent Ginzburg Landau equations 30 with the external correlated random force responsible for thermal fluctuations:
| (6) |
| (7) |
where is the relaxation constant is the electric potential, is the vector potential, is the normal conductivity.
Taking order parameter in the form where is the order parameter in the absence of the electric field, and substituting it into Eqs.6,7 one obtains in the case of zero magnetic field for the dc superconducting current:
| (8) |
where
| (9) |
Using 8 one obtains for the Aslamazov-Larkin conductivity:
| (10) |
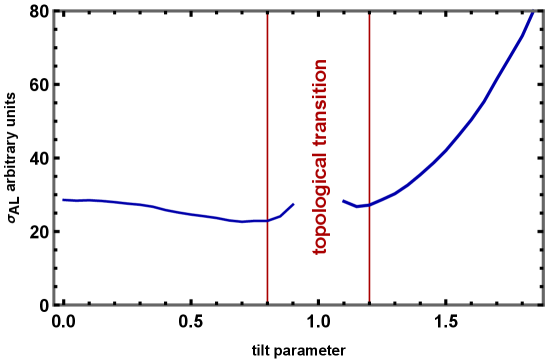
Performing integration one obtains for different dimensionality. For 3D case the tilt and temperature dependence of the ALC has the form:
| (11) |
Where
The reduced ALC is shown in Fig.2 and demonstrates strong dependence on the tilt parameter in Type-II phase.
Here is the film thickness and is the cross-section of the wire, .
V Aslamazov-Larkin conductivity in magnetic field.
The ALC in magnetic field was calculated earlier for both for isotropic system Terley and for layered structure with Josephson interaction between the layers Varlamov but these results cannot be used in WSM with a strong anisotropies of the coherence lengths. In our case with the external magnetic field directed parallel to the axis and the vector-potential , the ac ALC can be calculated from the dissipative-fluctuation theorem in the Kubo Kubo form:
| (13) |
Here is the Fourier transform of the current density 7 with the fluctuating order parameter in the form:
| (14) |
where are the normalized eigenfunction of the electron in magnetic field
| (15) |
with the eigenvalues
| (16) |
Here is the Hermit polynome,
| (17) | |||||
| (18) | |||||
| (19) |
where
| (20) |
Using the random force correlator in the right side of the Eq.(6) one obtains for the correlator of the order parameter where
Substituting this correlator into the Kubo relation for conductivity and performing the integrations one obtains
for ALC in magnetic field
| (21) |
It gives in the limit of a small magnetic fields where is the upper critical magnetic field, is the unit flux
| (22) |
In a strong magnetic field ALC diverges close to the . In this case the main term in the sum is the second ones with 21
| (23) |
and diverges at the coexistence line.
VI Discussion and conclusions.
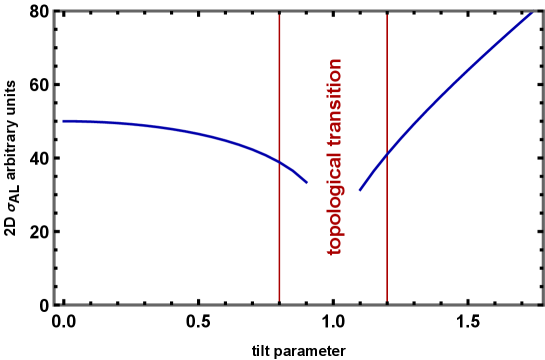
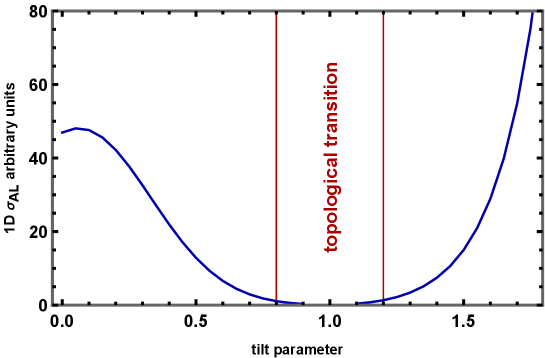
The Aslamazov-Larkin conductivity in the Weyl metals is described by the Eqs. 11,12 in the absence of the magnetic field and 21,22, 23 in the presence of the magnetic field for different dimensionality and demonstrate typical for AL conductivity temperature and field dependences. However, the coherence lengths are the cone slope dependent (see Figs.2-4 and Fig. 6) demonstrated the main results. While for 3D and 2D the Aslamazov -Larkin conductivity demonstrate similar dependence on the tilt parameter (weak variation in Type-I phase and essential increase in the Type-II phase, the ALC in 1D looks very different significantly reduces close to the border between Type-I and Type-II phases.
As it was predicted in Ref. seven , eigth , nine the static pressure can control the cone slope parameter in Weyl semimetals. In particular, the type-I WSM realized at large range of the pressures, while the type-II appears at low pressures. Recently, the resistance in the WSM was measured in the 3D layered material 14 .
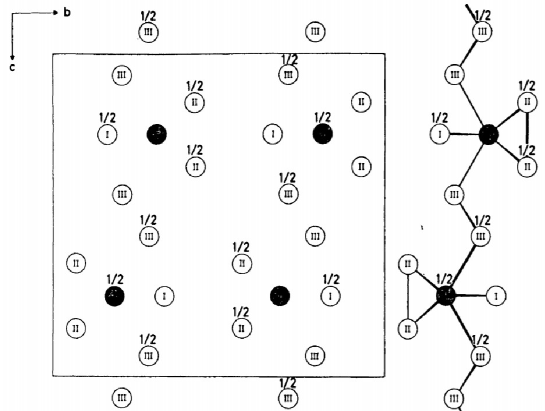
The crystal structure of has been determined by powder X-ray diffraction experiments 13 . Trigonal prismatic chains of run along the a axis, and these prismatic chains are linked via parallel zigzag chains of Te atoms along the c axis to form a 2D sheet of in the ac plane (along the z direction in our notation). The sheets of stack along the b axis, forming a layered structure 14 where metallic atoms are surrounded by dielectric as it is shown in Fig. 5 ( 31 ).
This material shows a well pronounced dependence of the resistivity on the static pressure. In particular, it was established that below the type-I WSM is realized while the type- II is realized above . In the range the type-II and type-I Dirac cones coexist. The critical temperature non-monotonic depending on the pressure allows to assume that the pressure is directly related to the cone slope parameter. It is naturally to assume that the Type-II WSM is established at large pressure and small .
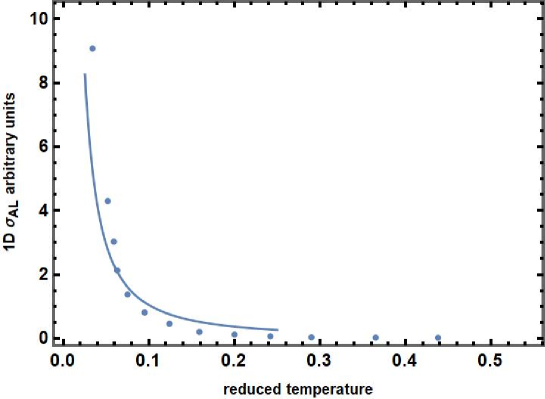
The resistivity was measured in the direction perpendicular to the layers. The comparison with the theory is presented in Fig.6 and demonstrates a good agreement with 1D ALC formulae. It shows that the conductivity obeyed the 1D AL Eq. 12 (see Fig.4). Measurements of the magnetoresistance when the current flows perpendicular to the layers (direction) show that its temperature dependence is well described by the one-dimensional formula for Aslamazov-Larkin fluctuations. This indicates that the current flows along the chains of the metal atoms forming one-dimensional channels crossing the layers.
Acknowledgements.
I am grateful Prof. Rosenstein for his attention and assistance.
References
- (1) Weng H., Dai X., and Fang Z., Topological semimetals predicted from first-principles calculations, J. Phys. Cond. Matter. 2016 28 303001; Bansil A. ,H. Lin, and Das T. , Topological band theory 2016 Rev. Mod. Phys. 88, 021004; Weng H. , Fang C. ,Fang Z. ,Bernevig B. A. , and Dai X., Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides, 2015 Phys. Rev. X 5, 011029; Lv B. Q. et al., Experimental Discovery of Weyl Semimetal TaAs, 2015 Phys. Rev. X 5, 031013; S.-Y. Xu et al., Discovery of a Weyl fermion semimetal and topological Fermi arcs, 2015 Science 349, 613.
- (2) Huang L. ,McCormick T. M. ,Ochi M. ,Zhao Z. ,Suzuki M.-T. ,Arita R. ,Wu Y. ,Mou D. ,Cao H. ,Yan J. ,Trivedi N. & Kaminski A. , Spectroscopic evidence for a type II Weyl semimetallic state in , 2016 Nature Materials 15 1155; Wang Y., et al, Gate-tunable negative longitudinal magnetoresistance in the predicted type-II Weyl semimetal 2016 Nature Com. 7, 13142; Cao J. ,Liang S. , Zhang C. ,Liu Y. , Huang J. ,Jin Z. ,Che Z.-G. , Wang Z.,Wang Q. ,Zhao J. ,Li S. , Dai X. , Zou J. ,Xia Z. , Li L. and Xiu F. , Landau level splitting in under high magnetic fields, 2015 Nat. Comm. 6, 7779; Yu W. , Jiang Y. ,Yang J. ,Dun Z.L. ,Zhou H.D. ,Jiang Z. , Lu P. and Pan W. Quantum Oscillations at Integer and Fractional Landau Level Indices in Single-Crystalline , 2016 Scientific Rep. 6, 35357.
- (3) Lv Y.-Y. et al., Experimental Observation of Anisotropic Adler-Bell-Jackiw Anomaly in Type-II Weyl Semimetal Crystals at the Quasiclassical Regime, 2017 Phys. Rev. Lett. 118, 096603;Udagawa M. and Bergholtz E. J., 2016 Field-Selective Anomaly and Chiral Mode Reversal in Type-II Weyl Materials, Phys. Rev. Lett. , 117 086401.
- (4) Li D. , Rosenstein B.,Shapiro B. Ya. , and Shapiro I. , Effect of the type-I to type-II Weyl semimetal topological transition on superconductivity, 2017 Phys. Rev. B 95, 094513.
- (5) Yu Z.-M. ,Yao Y. , and Yang S. A. , Predicted Unusual Magnetoresponse in Type-II Weyl Semimetals 2016 Phys. Rev. Lett. 117, 077202; O’Brien T. E. , Diez M. , and J. Beenakker C. W. , Magnetic Breakdown and Klein Tunneling in a Type-II Weyl Semimetal, 2016 Phys.Rev. Lett. 116, 236401.
- (6) Soluyanov A. A. ,Gresch D. ,Wang Z. ,Wu Q. ,Troyer M. ,Dai X. &Bernevig B. A. , Type-II Weyl semimetals, 2015 Nature 527, 495.
- (7) Katayama S.,Kobayashi A. ,Suzumura Y. , Pressure-Induced Zero-Gap Semiconducting State in Organic Conductor -(BEDT-TTF)2I3 Salt 2006 J. Phys. Soc. Japan 75, 054705; Zhang J.-L. et al. Superconductivity of topological matters induced via pressure, 2012 Front. Phys., 7, 193;Goerbig M. O. ,Fuchs J. -N. ,. Montambaux G.,Piéchon F. , Tilted anisotropic Dirac cones in quinoid-type graphene and -(BEDT-TTF)2I3 2008 Phys. Rev. B 78, 045415; Hirata M., Ishikawa K., Miyagawa K.,, Tamura M., Berthier C, Basko D., Kobayashi A., Matsuno G., & Kanoda K, Observation of an anisotropic Dirac cone reshaping and ferrimagnetic spin polarization in an organic conductor, 2016 Nature Commun. 7, 12666.
- (8) Zhou Y. et al, Pressure-Induced New Topological Weyl Semimetal Phase in TaAs, 2016 Phys. Rev. Let., 117, 146402; Zhou Y. et al, 2016 Pressure-induced superconductivity in a three-dimensional topological material PNAS 113 2904 ;Qi Y. ,Shi W. ,Naumov P. G. ,Kumar N. ,Schnelle W. ,Barkalov O. ,Shekhar C. , Borrmann H.,Felser C. ,Yan B. , and Medvedev S. A. , Pressure-driven superconductivity in the transition-metal pentatelluride 2016 Phys. Rev. B 94, 054517.
- (9) Ruan J. ,Jian S.-K. ,Yao H. ,Zhang H. , Zhang S.-C. &Xing D. , Symmetry-protected ideal Weyl semimetal in -class materials, 2016 Nature Com. 7 11136; Qi Y et al Superconductivity in Weyl semimetal candidate 2016 Nat. Commun. 7 11038.
- (10) Monteverde M. ,Goerbig M. O. Auban-Senzier, P., Navarin F. , Henck H. , Pasquier C. R. , Mèziére C. , and Batail P. Coexistence of Dirac and massive carriers in under hydrostatic pressure 2013 Phys. Rev B 87, 245110.
- (11) Sun F. and Ye J. , Type-I and type-II Weyl fermions, topological depletion, and universal subleading scaling across topological phase transitions 2017 Phys. Rev. B 96, 035113.
- (12) Sun Y. ,Wu S.-C. ,Ali M. N. ,Felser C. , and Yan B. , Prediction of Weyl semimetal in orthorhombic 2015 Phys. Rev. B 92, 161107(R);
- (13) Zhang K and Volovik G.E. ,Lifshitz transitions via the type-II dirac and type-II Weyl points, 2017 JETP Lett.105, 519 ; Xu Y. ,Zhang F. , and Zhang C. , Structured Weyl Points in Spin-Orbit Coupled Fermionic Superfluids, 2015 Phys. Rev. Lett., 115, 265304.
- (14) Liu Y. et al. Superconductivity in across weak to strong topological insulator transition induced via pressures, 2017 Scientific Reports, 7 44367.
- (15) Rosenstein B. , Shapiro B. Ya., Li D. , and Shapiro I. , Upper critical magnetic field in superconducting Dirac semimetal 2018 Europhys. Lett 124 27004.
- (16) Shapiro B.Ya. , Shapiro I , Li D , Rosenstein B , Type I superconductivity in Dirac materials 2018 J. Phys.: Condens. Matter 30 335403.
- (17) Rosenstein B , Shapiro B.Ya. , Li D ,Shapiro I , Magnetic properties of type-I and type-II Weyl semimetals in the superconducting state 2018 Phys. Rev. B 97, 144510.
- (18) Galitski V. and Larkin A.I. , Superconducting fluctuations at low temperature 2001 Phys. Rev. B 63, 174506.
- (19) Aslamazov L. G. and Larkin A. I. , Effect of fluctuations on the properties of a superconductor above the critical temperature 1968 Fiz. Tverd. Tela 10, 1104 [Sov. Phys. Solid State 10, 875].
- (20) Maki K. , Critical Fluctuation of the Order Parameter in a Superconductor. 1968 Prog. Theor. Phys. 40, 193.
- (21) Thomson R. S. , Microwave, Flux Flow, and Fluctuation Resistance of Dirty Type-II Superconductors, 1970 Phys. Rev. B 1, 327.
- (22) Hikami S. and Larkin A. I. , Magnetoresistance of high temperature superconductors, 1988 Mod. Phys. Lett. B 2, 693.
- (23) Ami S. and Maki K. ,Fluctuation-induced electric conductivity in dirty type-II superconductors 1978 Phys. Rev. B 18 4714.
- (24) Aronov A. G. ,Hikami S. andLarkin A. I. , Gauge invariance and transport properties in superconductors above 1995 Phys. Rev. B 51, 3880.
- (25) Huang C. et al Proximity-induced surface superconductivity in Dirac semimetal 2019 Nature Communs. 10 2217.
- (26) Li D, Rosenstein B, Shapiro B Ya and Shapiro I Strong magnetic field induces superconductivity in a Weyl semimetal, 2017 Phys.Rev. B 96 224517.
- (27) Alidoust M, Halterman K and Zyuzin A A Superconductivity in type-II Weyl semimetals 2017 Phys. Rev. B 95 155124.
- (28) Li D, Rosenstein B, Shapiro B Ya and Shapiro I., Effect of the type-I to type-II Weyl semimetal topological transition on superconductivity, 2017 Phys.Rev. B 95 094513;.
- (29) Li D, Rosenstein B, Shapiro B Ya and Shapiro I Quantum critical point in the superconducting transition on the surface of a topological insulator, 2014 Phys.Rev. B 90 054517.
- (30) Kopnin N. , 2001 Theory of Nonequillibrium Superconductivity, Clarendon Press, Oxford, p. 18.
- (31) Tilley D. R. and Parkinson J. B. Theory of resistive anomaly in a superconductor above a second-order critical magnetic field 1969 J. Phys. C: Solid State Phys. 2 2175.
- (32) Larkin A. and Varlamov A., 2007 Theory of fluctuations in Superconductors, Clarendon Press, Oxford, p.34.
- (33) Kubo R. ,Ichimura H. ,Usui T. , Hashitsume N. Statistical Mechanics, North-Holland Personal Library 1st Edition p.400.
- (34) Furuseth S. ,Brattas L. and Kjekshus A. , 1973 Crystal Structure of Acta Chemica Scandinavica, 27 2367.