Area-Optimal Simple Polygonalizations: The CG Challenge 2019

Erik D. Demaine [email protected] 0000-0003-3803-5703 CSAIL, MITCambridge, MAUSA , Sándor P. Fekete [email protected] 0000-0002-9062-4241 Department of Computer Science, TU BraunschweigBraunschweigGermany , Phillip Keldenich [email protected] 0000-0002-6677-5090 Department of Computer Science, TU BraunschweigBraunschweigGermany , Dominik Krupke [email protected] 0000-0003-1573-3496 Department of Computer Science, TU BraunschweigBraunschweigGermany and Joseph S. B. Mitchell [email protected] 0000-0002-0152-2279 Department of Applied Mathematics and Statistics, Stony Brook UniversityStony Brook, NYUSA

Abstract.

We give an overview of theoretical and practical aspects of finding a simple polygon of minimum (Min-Area) or maximum (Max-Area) possible area for a given set of $n$ points in the plane. Both problems are known to be $\mathcal{NP}$ -hard and were the subject of the 2019 Computational Geometry Challenge, which presented the quest of finding good solutions to more than 200 instances, ranging from $n=10$ all the way to $n=1,000,000$ .

^†^†copyright: acmcopyright^†^†journal: JEA^†^†journalvolume: 99^†^†journalnumber: 99^†^†article: 99^†^†publicationmonth: 13^†^†ccs: Theory of computation Design and analysis of algorithms^†^†ccs: Theory of computation Computational Geometry

1. Introduction

1.1. The Computational Geometry Challenge

The “CG:SHOP Challenge” (Computational Geometry: Solving Hard Optimization Problems) originated as a workshop at the 2019 Computational Geometry Week (CG Week) in Portland, Oregon in June, 2019. The goal was to conduct a computational challenge competition that focused attention on a specific hard geometric optimization problem, encouraging researchers to devise and implement solution methods that could be compared scientifically based on how well they performed on a database of instances. While much of computational geometry research has targeted theoretical research, often seeking provable approximation algorithms for $\mathcal{NP}$ -hard optimization problems, the goal of the CG Challenge was to set the metric of success based on computational results on a specific set of benchmark geometric instances. The 2019 CG Challenge focused on the problem of computing simple polygons whose vertices were a given set of points in the plane.

A tangible outcome is a new type of special issue, presented in this volume: a series of papers focusing on algorithm engineering methods for one difficult optimization problem. In this survey, we provide background and foundations of the underlying problem and give an overview of the results and contributions.

1.2. The 2019 Challenge Problem: Polygonizations of Optimal Area

The Traveling Salesman Problem (TSP) is one of the classic optimization problems: For a given set of locations and pairwise distances, find a shortest roundtrip that visits each position exactly once and returns to the start. In a geometric setting, in which locations correspond to a given set $P$ of $n$ points in the plane, and distances between points are induced by the Euclidean metric, it is a straighforward consequence of the triangle inequality that an optimal tour corresponds to a simple polygon $\mathcal{P}$ with vertex set $P$ , such that $\mathcal{P}$ has minimum total perimeter length.

This geometric motivation makes it natural to consider simple polygons with a given set of vertices that minimize another basic geometric measure: the enclosed area. This was considered in the past in the context of surface reconstruction, e.g., by O’Rourke (O’Rourke, 1980); as sketched in Section 2, there is also a close connection to point separation, which has gained importance in Artificial Intelligence. The same context has also raised interest in the corresponding maximization problem: For a given set $P$ of $n$ points in the plane, find a simple polygon $\mathcal{P}$ with vertex set $P$ of maximum possible area. In the following, we refer to these two problems as Min-Area and Max-Area, respectively.

Problem: Min-Area and Max-Area

Given: A set $P$ of $n$ points in the plane.

Goal: A simple polygon with vertex set $P$ of minimum (Min-Area) or maximum (Max-Area) possible enclosed area.

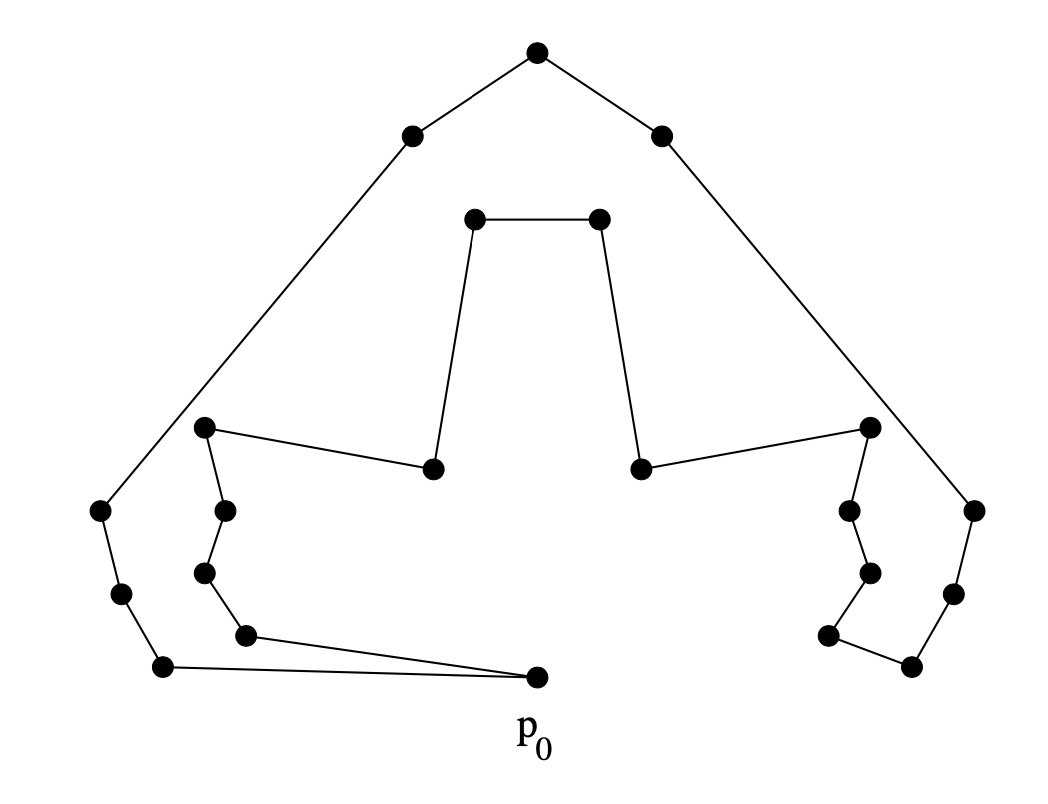
There are a number of features that make these problems suitable for optimization challenges, based on notable similarities to and differences from the TSP. As shown by Fekete (Fekete, 1992; Fekete and Pulleyblank, 1993; Fekete, 2000), both Min-Area and Max-Area are $\mathcal{NP}$ -hard; however, while membership in $\mathcal{NP}$ for the Euclidean TSP is a long-standing, famous open problem (e.g., Problem #33 in The Open Problems Project (Demaine et al., 2001)), it is straightforward for area optimization, so issues of numerical stability and checking vailidity of solutions do not come into play. On the other hand, edges in a polygon with small area need not be short, as shown in Figure 1. This makes it challenging to restrict potential neighbors of a point in a good polygonization, increasing the difficulty of employing local search methods for efficient algorithms. This explains an apparent practical distinction to the TSP: While provably optimal solutions for TSP benchmark instances of considerable size have been known for a while, exact methods for area optimization appear more elusive.

Refer to caption — Figure 1. A point set $P$ and its only minimum-area polygon $\mathcal{P}$ , containing several long edges. (Example from (Fekete, 1992, 2000).)

1.3. Related Work

1.3.1. History and Background

The origins of the problem of finding area-optimal polygons can be traced back at least to the early days of Computational Geometry (O’Rourke (O’Rourke, 1980) in 1980). Resolving the complexity was posed by Suri in 1989 at CCCG, and restated in a different context by Mitchell (Mitchell, 1993) and Mitchell and Suri (Mitchell and Suri, 1995).

Studying the set of possible polygonizations is of great interest in various applications (Aichholzer et al., 2002; Zhu et al., 1996; Ackerman et al., 2009; Abellanas et al., 1993; Arkin et al., 2003). Auer and Held (Auer and Held, 1996) gave methods for generating random polygonizations. O’Rourke and Suri (O’Rourke et al., 2017) raised the question of estimating the number of polygonizations as a function of the number $n$ of points. At this point, this is known to lie between $4.642^{n}$ (Garcıa et al., 2000) and $56^{n}$ (Sharir et al., 2013).

1.3.2. Complexity

Fekete (Fekete, 2000, 1992) gave a proof of $\mathcal{NP}$ -completeness for both problems, based on a reduction from Hamiltonicity of Planar Cubic Directed Graphs, and generalized this proof to higher dimensions: For any fixed $1\leq k\leq d$ and $2\leq d$ , it is $\mathcal{NP}$ -hard to find the polyhedron with $k$ -dimensional faces of minimum total volume for given vertices in $d$ -dimensional space. He also showed that no polynomial-time approximation scheme (PTAS) exists for Min-Area and presented a $\frac{1}{2}$ -approximation algorithm for Max-Area (Fekete and Pulleyblank, 1993; Fekete, 1992). Moreover, he proved that the $\mathcal{NP}$ -hardness of the minimization problem also applies for higher dimensions. More specifically he showed that for given $1\leq k\leq d$ and $2\leq d$ it is $\mathcal{NP}$ -hard to find the minimal volume polyhedron with $k$ -dimensional faces for given vertices.

1.3.3. Heuristics

Recent work was mainly focused on finding new heuristics for both Min-Area and Max-Area. Taranilla et al. (Taranilla et al., 2011) proposed three different heuristics. Peethambaran et al. (Peethambaran et al., 2016, 2015) proposed randomized and greedy algorithms for Min-Area and $d$ -dimensional variants of both problems.

1.3.4. Other Challenges

The Open Problems Project (TOPP), maintained by Demaine, Mitchell and O’Rourke (Demaine et al., 2001), is a library of long-standing unsolved problems. On the more practical side, there have been different efforts, based on benchmark libraries, such as the TSPLIB (Reinelt, 1991). Since 1990, the DIMACS implementation challenges have addressed questions of determining realistic algorithm performance where worst-case analysis is overly pessimistic and probabilistic models are too unrealistic. Since 1994, the Graph Drawing (GD) community has held annual contests in conjunction with its annual symposium to monitor and challenge the current state of the graph-drawing technology and to stimulate new research directions for graph layout algorithm. More recently, a variety of implementation challenges have gained traction in the world of programming and optimization, but not yet in the field of Computational Geometry.

1.4. Outcomes

The contest generated a large number of contributions, both for Min-Area and Max-Area. In the aftermath, the top teams were invited to describe their methods in detailed papers, which form the substance of this special issue.

•

Julien Lepagnot, Laurent Moalic, Dominique Schmitt: Optimal area polygonization by triangulation and ray-tracing (Lepagnot et al., 2022)
•

Loïc Crombez, Guilherme D. da Fonseca, Yan Gerard: Greedy and Local Search Solutions to the Minimum and Maximum Are (Crombez et al., 2022)
•

Nir Goren, Efi Fogel, Dan Halperin: Area-optimal polygonization using simulated annealing (Goren et al., 2022)
•

Günther Eder, Martin Held, Steinpor Jasonarson, Philipp Mayer, Peter Palfrader: 2-Opt moves and flips for area-optimal polygonizations (Eder et al., 2022)
•

Natanael Ramos, Rai Caetan de Jesus, Pedro de Rezende, Cid de Souza, Fabio Luiz Usberti: Heuristics for area optimal polygonizations (Ramos et al., 2022)

In addition, there is one paper focusing on exact methods for computing provably optimal solutions.

•

Sándor P. Fekete, Andreas Haas, Phillip Keldenich, Michael Perk, Arne Schmidt: Computing area-optimal simple polygonization (Fekete et al., 2022)

In the rest of this survey paper, we provide a discussion of specific aspects of mathematical connections between area optimization and grid points (Section 2), approximation algorithms (Section 3), and an overview of contest results (Section 4).

2. Pick’s Theorem and Integrality

For a simple polygon $\mathcal{P}$ with $n$ vertices, computing the Euclidean length of its perimeter involves evaluating a sum of square roots, for which membership in $\mathcal{NP}$ is a long-standing open problem (Demaine et al., 2001). This differs from computing the area of $\mathcal{P}$ , which can be evaluated quite efficiently, e. g., see O’Rourke (O’Rourke, 1998). An elegant combinatorial answer is given by Pick’s theorem. (This also implies benign objective values, in particular for vertices whose coordinates are all even numbers, as chosen in the contest.)

Theorem 1 (Pick (Pick, 1899)).

Let $\mathcal{P}$ be a simple polygon with integer vertices; let $i(\mathcal{P})$ be the number of grid points contained in the interior of $\mathcal{P}$ , and let $b(\mathcal{P})$ be the number of grid points on the boundary of $\mathcal{P}$ . Then

\mbox{AR}(\mathcal{P})=\frac{1}{2}b(\mathcal{P})+i(\mathcal{P})-1.

There are several elegant ways to prove Pick’s theorem, three of which can be found in (Funkenbusch, 1974; Coxeter, 1969; Gaskell et al., 1976). For a discussion of alternative approaches see the article by Niven and Zuckermann (Niven and Zuckerman, 1967). There are numerous generalizations to other than the orthogonal grid, e. g., by Ren and Reay (Ren and Reay, 1987); see Reeve (Reeve, 1957) for a generalization to higher dimensions.

Pick’s theorem also provides a bridge to issues of point separation: Maximizing the enclosed area amounts to finding a simple polygon that captures as many additional grid points as possible, while minimizing the area corresponds to excluding as many as possible. As the $n$ given points must lie on the boundary of $\mathcal{P}$ , and only points within the convex hull of $P$ come into play, we get the following lower and upper bounds for the area.

Theorem 2.

Let $P$ be a set of $n$ points in the plane that all have integer coordinates. Let $h_{i}(P)$ denote the number of points of the integer grid that are not contained in $P$ and strictly inside the convex hull, and let $h_{b}(P)$ be the number of grid points not in $P$ that are on the boundary of the convex hull.

Then for any simple polygon $\mathcal{P}$ on the vertex set $P$ , we have

\frac{n}{2}-1\leq\mbox{\emph{AR}}(\mathcal{P})\leq\frac{n}{2}+\frac{h_{b}(P)}{2}+h_{i}(P)-1.

See Figure 3 for an illustration. Deciding whether either of these bounds can be met is already $\mathcal{NP}$ -complete (Fekete, 2000). At the same time, they motivate using the area of the convex hull as a reference, which was used in the contest.

3. Approximation

Using the area of the convex hull as an upper bound can also be used for approximating Max-Area.

Theorem 1 ((Fekete, 1992)).

Let $P$ be a set of $n$ points in the plane. We can determine a simple polygon $\mathcal{P}$ on $P$ that has area larger than $\frac{1}{2}\mbox{\emph{AR}}(P)$ , where $\mbox{\emph{AR}}(P)$ denotes the area of $\mbox{\emph{conv}}(P)$ . This can be done in time $O(n\log n)$ .

Proof.

Let $p_{0}$ be a point on the convex hull of $P$ . In time $O(n\log n)$ , sort the points $p_{i}$ of $P$ by the slope of the lines $l(p_{0},p_{i})$ , such that the neighbors of $p_{0}$ on the convex hull are the first and the last point, respectively. If there is a set of points for which the slope is the same, break the tie by ordering them in increasing distance from $p_{0}$ , except when those points have the smallest of all slopes, in which case we take them in order of decreasing distance from $p_{0}$ . Connecting the points $p_{i}$ in this order yields a simple polygon $\mathcal{P}_{1}$ on $P$ .

If $\mbox{\emph{AR}}(\mathcal{P}_{1})>\frac{1}{2}\mbox{\emph{AR}}(P)$ , we are done. Suppose this is not the case. Then the set $\mathcal{Q}:=\mbox{\emph{conv}}(P)\setminus\mathcal{P}_{1}$ has area at least $\frac{1}{2}\mbox{\emph{AR}}(P)$ . Now it is not hard to see that there is a simple polygon $\mathcal{P}_{2}$ that contains $\mathcal{Q}$ , implying the claim. ∎

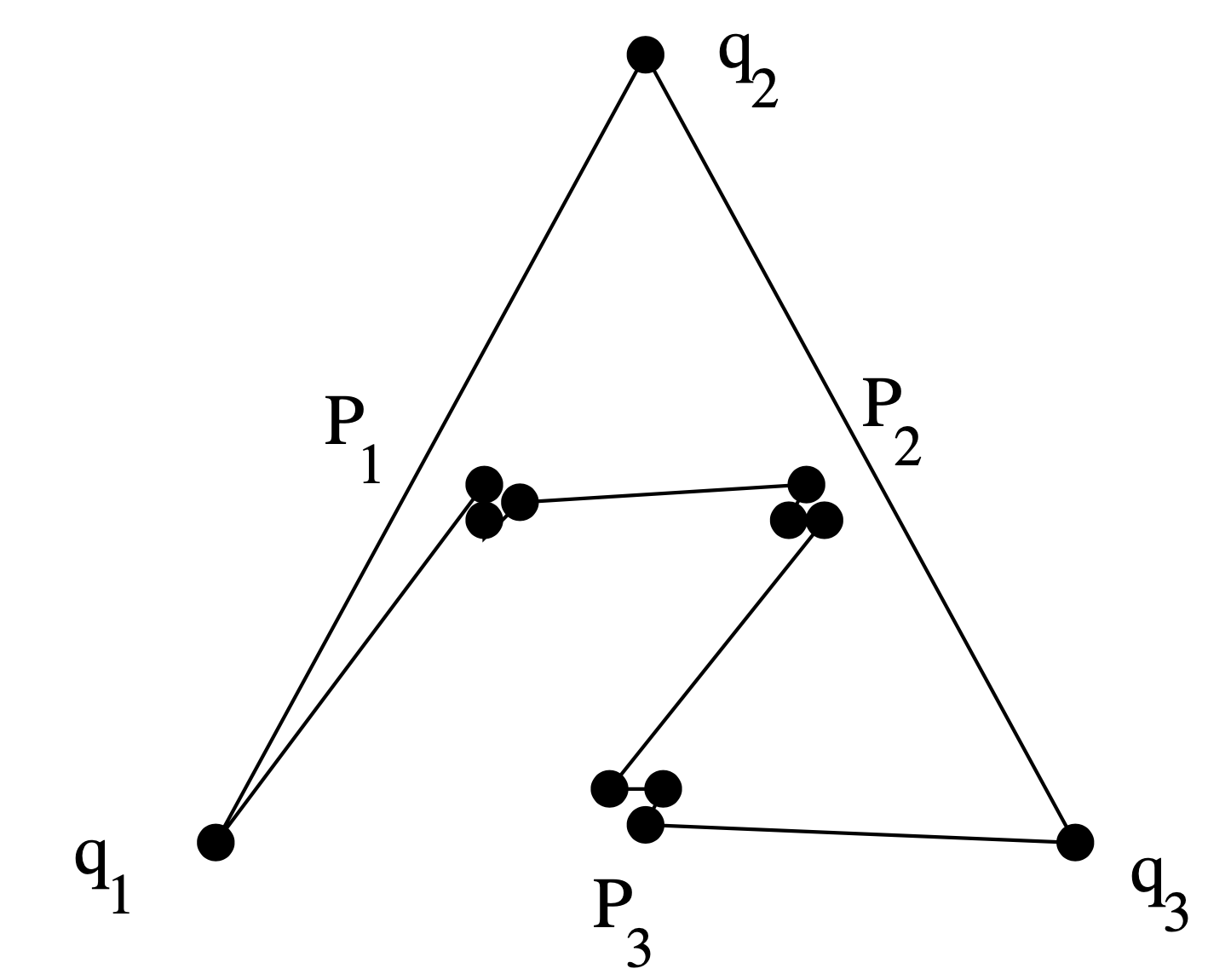
As shown in Figure 5, $\frac{1}{2}$ is a tight bound for this approach, even if all possible choices for $p_{0}$ are tested. Moreover, it was shown in (Fekete, 1992) that it is $\mathcal{NP}$ -complete to decide whether there is a simple polygon that contains strictly more than $\frac{2}{3}$ of the area of the convex hull;

At this time, no constant-factor approximation algorithm for Min-Area is known, hinting at a higher level of difficulty of the minimization problem. It may well be the case that no such approximation can be computed in polynomial time.

4. Contest and Outcomes

The 2019 Challenge was well received, with 28 teams from all over the world and a range of different scientific areas competing; participation was open to anyone. The contest itself was run through a dedicated server at TU Braunschweig, hosted at https://cgshop.ibr.cs.tu-bs.de/competition/cg-shop-2019/. It opened on February 28, 2019, and closed on May 31, 2019.

4.1. Instances

The contest started with a total of 247 benchmark instances, as follows. Each of these instances consisted of $n$ points in the plane with integer coordinates. For $n\in\{10$ , $15$ , $20$ , $25$ , $30$ , $35$ , $40$ , $45$ , $50$ , $60$ , $70$ , $80$ , $90$ , $100$ , $200$ , $300$ , $400$ , $500$ , $600$ , $700$ , $800$ , $900$ , $1000$ , $2000$ , $3000$ , $4000$ , $5000$ , $6000$ , $7000$ , $8000$ , $9000,10000,20000,30000,40000,50000,60000,70000,80000$ , $90000,100000\}$ , there were six instances each. In addition, there is one instance of size $n=1000000$ .

The instances were of four different types; see Fekete et al. (Fekete et al., 2017) for a more detailed description of how to generate benchmark instances through illumination maps.

•

uniform: uniformly distributed at random from a square
•

edge: randomly generated according to the distribution of the rate of change (the “edges”) from various images
•

illumination: randomly generated according to the distribution of brightness of an image (such as an illumination map)
•

orthogonally collinear points: randomly generated on an integral grid, resulting in a large number of collinear points (similar to printed circuit boards and distorted blueprints). .

4.2. Evaluation

The comparison between different teams was based on an overall score. For each instance, this score is the ratio given by the achieved area divided by the area of the convex hull; thus, the score is a number between 0 and 1. The total score achieved by each team was the sum of all 247 individual instance scores. Feasibility of submitted solutions was checked at the time of upload; for instances without a feasible solution, a default score of 1 (for minimization) or 0 (for maximization) was used. For multiple submissions by the same team, only the best feasible solution submitted was used to compute the score. In case of ties, the tiebreaker was set to be the date/time a specific score was obtained. This turned out not to be necessary.

4.3. Results

In the end, the top 10 in the leaderboard looked as shown in Table 1; note that according to the scoring function, a lower score is better for Min-Area, while a higher score is better for Max-Area. The progress over time of each team’s score can be seen in Figure 6 (for Min-Area) and Figure 7 (for Max-Area).

Table 1. The top of the final leaderboard. Shown are the scores in both categories, along with the achieved average percentages of the convex hull of points. Teams CGA and UNICAMP were overall tied, according to different positions for Min-Area and Max-Area, as were mperk and AQ_PG. The teams mperk (Michael Perk, TU Braunschweig) and zhengdw (David Zheng, University of British Columbia) were both individual, first-year Masters students.

Rk.	Team	Score (Min)	Score (Max)	# best	(unique)	# best	(unique)
				Min	sols.	Max	sols.
1	OMEGA/Mulhouse (FR)	23.393 ( 9.47%)	227.247 (92.00%)	223	(181)	184	(138)
2	lcrombez/Clermont (FR)	25.751 (10.43%)	226.691 (91.78%)	66	(23)	109	(4)
3	cgl@tau/Tel Aviv (IS)	35.289 (14.29%)	206.612 (83.65%)	13	(0)	12	(0)
4	CGA/Salzburg (AU)	36.069 (14.60%)	197.568 (79.99%)	26	(0)	23	(0)
4	UNICAMP/Campinas (BR)	46.432 (18.80%)	201.839 (81.72%)	3	(0)	3	(0)
6	mperk/Braunschweig (GE)	68.431 (27.70%)	191.483 (77.52%)	24	(0)	23	(0)
6	L’Aquila-Perugia (IT)	57.373 (23.23%)	179.752 (72.77%)	19	(0)	18	(0)
8	Stony Brook (US)	85.179 (34.49%)	162.031 (65.60%)	1	(0)	1	(0)
9	zhengdw (CA)	89.437 (36.21%)	154.723 (62.64%)	0	(0)	1	(0)
10	TGP/Eindhoven (NL)	112.561 (45.57%)	154.548 (62.57%)	18	(0)	26	(0)

The top 5 finishers were invited for contributions to this special issue, as follows.

(1)

Team OMEGA/Mulhouse (France): Julien Lepagnot, Laurent Moalic, Dominique Schmitt (Lepagnot et al., 2022)
(2)

Team lcrombez/Clermont Auvergne(France): Loïc Crombez, Guilherme D. da Fonseca, Yan Gerard (Crombez et al., 2022)
(3)

Team cgl@tau/Tel Aviv (Israel): Nir Goren, Efi Fogel, Dan Halperin (Goren et al., 2022)
(4)

Team CGA/Salzburg (France): Günther Eder, Martin Held, Steinthor Jasonarson, Philipp Mayer, Peter Palfrader (Eder et al., 2022).
(5)

Team UNICAMP/Campinas (Brazil): Natanael Ramos, Rai Caetan de Jesus, Pedro de Rezende, Cid de Souza, Fabio Luiz Usberti (Ramos et al., 2022)

Figure 6 shows the development of total scores over time for Min-Area and all teams; it can be seen that OMEGA passed lcrombez shortly before the deadline, with cgl@tau just squeezing by CGA. A similar and even tighter outcome between OMEGA and lcrombez for Max-Area can be seen in Figure 7; for that problem, cgl@tau also placed third, but UNICAMP managed to beat out CGA for fourth place. Thus, the ranking was consistent for both Min-Area and Max-Area, except for Campinas doing better than Salzburg in Max-Area, so they both shared fourth place. All five teams engineered their solutions with the use of a variety of specific tools. Details of their methods and the engineering decisions they made are given in their respective papers.

Figure 8 shows the spread of results for all Min-Area instances; it can be seen that there is a strong deviation over all instance sizes, even for the small ones. This is surprising as one would expect simple heuristics to perform reasonably well for small instances; however, it appears that even for very small instances with $10$ points of Min-Area, more advanced ideas are necessary to achieve good results. (See the contribution by Fekete et al. (Fekete et al., 2022) for a detailed study of exact methods.) At around $5000$ points, the mean score drops visibly; the best teams are able to obtain nearly the same score for all instances sizes above $50$ points. A similar overview for Max-Area is given in Figure 9. Here the deviation is very small for the small instances, showing that all teams where able to obtain reasonably good solutions for small instances. The deviation increases with the problem size until around $300$ points, after which it remains homogenous but smaller than for Min-Area. Like for Min-Area, the best teams obtained nearly equal scores for all instances sizes, while the mean score drops visibly after $900$ points.

5. Conclusions

The 2019 CG Challenge motivated a considerable number of teams to engage in intensive optimization studies. This success has not only led to practical progress on the problem of area optimization, but also turned the CG Challenge into a continuing feature of CGWeek, spawning considerable work through the 2020 Challenge problem (Minimum Convex Partition) and the 2021 problem (Coordinated Motion Planning). This promises to motivate further work on the involved problems, as well as other practical geometric optimization work. We are confident that this will further strengthen the bridges between optimization theory and practical algorithm engineering.

Acknowledgment

This work was supported by DFG project “Computational Geometry: Solving Hard Optimization Problems” (CG:SHOP), FE 407/21-1.

References

(1)
Abellanas et al. (1993) Manuel Abellanas, Jesús García, Gregorio Hernández Peñalver, Ferran Hurtado, Oriol Serra, and Jorge Urrutia. 1993. Updating polygonizations. In Computer Graphics Forum, Vol. 12. Wiley Online Library, 143–152. Issue 3.
Ackerman et al. (2009) Eyal Ackerman, Oswin Aichholzer, and Balázs Keszegh. 2009. Improved upper bounds on the reflexivity of point sets. Computational Geometry 42, 3 (2009), 241–249.
Aichholzer et al. (2002) Oswin Aichholzer, Franz Aurenhammer, and Hannes Krasser. 2002. Enumerating order types for small point sets with applications. Order 19, 3 (2002), 265–281.
Arkin et al. (2003) Esther M. Arkin, Joseph S. B. Mitchell, Sándor P. Fekete, Ferran Hurtado, Marc Noy, Vera Sacristán, and Saurabh Sethia. 2003. On the reflexivity of point sets. In Discrete and Computational Geometry. Springer, 139–156.
Auer and Held (1996) Thomas Auer and Martin Held. 1996. RPG-heuristics for the generation of random polygons. In Canadian Conference on Computational Geometry (CCCG). 38–44.
Coxeter (1969) Harold Scott Macdonald Coxeter. 1969. Introduction to Geometry. Wiley, New York.
Crombez et al. (2022) Loïc Crombez, Guilherme D. da Fonseca, and Yan Gerard. 2022. Greedy and Local Search Heuristics to Build Area-Optimal Polygons. Journal of Experimental Algorithmics (2022). This issue.
Demaine et al. (2001) Erik D. Demaine, Joseph S. B. Mitchell, and Joseph O’Rourke. 2001. The Open Problems Project. , 573–582 pages. http://cs.smith.edu/~orourke/TOPP/.
Eder et al. (2022) Günther Eder, Martin Held, Steinthor Jasonarson, Philipp Mayer, and Peter Palfrader. 2022. 2-Opt moves and flips for area-optimal polygonalizations. Journal of Experimental Algorithmics (2022). This issue.
Fekete (1992) Sándor P. Fekete. 1992. Geometry and the Travelling Salesman Problem. Ph.D. Thesis. Department of Combinatorics and Optimization, University of Waterloo, Waterloo, ON, Canada.
Fekete (2000) Sándor P. Fekete. 2000. On simple polygonizations with optimal area. Discrete & Computational Geometry 23, 1 (2000), 73–110.
Fekete et al. (2017) Sándor P. Fekete, Andreas Haas, Michael Hemmer, Michael Hoffmann, Irina Kostitsyna, Dominik Krupke, Florian Maurer, Joseph S. B. Mitchell, Arne Schmidt, Christiane Schmidt, and Julian Troegel. 2017. Computing Nonsimple Polygons of Minimum Perimeter. Journal of Computational Geometry 8 (2017), 340–365. Issue 1.
Fekete et al. (2022) Sándor P. Fekete, Andreas Haas, Phillip Keldenich, Michael Perk, and Arne Schmidt. 2022. Computing area-optimal simple polygonalization. Journal of Experimental Algorithmics (2022). This issue.
Fekete and Pulleyblank (1993) Sándor P. Fekete and William R. Pulleyblank. 1993. Area optimization of simple polygons. In Symposium on Computational Geometry (SoCG). ACM, 173–182.
Funkenbusch (1974) Walter W. Funkenbusch. 1974. From Euler’s formula to Pick’s formula using an edge theorem. The American Mathematical Monthly 81, 6 (1974), 647–648.
Garcıa et al. (2000) Alfredo Garcıa, Marc Noy, and Javier Tejel. 2000. Lower bounds on the number of crossing-free subgraphs of KN. Computational Geometry 16, 4 (2000), 211–221.
Gaskell et al. (1976) R. W. Gaskell, M. S. Klamkin, and P. Watson. 1976. Triangulations and Pick’s theorem. Mathematics Magazine 49, 1 (1976), 35–37.
Goren et al. (2022) Nir Goren, Efi Fogel, and Dan Halperin. 2022. Area optimal polygonization using simulated annealing. Journal of Experimental Algorithmics (2022). This issue.
Lepagnot et al. (2022) Julien Lepagnot, Laurent Moalic, and Dominique Schmitt. 2022. Optimal Area Polygonization by Triangulation and Visibility Search. Journal of Experimental Algorithmics (2022). This issue.
Mitchell (1993) Joseph S. B. Mitchell. 1993. Approximation algorithms for geometric separation problems. Technical Report. SUNY Stony Brook.
Mitchell and Suri (1995) Joseph S. B. Mitchell and Subhash Suri. 1995. Separation and approximation of polyhedral objects. Computational Geometry: Theory and Applications 5, 2 (1995), 95–114.
Niven and Zuckerman (1967) Ivan Niven and Herbert S. Zuckerman. 1967. Lattice points and polygonal area. The American Mathematical Monthly 74, 10 (1967), 1195–1200.
O’Rourke (1980) Joseph O’Rourke. 1980. Polyhedral object models from 3D points. Technical Report IFI-HH-M-77/80. Universität Hamburg.
O’Rourke (1998) Joseph O’Rourke. 1998. Computational geometry in C. Cambridge university press.
O’Rourke et al. (2017) Joseph O’Rourke, Subhash Suri, and Csaba D. Tóth. 2017. Polygons. In Handbook of discrete and computational geometry, Csaba D. Toth, Joseph O’Rourke, and Jacob E. Goodman (Eds.). CRC Press, Chapter 30, 787–810.
Peethambaran et al. (2015) Jiju Peethambaran, Amal Dev Parakkat, and Ramanathan Muthuganapathy. 2015. A randomized approach to volume constrained polyhedronization problem. Journal of Computing and Information Science in Engineering 15, 1 (2015), 011009.
Peethambaran et al. (2016) Jiju Peethambaran, Amal Dev Parakkat, and Ramanathan Muthuganapathy. 2016. An Empirical Study on Randomized Optimal Area Polygonization of Planar Point Sets. Journal of Experimental Algorithmics 21 (2016), 1–10.
Pick (1899) Georg Pick. 1899. Geometrisches zur Zahlenlehre. Sitzungsberichte des Deutschen Naturwissenschaftlich-Medicinischen Vereines für Böhmen “Lotos” in Prag 19 (1899), 311–319.
Ramos et al. (2022) Natanael Ramos, Rai Caetan de Jesus, Pedro de Rezende, Cid de Souza, and Fabio Luiz Usberti. 2022. Triangle-based heuristics for area optimal polygonizations. Journal of Experimental Algorithmics (2022). This issue.
Reeve (1957) John E. Reeve. 1957. On the volume of lattice polyhedra. Proceedings of the London Mathematical Society 3, 1 (1957), 378–395.
Reinelt (1991) Gerhard Reinelt. 1991. TSPlib – A Traveling Salesman Problem library. ORSA J. on Computing 3, 4 (1991), 376–384.
Ren and Reay (1987) Ding Ren and John R. Reay. 1987. The boundary characteristic and Pick’s theorem in the Archimedean planar tilings. Journal of Combinatorial Theory, Series A 44, 1 (1987), 110–119.
Sharir et al. (2013) Micha Sharir, Adam Sheffer, and Emo Welzl. 2013. Counting plane graphs: Perfect matchings, spanning cycles, and Kasteleyn’s technique. Journal of Combinatorial Theory, Series A 120, 4 (2013), 777–794.
Taranilla et al. (2011) Maria Teresa Taranilla, Edilma Olinda Gagliardi, and Gregorio Hernández Peñalver. 2011. Approaching minimum area polygonization. In XVII Congreso Argentino de Ciencias de la Computacion. 31–40.
Zhu et al. (1996) Chong Zhu, Gopalakrishnan Sundaram, Jack Snoeyink, and Joseph S. B. Mitchell. 1996. Generating random polygons with given vertices. Computational Geometry 6, 5 (1996), 277–290.