Are the $a_{0}(1710)$ or $a_{0}(1817)$ resonances in the $D_{s}^{+}\rightarrow K_{S}^{0}K^{+}\pi^{0}$ decay?

Recently, the BESIII Collaboration performed the amplitude analysis of the decay $D_{s}^{+}\rightarrow K_{S}^{0}K^{+}\pi^{0}$, and reported the branching fraction $\mathcal{B}\left(D_{s}^{+}\rightarrow K_{S}^{0}K^{+}\pi^{0}\right)=\left(1.46\pm 0.06\pm 0.05\right)\%$ BESIII:2022npc , which was consistent with the measurement of the CLEO Collaboration CLEO:2013bae . The isovector partner of the $f_{0}(1710)$, a state $a_{0}(1710)^{+}$ was observed in the $K_{S}^{0}K^{+}$ invariant mass spectrum of the decay $D_{s}^{+}\rightarrow K_{S}^{0}K^{+}\pi^{0}$ BESIII:2022npc ¹¹1In the published version, they assumed to be a new $a_{0}(1817)$ resonance., of which the mass and width were measured as,

$$M_{a_{0}(1710)}=(1.817\pm 0.008\pm 0.020)\textrm{ GeV},~{}\Gamma_{a_{0}(1710)}=(0.097\pm 0.022\pm 0.015)\textrm{ GeV}.$$

In fact, previously, the BABAR Collaboration performed the Dalitz plot analyses of $\eta_{c}\rightarrow\eta\pi^{+}\pi^{-}$ decay and found a new state $a_{0}(1700)$ in the $\pi\eta$ invariant mass spectrum BaBar:2021fkz ,

$$M_{a_{0}(1700)}=(1.704\pm 0.005\pm 0.002)\textrm{ GeV},~{}\Gamma_{a_{0}(1700)}=(0.110\pm 0.015\pm 0.011)\textrm{ GeV},$$

which might also be the same state as $a_{0}(1710)$ and corroborated the evidence found in Ref. BaBar:2018uqa . In Ref. BESIII:2021anf , a peak around $1.710$ GeV was observed in the $K_{S}^{0}K_{S}^{0}$ mass distribution in the decay $D_{s}^{+}\rightarrow\pi^{+}K_{S}^{0}K_{S}^{0}$ by the BESIII Collaboration. Due to the strong overlap and common quantum numbers $J^{PC}=0^{++}$, the states $a_{0}(1710)$ and $f_{0}(1710)$ were not distinguished, and then together denoted as $S(1710)$, where the mass and width were determined as BESIII:2021anf ,

$$M_{S(1710)}=(1.723\pm 0.011\pm 0.002)\textrm{ GeV},~{}\Gamma_{S(1710)}=(0.140\pm 0.014\pm 0.004)\textrm{ GeV}.$$

From these reported results of the BESIII BESIII:2022npc ; BESIII:2021anf and BABAR BaBar:2021fkz Collaborations, the extracted Breit-Wigner masses of $a_{0}(1710)$ are quite different. Actually, these experimental results have extraordinary significance, because searching for the $a_{0}(1710)$ is crucial to understand the nature of its isoscalar partner state $f_{0}(1710)$. In the present work, based on the recent results of the BESIII Collaboration BESIII:2022npc , we try to understand the properties of the state $a_{0}(1710)$ by exploiting the final state interaction formalism.

In the quark model, the $f_{0}(1710)$ was interpreted as an $I^{G}(J^{PC})=0^{+}(0^{++})$ light scalar meson by the Godfrey and Isgur model Godfrey:1985xj , which should also have an isovector partner at $1.78$ GeV. Similar results were obtained in Ref. Segovia:2008zza with a constituent quark model. However, the $f_{0}(1710)$ mainly decays to the channels $K\bar{K}$ and $\eta\eta$, indicating that it may have large $s\bar{s}$ quarks components Chanowitz:2005du ; Chao:2007sk . The $f_{0}(1710)$ was also regarded as a scalar glueball or containing a large glueball components in Refs. Close:2005vf ; Giacosa:2005zt ; Cheng:2006hu ; Albaladejo:2008qa ; Gui:2012gx ; Janowski:2014ppa ; Ochs:2013gi ; Cheng:2015iaa ; Klempt:2021wpg , which were supported by the experimental resuts of the BESIII Collaboration BESIII:2022riz ; BESIII:2022iwi . Searching for the isovector partner of the $f_{0}(1710)$ is the key to identify whether it is a scalar glueball. On the other hand, based on the chiral unitary approach (ChUA) Oller:1997ti ; Oset:1997it ; Oller:2000ma ; Oller:2000fj ; Oset:2008qh , the $f_{0}(1710)$ was dynamically generated in the interactions of vector mesons and assumed to be a molecular state of $K^{*}\bar{K}^{*}$ in Ref. Geng:2008gx , where its pole located at $1.726$ GeV and another $a_{0}$ state at $1.78$ GeV with isospin $I=1$ was predicted. Similar results were obtained in the extended research works of Du:2018gyn ; Wang:2021jub . Indeed, this $a_{0}$ state at $1.78$ GeV was arranged as the new found $a_{0}(1710)$ state in a further work of Wang:2022pin , which was also a bound state of $K^{*}\bar{K}^{*}$, a molecular state. More discussions about the molecular states can be referred to the review of Ref. Guo:2017jvc .

Furthermore, based on the results from the BESIII Collaboration BESIII:2021anf ; BESIII:2020ctr , Ref. Dai:2021owu studied the decay modes $D_{s}^{+}\rightarrow\pi^{+}K^{+}K^{-}$, $\pi^{+}K^{0}\bar{K}^{0}$, and $\pi^{0}K^{+}\bar{K}^{0}$, where the $f_{0}(1710)$ and $a_{0}(1710)$ states were dynamically generated from the final state interactions of $K^{*}\bar{K}^{*}$, and the branching ratio of $D_{s}^{+}\rightarrow\pi^{0}K^{+}K_{S}^{0}$ reaction was predicted. Analogously, the decay $D_{s}^{+}\rightarrow\pi^{+}K_{S}^{0}K_{S}^{0}$ was investigated in details in Ref. Zhu:2022wzk , where the $K_{S}^{0}K_{S}^{0}$ and $\pi^{+}K_{S}^{0}$ invariant mass distributions were calculated with the resonance contributions of the scalar $f_{0}(1710)$ and the isovector partner $a_{0}(1710)$, and the results obtained were consistent with the measurements from the BESIII Collaboration BESIII:2021anf . However, in Ref. Guo:2022xqu , the $a_{0}(1710)$ state, newly observed by the BESIII Collaboration BESIII:2022npc , was renamed as $a_{0}(1817)$, which was regarded as the isovector partner of the $X(1812)$ found in Ref. BES:2006vdb and classified into the isovector scalar meson family according to the standard Regge trajectory.

Therefore, it is meaningful to understand the nature of the state $a_{0}(1710)$, which is critical for further revealing the property of its isoscalar partner state $f_{0}(1710)$. The latest experimental measurement of the decay $D_{s}^{+}\rightarrow K_{S}^{0}K^{+}\pi^{0}$ by the BESIII Collaboration BESIII:2022npc gives us an opportunity to identify the nature of the $a_{0}(1710)$. In the present work, with the framework of the ChUA, we investigate the resonance contributions of the process $D_{s}^{+}\rightarrow K_{S}^{0}K^{+}\pi^{0}$ based on the final state interactions, where the states $a_{0}(980)^{+}$ and $a_{0}(1710)^{+}$ are dynamically generated in the coupled channel interactions of the channels $K\bar{K}$ and $K^{*}\bar{K}^{*}$. In the interactions of coupled channels, both the pseudoscalar and vector channels are considered, where five channels $K^{*}\bar{K}^{*}$, $\rho\omega$, $\rho\phi$, $K\bar{K}$, and $\pi\eta$, are involved. To describe the invariant mass spectra, we also take into account the contributions from the $\bar{K}^{*}(892)^{0}$ and ${K}^{*}(892)^{+}$ in the $P$-wave, which play a crucial role in the intermediate processes $D_{s}^{+}\rightarrow\bar{K}^{*}(892)^{0}K^{+}$ and ${K}^{*}(892)^{+}K_{S}^{0}$, but omit the contribution of the resonance $\bar{K}^{*}(1410)^{0}$, of which the contribution was small as implied in Ref. BESIII:2022npc . The manuscript is organized as follows. In Sec. II, we present the theoretical formalism of the decay $D_{s}^{+}\rightarrow K_{S}^{0}K^{+}\pi^{0}$ with the final state interaction. Next, our results are shown in Sec. III. A short conclusion is made in Sec. IV.

For the three-body weak decay $D_{s}^{+}\rightarrow K_{S}^{0}K^{+}\pi^{0}$, we start from the dynamics at the quark level, where the dominant external and internal $W$-emission mechanisms Chau:1982da ; Chau:1987tk are taken into account. In the next step, in the hadron level we consider the final state interactions in the $S$-wave and the vector meson productions in the $P$-wave, which will be discussed later. First, the Feynman diagrams of the external $W$-emission mechanisms are shown in Fig. 1, and the ones with the internal $W$-emission mechanisms are given in Fig. 2. As shown in Fig. 1 for the weak decays of $D_{s}^{+}$, the $c$ quark decays into a $W^{+}$ boson and an $s$ quark, and the $\bar{s}$ quark in $D_{s}^{+}$ as a spectator remains unchanged, then the $W^{+}$ boson decays into an $u\bar{d}$ quark pair. In the following procedures, there are two possibilities for the hadonization progresses. In Fig. 1(a), the $u\bar{d}$ pair forms a $\pi^{+}$ or $\rho^{+}$ meson, along with this process, the $s\bar{s}$ quark pair hadronizes into two mesons with $\bar{q}q=\bar{u}u+\bar{d}d+\bar{s}s$ produced from the vacuum. Contrarily, in Fig. 1(b), the $s\bar{s}$ quark pair goes into an $\eta$ or $\phi$ meson, the $u\bar{d}$ quark pair made by the $W^{+}$ boson hadronizes into two mesons with the $\bar{q}q$ pairs generated from the vacuum. The corresponding processes for these hadonizations can be given by the formulae below for Fig. 1(a) and Fig. 1(b), respectively,

	$\displaystyle|H^{(1a)}\rangle=$	$\displaystyle V_{P}^{(1a)}V_{cs}V_{ud}(u\bar{d}\rightarrow\pi^{+})|s(\bar{u}u+\bar{d}d+\bar{s}s)\bar{s}\rangle$		(1)
		$\displaystyle+V_{P}^{*(1a)}V_{cs}V_{ud}(u\bar{d}\rightarrow\rho^{+})|s(\bar{u}u+\bar{d}d+\bar{s}s)\bar{s}\rangle$
	$\displaystyle=$	$\displaystyle V_{P}^{(1a)}V_{cs}V_{ud}\pi^{+}(M\cdot M)_{33}+V_{P}^{*(1a)}V_{cs}V_{ud}\rho^{+}(M\cdot M)_{33},$

	$\displaystyle|H^{(1b)}\rangle=$	$\displaystyle V_{P}^{(1b)}V_{cs}V_{ud}(s\bar{s}\rightarrow\frac{-2}{\sqrt{6}}\eta)|u(\bar{u}u+\bar{d}d+\bar{s}s)\bar{d}\rangle$		(2)
		$\displaystyle+V_{P}^{*(1b)}V_{cs}V_{ud}(s\bar{s}\rightarrow\phi)|u(\bar{u}u+\bar{d}d+\bar{s}s)\bar{d}\rangle$
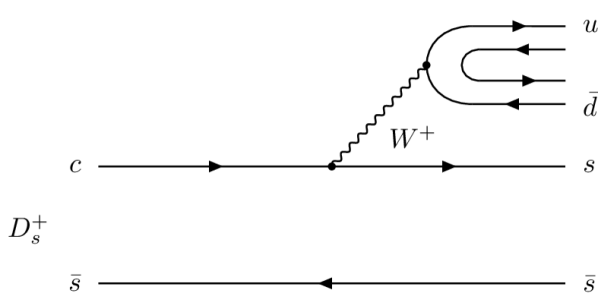
	$\displaystyle=$	$\displaystyle V_{P}^{(1b)}V_{cs}V_{ud}\frac{-2}{\sqrt{6}}\eta(M\cdot M)_{12}+V_{P}^{*(1b)}V_{cs}V_{ud}\phi(M\cdot M)_{12},$

where the $V_{P}^{(1a)}$ and $V_{P}^{*(1a)}$ are the weak interaction strengths of the production vertices Liang:2015qva ; Ahmed:2020qkv for the generations $\pi^{+}$ and $\rho^{+}$, respectively, for the case of Fig. 1(a), and the $V_{P}^{(1b)}$ and $V_{P}^{*(1b)}$ are the ones for the productions $\eta$ and $\phi$, severally, for the other case of Fig. 1(b). The factors $V_{cs}$ and $V_{ud}$ are the elements of the Cabibbo-Kobayashi-Maskawa (CKM) matrix, which indicate from $q_{1}\rightarrow q_{2}$ quarks. The symbol $M$ is the $q\bar{q}$ matrix in $SU{(3)}$, defined as

$\displaystyle M=\left(\begin{array}[]{lll}{u\bar{u}}&{u\bar{d}}&{u\bar{s}}\\ {d\bar{u}}&{d\bar{d}}&{d\bar{s}}\\ {s\bar{u}}&{s\bar{d}}&{s\bar{s}}\end{array}\right).$

(3)

Analogously, in the mechanisms of internal $W$-emission, see in Fig. 2, the $s\bar{d}$ pair goes into a $\bar{K}^{0}$ or $\bar{K}^{*0}$ meson, and the remnant $u\bar{s}$ quark pair hadronizes into two mesons with $\bar{q}q$ pairs produced from the vacuum, as shown in Fig. 2(a). On the other hand, in Fig. 2(b), the $u\bar{s}$ pair forms a $K^{+}$ or $K^{*+}$ meson, and the $s\bar{d}$ quark pair hadronizes into two mesons with $\bar{q}q$ pairs created from the vacuum. One can write these processes in the following way for Fig. 2(a) and Fig. 2(b), respectively,

	$\displaystyle|H^{(2a)}\rangle=$	$\displaystyle V_{P}^{(2a)}V_{cs}V_{ud}(s\bar{d}\rightarrow\bar{K}^{0})|u(\bar{u}u+\bar{d}d+\bar{s}s)\bar{s}\rangle$		(4)
		$\displaystyle+V_{P}^{*(2a)}V_{cs}V_{ud}(s\bar{d}\rightarrow\bar{K}^{*0})|u(\bar{u}u+\bar{d}d+\bar{s}s)\bar{s}\rangle$
	$\displaystyle=$	$\displaystyle V_{P}^{(2a)}V_{cs}V_{ud}\bar{K}^{0}(M\cdot M)_{13}+V_{P}^{*(2a)}V_{cs}V_{ud}\bar{K}^{*0}(M\cdot M)_{13},$

	$\displaystyle|H^{(2b)}\rangle=$	$\displaystyle V_{P}^{(2b)}V_{cs}V_{ud}(u\bar{s}\rightarrow K^{+})|s(\bar{u}u+\bar{d}d+\bar{s}s)\bar{d}\rangle$		(5)
		$\displaystyle+V_{P}^{*(2b)}V_{cs}V_{ud}(u\bar{s}\rightarrow K^{*+})|s(\bar{u}u+\bar{d}d+\bar{s}s)\bar{d}\rangle$
	$\displaystyle=$	$\displaystyle V_{P}^{(2b)}V_{cs}V_{ud}K^{+}(M\cdot M)_{32}+V_{P}^{*(2b)}V_{cs}V_{ud}K^{*+}(M\cdot M)_{32},$

where the $V_{P}^{(2a)}$ and $V_{P}^{*(2a)}$ are the weak interaction strengths of the production vertices for the creations $\bar{K}^{0}$ and $\bar{K}^{*0}$, respectively, and the $V_{P}^{(2b)}$ and $V_{P}^{*(2b)}$ are the ones for the formations $K^{+}$ and $K^{*+}$, severally. Afterward, the matrix $M$ for the hadronization can be revised in terms of the pseudoscalar ($P$) or vector ($V$) mesons, written as

$\displaystyle P=\left(\begin{array}[]{ccc}{\frac{1}{\sqrt{2}}\pi^{0}+\frac{1}{\sqrt{6}}\eta}&{\pi^{+}}&{K^{+}}\\ {\pi^{-}}&{-\frac{1}{\sqrt{2}}\pi^{0}+\frac{1}{\sqrt{6}}\eta}&{K^{0}}\\ {K^{-}}&{\bar{K}^{0}}&{-\frac{2}{\sqrt{6}}\eta}\end{array}\right),$

(6)

$\displaystyle V=\left(\begin{array}[]{ccc}{\frac{1}{\sqrt{2}}\rho^{0}+\frac{1}{\sqrt{2}}\omega}&{\rho^{+}}&{K^{*+}}\\ {\rho^{-}}&{-\frac{1}{\sqrt{2}}\rho^{0}+\frac{1}{\sqrt{2}}\omega}&{K^{*0}}\\ {K^{*-}}&{\bar{K}^{*0}}&{\phi}\end{array}\right),$

(7)

where we take $\eta\equiv\eta_{8}$ Liang:2014tia . In Eqs. (1), (2), (4), and (5), the $M\cdot M$ has four possible situations with two matrices of physical mesons, i.e., $P\cdot P$, $V\cdot V$, $P\cdot V$, and $V\cdot P$. And thus, these hadronization processes can be reexpressed as

$\displaystyle|H^{(1b)}\rangle=V_{P}^{*(1b)}V_{cs}V_{ud}\phi(\frac{-1}{\sqrt{2}}\rho^{+}\pi^{0})+V_{P}^{*(1b)^{\prime}}V_{cs}V_{ud}\phi(\frac{1}{\sqrt{2}}\rho^{+}\pi^{0}),$

(8)

$\displaystyle|H^{(2a)}\rangle=V_{P}^{(2a)}V_{cs}V_{ud}\bar{K}^{0}(\frac{1}{\sqrt{2}}K^{+}\pi^{0})+V_{P}^{*(2a)}V_{cs}V_{ud}\bar{K}^{*0}(\frac{1}{\sqrt{2}}K^{*+}\pi^{0}),$

(9)

$\displaystyle|H^{(2b)}\rangle=V_{P}^{(2b)}V_{cs}V_{ud}K^{+}(-\frac{1}{\sqrt{2}}\bar{K}^{0}\pi^{0})+V_{P}^{*(2b)}V_{cs}V_{ud}K^{*+}(-\frac{1}{\sqrt{2}}\bar{K}^{*0}\pi^{0}),$

(10)

where we only keep the terms that contribute to the final states $K_{S}^{0}K^{+}\pi^{0}$. It should be mentioned that there is no term for the Fig. 1(a) contributed to these final states of present $D_{s}^{+}$ decay process. Besides, in Eq. (8), the factors $V_{P}^{*(1b)}$ and $V_{P}^{*(1b)^{\prime}}$ are different because they come from $(V\cdot P)_{12}$ and $(P\cdot V)_{12}$, respectively. Then, we obtain the total contributions in the $S$-wave,

	$\displaystyle|H\rangle=$	$\displaystyle|H^{(1b)}\rangle+|H^{(2a)}\rangle+|H^{(2b)}\rangle$		(11)
	$\displaystyle=$	$\displaystyle\frac{1}{\sqrt{2}}(V_{P}^{*(1b)^{\prime}}-V_{P}^{*(1b)})V_{cs}V_{ud}\rho^{+}\phi\pi^{0}+\frac{1}{\sqrt{2}}(V_{P}^{(2a)}-V_{P}^{(2b)})V_{cs}V_{ud}K^{+}\bar{K}^{0}\pi^{0}$
		$\displaystyle+\frac{1}{\sqrt{2}}(V_{P}^{*(2a)}-V_{P}^{*(2b)})V_{cs}V_{ud}K^{*+}\bar{K}^{*0}\pi^{0},$
	$\displaystyle=$	$\displaystyle\frac{1}{\sqrt{2}}V_{P}^{*^{\prime}}V_{cs}V_{ud}\rho^{+}\phi\pi^{0}+\frac{1}{\sqrt{2}}V_{P}V_{cs}V_{ud}K^{+}\bar{K}^{0}\pi^{0}+\frac{1}{\sqrt{2}}V_{P}^{*}V_{cs}V_{ud}K^{*+}\bar{K}^{*0}\pi^{0},$

where we define $V_{P}^{*^{\prime}}=V_{P}^{*(1b)^{\prime}}-V_{P}^{*(1b)}$, $V_{P}=V_{P}^{(2a)}-V_{P}^{(2b)}$, and $V_{P}^{*}=V_{P}^{*(2a)}-V_{P}^{*(2b)}$. Note that there are also the final states $\bar{K}^{0}K^{+}\pi^{0}$ produced directly in the hadronization processes in Eq. (11). Taking into account the final state interactions, we can get these final states via the rescattering procedures, such as $K^{+}\bar{K}^{0}\rightarrow K^{+}\bar{K}^{0}$, $\rho^{+}\phi\rightarrow K^{+}\bar{K}^{0}$, and $K^{*+}\bar{K}^{*0}\rightarrow K^{+}\bar{K}^{0}$, which are depicted in Fig. 3. One more thing should be mentioned that there is no direct term $\eta\pi^{+}\pi^{0}$ contributed in Eq. (11) due to its two terms in $|H^{(1b)}\rangle$ cancelled, which is consistent with the evaluation of Ref. Molina:2019udw , where the experimental findings for the decay $D^{+}_{s}\to\eta\pi^{+}\pi^{0}$ BESIII:2019jjr were investigated. In Ref. Molina:2019udw , the larger decay rate of $D^{+}_{s}\to\eta\pi^{+}\pi^{0}$ was explained via the internal $W$-emission mechanism for the decay process rather than the $W$-annihilation procedure as assumed in Ref. BESIII:2019jjr . In the further study of the decay $D^{+}_{s}\to\eta\pi^{+}\pi^{0}$, no tree diagram of $D^{+}_{s}\to\eta\pi^{+}\pi^{0}$ decay was taken into account in Refs. Hsiao:2019ait ; Ling:2021qzl . Therefore, under the dominant external and internal $W$-emission mechanisms, the amplitude of decay $D_{s}^{+}\rightarrow\bar{K}^{0}K^{+}\pi^{0}$ in the $S$-wave is given by

	$\displaystyle t_{S\text{-wave}}(M_{12})\big{|}_{\bar{K}^{0}K^{+}\pi^{0}}=$	$\displaystyle\frac{1}{\sqrt{2}}\mathcal{C}_{1}G_{\rho^{+}\phi}(M_{12})T_{\rho^{+}\phi\rightarrow K^{+}\bar{K}^{0}}(M_{12})$		(12)
		$\displaystyle+\frac{1}{\sqrt{2}}\mathcal{C}_{2}+\frac{1}{\sqrt{2}}\mathcal{C}_{2}G_{K^{+}\bar{K}^{0}}(M_{12})T_{K^{+}\bar{K}^{0}\rightarrow K^{+}\bar{K}^{0}}(M_{12})$
		$\displaystyle+\frac{1}{\sqrt{2}}\mathcal{C}_{3}G_{K^{*+}\bar{K}^{*0}}(M_{12})T_{K^{*+}\bar{K}^{*0}\rightarrow K^{+}\bar{K}^{0}}(M_{12}),$

where the factors $V_{P}^{*^{\prime}}V_{cs}V_{ud}$, $V_{P}V_{cs}V_{ud}$, and $V_{P}^{*}V_{cs}V_{ud}$ in Eq. (11) have been absorbed into the parameters $\mathcal{C}_{1}$, $\mathcal{C}_{2}$, and $\mathcal{C}_{3}$, respectively. In the present work, we take them as the free constants, which are independent on the invariant masses and contain the global normalization factor for matching the events of the experimental data. $M_{ij}$ is the energy of two particles in the center-of-mass (c.m.) frame, where the lower indices $i,j=1,2,3$ denote the three final states of $K_{S}^{0}(\bar{K}^{0})$, $K^{+}$, and $\pi^{0}$, respectively. Besides, $G_{PP^{{}^{\prime}}(VV^{{}^{\prime}})}$ and $T_{PP^{{}^{\prime}}(VV^{{}^{\prime}})\rightarrow PP^{{}^{\prime}}}$ are the loop functions and the two-body scattering amplitudes, respectively. Then, as done in Ref. Dai:2021owu , we take $|K_{S}^{0}\rangle=\frac{1}{\sqrt{2}}(|K^{0}\rangle-|\bar{K}^{0}\rangle)$, and change the final state from $\bar{K}^{0}$ to $K_{S}^{0}$, where Eq. (12) becomes

	$\displaystyle t_{S\text{-wave}}(M_{12})\big{|}_{K^{0}_{S}K^{+}\pi^{0}}=$	$\displaystyle-\frac{1}{2}\mathcal{C}_{1}G_{\rho^{+}\phi}(M_{12})T_{\rho^{+}\phi\rightarrow K^{+}\bar{K}^{0}}(M_{12})$		(13)
		$\displaystyle-\frac{1}{2}\mathcal{C}_{2}-\frac{1}{2}\mathcal{C}_{2}G_{K^{+}\bar{K}^{0}}(M_{12})T_{K^{+}\bar{K}^{0}\rightarrow K^{+}\bar{K}^{0}}(M_{12})$
		$\displaystyle-\frac{1}{2}\mathcal{C}_{3}G_{K^{*+}\bar{K}^{*0}}(M_{12})T_{K^{*+}\bar{K}^{*0}\rightarrow K^{+}\bar{K}^{0}}(M_{12}).$

Furthermore, the rescattering amplitudes $T_{\rho^{+}\phi\rightarrow K^{+}\bar{K}^{0}}$, $T_{K^{+}\bar{K}^{0}\rightarrow K^{+}\bar{K}^{0}}$, and $T_{K^{*+}\bar{K}^{*0}\rightarrow K^{+}\bar{K}^{0}}$ in Eq. (13) can be calculated by the coupled channel Bethe-Salpeter equation of the on-shell form,

$\displaystyle T=[1-vG]^{-1}v,$

(14)

where the matrix $v$ is constituted by the $S$-wave interaction potentials in the coupled channels. In the present work, we consider the interactions of five channels $K^{*+}\bar{K}^{*0}$, $\rho^{+}\omega$, $\rho^{+}\phi$, $K^{+}\bar{K}^{0}$, and $\pi^{+}\eta$, where one can expect that the states $a_{0}(980)$ and $a_{0}(1710)$ will be dynamically generated. Among them, the potential elements of $v_{VV\rightarrow VV}$ are taken from the Appendix of Ref. Geng:2008gx (the arXiv version), which included the contact and exchange vector meson terms. The $VVP$ vertex is suppressed, and thus, the contributions of exchange pseudoscalar meson are ignored. As done in Ref. Wang:2019niy , the potentials $v_{PP\rightarrow PP}$ are taken from Refs. Oller:1997ti ; Duan:2020vye ; Xie:2014tma , which only included the contact items from the chiral Lagrangian. The ones $v_{VV\rightarrow PP}$ are evaluated with the approach of Ref. Wang:2022pin , where the Feynman diagrams of t- and u-channels were considered, as depicted in Fig. 4. The interaction Lagrangian for the $VPP$ vertex is given by Bando:1984ej ; Bando:1987br ,

$\displaystyle\mathcal{L}_{VPP}=-ig\left\langle V_{\mu}\left[P,\partial^{\mu}P\right]\right\rangle,$

(15)

with $g=M_{V}/(2f_{\pi})$, where taking $M_{V}=0.84566$ GeV is the averaged vector-meson mass and $f_{\pi}=0.093$ GeV pion decay constant, which are taken from Ref. Wang:2022pin . Thus, the interaction potentials are given by

		$\displaystyle v_{K^{*+}\bar{K}^{*0}\rightarrow K^{+}\bar{K}^{0}}=\left(\frac{2}{t-m_{\pi}^{2}}-\frac{6}{t-m_{\eta}^{2}}\right)g^{2}\epsilon_{1\mu}k_{3}^{\mu}\epsilon_{2\nu}k_{4}^{\nu},$		(16)
		$\displaystyle v_{K^{*+}\bar{K}^{*0}\rightarrow\pi^{+}\eta}=-2\sqrt{6}\left(\frac{g^{2}}{t-m_{K}^{2}}\epsilon_{1\mu}k_{3}^{\mu}\epsilon_{2\nu}k_{4}^{\nu}+\frac{g^{2}}{u-m_{K}^{2}}\epsilon_{1\mu}k_{4}^{\mu}\epsilon_{2\nu}k_{3}^{\nu}\right),$
		$\displaystyle v_{\rho^{+}\omega\rightarrow K^{+}\bar{K}^{0}}=-2\sqrt{2}\left(\frac{g^{2}}{t-m_{K}^{2}}\epsilon_{1\mu}k_{3}^{\mu}\epsilon_{2\nu}k_{4}^{\nu}+\frac{g^{2}}{u-m_{K}^{2}}\epsilon_{1\mu}k_{4}^{\mu}\epsilon_{2\nu}k_{3}^{\nu}\right),$
		$\displaystyle v_{\rho^{+}\omega\rightarrow\pi^{+}\eta}=0,$
		$\displaystyle v_{\rho^{+}\phi\rightarrow K^{+}\bar{K}^{0}}=4\left(\frac{g^{2}}{t-m_{K}^{2}}\epsilon_{1\mu}k_{3}^{\mu}\epsilon_{2\nu}k_{4}^{\nu}+\frac{g^{2}}{u-m_{K}^{2}}\epsilon_{1\mu}k_{4}^{\mu}\epsilon_{2\nu}k_{3}^{\nu}\right),$
		$\displaystyle v_{\rho^{+}\phi\rightarrow\pi^{+}\eta}=0,$

where $t=(k_{1}-k_{3})^{2}$ and $u=(k_{1}-k_{4})^{2}$ are defined, $\epsilon_{i}$ is polarization vector, and $k_{i}$ three-momentum of the corresponding particles with the lower index $i$ ($i=1,2,3,4$) denoting the particles in scattering process $V(1)V(2)\rightarrow P(3)P(4)$. Compared with $v_{VV\rightarrow VV}$, the potentials of $v_{VV\rightarrow PP}$ are much strengthened, and thus, a monopole form factor is introduced at each $VPP$ vertex of the exchanged pseudoscalar meson as done in Refs. Molina:2008jw ; Oset:2012zza ; Wang:2021jub ,

$\displaystyle F=\frac{\Lambda^{2}-m_{ex}^{2}}{\Lambda^{2}-q^{2}},$

(17)

where $m_{ex}$ is the mass of the exchanged pseudoscalar meson, and $q$ the transferred momentum. The value of parameter $\Lambda$ is empirically chosen as $1.0$ GeV. After performing the partial wave projection, one can obtain the $S$-wave potentials $v$.

The diagonal matrix $G$ is made up of the meson-meson two-point loop functions, where the explicit form of the element of matrix $G$ with the dimensional regularization is given by Oller:2000fj ; Oller:1998zr ; Gamermann:2006nm ; Alvarez-Ruso:2010rqm ; Guo:2016zep ,

	$\displaystyle G_{ii}(M_{inv})=$	$\displaystyle\frac{1}{16\pi^{2}}\left\{a_{ii}(\mu)+\ln\frac{m_{1}^{2}}{\mu^{2}}+\frac{m_{2}^{2}-m_{1}^{2}+M_{inv}^{2}}{2M_{inv}^{2}}\ln\frac{m_{2}^{2}}{m_{1}^{2}}\right.$		(18)
		$\displaystyle+\frac{q_{cmi}(M_{inv})}{M_{inv}}\left[\ln\left(M_{inv}^{2}-\left(m_{2}^{2}-m_{1}^{2}\right)+2q_{cmi}(M_{inv})M_{inv}\right)\right.$
		$\displaystyle+\ln\left(M_{inv}^{2}+\left(m_{2}^{2}-m_{1}^{2}\right)+2q_{cmi}(M_{inv})M_{inv}\right)$
		$\displaystyle-\ln\left(-M_{inv}^{2}-\left(m_{2}^{2}-m_{1}^{2}\right)+2q_{cmi}(M_{inv})M_{inv}\right)$
		$\displaystyle\left.\left.-\ln\left(-M_{inv}^{2}+\left(m_{2}^{2}-m_{1}^{2}\right)+2q_{cmi}(M_{inv})M_{inv}\right)\right]\right\},$

where $m_{1}$ and $m_{2}$ are the masses of the intermediate mesons in the loops, $M_{inv}$ is the invariant mass of the meson-meson system, $\mu$ the regularization scale, of which the value will be discussed in Sec. III, and the $a_{ii}(\mu)$ the subtraction constant. As done in Refs. Duan:2020vye ; Wang:2021kka , its value can be evaluated by Eq. (17) of Ref. Oller:2000fj ,

$\displaystyle a_{ii}(\mu)=-2\ln\left(1+\sqrt{1+\frac{m_{1}^{2}}{\mu^{2}}}\right)+\cdots,$

(19)

where $m_{1}$ is the mass of a larger-mass meson in the corresponding channels, and the ellipses indicates the ingnored higher order terms in the nonrelativistic expansion Guo:2018tjx . Besides, $q_{cmi}(M_{inv})$ is the three-momentum of the particle in the c.m. frame,

$\displaystyle q_{cmi}(M_{inv})=\frac{\lambda^{1/2}\left(M_{inv}^{2},m_{1}^{2},m_{2}^{2}\right)}{2M_{inv}},$

(20)

with the usual Källen triangle function $\lambda(a,b,c)=a^{2}+b^{2}+c^{2}-2(ab+ac+bc)$.

In addition, we also consider the contributions of the vector resonances in the intermediate states in the $P$-wave as discussed above, such as the ones $\bar{K}^{*}(892)^{0}$ and $K^{*}(892)^{+}$, which are not produced in the meson-meson scattering amplitudes. The production mechanisms are depicted in Fig. 5. Referring to Refs. Toledo:2020zxj ; Roca:2020lyi , the relativistic amplitude for the decay $D_{s}^{+}\rightarrow\bar{K}^{*}(892)^{0}K^{+}\rightarrow K_{S}^{0}\pi^{0}K^{+}$ can be written as,

	$\displaystyle t_{\bar{K}^{*}(892)^{0}}(M_{12},M_{13})=$	$\displaystyle\frac{\mathcal{D}_{1}e^{i\phi_{\bar{K}^{*}(892)^{0}}}}{M_{13}^{2}-m_{\bar{K}^{*}(892)^{0}}^{2}+im_{\bar{K}^{*}(892)^{0}}\Gamma_{\bar{K}^{*}(892)^{0}}}$		(21)
		$\displaystyle\times\left[(m_{K_{S}^{0}}^{2}-m_{\pi^{0}}^{2})\frac{m_{D_{s}^{+}}^{2}-m_{K^{+}}^{2}}{m_{\bar{K}^{*}(892)^{0}}^{2}}-M_{12}^{2}+M_{23}^{2}\right],$

where $\mathcal{D}_{1}$ is a unknown constant, $\phi_{\bar{K}^{*}(892)^{0}}$ a phase for the interference effect, the mass of $\bar{K}^{*}(892)^{0}$ taken as $m_{\bar{K}^{*}(892)^{0}}=0.89555$ GeV, and the width taken as $\Gamma_{\bar{K}^{*}(892)^{0}}=0.0473$ GeV, both of which are taken from the Particle Data Group (PDG) Workman:2022ynf . Note that the invariant masses $M_{ij}$ fulfil the constraint condition,

$\displaystyle M_{12}^{2}+M_{13}^{2}+M_{23}^{2}=m_{D_{s}^{+}}^{2}+m_{K_{S}^{0}}^{2}+m_{K^{+}}^{2}+m_{\pi^{0}}^{2}.$

(22)