Arbitrarily Structured Laser Pulses
Abstract
Spatiotemporal control refers to a class of optical techniques for structuring a laser pulse with coupled space-time dependent properties, including moving focal points, dynamic spot sizes, and evolving orbital angular momenta. Here we introduce the concept of arbitrarily structured laser (ASTRL) pulses which generalizes these techniques. The ASTRL formalism employs a superposition of prescribed pulses to create a desired electromagnetic field structure. Several examples illustrate the versatility of ASTRL pulses to address a range of laser-based applications.
Light can exhibit structures in space, time, or coupled space-time. The realization that these structures can be shaped using optical techniques has led to a deeper understanding of the fundamental properties of light and advances in multiple laser-based applications. Spatial shaping involves the use of static optical elements, such as phase plates, deformable mirrors, or spatial light modulators, to form transverse structures with orbital angular momentum, Airy or Bessel profiles, or tailored speckle patterns [1, 2, 3, 4]. Temporal shaping typically employs Fourier methods, in which frequency components are separated by diffraction gratings and separately modified, to synthesize pulses with nearly arbitrary time-dependent waveforms and polarizations [5, 6, 7].
Spatiotemporal pulse shaping invokes some combination of these techniques. Examples go back as far as smoothing by spectral dispersion (1989) [8] and pulse front tilt (1996) [9]. More modern examples include spatiotemporal optical vortices (STOVs) [10, 11, 12], diffraction-free light sheets [13, 14, 15], and flying focus concepts [16, 17, 18, 19]. Flying focus pulses, in particular, feature intensity peaks with programmable trajectories that can travel distances far greater than a Rayleigh range while maintaining a near-constant profile. The trajectory control afforded by these pulses has been proposed as a means to overcome limitations of traditional pulses in a number of applications, including laser wakefield acceleration [20, 21, 22], Raman amplification [23], photon acceleration [24], vacuum electron acceleration [25], and nonlinear Thomson scattering [26], as well as for the exploration of fundamental physics, such as radiation reaction [27] and nonlinear Compton scattering [28].
There are two approaches for creating spatiotemporally structured pulses. The first approach requires identifying a specific solution to Maxwell’s equations. Once known, this solution can be synthesized using programmable phase modulation techniques. This is the approach taken to create light sheets and STOVs. However, this approach does not provide a method to systematically identify new solutions of Maxwell’s equations with features that are desirable for a particular application. In the second approach, one imagines an electromagnetic structure with desirable features and synthesizes this structure using a superposition of solutions to Maxwell’s equations with known properties. This is the approach presented here.
In this letter, we introduce a concept and theoretical formalism for generating laser pulses with arbitrary structure. These arbitrarily structured laser (ASTRL) pulses are synthesized using a superposition of traditional laser pulses with controlled and varying properties. The ASTRL formalism generalizes the creation of pulses with evolving focal points (flying foci), spot size, orbital angular momentum, and polarization, and can also describe pulses with exotic topological structure such as STOVs. An example of each of these is presented. The flexibility of the ASTRL concept opens new and previously unimagined possibilities for structured light with the potential to improve a wide range of laser-based applications, while its simplicity facilitates implementation into simulations.
The formulation of the ASTRL concept begins with the vacuum wave equation for the electric field of a laser pulse:
| (1) |
ASTRL pulses are constructed by superposing solutions to Eq. 1 with varying properties. The electric field of an ASTRL pulse can be expressed either as a sum or an integral over these solutions:
| (2) |
where parameterizes the varying properties of the solutions. For example the amplitude, spot size, focal point, pulse duration, or relative delay of each can all depend on . Equation 2 is the most general representation of an ASTRL pulse in vacuum.
Analytic solutions for simplify the process of designing an ASTRL pulse for a specific application. Paraxial solutions, in particular, are expressed in terms of familiar quantities that can be parameterized in terms of . To derive such solutions, consider a laser pulse propagating in the -direction with constant polarization . The transverse electric field can be expressed as an envelope modulated by a carrier
| (3) |
where is the central wavenumber and . Substituting Eq. 3 into Eq. 1 and performing the Galilean change of variables provides
| (4) |
Upon applying the slowly-varying envelope approximation (), Eq. 4 reduces to
| (5) |
Equation 5 is the paraxial wave equation and its operator is independent of . This independence admits separable solutions, i.e., solutions with no spatiotemporal coupling, of the form
| (6) |
where satisfies and is an arbitrary function. For example, may be any Laguerre-, Hermite-, or Ince-Gaussian mode and the longitudinal profile may be .
The transverse electric field of a coherent ASTRL pulse can be approximated by summing or integrating over paraxial solutions:
| (7) |
where the properties of , , and may vary with respect to . The integral over may introduce spatiotemporal coupling, such that in general, Eq. 7 cannot be written as a separable function. Thus, may possess a high degree of spatiotemporal coupling despite the absence of coupling in Eq. 6.
The -dependence of may encode a delay , duration , and weight for each constituent pulse as
| (8) |
The durations set the fastest timescale over which the properties of the ASTRL pulse can vary and determine the number of pulses required for discrete approximation of Eq. 7 (see Supplemental). Unless otherwise stated, and will be independent of for the examples presented here.
A natural example for the -dependence of is an -indexed Gaussian-beam:
| (9) |
where is the complex beam parameter and is the number of transverse dimensions. In Eq. 9, the longitudinal focal position , transverse focal position , and Rayleigh range (and associated spot size ) may all be expressed as functions of the integration variable , which allows for extended focal ranges and evolving transverse structure. More generally, the mode numbers of the transverse profile can depend on , e.g., the radial or orbital angular momentum (OAM) quantum numbers of a Laguerre-Gaussian mode. Finally, may encode an evolving polarization.
The utility and generality of the ASTRL concept will be demonstrated by using Eq. 7 to construct several examples of spatiotemporally structured laser pulses. To begin, consider the flying focus [16, 17]. Each time slice in a flying focus pulse has a different focal point along the propagation axis. The time and location at which each slice comes to focus can be controlled to produce an intensity peak that travels at any velocity, including backwards or faster than the speed of light. Within the ASTRL formalism, a flying focus pulse may be described using a Gaussian transverse profile (Eq. 9) with and . This choice of produces a focal range extending from to , where can be much larger than . At each in the focal range, the focus will occur at a time determined by the condition . The delay required for a given focal trajectory can be derived from geometric optics as in Ref [20]. For example, motion of the focal point at a constant velocity is attained with .
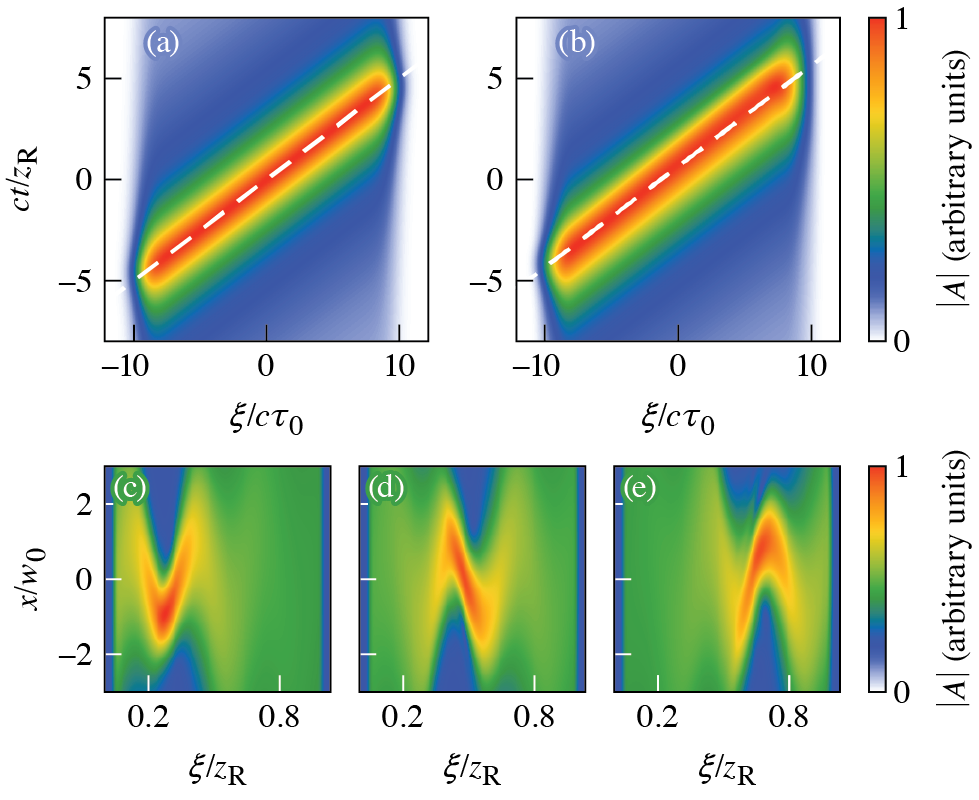
Figure 1(a) displays the on-axis envelope of a superluminal () flying focus pulse obtained by evaluating Eq. 7. The white dashed line shows the spacetime trajectory and demonstrates that the laser envelope travels at the expected velocity over 10 Rayleigh ranges. A finite-difference time-domain (FDTD) simulation of the full set of Maxwell’s equations produces nearly identical results [Fig. 1(b)]. The simulation used Eq. 7 to initialize the fields, but did not make the approximations leading to Eq. 5. A slight discrepancy can be observed near due to the inexactness of Eq. 6. The simulation was conducted using the code OSIRIS [29] with quasi-3D azimuthal decomposition [30] and the solver introduced in Ref [31] to mitigate numerical dispersion.
The ASTRL concept can also be used to describe new types of generalized flying focus pulses. For instance, a pulse whose focal point oscillates in the transverse direction as it translates along the propagation axis could serve as a controllable wiggler for generating radiation from relativistic electron bunches or enhance direct laser acceleration of electrons through new parametric resonances. Such a pulse can be constructed by parameterizing both the transverse and longitudinal focal coordinates: and , where, as before, . Figures 1(c)–(e) display the envelope from 2D OSIRIS simulations of this configuration. The intensity peak undergoes the expected oscillatory motion. Here, is given by Eq. 9 and , i.e., the focal point moves with a constant axial velocity.
Aside from moving focal points, many applications can benefit from pulses that have a fixed focal point with prescribed spatiotemporal profiles or time-dependent polarization (Fig. 2). Traditional Fourier techniques for temporal pulse shaping, as in Ref [6], produce pulses described by Eq. 6 with a customized . Similarly, previous polarization-structuring methods amount to evaluating Eq. 7 with a prescribed and , but with a that is independent of . Figure 2(a) shows an example. This particular ASTRL pulse is constructed from a discrete sum of seven pulses, indexed by , that share a common focal point, . The delay and polarization of each pulse is given by and while is given by Eq. 9. Evolving polarization structures as in this example have led to advances in nonlinear spectroscopy [32], quantum control [33, 34], nanophotonics [35], and a number of other areas [36, 37]. More exotic pulses with continuous polarization evolution can also be described using the ASTRL concept.
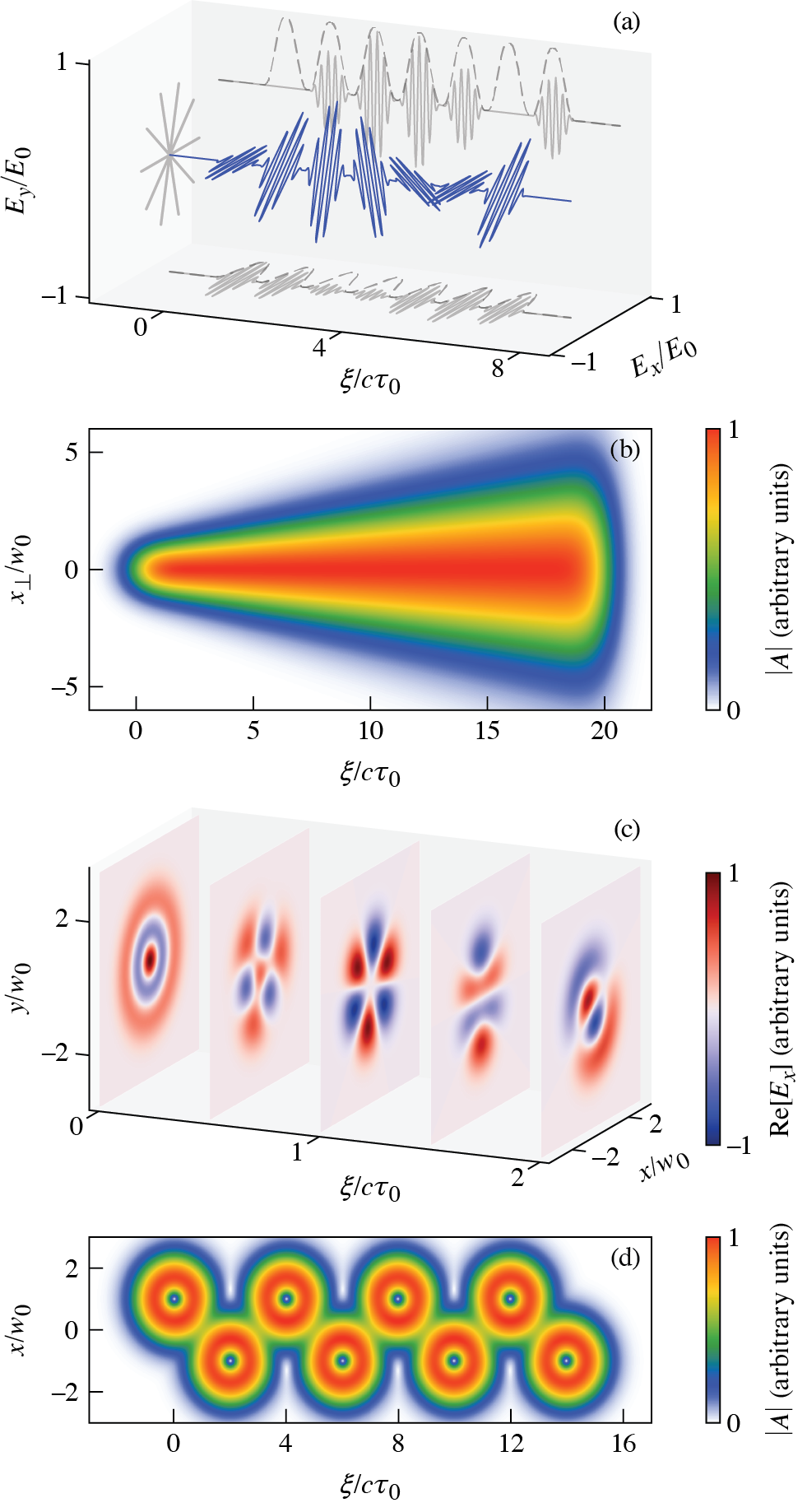
A time-dependent spot size can improve the performance of applications including laser wakefield acceleration [38] and inertial confinement fusion [39, 40, 41]. In laser wakefield acceleration, a spot size that increases in time can stabilize the propagation of an intense laser pulse in a plasma channel [38]. While in inertial confinement fusion, a spot size that decreases continuously in time can mitigate cross-beam energy transfer [39, 40, 41]. As demonstrated in Fig. 2(b), such a pulse can be described by Eqs. 7, 8, and 9 with a spot size parameterized as and the delay , where .
The orbital angular momentum and radial mode numbers ( and , respectively) of Laguerre-Gaussian modes provide additional degrees of freedom to structure the time-dependence of the transverse profile. Figure 2(c) displays a sequence of time slices in an ASTRL pulse formed by superposing three pulses that partially overlap in time with . Each pulse is indexed by , has a delay , and a weight . This construction produces a quasi-continuous transformation in angular momentum. In the first, third, and fifth frames, one pulse dominates, and the transverse profile is nearly a pure Laguerre-Gaussian mode; in the second and fourth frames, two pulses interfere to produce a hybrid mode. Investigations into structured OAM have only recently begun [42, 43, 44], but its potential for ultrafast probing of chiral systems has already drawn attention [44]. Many other applications based on OAM [45], including optical trapping and manipulation [46, 47, 48, 49], imaging [50, 51, 52], quantum optics [53, 54], nonlinear optics [55], and laser-plasma interactions [56, 57, 58, 59, 60, 61, 62, 63], may also benefit from added control over its structure.
As a final example, the ASTRL concept can be used to construct STOVs. In fact, the vacuum STOV solution introduced in Ref. [10],
| (10) |
is a superposition of two separable solutions as in Eq. 6, where the functions are Hermite-Gaussian modes of order and . Here the -dependence has been included, , and is the complex conjugate of . The generalization of Eq. 10 to higher-order vortex topologies (see Ref. [12]) can also be expressed as a superposition of separable solutions. Figure 2(d) illustrates a novel STOV “lattice” assembled by superposing solutions in the form of Eq. 10. The solutions are indexed by with delays , transverse displacements alternating between , and polarities (the sign in Eq. 10) alternating between .
The ASTRL description is particularly useful for simulations of structured light and its applications. Previous simulations of flying focus pulses required a Fresnel integral to propagate the field from the optic plane of a specific experimental design to the simulation plane. In contrast, the ASTRL description enables direct field initialization in the simulation plane, which simplifies implementation. Further, by decoupling the structured light-matter interaction physics from the details of a particular optical configuration, the ASTRL description expedites prototyping of new concepts. For example, the axiparabola-echelon pair used in Ref. [20] would not need to be redesigned for every simulation. An optical configuration capable of delivering the desired pulse can be designed or implemented in a simulation after a concept shows promise (see Supplemental).
As demonstrated by the examples above, an ASTRL pulse may generally exhibit spatiotemporal coupling despite being assembled from pulses with no spatiotemporal coupling (i.e., Eq. 6). The separability of Eq. 6 was derived by reducing the full wave equation (Eq. 4) to the paraxial wave equation (Eq. 5). The validity of the approximations leading to Eq. 5 may be determined by evaluating derivatives of the approximate solution . At any location, when ; this is the usual paraxial approximation, which fails only for tightly focused laser pulses. On the other hand, when . This condition only fails for pulses with durations less than a few-cycles. These two conditions, i.e., and , place constraints on and , respectively.
For an envelope that is initially separable at some , spatiotemporal coupling will develop beyond a range because of the term in Eq. 4 (see Supplemental). There are two common scenarios that can be considered. In the first scenario, every pulse comprising an ASTRL pulse is separable at its focus. Because each pulse only contributes significantly within a Rayleigh range of its focus, the condition on the accuracy of Eq. 6 can be expressed as or, equivalently, . In the second scenario, which is more applicable to field initialization in a simulation, every pulse is separable at a specified distance from focus. The condition on the accuracy of Eq. 6 is then given by . For example, in Fig. 1(a-b) , which contributes to the slight discrepancy at the end of the focal region. However, even if and spatiotemporal coupling develops in the constituent pulses, the qualitative features of the desired electromagnetic structure would remain intact.
The generality of the ASTRL concept extends well beyond Eq. 7 and the examples presented here. The time-dependence of any combination of parameters, such as the longitudinal focal point and OAM, can be simultaneously structured. Further, the ASTRL concept can be extended to accommodate multi-color pulses [64, 65], superpositions of pulses with vector polarization [66, 67, 68, 69], and pulses structured in the spatiospectral domain. In fact, using a wavelet transform one can show that arbitrary monochromatic laser fields may be decomposed as a generalized version of Eq. 7 (see Supplemental).
The ASTRL formalism provides a framework for constructing laser pulses with desired spatiotemporal structure. An ASTRL pulse is synthesized using superpositions of known solutions to Maxwell’s equations, such as an ensemble of traditional laser pulses. The flexibility of the ASTRL concept was illustrated with several examples, including pulses with moving focal points, dynamic polarization, evolving angular momentum, and nontrivial topological structure. In addition to facilitating the creation of new and previously unimagined electromagnetic structures, the ASTRL formalism simplifies the injection of structured light in simulations. New pulses based on this concept may enable or enhance techniques in a range of scientific disciplines, including microscopy, non-linear optics, quantum optics, and laser-plasma interactions.
Acknowledgements.
The authors graciously acknowledge C. Joshi, D. H. Froula, M. Vranic, E. P. Alves, SJ Spencer, A. Di Piazza, M. Formanek, T. Carbin, and C. Barkan for their lucid insights. Work supported by the National Science Foundation award 2108970, the Department of Energy contracts DE-SC00215057 and DE-SC0010064, the Scientific Discovery through Advanced Computing (SciDAC) program through a Fermi National Accelerator Laboratory (FNAL) subcontract No. 644405, and the Unversity of Rochester, Laboratory for Laser Energetics. Computer simulations were performed on NERSC’s Cori cluster (account m1157). J. Pierce was supported by a scholarship from the Directed Energy Professional Society.References
- Beijersbergen et al. [1994] M. Beijersbergen, R. Coerwinkel, M. Kristensen, and J. Woerdman, Helical-wavefront laser beams produced with a spiral phaseplate, Optics Communications 112, 321 (1994).
- Siviloglou et al. [2007] G. A. Siviloglou, J. Broky, A. Dogariu, and D. N. Christodoulides, Observation of accelerating airy beams, Phys. Rev. Lett. 99, 213901 (2007).
- Chattrapiban et al. [2003] N. Chattrapiban, E. A. Rogers, D. Cofield, I. Wendell T. Hill, and R. Roy, Generation of nondiffracting bessel beams by use of a spatial light modulator, Opt. Lett. 28, 2183 (2003).
- Kato et al. [1984] Y. Kato, K. Mima, N. Miyanaga, S. Arinaga, Y. Kitagawa, M. Nakatsuka, and C. Yamanaka, Random phasing of high-power lasers for uniform target acceleration and plasma-instability suppression, Phys. Rev. Lett. 53, 1057 (1984).
- Weiner [2000] A. M. Weiner, Femtosecond pulse shaping using spatial light modulators, Review of Scientific Instruments 71, 1929 (2000), https://doi.org/10.1063/1.1150614 .
- Weiner [2011] A. M. Weiner, Ultrafast optical pulse shaping: A tutorial review, Optics Communications 284, 3669 (2011).
- Brixner and Gerber [2001] T. Brixner and G. Gerber, Femtosecond polarization pulse shaping, Optics letters 26, 557 (2001).
- Skupsky et al. [1989] S. Skupsky, R. Short, T. Kessler, R. Craxton, S. Letzring, and J. Soures, Improved laser-beam uniformity using the angular dispersion of frequency-modulated light, Journal of Applied Physics 66, 3456 (1989).
- Hebling [1996] J. Hebling, Derivation of the pulse front tilt caused by angular dispersion, Optical and Quantum Electronics 28, 1759 (1996).
- Jhajj et al. [2016] N. Jhajj, I. Larkin, E. Rosenthal, S. Zahedpour, J. Wahlstrand, and H. Milchberg, Spatiotemporal optical vortices, Physical Review X 6, 031037 (2016).
- Hancock et al. [2019] S. Hancock, S. Zahedpour, A. Goffin, and H. Milchberg, Free-space propagation of spatiotemporal optical vortices, Optica 6, 1547 (2019).
- Hancock et al. [2021] S. W. Hancock, S. Zahedpour, and H. M. Milchberg, Mode structure and orbital angular momentum of spatiotemporal optical vortex pulses, Phys. Rev. Lett. 127, 193901 (2021).
- Kondakci and Abouraddy [2016] H. E. Kondakci and A. F. Abouraddy, Diffraction-free pulsed optical beams via space-time correlations, Optics Express 24, 28659 (2016).
- Kondakci and Abouraddy [2017] H. E. Kondakci and A. F. Abouraddy, Diffraction-free space–time light sheets, Nature Photonics 11, 733 (2017).
- Kondakci and Abouraddy [2019] H. Kondakci and A. F. Abouraddy, Optical space-time wave packets having arbitrary group velocities in free space, Nature communications 10, 1 (2019).
- Sainte-Marie et al. [2017] A. Sainte-Marie, O. Gobert, and F. Quéré, Controlling the velocity of ultrashort light pulses in vacuum through spatio-temporal couplings, Optica 4, 1298 (2017).
- Froula et al. [2018] D. H. Froula, D. Turnbull, A. S. Davies, T. J. Kessler, D. Haberberger, J. P. Palastro, S.-W. Bahk, I. A. Begishev, R. Boni, S. Bucht, J. Katz, and J. L. Shaw, Spatiotemporal control of laser intensity, Nature Photonics 12, 262 (2018).
- Simpson et al. [2020] T. T. Simpson, D. Ramsey, P. Franke, N. Vafaei-Najafabadi, D. Turnbull, D. H. Froula, and J. P. Palastro, Nonlinear spatiotemporal control of laser intensity, Opt. Express 28, 38516 (2020).
- Simpson et al. [2022] T. T. Simpson, D. Ramsey, P. Franke, K. Weichman, M. V. Ambat, D. Turnbull, D. H. Froula, and J. P. Palastro, Spatiotemporal control of laser intensity through cross-phase modulation, Opt. Express 30, 9878 (2022).
- Palastro et al. [2020] J. Palastro, J. Shaw, P. Franke, D. Ramsey, T. Simpson, and D. Froula, Dephasingless laser wakefield acceleration, Physical Review Letters 124, 10.1103/physrevlett.124.134802 (2020).
- Palastro et al. [2021] J. P. Palastro, B. Malaca, J. Vieira, D. Ramsey, T. T. Simpson, P. Franke, J. L. Shaw, and D. H. Froula, Laser-plasma acceleration beyond wave breaking, Physics of Plasmas 28, 013109 (2021).
- Caizergues et al. [2020] C. Caizergues, S. Smartsev, V. Malka, and C. Thaury, Phase-locked laser-wakefield electron acceleration, Nature Photonics 14, 475 (2020).
- Turnbull et al. [2018] D. Turnbull, S. Bucht, A. Davies, D. Haberberger, T. Kessler, J. Shaw, and D. Froula, Raman amplification with a flying focus, Physical Review Letters 120, 10.1103/physrevlett.120.024801 (2018).
- Howard et al. [2019] A. Howard, D. Turnbull, A. Davies, P. Franke, D. Froula, and J. Palastro, Photon acceleration in a flying focus, Physical Review Letters 123, 10.1103/physrevlett.123.124801 (2019).
- Ramsey et al. [2020] D. Ramsey, P. Franke, T. T. Simpson, D. H. Froula, and J. P. Palastro, Vacuum acceleration of electrons in a dynamic laser pulse, Physical Review E 102, 10.1103/physreve.102.043207 (2020).
- Ramsey et al. [2022] D. Ramsey, B. Malaca, A. Di Piazza, M. Formanek, P. Franke, D. Froula, M. Pardal, T. Simpson, J. Vieira, K. Weichman, et al., Nonlinear thomson scattering with ponderomotive control, Physical Review E 105, 065201 (2022).
- Formanek et al. [2022] M. Formanek, D. Ramsey, J. P. Palastro, and A. Di Piazza, Radiation reaction enhancement in flying focus pulses, Phys. Rev. A 105, L020203 (2022).
- Piazza [2021] A. D. Piazza, Unveiling the transverse formation length of nonlinear compton scattering, Physical Review A 103, 10.1103/physreva.103.012215 (2021).
- Fonseca et al. [2002] R. A. Fonseca, L. O. Silva, F. S. Tsung, V. K. Decyk, W. Lu, C. Ren, W. B. Mori, S. Deng, S. Lee, T. Katsouleas, and J. C. Adam, OSIRIS: A three-dimensional, fully relativistic particle in cell code for modeling plasma based accelerators, in Lecture Notes in Computer Science (Springer Berlin Heidelberg, 2002) pp. 342–351.
- Davidson et al. [2015] A. Davidson, A. Tableman, W. An, F. Tsung, W. Lu, J. Vieira, R. Fonseca, L. Silva, and W. Mori, Implementation of a hybrid particle code with a PIC description in r–z and a gridless description in into OSIRIS, Journal of Computational Physics 281, 1063 (2015).
- Li et al. [2021] F. Li, K. G. Miller, X. Xu, F. S. Tsung, V. K. Decyk, W. An, R. A. Fonseca, and W. B. Mori, A new field solver for modeling of relativistic particle-laser interactions using the particle-in-cell algorithm, Computer Physics Communications 258, 107580 (2021).
- Silberberg [2009] Y. Silberberg, Quantum coherent control for nonlinear spectroscopy and microscopy, Annual review of physical chemistry 60, 277 (2009).
- Villeneuve et al. [2000] D. Villeneuve, S. Aseyev, P. Dietrich, M. Spanner, M. Y. Ivanov, and P. Corkum, Forced molecular rotation in an optical centrifuge, Physical Review Letters 85, 542 (2000).
- Brixner et al. [2004] T. Brixner, G. Krampert, T. Pfeifer, R. Selle, G. Gerber, M. Wollenhaupt, O. Graefe, C. Horn, D. Liese, and T. Baumert, Quantum control by ultrafast polarization shaping, Physical review letters 92, 208301 (2004).
- Aeschlimann et al. [2007] M. Aeschlimann, M. Bauer, D. Bayer, T. Brixner, F. J. García de Abajo, W. Pfeiffer, M. Rohmer, C. Spindler, and F. Steeb, Adaptive subwavelength control of nano-optical fields, Nature 446, 301 (2007).
- Rubinsztein-Dunlop et al. [2016] H. Rubinsztein-Dunlop, A. Forbes, M. V. Berry, M. R. Dennis, D. L. Andrews, M. Mansuripur, C. Denz, C. Alpmann, P. Banzer, T. Bauer, et al., Roadmap on structured light, Journal of Optics 19, 013001 (2016).
- Misawa [2016] K. Misawa, Applications of polarization-shaped femtosecond laser pulses, Advances in Physics: X 1, 544 (2016).
- Benedetti et al. [2012] C. Benedetti, C. B. Schroeder, E. Esarey, and W. P. Leemans, Quasi-matched propagation of high-intensity, ultra-short laser pulses in plasma channels, AIP Conference Proceedings 1507, 252 (2012), https://aip.scitation.org/doi/pdf/10.1063/1.4773702 .
- Igumenshchev et al. [2013] I. V. Igumenshchev, D. H. Froula, D. H. Edgell, V. N. Goncharov, T. J. Kessler, F. J. Marshall, R. L. McCrory, P. W. McKenty, D. D. Meyerhofer, D. T. Michel, T. C. Sangster, W. Seka, and S. Skupsky, Laser-beam zooming to mitigate crossed-beam energy losses in direct-drive implosions, Physical Review Letters 110, 10.1103/physrevlett.110.145001 (2013).
- Froula et al. [2013] D. Froula, T. Kessler, I. Igumenshchev, R. Betti, V. Goncharov, H. Huang, S. Hu, E. Hill, J. Kelly, D. Meyerhofer, et al., Mitigation of cross-beam energy transfer: Implication of two-state focal zooming on omega, Physics of Plasmas 20, 082704 (2013).
- Huang et al. [2016] X. Huang, D. Hu, W. Zhou, W. Dai, X. Deng, Q. Yuan, Q. Zhu, and F. Jing, Optical zooming based on focusing grating in direct drive icf, Optics Express 24, 22051 (2016).
- Zhou et al. [2022] Z. Zhou, C. Min, H. Ma, Y. Zhang, X. Xie, H. Zhan, and X. Yuan, Time-varying orbital angular momentum in tight focusing of ultrafast pulses, Opt. Express 30, 13416 (2022).
- Rego et al. [2019] L. Rego, K. M. Dorney, N. J. Brooks, Q. L. Nguyen, C.-T. Liao, J. San Román, D. E. Couch, A. Liu, E. Pisanty, M. Lewenstein, et al., Generation of extreme-ultraviolet beams with time-varying orbital angular momentum, Science 364, eaaw9486 (2019).
- Dorney et al. [2019] K. M. Dorney, L. Rego, N. J. Brooks, J. San Román, C.-T. Liao, J. L. Ellis, D. Zusin, C. Gentry, Q. L. Nguyen, J. M. Shaw, et al., Controlling the polarization and vortex charge of attosecond high-harmonic beams via simultaneous spin–orbit momentum conservation, Nature photonics 13, 123 (2019).
- Allen et al. [1992] L. Allen, M. W. Beijersbergen, R. Spreeuw, and J. Woerdman, Orbital angular momentum of light and the transformation of laguerre-gaussian laser modes, Physical review A 45, 8185 (1992).
- He et al. [1995] H. He, N. Heckenberg, and H. Rubinsztein-Dunlop, Optical particle trapping with higher-order doughnut beams produced using high efficiency computer generated holograms, Journal of Modern Optics 42, 217 (1995).
- Gahagan and Swartzlander [1996] K. Gahagan and G. J. Swartzlander, Optical vortex trapping of particles, Optics Letters 21, 827 (1996).
- Prentice et al. [2004] P. Prentice, M. MacDonald, T. Frank, A. Cuschieri, G. Spalding, W. Sibbett, P. Campbell, and K. Dholakia, Manipulation and filtration of low index particles with holographic laguerre-gaussian optical trap arrays, Optics Express 12, 593 (2004).
- Lorenz et al. [2007] R. M. Lorenz, J. S. Edgar, G. D. Jeffries, Y. Zhao, D. McGloin, and D. T. Chiu, Vortex-trap-induced fusion of femtoliter-volume aqueous droplets, Analytical chemistry 79, 224 (2007).
- Fürhapter et al. [2005a] S. Fürhapter, A. Jesacher, S. Bernet, and M. Ritsch-Marte, Spiral phase contrast imaging in microscopy, Optics Express 13, 689 (2005a).
- Fürhapter et al. [2005b] S. Fürhapter, A. Jesacher, S. Bernet, and M. Ritsch-Marte, Spiral interferometry, Optics letters 30, 1953 (2005b).
- Maurer et al. [2011] C. Maurer, A. Jesacher, S. Bernet, and M. Ritsch-Marte, What spatial light modulators can do for optical microscopy, Laser & Photonics Reviews 5, 81 (2011).
- Mair et al. [2001] A. Mair, A. Vaziri, G. Weihs, and A. Zeilinger, Entanglement of the orbital angular momentum states of photons, Nature 412, 313 (2001).
- Malik et al. [2016] M. Malik, M. Erhard, M. Huber, M. Krenn, R. Fickler, and A. Zeilinger, Multi-photon entanglement in high dimensions, Nature Photonics 10, 248 (2016).
- Dholakia et al. [1996] K. Dholakia, N. Simpson, M. Padgett, and L. Allen, Second-harmonic generation and the orbital angular momentum of light, Physical Review A 54, R3742 (1996).
- Mendonça et al. [2009] J. T. Mendonça, B. Thidé, and H. Then, Stimulated raman and brillouin backscattering of collimated beams carrying orbital angular momentum, Physical review letters 102, 185005 (2009).
- Ali et al. [2010] S. Ali, J. Davies, and J. Mendonca, Inverse faraday effect with linearly polarized laser pulses, Physical review letters 105, 035001 (2010).
- Gariepy et al. [2014] G. Gariepy, J. Leach, K. T. Kim, T. J. Hammond, E. Frumker, R. W. Boyd, and P. B. Corkum, Creating high-harmonic beams with controlled orbital angular momentum, Physical review letters 113, 153901 (2014).
- Vieira and Mendonça [2014] J. Vieira and J. Mendonça, Nonlinear laser driven donut wakefields for positron and electron acceleration, Physical Review Letters 112, 215001 (2014).
- Vieira et al. [2016a] J. Vieira, R. M. Trines, E. P. Alves, R. Fonseca, J. Mendonça, R. Bingham, P. Norreys, and L. Silva, High orbital angular momentum harmonic generation, Physical review letters 117, 265001 (2016a).
- Vieira et al. [2016b] J. Vieira, R. M. Trines, E. P. Alves, R. Fonseca, J. Mendonça, R. Bingham, P. Norreys, and L. Silva, Amplification and generation of ultra-intense twisted laser pulses via stimulated raman scattering, Nature communications 7, 1 (2016b).
- Shi et al. [2018] Y. Shi, J. Vieira, R. Trines, R. Bingham, B. Shen, R. Kingham, et al., Magnetic field generation in plasma waves driven by copropagating intense twisted lasers, Physical Review Letters 121, 145002 (2018).
- Nuter et al. [2022] R. Nuter, P. Korneev, and V. Tikhonchuk, Raman scattering of a laser beam carrying an orbital angular momentum, Physics of Plasmas 29, 062101 (2022).
- Kim et al. [2007] K. Y. Kim, J. H. Glownia, A. J. Taylor, and G. Rodriguez, Terahertz emission from ultrafast ionizing air in symmetry-broken laser fields, Opt. Express 15, 4577 (2007).
- Edwards et al. [2014] M. R. Edwards, V. T. Platonenko, and J. M. Mikhailova, Enhanced attosecond bursts of relativistic high-order harmonics driven by two-color fields, Optics Letters 39, 6823 (2014).
- Zhan [2009] Q. Zhan, Cylindrical vector beams: from mathematical concepts to applications, Advances in Optics and Photonics 1, 1 (2009).
- Wang et al. [2010] X.-L. Wang, Y. Li, J. Chen, C.-S. Guo, J. Ding, and H.-T. Wang, A new type of vector fields with hybrid states of polarization, Optics Express 18, 10786 (2010).
- Milione et al. [2011] G. Milione, H. I. Sztul, D. A. Nolan, and R. R. Alfano, Higher-order poincaré sphere, stokes parameters, and the angular momentum of light, Physical Review Letters 107, 10.1103/physrevlett.107.053601 (2011).
- Naidoo et al. [2016] D. Naidoo, F. S. Roux, A. Dudley, I. Litvin, B. Piccirillo, L. Marrucci, and A. Forbes, Controlled generation of higher-order poincaré sphere beams from a laser, Nature Photonics 10, 327 (2016).