Applying Surface Normal Information in Drivable Area and Road Anomaly Detection for Ground Mobile Robots
Abstract
The joint detection of drivable areas and road anomalies is a crucial task for ground mobile robots. In recent years, many impressive semantic segmentation networks, which can be used for pixel-level drivable area and road anomaly detection, have been developed. However, the detection accuracy still needs improvement. Therefore, we develop a novel module named the Normal Inference Module (NIM), which can generate surface normal information from dense depth images with high accuracy and efficiency. Our NIM can be deployed in existing convolutional neural networks (CNNs) to refine the segmentation performance. To evaluate the effectiveness and robustness of our NIM, we embed it in twelve state-of-the-art CNNs. The experimental results illustrate that our NIM can greatly improve the performance of the CNNs for drivable area and road anomaly detection. Furthermore, our proposed NIM-RTFNet ranks 8th on the KITTI road benchmark and exhibits a real-time inference speed.
I Introduction
Ground mobile robots, such as sweeping robots and robotic wheelchairs, are playing significant roles in improving the quality of human life [1, 2, 3]. Visual environment perception and autonomous navigation are two fundamental components for ground mobile robots. The former takes as input sensory data and outputs environmental perception results, with which the latter automatically moves the robot from point A to point B. Among the environment perception tasks for ground mobile robots, the joint detection of drivable areas and road anomalies is a critical component that labels the image as the drivable area or road anomaly at the pixel-level. In this paper, the drivable area refers to a region where ground mobile robots can pass through, while a road anomaly refers to an area with a large difference in height from the surface of the drivable area. Accurate and real-time drivable area and road anomaly detection could avoid accidents for ground mobile robots.
With the great advancement of deep learning technologies, many effective semantic segmentation networks that could be used for the task of drivable area and road anomaly detection have been proposed [4, 5]. Specifically, Chen et al. [4] proposed DeepLabv3+, which combines the spatial pyramid pooling (SPP) module and the encoder-decoder architecture to generate accurate semantic predictions. However, most of the networks simply use RGB images, which suffer from degraded illumination conditions [6]. Recently, some data-fusion convolutional neural networks (CNNs) have been proposed to improve the accuracy of semantic segmentation. Such architectures generally utilize two different types of sensory data to learn informative learning representations. For example, Wang et al. [5] proposed a novel depth-aware CNN to fuse depth images with RGB images, which has improved the performance of semantic segmentation. Thus, the fusion of different modalities of data is a promising research direction that deserves more attention.
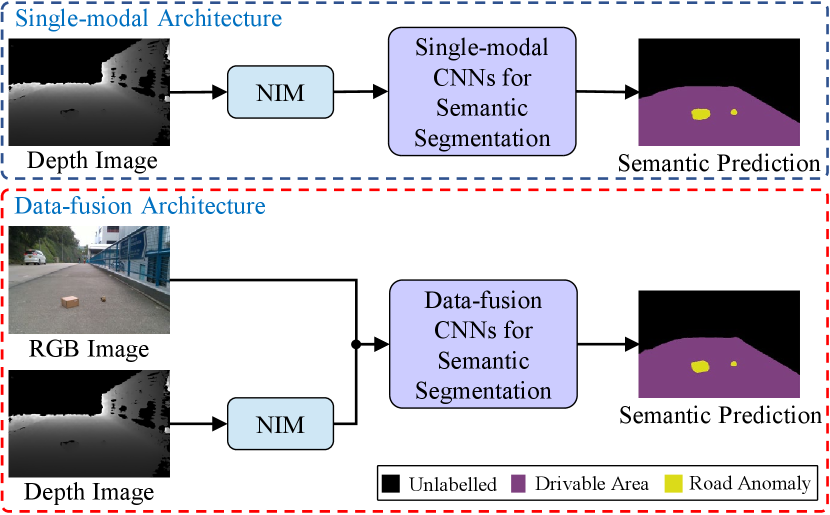
In this paper, we first introduce a novel module named Normal Inference Module (NIM), which generates surface normal information from dense depth images with high accuracy and efficiency. The surface normal information serves as a different modality of data, which can be deployed in existing semantic segmentation networks to improve performance, as illustrated in Fig. 1. To validate the effectiveness and robustness of our proposed NIM, we use our previous ground mobile robots perception (GMRP) dataset111https://github.com/hlwang1124/GMRPD [1] to train twelve state-of-the-art CNNs (eight single-modal CNNs and four data-fusion CNNs) with and also without our proposed NIM embedded. The experimental results demonstrate that our proposed NIM can greatly enhance the performance of the aforementioned CNNs for the task of drivable area and road anomaly detection. Furthermore, our proposed NIM-RTFNet ranks 8th on the KITTI road benchmark222www.cvlibs.net/datasets/kitti/eval_road.php [7] and exhibits a real-time inference speed. The contributions of this paper are summarized as follows:
-
•
We develop a novel NIM and show its effectiveness on improving the semantic segmentation performance.
-
•
We conduct extensive studies on the impact of different modalities of data on semantic segmentation networks.
-
•
Our proposed NIM-RTFNet greatly minimizes the trade-off between speed and accuracy on the KITTI road benchmark.
II Related Work
In this section, we briefly overview twelve state-of-the-art semantic segmentation networks, including eight single-modal networks, i.e., fully convolutional network (FCN) [8], SegNet [9], U-Net [10], DeepLabv3+ [4], DenseASPP [11], DUpsampling [12], ESPNet [13] and Gated-SCNN (GSCNN) [14], as well as four data-fusion networks, i.e., FuseNet [15], Depth-aware CNN [5], MFNet [16] and RTFNet [17].
II-A Single-modal CNN Architectures
FCN [8] was the first end-to-end semantic segmentation network. Of the three FCN variants, FCN-32s, FCN-16s and FCN-8s, we use FCN-8s in our experiments. SegNet [9] first presented the encoder-decoder architecture, which is widely used in current networks. U-Net [10] was designed based on an FCN [8], and adds skip connections between the encoder and decoder to improve the information flow.
DeepLabv3+ [4] was designed to combine the advantages of both the SPP module and the encoder-decoder architecture. To make the feature resolution sufficiently dense for autonomous driving, DenseASPP [11] was proposed to connect a set of atrous convolutional layers in a dense way.
Different from the networks mentioned above, DUpsampling [12] adopts a data-dependent decoder, which exploits the redundancy in the label space of semantic segmentation and has the ability to recover the pixel-wise prediction from low-resolution outputs of networks. ESPNet [13] employs a novel convolutional module named efficient spatial pyramid (ESP) to save computation and memory cost. GSCNN [14] utilizes a novel architecture consisting of a shape branch and a regular branch to focus on the boundary information.
II-B Data-fusion CNN Architectures
FuseNet [15] was proposed for the problem of semantic image segmentation using RGB-D data. It employs the popular encoder-decoder architecture, and adopts element-wise summation to combine the feature maps of the RGB stream and the depth stream. Depth-aware CNN [5] introduces two novel operations: depth-aware convolution and depth-aware average pooling, and leverages depth similarity between pixels to incorporate geometric information into the CNN.
MFNet [16] was proposed for semantic image segmentation using RGB-thermal images. It focuses on retaining the segmentation accuracy during real-time operation. RTFNet [17] was developed to enhance the performance of semantic image segmentation using RGB-thermal images. The key component of RTFNet is the novel decoder, which includes short-cuts to keep more detailed information.
III Methodology
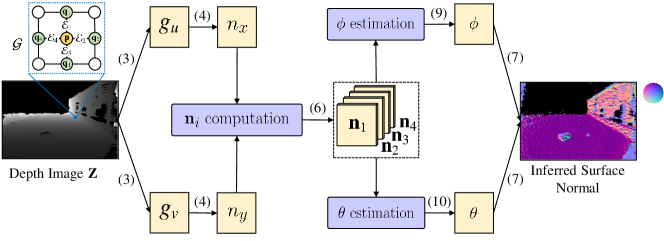
Our proposed NIM, as illustrated in Fig. 2, can generate surface normal information from dense depth images with both high precision and efficiency. The most common way of estimating the surface normal of a given 3D point in the camera coordinate system (CCS) is to fit a local plane: to , where are a collection of nearest neighboring points of . For a pinhole camera model, is linked with a pixel in the depth image by [18]:
| (1) |
A depth image can be considered as an undirected graph [19], where is a set of nodes (vertices) connected by edges . Please note that in this paper, are simply written as . Plugging (1) into the local plane equation obtains [20]:
| (2) |
Differentiating (2) with respect to and leads to
| (3) |
Rearranging (3) results in
| (4) |
Given a pair of and , we can work out the corresponding as follows:
| (5) |
where . Therefore, each neighboring point of can produce a surface normal candidate as follows [21]:
| (6) |
The optimal surface normal
| (7) |
can, therefore, be determined by finding the position at which the projections of distribute most intensively [6]. The visual perception module in a ground mobile robot should typically perform in real time, and taking more candidates into consideration usually makes the inference of more time-consuming. Therefore, we only consider the four neighbors adjacent to in this paper. can be estimated by solving [6]
| (8) |
which has a closed-form solution as follows:
| (9) |
| (10) |
Substituting (10) and (9) into (7) results in the optimal surface normal inference, as shown in Fig. 2.
IV Experimental Results and Discussions
IV-A Dataset Preparation and Experimental Setup
We recently published a pixel-level drivable area and road anomaly detection dataset for ground mobile robots, named the GMRP dataset [1]. Different from existing datasets, such as KITTI [7] and Cityscapes [22], our GMRP dataset covers the scenes and road anomalies that are common for ground mobile robots, e.g., sweeping robots and robotic wheelchairs. We refer readers to our previous paper [1] for the details of the dataset.
In order to evaluate the effectiveness and robustness of our proposed NIM, we use our GMRP dataset to train twelve CNNs as mentioned above, including eight single-modal CNNs and four data-fusion CNNs. We train each single-modal CNN with seven setups. Specifically, we first train each one with input RGB, depth and HHA images (denoted as RGB, Depth and HHA), separately, where HHA [15] is a three-channel feature map computed from the depth. Then, we train each one with input four-channel RGB-Depth and six-channel RGB-HHA (denoted as RGB+D and RGB+HHA), separately. Finally, we embed our proposed NIM in each single-modal CNN and train it with input depth images and four-channel RGB-Depth (denoted as NIM-Depth and NIM-RGB+D), separately. Similarly, we train each data-fusion CNN with three setups, separately denoted as RGB+D, RGB+HHA and NIM-RGB+D.
The total 3896 images in our GMRP dataset are split into a training set, a validation set and a testing set that contains 2726, 585 and 585 images, respectively. We train each network until the loss convergence and then select the best model according to the performance of the validation set. We adopt two metrics for the quantitative evaluations, the F-score and the Intersection over Union (IoU) for each class. We also compute the average values across two classes for the F-score and the IoU. The experimental results are presented in Section IV-B.
To validate the effectiveness and robustness of our proposed NIM for autonomous cars, we also conduct experiments on the KITTI dataset. Since we focus on the detection of drivable areas and road anomalies, our task does not match the KITTI semantic image segmentation benchmark. However, our drivable area detection task perfectly matches the KITTI road benchmark [7]. Therefore, we submit our best approach to the KITTI road benchmark. The experimental results are presented in Section IV-C.
IV-B Evaluations on Our GMRP Dataset
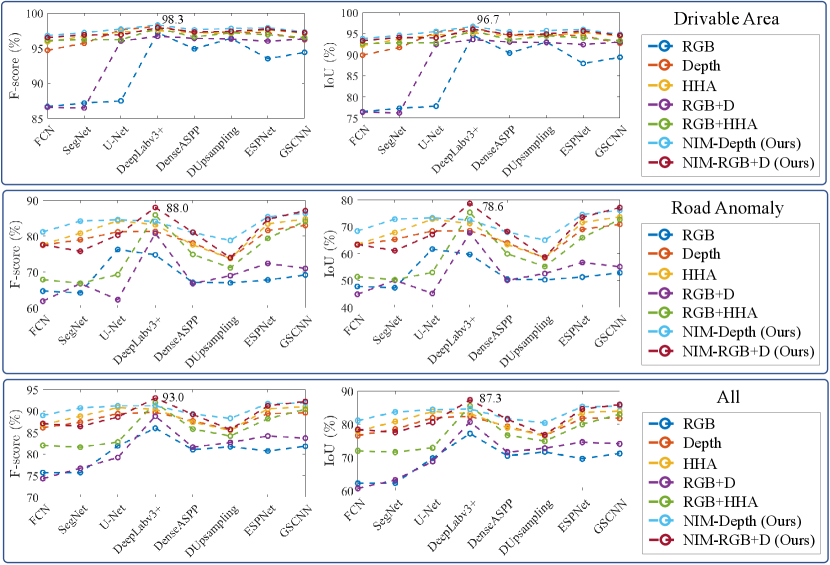
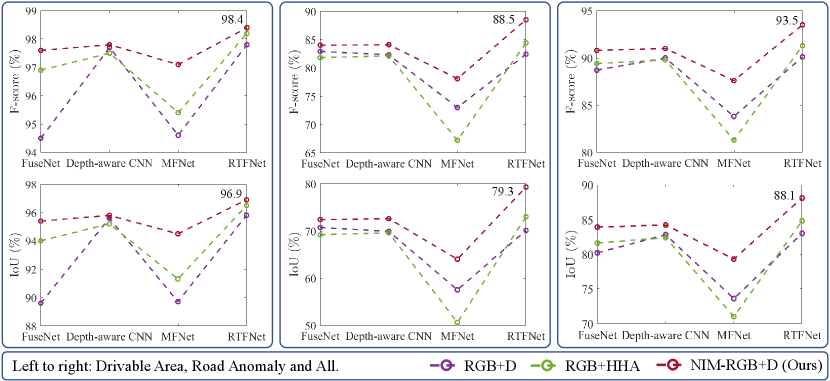
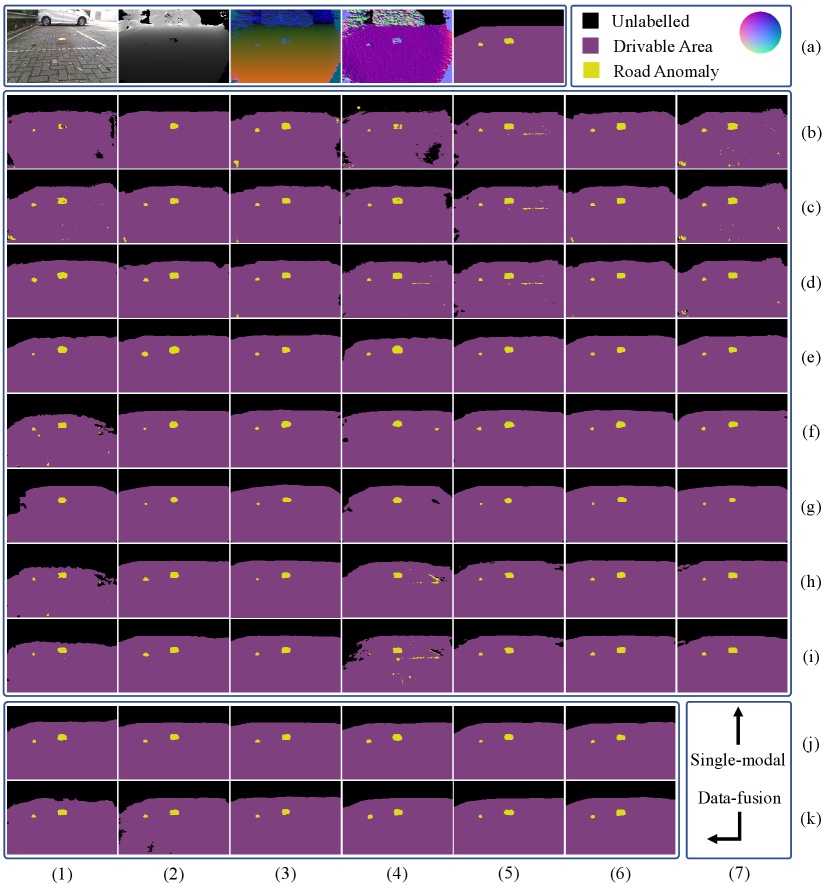
The performances of the single-modal and data-fusion CNNs mentioned above are compared in Fig. 3 and Fig. 4, respectively. We can observe that the CNNs with our proposed NIM embedded (NIM-Depth or NIM-RGB+D) outperform those without NIM embedded. Fig. 5 presents the sample qualitative results, where we can see that our proposed NIM greatly reduces the noise in the semantic predictions, especially for road anomaly detection. Specifically, for the networks with Depth and RGB+D setup, embedding our proposed NIM increases the average F-score and IoU by around 3.3-12.8 and 5.1-17.7, respectively. Furthermore, RTFNet [17] achieves the best overall performance.
IV-C Evaluations on the KITTI Road Benchmark
As previously mentioned, we select our best approach, NIM-RTFNet, and submit its results to the KITTI road benchmark [7]. The overall performance of our NIM-RTFNet ranks 8th on the KITTI road benchmark. Fig.6 illustrates an example of KITTI road testing images, and Table I presents the evaluation results. We can observe that our proposed NIM-RTFNet outperforms most existing approaches, which confirms the effectiveness and good generalization ability of our proposed NIM. Additionally, although the MaxF of LidCamNet [23] presents slight advantages over ours, our NIM-RTFNet runs much faster than it, and therefore greatly minimizes the trade-off between speed and accuracy.
| Approach | MaxF () | AP () | Runtime (s) |
|---|---|---|---|
| MultiNet [24] | 94.88 | 93.71 | 0.17 |
| StixelNet II [25] | 94.88 | 87.75 | 1.20 |
| RBNet [26] | 94.97 | 91.49 | 0.18 |
| LC-CRF [27] | 95.68 | 88.34 | 0.18 |
| LidCamNet [23] | 96.03 | 93.93 | 0.15 |
| NIM-RTFNet (Ours) | 96.02 | 94.01 | 0.05 |

V Conclusions
In this paper, we proposed a novel module NIM, which can be easily deployed in various CNNs to refine semantic image segmentation. The experimental results demonstrate that our NIM can greatly enhance the performance of CNNs for the joint detection of drivable areas and road anomalies. Furthermore, our NIM-RTFNet ranks 8th on the KITTI road benchmark and exhibits a real-time inference speed. In the future, we plan to propose a more feasible and computationally efficient cost function for our NIM.
References
- [1] H. Wang, Y. Sun, and M. Liu, “Self-Supervised Drivable Area and Road Anomaly Segmentation Using RGB-D Data For Robotic Wheelchairs,” IEEE Robot. Autom. Lett., vol. 4, no. 4, pp. 4386–4393, Oct 2019.
- [2] Y. Sun, M. Liu, and M. Q.-H. Meng, “Improving rgb-d slam in dynamic environments: A motion removal approach,” Robot. Auton. Syst., vol. 89, pp. 110–122, 2017.
- [3] Y. Sun et al., “Motion removal for reliable rgb-d slam in dynamic environments,” Robot. Auton. Syst., vol. 108, pp. 115–128, 2018.
- [4] L.-C. Chen et al., “Encoder-decoder with atrous separable convolution for semantic image segmentation,” in Proc. Eur. Conf. Comput Vis. (ECCV), 2018, pp. 801–818.
- [5] W. Wang and U. Neumann, “Depth-aware CNN for RGB-D segmentation,” in Proc. Eur. Conf. Comput Vis., 2018, pp. 135–150.
- [6] R. Fan, U. Ozgunalp, B. Hosking, M. Liu, and I. Pitas, “Pothole detection based on disparity transformation and road surface modeling,” IEEE Trans. Image Process., vol. 29, pp. 897–908, 2019.
- [7] J. Fritsch, T. Kuehnl, and A. Geiger, “A new performance measure and evaluation benchmark for road detection algorithms,” in Inter. Conf. Intell. Transp. Syst., 2013.
- [8] J. Long, E. Shelhamer, and T. Darrell, “Fully convolutional networks for semantic segmentation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2015, pp. 3431–3440.
- [9] V. Badrinarayanan et al., “SegNet: A deep convolutional encoder-decoder architecture for image segmentation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 39, no. 12, pp. 2481–2495, 2017.
- [10] O. Ronneberger, P. Fischer, and T. Brox, “U-Net: Convolutional networks for biomedical image segmentation,” in Int. Conf. Medical Image Comput. Comput.-Assisted Intervention, 2015, pp. 234–241.
- [11] M. Yang, K. Yu, C. Zhang, Z. Li, and K. Yang, “DenseASPP for semantic segmentation in street scenes,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2018, pp. 3684–3692.
- [12] Z. Tian et al., “Decoders matter for semantic segmentation: Data-dependent decoding enables flexible feature aggregation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2019, pp. 3126–3135.
- [13] S. Mehta, M. Rastegari, A. Caspi, L. Shapiro, and H. Hajishirzi, “ESPNet: Efficient spatial pyramid of dilated convolutions for semantic segmentation,” in Proc. Eur. Conf. Comput Vis., 2018, pp. 552–568.
- [14] T. Takikawa, D. Acuna, V. Jampani, and S. Fidler, “Gated-SCNN: Gated shape CNNs for semantic segmentation,” in Proc. IEEE Int. Conf. Comput. Vis., 2019, pp. 5229–5238.
- [15] C. Hazirbas et al., “Fusenet: Incorporating depth into semantic segmentation via fusion-based CNN architecture,” in Asian Conf. Comput. Vision. Springer, 2016, pp. 213–228.
- [16] Q. Ha et al., “MFNet: Towards real-time semantic segmentation for autonomous vehicles with multi-spectral scenes,” in IEEE/RSJ Int. Conf. Intell. Robots Syst. IEEE, 2017, pp. 5108–5115.
- [17] Y. Sun, W. Zuo, and M. Liu, “RTFNet: RGB-thermal fusion network for semantic segmentation of urban scenes,” IEEE Robot. Autom. Lett., vol. 4, no. 3, pp. 2576–2583, 2019.
- [18] R. Fan, “Real-time computer stereo vision for automotive applications,” Ph.D. dissertation, University of Bristol, 2018.
- [19] R. Fan, X. Ai, and N. Dahnoun, “Road surface 3D reconstruction based on dense subpixel disparity map estimation,” IEEE Transactions on Image Processing, vol. 27, no. 6, pp. 3025–3035, 2018.
- [20] R. Fan, H. Wang, B. Xue, H. Huang, Y. Wang, M. Liu, and I. Pitas, “Three-filters-to-normal: An accurate and ultrafast surface normal estimator,” arXiv preprint arXiv:2005.08165, 2020.
- [21] R. Fan, H. Wang, P. Cai, and M. Liu, “SNE-RoadSeg: Incorporating Surface Normal Information into Semantic Segmentation for Accurate Freespace Detection,” in Proc. Eur. Conf. Comput Vis. (ECCV). Springer, Aug. 2020.
- [22] M. Cordts et al., “The cityscapes dataset for semantic urban scene understanding,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2016, pp. 3213–3223.
- [23] L. Caltagirone, M. Bellone, L. Svensson, and M. Wahde, “Lidar–camera fusion for road detection using fully convolutional neural networks,” Robot. Auton. Syst., vol. 111, pp. 125–131, 2019.
- [24] M. Teichmann, M. Weber, M. Zoellner, R. Cipolla, and R. Urtasun, “MultiNet: Real-time joint semantic reasoning for autonomous driving,” in IEEE Intell. Vehicles Symp. IEEE, 2018, pp. 1013–1020.
- [25] N. Garnett et al., “Real-time category-based and general obstacle detection for autonomous driving,” in Proc. IEEE Int. Conf. Comput. Vis. Workshops, 2017, pp. 198–205.
- [26] Z. Chen and Z. Chen, “RBNet: A deep neural network for unified road and road boundary detection,” in International Conference on Neural Information Processing. Springer, 2017, pp. 677–687.
- [27] S. Gu et al., “Road Detection through CRF based LiDAR-Camera Fusion,” in IEEE Int. Conf. Robot. Autom., 2019, pp. 3832–3838.