Applicability of Modified Gauss-Bonnet Gravity Models on the Existence of Stellar Structures
Abstract
In this paper, we explore the existence of spherically symmetric strange quark configurations coupled with anisotropic fluid setup in the framework of modified Gauss-Bonnet theory. In this regard, we adopt two models such as (i) , and (ii) , and derive the field equations representing a static sphere. We then introduce bag constant in the gravitational equations through the use of MIT bag model, so that the quarks’ interior can be discussed. Further, we work out the modified equations under the use of Tolman IV ansatz to make their solution possible. Junction conditions are also employed to find the constants involved in the considered metric potentials. Afterwards, different values of model parameters and bag constant are taken into account to graphically exploring the resulting solutions. This analysis is done by considering five strange quark objects like Her X-I, LMC X-4, 4U 1820-30, PSR J 1614-2230, and Vela X-I. Certain tests are also applied on the developed models to check their physical feasibility. It is much interesting that this modified gravity under its both considered functional forms yield physically viable and stable results for certain parametric values.
Keywords: Gauss-Bonnet gravity; Anisotropy; MIT bag model; Stability.
PACS: 04.20.Jb; 04.50.Kd; 95.30.-k; 04.40.Dg.
1 Introduction
The universe is home to a diverse array of celestial objects, from the simplest to the most complex. The presence of extraordinary elements throughout the cosmos fuels the curiosity of researchers, who strive to unreveal the unique properties of these components in hopes of shedding light on the enigmas of the universe. The core of celestial bodies is the site of numerous nuclear reactions, which generate the heat and illumination that permeate the cosmos. During this, a celestial body reaches at a point where the inward pull of gravity overcomes the outward force of pressure. This causes the object to explode, leading to the formation of unique stellar remnants. One of them is the neutron stars in which the intense gravitational force compresses matter to the point where electrons combine with protons, creating a sea of neutrons. These neutrons exhibit quantum degeneracy, exerting an opposing force to gravity that prevents the star from collapsing further. Neutron stars, which are incredibly dense stellar objects, were theoretically predicted in 1934, even though their actual existence was confirmed at a later stage [1]. Interestingly, between the realms of black holes and neutron stars, there exists a hypothetical state known as a strange star. These strange stars are believed to be even denser than neutron stars, with their interiors composed of a unique combination of different (strange, down, and up) quarks. Several researchers have made attempts to understand and study these fictitious bodies [2]-[4].
Studying anisotropic systems, where the physical characteristics vary with direction, can provide valuable insights into the structure and evolution of astronomical bodies. Numerous physical phenomena occur that cause these systems to depart from uniform isotropy, where the properties are the same in all directions [5]. Jeans [6] introduced innovative concepts suggesting that anisotropy could arise from diverse factors, implying non-uniform pressure distribution within the interior. This non-uniformity manifests when pressures acting tangentially and radially differ, leading to the emergence of anisotropy. Ruderman [7] postulated the existence of massive interstellar entities with densities exceeding g/cm3 and inferred that these objects could exhibit anisotropic characteristics based on theoretical analyzes. Research has shown that the presence of a powerful magnetic field [8]-[10] or other influential factors [11]-[13] around a star can lead to anisotropy. Furthermore, Herrera’s work [14] demonstrated that the emergence of dissipative flux, inhomogeneous energy density, or shear, either individually or in combination, can disrupt the isotropic structure within a star, resulting in anisotropy.
Anisotropic fluid distributions showcase a variety of captivating physical processes, which are thought to be the essential constituents of more realistic compact structures. These processes encompass the presence of a superfluid, or boson stars [15, 16], etc. In a study conducted by Dev and Gleiser [17], specific equations of state (EoSs) were employed to investigate the anisotropic behavior exhibited by celestial objects. To investigate the characteristics of 4U 1820-30, Hossein and colleagues [18] incorporated into the gravitational equations and generated graphical models to analyze the system’s properties. Kalam et al. [19] evaluated the feasibility of various neutron star configurations, assessing their potential to exist as stable celestial objects. Maurya et al. [20] employed the embedding condition in order to determine the conditions necessary for 4U 1820-30 to be considered a physically relevant system. According to different investigations done by us, multiple anisotropic structures meet all physically acceptable conditions across various metric ansatz [21]-[31]. It has been revealed that the EoS for neutron stars failed to accurately predict the compactness of some stars like SAX J 1808.4-3658, Her X-1, and 4U 1820-30, etc. Hence, there is a need for another EoS that does not fail to do so. In this regard, MIT bag model is of great significance which helps in predicting the compactness of the above star models correctly [32]-[37].
The MIT bag model has been instrumental in probing the intricate details of quark structures. This model suggests that as the bag constant, which represents the energy density required to confine quarks, takes on larger values, the pressure exerted by quarks decreases correspondingly. Extensive research has been conducted using this EoS to shed light on the internal composition of strange objects. In a study of the extremely dense pulsar PSR J 1614-2230, Demorest et al. [38] found that the MIT bag model provided a suitable framework for modeling and understanding the properties of such ultra-dense stellar objects. Rahaman et al. [39] employed an interpolation function to estimate the mass of a hypothetical quark star, and then leveraged this result to elucidate various physical phenomena associated with such compact objects. Additionally, Bhar [40] investigated the necessary conditions for physically realistic stellar models by adopting the MIT EoS in conjunction with the Krori-Barua ansatz. Deb et al. [41, 42] explored distinct uncharged and charged fluid models using this bag model. Similarly, Sharif and his colleagues [43, 44] adopted the same approach to analyze stable anisotropic configurations.
A widely accepted theory among scientists, named the general relativity (GR), has been put forwarded by Albert Einstein in 1915. The proposal of this fundamental theory is thought to be his one of the biggest accomplishments. Such a highly recognized theory over more than one hundred years provides a cornerstone to discuss stellar and interstellar bodies in relation with their gravitational interaction at enormous scales. Moreover, this theory has opened many pathways in detecting mysterious celestial objects. Nevertheless, some inconsistencies occur in this theory when researchers explored the origin of cosmic dark components such as dark energy and dark matter. It is important to know that the former element produces large enough pressure opposite to the gravity that leads to the current cosmic rapid expansion era. In order to deal with such issues, some alternate proposals to GR have been established in recent years through the modification of the Einstein-Hilbert action function. The theory, refers to the first-ever modification of GR is known as the gravity which was accomplished through the replacement of (the Ricci scalar) with its generic functional. Several gravity models have been used to examine different cosmic eras [45]-[47]. In addition, using a class of different strategies, a large number of acceptable astrophysical results have been made in the literature in the context of theory [48, 49].
Many other modifications of GR have been proposed and explored in different astrophysical as well as cosmological scenarios. Nojiri and Odintsov [50] contributed in this context and gave a proposal named as gravity theory, where symbolizes the Gauss-Bonnet invariant (a sum of multiple curvature terms). This extension was also produced by modifying the action, but this time the Ricci scalar is not replaced by any function rather they added a generic function of in the curvature scalar. Bamba with his collaborators [51] reconstructed this modified gravity model in order to discuss several future singularities in relation with phantom/quintessence cosmic phase. Myrzakulov and his colleagues [52] solved gravitational equations without including the cosmological constant and explored the existence of anti-gravity force in an inflationary epoch. The expansion of our universe has been analyzed with the help of some symmetry generators obtained via Noether symmetry approach in this modified gravity. Bamba et al. [53] considered multiple Gauss-Bonnet gravity models and calculated some parametric values for Hubble, snap, jerk, and deceleration parameters, leading to the presence of normal fluid source. The spherical stellar structures and their geometry have also been investigated under the formalism of this gravity [54]. Some other interesting works are [55]-[58].
Our aim to do this work is to explore the applicability of modified Gauss-Bonnet gravity models on the existence of anisotropic stellar structures admitting spherical symmetry. The following lines indicate the pattern of this article. Some fundamentals to understand the formulation of this theory and its field equations are presented in section 2. We also assume the MIT bag model and Tolman IV ansatz to deal with the gravitational equations. Section 3 explores the matching conditions which are necessary in finding the constants in the considered spacetime under the observational data of multiple distinct stars. A detailed discussion through graphical interpretation is done is section 4 for two different modified models and several parametric values. Lastly, section 5 presents some concluding remarks about what we have achieved.
2 Modified Gauss-Bonnet Gravity Theory
The following modification in the Einstein-Hilbert action in the presence of fluid’s Lagrangian density leads to the modifed Gauss-Bonnet gravity theory as
| (1) |
where with being the metric tensor and represents an infinitesimal four-volume element in the spacetime manifold. Also, the Lagrangian term appeared in the above action can be associated with the energy-momentum tensor representing fluid source in the self-gravitating interior as
| (2) |
In the current setup, we derive the following gravitational equations through implementing the variational principle on the action (1) given by
| (3) |
where geometrical aspects of the considered spacetime structure are exposed by the Einstein tensor . Further, is the mathematical expression for the covariant derivative. When the function is differentiated w.r.t. , we represent it by . Once this functional is removed from the action (1), we are left with the GR framework. One can write Eq.(3) in an alternative way as follows
| (4) |
Here, the term on right side represents total fluid distribution and is classified as follows
| (5) |
where is the usual matter existing in any celestial body and all other quantities appear due to the modification of action (1).
In the presence of strong gravitational fields, such as around compact objects like neutron stars, the energy-momentum tensor can exhibit significant pressure anisotropy. Further, these kinds of fluid play a crucial role in cosmological models. In the following, we express such matter distributions by [59, 60]
| (6) |
where and are the four-vector and four-velocity in the covariant form, satifying and . Furthermore, the triplet symbolize the energy density, tangential and radial pressures, respectively. The spherical line element encodes the symmetries of the spacetime and allows modeling gravitational fields around compact objects. It is a crucial tool for studying GR or modified theories in spherical symmetry. The interior region of such a geometry is represented by
| (7) |
where and , showing that this metric is of static nature. The quantities appeared in the energy-momentum tensor (6) are now become in the light of metric (7) as
| (8) |
The methodology utilizing the MIT bag model EoS (describing the quark’s interior) alongside Tolman IV ansatz (which we shall take into account later) is a widely recognized approach for studying quark stars. However, the current study offers a new perspective by applying modified gravity, which has not been previously explored in the context of quark stellar structures. Adopting specific modified gravity models allow researchers to explore deviations from standard GR and assess their impact on the behavior of gravity. Moreover, they are used for the interpretation of observational data more efficiently. In this regard, we employ two models in the framework of gravity.
-
•
Model 1: A quadratic model used to understand the impact of bag constant in this theory is given as
(9) where represents an arbitrary constant.
-
•
Model 2: Another model is also considered as a realistic one, and is being able to describe the current cosmic expansion [51]
(10) where , and and are free parameters.
This combination enables a more detailed exploration of how higher-order curvature terms influence the properties of stars, especially under intense gravitational fields. Hence, this analysis offers a clearer insight into the behavior of quark stars in the context of this modified gravity theory. In the context of our chosen models, the issue of ghost modes emerges due to the higher-order derivatives introduced by the functional form. These higher-order terms result in fourth-order equations of motion, which are typically linked to ghost modes. Although the presence of ghosts presents a theoretical challenge, these models still play an important role in advancing our understanding of the behavior of modified gravitational theories. They underscore the necessity for more refined models to tackle both cosmological challenges and ensure theoretical consistency. Nonetheless, they remain significant in the ongoing exploration of alternative gravitational theories. Using Eqs.(4) and (6) along with the metric (7) and model 1 yield the field equations as
| (11) | ||||
| (12) | ||||
| (13) |
where . It must be stated here that the field equations corresponding to model 2 are found to be much lengthy, so we do not include them here. However, the results corresponding to this model shall be interpreted graphically. Further, the Gauss-Bonnet term
leads to the following expression expressed by
| (14) |
whose derivatives up to second order are given in Appendix A. When inserting the overhead values into Eqs.(11)-(13), the matter variables take the form presented in Appendix A.
It has been already discussed the importance of some particular constraints, say an EoS that can help in understanding the features of consider structures in a more better way. The main purpose to take EoSs into account is that each of them associate different physical parameters in a certain manner. One of the fascinating events occurring in our universe is the existence of neutron star like structure which are the results of collapse of highly massive stars. Such a structure has much powerful field of attraction around it with being of small size. Among these objects, the one comprising of low density converts into the quark star. A non-linear system (A3)-(A5) with five unknowns require an EoS to discuss the quark interior. A suitable candidate in this regard is the MIT bag model, providing a simple yet effective way to model the confinement of quarks inside hadrons. By confining the quarks within a bag with appropriate boundary conditions, the model captures the essential features of color confinement.
Quark pressure and quark density are important properties of the quark-gluon plasma. We define the former element in relation with the bag constant as
| (15) |
where we observe that such a matter usually classifies into three flavors, namely down (d), up (u) and strange (s). In addition, the quark pressures , and correspond to these flavors, respectively. We now define the quark density as
| (16) |
It is important to mention here that the relation between quark pressure and density can be seen from . Using this along with Eqs.(15) and (16) at the same time leads to the construction of the desired MIT bag model having the following form
| (17) |
The literature is full of exploration of certain salient properties linked with strange quark stars by choosing multiple values of the bag constant [61]-[63]. Hence, this constant comprises of a broader range of values.
Quantum Chromodynamics (QCD) is the fundamental theory that governs the strong nuclear force, one of the four basic forces of nature. A key aspect of QCD is confinement, which means that quarks cannot be found in isolation but are always confined within particles like protons and neutrons by the strong force. However, under extreme conditions of temperature and density, such as those in the early universe or within neutron stars, quarks and gluons can break free from confinement and form a state known as quark-gluon plasma. Investigating this plasma state provides crucial insights into how QCD behaves under such extreme conditions. In astrophysical contexts, QCD is vital for understanding the properties of ultra-dense matter inside objects like neutron stars or theoretical quark stars, where quarks may exist in a deconfined state. The MIT bag model (17) is a theoretical framework that models quark matter, incorporating concepts from QCD to describe its behavior.
Plugging the above-mentioned constraint into the field equations (A3)-(A5), they contain the significant role of the bag constant. After taking EoS (17) into account, we have four equations with six unknowns (). At this stage, the unique solution to this system is only possible when we adopt a metric ansatz. Therefore, in order to make it sure, we adopt non-singular Tolman IV metric potentials [64], described as
| (18) |
involving a constant triplet (). The Appendix B contains the values of fluid parameters after substituting the ansatz (18) into them.
3 Boundary Conditions
Boundary conditions are important in providing better understanding of the structural development of any celestial body. These are the constraints that help in matching the two regions, i.e., interior and exterior of a compact star at some boundary, named as hypersurface. Since the interior spacetime is a static sphere, it is better to adopt the Schwarzschild metric as an exterior geometry. This metric is defined as follows
| (19) |
where the exterior mass is symbolized by . In accordance with the first fundamental form of the boundary conditions, both and as well as the radial derivative of the later component corresponding to exterior and interior geometries are continuous across the spherical interface. Following this, we get
| (20) | ||||
| (21) | ||||
| (22) |
The above three equations are simultaneously solved, providing the Tolman IV triplet . We express them in the following
| (23) |
It is well recognized outcome in the study of compact stars that the radial pressure must be a decreasing function of the radial coordinate and disappears for maximum possible value of , i.e., at the interface. We use this condition for the radial pressure (presented in Appendix B) corresponding to model 1 as
| (24) |
The above equation leads to the following value of bag constant for model 1
| (25) |
whereas for model 2, the bag constant is not specified here due to lengthy expression. Five different strange quark candidates are chosen along with their observational data (masses and radii) and we present them in Table 1 along with their compactness. It is important to note that the limit for this factor has been suggested by a researcher, referred to the Buchdhal limit [65] defined as . From Table 1, we see that the considered stars are in agreement with this limit. We use this experimental data to compute the unknown constants, i.e., and and present them in Table 2. The bag constant is also numerically determined in Tables 3 and 4 corresponding to models 1 and 2, respectively.
| Strange Stars | Her X-I | LMC X-4 | PSR J 1614-2230 | Vela X-I | 4U 1820-30 |
|---|---|---|---|---|---|
| Mass | 0.85 | 1.04 | 1.97 | 1.77 | 1.58 |
| (km) | 8.1 | 8.3 | 9.69 | 9.56 | 9.1 |
| 0.1546 | 0.1846 | 0.2996 | 0.2728 | 0.2559 |
| Strange Stars | Her X-I | LMC X-4 | PSR J 1614-2230 | Vela X-I | 4U 1820-30 |
|---|---|---|---|---|---|
| 227.339 | 166.325 | 32.0351 | 62.6318 | 75.141 | |
| 0.535963 | 0.445918 | 0.101924 | 0.184694 | 0.232224 | |
| 424.169 | 372.995 | 314.305 | 339.112 | 323.571 |
| Strange Stars | Her X-I | LMC X-4 | PSR J1614-2230 | Vela X-I | 4U 1820-30 |
|---|---|---|---|---|---|
| (=0.5) | 0.000114958 | 0.000123759 | 0.000108751 | 0.000110312 | 0.000121002 |
| (=5.5) | 0.000114947 | 0.000123724 | 0.000108699 | 0.000110255 | 0.000120925 |
| Strange Stars | Her X-I | LMC X-4 | PSR J1614-2230 | Vela X-I | 4U 1820-30 |
|---|---|---|---|---|---|
| (=0.2, =0.5) | 0.000114958 | 0.000123759 | 0.000110935 | 0.000110312 | 0.000121002 |
| (=0.2, =8.5) | 0.000114956 | 0.000123751 | 0.000108739 | 0.000110298 | 0.000120983 |
| (=5, =0.5) | 0.000114954 | 0.000123745 | 0.00010873 | 0.000110289 | 0.000120971 |
| (=5, =8.5) | 0.000114865 | 0.000123466 | 0.000108315 | 0.000109835 | 0.000121363 |
The range of the bag constant is found to be within the interval for the strange compact bodies having not sufficient mass [66]. However, when the quark bodies having mass approximately equal to 154 are concerned, the above range becomes 56 to 78 [67]. The literature stresses multiple works on the use of bigger values of this constant from which several remarkable results have been achieved. In the light of this, it was shown by Xu [68] that a particular celestial structure, namely LMXB EXO 0748-676 behaves like a quark like star when choosing and . Some other experiments, in particular, CERN-SPS and RHIC, suggested that the quantity can take a more wider range for the density-dependent structures. The values of bag constant (in ) corresponding to the strange stars Her X-I, Vela X-I, PSR J1614-2230, LMC X-4 and 4U 1820-30, respectively, for model 1 with mentioned parametric values come out to be
-
•
: the values are 86.87, 83.36, 82.18, 93.52 and 91.43.
-
•
: the values are 86.86, 83.31, 82.14, 93.49 and 91.38.
For model 2, they are
-
•
: the values are 86.86, 83.35, 83.82, 93.51 and 91.42.
-
•
: the values are 86.86, 83.34, 82.16, 93.51 and 91.41.
-
•
: the values are 86.86, 83.33, 82.16, 93.50 and 91.40.
-
•
: the values are 86.79, 82.99, 81.84, 93.29 and 90.95.
4 Graphical Exploration of Strange Quark Stars
In this section, we illustrate the graphical plots to elucidate the significant impact of gravity on certain astronomical structures. To delve into their fundamental attributes, we focus on the masses and radii of constructed quark entities. The models facilitate this exploration by choosing different values of the constants involved in these models. The stars are graphically interpreted on the basis of the following selected values of the constants in the models
-
•
For model 1, two values are chosen as and .
-
•
For model 2, two values of both parameters are adopted as and along with .
Our analysis commences with an examination of the viability of the temporal and radial metric functions. Subsequently, we plot the matter variables, anisotropy, and energy conditions. Following this, we employ two distinct criteria to assess the stability of the assumed stars. It is crucial to note that the plots of metric functions should exhibit an increasing trend with to ensure the compatibility of the solution. The metric coefficients, represented by Eq.(18), involve three unknowns (), whose values are provided in Table 2. Additionally, the compatibility of the solution can be verified from Figure 1.


4.1 Profile of Physical Determinants









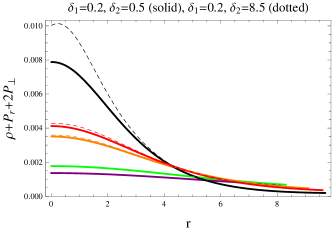
The significance of energy density and pressure components within anisotropic stars cannot be overlooked as they play pivotal roles in the structural evolution. The feasibility of these compact bodies hinges greatly upon the behavior of these physical parameters. Specifically, if these factors exhibit maximum values at the center, maintain a positive trend throughout, and smoothly decrease towards the boundary, then such behavior ensure the regularity of the models. Notably, the density of the system peaks at the central point for all stars and decreases as the radial coordinate, denoted by , increases (see Figure 2). This trend is also mirrored by the tangential and radial pressures, as illustrated in Figure 2, with reaching to zero at the boundary. Additionally, specific constraints, referred to the maximality conditions must be satisfied to ensure the acceptability of the solution, given as
All the requirements for the regularity of solution are satisfied by every considered candidate for all the mentioned values of both models’ parameters. However, their plots are not added.
4.2 Anisotropic Factor
Anisotropy is created when the system has different pressures in different directions (radial and transversal), expressed by . The pressure ingredients presented in Appendix B are utilized to compute the anisotropic factor for model 1 in terms of bag constant and Tolman IV solution, and is given in the same Appendix. For model 2, the corresponding expression is not included here. The structural changes in the strange candidates produced as a result of anisotropy are observed by utilizing the observational data of stars, as provided in Table 1. The anisotropy of the system in which the pressure in the radial direction is smaller than the tangential direction comes out to be positive. Under such circumstances, repulsive pressure is released to make the structure stable. On the other hand, attractive force is observed for the system having larger radial pressure than tangential pressure. In our current setup, the anisotropy in Figure 3 shows the positive behavior for all the considered quark stars.



4.3 Energy Conditions
To ensure the existence of usual matter configuration within the interiors of the celestial bodies, several mathematical constraints are considered. These constraints, known as energy conditions, serve as effective means to distinguish between usual and exotic fluid sources. Fulfillment of these conditions validates the viability of the derived solution and confirms the presence of ordinary fluid within compact structures. In cases of anisotropic composition, these conditions are categorized into strong, dominant, null, and weak energy conditions
| Strong energy conditions: | ||||
| Dominant energy conditions: | ||||
| Null energy conditions: | ||||
| Weak energy conditions: | (26) |
Figures 4-6 illustrate the energy plots depicting all compact entities under investigation, each corresponding to chosen values of prescribed models. Analysis of these plots reveals that all imposed constraints are effectively met, affirming the viability of the proposed solutions. Consequently, it can be inferred that all quark entities contain ordinary sources within their structures, thus indicating a coherent and viable model within this modified theoretical framework.














4.4 Stability Tests
We shall investigate the stability (which is a significant topic within the cosmic universe) of spherically symmetric anisotropic stars in this subsection. This shall be performed through two distinct methods. At first, the causality condition is utilized as a mean to understand the stability of stellar bodies by considering its various components such as
| (27) |
where and signify the radial and transversal sound speed components, respectively. This criterion is satisfied when both inequalities and hold [69, 70], and alternatively, one can say that sound speed in every direction must be less than the speed of light. The other technique used to determine the stable quarks is adiabatic index, whose expression is delineated as
| (28) |
The anisotropic stars depict stable interior if the value of is greater than [71]. Figure 7 represents the plots of the two considered tests for both the respective models (9) and (10). From this Figure, it can be easily observed that the model 1 portrays the stable quarks for both the proposed values of . The middle row indicates that all the five stars corresponding to and are stable. While on the contrary, the stars 4U 1820-30, Vela X-1 and PSR J 1614-2230 concerning and could not fulfill the stability tests and hence, are unstable. The last row also illustrates the stability approach for a couple of considered parametric values and one can notice that all the stars are underlying in the stable regions.









4.5 Some other Essential Factors
A fundamental quantity linked with the heavily celestial structures is the mass function. For spherically symmetric configurations, this function can be calculated through the following integral equation
| (29) |
We utilize a particular initial condition on this function, i.e., to solve Eq.(29). Keep in mind that we use the above definition instead of the one in terms of radial metric potential so that the effect of modification of functional form can be explored on strange stellar structures. It is important to gather some information about a factor related to the mass, referred to the compactness. It is widely used in literature while discussing compact celestial objects and expressed as a ratio between mass and radius, i.e., . When matching two (interior and exterior) regions of a spherical geometry, Buchdahl [65] came to know the expected possible value of this factor. He deduced it not to be more than everywhere to get a physically existing star model.
Almost all the astrophysical structures produce electromagnetic beams or radiations when influenced from the strong force of attraction produced by other nearby objects. These radiations are increased in terms of their wavelength and this can be found through the following expression
Since this is also dependent on the mass, the graphical behavior of this factor must be an increasing function of . As its acceptable value/range is concerned, researchers found this to be less than only when isotropic fluid configurations are discussed. On the other hand, when anisotropy in the interior is considered, this value reaches to . The profiles of all the above physical factors depicted in Figure 8 show that they are consistent with their limits for every parametric choice.









5 Conclusions
We have explored the possible existence of spherically symmetric anisotropic quark configurations for two different models of gravity. The field equations have been formulated corresponding to both the models, characterizing a static spherical fluid distribution. We have then introduced bag constant in the gravitational equations through the use of MIT bag model to explore the quarks’ interior. As candidates of quark strange stars, we have taken Her X-I, LMC X-4, 4U 1820-30, PSR J 1614-2230, and Vela X-I into account along with their observational data from the literature (Table 1). The equations of motion have been linked with the MIT model to make sure the presence of the bag constant in them. Further, we have worked out the modified equations under the use of Tolman IV metric potentials to make their unique solution possible. It is then observed that this ansatz involves a triplet of unknowns which have been determined through the implementation of junction conditions (Table 2). Tables 3 and 4 present the numerical values of for both models whose expression has been obtained through null radial pressure at the interface. Additionally, different values of model parameters and bag constant (25) have been chosen to graphically explore the resulting solutions. For instance,
-
•
For model 1, we have adopted .
-
•
For model 2, we have chosen and .
The fluid triplet has been plotted and observed to be consistent with their required behavior such that they are maximum and finite at and reach their minimum at the spherical junction. It has been noticed that the considered structures become more dense/massive for model 1. Also, a remarkable observation has been made about the values of bag constant which lie within their acceptable range. All energy conditions have been satisfied, guaranteeing the viability of our both models. Certain tests have been applied on the developed models to check their physical stability. Finally, we have concluded that the modified Gauss-Bonnet gravity under its first considered functional form yields physically relevant results for both parametric values. However, for the second functional form, the strange stars 4U 1820-30, Vela X-1 and PSR J 1614-2230 are unstable for and .
Similar to our present manuscript, Biswas et al. [72] also found an acceptable range for the bag constant in their study of strange stars, which is consistent with our findings. Naseer and Sharif [73] used the MIT bag EoS to analyze the impact on several quark stars in the context of non-minimally coupled gravity, and they determined that the star 4U 1820-30 satisfies all physical requirements, in contrast with our current results. Das and Debnath [74] discussed the essential characteristics and physical viability of two strange stars using the respective EoS, proposing them as examples of acceptable behavior. Our analysis offers a more comprehensive study of the internal properties of strange stars compared to the work done in [75]. Sharif and Hassan [76] have chosen a specific model of modified Gauss-Bonnet gravity to examine quark stars and found that the star PSR J1614-2230 becomes unstable for higher parameter values. It must be stated here that the results of this theory can be reduced in GR for and under models 1 and 2, respectively.
Appendix A
The derivatives of the Gauss-Bonnet term up to second order are
| (A1) | ||||
| (A2) |
Appendix B
The anisotropic factor for model 1 is given by
| (B4) |
Data Availability Statement: This manuscript has no associated data.
References
- [1] W. Baade, F. Zwicky, Remarks on super-novae and cosmic rays, Phys. Rev. 46 (1934) 76.
- [2] E. Witten, Cosmic separation of phases, Phys. Rev. D 30 (1984) 272.
- [3] X.D. Li, Z.G. Dai, Z.R. Wang, Is HER X-1 a strange star?, Astron. Astrophys. 303 (1995) L1.
- [4] I. Bombaci, Strangeness in neutron stars, Nucl. Phys. A 754 (2005) 335-344.
- [5] L. Herrera, N.O. Santos, Local anisotropy in self-gravitating systems, Phys. Rep. 286 (1997) 53.
- [6] J.H. Jeans, The motions of stars in a Kapteyn universe, Mon. Not. R. Astron. Soc. 82 (1922) 122.
- [7] M. Ruderman, Pulsars: structure and dynamics, Annu. Rev. Astron. Astrophys. 10 (1972) 427.
- [8] S.S. Yazadjiev, Relativistic models of magnetars: Nonperturbative analytical approach, Phys. Rev. D 85 (2012) 044030.
- [9] C.Y. Cardall, M. Prakash, J.M. Lattimer, Effects of strong magnetic fields on neutron star structure, Astrophys. J. 554 (2001) 322.
- [10] R. Ciolfi, V. Ferrari, L. Gualtieri, Structure and deformations of strongly magnetized neutron stars with twisted torus configurations, Mon. Not. R. Astron. Soc. 406 (2010) 2540.
- [11] A. Sokolov, Phase transitions in a superfluid neutron liquid, Sov. Phys. JETP 52 (1980) 575.
- [12] F. Weber, Quark matter in neutron stars, J. Phys. G: Nucl. Part. Phys. 25 (1999) R195.
- [13] S.K. Maurya, B. Mishra, S. Ray, R. Nag, Anisotropic stars in modified gravity: An extended gravitational decoupling approach, Chin. Phys. C 46 (2022) 105105.
- [14] L. Herrera, Stability of the isotropic pressure condition, Phys. Rev. D 101 (2020) 104024.
- [15] R. Rufini, S. Bonazzola, Systems of self-gravitating particles in general relativity and the concept of an equation of state, Phys. Rev. 187 (1969) 1767.
- [16] M. Gleiser, Stability of boson stars, Phys. Rev. D 38 (1988) 2376.
- [17] K. Dev, M. Gleiser, Anisotropic stars: exact solutions, Gen. Relativ. Gravit. 34 (2002) 1793.
- [18] S.K.M. Hossein, F. Rahaman, J. Naskar, M. Kalam, S. Ray, Anisotropic compact stars with variable cosmological constant, Int. J. Mod. Phys. D 21 (2012) 1250088.
- [19] M. Kalam, F. Rahaman, S. Molla, S.K.M. Hossein, Anisotropic quintessence stars, Astrophys. Space Sci. 349 (2014) 865.
- [20] S.K. Maurya, Y.K. Gupta, S. Ray, D. Deb, Generalised model for anisotropic compact stars, Eur. Phys. J. C 76 (2016) 693.
- [21] M. Sharif, T. Naseer, Extended decoupled anisotropic solutions in gravity, Int. J. Mod. Phys. D 31 (2022) 2240017.
- [22] M. Sharif, K. Hassan, Electromagnetic effects on the complexity of static cylindrical object in gravity, Eur. Phys. J. Plus 137 (2022) 1380.
- [23] M. Sharif, T. Naseer, Effects of charge and gravitational decoupling on complexity and isotropization of anisotropic models, Phys. Dark Universe 42 (2023) 101324.
- [24] K. Hassan, M. Sharif, Decoupled Anisotropic Solutions Using Karmarkar Condition in Gravity, Universe 9 (2023) 165.
- [25] T. Naseer, M. Sharif, S. Manzoor, A. Fatima, Anisotropic Durgapal Fuloria neutron stars in gravity, Mod. Phys. Lett. A 39 (2024) 2450048.
- [26] T. Naseer, M. Sharif, A. Fatima, S. Manzoor, Constructing traversable wormhole solutions in theory, Chin. J. Phys. 86 (2023) 350.
- [27] M. Sharif, T. Naseer, Charged anisotropic spherical collapse in gravity, Chin. J. Phys. 81 (2023) 37.
- [28] E. Demir, T. Naseer, A. Ashraf, E. Gudekli, Investigating physical existence of charged stellar models, Chin. J. Phys. 91 (2024) 299.
- [29] T. Naseer, M. Sharif, Decoupled anisotropic Buchdahl’s relativistic models in theory, Phys. Scr. 99 (2024) 035001.
- [30] Y. Feng, T. Naseer, A. Ashraf, D. Sofuoglu, Analysis of some newly constructed compact models in theory, Phys. Scr. 99 (2024) 085034.
- [31] T. Naseer, M. Sharif, Implications of vanishing complexity condition in theory, Eur. Phys. J. C 84 (2024) 554.
- [32] P. Haensel, J.L. Zdunik, R. Schaefer, Strange quark stars, Astron. Astrophys. 160 (1986) 121.
- [33] F. Weber, Strange quark matter and compact stars, Prog. Part. Nucl. Phys. 54 (2005) 193.
- [34] M.A. Perez-Garcia, J. Silk, J.R. Stone, Dark matter, neutron stars, and strange quark matter, Phys. Rev. Lett. 105 (2010) 141101.
- [35] H. Rodrigues, S.B. Duarte, J.C.T. De Oliveira , Massive compact stars as quark stars, Astrophys. J. 730 (2011) 31.
- [36] M. Sharif, T. Naseer, Charge effect on isotropization and complexity of extended decoupled anisotropic stellar models, Chin. J. Phys. 86 (2023) 596.
- [37] Y. Feng, T. Naseer, A. Ashraf, D. Sofuoglu, I Abdullayeva, A brief analysis of isotropic Karmarkar models in modified gravity theory, Chin. J. Phys. 90 (2024) 372.
- [38] P.B. Demorest, T. Pennucci, S.M. Ransom, M.S.E. Roberts, J. Hessels, A two solar mass neutron star measured using Shapiro delay, Nature 467 (2010) 1081.
- [39] F. Rahaman, K. Chakraborty, P.K.F. Kuhfittig, G.C. Shit, M. Rahman, A new deterministic model of strange stars, Eur. Phys. J. C 74 (2014) 3126.
- [40] P. Bhar, A new hybrid star model in Krori Barua spacetime, Astrophys. Space Sci. 357 (2015) 46.
- [41] D. Deb, S.R. Chowdhury, S. Ray, F. Rahaman, B.K. Guha, Relativistic model for anisotropic strange stars, Ann. Phys. 387 (2017) 239.
- [42] D. Deb, M. Khlopov, F. Rahaman, S. Ray, B.K. Guha, Anisotropic strange stars in the Einstein Maxwell spacetime, Eur. Phys. J. C 78 (2018) 465.
- [43] M. Sharif, T. Naseer, Study of charged compact stars in non minimally coupled gravity, Fortschr. Phys. 71 (2023) 2200147.
- [44] M. Sharif, K. Hassan, Influence of modified gravity on self gravitating stellar objects, New Astron. 107 (2024) 102158.
- [45] S. Capozziello, A. Stabile, A. Troisi, Spherical symmetry in gravity, Class. Quantum Grav. 25 (2008) 085004.
- [46] S. Capozziello, E. De Filippis, V. Salzano, Modelling clusters of galaxies by gravity, Mon. Not. R. Astron. Soc. 394 (2009) 947.
- [47] S. Nojiri, S.D. Odintsov, Unified cosmic history in modified gravity: from theory to Lorentz non invariant models, Phys. Rep. 505 (2011) 59.
- [48] A.V. Astashenok, S. Capozziello, S.D. Odintsov, Extreme neutron stars from extended theories of gravity, J. Cosmol. Astropart. Phys. 01 (2015) 001.
- [49] A.V. Astashenok, S. Capozziello, S.D. Odintsov, Nonperturbative models of quark stars in gravity, Phys. Lett. B 742 (2015) 160.
- [50] S. Nojiri, S.D. Odintsov, Modified Gauss Bonnet theory as gravitational alternative for dark energy, Phys. Lett. B 631 (2005) 1.
- [51] K. Bamba, S.D. Odintsov, L. Sebastiani, S. Zerbini, Finite time future singularities in modified Gauss Bonnet and gravity and singularity avoidance, Eur. Phys. J. C 67 (2010) 295.
- [52] R. Myrzakulov, D. Saez-Gomez, A. Tureanu, On the CDM universe in gravity, Gen. Relativ. Gravit. 43 (2011) 1671.
- [53] K. Bamba, et al., Energy conditions in modified gravity, Gen. Relativ. Gravit. 49 (2017) 112.
- [54] S. Nojiri, S.D. Odintsov, V.K. Oikonomou, Ghost free Gauss Bonnet theories of gravity, Phys. Rev. D 99 (2019) 044050.
- [55] P.G.S. Fernandes, P. Carrilho, T. Clifton, D.J. Mulryne, Derivation of regularized field equations for the Einstein Gauss Bonnet theory in four dimensions, Phys. Rev. D 102 (2020) 024025.
- [56] R.A. Hennigar, D. Kubiznak, R.B. Mann, C. Pollack, On taking the limit of Gauss Bonnet gravity: theory and solutions, J. High Energy Phys. 2020 (2020) 27.
- [57] R. Kumar, S.U. Islam, S.G. Ghosh, Gravitational lensing by charged black hole in regularized 4D Einstein Gauss Bonnet gravity, Eur. Phys. J. C 80 (2020) 1128.
- [58] P.G.S. Fernandes, P. Carrilho, T. Clifton, D.J. Mulryne, The 4D Einstein Gauss Bonnet theory of gravity: a review, Class. Quantum Grav. 39 (2022) 063001.
- [59] M. Sharif, T. Naseer, Influence of charge on extended decoupled anisotropic solutions in gravity, Indian J. Phys. 96 (2022) 4373.
- [60] M. Sharif, T. Naseer, Impact of charge on complexity analysis and isotropic decoupled solutions in gravity, Phys. Scr. 98 (2023) 115012.
- [61] M. Kalam, A.A. Usmani, F. Rahaman, S.K.M. Hossein, I. Karar, R. Sharma, A relativistic model for strange quark star, Int. J. Theor. Phys. 52 (2013) 3319.
- [62] J.D.V. Arbanil, M. Malheiro, Radial stability of anisotropic strange quark stars, J. Cosmol. Astropart. Phys. 11 (2016) 012.
- [63] M. Sharif, T. Naseer, Study of anisotropic compact stars in gravity, Pramana 96 (2022) 119.
- [64] R.C. Tolman, Static solutions of Einsteins field equations for spheres of fluid, Phys. Rev. 55 (1939) 364.
- [65] H.A. Buchdahl, General relativistic fluid spheres, Phys. Rev. 116 (1959) 1027.
- [66] E. Farhi, R.L. Jaffe, Strange matter, Phys. Rev. D 30 (1984) 2379.
- [67] N. Stergioulas, Rotating stars in relativity, Living Rev. Relativ. 6 (2003) 3.
- [68] R.X. Xu, What Can the Redshift Observed in EXO 0748-676 Tell Us?, Chin. J. Astron. Astrophys. 3 (2003) 33.
- [69] H. Abreu, H. Hernandez, L.A. Nunez, Sound speeds, cracking and the stability of self gravitating anisotropic compact objects, Class. Quantum Grav. 24 (2007) 4631.
- [70] T. Naseer, J.L. Said, Existence of non singular stellar solutions within the context of electromagnetic field: a comparison between minimal and non minimal gravity models, Eur. Phys. J. C 84 (2024) 808.
- [71] H. Heintzmann, W. Hillebrandt, Neutron stars with an anisotropic equation of state mass, redshift and stability, Astron. Astrophys. 38 (1975) 51.
- [72] S. Biswas, D. Shee, S. Ray, F. Rahaman, B.K. Guha, Relativistic strange stars in Tolman Kuchowicz spacetime, Ann. Phys. 409 (2019) 167905.
- [73] T. Naseer, M. Sharif, Estimating the role of bag constant and modified theory on anisotropic stellar models, Chin. J. Phys. 88 (2024) 10.
- [74] K.P. Das, U. Debnath, Anisotropic strange stars in extended gravity with electromagnetic field, Chin. J. Phys. 88 (2024) 439.
- [75] K. Komathiraj, R. Sharma, Exact solution for an anisotropic star admitting the MIT Bag model equation of state, J. Sci. 01 (2020) 22.
- [76] M. Sharif, K. Hassan, Study of charged celestial objects in modified gravity, Chin. J. Phys. 86 (2023) 227.