Anytime Solvers for Variational Inequalities:
the (Recursive) Safe Monotone Flows
Abstract
This paper synthesizes anytime algorithms, in the form of continuous-time dynamical systems, to solve monotone variational inequalities. We introduce three algorithms that solve this problem: the projected monotone flow, the safe monotone flow, and the recursive safe monotone flow. The first two systems admit dual interpretations: either as projected dynamical systems or as dynamical systems controlled with a feedback controller synthesized using techniques from safety-critical control. The third flow bypasses the need to solve quadratic programs along the trajectories by incorporating a dynamics whose equilibria precisely correspond to such solutions, and interconnecting the dynamical systems on different time scales. We perform a thorough analysis of the dynamical properties of all three systems. For the safe monotone flow, we show that equilibria correspond exactly with critical points of the original problem, and the constraint set is forward invariant and asymptotically stable. The additional assumption of convexity and monotonicity allows us to derive global stability guarantees, as well as establish the system is contracting when the constraint set is polyhedral. For the recursive safe monotone flow, we use tools from singular perturbation theory for contracting systems to show KKT points are locally exponentially stable and globally attracting, and obtain practical safety guarantees. We illustrate the performance of the flows on a two-player game example and also demonstrate the versatility for interconnection and regulation of dynamical processes of the safe monotone flow in an example of a receding horizon linear quadratic dynamic game.
1 Introduction
Variational inequalities encompass a wide range of problems arising in operations research and engineering applications, including minimizing a function, characterizing Nash equilibria of a game, and seeking saddle points of a function. This paper synthesizes continuous-time flows whose trajectories converge to the solution set of a monotone variational inequality while respecting the constraints at all times.
Our motivation for considering this problem is two-fold. First, iterative algorithms in numerical computing can be interpreted as dynamical systems. This opens the door for the use of controls and system-theoretic tools to characterize their qualitative and quantitative properties, e.g., stability of solutions, convergence rate, and robustness to disturbances. In turn, the availability of such characterization sets the stage for developing sample-data implementations and systematically designing new algorithms equipped with desired properties.
The second motivation stems from problems where the solution to the variational inequality is used to regulate a physical process modeled as a dynamically evolving plant (e.g., providing setpoints, specifying optimization-based controllers, steering the plant toward an optimal steady-state). This type of problem arises in multiple application areas, including power systems, network congestion control, and traffic networks. In these settings, the algorithm used to solve the variational inequality is interconnected with a plant, and thus the resulting coupled system naturally lends itself to system-theoretic analysis and design. We are particularly interested in situations where the problem incorporates constraints which, when violated, would threaten the safe operation of the physical system. In such cases, it is desirable that the algorithm is anytime, meaning that it is guaranteed to return a feasible point even when terminated before it has converged to a solution. The anytime property ensures that the specifications conveyed to the plant remain feasible at all times.
1.1 Related Work
The study of the interplay between continuous-time dynamical systems and variational inequalities has a rich history. In the context of optimization, classical references include [2, 3, 4, 5]. For general variational inequalities, flows solving them can be obtained through differential inclusions involving monotone set-valued maps, originally introduced in [6]. These systems have been equivalently described as a projected dynamical systems [7] and complementarity systems [8, 9]. Recently, this framework has been extended to settings where monotonicity holds with respect to non-Euclidean norms [10], and when the system evolves on a Riemannian manifold [11]. One limitation of these systems is that they are, in general, discontinuous, which poses challenges both for their theoretical analysis and practical implementation.
The interconnection of algorithms with physical plants has attracted much attention recently. The interconnected system can often be viewed as the coupling of a dynamical system with a set valued operator (cf. [12, 13] for a comprehensive survey of systems having this form). The specific setting where the algorithm optimizes the steady-state of the plant is typically referred to as online feedback optimization[14, 15] and has been studied in continuous time in the context of power systems [16, 17], network congestion control [18], and traffic networks [19], as well as discrete time in [20]. Recently this framework has also been studied in game scenarios [21, 22].
A complementary approach uses extremum seeking control [23], which has been generalized to the setting of games in [24]. Extremum seeking differs from the methods introduced here in that they are typically zeroth-order methods, and do not offer exact stability guarantees. The recent work [25] considers safety guarantees for extremum seeking control for the special case of a single inequality constraint. In fact, the proposed algorithm can be understood as an approximation of the safe gradient flow in [26], which is a precursor for constrained optimization of the algorithms proposed here for constraint sets parameterized by multiple inequality and equalities.
To synthesize our flows, we employ techniques from safety-critical control [27, 28], which refers to the problem of designing a feedback controller that ensures that the state of the system satisfies certain constraints. The problem of ensuring safety is typically formalized by specifying a set of states where the system is said to remain safe, and ensuring the safe set is forward invariant. The work [29] reviews set invariance in control. A popular technique for synthesizing safe controllers uses the concept of control barrier functions (CBFs), see [30, 31, 32] and references therein, to specify optimization-based feedback controllers which “filter” a nominal system to ensure it remains in the safe set. Here, we apply this strategy to synthesize anytime algorithms, viewing the constraint set as a safety set and the monotone operator of the variational inequality as the nominal system. This view has connections to projected dynamical systems, whose relationship with CBF-based control design has recently been explored in [33, 34], and leads to the alternative “projection-based” interpretation of the projected monotone flow and safe monotone flow proposed here.
1.2 Statement of Contributions
We consider the synthesis of continuous-time dynamical systems solving variational inequalities while respecting the constraints at all times. We work primarily with continuous-time systems since we are motivated by online feedback optimization, where the evolution of a physical process determines the functions that define the variational inequality, which in turn regulates the dynamically evolving plant. The methods introduced here can be implemented on digital hardware by discretizing the resulting dynamics.
We discuss three flows that solve this problem. The projected monotone flow is already known, but we provide a novel control-theoretic interpretation as a control system whose closed-loop behavior is as close as possible to the monotone operator while still belonging to the tangent cone of the constraint set. The safe monotone flow can be interpreted either as a control system with a feedback controller synthesized using techniques from safety-critical control or as an approximation of the projected monotone flow. The latter interpretation relies on the novel notion of restricted tangent set, which generalizes the usual concept of tangent cone from variational geometry. We show that equilibria correspond exactly with critical points of the original problem, establish existence and uniqueness of solutions, and characterize the regularity properties of flow. We also show that the constraint set is forward invariant and asymptotically stable, and derive global stability guarantees under the additional assumption of convexity and monotonicity. Our technical analysis relies on a suite of Lyapunov functions to establish stability properties with respect to the constraint set and the whole state space. When the constraint set is polyhedral, we establish that the system is contracting and exponentially stable. Finally, the recursive safe monotone flow bypasses the need for continuously solving quadratic programs along the trajectories by incorporating a dynamics whose equilibria precisely correspond to such solutions, and interconnecting the dynamical systems on different time scales. Using tools from singular perturbation theory for contracting systems, we show that for variational inequalities with polyhedral constraints, the KKT points are locally exponentially stable and globally attracting, and obtain practical safety guarantees. We compare the three flows on a simple two-player game and demonstrate how the safe monotone flow can be interconnected with dynamical processes on an example of a receding horizon linear quadratic dynamic game.
The flows introduced here generalize the safe gradient flow, a continuous-time system proposed in our previous work [26] (in parallel, [20] introduced a discrete-time implementation of a simplified version of it). With respect to the safe gradient flow, our treatment extends the results in three key ways. First, we consider variational inequalities, rather than just constrained optimization problems, making the flows introduced here applicable to a much broader range of problems. Second, with assumptions of monotonicity and convexity of the constraints, we obtain global stability and convergence results, rather than local stability results. Third, the rigorous characterization of the contractivity properties of the safe monotone flow paves the way for its interconnection with other dynamically evolving processes. In fact, the proposed recursive safe monotone flow critically builds on this analysis by leveraging different timescales and singular perturbation theory.
2 Preliminaries
We review here basic notions from variational inequalities, projections, and set invariance. Readers familiar with these concepts can safely skip this section.
2.1 Notation
Let denote the set of real numbers. For , . For , denotes the th component and denotes all components of excluding . For , (resp. ) denotes (resp. ) for . We let denote the Euclidean norm. We write (resp., ) to denote is positive semidefinite (resp., is positive definite). Given , let denote the seminorm where . For a symmetric , and denote the minimum and maximum eigenvalues of , resp. Given , the distance of to is . The projection map onto is , where . Given a closed and convex set , the normal cone to at is and the tangent cone to at is .
Given , we denote its gradient by . For , denotes its Jacobian. For , we denote by the matrix whose rows are . Given a function , we say it is directionally differentiable if for all , the following limit exists
Given a vector field and a function , the Upper-right Dini derivative of along is
where is the flow map111 For , the flow map is defined by , where is the unique trajectory solving with . corresponding to the system . When is directionally differentiable and when is differentiable, then .
2.2 Variational Inequalities
Here we review the basic theory of variational inequalities following [35]. Let be a map and a set of constraints. A variational inequality refers to the problem of finding such that
| (1) |
We use to refer to the problem (1) and to denote its set of solutions. Variational inequalities provide a framework to study many different analysis and optimization problems, including
-
•
Solving the nonlinear equation , which corresponds to ;
-
•
Minimizing the function subject to the constraint that , which corresponds to ;
-
•
Finding saddle points of the function subject to the constraints that and , which corresponds to .
-
•
Finding the Nash equilibria of a game with agents, where the th agent wants to minimize the cost subject to the constraint , which corresponds to , where is the pseudogradient operator defined by , and .
The map is monotone if , for all , and is -strongly monotone if there exists such that , for all . When is a gradient map, i.e., for some function , then monotonicity (resp. -strong monotonicity) is equivalent to convexity (resp. strong convexity) of . When is monotone and is convex, is a monotone variational inequality.
In order to provide a characterization of the solution set , we need to introduce a more explicit description of the set of constraints. Suppose that and are continuously differentiable and is described by inequality constraints and affine equality constraints,
| (2) |
where and . For , we denote the active constraint, inactive constraint, and constraint violation sets, resp., as
The problem (1) satisfies the constant-rank condition at if there exists an open set containing such that for all , the rank of remains constant for all . The problem (1) satisfies the Mangasarian-Fromovitz Constraint Qualification (MFCQ) condition at if are linearly independent, and there exists such that for all , and for all . If MFCQ holds at , then, if satisfies (1), there exists such that
| (3a) | ||||
| (3b) | ||||
| (3c) | ||||
| (3d) | ||||
| (3e) | ||||
Equations (3) are called the KKT conditions. A point satisfying them is a KKT triple and the pair is a Lagrange multiplier. For monotone variational inequalities, when MFCQ holds at , then the KKT conditions are both necessary and sufficient for . When is monotone is closed and convex. If is additionally -strongly monotone, then the set of solutions is a singleton.
2.3 Controller Synthesis for Set Invariance
We review here notions from the theory of set invariance for control systems following [29] and discuss methods for synthesizing feedback controllers that ensure it. Consider a control-affine system
| (4) | ||||
with Lipschitz-continuous vector fields , for , and a set of valid control inputs . Let be a constraint set of the form (2) to which we want to restrict the evolution of the system. We consider the problem of designing a feedback controller such that is forward invariant with respect to the closed-loop dynamics . In applications, often corresponds to the set of states for which the system can operate safely. For this reason, we refer to as the safety set, and call the system safe under a controller if is forward invariant. A controller ensuring safety is safeguarding. We discuss two optimization-based strategies for synthesizing safeguarding controllers.
2.3.1 Safeguarding Control via Projection
The first strategy ensures the closed-loop dynamics lie in the tangent cone of the safety set. Whenever MFCQ holds at , the tangent cone can conveniently be expressed as, cf. [36, Theorem 6.31], . We then define the set-valued map which characterizes the set of inputs that ensure the system remains inside the safety set. The set has the form,
As we in the following result, the feedback such that for renders forward invariant. The proof is omitted for brevity, though it follows directly from Nagumo’s Theorem [37, Theorem 2].
Lemma 2.1 (Projection-based Safeguarding Feedback).
Consider the system (4) with safety set and suppose that for all . Then, the feedback controller is safeguarding if for all and the closed-loop system admits a unique solution for all initial conditions.
To synthesize a safeguarding controller, we propose a strategy where at each is expressed as the solution to a mathematical program. Because is defined in terms of affine constraints on the control input , we can readily express a feedback satisfying the hypotheses of Lemma 2.1 in the form of a mathematical program,
| (5) |
for an appropriate choice of cost function . In general, care must be taken to ensure that the set is nonempty and that the controller in (5) satisfies appropriate regularity conditions to ensure existence and uniqueness for solutions of the resulting closed-loop dynamics. Even if these properties hold, the approach has several limitations: the controller is ill-defined for initial conditions lying outside the safety set and the closed-loop system in general is nonsmooth.
2.3.2 Safeguarding Control via Control Barrier Functions
The second strategy for synthesizing safeguarding controllers addresses the limitations of projection-based methods. The approach relies on the notion of a vector control barrier functions [27, 26]. Given a set and set of valid control inputs , we say the pair is a -vector control barrier function (VCBF) for on relative to if there exists such that the map given by
takes nonempty values for all . Similar to the previous strategy, the set characterizes the set of inputs which ensure that the state remains inside the safe set. Unlike the previous strategy, this assurance is implemented gradually: the parameter corresponds to how tolerant we are of increasing the value of inactive constraints, with small values of corresponding to more aggressive bounds on the growth rate. To see this, note that if then the left-hand sides of the constraints parameterizing decrease as increases, making the constraint easier to satisfy. For , if , then the left-hand side of the corresponding constraint becomes , thus the only nontrivial constraints correspond to where , and for the set corresponds to .
When and , an -vector control barrier function is equivalent to the usual notion of a control barrier function [27, Definition 2]. The generalization provided by VCBFs allows us to consider a broader class of safety sets.
Lemma 2.2 (VCBF-based Safeguarding Feedback).
Consider the system (4) with safety set and suppose is a vector control barrier function for on relative to and MFCQ holds on . Then, the feedback controller is safeguarding and ensures asymptotic stability of on if for all and the closed-loop system admits a unique solution for all initial conditions.
The proof of the Lemma 2.2 is omitted for space, but the result follows by Nagumo’s Theorem [37, Theorem 2] since one can show that the closed-loop dynamics are contained in the tangent cone. To synthesize a safeguarding feedback controller, one can pursue a design using a similar approach to Section 2.3.1. Given a cost function , we let solve the following mathematical program:
| (6) |
Similarly to the case of projection-based safeguarding feedback control, care must be taken to verify the existence and uniqueness of solutions to the closed-loop system, as well as to handle situations where (6) does not have unique solutions. If these properties hold, then the control design addresses the challenges of projection-based methods. In particular, we can ensure that a controller of the form (6) is well-defined outside the safety set and results in closed-loop system with continuous solutions, under mild conditions which we discuss in the following sections.
3 Problem Formulation
Consider a variational inequality defined by a continuously differentiable map and a convex set of the form (2), where is continuously differentiable. We assume throughout that . Our goal is to synthesize a solver for this problem in the form of a continuous-time dynamical system.
Problem 1 (Anytime solver of variational inequality).
Design a dynamical system, , which is well defined on a set containing such that
-
(i)
Trajectories of the system converge to ;
-
(ii)
is forward invariant;
-
(iii)
is asymptotically stable as a set.
Item (i) ensures that the dynamical system can be viewed as a solver of the problem (1): solutions can be obtained by simulating system trajectories and taking the limit as of . Furthermore, the solver can be implemented on computational platforms by discretizing the dynamics. Item (ii) ensures that this solver is anytime, meaning that even if terminated early, it is guaranteed to return a feasible solution provided the initial condition is feasible. Item (iii) accounts for infeasible initial conditions, and ensures asymptotic safety. Both the expression of the algorithm in the form of a continuous-time dynamical system and the anytime property are particularly useful for real-time applications, where the algorithm might be interconnected with other physical processes – e.g., when the algorithm output is used to regulate a physical plant and constraints of the optimization problem ensure the safe operation of the plant.
In the following, we introduce three dynamics to solve Problem 1. The first, synthesized using the technique outlined in Section 2.3.1, is the projected monotone flow. This dynamics is already well-known but we reinterpret it here through the lens of control theory. The next two, synthesized using the technique outlined in Section 2.3.2, are the safe monotone flow and the recursive safe monotone flow. Both dynamics are entirely novel.
4 Projected Monotone Flow
Here, we discuss our first solution to Problem 1, in the form of the projected monotone flow. We show that the system can be viewed in two equivalent ways: either as a control system with a feedback controller designed using the strategy outlined in Section 2.3.1, or as a projected dynamical system. In fact, this system admits many other equivalent descriptions, for example in terms of monotone differential inclusions, or complementarity systems [8, 9, 37] (see [13] for a modern survey on the relationships between systems in various formalisms). Its properties have been extensively studied [7] and techniques for computational implementation have been considered in [38]. However, we focus here on the control-based and projection-based forms. In the coming sections we describe in detail the derivation of each implementation, show their equivalence, and discuss the properties of the resulting flow regarding safety and stability.
4.1 Control-Based Implementation
Our design strategy originates from the observation that, when is monotone, the system finds solutions to the unconstrained variational inequality . However, trajectories flowing along this dynamics might leave the constraint set . This leads us to consider the control-affine system:
| (7) | ||||
Here, we have augmented the system with inputs from the admissible set to modify the flow of the original drift to account for the constraints in a way that ensures that the solutions to (7) stay inside of or approach . The idea is that if the constraint is in danger of being violated, the corresponding input can be increased to ensure trajectories continue to satisfy it. Likewise, the input can be increased or decreased to ensure the corresponding constraint is satisfied along trajectories.
Our design proceeds by thinking of as a safety set for the system and using the approach outlined in Section 2.3.1 to synthesize a safeguarding feedback controller . Assuming that MFCQ holds for all , the map takes the form
| (8) | ||||
The following result states that the set of admissible controls is nonempty. We omit its proof for space reasons, but note that it readily follows from Farka’s Lemma [39].
Lemma 4.1.
(Projection onto Tangent Cone is Feasible) If and MFCQ holds at , then .
We then use the feedback controller
| (9) |
where we set the objective function to be
| (10) |
This function measures the magnitude of the “modification” of the drift term in (7). Thus, the QP-based controller (9) has the interpretation, at each , of finding the control input such that the closed-loop system dynamics are as close as possible to , while still being in . In general, the program given by (9) does not have unique solutions. Despite this, we show below that the closed-loop dynamics of (7) is well defined regardless of which solution to (5) is chosen. We refer to it as the projected monotone flow.
4.2 Projection-Based Implementation
The second implementation of the projected monotone flow consists of projecting onto the tangent cone of the constraint set. In general, the tangent cone does not have a representation that allows us to compute the projection easily. However, when the appropriate constraint qualification condition holds, the tangent cone admits a convenient parameterization which allows for the projection to be implemented as a quadratic program. Let and suppose that MFCQ holds at . It follows that the tangent cone can be parameterized222 The right hand side of (11) is called the linearization cone of , and denoted as . In general, , and we say that Abadie’s Constraint Qualification (ACQ) [40] holds at if the reverse inclusion holds, i.e., . MFCQ is a stronger condition that implies ACQ. Many of the results we state in the paper can be generalized to hold under the weaker assumption of ACQ, however for simplicity, we avoid a detailed technical discussion of constraint qualifications. as
| (11) |
The projection-based implementation of the projected monotone flow takes then the following form:
| (12) | ||||
The projection onto the tangent ensures that is forward invariant, by Nagumo’s Theorem [29, Theorem 3.1].
4.3 Properties of Projected Monotone Flow
Here, we lay out the properties of the projected monotone flow. We begin by establishing the equivalence between the control- and projection-based implementations. We then discuss existence and uniqueness of solutions, and finally the stability and safety properties of the dynamics.
4.3.1 Equivalence of Control-Based and Projection-Based Implementations
Equivalence follows directly from the properties of the tangent cone, as we show next.
Proposition 4.2.
(Equivalence of Control-Based and Projected-Based Implementations) Assume MFCQ holds at and let be any solution to (9). Then, .
Proof.
Let be any solution to (9) and . Then , so it follows immediately by optimality of that
Next, because is given by a projection, there exists such that , see e.g., [8, Corollary 2]. If MFCQ holds at , by [36, Theorem 6.14], there exists such that can be written as
Combining this expression with the fact that and using the parameterization of the tangent cone in (11), we deduce that . By optimality of ,
But since the projection onto the tangent cone must be unique, we conclude . ∎
The value of Proposition 4.2 stems from showing that safety-critical control can be used to design algorithms that solve variational inequalities. Though the control strategy pursued in Section 4.1 results in a known flow, this sets up the basis for employing other design strategies from safety-critical control to yield novel methods, as we show later.
4.3.2 Existence and Uniqueness of Solutions
The projected monotone flow is discontinuous, and hence one must consider notions of solutions beyond the classical ones, see e.g., [41]. Here, we consider Carathéodory solutions, which are absolutely continuous functions that satisfy (12) almost everywhere. The existence and uniqueness of solutions for all initial conditions follows readily from [37, Chapter 3.2, Theorem 1(i)] or [13, Theorem 5.8].
4.3.3 Safety and Stability of Projected Monotone Flow
We now show that the projected monotone flow is safe, meaning that the constraint set is forward invariant, and the solution set is stable. Forward invariance of follows directly from Nagumo’s Theorem. The equilibria of the projected monotone flow correspond to solutions to . Finally, stability of a solution can be certified using the Lyapunov function
as a consequence of [37, Chapter 3.2, Theorem 1(ii)] or [42, Theorems 1 and 2]. These properties are summarized next.
Theorem 4.3.
(Safety and Stability Properties of Projected Monotone Flow) Let be convex and suppose MFCQ holds everywhere on . The following hold for the projected monotone flow:
-
(i)
is forward invariant;
-
(ii)
is an equilibrium of the projected monotone flow if and only if ;
-
(iii)
If and is monotone, then is globally Lyapunov stable relative to ;
-
(iv)
If is -strongly monotone, then the projected monotone flow is contracting at rate . In particular, the unique solution is globally exponentially stable relative to .
5 Safe Monotone Flow
In this section, we discuss a second solution to Problem 1, which results in an entirely novel flow, termed safe monotone flow. Similar to the projected monotone flow, this system admits two equivalent implementations: either as a control-system with a safeguarding feedback controller or as a projected dynamical system. Because of its continuity properties, the system can be solved using standard ODE discretization schemes, cf. [26, Remark 5.6], but we leave the formal analysis of this for future work.
5.1 Control-Based Implementation
We start with the control system (7) with the admissible control set , viewing as a safety set, and design a safeguarding controller. We synthesize this controller using the function as a VCBF, following the approach outlined in Section 2.3.2.
Letting be a parameter, the set of control inputs ensuring safety is given by
The next result shows that this set is nonempty on an open set containing .
Lemma 5.1 (Vector Control Barrier Function for (7)).
Assume MFCQ holds for all . Then there exists an open set on which is a vector-control barrier function of (7) for , on , relative to .
The proof of this result is identical to [26, Lemma 4.1] and we omit it for brevity. By Lemma 5.1, the feedback controller where
| (13) |
and is given by (10), is well defined on . This controller has the same interpretation as before: determining the control input belonging to such that the closed-loop system dynamics are as close as possible to . Similar to the case with projection-based methods, the problem (6) does not necessarily have unique solutions. However, we show below that the closed-loop system is well-defined regardless of which solution is chosen. We refer to it as the safe monotone flow with safety parameter , denoted .
5.2 Projection-Based Implementation
Here we describe the implementation of the safe monotone flow as a projected dynamical system. Similar to the projected monotone flow, the projected system is obtained by projecting onto a set-valued map. However, because the projection onto the tangent cone is in general discontinuous as a function of the state, we replace the tangent cone with the -restricted tangent set (here ), denoted , defined as
| (14) |
Figure 1 illustrates this definition. This set can be interpreted as an approximation of the usual tangent cone, but differs in several key ways. First, the restricted tangent set is not a cone, meaning that vectors in cannot be scaled arbitrarily: in certain direction, the magnitude of vectors in is restricted. An important property of is that, even though the tangent cone is undefined for , this is not the case for the restricted tangent set. In fact, it can be shown that takes nonempty values on an open set containing . This property allows for the safe monotone flow to be well-defined for infeasible initial conditions. The next result states properties of the -restricted tangent set.

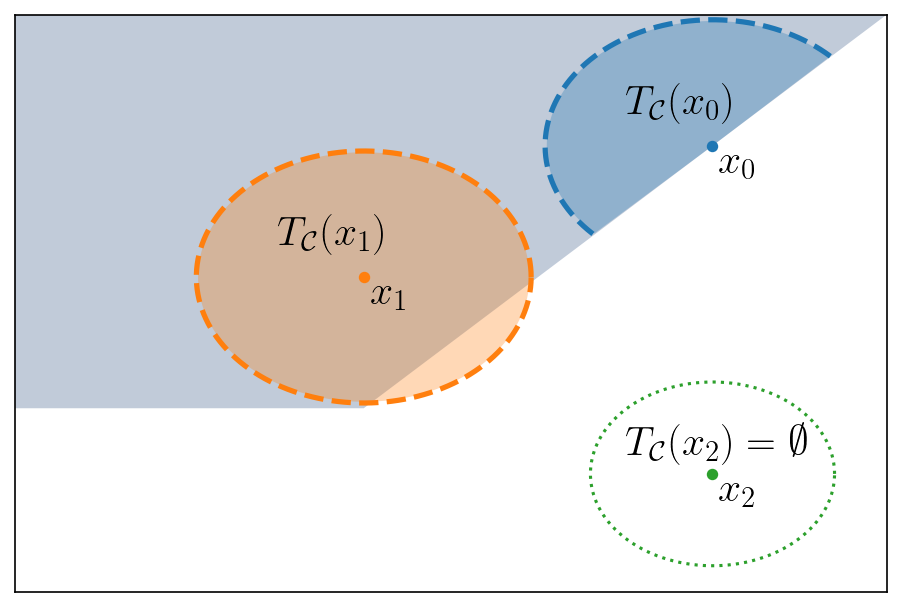
Proposition 5.2.
(Properties of -Restricted Tangent Set) Assume MFCQ holds for all . The set-valued map satisfies:
-
(i)
is convex for all ;
-
(ii)
For any fixed , the set satisfies MFCQ at all .
-
(iii)
There exists an open set containing such that for all ;
-
(iv)
If , then .
Proof.
We observe that (i) follows from the fact that the constraints characterizing are affine in the variable . We prove (ii) using the same strategy as [26, Lemma 4.5], which we sketch here. If MFCQ holds at , then the inequalities defining (14) satisfy Slater’s condition [43, Chapter 5.2.3] at and therefore MFCQ holds for all . To show (iii), we note that Slater’s condition implies that the affine constraints parameterizing are regular [44, Theorem 2], meaning that the system remains feasible with respect to perturbations. Since is nonempty for all , it follows that there exists an open set containing such that is nonempty for all . Finally, (iv) follows from the definition of the tangent cone. ∎
Using the -restricted tangent set, we can define the projected dynamical system
| (15) | ||||
Similar to the projected monotone flow, the projection operation ensures that the trajectories of the system remain in the safety set. However, as we show next, the advantages of projecting onto the restricted tangent cone is that the system is well defined for infeasible initial conditions, and trajectories of the system are smooth.
5.3 Properties of Safe Monotone Flow
We now discuss the properties of the safe monotone flow. We begin by establishing the equivalence of the control-based and projection-based implementations. Next, we discuss its stability and safety properties.
5.3.1 Equivalence of Control-Based and Projection-Based Implementations
We establish here that the control-based and projection-based implementations of the safe monotone flow are equivalent. The next result states that the closed-loop dynamics resulting from the implementation of (6) over (7) is equivalent to the projection onto . The structure of the proof mirrors that of Proposition 4.2.
Proposition 5.3.
(Equivalence of Control-Based and Projection-Based Implementations) Assume MFCQ holds for everywhere on and let be an open set containing on which takes nonempty values. Let be any solution to (13) at (note that ). Then, .
Proof.
Let be any solution to (13) and . Then , so it follows immediately by optimality of that
Next, because is given by a projection, there exists , where such that , see e.g., [8, Corollary 2], and where
Combining this expression with the fact that and using the definition of the -restricted tangent cone, we deduce that . By optimality of , we have
But since the projection onto the -restricted tangent set is unique, we conclude . ∎
5.3.2 Existence and Uniqueness of Solutions
We now discuss conditions for the existence and uniqueness of solutions of the safe monotone flow.
Proposition 5.4.
(Existence and Uniqueness of Solutions to Safe Monotone Flow) Assume MFCQ and the constant-rank condition hold on for all and let be the open set containing in Proposition 5.2(iii). Then
-
(i)
For all , there exists a unique solution to the safe monotone flow with .
-
(ii)
For all , there exists a unique solution such that . Furthermore, the solution can be extended so that either or as .
Proof.
We first note that the program (15) satisfies the General Strong Second-Order Sufficient Condition (cf. [45]) and Slater’s condition at . Because the objective function and constraints of (15) are twice continuously differentiable, we can apply [45, Theorem 3.6] to conclude that is locally Lipschitz at . Therefore, is also lower semicontinuous and by [37, Chapter 2, Theorem 1] there exists for all a solution for some with . Furthermore, either or as . Uniqueness of solutions holds by local Lipschitznes and (ii) follows.
To show (i), we note that , and by [29, Theorem 3.1], for any solution with , we have that for all on the interval on which the solution exists. Since , solutions beginning in cannot approach , and exist for all time. ∎
5.3.3 Safety of Safe Monotone Flow
Here we establish the safety properties of the safe monotone flow. We begin by characterizing optimality conditions for the closed-loop dynamics.
Lemma 5.5.
Proof.
Let . Then is a solution to the monotone variational inequality , parameterized by . Since MFCQ holds at all by Proposition 5.2(iii), we can use the KKT conditions to characterize , which correspond to (16). Further, by Proposition 5.2(iv), solutions to (16) exist on an open set containing . Since is strongly monotone with respect to , the solution to is unique, proving the result. ∎
We rely on the optimality conditions in Lemma 5.5 to establish the following result characterizing the equilibria and safety properties of the safe monotone flow.
Theorem 5.6.
(Equilibria and Safety of Safe Monotone Flow) Let , be convex, and suppose MFCQ and the constant rank condition holds everywhere on . The following hold for the safe monotone flow:
-
(i)
is forward invariant and asymptotically stable on ;
-
(ii)
is an equilibrium if and only if ;
Proof.
To show (i), note that by Proposition 5.3, for all there exists such that . Given the existence and uniqueness of solutions of the closed-loop system, cf. Propositions 5.4, the result follows from Lemma 2.2 since is a VCBF. Statement (ii) follows from the observation that, if , by Lemma 5.5, there exists such that solves (16), which holds if and only if solves (3). ∎
5.3.4 Stability of Safe Monotone Flow
Here we characterize the stability properties of the safe monotone flow. We begin by establishing conditions for stability relative to .
Theorem 5.7.
(Stability of Safe Monotone Flow Relative to ) Assume MFCQ holds everywhere on . Then
-
(i)
If and is monotone, then is globally Lyapunov stable relative to ;
-
(ii)
If and is -strongly monotone, then is globally asymptotically stable relative to .
Before proving Theorem 5.7, we provide several intermediate results. Our strategy relies on fixing and considering the candidate Lyapunov function
| (17) |
We first present bounds on the Dini derivative of along . The result is proven in Appendix A.
Lemma 5.8 (Dini Derivative of ).
Assume MFCQ holds everywhere on . For , let be Lagrange multipliers corresponding to . For and , then
if is -strongly monotone (the inequality holds with if F is monotone instead).
We now move on to characterizing properties of . The following result is proven in Appendix B.
Lemma 5.9 (Properties of ).
Assume MFCQ holds everywhere on . Define the matrix-valued function by
Then, for all and ,
| (18) |
and
| (19) |
We are now ready to prove Theorem 5.7.
Proof of Theorem 5.7.
Let and suppose the hypotheses of (i) hold. Consider the function defined by (17). We show that is a (strict) Lyapunov function when is (-strongly) monotone. Let and . Then, using (16d),
so by examining the expression in (18) we see that for all with equality if and only if . Thus is positive definite with respect to . Next,
Since and , we have and , and therefore
Similarly, since , and , we have and , and therefore
Finally, since is monotone and is convex, it follows that is positive semi-definite, and therefore . To show (ii), we can use the same reasoning above to show that . ∎
Next, we discuss stability with respect to the entire state space, which ensures the safe monotone flow can be used to solve even for infeasible initial conditions.
Theorem 5.10.
(Stability of Safe Monotone Flow with Respect to n) Assume MFCQ and the constant-rank condition holds on . Then
-
(i)
If and is monotone, then is globally Lyapunov stable;
-
(ii)
If and is -strongly monotone, then is globally asymptotically stable.
To prove Theorem 5.10, we can no longer rely on the Lyapunov function defined in (17) because it is no longer positive definite and may take negative values for . Instead, we consider the new candidate Lyapunov function
| (20) |
where and is the penalty function given by
Before proceeding to the proof of Theorem 5.10, we provide a bound for the Dini derivative of along , which is proven in Appendix C.
Lemma 5.11 (Dini Derivative of ).
For all and , is directionally differentiable at along the direction . In particular,
| (21) |
where .
We are now ready to prove Theorem 5.10.
Proof of Theorem 5.10.
We begin by showing (i). Let . Note that, from the optimality conditions (16), corresponds to the set of Lagrange multipliers of the solution to . Because MFCQ holds at , it follows that is bounded. Thus, it is possible to choose small enough so that
| (22) |
Next, we observe that it follows immediately from the definition (20) that is positive definite with respect to . Finally, we compute and show that it is negative semidefinite. Let . We consider three cases: , , and . In the case where ,
Combining the bounds in Lemmas 5.8, 5.9, and 5.11,
| (23) |
Since satisfies (22), it follows that .
For the case where , we rearrange (18) to write
Then, we have
| (24) | ||||
and . In the case where ,
which leads us to two subcases: (a) and (b) . In subcase (a), satisfies the bound in (23) and, therefore, . In subcase (b),
and therefore satisfies the bound in (24), so . To prove (ii), we can use the same arguments above to show in each case . ∎
We conclude this section by discussing the contraction properties of the safe monotone flow. Contraction refers to the property that any two trajectories of the system approach each other exponentially (cf. [46, 47] for a precise definition), and implies exponential stability of an equilibrium. We show that, for sufficiently large , the safe monotone flow system is contracting provided is globally Lipschitz and the constraint set is polyhedral. Our analysis relies relies on the following result, which follows as a direct consequence of [48, Lemma 2.1].
Lemma 5.12 ([48, Lemma 2.1]).
Consider the following quadratic program
| (25) |
where . Then solves (25) if and only if it is a solution to the linear program
| (26) |
We now show that the safe monotone flow is contracting.
Theorem 5.13.
(Contraction and Exponential Stability of Safe Monotone Flow) Let be -strongly monotone and globally Lipschitz with constant and a polyhedral set defined by (2) with and . If
| (27) |
then the safe monotone flow is contracting with rate . In particular, the unique solution is globally exponentially stable.
Proof.
We claim that if the assumptions hold, then
| (28) |
in which case the system is contracting by [46, Theorem 31], and exponential stability of follows as a consequence. To show the claim, from (16a), note that
for any . Let then and and . Then, using the strong monotonicity of ,
| (29) | ||||
Next, let , where is the Lagrangian of (15), defined as
| (30) |
and is given by
| (31) |
For , is minimized when , and therefore
| (32) |
If , then is a solution to the program
which is the Lagrangian dual333By convention, the Lagrangian dual problem is a maximization problem (cf. [43, Chapter 5]). However, the minus sign in the definition of ensures that here it is a minimization. The reason for this sign convention is to make the notation simpler. of (15). By Lemma 5.12, is also a solution to the linear program,
Since is also feasible for the previous linear program, by optimality of ,
By a similar line of reasoning,
Combining the previous two expressions, we obtain
where we used , with . For any , by Young’s Inequality [49, pp. 140] it follows that
Substituting into (29), we obtain
Therefore, (28) holds with if satisfies
Such can be chosen if , which corresponds to the condition (27). The optimal estimate of the contraction rate is . ∎
Remark 5.14 (Connection with Safe Gradient Flow).
The safe monotone flow is a generalization of the safe gradient flow introduced in [26]. The latter was originally studied in the context of nonconvex optimization and, similar to the case of the safe monotone flow, enjoys safety of the feasible set and correspondence between equilibria and critical points. Further, under certain constraint qualifications, the local stability of equilibria relative to the constraint set under the safe gradient flow can be established using the objective function as a Lyapunov function. Because we are working with variational inequalities, may not correspond to the gradient of a scalar-valued function, so the Lyapunov functions used in [26] are not directly applicable. However, the assumption of convexity and monotonicity here allows us to construct novel Lyapunov functions to obtain global stability results. The interested reader can check [26, Section VI] for a comparison of the safe gradient flow with other continuous-time methods for optimization.
6 Recursive Safe Monotone Flow
A drawback of the projected and safe monotone flows is that, in order to implement them, one needs to solve either the quadratic programs (9) or (13) at each time along the trajectory of the system. As a third algorithmic solution to Problem 1, in this section we introduce the recursive safe monotone flow which gets around this limitation by incorporating a dynamics whose equilibria correspond to the solutions of the quadratic program. We begin by showing how to derive the dynamics for general constraint sets by interconnecting two systems on multiple time scales. Next, we use the theory of singular perturbations of contracting flows to obtain stability guarantees in the case where is polyhedral, and show that trajectories of the recursive safe monotone flow track those of the safe monotone flow. The latter property enables us to formalize a notion of “practical safety” that the recursive safe monotone flow satisfies.
6.1 Construction of the Dynamics
We discuss here the construction of the recursive safe monotone flow. The starting point for our derivation is the control-affine system (7). The safe monotone flow consists of this system with a feedback controller specified by the quadratic program (13). Rather than solving this program exactly, the approach we take is to replace it with a monotone variational inequality parameterized by the state. For fixed , we can solve solve this inequality, and hence obtain the feedback , using the safe monotone flow corresponding to this problem. Coupling this flow with the control system (7) yields the recursive safe monotone flow. The reason for using the term “recursive” is that the system can be interpreted as coupling one instance of the safe monotone flow (corresponding to the problem (1)), with another instance of the safe monotone flow (corresponding to the problem (6)).
In this section we carry out this strategy in mathematically precise terms. We rely on the following result, which provides an alternative characterization of the CBF-QP (13).
Lemma 6.1.
Proof.
Note that the constraints of (33) satisfy MFCQ for all . Since the objective function in (33) is convex in , one can see that necessary and sufficient conditions for optimality are given by a KKT system that, after some manipulation, takes the form
It follows immediately that if satisfies the above equations, then . ∎
The rationale for considering (33), rather than working with (13) directly, is that the constraints of (33) are independent of , which will be important for reasons we show next. Being a constrained optimization problem, (33) can be expressed in terms of a variational inequality (parameterized by ). Formally, let be given by
| (34) |
where is given by (7) and let , which we parameterize as
| (35) |
The optimization problem (33) corresponds to the variational inequality .
Our next step is to write down the safe monotone flow with safety parameter corresponding to the variational inequality . Note that the -restricted tangent set (14) of is The projection onto has the following closed-form solution
Using this expression and applying Proposition 5.3, we write the safe monotone flow corresponding to the variational inequality as
| (36) | ||||
Under certain assumptions, which we formalize in the sequel, for a fixed , trajectories of (36) converge to solutions of the QP (13).
This discussion suggests a system solving the original variational inequality can be obtained by coupling (36) with the dynamics (7) as follows:
| (37a) | ||||
| (37b) | ||||
| (37c) | ||||
We refer to the system (37) as the recursive safe monotone flow. The parameter characterizes the separation of timescales between the system (37a) and (37b)-(37c). The interpretation of the dynamics is that, when is sufficiently small, (37b)-(37c) evolve on a much faster timescale and rapidly approach the solution set of (13). The system on the slower timescale (37a) then approximates the safe monotone flow. We formalize this analysis next.
Remark 6.2.
(Relationship to Primal-Dual Flows) This recursive safe monotone flow is closely related to primal-dual flows, which seek a solution to (3) by flowing along a monotone operator in the primal variable, and performing a gradient ascent in the dual variables:
| (38a) | ||||
| (38b) | ||||
| (38c) | ||||
This method has been well-studied classically [2, 50], and has attracted recent attention due to its suitability for distributed implementation on network problems [51, 52, 53, 54]. One drawback of (38) is that it does not ensure that the primal variable remains in the feasible set . The recursive monotone flow can be interpreted as a primal-dual flow which overcomes this limitation, and provides practical safety guarantees, by modifying the dual-ascent term. One can show that the right hand side of (37) converges exactly to the right hand side of (38) by letting , , and , and taking the limit as . Future work will study further connections of the recursive safe monotone flow with primal-dual flows.
6.2 Stability of Recursive Safe Monotone Flow
To prove stability of the system (37), we rely on results from contraction theory [46]. Specifically, we derive conditions on the time-scale separation that ensures that (37) is contracting and, as a consequence, globally attractive and locally exponentially stable. Throughout the section, we assume the following assumption holds.
Assumption 1.
(Strong Monotonicity, Lipschitzness, and Polyhedral Constraints) The following holds:
-
(i)
is -strongly monotone and -Lipschitz;
-
(ii)
is a polyhedral set defined by (2) with and , and the matrix has full rank444 This assumption is slightly stronger than the Linear Independence Contraint Qualification (LICQ) assumption. LICQ requires linear independence of the gradients of only the active constraints, whereas here we require linear independence of the gradients of all constraints..
Next, we show that it is possible to tune the parameters so the system (36) is contracting, uniformly in .
Lemma 6.3.
Proof.
We now characterize the contraction and stability properties of the recursive safe monotone flow.
Theorem 6.4.
(Contractivity of Recursive Safe Monotone Flow) Assume is -strongly monotone and globally Lipschitz, and satisfies (27). Under Assumption 1 and chosen as in Lemma 6.3, then
-
(i)
the unique KKT triple, , corresponding to is the only equilibrium of (37).
Moreover, for all , there exists , such that for all ,
- (ii)
-
(iii)
the unique KKT triple is locally exponentially stable and globally attracting.
Proof.
We begin with (i). By direct examination of (37), we see that the equilibria correspond exactly with triples satisfying (3). Since the matrix has full rank, the gradients of all the constraints are linearly independent, and hence MFCQ holds on . Since is -strongly monotone, the solution is unique and there exists a unique Lagrange multiplier such that satisfies (3).
To show (ii), we verify that all hypotheses in [55, Theorem 4] hold. First, note that the map is -Lipschitz in uniformly in , and -Lipschitz in , uniformly in . Let denote the righthand side of (36). Because is piecewise affine in and globally Lipschitz, there exists constants , , such that is -Lipschitz in uniformly in and -Lipschitz in uniformly in . By Lemma 6.3, there exists such that (36) is -contracting, uniformly in . Finally, we note that the reduced system corresponding to (37) is , which is contracting by Theorem 5.13. Thus all the hypotheses of [55, Theorem 4] hold and (ii) follows. Finally (iii) follows from combining (i) and (ii). ∎
6.3 Safety of Recursive Safe Monotone Flow
Here we discuss the safety properties of the recursive safe monotone flow. In general, even if the initial condition belongs to , i.e., , it is not guaranteed that solutions of the system (37) satisfy for . However, under appropriate conditions, we can show that the system is “practically safe”, in the sense that remains in a slightly expanded form of the original constraint set .
Theorem 6.5.
To prove Theorem 6.5, we rely on the notion of input-to-state safety. Consider the system
| (39) |
This system can be interpreted as the safe monotone flow perturbed by a disturbance . The set is input-to-state safe (ISSf) with respect to (39), with gain , if there exists a class function such that, if , then is forward invariant under (39). This notion of input-to-state safety is a slight generalization of the standard definition, cf. [56], to the case where the safe set is parameterized by multiple equality and inequality constraints. We show next that (39) is ISSf.
Lemma 6.6 (Perturbed Safe Monotone Flow is ISSf).
Proof.
We are now ready to prove Theorem 6.5.
Proof of Theorem 6.5.
By Lemma 6.6, is input-to-state safe with respect to (39), with gain . Note that, for any solution of (37), the trajectory solves (39) with
Next, by Theorem 6.4, for all , there exists such that if , then for all , for some class function . Now, choose such that and let . Then, for all ,
Hence, for , since is input-to-state safe with respect to (39), we conclude for all . ∎
Remark 6.7 (Implementation of Recursive Safe Monotone Flow on Network Optimization Problem).
One drawback of the projected monotone flow and the safe monotone flow is that neither system admits a distributed implementation for network optimization problems. The reason for this is that both the feedback control and projected implementations of these systems introduce additional couplings between agents that require global knowledge to solve exactly.
We show here that the recursive safe monotone flow can be implemented in a distributed manner on constrained optimization problems with a separable objective function and locally expressible constraints, provided that agents can communicate with their two-hop neighbors. Consider an undirected network where is a set of agents, and is the set of edges. For each agent , let denote the set of neighbors of . Consider
| (40) | ||||||
| subject to |
where corresponds to the decision variable of the th agent. For problems with this structure, the constraints corresponding to each node are expressible as a function of information available to that node. This assumption is common in the distributed optimization literature (see e.g. [57]). When implementing (37), the state of the th agent consists of , and the dynamics are given by
Observe that from the previous expression, the th node can implement the dynamics corresponding to its state using only the state information of its two-hop neighbors.
7 Numerical Examples
Here we illustrate the behavior of the proposed flows on two example problems. The first example is a variational inequality on 2 corresponding to a two-player game with quadratic payoff functions. The second example is a constrained linear-quadratic dynamic game where we implement the safe monotone flow in a receding horizon manner to examine its anytime properties.
7.1 Nash Equilibria of Two-Player Game
The first numerical example we discuss is a variational inequality on 2 corresponding to a two-player game, where player wants to minimize a cost subject to the constraints that . We take . We have selected a two-dimensional example that allows us to visualize the constraint set and the trajectories of the proposed flows to better illustrate their differences. The problem of finding the Nash equilibria of a game of this form is equivalent to the variational inequality , where is the pseudogradient map, given by . For , let and be the quadratic function , with
The pseudogradient map is given by where
Because , it follows that the is -strongly monotone, and therefore the problem has a unique solution .
Figure 2 shows the results of implementing each of the proposed flows to find the Nash equilibrium. The projected monotone flow, cf. Figure 2(a), is only well defined in . However, the constraint set remains forward invariant and all trajectories converge to the solution . The safe monotone flow with , cf. Figure 2(b), also keeps the constraint set forward invariant and has all trajectories converge to . In addition, the system is well defined outside of , and trajectories beginning outside the feasible set converge to it.
In Figure 2(c), we consider the recursive safe monotone flow with , and , where . The trajectories converge to and closely approximate the trajectories of the safe monotone flow. Note, however, that the set is not safe but only practically safe. This is illustrated in the zoomed-in Figure 2(d), where it is apparent that the trajectories do not always remain in but remain close to it.




7.2 Receding Horizon Linear-Quadratic Dynamic Game
We now discuss a more complex example, where the input to a plant is specified by the solution to a variational inequality parameterized by the state of the plant. To solve it, we interconnect the plant dynamics with the safe monotone flow, and demonstrate that the anytime property of the latter ensures good performance and satisfaction of the constraints even when terminated terminated early. The plant takes the form of a discrete-time linear time-invariant system with two inputs,
| (41) |
where and for .
We consider a linear-quadratic dynamic game (LQDG) between two players, where each player can influence the system (41) by choosing the corresponding input . We fix a time horizon and an initial condition , and define as a quadratic payoff,
| (42) |
where and . The goal of player 1 is to minimize the payoff (42), whereas the goal of player 2 is to maximize it. This problem can be solved in closed form when the constraints are trivial (cf. [58, Chapter 6], [59]), but must be solved numerically for nontrivial constraints.
We first note the LQDG problem can be posed as a variational inequality. Indeed, let and, for , let . Define
Next, letting and , and using the fact that
we see that the payoff function (42) can be written as,
Finally, letting , we see that the LQDG problem corresponds to the variational inequality , where
and the constraint set is
We assume that the problem data satisfies
in which case is strongly monotone.
For simulation purposes, we take , , , , and a marginally stable matrix selected randomly. We use the safe monotone flow to solve the variational inequality and implement the solution in a receding horizon manner: given the initial state , we solve for the optimal input sequence over the entire time horizon, apply the input to (41) to obtain , update the initial condition and repeat. When is strongly monotone, on each iteration the flow converges to the exact solution as . However, we also consider here the effect of terminating the solver early at some .
Figure 3 shows the results of the simulation. In Figure 3(a), we plot for various values of termination times. We denote the exact solution with . The closed-loop dynamics with the exact solution to the receding horizon LQDG is stabilizing, and as grows larger, the early terminated solution drives the state of the system closer to the origin. In Figure 3(b), we plot the first component of in blue and the first component of in red. Regardless of when terminated, the inputs satisfy the input constraints on each iteration due to the safety properties of the safe monotone flow.


8 Conclusions
We have tackled the design of anytime algorithms to solve variational inequalities as a feedback control problem. Using techniques from safety-critical control, we have synthesized three continuous-time dynamics which find solutions to monotone variational inequalities: the projected monotone flow, already well known in the literature, and the novel safe monotone and recursive safe monotone flows. The equilibria of these flows correspond to solutions of the variational inequality, and so we have embarked in the precise characterization of their asymptotic stability properties. We have established asymptotic stability of equilibria in the case of strong monotonicity, and contractivity and exponential stability in the case of polyhedral constraints. We have also shown that the safe monotone flow renders the constraint forward invariant and asymptotically stable. The recursive safe monotone flow offers an alternative implementation that does not necessitate the solution of a quadratic program along the trajectories. This flow results from coupling two systems evolving on different timescales, and we have established local exponential stability and global attractivity of equilibria, as well as practical safety guarantees. We have illustrated in two game scenarios the properties of the proposed flows and, in particular, their amenability for interconnection and regulation of physical processes. Future work will develop methods for distributed network problems, study time-varying and parametric problems, consider applications to feedback optimization, explore connections between the recursive safe monotone flow and primal-dual flows, and analyze discretizations and the implementation on computational platforms of the proposed flows.
Appendix A Appendix: Proof of Lemma 5.8
Proof.
Note that
When is -strongly monotone,
and when is monotone, the previous inequality holds with . Next, we rearrange (3a) and use that is convex for all and is affine for all to obtain
where the last equality follows from the fact that . By a similar line of reasoning, we have
The result follows by summing the previous two expressions. ∎
Appendix B Appendix: Proof of Lemma 5.9
Proof.
We first show that the solution to the optimization problem in the definition of is . Note that the constraints in the definition of in (17) and (15) are identical. Let denote the objective function in the definition of . Then . Because the difference between the objective functions of (15) and the definition of is independent of , the two optimization problems have the same solution. The claim now follows because is the minimizer solving (15).
Next we show that can be expressed in closed form as (18). Because the optimizer is , we have
| (43) |
Note that satisfies the optimality conditions (16) for all . Therefore we can rearrange (16a) to obtain . Next
where the second equality follows by rearranging (16c) and (16e). Then, (18) follows by substituting the previous expression into (43).
Appendix C Appendix: Proof of Lemma 5.11
References
- [1] A. Allibhoy and J. Cortés. Safety-critical control as a design paradigm of anytime solvers of variational inequalities. In IEEE Conf. on Decision and Control, pages 6211–6216, Cancun, Mexico, December 2022.
- [2] K. Arrow, L Hurwitz, and H. Uzawa. Studies in Linear and Non-Linear Programming. Stanford University Press, Stanford, CA, 1958.
- [3] R. W. Brockett. Dynamical systems that sort lists, diagonalize matrices, and solve linear programming problems. Linear Algebra and Its Applications, 146:79–91, 1991.
- [4] U. Helmke and J. B. Moore. Optimization and Dynamical Systems. Springer, 1994.
- [5] C. Henry. An existence theorem for a class of differential equations with multivalued right-hand side. Journal of Mathematical Analysis and Applications, 41:179–186, 1973.
- [6] H. Brezis. Operateurs Maximaux Monotones et Semi-groupes de Contractions dans Les Espaces de Hilbert, volume 5 of North-Holland Mathematics Studies. Elsevier, Oxford, UK, 1973.
- [7] A. Nagurney and D. Zhang. Projected Dynamical Systems and Variational Inequalities with Applications, volume 2 of International Series in Operations Research and Management Science. Kluwer Academic Publishers, Dordrecht, The Netherlands, 1996.
- [8] B. Brogliato, A. Daniilidis, C. Lemaréchal, and V. Acary. On the equivalence between complementarity systems, projected systems, and differential inclusions. Systems & Control Letters, 55(1):45–51, 2006.
- [9] W. P. M. H. Heemels, J. M. Schumacher, and S. Weiland. Projected dynamical systems in a complementarity formalism. Operations Research Letters, 27:83–91, 2000.
- [10] W. P. M. H. Heemels, M. K. Camlibel, and M. F. Heertjes. Oblique projected dynamical systems and incremental stability under state constraints. IEEE Control Systems Letters, 4(4):1060–1065, 2020.
- [11] A. Hauswirth, S. Bolognani, and F. Dörfler. Projected dynamical systems on irregular, non-Euclidean domains for nonlinear optimization. SIAM Journal on Control and Optimization, 59(1):635–668, 2021.
- [12] A. Tanwani, B. Brogliato, and C. Prieur. Well-posedness and output regulation for implicit time-varying evolution variational inequalities. SIAM Journal on Control and Optimization, 56(2):751–781, 2018.
- [13] B. Brogliato and A. Tanwani. Dynamical systems coupled with monotone set-valued operators: Formalisms, applications, well-posedness, and stability. SIAM Review, 62(1):3–129, 2020.
- [14] M. Colombino, E. Dall’Anese, and A. Bernstein. Online optimization as a feedback controller: Stability and tracking. IEEE Transactions on Control of Network Systems, 7(1):422–432, 2020.
- [15] A. Hauswirth, Z. He, S. Bolognani, G. Hug, and F. Dörfler. Optimization algorithms as robust feedback controllers. Annual Reviews in Control, 57:100941, 2024.
- [16] E. Dall’Anese and A. Simonetto. Optimal power flow pursuit. IEEE Transactions on Smart Grid, 9(2):942–952, 2016.
- [17] L. S. P. Lawrence, J. W. Simpson-Porco, and E. Mallada. Linear-convex optimal steady-state control. IEEE Transactions on Automatic Control, 66(11):5377–5384, 2021.
- [18] S. H. Low, F. Paganini, and J. C. Doyle. Internet congestion control. IEEE Control Systems, 22(1):28–43, 2002.
- [19] G. Bianchin, J. Cortés, J. I. Poveda, and E. Dall’Anese. Time-varying optimization of LTI systems via projected primal-dual gradient flows. IEEE Transactions on Control of Network Systems, 9(1):474–486, 2022.
- [20] V. Häberle, A. Hauswirth, L. Ortmann, S. Bolognani, and F. Dörfler. Non-convex feedback optimization with input and output constraints. IEEE Control Systems Letters, 5(1):343–348, 2021.
- [21] A. Agarwal, J. W. Simpson-Porco, and L. Pavel. Game-theoretic feedback-based optimization. IFAC-PapersOnLine, 55(13):174–179, 2022.
- [22] G. Belgioioso, D. Liao-McPherson, M. H. de Badyn, S. Bolognani, R. S. Smith, J. Lygeros, and F. Dörfler. Online feedback equilibrium seeking. IEEE Transactions on Automatic Control, 2024. To appear.
- [23] K. B. Ariyur and M. Krstić. Real-Time Optimization by Extremum-Seeking Control. Wiley, New York, 2003.
- [24] P. Frihauf, M. Krstić, and T. Başar. Nash equilibrium seeking in noncooperative games. IEEE Transactions on Automatic Control, 57(5):1192–1207, 2012.
- [25] A. Williams, M. Krstic, and A. Scheinker. Semi-global practical extremum seeking with practical safety. In IEEE Conf. on Decision and Control, pages 6774–6779. IEEE, 2023.
- [26] A. Allibhoy and J. Cortés. Control barrier function-based design of gradient flows for constrained nonlinear programming. IEEE Transactions on Automatic Control, 69(6):3499–3514, 2024.
- [27] A. D. Ames, S. Coogan, M. Egerstedt, G. Notomista, K. Sreenath, and P. Tabuada. Control barrier functions: theory and applications. In European Control Conference, pages 3420–3431, Naples, Italy, 2019.
- [28] M. Cohen and C. Belta. Adaptive and Learning-Based Control of Safety-Critical Systems. Springer, New York, 2023.
- [29] F. Blanchini. Set invariance in control. Automatica, 35(11):1747–1767, 1999.
- [30] P. Wieland and F. Allgöwer. Constructive safety using control barrier functions. IFAC Proceedings Volumes, 40(12):462–467, 2007.
- [31] A. D. Ames, X. Xu, J. W. Grizzle, and P. Tabuada. Control barrier function based quadratic programs for safety critical systems. IEEE Transactions on Automatic Control, 62(8):3861–3876, 2017.
- [32] W. Xiao, C. G. Cassandras, and C. Belta. Safe Autonomy with Control Barrier Functions: Theory and Applications. Synthesis Lectures on Computer Science. Springer, New York, 2023.
- [33] G. Delimpaltadakis and W. P. M. H. Heemels. On the relationship between control barrier functions and projected dynamical systems. In IEEE Conf. on Decision and Control, page 770–775, Singapore, 2023.
- [34] G. Delimpaltadakis, J. Cortés, and W. P. M. H. Heemels. Continuous approximations of projected dynamical systems via control barrier functions. IEEE Transactions on Automatic Control, 2024. Submitted.
- [35] F. Facchinei and J.-S. Pang. Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer, 2003.
- [36] R. T. Rockafellar and R. J. B. Wets. Variational Analysis, volume 317 of Comprehensive Studies in Mathematics. Springer, New York, 1998.
- [37] J. P. Aubin and A. Cellina. Differential Inclusions, volume 264 of Grundlehren der mathematischen Wissenschaften. Springer, New York, 1984.
- [38] V. Acary and B. Brogliato. Numerical Methods for Nonsmooth Dynamical Systems: Applications in Mechanics and Electronics, volume 35 of Lecture Notes in Applied and Computational Mechanics. Springer, New York, 2008.
- [39] R. T. Rockafellar. Convex Analysis. Princeton University Press, 1970.
- [40] D. W. Peterson. A review of constraint qualifications in finite-dimensional spaces. SIAM Review, 15(3):639–654, 1973.
- [41] J. Cortés. Discontinuous dynamical systems - a tutorial on solutions, nonsmooth analysis, and stability. IEEE Control Systems, 28(3):36–73, 2008.
- [42] D. Goeleven and B. Brogliato. Stability and instability matrices for linear evolution variational inequalities. IEEE Transactions on Automatic Control, 49(4):521–534, 2004.
- [43] S. Boyd and L. Vandenberghe. Convex Optimization. Cambridge University Press, Cambridge, UK, 2009.
- [44] S. M. Robinson. Stability theory for systems of inequalities. Part I: Linear systems. SIAM Journal on Numerical Analysis, 12(5):754–769, 1975.
- [45] J. Liu. Sensitivity analysis in nonlinear programs and variational inequalities via continuous selections. SIAM Journal on Control and Optimization, 33(4):1040–1060, 1995.
- [46] A. Davydov, S. Jafarpour, and F. Bullo. Non-Euclidean contraction theory for robust nonlinear stability. IEEE Transactions on Automatic Control, 67(12):6667–6681, 2022.
- [47] F. Bullo. Contraction Theory for Dynamical Systems. Kindle Direct Publishing, 1.1 edition, 2023.
- [48] N. D. Yen. Lipschitz continuity of solutions of variational inequalities with a parametric polyhedral constraint. Mathematics of Operations Research, 20(3):695–708, 1995.
- [49] H. L. Royden and P. Fitzpatrick. Real Analysis. Prentice Hall, 2010.
- [50] T. Kose. Solutions of saddle value problems by differential equations. Econometrica, 24(1):59–70, 1956.
- [51] D. Feijer and F. Paganini. Stability of primal-dual gradient dynamics and applications to network optimization. Automatica, 46:1974–1981, 2010.
- [52] A. Cherukuri, B. Gharesifard, and J. Cortés. Saddle-point dynamics: conditions for asymptotic stability of saddle points. SIAM Journal on Control and Optimization, 55(1):486–511, 2017.
- [53] A. Cherukuri, E. Mallada, S. H. Low, and J. Cortés. The role of convexity in saddle-point dynamics: Lyapunov function and robustness. IEEE Transactions on Automatic Control, 63(8):2449–2464, 2018.
- [54] J. Cortés and S. K. Niederländer. Distributed coordination for nonsmooth convex optimization via saddle-point dynamics. Journal of Nonlinear Science, 29(4):1247–1272, 2019.
- [55] L. Cothren, F. Bullo, and E. Dall’Anese. Singular perturbation via contraction theory. arXiv preprint arXiv:2310.07966, 2023.
- [56] S. Kolathaya and A. D. Ames. Input-to-state safety with control barrier functions. IEEE Control Systems Letters, 3(1):108–113, 2018.
- [57] S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning, 3(1):1–122, 2011.
- [58] T. Başar and G. J. Olsder. Dynamic Noncooperative Game Theory. SIAM, 2 edition, 1999.
- [59] M. Pachter and K. D. Pham. Discrete-time linear-quadratic dynamic games. Journal of Optimization Theory & Applications, 146:151–179, 2010.
- [60] V. Bondarevsky, A. Leschov, and L. Minchenko. Value functions and their directional derivatives in parametric nonlinear programming. Journal of Optimization Theory & Applications, 171(2):440–464, 2016.
- [61] G. Di Pillo and L. Grippo. Exact penalty functions in constrained optimization. SIAM Journal on Control and Optimization, 27(6):1333–1360, 1989.