Anonymous Learning via Look-Alike Clustering: A Precise Analysis of Model Generalization

Look-alike modeling in machine learning encompasses a range of techniques that focus on identifying users who possess similar characteristics, behaviors, or preferences to a specific target individual. This approach primarily relies on the principle that individuals with shared attributes are likely to exhibit comparable interests and behaviors. By analyzing the behavior of these look-alike users, look-alike modeling enables accurate predictions for the target user. This technique has been widely used in various domains, including targeted marketing and personalized recommendations, where it plays a crucial role in enhancing user experiences and driving tailored outcomes [SGD15, MWXC16, MWW⁺16, MRH⁺11].

In this paper, we use look-alike clustering for a different purpose, namely to anonymize sensitive information of users. Consider a supervised regression setup where the training set contains $n$ pairs $({\bm{x}}_{i},\bm{y}_{i})$, for $i\in[n]$, with $y_{i}\in\mathbb{R}$ denoting the response and ${\bm{x}}_{i}\in\mathbb{R}^{d}$ representing a high-dimensional vector of features. We consider two groups of features: sensitive features, which contain some personal information about users and should be protected from the leaner, and the non-sensitive features. We assume that that the learner has access to a clustering structure on users, which is non-private information (e.g. based on non-sensitive features or other non-sensitive data set on users).

We propose a look-alike clustering approach, where we anonymize the individuals’ sensitive features by replacing them with the cluster’s average values. Only the anonymized dataset will be shared with the learner who then uses it to train a model. We refer to Figure 1 for an illustration of this approach. Note that the learner never gets access to the individuals’ sensitive features and so this approach is safe from re-identification attacks where the learner is given access to the pool of individuals’ sensitive information (up to permutation) and may use the non-sensitive features to re-identify the users. Also note that since a common representation (average sensitive features) is used for all the users in a cluster, this approach offers $m$-anonymity provided that each cluster is of size at least $m$ (minimum size clustering) [weeney2002k].

Minimum size clustering has received an increased attention mainly as a tool for anonymization and when privacy considerations are in place [BKBL07, AFK⁺05, APF⁺10]. A particular application is for providing anonymity for user targeting in online advertising with the goal of replacing the use of third-party cookies with a more privacy-respecting entity [EMMZ22]. There are a variety of approximation algorithms for clustering with minimum size constraint [PS07, DHHL17, AKBCF16, SSR21], as well as parallel and dynamic implementation [EMMZ22].

In this paper, we focus on linear regression and derive a precise characterization of model generalization³³3the ability of the model to generalize to new, unseen data from the same distribution as the training data using the look-alike clustering approach, in the so-called proportional regime where the size of training set grows in proportion to the number of parameters (which for the linear regression is equal to the number of features). The proportional regime has attracted a significant attention as overparametrized models have become greatly prevalent. It allows to understand the effect under/overparametrization in feature-rich models, providing insights to several intriguing phenomena, including double-descent behavior in the generalization error [MM22, DKT22, HJ22].

Our precise asymptotic theory allows us to demystify the effect of different factors on the model generalization under look-alike clustering, such as the role of cluster size, number of clusters, signal-to-noise ratio of the model as well as the strength of sensitive and non-sensitive features. A key tool in our analysis is a powerful extension of Gordon’s Gaussian process inequality [Gor88] known as the Convex Gaussian Minimax Theorem (CGMT), which was developed in [TOH15] and has been used for studying different learning problems; see e.g, [TAH18, DKT22, JS22, HJ22, JSH20].

Initially, it might be presumed that look-alike clustering would hinder model generalization by suppressing sensitive features of individuals, suggesting a possible tradeoff between anonymity (privacy) and model performance. However, our analysis uncovers scenarios in which look-alike clustering actually enhances model generalization! We will develop further insights on these results by arguing that the proposed look-alike clustering can serve as a form of regularization, mitigating model overfitting and consequently improving the model generalization.

Before summarizing our key contributions in this paper, we conclude this section by discussing some of the recent work on the tradeoff between privacy and model generalization at large. An approach to study such potential tradeoff is via the lens of memorization. Modern deep neural networks, with remarkable generalization property, operate in the overparametrized regime where there are more tunable parameters than the number of training samples. Such overparametrized models tend to interpolate the training data and are known to fit well even random labels [ZBH⁺21, ZBH⁺20]. Similar phenomenon has been observed in other models, such as random forest [BFLS98], Adaboost [Sch13, WOBM17], and kernel methods [BMM18, LR20]. Beyond label memorization, [BBF⁺21] studies setting where learning algorithms with near-optimal generalization must encode most of the information about the entire high-dimensional (and high-entropy) covariates of the training examples. Clearly, memorization of training data imposes significant privacy risks when this data contains sensitive personal information, and therefore these results hint to a potential trade-off between privacy protection and model generalization [SS19, FZ20, MBG21]. Lastly, [Fel20] studies settings where data is sampled from a mixture of subpopulations, and shows that label memorization is necessary for achieving near-optimal generalization error, whenever the distribution of subpopulation frequencies is long-tailed. Intuitively, this corresponds to datasets with many small distinct subpopulations. In order to predict more accurately on a subpopulation from which only a very few examples are observed, the learning algorithm needs to memorize the labels of those examples.

We consider a linear regression setting, where we are given $n$ i.i.d pairs $({\bm{x}}_{i},y_{i})$, where the response $y_{i}$ is given by

We assume that there is a clustering structure on features ${\bm{x}}_{i}$, $i\in[n]$, independent from the responses. We model this structure via Gaussian-Mixture model.

Our goal in this paper is to precisely characterize the effect of look-alike clustering on model generalization. We focus on the high-dimensional asymptotic regime, where the number of training data $n$, and features sizes $d,p$ grow in proportion.

We formalize the high-dimensional asymptotic setting in the assumption below:

To study the generalization of a model ${\bm{\theta}}$ (performance on unseen data) via the out-of-sample prediction risk defined as ${\rm Risk}({\bm{\theta}}):=\operatorname{\mathbb{E}}[(y-{\bm{x}}^{\sf T}{\bm{\theta}})^{2}]$, where $(y,{\bm{x}})$ is generated according to (2.1). Our next lemma characterizes the risk when the feature ${\bm{x}}$ is drawn from GMM.

The proof of Lemma 2.1 is deferred to the supplementary.

Consider the minimum $\ell_{2}$ norm (min-norm) least squares regression estimator of $\bm{y}$ on $\bm{X}$ defined by

where $(\bm{X}\bm{X}^{\sf T})^{\dagger}$ denotes the Moore-Penrose pseudoinverse of $\bm{X}\bm{X}^{\sf T}$. This estimator can also be formulated as

We also define the “look-alike estimator” denoted by ${\widehat{\bm{\theta}}}_{L}$, where the sensitive features are first anonymized via look-like modeling, and then the min-norm estimator is computed based on the resulting features. Specifically the sensitive feature $\bm{x}_{{\rm s}}$ of each sample is replaced by the center of its cluster. In our notation, writing $\bm{X}^{\sf T}=[\bm{X}_{{\rm s}}^{\sf T},\bm{X}_{{\rm ns}}^{\sf T}]$ , we define $\bm{X}_{L}^{\sf T}=[(\bm{M}_{{\rm s}}\bm{\Lambda})^{\sf T},\bm{X}_{{\rm ns}}^{\sf T}]$ the features matrix obtained after look-alike modeling on the sensitive features. The look-alike estimator is then given by

Our main result is to provide a precise characterization of the risk of look-alike estimator ${\widehat{\bm{\theta}}}_{L}$ as well as ${\widehat{\bm{\theta}}}$ (non-look-alike) in the asymptotic regime, as described in Assumption 1. We then discuss regimes where look-alike clustering offers better generalization.

As our analysis shows there are two majorly different setting in the behavior of the look-alike estimator:

• $(i)$

  $\psi_{d}-\psi_{p}\leq 1$. In words, the sample size $n$ is asymptotically larger than $d-p$, the number of non-sensitive features. This regime is called underparametrized asymptotics.

• $(ii)$

  $\psi_{d}-\psi_{p}\geq 1$, which is referred to as overparametrized asymptotics.

Our first theorem is on the risk of look-alike estimator in the underparametrized setting. To present our result, we consider the following singular value decomposition for $\bm{M}_{{\rm s}}$, the matrix of cluster centers restricted to sensitive features:

where $r={\rm rank}(\bm{M}_{{\rm s}})\leq k$.

There are several intriguing observations about this result. In the underparametrized regime:

1. 1.

   The risk depends on ${\bm{\theta}}_{0,{\rm s}}$ (model component on the sensitive features), only through the norms $\|{\bm{\theta}}_{0,{\rm s}}\|=r_{\rm s}$ and $\|\bm{U}_{{\rm s}}^{\sf T}{\bm{\theta}}_{0,{\rm s}}\|=\sqrt{\rho}r_{\rm s}$. Note that $\|\bm{U}_{{\rm s}}^{\sf T}{\bm{\theta}}_{0,{\rm s}}\|$ measures the alignment of the model with the left singular vectors of the cluster centers.

2. 2.

   The cluster structure on the non-sensitive features plays no role in the risk, nor does ${\bm{\theta}}_{0,{\rm ns}}$ the model component corresponding to the non-sensitive features.

3. 3.

   The cluster prior probabilities $\bm{\pi}$ does not impact the risk.

We next proceed to the overparametrized setting. For technical convenience, we make some simplifying assumption, however, we believe a similar derivation can be obtained for the general case, albeit with a more involved analysis.

Our next theorem characterizes the risk of look-alike estimator in the underparametrized regime.

As discussed in the introduction, one of the focal interest in this work is to understand cases where look-alike modeling improves generalization. In Section 5 we discuss this by comparing the look-alike estimator ${\widehat{\bm{\theta}}}_{L}$ with the min-norm estimator ${\widehat{\bm{\theta}}}$, given by (3.1) which utilizes the full information on the sensitive features. In order to do that, we next derive a precise characterization of the risk of ${\widehat{\bm{\theta}}}$ in the asymptotic setting.

In this section, we validate our theory with numerical experiments. We consider GMM with $k$ clusters, where the centers of clusters are given by $\mu\bm{u}_{\ell}$, for $\ell\in[k]$, where $\bm{u}_{\ell}\in\mathbb{R}^{d}$ are of unit $\ell_{2}$-norm. Also the vectors $\bm{u}_{\ell}$ are non-zero only on the first $p$ entries, and their restriction to these entries form a random orthogonal constellation. Therefore, defining $\bm{U}=[\bm{u}_{1},\dotsc,\bm{u}_{k}]$, we have $\bm{U}=\begin{bmatrix}\bm{U}_{{\rm s}}\\ {\mathbf{0}}\end{bmatrix}$, with $\bm{U}_{{\rm s}}^{\sf T}\bm{U}_{{\rm s}}={\bm{I}}_{k}$. In this setting there is no cluster structure on the non-sensitive features and the cluster centers on the sensitive features are orthogonal and of same norm.

Recall the decomposition of the model ${\bm{\theta}}_{0}=({\bm{\theta}}_{0,{\rm s}},{\bm{\theta}}_{0,{\rm ns}})$, with ${\bm{\theta}}_{0}$ the true underlying model (2.1) and ${\bm{\theta}}_{0,{\rm s}}$, ${\bm{\theta}}_{0,{\rm ns}}$ the components corresponding to sensitive and non-sensitive features. We generate ${\bm{\theta}}_{0,{\rm ns}}\in\mathbb{R}^{d-p}$ to have i.i.d standard normal entries and then normalize it to have $\left\|{\bm{\theta}}_{0,{\rm ns}}\right\|_{\ell_{2}}=r_{\rm ns}$. For ${\bm{\theta}}_{0,{\rm s}}$, we generate $\bm{Z}_{1},\bm{Z}_{2}\sim{\sf N}({\mathbf{0}}_{p},{\bm{I}}_{p})$, independently and let

where ${\sf P}_{\bm{U}_{{\rm s}}}:=\bm{U}_{{\rm s}}\bm{U}_{{\rm s}}^{\sf T}$ is the projection onto column space of $\bm{U}_{{\rm s}}$. Therefore, $\left\|{\bm{\theta}}_{0,{\rm s}}\right\|_{\ell_{2}}=r_{\rm s}$ and $\left\|\bm{U}_{{\rm s}}^{\sf T}{\bm{\theta}}_{0,{\rm s}}\right\|_{\ell_{2}}=\sqrt{\rho}r_{\rm s}$. Note that $\rho$ quantifies the alignment of the model with the cluster centers, confined to the sensitive features.)

We will vary the values of $r_{\rm s}$ and $r_{\rm ns}$ in our experiments. We also consider the case of balanced clusters, so the cluster prior probabilities are all equal, $\pi_{\ell}=1/k$, for $\ell\in[k]$.

We set the number of cluster $k=3$, dimension of sensitive features $p=200$ and the dimension of entire features vector $d=500$. We also set $\mu=5$ and $\rho=0.3$.

In our experiments, we vary the sample size $n$ and plot the risk of ${\widehat{\bm{\theta}}}_{L}$ and ${\widehat{\bm{\theta}}}$ versus $\psi_{d}-\psi_{p}=(d-p)/n$. We consider different settings, where we vary $r_{\rm s}$, $r_{\rm ns}$ and $\sigma$ (noise variance in model (2.1)).

In Figure 2, we report the results. Curves correspond to our asymptotic theory and does to the numerical simulations. (Each dot is obtained by averaging over 20 realizations of that configuration.) As we observe, in all scenarios our theoretical predictions are a perfect match to the empirical performance.

In Section 3, we provided a precise characterization of the risk of look-alike estimator ${\widehat{\bm{\theta}}}_{L}$ and its counterpart, the min-norm estimator ${\widehat{\bm{\theta}}}$ which utilizes the full information on the sensitive features. By virtue of these characterizations, we would like to understand regimes where the look-alike clustering helps with the model generalization, and the role of different problem parameters in achieving this improvement. Notably, since the look-alike estimator offers $m$-anonymity on the sensitive features (with $m$ the minimum size of clusters), our discussion here points out instances where data anonymization and model generalization are not in-conflict.

We define the gain of look-alike estimator $\Delta$ as follows:

which indicates the gain obtained in generalization via look-alike clustering.

For ease in presentation, we focus on the case of balanced clusters (equal priors $\pi_{1}=\dotsc=\pi_{k}=1/k$), and consider three cases:

In Figure 3(b) we report similar curves, where this time $\psi_{p}=0.5$ and we consider several values of $\rho$. As we observe, at fixed SNR the gain $\Delta$ is increasing in $\rho$. This is expected since $\rho$ measures the alignment of the underlying model ${\bm{\theta}}_{0}$ with the (left eigenvectors of) cluster centers and so higher $\rho$ is to advantage of the look-alike estimator which uses the cluster centers instead of individuals’ sensitive features.

We refer to the appendix for the proof of Theorem 5.1.

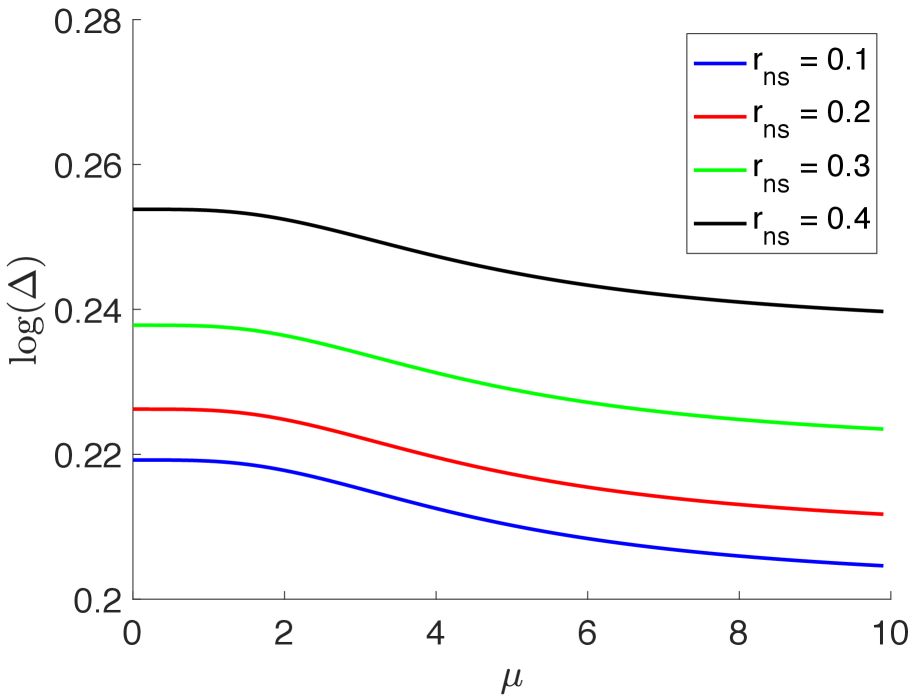
In Figure 4(a) we plot $\log(\Delta)$ versus $\mu$ for several values of $r_{\rm ns}$. Here, $\psi_{d}=2$, $\psi_{p}=1.7$, $\sigma=1$, $r_{\rm s}=0.5$ and so condition (5.1) holds. As we observe $\log(\Delta)$ is positive, decreasing in $\mu$ and also at any fixed $\mu$, it is increasing in $r_{\rm ns}$, all of which are consistent with the Theorem 5.1. In Figure 4(b), we plot similar curves where this time $r_{\rm ns}=0.2$ and we try several values of $\rho$. As we see the look-alike estimator has larger gain $\Delta$ at larger values of $\rho$.

Let us first focus on $r_{\rm ns}$, the energy of the model on the non-sensitive features. Invoking the equations (3.3) and (3.4) and hiding the terms that do not depend on $r_{\rm ns}$ in constants $C_{1}$, $C_{2}$ we arrive at

Therefore, $\lim_{r_{\rm ns}\to\infty}\Delta=(1-\psi_{d}^{-1})/(1-(\psi_{d}-\psi_{p})^{-1})>1$, indicating a gain for the look-alike estimator over ${\widehat{\bm{\theta}}}$. In Figure 5(a), we plot $\log(\Delta)$ versus $r_{\rm ns}$ for several values of $\psi_{p}$. As we observe, when $r_{\rm ns}$ is large enough we always have a gain, which is increasing in $\psi_{p}$.

We next consider the effect of SNR = $r_{\rm s}/\sigma$. In Figure 5(b) we plot $\log(\Delta)$ versus SNR, for several values of $\psi_{p}$. Similar to the underparametrized regime, we observe that in low SNR, the look-alike estimator has better generalization $(\log(\Delta)>0)$.

In previous section, we used our theory for linear models to show that at low SNR, look-alike modeling improves model generalization. We also provided an insight for this phenomenon by arguing that look-alike modeling acts as a form of regularization and avoids over-fitting at low SNR regime. In this section we show empirically that this phenomenon also extends to non-linear models.

Consider the following data generative model:

where $\varepsilon\sim{\sf N}(0,\sigma^{2})$. We construct the model ${\bm{\theta}}_{0}=({\bm{\theta}}_{0,{\rm s}},{\bm{\theta}}_{0,{\rm ns}})$ similar to the setup in Section 4. We set $n=200$, $d=180$, $k=3$, $\mu=5$, $\sigma=1$, $\rho=0.3$, $r_{\rm ns}=2$ and $N=1000$ (number of trials in Binomial distribution).

We vary SNR by changing $r_{\rm s}$ in the set $\{0.1,0.3,\dotsc,1.9\}$. The estimators ${\widehat{\bm{\theta}}}$ and ${\widehat{\bm{\theta}}}_{L}$ are obtained by fitting a GLM with logit link function and binomial distribution. We compute the risks of ${\widehat{\bm{\theta}}}$ and ${\widehat{\bm{\theta}}}_{L}$ by averaging over a test set of size $50K$. In Figure 6, we plot the gain $\log(\Delta)$ versus $r_{\rm s}$ where each data point is by averaging over $50$ different realizations of data. As we observe at low SNR, $\log(\Delta)>0$ indicating that the look-alike estimator ${\widehat{\bm{\theta}}}_{L}$ obtains a lower risk than the min-norm estimator.

Our analysis of the generalization error is based on an extension of Gordon’s Gaussian process inequality [Gor88], called Convex-Gaussian Minimax Theorem (CGMT) [TOH15]. Here, we outline the general steps of this framework and refer to the supplementary for complete details and derivations.

Consider the following two Gaussian processes:

where $\bm{G}\in\mathbb{R}^{n\times d}$, $\bm{g}\in\mathbb{R}^{n}$ and $\bm{h}\in\mathbb{R}^{d}$, all have i.i.d standard normal entries. Further, $\psi:\mathbb{R}^{d}\times\mathbb{R}^{n}\to\mathbb{R}$ is a continuous function, which is convex in the first argument and concave in the second argument.

Given the above two processes, consider the following min-max optimization problems, which are respectively referred to as the Primary Optimization (PO) and the Auxiliary Optimization (AO) problems:

The main result of CGMT is to connect the above two random optimization problems. As shown in [TOH15](Theorem 3), if $\bm{S}_{\bm{u}}$ and $\bm{S}_{\bm{v}}$ are compact and convex then, for any $\lambda\in\mathbb{R}$ and $t>0$,

An immediate corollary of this result (by choosing $\lambda=\mathbb{E}[\Phi_{\rm AO}(\bm{g},\bm{h})$]) is that if the optimal cost of the AO problem concentrates in probability, then the optimal cost of the corresponding PO problem also concentrates, in probability, around the same value. In addition, as shown in part (iii) of  [TOH15](Theorem 3), concentration of the optimal solution of the AO problem implies concentration of the optimal solution of the PO around the same value. Therefore, the two optimization are intimately connected and by analyzing the AO problem, which is substantially simpler, one can derive corresponding properties of the PO problem.

The CGMT framework has been used to infer statistical properties of estimators in certain high-dimensional asymptotic regime. The intermediate steps in the CGMT framework can be summarized as follows: First form an PO problem in the form of (7.1) and construct the corresponding AO problem. Second, derive the point-wise limit of the AO objective in terms of a convex-concave optimization problem, over only few scalar variables. This step is called ‘scalarization’. Next, it is possible to establish uniform convergence of the scalarized AO to the (deterministic) min-max optimization problem using convexity conditions. Finally, by analyzing the latter deterministic problem, one can derive the desired asymptotic characterizations.

Of course implementing the above steps involved problem-specific intricate calculations. Our proofs of Theorems 3.1, 3.2, 3.3 in the supplementary follow this general strategy.

We would like to thank Sugato Basu, Kedar Dhamdhere, Alessandro Epasto, Rezsa Farahani, Asif Islam, Omkar Muralidharan, Dustin Zelle and Peilin Zhong for helpful discussion about this work. We also thank the anonymous reviewers of NeurIPS for their thoughtful comments. This work is supported in part by the NSF CAREER Award DMS-1844481 and the NSF Award DMS-2311024.