Anomaly-Aware Semantic Segmentation by Leveraging Synthetic-Unknown Data
Abstract
Anomaly awareness is an essential capability for safety-critical applications such as autonomous driving. While recent progress of robotics and computer vision has enabled anomaly detection for image classification, anomaly detection on semantic segmentation is less explored. Conventional anomaly-aware systems assuming other existing classes as out-of-distribution (pseudo-unknown) classes for training a model will result in two drawbacks. (1) Unknown classes, which applications need to cope with, might not actually exist during training time. (2) Model performance would strongly rely on the class selection. Observing this, we propose a novel Synthetic-Unknown Data Generation, intending to tackle the anomaly-aware semantic segmentation task. We design a new Masked Gradient Update (MGU) module to generate auxiliary data along the boundary of in-distribution data points. In addition, we modify the traditional cross-entropy loss to emphasize the border data points. We reach the state-of-the-art performance on two anomaly segmentation datasets. Ablation studies also demonstrate the effectiveness of proposed modules.
I INTRODUCTION
The machine capability of realizing out-of-distribution (OOD) samples is essential for deploying learning systems to safety-critical real-world applications. For example, a self-driving vehicle is likely to encounter an object or a condition that is unknown or even does not exist during the training phase. However, modern deep learning-based methods, despite reaching remarkable performance on various computer vision and robotic tasks, are inclined to make overconfident predictions towards unknown samples and therefore result in myriad safety issues, as confirmed by recent studies [1, 2, 3, 4].
Recent anomaly detection research has made progress in detecting OOD samples on image classification tasks [5, 6, 7, 8, 9]. Auxiliary data, in particular, is proposed to actually enable the model capability of realizing unknown samples by fine-tuning a trained learning system, instead of manipulating predicted results (e.g., threshold-based methods [5, 6]). In addition, prior works [7, 8, 9] have demonstrated that training with auxiliary data sampled outside the training distribution can improve accuracy by effectively lowering the confidence scores of those anomalies on classification tasks. Nevertheless, various robotic applications such as auto-driving vehicles or medical robots require per-pixel prediction (i.e., semantic segmentation), which remains less explored, to make decisions. Moreover, it is inapplicable to directly adapt anomaly detection methods aiming for classification as they mostly assume one category per image, which is not the case for semantic segmentation tasks.

Several previous methods [8, 10] utilize existing classes that are out-of-distribution as auxiliary samples. Despite being able to tackle segmentation tasks theoretically, this principle of using “known-unknown” classes assumes that they represent all potential anomalies and leads to two drawbacks. (1) It is impossible to train with all the unknown or even non-existing objects in the real world. (2) The performance of anomaly awareness strongly relies on the known-unknown class selection. For example, our experiment shows that the AUROC of models trained could vary from to with merely a different class selection of auxiliary samples (see Tab. I).
Intuitively, out-of-distribution data covers the whole space excluding in-distribution data and it is infeasible to enumerate several classes with any selection method to overlay the remaining space. Therefore, we hypothesize that the model could maximize the gain from auxiliary data points that are along the in-distribution boundaries. Hence, we propose a novel model-agnostic data generation algorithm to address the dilemma. As illustrated in Fig. 1(a), our Masked Gradient Update (MGU) adaptively generates synthetic-unknown regions of auxiliary samples around the boundary of in-distribution data. In this way, the auxiliary data no longer suffer from the non-existing object issue and class selection bias. Furthermore, our MGU generated data could be utilized in any model or fine-tuning strategy. We design an anomaly-aware fine-tune (AaFt) module, as shown in Fig. 1(b), by fine-tuning on synthetic-unknown samples with a modified cross-entropy loss. Following our principle of paying attention to the boundary, AaFt modifies the cross-entropy to emphasize the near boundary samples and further improves the performance. This experimental finding not only echos our hypothesis of the benefit from boundary samples but indicates that boundary-based approaches deserve further investigation.
The overall contributions of this work can be summarized as follows: 1) We are the first to quantify and tackle the selection bias of auxiliary data for anomaly segmentation. 2) The proposed method comprised of MGU and AaFt is model-agnostic and can train anomaly segmentation models in an adaptive manner. 3) We propose a novel entropy ratio loss to better separate the in- and out-of-distribution samples. 4) We achieve state-of-the-art results without building costly post-processing or ensemble models.
II Related work
II-A Anomaly Detection with Deep Neural Networks.
Anomaly detection, also known as out-of-distribution (OOD) detection, is formulated as a problem to determine whether an input is in-distribution (, the training distribution) or out-of-distribution (, the other distributions). The issue has been studied in several aspects, such as selective classification [11] and open-set recognition [3]. Hendrycks et al. [5] demonstrated that deep classifiers have a tendency to assign lower maximum softmax probability (MSP) to anomalous inputs than in-distribution samples. Such property enables models to perform OOD classification by simple thresholding. Liang et al. [6] further proposed temperature scaling and input preprocessing to make the MSP score become a more effective measurement for anomaly detection. Monte Carlo dropout (MCDropout) has also been studied in previous works to measure network uncertainty [12, 13], but the post-processing of such methods is rather expensive. Some approaches based on ensemble learning have shown remarkable performance [14], but training multiple models requires considerable resources.
The threshold-based methods [5] are notable for their computational efficiency, yet the pre-trained classifiers they used might fail to separate in- and out-of-distribution samples due to the overconfident prediction issue. To address the overconfident prediction issue of the threshold-based methods [5, 6], [7, 8] trained anomaly detectors against an auxiliary dataset of outliers [15] so the models could be capable of generalizing to unseen anomalies. In order to obtain more representative samples, [7] leveraged GAN [16] to synthesize adversarial examples around the in-distribution boundaries; [10] proposed a re-sampling strategy to construct a compact yet effective subset for training. Additionally, [8] proposed an extra loss term to penalize non-uniform predictions when out-of-distribution data are given, regularizing the learning so that OOD samples will have much lower confidence scores.
II-B Semantic Segmentation.
Recent studies have made significant progress on semantic segmentation, which is one of the essential problems in computer vision and has shown great potential in a myriad of applications. FCN [17] is regarded as a fundamental work in semantic segmentation, which included only convolutional layers and can process images of arbitrary sizes. Feature pyramid [18] is also widely used in segmentation models to better capture multi-scale information. DeepLabv3 [19] achieves admirable performance with computational efficiency by exploiting dilated convolutions. Though these approaches have shown robustness and effectiveness, they have a tendency to make overconfident decisions as OOD inputs are given. Such an insufficiency would seriously restrict these methods from deployment to real-world scenarios.
II-C Anomaly Segmentation.
While prior attempts have studied OOD detection in multiple views, the task of anomaly segmentation remains rarely explored. Wilddash dataset [20] was proposed to offer evaluations that reflect algorithmic robustness against visual hazards (, illumination changes, distortions, image noise), yet the OOD detection in [20] still remains at the image-wise level. Therefore, the CAOS benchmark [21] comprised of real-world driving scenes and synthetic anomalies is proposed, attempting to bridge the gap between anomaly detection and semantic segmentation. Xia et al. [22] proposed a framework consisting of both generative and comparison modules, identifying OOD regions by comparing the synthesized image to the original input. Franchi et al. [23] achieved state-of-the-art results by tracking the trajectory of weights and using an ensemble of networks. Both [22, 23] demonstrated remarkable performance, however, these approaches require additional models to refine the output. In this paper, we show our framework achieves superior performance by directly thresholding the softmax scores without exploiting generative modules, and such computational efficiency is highly desired in real-world applications.

III Method
In this paper, we aim to present an anomaly segmentation model based on existing semantic segmentation frameworks. To tackle the Anomaly-aware Semantic Segmentation task, we propose two novel components. First, Masked Gradient Updating (III-B) generates auxiliary data on the boundary of in-distribution data without referencing additional existing data classes and labels. Second, Anomaly-aware Fine-tuning (III-C) learns anomaly-aware decision boundaries by adding additional loss for synthetic-unknown regions.
III-A Preliminary
In this paper, we consider the problem of anomaly segmentation. Unlike conventional OOD classification [5, 6, 7] treating a whole image as an anomalous sample, in anomaly segmentation, we must segment anomalous regions with pixel-level accuracy. Let and denote two distinct distributions, known and unknown, respectively. Those pixels of instances within training data are drawn from , while the pixels of anomalous instances are sampled from . We further define a synthetic-unknown distribution , which indicates the space of those synthetic pixels. We assume a well-trained semantic segmentation model and the ground truth pixel labels associated with the input image are available. For the convenience of interpretation, we define the well-known softmax probability as
| (1) |
where is the model output score of category at pixel ; is the number of classes in the dataset. In the inference stage, we follow previous threshold-based methods [5] to classify image pixels into anomalous objects if
| (2) |
where denotes the threshold. An ideal anomaly segmentation model is expected to predict a class distribution which is extremely close to the uniform distribution as an anomalous pixel is given. In the following sections, we will focus on explaining the training process of our anomaly segmentation framework.
III-B Generating auxiliary data by Masked Gradient Updating
The auxiliary data plays a crucial role in our approach and is widely adopted in existing anomaly classification methods [7, 8, 10]. Nonetheless, the selection bias of known-unknown samples raises serious concern and remains rarely explored in anomaly segmentation (see Tab. I). Furthermore, within the more complicated problem setting of semantic segmentation, we cannot simply leverage a whole image drawn from another dataset as an auxiliary sample.
To solve the above problems, we propose Masked Gradient Update (MGU) addressing the aforementioned issues by producing auxiliary images comprised of both in- and out-of-distribution regions in an adaptive manner. As shown in algorithm 1, we use to indicate the indices of those pixels belonging , and denotes the indices of pixels predicted as correctly. Given an initialized auxiliary image , we arbitrarily choose one of the classes existing in that image as the adversarial class . Then, our proposed MGU will iteratively update the pixels included in conditioned on the cost function . The cost function is defined as
| (3) |
During the process, the parameters of are frozen and only the pixels within the target regions will be updated along the descending gradient direction of . By minimizing the softmax probability of , those would be transformed into the synthetic-unknown pixels, which can also be regarded as the pseudo-unknown samples used for training an anomaly segmentation model. The auxiliary dataset can therefore be constructed by obtaining such synthetic-unknown images for each of the categories.
The concept of MGU is illustrated in Fig 2(a). Unlike previous methods [8, 10] treating a known class as unknown objects, we aim to enforce the embeddings of synthetic-unknown instances to locate outside the decision boundary of known categories. Punishing the pixels for having large can be regarded as a process to enforce the embeddings of these pixels to move from their cluster center towards the decision boundary. Note that once a pixel has been updated and predicted ”incorrectly”, it will immediately stop being updated. Besides, the encourages the pixels to be updated against their ground truth labels, so it can be expected the of each pixel to be small at the last few updates. Therefore, we can expect the gradient of the last update of most pixels is too small to drag the samples far away from the boundary. Such a property is highly desired because the synthetic-unknown instances would be the most discriminative pseudo-unknown samples that clearly identify the boundary of known categories.
III-C Anomaly-aware Fine-tuning
After we generate the synthetic-unknown data through MGU, the next step is to fine-tune , which is pre-trained on a normal semantic segmentation task, with those auxiliary data. As illustrated in Fig. 2(b), the idea is that we could learn to distinguish anomalies between in-distribution samples and the synthetic-unknown samples around the original model decision boundaries. Following the threshold-based method in Equation 2, our goal is to lower the maximum probability value for those regions in while maintaining the original semantic segmentation output for regions in .
For pixels in , we apply the loss [7, 8, 10] to minimize KL divergence between the output probability distribution and uniform distribution. is defined as:
| (4) |
where is a pixel sampled from , and . This forces the output probability distribution towards uniform distribution for the anomaly areas.
Combined with the standard semantic segmentation cross-entropy loss , the objective function for fine-tuning is defined as:
| , | (5) |
where is weighting the hyper-parameter between the loss of standard semantic segmentation and anomaly segmentation. calculates on all the pixels in , and calculates on all the pixels in the .
In this paper, we also explore another loss function option, , for anomaly segmentation by measuring the entropy of softmax output. The entropy ratio loss is:
| , | (6) |
where is a regularization term. The aims to maximize the output entropy of the pixels belonging to .
Through the anomaly-aware fine-tuning, using the data generated from MGU, the model is able to perform the original semantic segmentation task and detect anomaly regions through thresholding.
IV Experimental Results
IV-A Training Setting
In order to verify the effectiveness of our proposed method, we conduct experiments on two anomaly segmentation datasets (StreetHazards and BDD-Anomaly datasets). StreetHazards dataset [21] is a large-scale anomaly segmentation dataset containing 5125 training images, 1031 validation images, and 1500 testing images with 12 object classes for self-driving applications. Noted that for the testing images, a total of 250 unique anomalous objects appear in the image. BDD-Anomaly dataset derives from the BDD100K semantic segmentation dataset [24], a semantic segmentation dataset with diverse driving conditions. We follow the experimental setup in [21], regarding the classes motorcycle and train as anomalous objects. The dataset contains 6688 training images, 951 validation images, and 361 testing images. For network architectures, we use two state-of-the-art backbones, Deeplabv3 [19] and PSPNet [18], to validate the performance of our method on the StreetHazards dataset, and we train a Deeplabv3 for anomaly-aware semantic segmentation on the BDD-Anomaly dataset.
For both backbones, we first train the model with Adam and the learning rate for epochs with batch size on standard semantic segmentation task. Then, for auxiliary data generating, we choose images for each in-distribution class to apply MGU. The Deeplabv3 model is fine-tuned with Adam and the learning rate for epochs with batch size . The PSPNet model is finetuned with Adam and the learning rate for epochs with batch size . The hyper-parameter in Equation. 5 is , and the regularization term in Equation. 6 is , where is in this case for the both backbones.
IV-B Evaluation Metrics
We use the following three standard metrics to evaluate the effectiveness of the anomaly-aware semantic segmentation model. In this paper, we treat the unknown pixels as positive samples for all three metrics.
AUPR is the Area Under the Precision-Recall curve. In safety-critical applications, it is necessary to detect all anomalous objects. AUPR score focuses on evaluating the model performance on positive samples (i.e. anomalous samples), and it is more sensitive to positive and negative class imbalances. When positive samples are relatively small, AUPR is a more comprehensive indicator that reflects the data imbalance in the score. It is a threshold-independent metric, but the random guess score is the ratio between the number of positive and negative samples.
AUROC is the Area Under the Receiver Operating Characteristic curve. It is the probability for a positive sample to get a higher score than a negative sample. AUROC is also a threshold-independent metric, and the score of random guesses is always regardless of the ratio of the number of positive samples to the number of negative samples.
FPR95 means the false positive rate at true positive rate. FPR at TPR tells how many false positives are inevitable for a given method to obtain the desired recall .
| sub-experiment |
|
|
|
|
|||||
|---|---|---|---|---|---|---|---|---|---|
| sub-exp 0 | 44.1 | 97.0 | 13.3 | 1.9 | |||||
| sub-exp 1 | 7.5 | 80.7 | 79.1 | 1.6 | |||||
| sub-exp 2 | 26.3 | 84.9 | 70.2 | 5.3 | |||||
| sub-exp 3 | 29.4 | 92.9 | 30.5 | 1.5 | |||||
| sub-average | 26.8 | 88.9 | 48.3 | 2.6 |
IV-C Selection Bias
To investigate the selection bias of known-unknown-based methods [8, 10], we conduct a pilot study with the same settings except for merely different instance categories serving as known-unknown samples. Specifically, the classes in StreetHazards dataset [21] are split into subsets. Each subset consists of classes without overlaps, and in each sub-experiment, one of the subsets will be chosen as the anomaly subset. Those instances in an image belonging to the categories of the anomaly subset should be regarded as anomalies for training. Such an experimental setting is consistent with those methods using auxiliary data [8, 10], except that we explore anomaly segmentation rather than classification.
As shown in Tab. I, the significantly fluctuating performance indicates that known-unknown class selection heavily influences the results. The results reveal our hypothesis of known-unknown class selection correlates to model performance. Therefore, known-unknown classes could barely represent the out-of-distribution regions. On the other hand, our proposed MDG can adaptively generate synthetic-unknown instances based on observing distribution instead of choosing particular categories as known-unknown instances.
IV-D Result
Tab. II demonstrates the experimental result on the StreetHazard dataset. Using the backbone of both Deeplabv3 and PSPNet, our MGU+AaFt with entropy ratio loss reaches state-of-the-art performance on AUPR and AUROC metrics while having a competitive FPR95 score. As there are only unknown pixels in the StreetHazards dataset, metrics that do not consider data imbalance might underestimate the significance of detecting unknown pixels. The impressive AUPR scores ( and enhancement with Deeplabv3 and PSPNet), which is the only one regarding data imbalance, suggest the capability of anomaly awareness of our proposed method. Besides, our method also performs well on the BDD-Anomaly dataset, as shown in Tab. III. The results reveal that our method outperforms the best previous score by in AUPR. The results indicate the effectiveness and the robustness of our proposed components.
Also, more than achieving remarkable performance, our method is more resource-efficient. Prior works either require multiple models (Deep Ensemble [14], TRADI [23]) or reconstruct original testing images (SynthCP [22]). Additionally, our approach is model-agnostic and has huge potential to further boost the performance of future models or applications.
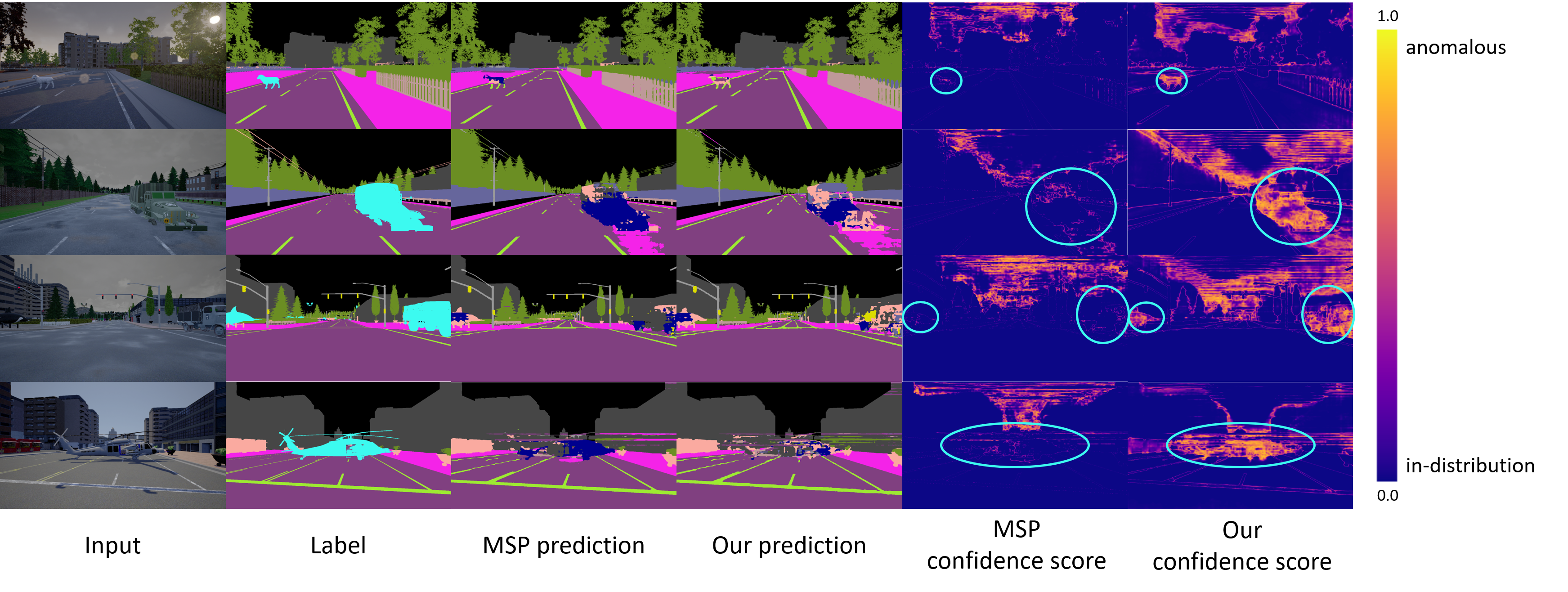
Fig. 3 demonstrates several cases on the StreetHazard dataset. MSP method alone is unable to tackle anomalies on the roads and leads to critical safety issues. With the same backbones, we finetune the model with our generated auxiliary data and enable the model to recognize unknown objects.
| Method | AUPR | AUROC | FPR95 |
|---|---|---|---|
| Dropout [12] | 7.5 | 79.4 | 69.9 |
| MSP [5] ( only) | 6.6 | 87.7 | 33.7 |
| MSP+CRF [21] | 6.5 | 88.1 | 29.9 |
| SynthCP [22] | 9.3 | 88.6 | 28.4 |
| TRADI [23] | 7.2 | 89.2 | 25.3 |
| Deep Ensemble [14] | 7.2 | 90.0 | 25.4 |
| MGU+AaFt(, pspnet) | 10.9 | 89.5 | 32.9 |
| MGU+AaFt(, deeplabv3) | 13.2 | 90.4 | 34.0 |
| MGU+AaFt(, deeplabv3) | 14.6 | 92.2 | 25.9 |
| Method |
|
|
|
|||
|---|---|---|---|---|---|---|
| Dropout [12] | 6.5 | 83.7 | 33.4 | |||
| MSP [5] | 6.3 | 84.2 | 31.9 | |||
| MSP+CRF [21] | 8.2 | 86.3 | 26 | |||
| TRADI [23] | 5.6 | 86.1 | 26.9 | |||
| Deep Ensemble [14] | 6 | 87 | 25 | |||
| MGU+AaFt(, deeplabv3) | 14.7 | 91.5 | 30.8 |
IV-E Ablation Study
In the ablation study, we measure the effectiveness of each designed module. As shown in Tab. II, by training with our MGU generated, we boost the MSP (first block, second row) from 6.6 AUPR to 13.2 (second block, second row). Considering MSP is a relatively simple method, the performance gain is impressive. Additionally, it reveals possible further performance improvement of training modern models with MGU generated data.
Our entropy ratio loss aims to investigate the influence of loss usage, further improving the performance from 13.2 AUPR to 14.6 (second block, third row). As a step toward, the result suggests a potential research direction for future work.
IV-F Threshold Analysis
The AUPR, AUROC, and FPR95 metrics measure the relative output confidence scores between in-distribution pixels and anomalous pixels regardless of the correctness of semantic segmentation. In this section, we introduce how thresholding influences the performance of semantic and anomaly segmentation. Fig. 4 shows the semantic and anomaly segmentation accuracy of our method and MSP. As increasing , more pixels are classified as anomalies. Note that the MSP model has not been fine-tuned with anomaly data, so ideally adjusting the threshold affects little in the semantic segmentation performance; however, it will encounter the overconfidence issue when fed with anomalous inputs. Overall, as increasing , the anomaly-aware semantic segmentation model trained with our method can significantly improve the anomaly segmentation accuracy, while the model still maintains desirable semantic segmentation performance.

V Conclusion
In this paper, we study a practical yet less explored anomaly-aware semantic segmentation task and, first-ever, leverage auxiliary data to tackle it. Observing the drawbacks of traditional known-unknown-based auxiliary data approaches, we propose a novel MGU module to generate samples along the border of in-distribution data. Moreover, we investigate the usage of loss function when fine-tuning and design an entropy ratio loss. Experimental results show the effectiveness of our proposed modules. We are optimistic that our work could pave a new path for future research.
References
- [1] D. Amodei, C. Olah, J. Steinhardt, P. F. Christiano, J. Schulman, and D. Mané, “Concrete problems in AI safety,” CoRR, vol. abs/1606.06565, 2016.
- [2] C. Guo, G. Pleiss, Y. Sun, and K. Q. Weinberger, “On calibration of modern neural networks,” in International Conference on Machine Learning. PMLR, 2017, pp. 1321–1330.
- [3] A. Bendale and T. E. Boult, “Towards open set deep networks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 1563–1572.
- [4] A. Nguyen, J. Yosinski, and J. Clune, “Deep neural networks are easily fooled: High confidence predictions for unrecognizable images,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 427–436.
- [5] D. Hendrycks and K. Gimpel, “A baseline for detecting misclassified and out-of-distribution examples in neural networks,” in 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings. OpenReview.net, 2017.
- [6] S. Liang, Y. Li, and R. Srikant, “Enhancing the reliability of out-of-distribution image detection in neural networks,” in 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net, 2018.
- [7] K. Lee, H. Lee, K. Lee, and J. Shin, “Training confidence-calibrated classifiers for detecting out-of-distribution samples,” in 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net, 2018.
- [8] D. Hendrycks, M. Mazeika, and T. G. Dietterich, “Deep anomaly detection with outlier exposure,” in 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, May 6-9, 2019. OpenReview.net, 2019.
- [9] A. Vyas, N. Jammalamadaka, X. Zhu, D. Das, B. Kaul, and T. L. Willke, “Out-of-distribution detection using an ensemble of self supervised leave-out classifiers,” in Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 550–564.
- [10] Y. Li and N. Vasconcelos, “Background data resampling for outlier-aware classification,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 13 218–13 227.
- [11] Y. Geifman and R. El-Yaniv, “Selective classification for deep neural networks,” in Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, I. Guyon, U. von Luxburg, S. Bengio, H. M. Wallach, R. Fergus, S. V. N. Vishwanathan, and R. Garnett, Eds., 2017, pp. 4878–4887.
- [12] Y. Gal and Z. Ghahramani, “Dropout as a bayesian approximation: Representing model uncertainty in deep learning,” in international conference on machine learning. PMLR, 2016, pp. 1050–1059.
- [13] A. Kendall and Y. Gal, “What uncertainties do we need in bayesian deep learning for computer vision?” in Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, I. Guyon, U. von Luxburg, S. Bengio, H. M. Wallach, R. Fergus, S. V. N. Vishwanathan, and R. Garnett, Eds., 2017, pp. 5574–5584.
- [14] B. Lakshminarayanan, A. Pritzel, and C. Blundell, “Simple and scalable predictive uncertainty estimation using deep ensembles,” in Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, I. Guyon, U. von Luxburg, S. Bengio, H. M. Wallach, R. Fergus, S. V. N. Vishwanathan, and R. Garnett, Eds., 2017, pp. 6402–6413.
- [15] I. J. Goodfellow, J. Shlens, and C. Szegedy, “Explaining and harnessing adversarial examples,” in 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings, Y. Bengio and Y. LeCun, Eds., 2015.
- [16] M. Mirza and S. Osindero, “Conditional generative adversarial nets,” arXiv preprint arXiv:1411.1784, 2014.
- [17] J. Long, E. Shelhamer, and T. Darrell, “Fully convolutional networks for semantic segmentation,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 3431–3440.
- [18] H. Zhao, J. Shi, X. Qi, X. Wang, and J. Jia, “Pyramid scene parsing network,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 2881–2890.
- [19] L.-C. Chen, G. Papandreou, F. Schroff, and H. Adam, “Rethinking atrous convolution for semantic image segmentation,” arXiv preprint arXiv:1706.05587, 2017.
- [20] O. Zendel, K. Honauer, M. Murschitz, D. Steininger, and G. F. Dominguez, “Wilddash-creating hazard-aware benchmarks,” in Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 402–416.
- [21] D. Hendrycks, S. Basart, M. Mazeika, M. Mostajabi, J. Steinhardt, and D. Song, “A benchmark for anomaly segmentation,” arXiv preprint arXiv:1911.11132, 2019.
- [22] Y. Xia, Y. Zhang, F. Liu, W. Shen, and A. L. Yuille, “Synthesize then compare: Detecting failures and anomalies for semantic segmentation,” in European Conference on Computer Vision. Springer, 2020, pp. 145–161.
- [23] G. Franchi, A. Bursuc, E. Aldea, S. Dubuisson, and I. Bloch, “Tradi: Tracking deep neural network weight distributions,” in European Conference on Computer Vision (ECCV) 2020. Springer, 2020.
- [24] F. Yu, W. Xian, Y. Chen, F. Liu, M. Liao, V. Madhavan, and T. Darrell, “Bdd100k: A diverse driving video database with scalable annotation tooling,” arXiv preprint arXiv:1805.04687, vol. 2, no. 5, p. 6, 2018.