Anomalous thermal transport and violation of Wiedemann-Franz law in the critical regime of a charge density wave transition
Abstract
ErTe3 is studied as a model system to explore thermal transport in a layered charge density wave (CDW) material. We present data from thermal diffusivity, resistivity, and specific heat measurements: There is a sharp decrease in thermal conductivity both parallel and perpendicular to the primary CDW at the CDW transition temperature. At the same time, the resistivity changes more gradually. Correspondingly, while well above and below , a consistent description of the thermal transport applies with essentially independent electron and phonon contributions (estimated using the Wiedemann Franz law), in the critical regime no such description is possible; the observed behavior corresponds to a strongly coupled electron-phonon critical ‘soup.’
I Introduction
Contrary to the standard paradigm [1, 2], in more than one spatial dimension, due to the lack of perfect nesting, charge density wave (CDW) order (unlike superconducting order) only emerges for interactions greater than a critical strength. Generically, both strong electron-electron and electron-phonon interactions are involved in the “mechanism.” Among other things, the strong-coupling aspect is reflected in large values of the induced gap to ratios - in the focus material for the present study, ErTe3, the gap associated with the primary CDW transition at K is meV, so that [3, 4]. However, especially since conventional notions of weakly interacting quasi-particles and well defined phonons give a good account of the normal state at and of the low temperature physics deep in the ordered phase, it is conventional (as is indeed common more generally in considering classical critical phenomena in metals) to adopt a phenomenological approach in which the low energy quasi-particles and the bulk of the phonons are weakly coupled to the “critical modes” associated directly with the CDW transition. This perspective is challenged by our present results.
Electrical and thermal transport measurements provide important information about the electronic structure and scattering processes in complex quantum materials. To the extent that the transport is dominated by weakly interacting (emergent) elementary excitations, the thermal conductivity can be expressed as the sum of an electronic and a phonon piece, . Moreover, to the extent that the scattering processes are quasi-elastic, is related to the electrical conductivity by the so-called Wiedemann-Franz (WF) law, i.e. the ratio between them, is determined by the universal constant, WK-2. Observing this ratio gives information about how “standard” the transport is in a given electronic system, with significant violations of the WF law plausibly indicating the breakdown of the quasiparticle description.
In this paper we examine electrical and thermal transport in the layered material ErTe3, which has two successive CDW transitions at K and K. Here marks the onset of the “primary” CDW order with ordering vector along the -direction, while below a “secondary” orthogonal CDW component with along the -direction appears (where and are in-plane lattice parameters in the standard space group setting for this structure type). Thus, despite the nearly tetragonal symmetry of the crystal (), the phase at has unidirectional CDW order, while the low temperature CDW is bidirectional, but with inequivalent amplitudes in the two directions. ErTe3 is an ideal “model system” in that it is stoichiometric and hence can be synthesized with a high degree of crystalline perfection and little disorder (in the sense both of very low residual resistivity - -cm at low - and resolution limited Bragg peaks associated with the CDW order). It boasts broad metallic bands with a plasma frequency which, depending on the global fit, is estimated in the range of eV [3] to eV [5] in the CDW state. Moreover, the effect of disorder can be explored systematically by Pd intercalation, as discussed in previous publications.[6, 7, 8]
Our primary result is that the thermal transport in a critical regime below appears inconsistent with quasi-particle transport. Specifically, by assuming separate electronic and phonon contributions to and that satisfies the WF law, one is forced to infer an unphysically large depression of the lattice thermal transport in this regime. The regime in which we deduce the breakdown of WF law, and hence the breakdown of the quasiparticle concept, is found to be strongly asymmetric around , extending farther below than above. In addition to this dramatic result, we also observe the following effects: i) Similar to other strongly interacting CDW systems, large anomalies are observed in the temperature derivative of the resistivity and the reflectivity (Fig. 2(b)), which, with the assumption that Fisher-Langer theory [9] applies, stands in sharp contrast to the small anomaly observed in heat capacity measurements [10]. ii) The behavior of the various linear response tensors near criticality (Figs. 1(b) and 2(a)) depends strongly on direction. As a function of decreasing , the resistivity along the -direction, , has a pronounced critical singularity at followed by a broad maximum before continuing to drop at lower temperatures, as has previously been discussed by Sinchenko et al.[11]. On the other hand, the critical anomaly in at is much weaker, and neither component shows any clear non-analyticity at . In contrast, the thermal diffusivity has a large and sharp decrease at along both the - and - directions, followed by a relatively faster recovery along the -direction. In fact, as can be inferred from Fig. 2(a), the thermal conductivity (see also Fig. 3 below) more closely resembles the temperature derivative of the resistivity, especially the -axis thermal diffusivity. iii) Thermal diffusivity in both directions show marked increases below , which through suppression of this effect by weak Pd-intercalation are shown to be electronic in origin (Fig. 4 below).




II Experiment
Samples of ErTe3 were grown using a Te self-flux technique, which ensures purity of the melt, and produces large crystals with a high degree of structural order [12]. The material is somewhat air sensitive, and crystals must be stored in an oxygen and moisture-free environment. Crystal orientation was determined with XRD.
The heat capacity of the single-crystal samples was measured using a relaxation time technique in a Quantum Design Physical Property Measurement System (PPMS). Crystals with a mass of approximately mg to mg and flat surfaces were selected for good thermal contact with the sample platform. Data were taken in zero applied field from to K.
Measurements of resistance versus temperature were performed in a Janis Supertran-VP continuous flow cryostat. The resistivity in the - plane was measured on thin rectangular crystals which had been cut with a scalpel and cleaved to expose a clean surface immediately before contacting. Crystals were cut in to bars such that current flows along the [101] axis, and contacts were attached to the surface in both longitudinal and transverse geometry, as described elsewhere [13]. In this geometry, the longitudinal and transverse contacts simultaneously measure the sum of the resistivity components along the crystal axes and the in-plane resistivity anisotropy respectively. This technique minimizes uncertainty in the resistivity anisotropy arising from geometric effects relative to using two different samples to measure and separately. Measured resistivity values were then rescaled to match existing literature [14, 13] at room temperature while preserving the same anisotropy.
Thermal diffusivity and temperature derivative reflectivity () measurements were performed using a photo-thermal microscope as described in [15]. Further details associated with the present experiment are described in the Supplemental Material section[16]. Using this apparatus, the thermal diffusivity is obtained directly, without the need to measure the thermal conductivity and specific heat separately. An advantage of this apparatus is the ability to measure the full in-plane anisotropy of the thermal diffusivity by orienting the pair of heating and probing laser spots at any arbitrary orientation with respect to the crystal axes. The mobility in the optics is further used for diagnostics of spatial uniformity of the thermal diffusivity and values. Dimensions of the measured crystal were around m by m by m. To minimize surface degradation from oxygen and water, samples were cleaved using Kapton tape immediately before being placed in the photo-thermal microscope and measured.
III Results
The specific heat of two different ErTe3 crystals over a wide temperature range is shown in Fig. 1(a) along with an ideal Debye approximation fit with a Debye temperature K. The data closely follow the Debye law both above and below each of the CDW transitions saturating at the Dulong-Petit value at high temperatures. Previous measurements of the specific heat anomaly at the CDW transition [10] find that J/molK, below the resolution of the present measurements, and surprisingly of “normal magnitude” given the large value of estimated via ARPES measurements[4]. Thermal diffusivity of a different ErTe3 crystal from the same growth batch is shown in Fig. 2(a) along with a guide to the eye curve. In contrast to the case of the specific heat, both CDW transitions produce large anomalies in the diffusivity data. In particular, at the diffusivity along both axes drops by over a third from cm2/s to cm2/s.
The sharp change in diffusivity can also be compared to the much broader change in electrical resistivity. Resistivity data on the same-batch crystals is presented in Fig. 1. The resistivity was rescaled to match existing literature as described previously. This data is similar in trend to previously measured data on RTe3 crystals [14], in particular on ErTe3 [13, 6]. The main feature in the resistivity data of this class of materials is the strong anomaly in the direction perpendicular to the primary CDW direction (-axis), as shown in Fig. 1. In contrast, the thermal diffusivity decreases along both axes. Moreover, below , the thermal diffusivity increases along both axes while the resistivity is little affected. However, the derivative of the resistivity , shows effects of the CDW transitions that are more like those seen in the thermal diffusivity (Fig. 2(a)). In all cases, there is a larger change at than at . Finally, it is illuminating to compare the critical evolution of these various DC probes with the temperature derivative of the reflectivity at eV (820 nm wavelength) as shown in Fig. 2. The derivative of the reflectivity shows a large and sharp decrease at while no anomaly is visible at .
The effect of purposefully introduced weak disorder on the temperature dependence of the thermal diffusivity is illustrated in Fig. 4, which shows a plot of the axis diffusivity of Pd0.003ErTe3 in green the data on pure ErTe3 already shown in Fig 2. is slightly suppressed upon the intercalation, from K to K, but the sharp drop in the diffusivity at the transition looks just like the one in pure ErTe3 (as shown in [7], no disorder effects appear in the -direction for this weak disorder). However, below (here around K) there is a striking intercalation induced difference; the pronounced upturn of the diffusivity in the pure material is eliminated with Pd intercalation.
IV Discussion
IV.1 Temperature derivative of the reflectivity and resistivity
The resistivity of ErTe3 has been measured before [14, 13] and the temperature dependence understood in terms of the band structure of the material [11]. Specifically, when the primary CDW forms along the -axis, the resistivity begins to increase along the perpendicular -direction. Likewise, at the formation of secondary CDW along the -axis, there is a larger change in along the perpendicular -direction.
The photothermal measurement used to extract thermal diffusivity information is a result of analyzing the phase delay in change of reflectivity from a probed point on the sample surface due to a propagating heat wave originating from a point-like source that is modulated at some frequency (see supplementary information [16]). The amplitude of the reflected light , (where is the frequency of the probing light with wavelength ) detected at the probing point can be shown to be proportional to . The optical reflectivity of ErTe3 was previously measured [3, 5] over the entire frequency range, exceeding the room-temperature plasma frequency, which depending on the global fit, is estimated in the range of cm-1 (nm) [3] to cm-1 (nm) [5]. At our probing wavelength of 820 nm, and with a Drude scattering rate () times smaller, a full Drude-Lorentz expression is needed to fit the experimental data in the whole frequency range [3, 5]. Since the range of interband transition described by a set of Lorentz harmonic oscillators is temperature independent, it is reasonable to assume that much of the temperature-dependent component of the reduction in reflectivity comes from the temperature dependence of the relaxation time, which is strongly affected by scattering from CDW fluctuations [3]. In that case we can write (e.g., we may attempt to extend the Hagen-Rubens relation to near infrared corresponding to our probing light, , where is the Drude resistivity), and thus .
In a seminal work, Fisher and Langer [9] showed that the leading (perturbative) effect of scattering of conduction electrons by classical (i.e. approximately static) critical modes leads to the relation , where is the specific heat associated with the critical fluctuations in the neighborhood of a finite phase transition. Examination of the temperature derivative of the resistivity data, particularly in the -direction, indeed reveals what appears to be a broadened discontinuity at , which is similar to the behavior of the reflectivity. This mean-field-like form is in agreement with the shape of the anomaly observed in direct measurements of specific heat in [10, 17], although the relative strength of the anomaly is much weaker in those measurements (and essentially invisible in our Fig. 1a). Despite their similar behaviors at , at lower temperatures and exhibit substantially different thermal evolutions. The former, but not the latter recovers rapidly to values comparable to those the CDW transition[18]. Furthermore, near , shows a relatively weak but still clear critical anomaly, while the the effect of the second CDW transition is difficult to discern in .
IV.2 Thermal Conductivity
More insight into the relation between electrical and thermal transport is obtained if we use the respective Einstein relations for these coefficients
| (1) |
where is the electronic compressibility, is its total specific heat, and and are the electronic and heat diffusivities respectively. While is a response function of only the electron system, the specific heat of the material, particularly at high temperatures may be dominated by the lattice. In a simple kinetic approach where electrons and phonons transport heat in parallel channels we may write , where and are the electronic and lattice specific heats and and are the respective diffusivities.
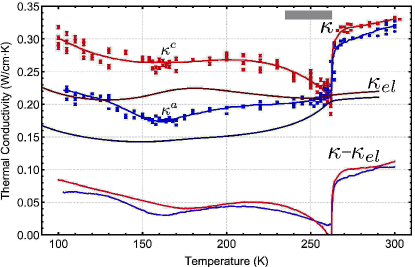
Measuring the specific heat and thermal diffusivity, the total thermal conductivity can be calculated following Eqn. 1. The resulting thermal conductivity is shown in Fig. 3 with blue and red showing the calculated thermal conductivity along the and axes respectively. A best-fit guide to the eye curve is drawn through the data points. Assuming that Wiedemann-Franz law holds, we can calculate the electronic thermal conductivity from the resistivity , which is also shown in Fig. 3. This allows us to define a “non-electronic” contribution . While it is conventional to identify with an independent phonon contribution, , it is apparent (as we will discuss below) that this is not plausible over much of the range of temperatures and especially in a region (indicated by the gray bar in Fig. 3)
We first consider the thermal conductivity around room temperature, above the CDW transitions. We note that the value of the total thermal conductivity is very high as compared to other chalcogenide-based CDW materials. For example, W/cmK for TaSe3 [19], W/cmK for NbSe3 [20], W/cmK for (TaSe4)2I [21], W/cmK for 2H-TaSe2 [22], W/cmK for HfTe5 [23], or W/cmK at 370K for 1T-TaS2 [22], to give a few examples. By contrast, ErTe3 exhibits W/cm-K at room temperature, which is more than 3 and up to 10 times larger thermal conductivity then those other compounds. However, using Wiedemann-Franz law and our measured resistivity to evaluate the electronic thermal conductivity, we obtain upon subtraction a value of which is comparable in magnitude to the aforementioned materials. Moreover, in light of the considerably larger resistivities of these other materials, the same Weidemann-Franz analysis is around 20% to 25% for most compounds, reaching 45% for NbSe3 nanowires [20]. Moreover, in all cases is very weakly dependent in this range of . It is thus natural to identify as an essentially independent phonon contribution to the thermal conductivity - as is commonly done.
While WF analysis is generally expected to work at temperatures comparable and above , analysis of the CDW transition region, particularly the anomaly at , implies a catastrophic breakdown of this approach. Firstly, while on the basis of the WF law, one would expect the the critical anomaly in the total thermal conductivity to be weak, as it is in the resistivity, in fact it is pronounced and resembles the behavior of . (Note also that the specific heat anomaly at is weak compared to the total heat capacity, primarily because of the high transition temperature where it is already in the Dulong-Petit regime). More dramatically, were we to use the WF law to subtract an electronic contribution to in the critical regime, we would be forced to conclude that the lattice contribution mysteriously vanishes, at least within degrees below - the region indicated by the gray bar in Fig. 3. We are aware of no plausible physical mechanism that could produce such an effect.
Cooling down below K, reaches a value of order W/cmK, which is common to these type of materials as discussed above, and hence may again be loosely interpretted in terms of a parallel lattice contribution. Using simple kinetic theory, our measured specific heat and a typical longitudinal sound velocity of cm/sec [10, 17], we obtain a mean free path of Å at , reduced from Å above . While below the primary CDW transition phonon mean free path might be expected to increase reflecting reduced phonon-electron scattering, CDW fluctuations in the transition region, and the CDW formation below that temperature could be additional sources of phonon scattering. (However, by contrast, in the other chalcogenide-based CDW materials mentioned above, is nearly constant with a slight tendency to increase with decreasing over the same range of .) In the same temperature range the total and electronic thermal conductivities reach an anisotropic value of , reflecting the effect of the primary CDW at . It is then interesting to note that this anisotropy is only weakly reduced below the secondary CDW transition at , where the primary effect is an increase in all components of the thermal transport. While the increase in the putative lattice part below could be due to further gapping of electronic states that decrease the phonon-electron scattering rate, the electronic increase in thermal conductivity simply reflects the increase of the mean free path of the remaining itinerant electrons. This hypothesis can be checked by introducing additional electron disorder scattering with small concentration of intercolated Pd atoms (). At the same time, this level of intercalation does not seem to markedly change the carrier density [6].


Figure 4 show the effect of Pd intercalation on resistivity and Pd intercalation effect on thermal conductivity. We first notice the respective decrease in the primary CDW transitions, which closely follows the phase diagram first introduced in [6]. Focusing on the -axis transport, where effects of disorder have been shown to the strong effect on the electronic component is observed, thermal diffusivity as shown in Fig. 4 did not change much below , but the characteristic increase increase below is missing. The respective electronic component shown in Fig. 4 also show a decrease, both reflect the increase in disorder which scatter both, electrons and phonons. The incomplete gapping of electronic states may also affect the phonon-electron scattering [7, 8].
V Broader Context
In many cases, the transport properties of metals can be successfully understood on the basis of the response of weakly interacting elementary excitations - fermionic-quasi-particles and bosonic phonons. In the last several decades, however, various transport regimes in certain “highly correlated” materials have been identified, in which the validity of such an approach has been called into question. However, it remains highly contravertial to what extent conventional quasi-particle ideas can be extended without fundamental changes in approach to strongly interacting regimes in which the quasiparticle identity is “marginally” maintained, or if entirely new paradigms (possibly involving some form of “non-Fermi liquid” or novel fractionalized quasiparticles) are needed.
One avenue of attack on this problem has been to investigate the way in which the usual quasiparticle picture can break down in the neighborhood of a quantum critical point. However, even at classical (finite ) critical points, the existence of non-trivial critical exponents describing the behavior in the critical regime provides clear evidence that the critical modes themselves cannot have a quasi-particle description. None-the-less, in many cases, as for instance in cases where the Fisher-Langer theory gives good account of transport anomalies, a treatment involving well-defined conduction electrons (and, presumably, phonons) weakly scattered by the critical modes, implies that the conventional mechanism of transport theory continues to apply even in the critical regime.
The dramatic failure of such an approach to give an adequate description of the thermal transport in ErTe3, most dramatically in a K range of below , may be a first indication of a potentially simpler context to study the breakdown of the quasi-particle paradigm. The discrepancies in the critical dependences of the thermal conductivity and the resistivity in this regime imply a complete breakdown of the WF law, the existence of independent electronic quasiparticles and phonon modes, or both. In fact, the observed behavior may more adequately described as a strongly coupled electron-phonon critical ‘soup.’
CDW formation, arising from a variety of physical mechanisms, is a relatively common phenomenon in quasi-low-dimensional materials. Although thermal transport measurements have not been performed for all such materials, they do exist for many of the well-known canonical examples, and in none of these cases has such a dramatic violation of the WF law been deduced. This raises an associated question as to why the effect should be so pronounced in this particular material system given the relative ubiquity of CDW compounds (for a recent survey of CDW systems see e.g. [24]). A wider survey of related materials might yet reveal that this effect is in fact not unique to the rare earth tritellurides, but at least for now ErTe3 occupies a unique position among known CDW compounds and presents an entirely new opportunity to explore unconventional transport properties of strongly interacting metals.
VI Acknowledgments
We would like to thank Alan Fang for helpful discussions. This work was supported by the Department of Energy, Office of Basic Energy Sciences, under contract no. DE-AC02-76SF00515. The photothermal apparatus was built using a grant from the Gordon and and Betty Moore Foundation through Emergent Phenomena in Quantum Systems Initiative Grant GBMF4529. JAWS was supported in part by an ABB Stanford Graduate Fellowship. AGS was supported in part by an NSF Graduate Research Fellowship (grant number DGE-1656518).
References
- Peierls [1955] R. E. Peierls, Quantum theory of solids (Clarendon Press, Oxford, 1955).
- Fröhlich [1954] H. Fröhlich, On the theory of superconductivity: The one-dimensional case, Proceedings of the Royal Society A 223, 296 (1954).
- Pfuner et al. [2010] F. Pfuner, P. Lerch, J.-H. Chu, H.-H. Kuo, I. R. Fisher, and L. Degiorgi, Temperature dependence of the excitation spectrum in the charge-density-wave ErTe3 and HoTe3 systems, Phys. Rev. B 81, 195110 (2010).
- Moore et al. [2010] R. G. Moore, V. Brouet, R. He, D. H. Lu, N. Ru, J.-H. Chu, I. R. Fisher, and Z.-X. Shen, Fermi surface evolution across multiple charge density wave transitions in , Phys. Rev. B 81, 073102 (2010).
- Hu et al. [2011] B. F. Hu, B. Cheng, R. H. Yuan, T. Dong, A. F. Fang, W. T. Guo, Z. G. Chen, P. Zheng, Y. G. Shi, and N. L. Wang, Optical study of the multiple charge-density-wave transitions in erte3, Phys. Rev. B 84, 155132 (2011).
- Straquadine et al. [2019] J. A. W. Straquadine, F. Weber, S. Rosenkranz, A. H. Said, and I. R. Fisher, Suppression of charge density wave order by disorder in Pd-intercalated ErTe3, Phys. Rev. B 99, 235138 (2019).
- Fang et al. [2019] A. Fang, J. A. W. Straquadine, I. R. Fisher, S. A. Kivelson, and A. Kapitulnik, Disorder-induced suppression of charge density wave order: Stm study of pd-intercalated , Phys. Rev. B 100, 235446 (2019).
- Fang et al. [2020] A. Fang, A. G. Singh, J. A. W. Straquadine, I. R. Fisher, S. A. Kivelson, and A. Kapitulnik, Robust superconductivity intertwined with charge density wave and disorder in pd-intercalated , Phys. Rev. Research 2, 043221 (2020).
- Fisher and Langer [1968] M. E. Fisher and J. S. Langer, Resistive anomalies at magnetic critical points, Phys. Rev. Lett. 20, 665 (1968).
- Saint-Paul et al. [2017] M. Saint-Paul, G. Remenyi, C. Guttin, P. Lejay, and P. Monceau, Thermodynamic and critical properties of the charge density wave system erte3, Physica B: Condensed Matter 504, 39 (2017).
- Sinchenko et al. [2014] A. A. Sinchenko, P. D. Grigoriev, P. Lejay, and P. Monceau, Spontaneous breaking of isotropy observed in the electronic transport of rare-earth tritellurides, Phys. Rev. Lett. 112, 036601 (2014).
- Ru and Fisher [2006] N. Ru and I. R. Fisher, Thermodynamic and transport properties of , , and , Phys. Rev. B 73, 033101 (2006).
- Walmsley and Fisher [2017] P. Walmsley and I. R. Fisher, Determination of the resistivity anisotropy of orthorhombic materials via transverse resistivity measurements, Review of Scientific Instruments 88, 043901 (2017), https://doi.org/10.1063/1.4978908 .
- Ru et al. [2008] N. Ru, C. L. Condron, G. Y. Margulis, K. Y. Shin, J. Laverock, S. B. Dugdale, M. F. Toney, and I. R. Fisher, Effect of chemical pressure on the charge density wave transition in rare-earth tritellurides , Phys. Rev. B 77, 035114 (2008).
- Zhang et al. [2017] J. Zhang, E. M. Levenson-Falk, B. J. Ramshaw, D. A. Bonn, R. Liang, W. N. Hardy, S. A. Hartnoll, and A. Kapitulnik, Anomalous thermal diffusivity in underdoped yba2cu3o6+x, Proceedings of the National Academy of Sciences 114, 5378 (2017).
- Sup [Note] (Note), See Supplemental Material at [URL will be inserted by publisher] .
- Saint-Paul and Monceau [2020] M. Saint-Paul and P. Monceau, Phenomenological approach of the thermodynamic properties of the charge density wave systems, Philosophical Magazine 0, 1 (2020), https://doi.org/10.1080/14786435.2020.1844917 .
- Lazarević et al. [2011] N. Lazarević, Z. V. Popović, R. Hu, and C. Petrovic, Evidence of coupling between phonons and charge-density waves in ErTe3, Phys. Rev. B 83, 024302 (2011).
- Zawilski et al. [2010] B. Zawilski, R. Littleton IV, N. Lowhorn, and T. Tritt, Observation of a two level thermal conductivity in the low-dimensional materials, Solid State Communications 150, 1299 (2010).
- Yang et al. [2019] L. Yang, Y. Tao, J. Liu, C. Liu, Q. Zhang, M. Akter, Y. Zhao, T. T. Xu, Y. Xu, Z. Mao, Y. Chen, and D. Li, Distinct signatures of electron-phonon coupling observed in the lattice thermal conductivity of nbse3 nanowires, Nano Letters 19, 415 (2019).
- Kwok and Brown [1989] R. S. Kwok and S. E. Brown, Thermal conductivity of the charge-density-wave systems and (i near the peierls transition, Phys. Rev. Lett. 63, 895 (1989).
- Núñez Regueiro et al. [1985] M. D. Núñez Regueiro, J. M. Lopez-Castillo, and C. Ayache, Thermal conductivity of -ta and -ta, Phys. Rev. Lett. 55, 1931 (1985).
- Zawilski et al. [2001] B. M. Zawilski, R. T. Littleton, and T. M. Tritt, Description of the parallel thermal conductance technique for the measurement of the thermal conductivity of small diameter samples, Review of Scientific Instruments 72, 1770 (2001), https://aip.scitation.org/doi/pdf/10.1063/1.1347980 .
- Saint-Paul and Monceau [2019] M. Saint-Paul and P. Monceau, Survey of the thermodynamic properties of the charge density wave systems, Advances in Condensed Matter Physics 2019, 2138264 (2019).