Anisotropic odd elasticity with Hamiltonian curl forces

An elastic body in continuum limit is modeled as a $d$-dimensional Riemannian manifold $(\mathcal{B},g_{ab})$ embedded in Euclidean space $\mathcal{E}$ in the study of its interior elastic deformation. The strain state is characterized by the metric tensor $g_{ab}$ defined on $\mathcal{B}$. For example, the strain-free elastic body prior to any deformation is described by a Riemannian manifold isometrically embedded in Euclidean space; the value of $g_{ab}$ is specified by the pullback of the Euclidean metric [23, 24]. Note that in this work we employ the abstract index notation in Latin letters to represent a tensor; the tensor components are labeled by Greek letters.

In general, the deformation of the body leads to the variation of the element of length, and thus the metric of the manifold [25, 26]. Therefore, the elastic deformation of the body could be characterized by a diffeomorphism $\phi$ from some reference configuration to the deformed one: $(\mathcal{B},g_{ab})\rightarrow(\mathcal{B},\tilde{g}_{ab})$. Note that subscripts ‘$ab$’ are to indicate that $g_{ab}$ is a covariant tensor field of order 2. The topology of $\mathcal{B}$ is preserved in elastic deformation. To illustrate the $\phi$ mapping, we present some examples in figure 1. Under the deformations as described by the mappings $\phi_{i}$ ($i=1,2,3$), any given point in the reference configuration, say $A$, is mapped to $\phi_{i}(A)$. The original 2D elastic body of square shape is deformed to a rectangle (by $\phi_{1}$ mapping), to the patches on the sphere (by $\phi_{2}$ mapping) and on the cylinder (by $\phi_{3}$ mapping), respectively. In these three kinds of deformations, $\tilde{g}_{ab}$ refers to the Euclidean metric, the spherical metric and the cylindrical metric, respectively.

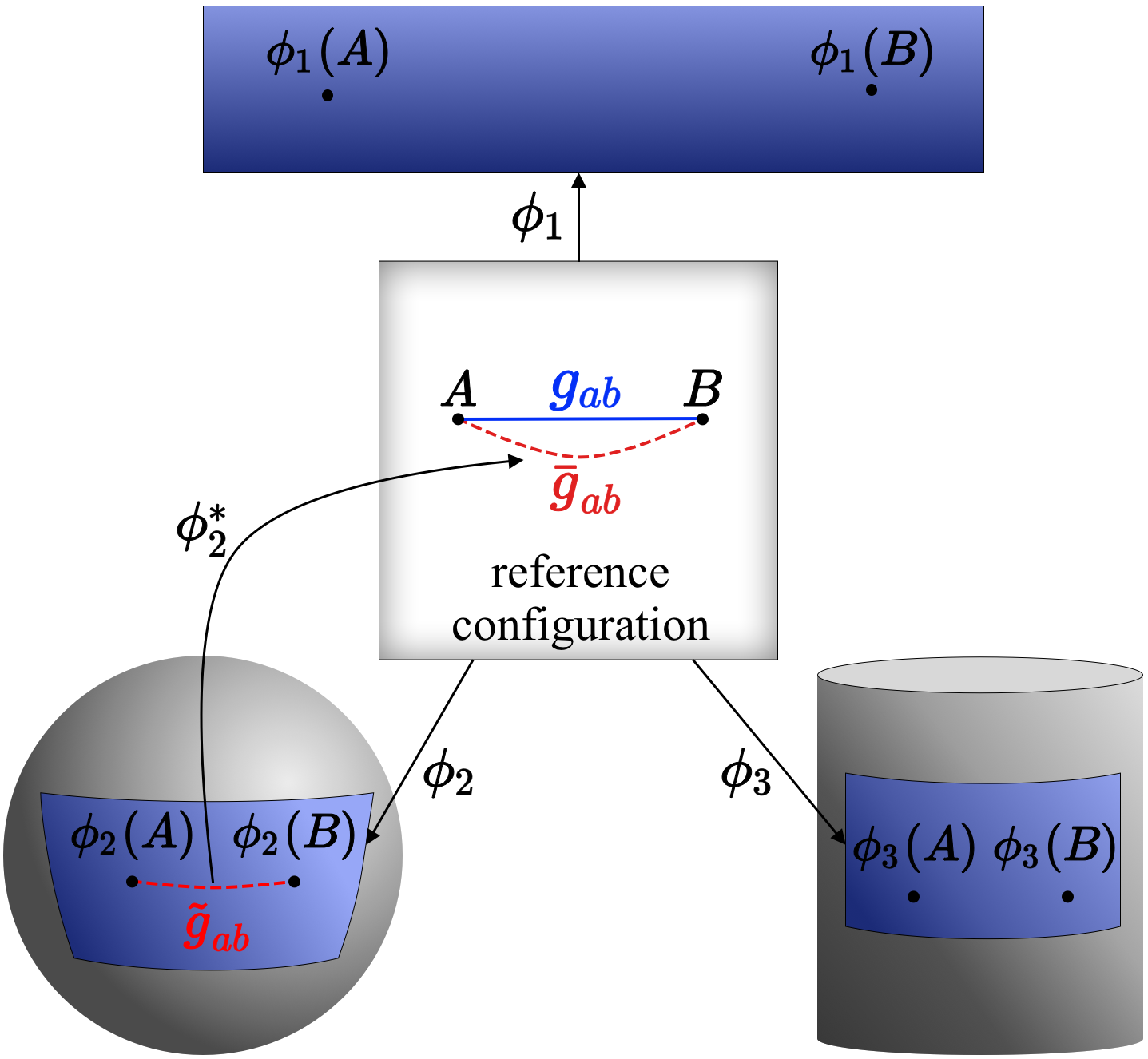
From the geometric perspective, the deformation is characterized by the variation of the metric from $g_{ab}$ to $\phi^{*}\tilde{g}_{ab}$, both of which are defined on the same manifold $\mathcal{B}$. Specifically, the information of the strain in the deformation is encoded in the difference between $\phi^{*}\tilde{g}_{ab}$ and $g_{ab}$. To illustrate this point, let us consider a curve $\gamma(t)\in(\mathcal{B},g_{ab})$, where $t\in[0,1]$. The length of the line element on $\gamma$ is measured by $g_{ab}$. After the deformation, the curve is mapped to $\phi(\gamma(t))\in(\mathcal{B},\tilde{g}_{ab})$. The length of a line element on $\phi(\gamma)$ measured by $\tilde{g}_{ab}$ is equal to the length of the corresponding line element on $\gamma$ measured by $\phi^{*}\tilde{g}_{ab}$. Therefore, the change of the curve length could be measured by $\phi^{*}\tilde{g}_{ab}-g_{ab}$. As such, it is natural to define the strain tensor on $\mathcal{B}$ as [27, 2, 28]

$\displaystyle u_{ab}=\frac{1}{2}\left(\bar{g}_{ab}-g_{ab}\right),$

(1)

where $\bar{g}_{ab}\equiv\phi^{*}\tilde{g}_{ab}$. The definition of strain in (1) is also applicable to large deformation [2].

In the following discussion, the Riemannian manifold $(\mathcal{B},\bar{g}_{ab})$ is denoted as $\Sigma$, representing the deformed configuration of the elastic body. The elastic body is initially free of stress, and is thus isometrically embedded in the $(d+1)$-dimensional Euclidean space $\mathcal{E}$. The metric $\bar{g}_{ab}$ on the manifold $\Sigma$ is induced from the metric $\delta_{ab}$ on $\mathcal{E}$ [24, 29, 30], i.e., $\bar{g}_{ab}=\delta_{ab}-N_{a}N_{b}$, where $N_{a}$ is the unit normal covector on $\Sigma$ in $\mathcal{E}$. For example, consider a 2D surface isometrically embedded in $\mathcal{E}$. One may construct the Cartesian coordinates $\{X^{1},X^{2},X^{3}\}$ centered at any point $P$ on the surface; $X^{3}$-axis is perpendicular to the tangent plane at point $P$. The first fundamental form (or the line element) is given explicitly by the metric: $\bar{g}_{\alpha\beta}(\mathrm{d}X^{\alpha})_{a}(\mathrm{d}X^{\beta})_{b}=\bar{g}_{\mu\nu}(\mathrm{d}s^{\mu})_{a}(\mathrm{d}s^{\nu})_{b}+(\mathrm{d}X^{3})_{a}(\mathrm{d}X^{3})_{b}-(\mathrm{d}X^{3})_{a}(\mathrm{d}X^{3})_{b}=\bar{g}_{\mu\nu}(\mathrm{d}s^{\mu})_{a}(\mathrm{d}s^{\nu})_{b}$, where $\{s^{1},s^{2}\}$ are local coordinates near the point $P$. Note that the Greek letters in the indices represent the components of the tensor, and they take the values from $1$ to $d+1$. Here, the convention of Einstein summation is applied. For spherical surface, $s^{1}=\theta$ and $s^{2}=\phi$, where the polar angle $\theta\in[0,\pi]$ and the azimuthal angle $\phi\in[0,2\pi)$. Note that due to the isometric embedding of $\Sigma$ in $\mathcal{E}$, all of the tensors in this work are regarded as being defined on the tangent space of $\mathcal{E}$, and the lowering (or raising) of the indices of a tensor is uniformly implemented by $\delta_{ab}$ (or $\delta^{ab}$).

Now, we characterize the displacement field associated with the deformation in terms of the geometric language introduced in the preceding paragraph. We first establish the Cartesian coordinates system of $\mathcal{E}$ by $\{X^{1},\dots,X^{d+1}\}$. The manifolds $(\mathcal{B},g_{ab})$ and $\Sigma$ are thus represented by the $\mathbb{R}^{d+1}$ -valued functions $X_{0}^{\mu}(p)$ and $X^{\mu}(\phi(p))$ ($\forall p\in\mathcal{B}$), respectively. $\bar{X}^{\mu}(p)\equiv X^{\mu}(\phi(p))$. The displacement field on $\mathcal{B}$ is

$\displaystyle U^{a}=U^{\mu}\left(\frac{\partial}{\partial X^{\mu}}\right)^{a},$

(2)

where the $\mu$-component of the displacement field $U^{\mu}(p)=\bar{X}^{\mu}(p)-X_{0}^{\mu}(p),\forall p\in\mathcal{B}.$

The displacement fields $U^{a}$ constitute an infinite dimensional manifold called the configuration space. The Hamiltonian of the elastic body is a scalar on the cotangent bundle of the configuration space, and it can be written formally as [30]:

$\displaystyle H=T+W=\int_{\Sigma}\rho\left(\mathscr{T}+\mathscr{W}\right)\bm{\varepsilon},$

(3)

where $\mathscr{T}$ and $\mathscr{W}$ are the kinetic energy and elastic potential per unit mass, respectively. $\bm{\varepsilon}$ is the Riemannian volume form compatible with $\bar{g}_{ab}$. $\rho$ is the mass density of the deformed configuration. In this work, $\mathscr{W}$ is a quadratic local function of $u_{ab}$. The gradient of $\mathscr{W}$ is recognized as the Kirchhoff stress tensor:

$\displaystyle\tau^{ab}=\frac{\partial\mathscr{W}}{\partial u_{ab}}.$

(4)

$\tau^{ab}$ is a symmetric tensor field on $\Sigma$. It measures the stress experienced by the unit mass of the deformed configuration. Note that the Cauchy stress tensor $\sigma^{ab}$ is related to the Kirchhoff stress tensor by $\sigma^{ab}=\rho\tau^{ab}$, and it measures the stress on the unit volume of the deformed configuration [30]. In (3), $\mathscr{T}$ could be written as a quadratic function of the generalized momentum density field $P_{a}$ that is conjugated to $U^{a}$:

$\displaystyle\mathscr{T}=\frac{1}{2}\mathscr{M}^{ab}P_{a}P_{b}.$

(5)

It is important to point out that here we introduce the effective mass tensor $\mathscr{M}^{ab}$. $\mathscr{M}^{ab}$ is anisotropic and symmetric, and it is invariant in the deformation of the elastic body. In connection to possible experimental realizations, the anisotropy of $\mathscr{M}^{ab}$ may be introduced by designing a local resonance cavity structure composed of an internal mass that is connected to the wall by two perpendicular Hookean springs; such anisotropic mechanical microstructures have been used to regulate the propagation of acoustic waves in metamaterials [31, 32]. An explanatory example based on the modified mass-in-mass model is presented in section 3.4 to show the realization of anisotropic effective mass units. The idea of introducing the anisotropy in the construction of the kinetic energy is inspired by the work on Hamiltonian curl forces [20, 21, 22]. The concept of inducing Hamiltonian curl forces through anisotropic mass was initially introduced in systems with finite degrees of freedom by Berry and Shukla [20, 21, 22]. Specifically, it has been proved that a class of non-conservative (i.e., whose curl is not zero) position depending forces can be generated by the element of anisotropy in the kinetic energy term in Hamiltonian. Here, we extend this idea to the continuum elastic system by incorporating the non-conservative nature into $\mathscr{M}^{ab}$. Consequently, (3) admits a non-conservative force density, which is crucial for understanding odd elasticity.

The Hamilton’s equations based on (3) are

	$\displaystyle\frac{\partial U^{a}}{\partial t}=\frac{\delta H}{\delta P_{a}}=\rho\sqrt{\bar{g}}\mathscr{M}^{ab}P_{b},$		(6a)
	$\displaystyle\frac{\partial P_{a}}{\partial t}=-\frac{\delta H}{\delta U^{a}}=\sqrt{\bar{g}}f_{a},$		(6b)

where $f_{a}=\bar{g}_{b}{}^{c}\partial_{c}(\bar{g}_{ad}\sigma^{db})$. Note that the repeated indices in pairs represents tensor contraction. $\bar{g}$ is the determinant of $\bar{g}_{ab}$; $\partial_{c}$ is the Cartesian derivative operator on $\mathcal{E}$ acting on the embedding coordinates $\{\bar{X}^{\mu}\}$ of $\Sigma$. The detailed information is presented in A and B. Note that the generalized coordinates $U^{a}$ in the Hamiltonian formalism is closely related to the strain of an elastic body.

By combining (6a) and (6b), we obtain the dynamic equation of the manifold $\Sigma$ as

$\displaystyle\frac{\partial V^{a}}{\partial t}=M^{ab}f_{b}\equiv F^{a},$

(6g)

where the displacement velocity field $V^{a}\equiv\partial{U^{a}}/\partial{t}$ and the symmetric tensor field $M^{ab}\equiv\rho\bar{g}\mathscr{M}^{ab}$. According to (6g), $F^{a}$ regulates the acceleration of unit mass in the elastic body, and it is recognized as the Newtonian force per unit mass. (6g) suggests that the dynamics of a continuum elastic body with anisotropic mass $\mathscr{M}^{ab}$ under $f^{a}$ is equivalent to the dynamics of a unit scalar mass under $F^{a}$; the velocity $V^{a}$ as associated to the displacement field is the common dynamics variable.

Without any loss of generality, $M^{ab}$ is decomposed as

$\displaystyle M^{ab}=M\delta^{ab}+\Omega^{ab},$

(6h)

where $M=\delta_{ab}M^{ab}/(d+1)$, and $\Omega^{ab}$ is a traceless symmetric tensor field. Here, we shall emphasize that the anisotropic effect in the kinetic energy is captured by $\Omega^{ab}$. By (6h), the kinetic energy density $\mathscr{T}$ is divided into the isotropic and the anisotropic parts:

$\displaystyle\mathscr{T}=\frac{1}{2\rho^{2}\bar{g}}P_{a}P^{a}+\frac{1}{2\rho\bar{g}}\Omega^{ab}P_{a}P_{b}.$

(6i)

We also cast $F^{a}$ in the following form

$\displaystyle F^{a}=Mf^{a}+\Omega^{ab}f_{b}.$

(6j)

Now, let us focus on (6j). The first term in (6j) is recognized as the force per unit mass as a derivative of the elastic potential for $M=1/\rho$ [28, 33, 34, 35]. According to (6a) and (6b), the power of $Mf^{a}$ is expressed as:

$\displaystyle Mf_{a}V^{a}=\mathscr{M}^{ab}\frac{\partial P_{a}}{\partial t}P_{b}=\frac{\mathrm{d}\mathscr{T}}{\mathrm{d}t}=-\frac{\mathrm{d}\mathscr{W}}{\mathrm{d}t}.$

(6k)

In the last equality, the conservation of the total energy is applied, i.e., $\mathrm{d}{H}/\mathrm{d}{t}=0$. According to (6k), the power of $Mf^{a}$ is equal to the reduction rate of $\mathscr{W}$. Due to the conservation of the total energy, it indicates that the work done by $Mf^{a}$ is equal to the energy transfer from the potential energy to the kinetic energy per unit mass in the deformation of the elastic body. Note that for a single-valued $\mathscr{W}$ function, the integration of (6k) over any closed orbits in $\mathcal{E}$ is zero, implying that $Mf^{a}$ is a conservative force. As such, the first term of $F^{a}$ in (6j) does not alter the value of either $\mathscr{W}$ or $\mathscr{T}$ in a cyclic deformation of the elastic body.

We proceed to examine the second term $\Omega^{ab}f_{b}$ in (6j). The power of $\Omega^{ab}f_{b}$ is:

	$\displaystyle\Omega^{ab}f_{b}V_{a}$	$\displaystyle=\rho\Omega^{ab}\frac{\partial P_{b}}{\partial t}\mathscr{M}_{a}{}^{c}P_{c}$			(6l)
		$\displaystyle=\frac{1}{\rho\bar{g}}\Omega^{ab}\left(\delta_{a}{}^{c}+\rho\Omega_{a}{}^{c}\right)P_{c}\frac{\partial P_{b}}{\partial t}.$

Under the assumption that the anisotropic tensor $\rho\Omega^{ab}$ is small compared with $\delta^{ab}$, (6l) becomes

$\displaystyle\Omega^{ab}f_{b}V_{a}=\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{1}{2\rho\bar{g}}\Omega^{ab}P_{a}P_{b}\right).$

(6m)

Here, it is important to point out that the R.H.S. of (6m) is identified as the rate of the increase of the anisotropic part of $\mathscr{T}$. In other words, the work done by $\Omega^{ab}f_{b}$ causes the increase in the anisotropic part of the kinetic energy per unit mass.

In the following, we will show that the second term $\Omega^{ab}f_{b}$ in (6j) is a non-conservative force. To this end, we first substitute the expression of $f_{a}$ in (6j), and obtain the expression for the Newtonian force per unit volume as

	$\displaystyle\rho F^{a}$	$\displaystyle=\bar{g}_{b}{}^{c}\partial_{c}\sigma^{ab}+\rho\Omega^{ad}\bar{g}_{b}{}^{c}\partial_{c}\left(\bar{g}_{de}\sigma^{eb}\right)$			(6n)
		$\displaystyle=\bar{g}_{b}{}^{c}\partial_{c}\left(\sigma^{ab}+\hat{\sigma}^{ab}\right)-\bar{g}_{bd}\sigma^{dc}\partial_{c}\left(\rho\Omega^{ab}\right),$

where $\hat{\sigma}^{ab}\equiv\rho\Omega^{ac}\bar{g}_{cd}\sigma^{db}$. Note that $\hat{\sigma}^{ab}$ is not symmetric. Furthermore, $\hat{\sigma}^{ab}$ does not live in the tangent space of $\Sigma$ because of the acting of $\Omega^{ac}\bar{g}_{cd}$. For spatially-slowly-varying $\rho\Omega^{ab}$, its gradient could be regarded as a small quantity. Therefore, the last term in (6n) is much smaller than the second term; note that $\bar{g}_{b}{}^{c}\partial_{c}\hat{\sigma}^{ab}=\bar{g}_{b}{}^{c}\partial_{c}(\rho\Omega^{ad}\bar{g}_{de}\sigma^{eb})$. As such, the last term could be neglected. The anisotropic effect boils down to the modification of $\hat{\sigma}^{ab}$ in $\sigma^{ab}$ as shown in the first bracket in (6n).

Now, to reveal the non-conservative nature of the second term in (6j), we analyze the work done by the total stress per unit mass in a cyclic deformation. In the deformation process, the instantaneous strain state of the elastic body is denoted by $u_{ab}(t)$, which is represented by a point in the space of the strain field $u_{ab}$. The cycle of deformation is thus described by a loop $\eta(t)$ in the strain space. $t\in[0,T]$. $\eta(0)=\eta(T)$. The work done per unit mass in a cycle of deformation is [6, 10]:

	$\displaystyle\Delta\mathscr{A}$	$\displaystyle=\oint_{\eta(t)}\left(\tau^{ab}+\hat{\tau}^{ab}\right)\mathrm{d}u_{ab}$			(6o)
		$\displaystyle=\int_{S}\left(\frac{\partial\tau^{ab}}{\partial u_{cd}}+\frac{\partial\hat{\tau}^{ab}}{\partial u_{cd}}\right)\mathrm{d}u_{cd}\wedge\mathrm{d}u_{ab},$
		$\displaystyle\equiv\int_{S}T^{abcd}\mathrm{d}u_{cd}\wedge\mathrm{d}u_{ab},$

where $\hat{\tau}^{ab}=\hat{\sigma}^{ab}/\rho$, and $S$ is the surface enclosed by $\eta(t)$. Stokes’s theorem is used in the derivation for (6o). Since the exterior product is antisymmetric, the stress is conservative (such that $\Delta\mathscr{A}=0$ in the cyclic deformation) if and only if $T^{abcd}$ possesses the major index symmetry, i.e., $T^{abcd}=T^{cdab}$. Especially, quasi-static cyclic deformation can be realized by applying suitable external force on $\Sigma$. $\Delta\mathscr{A}$ is then equal to the work done by the external force.

We analyze the first term of $T^{abcd}$ in (6o). From the expression for $\mathscr{W}$

$\displaystyle\mathscr{W}=\frac{1}{2}C^{abcd}u_{ab}u_{cd},$

(6p)

where $C^{abcd}$ is the elastic modulus tensor with major index symmetry (i.e, $C^{abcd}=C^{cdab}$), we obtain the linear constitutive relation

$\displaystyle\tau^{ab}=C^{abcd}u_{cd}.$

(6q)

Due to the major index symmetry of $C^{abcd}$, the first term of $T^{abcd}$ satisfies $\partial{\tau^{ab}}/\partial{u_{cd}}=\partial{\tau^{cd}}/\partial{u_{ab}}$, which indicates the conservative nature of $\tau^{ab}$. In other words, the work done by $\tau^{ab}$ is zero in a cyclic deformation.

For the second term in $T^{abcd}$, from the definition of $\hat{\sigma}^{ab}$ and (6q), we have

	$\displaystyle\hat{\tau}^{ab}$	$\displaystyle=$	$\displaystyle\rho\Omega^{ac}\bar{g}_{cd}\tau^{db}$		(6r)
		$\displaystyle=$	$\displaystyle\rho\Omega^{ae}\left(g_{ef}+2u_{ef}\right)C^{fbcd}u_{cd}$
		$\displaystyle=$	$\displaystyle\hat{C}^{abcd}u_{cd}+\hat{D}^{abcdef}u_{cd}u_{ef},$

where

$\displaystyle\hat{C}^{abcd}=\rho\Omega^{ae}g_{ef}C^{fbcd},\quad\hat{D}^{abcdef}=2\rho\Omega^{ac}C^{dbef}.$

(6s)

In the nonlinear constitutive relation in (6r), the quadratic term naturally arises in the expansion of $\bar{g}_{cd}$ as the sum of the metric $g_{cd}$ of the reference configuration and the strain field $2u_{cd}$. Furthermore, the anisotropic tensor $\Omega^{ab}$ leads to the anisotropic nature of the elastic modulus $\hat{C}^{abcd}$ and $\hat{D}^{abcdef}$. Here, we shall point out that in the Hamiltonian formalism based on anisotropic mass tensor, the resulting odd elastic modulus are naturally anisotropic. The anisotropy of $\hat{C}^{abcd}$ and $\hat{D}^{abcdef}$ is inherent in our formalism. A detailed discussion about the symmetry of $\hat{C}^{abcd}$ and $\hat{D}^{abcdef}$ is in D. In general, the odd elastic modulus are not necessarily anisotropic in 2D [6]. By (6r), the second term of $T^{abcd}$ is obtained

$\displaystyle\frac{\partial\hat{\tau}^{ab}}{\partial u_{cd}}=\hat{C}^{abcd}+\left(\hat{D}^{abcdef}+\hat{D}^{abef(cd)}\right)u_{ef}.$

(6t)

The bracket in the superscript of $\hat{D}$ indicates the symmetric part of the tensor. Here, it is important to point out that in (6s), the involvement of the $\Omega^{ab}$-tensor breaks the major index symmetry of $\hat{C}^{abcd}$, as well as that of the second and the third terms in the right hand side of (6t). Consequently, $\hat{\tau}^{ab}$ is non-conservative according to (6t).

Note that both $\hat{C}^{abcd}$ and $\hat{D}^{abcdef}$ in (6s) are invariant in the deformation of $\Sigma$. The reason is as follows. In the expressions for $\hat{C}^{abcd}$ and $\hat{D}^{abcdef}$, both the elastic modulus tensor $C^{abcd}$ and the metric $g_{ab}$ are independent of the deformation of $\Sigma$. Regarding the factor $\rho\Omega^{ab}$, according to (6h) and the definition for $M^{ab}$, $\rho\Omega^{ab}=\rho^{2}\bar{g}\mathscr{M}^{ab}-\delta^{ab}=\rho_{0}^{2}g\mathscr{M}^{ab}-\delta^{ab}$, where $\rho_{0}$ is the mass density of the reference configuration. $\rho\Omega^{ab}$ is therefore invariant in the deformation of $\Sigma$.

In the regime of small deformation, where the quadratic term in (6r) can be neglected, the constitutive relation of $\hat{\tau}^{ab}$ becomes linear:

$\displaystyle\hat{\tau}^{ab}=\hat{C}^{abcd}u_{cd}.$

(6u)

The broken major index symmetry of $\hat{C}^{abcd}$ indicates the presence of the antisymmetric (odd) part in the elastic modulus tensor, which is responsible for the non-conservativity of the stress and the extra work occurring in cyclic deformations. As such, $\hat{C}^{abcd}$ is called the odd elastic modulus in literature [6]. Microscopic mechanism for odd elasticity has been attributed to various non-conservative interparticle forces. Here, the odd elasticity as characterized by the $\hat{C}^{abcd}$-tensor in (6u) is derived from the anisotropic effective mass in the Hamiltonian formalism in the continuum level.

We shall point out that in the model of odd elasticity based on the Hamiltonian formalism, the total energy is conserved. The work extracted by $\hat{\tau}^{ab}$ during cyclic deformations is from the conversion of the kinetic energy pre-stored in the internal degree of freedom of the system, rather than from the external energy inputs (see section 3.4 for detailed discussions). The anisotropy of the effective mass $\mathscr{M}^{ab}$ arises from the coarse-grained internal degrees of freedom. In a cyclic process, according to (6m), the non-conservative curl force transfers the kinetic energy between the (coarse-grained) anisotropic parts of $\mathscr{T}$ and the isotropic parts of $\mathscr{T}$. As such, for a cyclic deformation starting and ending at zero velocity, no work can be extracted.

In this section, we illustrate the emergence of odd elasticity for the simple case of planar deformation of a 2D elastic body under small deformation approximation.

The strain tensor $u_{ab}$ in the deformation can be expanded as $u_{ab}=u_{\mu}\mathfrak{e}^{\mu}{}_{ab}$, where $\mathfrak{e}^{\mu}{}_{ab}$ is a set of orthogonal tensor bases on the reference configuration equipped with a local orthonormal frame fields $\{e_{1}{}^{a},e_{2}{}^{a}\}$ [6]:

	$\displaystyle\mathfrak{e}^{1}{}_{ab}=e^{1}{}_{a}e^{1}{}_{b}+e^{2}{}_{a}e^{2}{}_{b},$		(6va)
	$\displaystyle\mathfrak{e}^{2}{}_{ab}=e^{2}{}_{a}e^{1}{}_{b}-e^{1}{}_{a}e^{2}{}_{b},$		(6vb)
	$\displaystyle\mathfrak{e}^{3}{}_{ab}=e^{1}{}_{a}e^{1}{}_{b}-e^{2}{}_{a}e^{2}{}_{b},$		(6vc)
	$\displaystyle\mathfrak{e}^{4}{}_{ab}=e^{1}{}_{a}e^{2}{}_{b}+e^{2}{}_{a}e^{1}{}_{b}.$		(6vd)

$u_{\mu}$ characterizes the following local modes of deformation: dilation, rotation, and shearing. The stress tensor can also be expanded as $\tau^{ab}=\tau^{\mu}\mathfrak{e}_{\mu}{}^{ab}$, where $\tau^{\mu}$ are associated with pressure, torque density and shear stress.

The rotationally symmetric elastic modulus tensor field $C^{abcd}$ could be written as (see C for details):

$\displaystyle C^{abcd}=\lambda g^{ab}g^{cd}+2\mu g^{a(c}g^{d)b},$

(6vw)

where $\lambda$ and $\mu$ are Lamé coefficients. In the tensor bases of $\{\mathfrak{e}^{\mu}{}_{ab}\}$, $g_{ab}=\mathfrak{e}^{1}{}_{ab}$, and $C^{abcd}=C^{\mu\nu}\mathfrak{e}_{\mu}{}^{ab}\mathfrak{e}_{\nu}{}^{cd}$. From (6vw), we obtain

$\displaystyle C^{\mu\nu}=\begin{bmatrix}\lambda+\mu&0&0&0\\ 0&0&0&0\\ 0&0&\mu&0\\ 0&0&0&\mu\\ \end{bmatrix}.$

(6vx)

Correspondingly, (6q) is expressed as $\tau^{\mu}=C^{\mu\nu}u_{\nu}$. $\lambda+\mu$ and $\mu$ characterize the isotropic stretching rigidity and the isotropic shear rigidity, respectively. Note that the matrix in 6vx is invariant under the rotation of $\{e_{1}{}^{a},e_{2}{}^{a}\}$.

We proceed to discuss the components $\hat{C}^{\mu\nu}$. By expanding the traceless tensor $\rho\Omega^{ab}$ in the tensor bases of $\{e_{1}{}^{a},e_{2}{}^{a}\}$ as

$\displaystyle\rho\Omega^{ab}=\kappa e_{1}{}^{a}e_{1}{}^{b}+\zeta e_{1}{}^{a}e_{2}{}^{b}+\zeta e_{2}{}^{a}e_{1}{}^{b}-\kappa e_{2}{}^{a}e_{2}{}^{b},$

(6vy)

where $\kappa$ and $\zeta$ are scalars, we finally have

$\displaystyle\hat{C}^{\mu\nu}=\begin{bmatrix}0&0&\kappa\mu&\zeta\mu\\ 0&0&\zeta\mu&-\kappa\mu\\ \kappa(\lambda+\mu)&0&0&0\\ \zeta(\lambda+\mu)&0&0&0\end{bmatrix}.$

(6vz)

Since $\hat{C}^{abcd}=\hat{C}^{\mu\nu}\mathfrak{e}_{\mu}{}^{ab}\mathfrak{e}_{\nu}{}^{cd}$, the abstract index exchange $ab\leftrightarrow cd$ in $\hat{C}^{abcd}$ is identical to the label exchange $\mu\leftrightarrow\nu$ in $\hat{C}^{\mu\nu}$. (6vz) shows that $\hat{C}^{\mu\nu}\neq\hat{C}^{\nu\mu}$, and therefore $\hat{C}^{abcd}\neq\hat{C}^{cdab}$. This key feature of the broken major symmetry is exactly the mathematical structure underlying the phenomenon of odd elasticity. The upper right $2\times 2$ submatrix in (6vz) connects shear strain with pressure and torque, and the lower left $2\times 2$ submatrix connects dilation with shear stress. The existence of these two non-zero submatrices is an indicator for the anisotropy of $\hat{C}^{abcd}$ [6].

In the following, we employ the modified mass-in-mass model as an example to show the emergence of the anisotropic inertial mass and the non-conservative force.

Consider a 2D cavity of mass $m_{1}$ that contains an internal mass $m_{2}$, as illustrated in figure 2. The internal mass is connected to the cavity via a spring of resonance frequency $\omega_{\mathrm{I}}$ and a damper of damping constant $\Omega_{\mathrm{I}}$. The cavity is subject to an external potential $W$. The dynamic equations for this mass-in-mass model are

	$\displaystyle m_{1}\frac{\mathrm{d}^{2}X_{1}}{\mathrm{d}t^{2}}=-\frac{\partial W}{\partial X_{1}}-m_{2}\omega_{\mathrm{I}}^{2}D-\Omega_{\mathrm{I}}\frac{\mathrm{d}D}{\mathrm{d}t},$		(6vaaa)
	$\displaystyle m_{2}\frac{\mathrm{d}^{2}X_{2}}{\mathrm{d}t^{2}}=m_{2}\omega_{\mathrm{I}}^{2}D+\Omega_{\mathrm{I}}\frac{\mathrm{d}D}{\mathrm{d}t},$		(6vaab)
	$\displaystyle m_{1}\frac{\mathrm{d}^{2}Y_{1}}{\mathrm{d}t^{2}}=-\frac{\partial W}{\partial Y_{1}},$		(6vaac)
	$\displaystyle m_{2}\frac{\mathrm{d}^{2}Y_{2}}{\mathrm{d}t^{2}}=0,$		(6vaad)

where $(X_{1},\ Y_{1})$ and $(X_{2},\ Y_{2})$ represent the Cartesian coordinates of displacements of $m_{1}$ and $m_{2}$ respectively, and $D=X_{1}-X_{2}$.

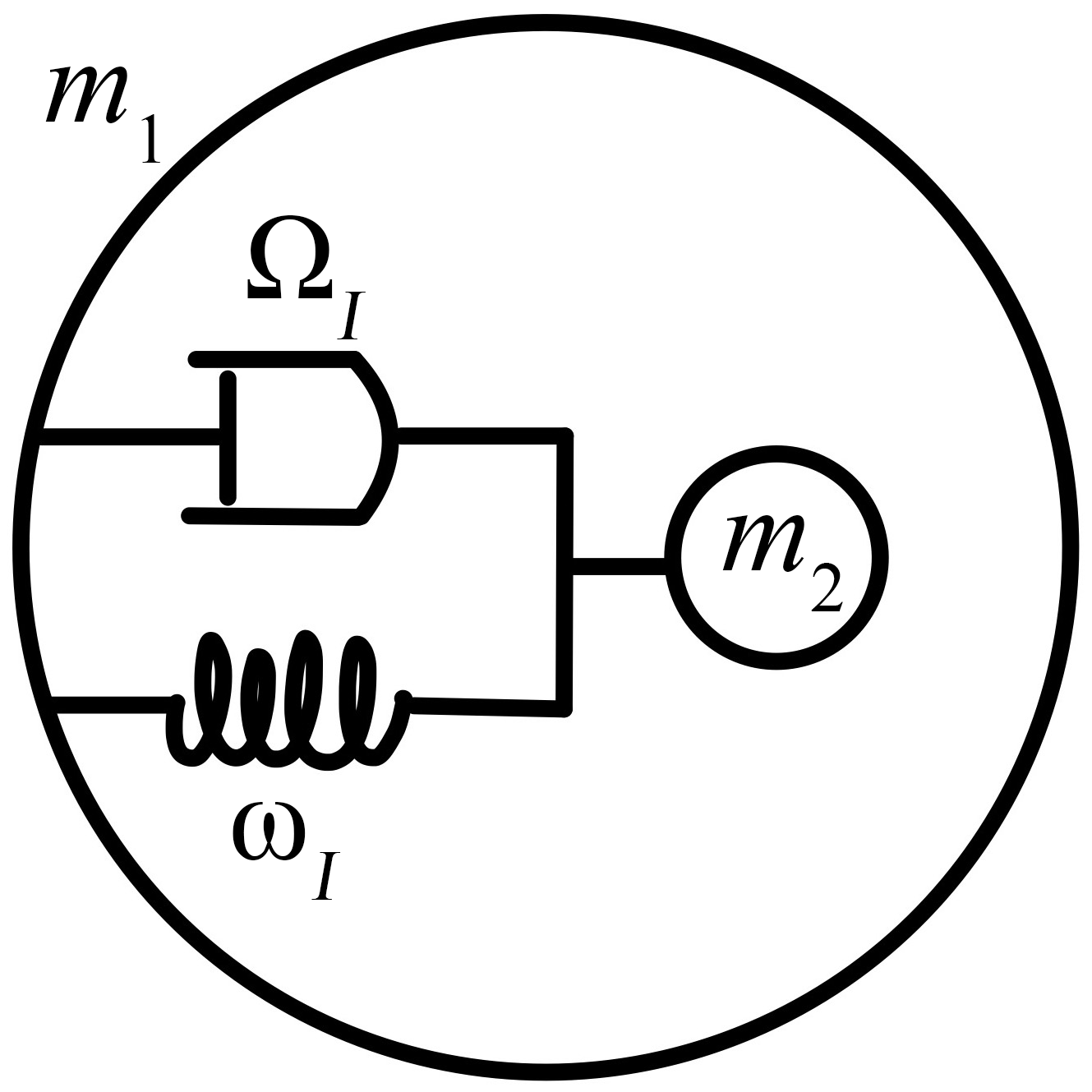
We focus on the motion along the x-direction. Adding and subtracting (6vaaa) and (6vaab) lead to:

	$\displaystyle\left(m_{1}+m_{2}\right)\frac{\mathrm{d}^{2}X_{1}}{\mathrm{d}\hat{t}^{2}}-m_{2}\frac{\mathrm{d}^{2}D}{\mathrm{d}\hat{t}^{2}}=f_{x},$		(6vaaaba)
	$\displaystyle m_{1}\frac{\mathrm{d}^{2}D}{\mathrm{d}\hat{t}^{2}}+\left(m_{1}+m_{2}\right)\left(\hat{\omega}^{2}D+\hat{\Omega}\frac{\mathrm{d}D}{\mathrm{d}\hat{t}}\right)=f_{x},$		(6vaaabb)

where the external force:

$\displaystyle f_{x}=-\frac{1}{\omega_{\mathrm{E}}^{2}}\frac{\partial W}{\partial X_{1}},$

(6vaaabac)

and the dimensionless quantities are

$\displaystyle\hat{t}=t\omega_{\mathrm{E}},\quad\hat{\omega}=\frac{\omega_{\mathrm{I}}}{\omega_{\mathrm{E}}},\quad\hat{\Omega}=\frac{\Omega_{\mathrm{I}}}{m_{2}\omega_{\mathrm{E}}}.$

(6vaaabad)

We focus on the regime of $\hat{\omega}\gg 1$ and $\hat{\Omega}\gg 1$, i.e., the dynamics of the internal degree of freedom is much faster than the that of the cavity.

We first analyze (6vaaabb) by introducing the following Green’s function $G_{\omega}$:

	$\displaystyle D(\hat{t})$	$\displaystyle=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\mathrm{d}\omega\int_{-\infty}^{+\infty}\mathrm{d}\hat{t}^{\prime}\exp[-\mathrm{i}\omega(\hat{t}-\hat{t}^{\prime})]G_{\omega}f_{x}(\hat{t}^{\prime})$			(6vaaabae)
		$\displaystyle=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\mathrm{d}\omega\int_{-\infty}^{+\infty}\mathrm{d}\hat{t}^{\prime}\exp(-\mathrm{i}\omega\hat{t}^{\prime})G_{\omega}f_{x}(\hat{t}-\hat{t}^{\prime}),$

where

$\displaystyle G_{\omega}=\frac{1}{(m_{1}+m_{2})\left(\hat{\omega}^{2}-\mathrm{i}\hat{\Omega}\omega\right)-m_{1}\omega^{2}}.$

(6vaaabaf)

We thus have:

$\displaystyle\frac{\mathrm{d}^{2}D}{\mathrm{d}\hat{t}^{2}}=-\frac{1}{2\pi}\int_{-\infty}^{+\infty}\mathrm{d}\omega\int_{-\infty}^{+\infty}\mathrm{d}\hat{t}^{\prime}\exp(-\mathrm{i}\omega\hat{t}^{\prime})\omega^{2}G_{\omega}f_{x}(\hat{t}-\hat{t}^{\prime}).$

(6vaaabag)

The integration over $\omega$ in (6vaaabag) is implemented by the residue theorem. Specifically,

	$\displaystyle\int_{-\infty}^{+\infty}\mathrm{d}\omega\exp(-\mathrm{i}\omega\hat{t}^{\prime})\omega^{2}G_{\omega}=\int_{-\infty}^{+\infty}\mathrm{d}\omega\frac{\exp(-\mathrm{i}\omega\hat{t}^{\prime})\omega^{2}}{\left(m_{1}+m_{2}\right)\left(\hat{\omega}^{2}-\mathrm{i}\hat{\Omega}\omega\right)-m_{1}\omega^{2}}$
	$\displaystyle=\int_{-\infty}^{+\infty}\mathrm{d}\omega\frac{\exp(-\mathrm{i}\omega\hat{t}^{\prime})\left(m_{1}+m_{2}\right)\left(\hat{\omega}^{2}-\mathrm{i}\hat{\Omega}\omega\right)}{m_{1}\left(m_{1}+m_{2}\right)\left(\hat{\omega}^{2}-\mathrm{i}\hat{\Omega}\omega\right)-m_{1}^{2}\omega^{2}}-\frac{1}{m_{1}}\int_{-\infty}^{+\infty}\mathrm{d}\omega\exp(-\mathrm{i}\omega\hat{t}^{\prime})$
	$\displaystyle=\int_{-\infty}^{+\infty}\mathrm{d}\omega\frac{\exp(-\mathrm{i}\omega\hat{t}^{\prime})\left(m_{1}+m_{2}\right)\left(\mathrm{i}\hat{\Omega}\omega-\hat{\omega}^{2}\right)}{m_{1}^{2}\left(\omega-\omega_{+}\right)\left(\omega-\omega_{-}\right)}-\frac{2\pi}{m_{1}}\delta(\hat{t}^{\prime}).$		(6vaaabah)

The integrand has two poles in the lower half complex $\omega$-plane at:

$\displaystyle\omega_{\pm}=\frac{-\mathrm{i}\left(m_{1}+m_{2}\right)\hat{\Omega}\pm\sqrt{\left(m_{1}+m_{2}\right)\left[\left(m_{1}+m_{2}\right)\hat{\Omega}^{2}-4m_{1}\hat{\omega}^{2}\right]}}{2m_{1}},$

(6vaaabai)

if $\left(m_{1}+m_{2}\right)\hat{\Omega}^{2}>4m_{1}\hat{\omega}^{2}$.

By the standard method of constructing a closed contour via introducing an infinitely large semicircle in the lower half-plane, and applying the residue theorem, the first term in (6vaaabah) becomes

		$\displaystyle-$	$\displaystyle\frac{1}{2\pi\mathrm{i}}\int_{-\infty}^{+\infty}\mathrm{d}\omega\frac{\exp(-\mathrm{i}\omega\hat{t}^{\prime})\left(m_{1}+m_{2}\right)\left(\hat{\omega}^{2}-\mathrm{i}\hat{\Omega}\omega\right)}{m_{1}\left(m_{1}+m_{2}\right)\left(\hat{\omega}^{2}-\mathrm{i}\hat{\Omega}\omega\right)-m_{1}^{2}\omega^{2}}$		(6vaaabaj)
		$\displaystyle=$	$\displaystyle\frac{\exp(-\mathrm{i}\omega_{+}\hat{t}^{\prime})\left(m_{1}+m_{2}\right)\left(\mathrm{i}\hat{\Omega}\omega_{+}-\hat{\omega}^{2}\right)}{m_{1}^{2}\left(\omega_{+}-\omega_{-}\right)}$
			$\displaystyle+\frac{\exp(-\mathrm{i}\omega_{-}\hat{t}^{\prime})\left(m_{1}+m_{2}\right)\left(\mathrm{i}\hat{\Omega}\omega_{-}-\hat{\omega}^{2}\right)}{m_{1}^{2}\left(\omega_{-}-\omega_{+}\right)}.$

By inserting (6vaaabah) and (6vaaabaj) into (6vaaabag), we obtain:

	$\displaystyle\frac{\mathrm{d}^{2}D}{\mathrm{d}\hat{t}^{2}}$	$\displaystyle=$	$\displaystyle\int_{0}^{+\infty}\mathrm{d}\hat{t}^{\prime}\frac{\mathrm{i}\exp(-\mathrm{i}\omega_{+}\hat{t}^{\prime})\left(m_{1}+m_{2}\right)\left(\mathrm{i}\hat{\Omega}\omega_{+}-\hat{\omega}^{2}\right)}{m_{1}^{2}\left(\omega_{+}-\omega_{-}\right)}f_{x}(\hat{t}-\hat{t}^{\prime})$		(6vaaabak)
			$\displaystyle+\int_{0}^{+\infty}\mathrm{d}\hat{t}^{\prime}\frac{\mathrm{i}\exp(-\mathrm{i}\omega_{-}\hat{t}^{\prime})\left(m_{1}+m_{2}\right)\left(\mathrm{i}\hat{\Omega}\omega_{-}-\hat{\omega}^{2}\right)}{m_{1}^{2}\left(\omega_{-}-\omega_{+}\right)}f_{x}(\hat{t}-\hat{t}^{\prime})+\frac{f_{x}(\hat{t})}{m_{1}}$
		$\displaystyle=$	$\displaystyle-\frac{f_{x}(\hat{t})}{m_{1}}+\frac{f_{x}(\hat{t})}{m_{1}}$
		$\displaystyle=$	$\displaystyle 0.$

Note that the initial value theorem of Laplace transform is used in the integration over $\hat{t}^{\prime}$. The theorem states that for large real $s$,

$\displaystyle\int_{0}^{+\infty}\mathrm{d}\hat{t}^{\prime}f(\hat{t}^{\prime})\exp(-s\hat{t}^{\prime})=\frac{f(0)}{s}.$

(6vaaabal)

Consequently, (6vaaaba) is simplified to:

$\displaystyle\left(m_{1}+m_{2}\right)\frac{\mathrm{d}^{2}X_{1}}{\mathrm{d}\hat{t}^{2}}=-\frac{1}{\omega_{\mathrm{E}}^{2}}\frac{\partial W}{\partial X_{1}}.$

(6vaaabam)

Along with (6vaac), the equations of motion for the displacement $R^{a}=(X_{1},\ Y_{1})$ are finally reduced to:

$\displaystyle m_{ab}\frac{\mathrm{d}^{2}R^{a}}{\mathrm{d}\hat{t}^{2}}=-\nabla_{a}\hat{W},$

(6vaaaban)

where $\hat{W}=W/\omega_{\mathrm{E}}^{2}$. Here, it is important to point out that the effective anisotropic mass arises in the mass-in-mass model. In Cartesian coordinates,

$\displaystyle m_{\mu\nu}=\begin{bmatrix}m_{1}+m_{2}&0\\ 0&m_{1}\end{bmatrix}.$

(6vaaabao)

Therefore, elastic media fabricated by connecting such cavity units with Hookean springs could manifest anisotropic mass density, and thus exhibit odd elasticity.

We proceed to discuss the Hamiltonian non-conservative force acting on the cavity. First of all, we construct the Hamiltonian corresponding to (6vaaaban) as

$\displaystyle H=T+\hat{W}.$

(6vaaabap)

The total kinetic energy $T$ includes the kinetic energies of $m_{1}$ and $m_{2}$:

$\displaystyle T=\frac{1}{2}M^{ab}P_{a}P_{b}=\frac{1}{2}m_{1}\left(u^{2}+v^{2}\right)+\frac{1}{2}m_{2}u^{2},$

(6vaaabaq)

where $M^{ab}=(m^{-1})^{ab}$, $u=\mathrm{d}{X_{1}}/\mathrm{d}{\hat{t}}$, $v=\mathrm{d}{Y_{1}}/\mathrm{d}{\hat{t}}$. The Hamilton’s equations are:

	$\displaystyle\frac{\mathrm{d}R^{a}}{\mathrm{d}\hat{t}}$	$\displaystyle=M^{ab}P_{b},$			(6vaaabara)
	$\displaystyle\frac{\mathrm{d}P_{a}}{\mathrm{d}\hat{t}}$	$\displaystyle=-\nabla_{a}\hat{W}.$			(6vaaabarb)

Combining (6vaaabara) and (6vaaabarb), the dynamics equation becomes:

$\displaystyle m\frac{\mathrm{d}^{2}R^{a}}{\mathrm{d}\hat{t}^{2}}=-mM^{ab}\nabla_{b}\hat{W}\equiv F^{a},$

(6vaaabaras)

where the effective scalar mass $m=2/M^{a}{}_{a}$. Note that (6vaaabaras) could also be derived by multiplying $mM^{ab}$ at both side of (6vaaaban). (6vaaabaras) shows the dynamics of an anisotropic mass $m_{ab}$ under the potential $\hat{W}$, which is equivalent to the dynamics of an isotropic mass $m$ subject to a non-conservative force $F^{a}$.