Anisotropic dressing of electrons in electron-doped cuprate superconductors
Abstract
The recent experiments revealed a remarkable possibility for the absence of the disparity between the phase diagrams of the electron- and hole-doped cuprate superconductors, while such an aspect should be also reflected in the dressing of the electrons. Here the phase diagram of the electron-doped cuprate superconductors and the related exotic features of the anisotropic dressing of the electrons are studied based on the kinetic-energy driven superconductivity. It is shown that although the optimized in the electron-doped side is much smaller than that in the hole-doped case, the electron- and hole-doped cuprate superconductors rather resemble each other in the doping range of the superconducting dome, indicating an absence of the disparity between the phase diagrams of the electron- and hole-doped cuprate superconductors. In particular, the anisotropic dressing of the electrons due to the strong electron’s coupling to a strongly dispersive spin excitation leads to that the electron Fermi surface is truncated to form the disconnected Fermi arcs centered around the nodal region. Concomitantly, the dip in the peak-dip-hump structure of the quasiparticle excitation spectrum is directly associated with the corresponding peak in the quasiparticle scattering rate, while the dispersion kink is always accompanied by the corresponding inflection point in the total self-energy, as the dip in the peak-dip-hump structure and dispersion kink in the hole-doped counterparts. The theory also predicts that both the normal and anomalous self-energies exhibit the well-pronounced low-energy peak-structures.
pacs:
74.25.Jb, 74.25.Dw, 74.20.Mn, 74.72.EkI Introduction
The parent compound of cuprate superconductors is classified as a half-filled Mott insulator with an antiferromagnetic (AF) long-range order (AFLRO) Bednorz86 ; Tokura89 , which occurs to be due to the very strong electron correlation Anderson87 . In the hole-doped case Bednorz86 , a small number of the doped holes destroys AFLRO quickly, and then superconductivity appears leaving only the AF short-range order (AFSRO) correlation still intact Fujita12 ; Damascelli03 ; Campuzano04 ; Fink07 . However, in the electron-doped side Tokura89 , both the doped electrons and annealing process in a low-oxygen environment are required to induce superconductivity, where the early experimental observations Armitage10 ; Armitage01 ; Matsui05 ; Matsui05a ; Matsui07 ; Santander-Syro11 ; Song12 revealed that in a clear contrast to the hole-doped case, AFLRO survives until superconductivity appears only in a narrow window of the highly doped electrons, around the optimal doping, and can persist into the superconducting (SC) phase. In particular, a large pseudogap opens at around the crossing points of the electron Fermi surface (EFS) with the AF Brillouin zone boundary due to the AFLRO correlation Armitage10 ; Armitage01 ; Matsui05 ; Matsui05a ; Matsui07 ; Santander-Syro11 ; Song12 . Moreover, unlike the universal dome-like shape doping dependence of the SC transition temperature in the hole-doped case Damascelli03 ; Campuzano04 ; Fink07 with an optimal doping at around , the SC phase in the electron-doped side shows a large variation Armitage10 . This disparity between the phase diagrams of the electron- and hole-doped cuprate superconductors implies that the electron doping and hole doping may affect the electronic structure in different manners Damascelli03 ; Campuzano04 ; Fink07 ; Armitage10 ; Armitage01 ; Matsui05 ; Matsui05a ; Matsui07 ; Santander-Syro11 ; Song12 .
Since the additional annealing process is crucial for realizing superconductivity in the electron-doped side Armitage10 ; Armitage01 ; Matsui05 ; Matsui05a ; Matsui07 ; Santander-Syro11 ; Song12 , the different annealing methods may result in distinct properties, reflecting a fact that the controversy of the phase diagram in the electron-doped side may be attributed to the conflicting experimental results associated with the annealing effect. Although the effect of the annealing is still not fully understood on the microscopic level Adachi13 ; Adachi17 , it is possible that the intrinsic aspects of the electron-doped cuprate superconductors are masked by the improper annealing condition. Recently, the substantial improvements in the materials synthesis technique Adachi17 ; Horio16 ; Song17 ; Lin20 ; Horio20b allow one to grow the single crystals of the electron-doped cuprate superconductors in the optimal annealing condition, where a strongly localized state of charge carriers accompanied by an AF pseudogap at around the crossing points in the improper annealing condition has been changed to a metallic- and SC-states with the optimal annealing condition. In particular, the experimental observations on these new single crystals in the proper annealing condition indicate clearly that the annealing and oxygen vacancy induce a sufficient change in the charge carrier density Adachi17 . In this case, the doping concentration should be considered in conjunction with the annealing and oxygen nonstoichiometry. This actual charge carrier concentration has been be used in building the new phase diagram Adachi17 ; Horio16 ; Song17 ; Lin20 ; Horio20b , where the SC-state that coexists with AFSRO is extended over a wide electron doping range with the maximum value of that occurs at around the optimal doping , while the deduced AFLRO phase boundary does not extend into the SC dome Horio16 ; Song17 ; Lin20 ; Horio20b . This new phase diagram of the electron-doped cuprate superconductors is in a striking analogy to the corresponding phase diagram in the hole-doped counterparts, and therefore reveals a possibility for the absence of the disparity between the phase diagrams of the electron- and hole-doped cuprate superconductors. With this new phase diagram, a critical question is whether or not SC mechanism in the electron-doped side is the same as in the hole-doped case.
The new phase diagram in the electron-doped cuprate superconductors is thus closely related to the actual electron doping concentration, while such an aspect should be reflected in the nature of the quasiparticle excitations resulting of the dressing of the electrons due to the electron interaction mediated by various bosonic excitations. The understanding of how strong coupling of the electrons with various bosonic excitations affects the electronic structure is especially important to explain the astonishing phenomena, including the question of the pairing mechanism Vekhter03 ; Carbotte11 ; Choi18 . Very recently, the intrinsic EFS reconstruction and its evolution with the electron doping in the new single crystals with the proper annealing condition have been observed experimentally from the angle-resolved photoemission spectroscopy (ARPES) measurements Horio16 ; Song17 ; Lin20 ; Horio20b , where the characteristic features can be summarized as: (a) a quasiparticle peak is observed on the entire EFS without the signature of an AF pseudogap at around the crossing points; and (b) the stronger quasiparticle scattering is observed in the antinodal region than in the nodal region, leading to the formation of the disconnected Fermi arcs centered around the nodal region. In the hole-doped case, the intrinsic features of the quasiparticle excitations, associated with the EFS reconstruction and characterized by the distinct depression in the electron density of states, reminiscent of the well-known peak-dip-hump (PDH) structure in the quasiparticle excitation spectrum, the kink in the quasiparticle dispersion, and the multiple nearly-degenerate electronic orders, have been observed experimentally by virtue of systematic studies using the scanning tunneling microscopy Neto14 ; Fujita14 and resonant X-ray scattering techniques Vishik18 ; Comin16 ; Comin14 , particularly the ARPES measurements Dessau91 ; Norman97 ; Campuzano99 ; Wei08 ; DMou17 ; Kaminski01 ; Lanzara01 ; Kordyuk06 ; Iwasawa08 ; Plumb13 . On the other hand, although a few experimental results for the dispersion kinks along the nodal and antinodal directions, associated with the new phase diagram and the intrinsic EFS reconstruction, has been observed very recently in the electron-doped side with the proper annealing condition Horio20b , the experimental data of the PDH structure are still lacking to date. Furthermore, to the best of our knowledge, these intrinsic properties of the quasiparticle excitations have also not been discussed starting from a SC theory so far. In this case, the crucial issue is to understand even from a theoretical analysis which intrinsic aspects of the quasiparticle excitations are universal to both the electron- and hole-doped cuprate superconductors, and how they might depend on the specifics of the participating electron- or hole-like states.
In our previous works Feng15a ; Gao18 ; Gao18a ; Gao19 ; Liu20 , the doping dependence of and the related dressing of the electrons in the hole-doped cuprate superconductors have been investigated within the framework of the kinetic-energy driven superconductivity, where we have shown that takes a dome-like shape with the underdoped and overdoped regimes on each side of the optimal doping , where reaches its maximum, and then the main aspects of the quasiparticle excitations observed from the experiments, including the EFS reconstruction Norman98 ; Kanigel07 ; Nakayama09 ; Kondo13 ; Chatterjee06 , the nature of the charge-order correlation Neto14 ; Fujita14 ; Vishik18 ; Comin16 ; Comin14 , the striking PDH structure in the quasiparticle excitation spectrum Dessau91 ; Norman97 ; Campuzano99 ; Wei08 ; DMou17 , the dispersion kink Kaminski01 ; Lanzara01 ; Kordyuk06 ; Iwasawa08 ; Plumb13 , and the remarkable ARPES autocorrelation and its connection with the quasiparticle scattering interference Chatterjee06 ; He14 , are qualitatively reproduced. In particular, we have also shown that all these exotic features are a natural result of the strong electron correlation characterized by the strong electron interaction mediated by a strongly dispersive spin excitation. However, a comprehensive discussion of the electron-doped counterparts has not been given. We believe that if the coupling of the electrons with a strongly dispersive spin excitation is of the same nature both in the electron- and hole-doped cuprate superconductors, it should reveal itself in the nature of the quasiparticle excitation of the electron-doped cuprate superconductors as it does in the hole-doped counterparts. In this paper, we try to study the phase diagram and the related intrinsic properties of the quasiparticle excitations in the electron-doped cuprate superconductors. We show explicitly that the maximal occurs around the optimal doping , and then decreases in both the underdoped and overdoped regimes. In particular, although the optimized in the electron-doped side is much smaller than that in the hole-doped case, the electron- and hole-doped cuprate superconductors rather resemble each other in the doping range of the SC dome, indicating an absence of the disparity between the phase diagrams of the electron- and hole-doped cuprate superconductors. Moreover, the characteristic features of the intrinsic EFS reconstruction, the PDH structure, and the dispersion kink in the electron-doped cuprate superconductors are a clear analogy to those obtained in the hole-doped counterparts. Our present results therefore also show that the essential physics is the same for both the electron- and hole-doped cuprate superconductors.
This paper is organized as follows. First, we present the basic formalism in Sec. II, where we express explicitly the single-particle diagonal and off-diagonal propagators (hence the single-particle spectral function) of the electron-doped cuprate superconductors based on the kinetic-energy driven superconductivity. We then discuss the doping dependence of in Sec. III, where a comparison of the phase diagrams between the electron- and hole-doped cuprate superconductors is made. In Sec. IV, we discuss the intrinsic aspects of the quasiparticle excitations, and show that a sharp quasiparticle peak emerges on the entire EFS without an AF pseudogap at around the crossing points. Finally, we give a summary and discussions in Sec. V.
II Formalism
Both the electron- and hole-doped cuprate superconductors have a layered crystal structure consisting of the two-dimensional CuO2 planes separated by insulating layers Bednorz86 ; Tokura89 , and it is then believed that the exotic features in these systems are closely related to the doped CuO2 planes Damascelli03 ; Campuzano04 ; Fink07 ; Armitage10 . In this case, as originally emphasized by Anderson Anderson87 , the essential physics of the doped CuO2 plane is properly captured by the - model on a square lattice Lee06 ; Edegger07 ,
| (1) | |||||
where the summation is over all sites , and for each , over its nearest-neighbors (NN) or the next NN , the hopping integrals and for the hole-doped case, while and in the electron-doped side. In particular, the NN hopping in the - model (1) has a electron-hole symmetry because the sign of can be absorbed by the change of the sign of the orbital on one sublattice. However, the electron-hole asymmetry can be properly accounted by the next NN hopping Hybertsen90 ; Gooding94 ; Kim98 . and are the electron creation and annihilation operators, respectively, with spin on site , is a localized spin operator, and is the chemical potential. The high complexity in the - model (1) comes mainly from the electron local constraint, i.e., this - model (1) is supplemented by a local constraint of no double electron occupancy in the hole-doped case: , while it acts on the space with no zero electron occupied sites in the electron-doped side: . However, for the electron doping, we can work in the hole representation via a particle-hole transformation , with () that is the hole creation (annihilation) operator, and then the local constraint of no zero electron occupancy in the electron representation is replaced by the local constraint of no double hole occupancy in the hole representation . In this case, the - model (1) in both the electron doping and hole doping is always subject to an important on-site local constraint to avoid the double occupancy, and the difference between the electron doping and hole doping is expressed as the sign difference of the hopping integrals as mentioned above. This local constraint of no double occupancy can be dealt properly by the fermion-spin theory Feng9404 ; Feng15 based on the charge-spin separation, and in particular, the constrained hole operators and are decoupled as,
| (2) |
where the spinful fermion operator describes the charge degree of freedom of the constrained hole together with some effects of spin configuration rearrangements due to the presence of the doped charge carrier itself, while the localized spin operator describes the spin degree of freedom of the constrained hole, and then the local constraint without double hole occupancy is satisfied in analytical calculations. Based on the - model in the fermion-spin representation, the kinetic-energy driven SC mechanism has been established Feng15 ; Feng0306 ; Feng12 , where in the doped regime without an AFLRO, the coupling of the charge carriers and spin excitations directly from the kinetic energy provides the attractive interaction between the charge carriers in the particle-particle channel that pairs charge carriers together to form d-wave charge-carrier pairing state, then the electron pairs with the d-wave symmetry originated from the d-wave charge-carrier pairing state are due to the charge-spin recombination Feng15a , and their condensation reveals the SC ground-state. The typical features of the kinetic energy driven SC mechanism can be summarized as: (a) the mechanism is purely electronic without phonons; (b) the mechanism indicates that the strong electron correlation favors superconductivity, since the main ingredient is identified into an electron pairing mechanism not involving the phonon, the external degree of freedom, but the internal spin degree of freedom of electron; (c) the electron pairing state is controlled by both the electron pair gap and single-particle coherence, which leads to that the maximal occurs around the optimal doping, and then decreases in both the underdoped and the overdoped regimes; (d) superconductivity coexists with the AFSRO correlation. Within the framework of this kinetic-energy driven superconductivity, the ARPES autocorrelation and the line-shape of the quasiparticle excitation spectrum in electron-doped cuprate superconductors have been studied recently Tan20 . Following these previous discussions Tan20 , the single-particle diagonal and off-diagonal propagators and of the electron-doped cuprate superconductors can be obtained explicitly as,
| (3a) | |||||
| (3b) | |||||
where is the single-electron band energy, with and , , while the total self-energy is a combination of the normal self-energy in the particle-hole channel and the anomalous self-energy in the particle-particle channel, and is given explicitly by,
| (4) |
In the kinetic-energy driven SC mechanism, both the normal and anomalous self-energies and quantify the interaction between electrons mediated by a strongly dispersive spin excitation, and have been given explicitly in Ref. Tan20, , where the sharp peak visible for temperature in the normal (anomalous) self-energy is actually a -functions, broadened by a small damping used in the numerical calculation at a finite lattice. The calculation in this paper for the normal (anomalous) self-energy is performed numerically on lattice in momentum space, with the infinitesimal replaced by a small damping .
The result in Eq. (3) also shows that the basic Eliashberg formalism Eliashberg60 with the d-wave type SC gap is still valid, although the pairing mechanism is driven by the kinetic energy by the exchange of spin excitations. The single-particle spectral function is related directly to the imaginary part of the single-particle diagonal propagator in Eq. (3a) as Damascelli03 ; Campuzano04 ; Fink07 ,
| (5) |
and then the quasiparticle excitation spectrum measured by ARPES experiments is proportional to this single-particle spectral function (5), where and are the real and imaginary parts of the total self-energy , respectively. In particular, the real part of the total self-energy offsets the single-electron band energy , while the imaginary part of the total self-energy is identified as the quasiparticle scattering rate,
| (6) |
which broadens the spectral peak in the ARPES spectrum, and therefore governs the lifetime of the quasiparticle Damascelli03 ; Campuzano04 ; Fink07 . This is why one can obtain the information about the total self-energy from ARPES experiments by analyzing the energy and momentum distribution data.
III Phase diagram
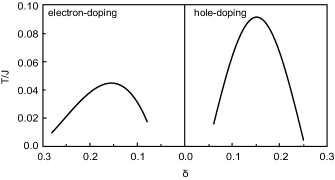
The understanding of the phase diagram of cuprate superconductors has been one of the central issues since its original discovery in 1986 Bednorz86 ; Tokura89 , through to the present day. Within the framework of the kinetic-energy driven superconductivity Feng15 ; Feng0306 ; Feng12 , the evolution of with the hole doping in the hole-doped cuprate superconductors has been obtained in our early studies Feng15a ; Feng12 in terms of the self-consistent calculation at the condition of the SC gap , where has a dome-like shape doping dependence with the maximum that occurs at around the optimal hole doping , in good agreement with the experimental results observed on the hole-doped cuprate superconductors Tallon95 . Following these early studies for the hole-doped case, we have also performed a self-consistent calculation for the doping dependence of in the electron-doped side, and the result of as a function of the electron doping for parameters and is plotted in the left panel of Fig. 1. In order to compare the present result of the electron-doped cuprate superconductors with that of the hole-doped counterparts, the corresponding result Feng15a of the doping dependence of in the hole-doped case for parameters and is also shown in the right panel of Fig. 1. One can immediately see from the results in Fig. 1 that the doping range of the SC dome in the electron-doped side is very similar to that in the hole-doped case, where with the increase of doping, is raised gradually in the underdoped regime, and reaches the maximum around the optimal doping , however, the optimized in the electron-doped side is much lower than that in the hole-doped case. With the further increase of doping, then turns into a monotonically decrease in the overdoped regime, and finally, superconductivity disappears in the heavily overdoped regime. Apart from this obvious similarity of the doping ranges of the SC domes in the electron- and hole-doped cuprate superconductors, the other typical features in Fig. 1 can be also summarized as: (a) there is no the disparity between the phase diagrams of the electron- and hole-doped cuprate superconductors; (b) superconductivity coexists with the AFSRO correlation; (c) as an evidence of the electron-hole asymmetry, in the hole-doped case is much higher than that in the electron-doped side. This electron doping dependence of in the left panel of Fig. 1 and the related typical features are well consistent with the true phase diagram observed recently on Pr1-xLaCexCuO4-δ under the proper annealing condition Song17 ; Lin20 and the corresponding SR experimental results Adachi16 . The good agreement between the present theoretical result of the phase diagram in Fig. 1 and experimental observations also show the existence of a common SC mechanism for both the electron- and hole-doped cuprate superconductors.
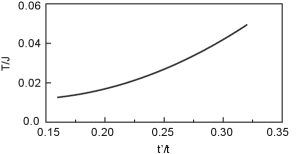
However, it should be noted that both in the electron- and hole-doped cuprate superconductors, the values of , , and are believed to vary somewhat from compound to compound Hybertsen90 ; Gooding94 ; Kim98 ; Park07 ; Nekrasov09 ; Ikeda09 ; Ikeda09a ; Harter12 ; Harter15 ; Tanaka04 ; Shih04 ; Pavarini01 , and then some differences among the different families such as the significant variation in the maximal at the optimal doping have been observed experimentally Damascelli03 ; Campuzano04 ; Fink07 ; Armitage10 . In particular, it has been shown experimentally and theoretically that the maximal (then the shape of the SC dome) for different families of the hole-doped cuprate superconductors Tanaka04 ; Shih04 ; Pavarini01 is strongly correlated with . In this case, we have made a series of calculations for the maximal at the optimal doping with different values of in the electron-doped cuprate superconductors, and the results show that the maximal is also correlated with . To see this correlation more clearly, we plot the maximal as a function of at the electron doping for in Fig. 2, where in a reasonably estimative range Hybertsen90 ; Gooding94 ; Kim98 ; Park07 ; Nekrasov09 ; Ikeda09 ; Ikeda09a ; Harter12 ; Harter15 of the parameter , the maximal is enhanced by , i.e., the maximal increases smoothly with the increase of . This anticipated result is also well consistent with the corresponding experimental data Tanaka04 of the hole-doped counterparts, and the numerical simulations Shih04 ; Pavarini01 in the same range of the parameter , where the enhancement of by has been observed experimentally and confirmed by the numerical simulations.
IV Exotic features of dressing of electrons
The dressing of the electrons due to the strong coupling of the electrons with various bosonic excitations leads to a rich variety phenomena. However, with the new phase diagram in Fig. 1, the immediate problem becomes to study which these astonishing phenomena that are universal to both the electron- and hole-doped cuprate superconductors, and how these astonishing phenomena depend on the specifics of the participating electron- or hole-like states.
IV.1 Intrinsic electron Fermi surface reconstruction
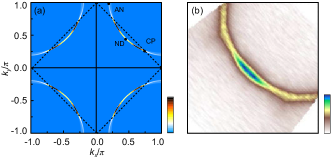
In ARPES experiments Damascelli03 ; Campuzano04 ; Fink07 , the weight of ARPES spectrum at zero energy is used to map out EFS. In other words, EFS is determined by the single-particle spectral function in Eq. (5) at zero energy to map out the locus of the maximum in the spectral weight of . For the understanding of the essential physics of an interacting system, the study of the nature of EFS is a starting point Mahan81 . This follows from a fact that the EFS topology is a fundamental ground-state property, and influences directly the low-energy transport properties. In particular, the shape of EFS in cuprate superconductors has been central to addressing the strong electron correlation effect and multiple nearly-degenerate electronic orders Neto14 ; Fujita14 ; Vishik18 ; Comin16 ; Comin14 ; Neto15 ; Neto16 . In this case, we first characterize the EFS topology. In the case without considering the electron interaction, a large EFS is characterized as a closed contour of the gapless quasiparticle excitations in momentum space, where the peaks of the quasiparticle excitation spectrum with the same weight distribute uniformly along with the EFS contour, and then the quasiparticle lifetime is infinitely long on this EFS contour. However, in the presence of the strong interaction of the electrons with a strongly dispersive spin excitation, which is manifested itself by the energy and momentum dependence of the total self-energy , the closed EFS contour is broken up into the disconnected Fermi arcs. To see this EFS reconstruction more clearly, we plot the underlying EFS map in the plane at the electron doping with for and in Fig. 3a. For comparison, the experimental result Song17 obtained from the ARPES measurement on Pr1-xLaCexCuO4-δ under the proper annealing at around the electron doping is also shown in Fig. 3b. In a qualitative analogy to the hole-doped counterparts Feng15a ; Gao18 , EFS has been reconstructed due to the strong redistribution of the spectral weight, where there are two typical regions: (a) the antinodal region, where the result shows a heavy suppression of the spectral weight, leading to that EFS at around the antinodal region is invisible. Moreover, the AF pseudogap at around the crossing points is totally absent; (b) the nodal region, where the result indicates a modest reduction of the spectral weight, and then EFS is clearly visible as the reminiscence of the EFS contour in the case without considering the electron interaction to form the Fermi arcs centered around the nodal region. However, the dressing from the quasiparticle scattering further moves the spectral weight from the Fermi arcs to the tips of the Fermi arcs, which leads to that although a quasiparticle peak emerges in the entire EFS, the spectral weight exhibits a largest value at around the tips of the Fermi arcs. This EFS reconstruction is also qualitatively consistent with the recent experimental observations on the electron-doped cuprate superconductors Horio16 ; Song17 ; Lin20 ; Horio20b , where upon the proper annealing, (a) the weight of the ARPES spectrum around the antinodal region is suppressed, and then EFS is truncated to form the Fermi arcs located around the nodal region; (b) the AF pseudogap is closed on the whole EFS, and then the quasiparticle peak is observed on the whole EFS. Moreover, as in the hole-doped case Gao19 ; Chatterjee06 ; He14 , these tips of the Fermi arcs linked up by the scattering wave vectors in the electron-doped side also can construct an octet scattering model Tan20 , and then different ordered electronic states determined by the quasiparticle scattering processes with the corresponding scattering wave vectors therefore are driven by this intrinsic EFS instability. This is also why a exotic feature in the electron-doped cuprate superconductor is the coexistence and competition between different ordered electronic states and superconductivity Armitage10 ; Neto15 ; Neto16 . In particular, it has been shown that the charge-order wave vector connecting the straight tips of the Fermi arcs smoothly increases with the increase of the electron doping Mou17 , which is consistent with the experimental results Neto16 . However, this is unlike the case in the hole-doped counterparts Gao18 ; Comin16 ; Comin14 , where the charge-order wave vector smoothly decreases with the increase of the hole doping, which is another evidence of the electron-hole asymmetry. Furthermore, we have also studied the doping dependence of the EFS reconstruction, and the results show that the EFS reconstruction can persist into the overdoped regime, also in agreement with the experimental observations Horio16 ; Song17 ; Lin20 ; Horio20b .
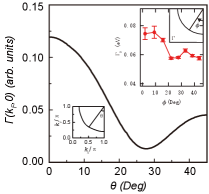
The physical origin of the EFS reconstruction in the electron-doped side is the same as that in the hole-doped case Gao18 , and can be also attributed to the highly anisotropic momentum dependence of the quasiparticle scattering rate (6). The EFS contour in momentum space is determined directly by the poles of the single-particle diagonal propagator (3a) at zero energy: , and then the spectral weight of the single-particle spectral function in Eq. (5) at EFS is governed by the inverse of the quasiparticle scattering rate . To reveal this highly anisotropic in momentum space clearly, we plot the angular dependence of along EFS from the antinode to the node at with for and in Fig. 4 in comparison with the corresponding ARPES result Horio16 observed on Pr1.3-xLa0.7CexCuO4 under the proper annealing condition (inset). Apparently, the main feature of the quasiparticle scattering rate along EFS observed from the ARPES experiment Horio16 is qualitatively reproduced, where the quasiparticle scattering rate increases as the momentum approaches the antinode, and then the strongest scattering emerges at the antinode, leading to a heavy suppression of the spectral weight at around the antinode. Moreover, the weak quasiparticle scattering occurs around the nodal region, and then the formation of the Fermi arcs is due to a modest reduction of the spectral weight around the nodal region. This strong redistribution of the spectral weight on EFS therefore induces the EFS reconstruction or instability. It is very interesting to note that the similar angular dependence of the quasiparticle scattering rate has been also observed experimentally in the hole-doped case Vishik09 , indicating a common quasiparticle scattering mechanism both in the hole- and electron-doped cuprate superconductors.
However, as seen by comparison with the experimental data Horio16 , there is also a substantial difference between theory and experiment, namely, the weakest quasiparticle scattering occurs at the crossing points in experiment Horio16 , while the calculation in the present parameters and anticipates it at the tips of the Fermi arcs. In the electron-doped cuprate superconductors, (a) as we have mentioned above in Section III, the values of , , and are different between different families Park07 ; Nekrasov09 ; Ikeda09 ; Ikeda09a ; Harter12 ; Harter15 ; (b) however, the positions of the tips of the Fermi arcs are strongly depend on the curvature of EFS, while this curvature Park07 ; Nekrasov09 ; Ikeda09 ; Ikeda09a ; Harter12 ; Harter15 is dominated by the next NN hopping . In other words, the difference in among the electron-doped cuprate superconductors Park07 ; Nekrasov09 ; Ikeda09 ; Ikeda09a ; Harter12 ; Harter15 leads to the difference of the positions of the tips of the Fermi arcs. In this case, we have also made a series of calculations for the different value of , and found that the positions of the tips of the Fermi arcs can locate exactly on the corresponding positions of the crossing points by the proper choice or adjustment of the parameter .
IV.2 Peak-dip-hump structure

The dressing of the electrons affects the quasiparticle excitation spectrum and the momentum and energy dependence of the quasiparticle scattering rate, which can be obtained respectively from the energy distribution curves and the widths of the corresponding peaks in ARPES experiments Damascelli03 ; Campuzano04 ; Fink07 . In the hole-doped cuprate superconductors, a hallmark of the spectral line-shape of the ARPES spectrum is the well-known PDH structure Dessau91 ; Norman97 ; Campuzano99 ; Wei08 ; DMou17 , which is closely associated with the EFS reconstruction, and now has been identified experimentally along the entire EFS. Since the strong coupling of the electrons with bosonic excitations has been observed experimentally in whole families of the hole-doped cuprate superconductors within a wide hole doping range, it is thus believed that the strong coupling of the electrons with bosonic excitations gives rise to the PDH structure Dessau91 ; Norman97 ; Campuzano99 ; Wei08 ; DMou17 . In particular, we Gao18 ; Gao18a have shown based on the kinetic-energy driven SC mechanism that this strong coupling of the electrons with bosonic excitations can be identified as the strong electron’s coupling to a strongly dispersive spin excitation. In this subsection, we discuss the spectral line-shape in the quasiparticle excitation spectrum of the electron-doped cuprate superconductors. We have performed a calculation for the single-particle spectral function (5), and the results of as a function of energy at (a) the antinode and (b) node for with for and are plotted in Fig. 5, where we find that the main features of the PDH structure in the electron-doped side are in a striking similarity to those obtained in the hole-doped case Dessau91 ; Norman97 ; Campuzano99 ; Wei08 ; DMou17 ; Gao18 ; Gao18a . In particular, the position of the dip in the PDH structure is shifted to the lower energy when one moves the momentum from the antinode to the node, while the coupling strength of the electrons with a strongly dispersive spin excitation appears to be weaker at around the nodal region than at around the antinodal region. Moreover, the results in Fig. 5 also show that the PDH structure is an intrinsic feature of the quasiparticle excitation spectrum in the electron-doped cuprate superconductors, and is found to be present all around EFS. Although the experimental data of the PDH structure in the quasiparticle excitation spectrum of the electron-doped cuprate superconductors under the proper annealing condition are still lacking to date, the similar PDH structure has been observed experimentally on the electron-doped cuprate superconductors under the improper annealing condition Armitage10 ; Armitage01 ; Matsui05 ; Matsui05a ; Matsui07 , while our present results in Fig. 5 are also qualitatively consistent with these experimental observations Armitage10 ; Armitage01 ; Matsui05 ; Matsui05a ; Matsui07 .

The mechanism of the PDH structure in the quasiparticle excitation spectrum of the electron-doped cuprate superconductors is also the same as in the hole-doped counterparts DMou17 ; Gao18 ; Gao18a , and is directly associated with the emergence of the corresponding sharp peak in the quasiparticle scattering rate. Following the single-particle spectral function in Eq. (5), the position of the peak in the momentum distribution curve, plotted as a function of energy in Fig. 5, is determined self-consistently by the quasiparticle dispersion,
| (7) |
while the weight of the peak (then the lifetime of the quasiparticle excitation) is dominated by the inverse of the quasiparticle scattering rate . In this case, the appearance of the dip in the PDH structure of the quasiparticle excitation spectrum along EFS is closely related to the emergence of the corresponding sharp peak in . To see this point more clearly, we plot as a function of energy at (a) the antinode and (b) the node for with for and in Fig. 6, where the sharp peaks emerge at the antinode and node, respectively. More specifically, we find that the position of the peak in at the antinode (node) in Fig. 6 is exactly corresponding to the position of the dip in the PDH structure in the quasiparticle excitation spectrum at the antinode (node) shown in Fig. 5, and then the spectral weight at around the dip is suppressed heavily by the corresponding sharp peak in , which leads to form the PDH structure in the quasiparticle excitation spectrum. In other words, the striking PDH structure in the quasiparticle excitation spectrum shown in Fig. 5 is caused directly by the the emergence of the sharp peak in shown in Fig. 6. Furthermore, we have also discussed the spectral line-shape in the electron-doped cuprate superconductors in the normal-state, and found the sharp peak in that can persist into the normal-state, indicating that the PDH structure is totally unrelated to superconductivity, as the PDH structure in the hole-doped counterparts Dessau91 ; Norman97 ; Campuzano99 ; Wei08 ; DMou17 .
IV.3 Dispersion kink
The strong coupling of the electrons and various bosonic excitations in cuprate superconductors manifested itself as a slope change (or a kink) in the quasiparticle dispersion Damascelli03 ; Campuzano04 ; Fink07 . In the hole-doped cuprate superconductors, the quasiparticle dispersion displays a kink at all around EFS Kaminski01 ; Lanzara01 ; Kordyuk06 ; Iwasawa08 ; Plumb13 , with the energy range meV at which the kink appears. In spite of the extensive studies, the controversy still exists on what bosonic mode causes the dispersion kink. In the recent studies for the hole-doped case Liu20 , we have shown within the framework of the kinetic-energy driven superconductivity that the quasiparticle dispersion is affected by a strongly dispersive spin excitation, and then the dispersion kink associated with the dressing of the electrons is electronic in nature. On the electron-doped side, although the experimental results of the PDH structure in the quasiparticle excitation spectrum under the proper annealing condition are still lacking to date as we have mentioned above in Section I, the dispersion kinks in the electron-doped cuprate superconductor Pr1.3-xLa0.7CexCuO4 under the proper annealing condition along the nodal and antinodal directions have been detected very recently from the ARPES spectra Horio20b , where the bare band structure Horio20b ; Horio18a has been well fitted in terms of the single-band tight-binding model with . In this subsection, we discuss the nature of the dispersion kink in the electron-doped cuprate superconductors, and adopt the parameters and in the - model (1) for a quantitative or semiquantitative comparison between the theory and experiment.
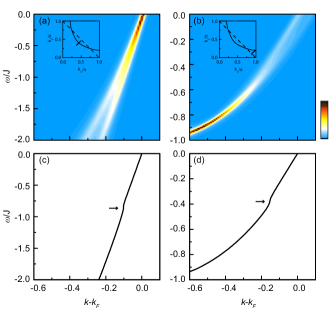
In Fig. 7, we plot the intensity map of the single-particle spectral function as a function of binding-energy along (a) the nodal cut and (b) the antinodal cut at with for and in the upper panel . In the lower panel, we plot the corresponding quasiparticle dispersions along (c) the nodal cut and (d) the antinodal cut extracted from the positions of the lowest-energy quasiparticle excitation peaks in (a) and (b), respectively. The arrow in Fig. 7 marks the kink where the the linear quasiparticle dispersion is separated as the low-energy and high-energy ranges with different slopes. It is especially interesting to note that these results of the dispersion kink in the electron-doped cuprate superconductors shown in Fig. 7 are quite similar to those obtained in the hole-doped counterparts Kaminski01 ; Lanzara01 ; Kordyuk06 ; Iwasawa08 ; Plumb13 ; Liu20 . In particular, with a reasonably estimative value of meV, the quasiparticle dispersion deviates from the low-energy linear dispersion at around the kink energy meV along the nodal cut, while this kink energy occurs at around meV along the antinodal cut, which are semiquantitatively consistent with the corresponding results Horio20b observed on the electron-doped cuprate superconductor Pr1.3-xLa0.7CexCuO4 under the proper annealing condition along the nodal and antinodal directions, respectively. The above these results in Fig. 7 also indicate that although the kink in the quasiparticle dispersion is present all around EFS, the kink energy decreases when the cut moves from the nodal region to the antinodal region. Moreover, it should be noted that the coupling of the electrons with bosonic excitations has been also observed early in all the electron-doped cuprate superconductors under the improper annealing condition Santander-Syro09 ; Schmitt08 ; Park08a ; Armitage03 , where the quasiparticle dispersions present the kinks at around meV along both the antinodal and nodal cuts, which are also semiquantitatively consistent with our present results in Fig. 7.
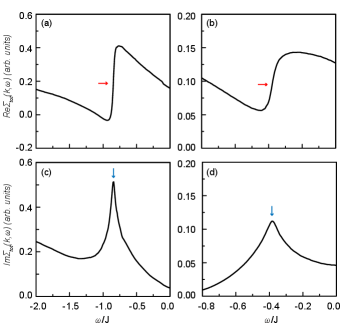
A natural and important question is which bosonic mode causes the dispersion kink in the electron-doped cuprate superconductors? Within the framework of the kinetic-energy driven superconductivity, the dispersion kink in the electron-doped cuprate superconductors arises from the strong coupling between the electrons and a strongly dispersive spin excitation. This follows a fact that from the quasiparticle dispersion in Eq. (7), the dispersion kink shown in Fig. 7 does not originate from the single-electron band energy , but it is due to the slope change in the real part of the total self-energy , while the drop seen at around the kink is directly associated with the corresponding peak in the quasiparticle scattering rate in Eq. (6) [then the imaginary part of the total self-energy]. To further explore how the total self-energy generates the dispersion kink, we plot the real part of the total self-energy as a function of binding-energy along (a) the nodal dispersion and (b) the antinodal dispersion as shown in Fig. 7c and Fig. 7d, respectively, at with for and in the upper panel of Fig. 8, where the red arrow indicates the inflection point (then the point of the slope change in the quasiparticle dispersion). In the lower panel, we plot the corresponding quasiparticle scattering rate as a function of binding-energy along (c) the nodal dispersion and (d) the antinodal dispersion, where the blue arrow denotes the peak position (then the point of the intensity depletion in the quasiparticle dispersion). It is obvious that a well-pronounced peak in is clearly visible with a corresponding inflection point in that appears at the exactly same energy in . This sharp peak in suppresses heavily the spectral weight at around the inflection point. More importantly, we find that the position of the dispersion kink in Fig. 7 matches exactly with the position of the inflection point in [then the position of the peak in ] in Fig. 8. In other words, the emergence of the dispersion kink is determined by both the inflection point in and the well-pronounced peak in . This is why the dispersion kink marks the crossover between two different slopes, while the weak spectral intensity appears always at around the kink position Santander-Syro09 ; Schmitt08 ; Park08a ; Armitage03 .
IV.4 Peak-structure in self-energy
In ARPES experiments Damascelli03 ; Campuzano04 ; Fink07 , the energy distribution curves are observed when the photoemission intensity is measured at constant momentum, while the momentum distribution curves are observed when the photoemission intensity is measured at constant energy. The information of the energy and momentum dependence of the electron self-energy then can be extracted in terms of the single-particle spectral function (5) by analyzing the spectral intensity of the energy and momentum distribution curves. However, as shown in the single-particle spectral function (5), only the total self-energy can be extracted directly from ARPES experiments Damascelli03 ; Campuzano04 ; Fink07 . In particular, for our exploration of the strongly dispersive spin excitation coupling in the kinetic-energy driven SC mechanism that is how the normal and anomalous self-energy effects compete in the SC-state, it thus is crucial to extract the normal and the anomalous self-energies separately. This also follows a basic fact that in the kinetic-energy driven superconductivity Feng15a ; Feng0306 ; Feng12 ; Feng15 , the SC-state is controlled by both the electron pair gap and single-particle coherence, where the single-particle coherence is dominated by the normal self-energy , and therefore antagonizes superconductivity, while the energy and momentum dependent electron pair gap is determined completely by the anomalous self-energy , and therefore is corresponding to the energy for breaking an electron pair. In this case, if both the normal and anomalous self-energies are deduced from the experimental data, it can be used to examine the microscopic theory of the kinetic-energy driven superconductivity and understand the essential physics of cuprate superconductors.
In the hole-doped cuprate superconductors, the machine learning technique has been applied recently to deduce both the normal and anomalous self-energies from the experimental data of the ARPES spectra observed in Bi2Sr2CaCu2O8+δ at the optimum doping and Bi2Sr2CuO6+δ in the underdoped regime Yamaji19 , and the deduced results show clearly that both the normal and anomalous self-energies exhibit the sharp low-energy peak-structures. Moreover, these machine learning ’experimental’ results confirm that the peak in the anomalous self-energy makes a dominant contribution to the SC gap, and therefore provide a decisive testimony for the origin of superconductivity Yamaji19 . In the very recent studies Liu20a , we have made a comparison of these deduced normal and anomalous self-energies in Ref. Yamaji19, with those obtained based on the kinetic-energy driven SC mechanism, and then show explicitly that the interaction between electrons by the exchange of spin excitations generates the sharp low-energy peak-structures both in the normal and anomalous self-energies, in striking agreement with the corresponding results in the normal and anomalous self-energies deduced via machine learning ’experiments’ Yamaji19 . In this subsection, we analyze the normal and anomalous self-energies in the electron-doped cuprate superconductors, and then compare these normal and anomalous self-energies with those obtained in the hole-doped counterparts Yamaji19 ; Liu20a .
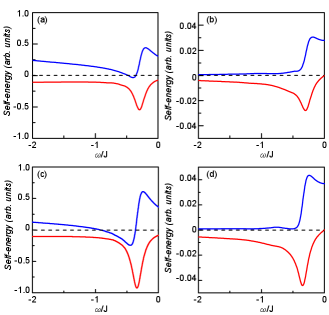
In Fig. 9, we plot (a) the real (blue line) and imaginary (red line) parts of the normal self-energy and (b) the real (blue line) and imaginary (red line) parts of the anomalous self-energy at the antinode as a function of energy in the electron doping with for and . For a better comparison, the corresponding results Liu20a of (c) the real and imaginary parts of the normal self-energy and (d) the real and imaginary parts of the anomalous self-energy at the antinode as a function of energy in the hole doping with for and are also shown in Fig. 9. Surprisedly, both the normal and anomalous self-energies in the electron-doped cuprate superconductors also exhibit the sharp low-energy peak-structures. More specifically, the main features of these low-energy peak-structures are in a stark similarity with the corresponding low-energy peak-structures in the normal and anomalous self-energies of the hole-doped cuprate counterparts obtained based on the kinetic energy driven superconductivity Liu20a , and deduced from the ARPES spectra via machine learning Yamaji19 . This is why the absence of the disparity between the phase diagrams of the electron- and hole-doped cuprate superconductors can be observed experimentally Song17 ; Lin20 ; Horio20b . In the SC-state, the pairing force and electron pair order parameter have been incorporated into the anomalous self-energy , which is identified as the SC gap, and therefore describes the strength of the electron pair. In this case, the dominant contribution to the strength of the electron pair arises from the sharp low-energy peaks both in and Yamaji19 ; Liu20a . On the other hand, from the total self-energy in Eq. (4), the dressing of the electrons are mainly dominated by the normal self-energy , indicating that the sharp low-energy peak in offsets mainly the single-electron band energy, while the sharp low-energy peak in governs mainly the lifetime of the quasiparticle excitation Liu20a . However, the sharp low-energy peak in the anomalous self-energy disappears in the normal-state, while the sharp low-energy peak in the normal self-energy can persist into the normal-state. This is also why the exotic features, including the intrinsic EFS reconstruction, the PDH structure in the quasiparticle excitation spectrum, the dispersion kink, and the ARPES autocorrelation and its connection with the quasiparticle scattering interference Tan20 , arisen from the dressing of the electrons that emerge in the SC-state also appear in the normal-state.
For a further understanding of the essential physics of the electron-doped cuprate superconductors, we have also studied the doping and momentum dependence of the low-energy peak structures both in the normal and anomalous self-energies, and all the obtained results are consistent with the corresponding results obtained in the hole-doped counterparts Yamaji19 ; Liu20a . We therefore complete the picture of the dressing of the electrons for the electron-doped cuprate superconductors, and show the existence of the common origin of the anisotropic dressing of the electrons both in the electron- and hole-doped cuprate superconductors, i.e., the dressing of the electrons arises from the interaction of the electrons with a strongly dispersive spin excitation. Since the remarkable low-energy peak-structures both in the normal and anomalous self-energies of the hole-doped cuprate superconductors Liu20a are well consistent with those deduced via machine learning ’experiments’ Yamaji19 , we therefore predict that the similar low-energy peak-structures both in the normal and anomalous self-energies can be also deduced from the experimental data of the ARPES spectra observed on the electron-doped cuprate superconductors in the proper annealing condition via machine learning.
V Conclusions
Within the framework of the kinetic-energy driven superconductivity, we have studied the phase diagram of the electron-doped cuprate superconductors and the related exotic features of the anisotropic dressing of the electrons. Our results show that although the optimized in the electron-doped superconductors is much smaller than that in the hole-doped counterparts, the electron- and hole-doped cuprate superconductors rather resemble each other in the doping range of the SC dome, indicating an absence of the disparity between the phase diagrams of the electron- and hole-doped cuprate superconductors. In particular, the anisotropic dressing of the electrons due to the strong electron’s coupling to a strongly dispersive spin excitation induces a EFS reconstruction, where the closed EFS contour in the case without considering the strong electron interaction is broken up into the disconnected Fermi arcs centered around the nodal region, in qualitative agreement with the available experimental data. Moreover, we reveal the spin excitation effect in the quasiparticle excitation spectrum, where the dip in the PDH structure developed in the quasiparticle excitation spectrum at around the antinodal (nodal) region is directly related to the corresponding sharp peak in the antinodal (nodal) quasiparticle scattering rate, while the appearance of the dispersion kink is always associated with the emergence of the inflection point in the real part of the total self-energy and the sharp peak in the quasiparticle scattering rate. By comparing directly with the corresponding results in the hole-doped cuprate superconductors, our present results therefore show that the EFS reconstruction to form the Fermi arcs, the PDH structure in the quasiparticle excitation spectrum, and the dispersion kink, are the intrinsic properties both of the electron- and hole-doped cuprate superconductors. Although some subtle differences between the electron- and hole-doped cuprate superconductors appear due to the electron-hole asymmetry, the coupling of the electrons with a strongly dispersive spin excitation is the common origin for the anisotropic dressing of the electrons both in the electron- and hole-doped cuprate superconductors. The theory also predicts that both the normal and anomalous self-energies exhibit the notable low-energy peak-structures, which should be verified by future machine learning ’experiments’.
Acknowledgements
This work was supported by the National Key Research and Development Program of China under Grant No. 2016YFA0300304, and the National Natural Science Foundation of China under Grant Nos. 11974051 and 11734002.
References
- (1) J. G. Bednorz and K. A. Müller, Z. Phys. B 64, 189 (1986).
- (2) Y. Tokura, H. Takagi, and S. Uchida, Nature 337, 345 (1989).
- (3) P. W. Anderson, Science 235, 1196 (1987).
- (4) See, e.g., the review, Masaki Fujita, Haruhiro Hiraka, Masaaki Matsuda, Masato Matsuura, John M. Tranquada, Shuichi Wakimoto, Guangyong Xu, and Kazuyoshi Yamada, J. Phys. Soc. Jpn. 81, 011007 (2012).
- (5) See, e.g., the review, A. Damascelli, Z. Hussain, and Z.-X. Shen, Rev. Mod. Phys. 75, 473 (2003).
- (6) See, e.g., the review, J. C. Campuzano, M. R. Norman, M. Randeira, in Physics of Superconductors, vol. II, edited by K. H. Bennemann and J. B. Ketterson (Springer, Berlin Heidelberg New York, 2004), p. 167.
- (7) See, e.g., the review, Joerg Fink, Sergey Borisenko, Alexander Kordyuk, Andreas Koitzsch, Jochen Geck, Volodymyr Zabalotnyy, Martin Knupfer, Bernd Buechner, and Helmut Berger, in Lecture Notes in Physics, vol. 715, edited by Stefan Hüfner (Springer-Verlag Berlin Heidelberg, 2007), p. 295.
- (8) See, e.g., the review, N. P. Armitage, P. Fournier, and R. L. Greene, Rev. Mod. Phys. 82, 2421 (2010).
- (9) N. P. Armitage, D. H. Lu, C. Kim, A. Damascelli, K. M. Shen, F. Ronning, D. L. Feng, P. Bogdanov, Z.-X. Shen, Y. Onose, Y. Taguchi, Y. Tokura, P. K. Mang, N. Kaneko, and M. Greven, Phys. Rev. Lett. 87, 147003 (2001).
- (10) H. Matsui, K. Terashima, T. Sato, T. Takahashi, S.-C. Wang, H.-B. Yang, H. Ding, T. Uefuji, and K. Yamada, Phys. Rev. Lett. 94, 047005 (2005).
- (11) H. Matsui, K. Terashima, T. Sato, T. Takahashi, M. Fujita, and K. Yamada, Phys. Rev. Lett. 95, 017003 (2005).
- (12) H. Matsui, T. Takahashi, T. Sato, K. Terashima, H. Ding, T. Uefuji and K. Yamada, Phys. Rev. B 75, 224514 (2007).
- (13) A. F. Santander-Syro, M. Ikeda, T. Yoshida, A. Fujimori, K. Ishizaka, M. Okawa, S. Shin, R. L. Greene, and N. Bontemps, Phys. Rev. Lett. 106, 197002 (2011).
- (14) Dongjoon Song, Seung Ryong Park, Chul Kim, Yeongkwan Kim, Choonshik Leem, Sungkyun Choi, Wonsig Jung, Yoonyoung Koh, Garam Han, Yoshiyuki Yoshida, Hiroshi Eisaki, D. H. Lu, Z.-X. Shen, and Changyoung Kim, Phys. Rev. B 86, 144520 (2012).
- (15) Tadashi Adachi, Yosuke Mori, Akira Takahashi, Masatsune Kato, Terukazu Nishizaki, Takahiko Sasaki, Norio Kobayashi, and Yoji Koike, J. Phys. Soc. Jpn. 82, 063713 (2013).
- (16) See, e.g., the review, T. Adachi, T. Kawamata, Y. Koike, Condensed Matter 2, 23 (2017).
- (17) M. Horio, T. Adachi, Y. Mori, A. Takahashi, T. Yoshida, H. Suzuki, L. C. C. Ambolode II, K. Okazaki, K. Ono, H. Kumigashira, H. Anzai, M. Arita, H. Namatame, M. Taniguchi, D. Ootsuki, K. Sawada, M. Takahashi, T. Mizokawa, Y. Koike and A. Fujimori, Nat. Commun. 7, 10567 (2016).
- (18) Dongjoon Song, Garam Han, Wonshik Kyung, Jeongjin Seo, Soohyun Cho, Beom Seo Kim, Masashi Arita, Kenya Shimada, Hirofumi Namatame, Masaki Taniguchi, Y. Yoshida, H. Eisaki, Seung Ryong Park and C. Kim, Phys. Rev. Lett. 118, 137001 (2017).
- (19) C. Lin, T. Adachi, M. Horio, T. Ohgi, M.A. Baqiya, T. Kawamata, H. Sato, T. Sumura, K. Koshiishi, S. Nakata, G. Shibata, K. Hagiwara, M. Suzuki, K. Ono, K. Horiba, H. Kumigashira, S. Ideta, K. Tanaka, Y. Koike, A. Fujimori, arXiv:2006.04524.
- (20) M. Horio, K. P. Kramer, Q. Wang, A. Zaidan, K. von Arx, D. Sutter, C. E. Matt, Y. Sassa, N. C. Plumb, M. Shi, A. Hanff, S. K. Mahatha, H. Bentmann, F. Reinert, S. Rohlf, F. K. Diekmann, J. Buck, M. Kalläne, K. Rossnagel, E. Rienks, V. Granata, R. Fittipaldi, A. Vecchione, T. Ohgi, T. Kawamata, T. Adachi, Y. Koike, A. Fujimori, M. Hoesch, J. Chang, arXiv:2006.13119.
- (21) I. Vekhter and C. M. Varma, Phys. Rev. Lett. 90, 237003 (2003).
- (22) See, e.g., the review, J. P. Carbotte, T. Timusk, and J. Hwang, Rep. Prog. Phys. 74, 066501 (2011).
- (23) See, e.g., the review, Han-Yong Choi and Jin Mo Bok, Int. J. Mod. Phys. B 32, 1840026 (2018).
- (24) Eduardo H. da Silva Neto, Pegor Aynajian, Alex Frano, Riccardo Comin, Enrico Schierle, Eugen Weschke, András Gyenis, Jinsheng Wen, John Schneeloch, Zhijun Xu, Shimpei Ono, Genda Gu, Mathieu Le Tacon, and Ali Yazdani, Science 343, 393 (2014).
- (25) K. Fujita, Chung Koo Kim, Inhee Lee, Jinho Lee, M. H. Hamidian, I. A. Firmo, S. Mukhopadhyay, H. Eisaki, S. Uchida, M. J. Lawler, E.-A. Kim, J. C. Davis, Science 344, 612 (2014).
- (26) See, e.g., the review, I. M. Vishik, Rep. Prog. Phys. 81, 062501 (2018).
- (27) See, e.g., the review, Riccardo Comin and Andrea Damascelli, Annu. Rev. Condens. Matter Phys. 7, 369 (2016).
- (28) R. Comin, A. Frano, M. M. Yee, Y. Yoshida, H. Eisaki, E. Schierle, E. Weschke, R. Sutarto, F. He, A. Soumyanarayanan, Yang He, M. Le Tacon, I. S. Elfimov, Jennifer E. Hoffman, G. A. Sawatzky, B. Keimer and A. Damascelli, Science 343, 390 (2014).
- (29) D. S. Dessau, B. O. Wells, Z.-X. Shen, W. E. Spicer, A. J. Arko, R. S. List, D. B. Mitzi, and A. Kapitulnik, Phys. Rev. Lett. 66, 2160 (1991).
- (30) M. R. Norman, H. Ding, J. C. Campuzano, T. Takeuchi, M. Randeria, T. Yokoya, T. Takahashi, T. Mochiku, and K. Kadowaki, Phys. Rev. Lett. 79, 3506 (1997).
- (31) J. C. Campuzano, H. Ding, M. R. Norman, H. M. Fretwell, M. Randeria, A. Kaminski, J. Mesot, T. Takeuchi, T. Sato, T. Yokoya, T. Takahashi, T. Mochiku, K. Kadowaki, P. Guptasarma, D. G. Hinks, Z. Konstantinovic, Z. Z. Li, and H. Raffy, Phys. Rev. Lett. 83, 3709 (1999).
- (32) J. Wei, Y. Zhang, H. W. Ou, B. P. Xie, D. W. Shen, J. F. Zhao, L. X. Yang, M. Arita, K. Shimada, H. Namatame, M. Taniguchi, Y. Yoshida, H. Eisaki, and D. L. Feng, Phys. Rev. Lett. 101, 097005 (2008).
- (33) Daixiang Mou, Adam Kaminski, and Genda Gu, Phys. Rev. B 95, 174501 (2017).
- (34) A. Kaminski, M. Randeria, J. C. Campuzano, M. R. Norman, H. Fretwell, J. Mesot, T. Sato, T. Takahashi, and K. Kadowaki, Phys. Rev. Lett. 86, 1070 (2001).
- (35) A. Lanzara, P. V. Bogdanov, X. J. Zhou, S. A. Kellar, D. L. Feng, E. D. Lu, T. Yoshida, H. Eisaki, A. Fujimori, K. Kishio, J.-I. Shimoyama, T. Noda, S. Uchida, Z. Hussain, and Z.-X. Shen, Nature 412, 510 (2001).
- (36) A. A. Kordyuk, S. V. Borisenko, V. B. Zabolotnyy, J. Geck, M. Knupfer, J. Fink, B. Büchner, C. T. Lin, B. Keimer, H. Berger, A. V. Pan, Seiki Komiya, and Yoichi Ando, Phys. Rev. Lett. 97, 017002 (2006).
- (37) H. Iwasawa, J. F. Douglas, K. Sato, T. Masui, Y. Yoshida, Z. Sun, H. Eisaki, H. Bando, A. Ino, M. Arita, K. Shimada, H. Namatame, M. Taniguchi, S. Tajima, S. Uchida, T. Saitoh, D. S. Dessau, and Y. Aiura, Phys. Rev. Lett. 101, 157005 (2008).
- (38) N. C. Plumb, T. J. Reber, H. Iwasawa, Y. Cao, M. Arita, K. Shimada, H. Namatame, M. Taniguchi, Y. Yoshida, H. Eisaki, Y. Aiura and D. S. Dessau, New J. Phys. 15, 113004 (2013).
- (39) Shiping Feng, Lülin Kuang, and Huaisong Zhao, Physica C 517, 5 (2015).
- (40) Deheng Gao, Yiqun Liu, Huaisong Zhao, Yingping Mou, and Shiping Feng, Physica C 551, 72 (2018).
- (41) Deheng Gao, Yingping Mou, and Shiping Feng, J. Low Temp. Phys. 192, 19 (2018).
- (42) Deheng Gao, Yingping Mou, Yiqun Liu, Shuning Tan, and Shiping Feng, Phil. Mag. 99, 752 (2019).
- (43) Yiqun Liu, Yu Lan, Yingping Mou, and Shiping Feng, Physica C 576, 1353661 (2020).
- (44) M. R. Norman, H. Ding, M. Randeria, J. C. Campuzano, T. Yokoya, T. Takeuchi, T. Takahashi, T. Mochiku, K. Kadowaki, P. Guptasarma, and D. G. Hinks, Nature, 157 392 (1998).
- (45) A. Kanigel, U. Chatterjee, M. Randeria, M. R. Norman, S. Souma, M. Shi, Z. Z. Li, H. Raffy, and J. C. Campuzano, Phys. Rev. Lett. 99, 157001 (2007).
- (46) K. Nakayama, T. Sato, Y. Sekiba, K. Terashima, P. Richard, T. Takahashi, K. Kudo, N. Okumura, T. Sasaki, and N. Kobayashi, Phys. Rev. Lett. 102, 227006 (2009).
- (47) Takeshi Kondo, Ari D. Palczewski, Yoichiro Hamaya, Tsunehiro Takeuchi, J. S. Wen, Z. J. Xu, Genda Gu, and Adam Kaminski, Phys. Rev. Lett. 111, 157003 (2013).
- (48) U. Chatterjee, M. Shi, A. Kaminski, A. Kanigel, H. M. Fretwell, K. Terashima, T. Takahashi, S. Rosenkranz, Z. Z. Li, H. Raffy, A. Santander-Syro, K. Kadowaki, M. R. Norman, M. Randeria, and J. C. Campuzano, Phys. Rev. Lett. 96, 107006 (2006).
- (49) Yang He, Yi Yin, M. Zech, Anjan Soumyanarayanan, Michael M. Yee, Tess Williams, M. C. Boyer, Kamalesh Chatterjee, W. D. Wise, I. Zeljkovic, Takeshi Kondo, T. Takeuchi, H. Ikuta, Peter Mistark, Robert S. Markiewicz, Arun Bansil, Subir Sachdev, E. W. Hudson, J. E. Hoffman, Science 344, 608 (2014).
- (50) See, e.g., the review, P. A. Lee, N. Nagaosa, and X.-G. Wen, Rev. Mod. Phys. 78, 17 (2006).
- (51) See, e.g., the review, B. Edegger, V. N. Muthukumar, and C. Gros, Adv. Phys. 56, 927 (2007).
- (52) Mark S. Hybertsen, E. B. Stechel, M. Schluter, and D. R. Jennison, Phys. Rev. B 41, 11068 (1990).
- (53) R. J. Gooding, K. J. E. Vos, and P. W. Leung, Phys. Rev. B 50, 12866 (1994).
- (54) C. Kim, P. J. White, Z.-X. Shen, T. Tohyama, Y. Shibata, S. Maekawa, B. O. Wells, Y. J. Kim, R. J. Birgeneau, and M. A. Kastner, Phys. Rev. Lett. 80, 4245 (1998).
- (55) Shiping Feng, Jihong Qin, and Tianxing Ma, J. Phys.: Condens. Matter 16, 343 (2004); Shiping Feng, Z. B. Su, and L. Yu, Phys. Rev. B 49, 2368 (1994).
- (56) See, e.g., the review, Shiping Feng, Yu Lan, Huaisong Zhao, Lülin Kuang, Ling Qin, and Xixiao Ma, Int. J. Mod. Phys. B 29, 1530009 (2015).
- (57) Shiping Feng, Phys. Rev B 68, 184501 (2003); Shiping Feng, Tianxing Ma, and Huaiming Guo, Physica C 436, 14 (2006).
- (58) Shiping Feng, Huaisong Zhao, and Zheyu Huang, Phys. Rev. B 85, 054509 (2012); Phys. Rev. B 85, 099902(E) (2012).
- (59) Shuning Tan, Yingping Mou, Yiqun Liu, and Shiping Feng, J. Supercond. Nov. Magn. 33, 2305-2311 (2020); Shuning Tan, Yingping Mou, Yiqun Liu, and Shiping Feng, Mod. Phys. Lett. B 34, 2040053 (2020).
- (60) G. M. Eliashberg, Sov. Phys. JETP 11, 696 (1960).
- (61) J. L. Tallon, C. Bernhard, H. Shaked, R. L. Hitterman, and J. D. Jorgensen, Phys. Rev. B 51, 12911 (1995).
- (62) Tadashi Adachi, Akira Takahashi, Kensuke M. Suzuki, Malik A. Baqiya, Takuya Konno, Tomohisa Takamatsu, Masatsune Kato, Isao Watanabe, Akihiro Koda, Masanori Miyazaki, Ryosuke Kadono, and Yoji Koike, J. Phys. Soc. Jpn. 85 114716 (2016).
- (63) S. R. Park, Y. S. Roh, Y. K. Yoon, C. S. Leem, J. H. Kim, B. J. Kim, H. Koh, H. Eisaki, N. P. Armitage, and C. Kim, Phys. Rev. B 75, 060501(R) (2007).
- (64) I. A. Nekrasov, N. S. Pavlov, E. Z. Kuchinskii, M. V. Sadovskii, Z. V. Pchelkina, V. B. Zabolotnyy, J. Geck, B. Büchner, S. V. Borisenko, D. S. Inosov, A. A. Kordyuk, M. Lambacher, and A. Erb, Phys. Rev. B 80, 140510(R) (2009).
- (65) M. Ikeda, T. Yoshida, A. Fujimori, M. Kubota, K. Ono, Hena Das, T. Saha-Dasgupta, K. Unozawa, Y. Kaga, T. Sasagawa, and H. Takagi, Phys. Rev. B 80, 014510 (2009).
- (66) M. Ikeda, T. Yoshida, A. Fujimori, M. Kubota, K. Ono, Y. Kaga, T. Sasagawa, and H. Takagi, Phys. Rev. B 80, 184506 (2009).
- (67) John W. Harter, Luigi Maritato, Daniel E. Shai, Eric J. Monkman, Yuefeng Nie, Darrell G. Schlom, and Kyle M. Shen, Phys. Rev. Lett. 109, 267001 (2012).
- (68) John W. Harter, Luigi Maritato, Daniel E. Shai, Eric J. Monkman, Yuefeng Nie, Darrell G. Schlom, and Kyle M. Shen, Phys. Rev. B 92, 035149 (2015).
- (69) K. Tanaka, T. Yoshida, A. Fujimori, D. H. Lu, Z.-X. Shen, X.-J. Zhou, H. Eisaki, Z. Hussain, S. Uchida, Y. Aiura, K. Ono, T. Sugaya, T. Mizuno, and I. Terasaki, Phys. Rev. B 70, 092503 (2004).
- (70) C. T. Shih, T. K. Lee, R. Eder, C.-Y. Mou, and Y. C. Chen, Phys. Rev. Lett. 92, 227002 (2004).
- (71) E. Pavarini, I. Dasgupta, T. Saha-Dasgupta, O. Jepsen, and O. K. Andersen, Phys. Rev. Lett. 87, 047003 (2001).
- (72) See, e.g., G. D. Mahan, Many-Particle Physics, (Plenum Press, New York, 1981).
- (73) Eduardo H. da Silva Neto, Riccardo Comin, Feizhou He, and Ronny Sutarto, Yeping Jiang, Richard L. Greene, George A. Sawatzky and Andrea Damascelli, Science 347, 282 (2015).
- (74) Eduardo H. da Silva Neto, Biqiong Yu, Matteo Minola, Ronny Sutarto, Enrico Schierle, Fabio Boschini, Marta Zonno, Martin Bluschke, Joshua Higgins, Yangmu Li, Guichuan Yu, Eugen Weschke, Feizhou He, Mathieu Le Tacon, Richard L. Greene, Martin Greven, George A. Sawatzky, Bernhard Keimer and Andrea Damascelli, Sci. Adv. 2, e1600782 (2016).
- (75) Yingping Mou and Shiping Feng, Phil. Mag. 97, 3361 (2017).
- (76) I. M. Vishik, E. A. Nowadnick, W. S. Lee, Z. X. Shen, B. Moritz, T. P. Devereaux, K. Tanaka, T. Sasagawa, and T. Fujii, Nat. Phys. 5, 718 (2009).
- (77) M. Horio, S. Sakai, K. Koshiishi, Y. Nonaka, H. Suzuki, J. Xu, M. Hashimoto, D. Lu, Z.-X. Shen, T. Ohgi, T. Konno, T. Adachi, Y. Koike, M. Imada, A. Fujimori, arXiv:1801.04247.
- (78) A. F. Santander-Syro, T. Kondo, J. Chang, A. Kaminski, S. Pailhes, M. Shi, L. Patthey, A. Zimmers, B. Liang, P. Li, R. L. Greene, arXiv:0903.3413.
- (79) F. Schmitt, W. S. Lee, D.-H. Lu, W. Meevasana, E. Motoyama, M. Greven, and Z.-X. Shen, Phys. Rev. B 78, 100505(R) (2008).
- (80) Seung Ryong Park, D. J. Song, C. S. Leem, Chul Kim, C. Kim, B. J. Kim, and H. Eisaki, Phys. Rev. Lett. 101, 117006 (2008).
- (81) N. P. Armitage, D. H. Lu, C. Kim, A. Damascelli, K. M. Shen, F. Ronning, D. L. Feng, P. Bogdanov, X. J. Zhou, W. L. Yang, Z. Hussain, P. K. Mang, N. Kaneko, M. Greven, Y. Onose, Y. Taguchi, Y. Tokura, and Z.-X. Shen, Phys. Rev. B 68, 064517 (2003).
- (82) Youhei Yamaji, Teppei Yoshida, Atsushi Fujimori, and Masatoshi Imada, arXiv:1903.08060.
- (83) Yiqun Liu, Yu Lan, and Shiping Feng, arXiv:2004.06489.