Angle structure on general hyperbolic -manifolds
Abstract
Let be a non-compact hyperbolic -manifold with finite volume and totally geodesic boundary components. By subdividing mixed ideal polyhedral decompositions of , under some certain topological conditions, we prove that has an ideal triangulation which admits an angle structure.
1 Introduction
Thurston’s geometrization conjecture (proved by Perelman [33]-[35], or see [6],[20],[31] for more details) tells us that any -manifold can be decomposed via J-S-J splitting into distinct geometric pieces, the majority of which are hyperbolic. A -manifold with a hyperbolic geometric structure is termed as a hyperbolic -manifold. Thus, determining the existence of a hyperbolic structure on a given -manifold is a significant research topic. Thurston [41] introduced the concept of ideal triangulations on -manifolds and proved that a solution of the hyperbolic gluing equations on the ideal triangulation can yield a hyperbolic structure on the -manifold. However, solving the hyperbolic gluing equations on general ideal triangulations is extremely challenging. In the 1990s, Casson [21] and Rivin [38] discovered a powerful technique for solving Thurston’s gluing equations. By introducing the concept of angle structures on ideal triangulations, they proved that if a maximal volume angle structure exists, it provides solutions to Thurston’s gluing equations, thereby yielding a hyperbolic structure on the -manifold. The converse is also true, and one can find a self-contained exposition of Casson-Rivin’s program in [9].
An angle structure on an ideal triangulation refers to assigning real numbers (called dihedral angle) in the interval at each edge of each ideal tetrahedron such that the sum of the dihedral angles at each ideal vertex is and the sum of dihedral angles around each edge is . Kang-Rubinstein [19] extended the real numbers assigned at each edge into , and called this structure as semi-angle structure. If the dihedral angles are only taken values or , then the structure is termed as taut structure by Lackanby [23]. Luo-Tillmann [26] further extended the assignment of dihedral angles to the whole real numbers , which is defined as generalized angle structure.
Conversely, to study the geometry and topology of hyperbolic -manifolds, a natural approach is to investigate their geometric ideal tetrahedra decompositions. The existence of geometric ideal triangulations are very important for studying hyperbolic 3-manifolds. On the one hand, Thurston’s proof of the famous Hyperbolic Dehn Filling Theorem takes it for granted that each cusped hyperbolic 3-manifold has a geometric ideal triangulation, see [5], [29], [36] for example. On the other hand, geometric ideal triangulations ensures that all three-dimensional hyperbolic manifolds can be constructed from ideal tetrahedra with the help of Thurston’s gluing equations. The first breakthrough on geometric ideal decomposition is due to Epstein-Penner [7]. They introduced canonical geometric ideal polyhedral decompositions on cusped hyperbolic manifolds with finite volume. Similarly, Kojima [28] obtained truncated hyperideal polyhedral decompositions on compact hyperbolic -manifolds with totally geodesic boundary. Recently, we [12] obtained mixed ideal polyhedral decompositions on non-compact hyperbolic -manifolds with finite volume and totally geodesic boundary. In all known examples, a cusped hyperbolic manifold admits at least one geometric ideal triangulation, but whether this holds true for arbitrary cusped hyperbolic -manifold is still an open question. As was pointed by Guéritaud and Schleimer in [15], “it is a difficult problem in general. General results are known only when is restricted to belong to certain classes of manifolds: punctured-torus bundles, two-bridge link complements, certain arborescent link complements and related objects, or covers of any of these spaces” (see [1]-[3], [13]-[14], [16], [18], [22], [32] for instance). For compact three-dimensional manifolds with boundary, Feng-Ge-Hua [8] established a deep connection between the combinatorial Ricci flow and geometric ideal triangulations, and proved that any topological ideal triangulation with degree greater than or equal to 10 are geometric. Although it was difficult to obtain geometric triangulations directly, Luo-Schleimer-Tillmann [25] proved the virtual existence of geometric triangulations. Furthermore, Futer-Hamilton-Hoffman [10] proved that there are infinitely many virtual geometric triangulations.
To a certain extent, the existence of angle structure is weaker than that of geometric triangulations. Hence, a quite natural question arises: for any hyperbolic -manifold , are there topological triangulations which admits an angle structure? Luo-Tillmann [26] gave a sufficient and necessary condition for the existence of angle structure on cusped hyperbolic -manifolds using the theory of normal surface. By using Epstein-Penner’s ideal geometric polyhedral decompositions and the results of Luo-Tillmann [26], Hodgson-Rubinstein-Segerman [17] proved that there exists an ideal triangulation which admits an angle structure on cusped hyperbolic -manifolds with a certain topological condition. By using Kojima’s hyperideal (truncated) polyhedral decompositions, Qiu-Zhang-Yang [37] obtained a hyperideal (truncated) triangulation which admits an angle structure on compact hyperbolic -manifolds with totally geodesic boundary. In this paper we consider a hyperbolic -manifold with both cusps and totally geodesic boundaries. By Moise’s work [30], there is always an ideal triangulation on . We want to know whether admits an angle structure. Based on our previous work on mixed ideal polyhedral decompositions [12] and Luo-Tillmann’s arguments in [26], we get a natural ideal triangulation (see Corollary 3.2) on directly without using Moise’s work [30]. Moreover, under some topological conditions, admits an angle structure. To be precise, we have:
Theorem 1.1.
Let be a non-compact finite-volume hyperbolic -manifold with totally geodesic boundary. Denote by the compact -manifold with boundary, with each torus (or Klein bottle) boundary component corresponds to a cusp of . In other words, after subtracting the torus (or Klein bottle) boundary components, is homeomorphic to . If is the zero map, then there is a topological ideal triangulation on such that it admits an angle structure.
To prove Theorem 1.1, the polyhedral decomposition theory [12], which parallels [7] and [28], will play a crucial role. In addition, we follow the spirits in Luo-Tillmann [26], Kang-Rubinstein [19] and Hodgson-Rubinstein-Segerman [17]. We outline the proof in three steps. Step 1, using our geometric polyhedral decompositions [12], we first decompose into hyperbolic ideal or truncated polyhedra. Then we triangulate each polyhedron. The triangulation of the common faces of adjacent polyhedra may not necessarily match. On the mismatched faces, by inserting flat ideal tetrahedra, we are able to achieve an ideal triangulation . Step 2, following Kang-Rubinstein [19] and Luo-Tillmann [26], there is a strong relationship between the angle structure of and the theory of normal surfaces in . On each individual of , there exist four types of normal triangles and three types of normal quadrilaterals, each of which is characterized by coordinates. These coordinates satisfy a system of compatibility equations with solution space denoted by . By introducing the generalized Euler characteristic function defined on and using Farkas’s lemma, we derive a sufficient combinatorial condition for the existence of angle structures, i.e.
Proposition 1.2.
Let be a non-compact hyperbolic -manifold with finite volume and totally geodesic boundary. There exists an ideal triangulation on , and if for all with all quadrilateral coordinates non-negative and at least one quadrilateral coordinates positive, then admits an angle structure.
Step 3, by excluding cases that do not satisfy the combinatorial conditions in Proposition 1.2, we get the topological conditions in Theorem 1.1 for the existence of angle structures.
The paper is organized as follows. We give some basic notions in Section 2, including the polyhedral decomposition theory, ideal triangulation, angle structure, normal surface and Farkas’s lemma. In Section 3, we derive an ideal triangulation directly and prove Proposition 1.2. In Section 4, we prove Theorem 1.1.
Acknowledgements: The authors are very grateful to Professor Ruifeng Qiu, Feng Luo, Tian Yang for many discussions on related problems in this paper. The first two authors would like to thank Professor Gang Tian for his long-term support and encouragement. Huabin Ge is supported by NSFC, no.12341102 and no.12122119. Faze Zhang is supported by NSFC, no.12471065.
2 Preliminaries
2.1 Polyhedral decomposition theory
Let us recall the definitions of the ideal tetrahedra and partially truncated tetrahedra first.
Definition 2.1.
An ideal tetrahedron in is a finite-volume region in bounded by four geodesic faces. Any two faces intersect each other, and any three faces intersect at the infinite boundary of . See the left picture of Figure 1 for example.
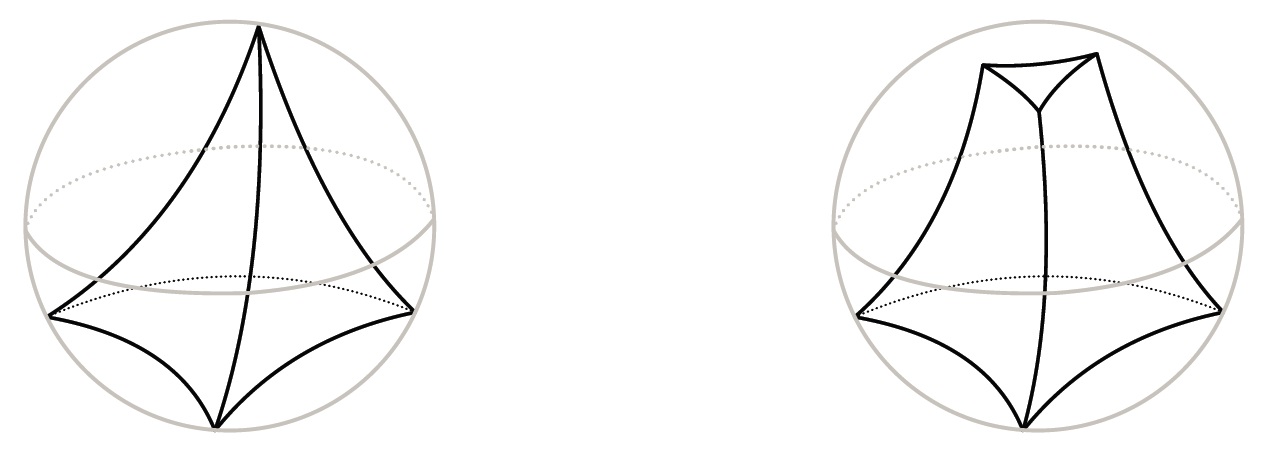
Denote by the open unite ball representing the hyperbolic 3-space via the projective Klein model. Following the terminology in [4], we have
Definition 2.2.
A hyperideal tetrahedron is a non-compact tetrahedron in which is just the intersection of with a projective tetrahedron whose vertices are all outside and whose edges all meet .
Given that the hyperideal tetrahedron has been extensively studied and used by several mathematicians, we would like to emphasize that the definition of a hyperideal tetrahedron varies from author to author. Some authors require that all four vertices of a hyperideal tetrahedron must be hyperideal vertices, i.e. points outside the closure of , e.g. [27]. It is called strictly hyperideal by Schlenker [39].
Definition 2.3.
A hyperideal tetrahedron of 1-3 type means that there are only one vertex of lies outside of the closure of and the other three vertices are all lie in . The truncation of a type 1-3 hyperideal tetrahedron at the vertex is defined as cutting off the thick end towards from by a geodesic plane which is perpendicular to the three adjacent geodesic faces at . After the truncation of at , the resulting polyhedron is called a partially truncated tetrahedron of 1-3 type. The unique face of induced by the truncation is called an external face and the other faces of are called internal faces. See the right picture of Figure 1 for example.
The concept of ideal tetrahedron, hyperideal tetrahedron and partially truncated tetrahedra of 1-3 type can be generalized to polyhedra case easily.
Definition 2.4.
An ideal polyhedron in is a finite-volume polyhedral region bounded by several geodesic faces. Any two faces intersect each other, and any three faces intersect at the infinite boundary of .
Definition 2.5.
A hyperideal polyhedron is a non-compact polyhedron in which is just the intersection of with a projective polyhedron whose vertices are all outside and whose edges all meet .
Definition 2.6.
A hyperideal polyhedron of 1-k type is defined as there is exactly one vertex (called hyperideal vertex) of the corresponding lies outside of and the other vertices (called ideal vertices) are all lie in . After the truncation of at the hyperideal vertex , the resulting polyhedron is defined as a partially truncated polyhedron of 1-k type. The unique face of induced by the truncation is called an external face and the other faces of are called internal faces.
Similarly, one can define the truncation of a hyperideal tetrahedron (or polyhedron resp.), which is truncated at all hyperideal vertices, i.e. points outside the closure of . After the truncating, one get a partially truncated tetrahedron (or polyhedron resp.).
Similar to the role of Epstein-Penner’s decomposition [7] played in [17], we developed a theory of decomposition of general hyperbolic 3-manifolds, which will paly essential role in the proof of our main theorem. The theory says any hyperbolic 3-manifold admits a geometric polyhedral decomposition.
Theorem 2.7 (Ge-Jiang-Zhang, [12]).
Let be a volume finite, non-compact, complete hyperbolic -dimensional manifold with totally geodesic boundary. Then admits a mixed geometric ideal polyhedral decomposition such that each cell is either an ideal polyhedron or a partially truncated polyhedron with only one hyperideal vertex.
Theorem 2.7 may be considered as a combination of Epstein-Penner’s decomposition [7] and Kojima’s decomposition [28]. However, to some extent, our conclusion is slightly stronger, and only ideal polyhedra and 1- type polyhedra appear in our decomposition. It is worth emphasizing that there are several advantages to choosing type 1-3 tetrahedra and type 1- polyhedra. Firstly, for polyhedral decomposition, it is more suitable for the algorithm. Secondly, it is very suitable for the proof of the main theorem in this paper, which can highlight the essence of the proof, and can also greatly simplify the expression, making the details clearer and more readable. See Section 3-4 for details.
2.2 Ideal triangulation
Strictly speaking, the ideal tetrahedron, as well as the hyperideal tetrahedron, have no real existent vertices. But for the sake of convenience, we often think that they all have four vertices. For example, a truncated type 1-3 tetrahedral has three real vertices, which are the three vertices of a hyperbolic triangle obtained by truncating a strictly hyperideal vertex, and four non-existent vertices, of which three are ideal vertices and one is a strictly hyperideal vertex. But we often think that these four unreal vertices are all the vertices of , while those three real vertices are not considered vertices of .
Additionally, it should be noted that the geometry of ideal tetrahedra, hyperideal tetrahedra, and truncated tetrahedra is hyperbolic. For each ideal tetrahedron, it corresponds to a topological tetrahedron with no geometry (i.e., on the boundary of a topological 3-ball, four marked vertices are selected, and each of the two marked points is connected to a marked edge, which does not intersect each other). It can even be considered equivalently that these topological tetrahedra are combinatorial tetrahedra with only combinatorial structures, where combinatorial structures refer to vertices, edges, faces, and connection relationships between them. We can also think of it as corresponding to a type of Euclidean tetrahedra, which may not be the same in shape, but have the same combinatorial structure. Similarly, each truncated hyperbolic tetrahedron corresponds to a combinatorial tetrahedron and a type of truncated Euclidean tetrahedron. For example, the following Figure 2 depicts the correspondence between a tetrahedron with only one truncated vertex (left) and a tetrahedron with four truncated vertices (right). If a (truncated) Euclidean tetrahedron corresponds to a (truncated) hyperbolic tetrahedron according to the above rules, then a vertex in is called an ideal vertex or a hyperideal vertex, defined according to its corresponding vertex type in the (truncated) hyperbolic tetrahedron.
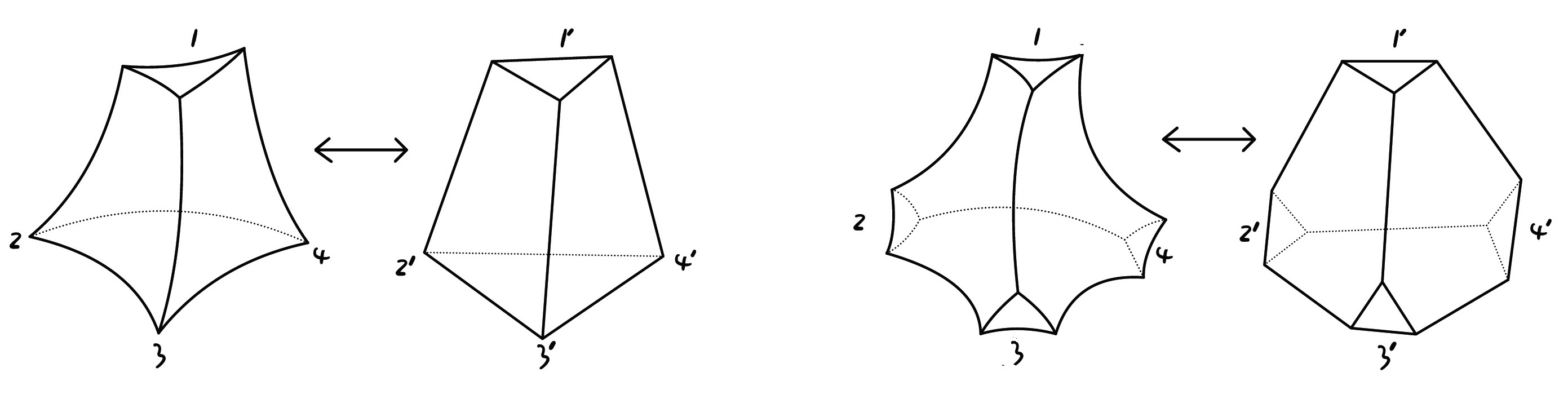
The surface generated by truncating a vertex is called an external surface. The remaining faces are called internal faces, or in other words, faces containing at least one ideal vertex are called internal faces. In Euclidean tetrahedra and combinatorial tetrahedra, external and internal faces can be defined similarly. The edges in the external faces are called the external edges, and the remaining edges are called the internal edges. Equivalently, the edges that contain at least one ideal vertex are called the internal edges. Thus, each tetrahedron, whether it is an ideal tetrahedron or a truncated tetrahedron, always has exactly six internal edges. Below we provide the precise meaning of an ideal triangulation.
Definition 2.8.
Given a topological three dimensional manifold with both topological cusps and boundaries whose connected components all have negative Euler characteristic numbers. For example, is derived from a volume finite, non-compact, complete hyperbolic -manifold with totally geodesic boundary, after forgetting the hyperbolic structure. Let be a topological space with each either an Euclidean tetrahedron or a truncated Euclidean tetrahedron. Let be a collection of affine homeomorphisms between the internal faces, and be the set of ideal vertices in . If is homomorphic to , then the cell decomposition is called an ideal triangulation of .
Note that the quotient of external faces in constitutes a triangulation of . The -simplices (-simplices resp.) in are called internal edges (faces resp.) of .
2.3 Angle structure
By definition, an angle structure on a single topological, or combinatorial ideal tetrahedron assigns to each edge of a positive number, called dihedral angle, such that the sum of the angles associated to the three edges meeting in a vertex is for each vertex of the tetrahedron. After a simple calculation, it can be found that the dihedral angles of opposite sides are equal. For a truncated tetrahedron with at least one hyperideal vertex, the definition of an angle structure is a little different. The main difference is that the sum of the dihedral angles associated to the three edges meeting in a strictly hyperideal vertex (or equivalently, a truncated face) is less than . Combining the above two definitions, the concept of an angle structure can be extended to the most general 3-dimensional pseudo-manifolds with ideal triangulations, see [11], [19], [21], [24], [26], [27] for instance.
Definition 2.9.
Let be an ideal triangulation on a topological 3-manifold with 3-simplices . An angle structure on is a function that, for each internal edge of (, ), assigns a values which is called the dihedral angle, so that:
-
1.
for any internal edge in , the sum of all dihedral angles around is ;
-
2.
if is a vertex of some with , and is not in the external faces of , the sum of all dihedral angles adjacent to in is ;
-
3.
if is an external face of some truncated tetrahedron with , the sum of all dihedral angles adjacent to in is less than .
In the above definition, if all the dihedral angles are allowed to be taken in the closed interval , it is said to be a semi-angle structure. By the work of Bao-Bonahon [4] ( or see [27] and [39]), any angle structure on endows each single 3-simplex with a hyperbolic geometry, making it an ideal tetrahedron or hyperideal truncated tetrahedron according to its type. However, it must be pointed out that due to the possible differences in edge lengths (even after choosing decorations), these hyperbolic tetrahedra generally cannot be glued together to obtain a hyperbolic structure on .
2.4 Normal surface and generalised Euler characteristic
Let be an ideal triangulation on a topological 3-manifold with 3-simplex .
Definition 2.10.
Let be an internal face. A normal arc is an embedding of an arc into such that lie on different internal edges of . A normal disk in () is an embedding of a disk into () such that is either empty or consists of disjoint normal arcs.
For each , there are seven types of normal disks on , of which 4 are normal triangles, corresponding to 4 vertices; 3 normal quadrilaterals, corresponding to 3 sets of opposing edges. For example, Figure 3 shows a special normal triangle, as well as an example of a special normal quadrilateral.
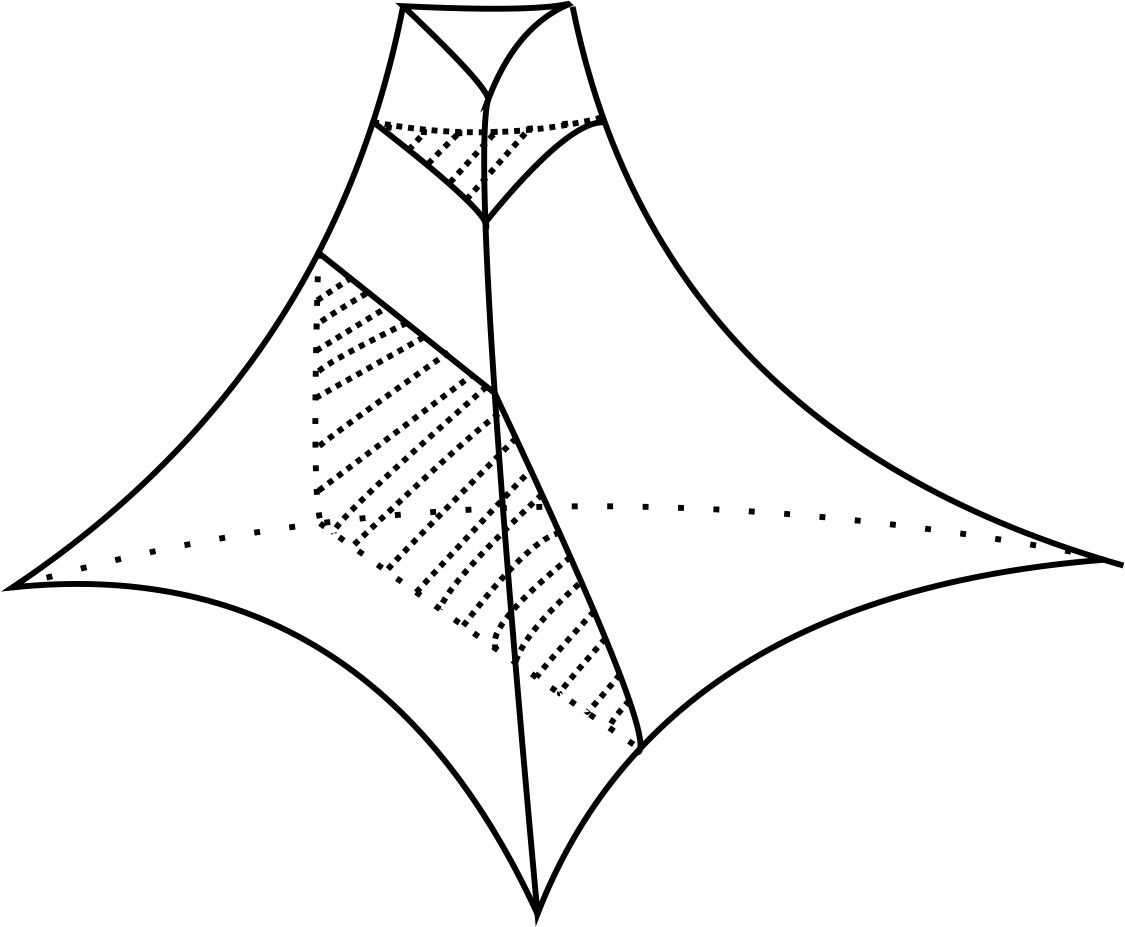
Definition 2.11.
A compact surface in is called normal with respect to , if is either empty or consists of disjoint normal disks of for each .
Recall is the number of all types of tetrahedra in the triangulation . We fix an ordering of all normal disc types in , where denotes a normal quadrilateral type and a normal triangle type. For any given normal surface , its normal coordinate is a vector in , where is the number of normal discs of type in , and is the number of normal discs of type in . A properly embedded normal surface is uniquely determined up to normal isotopy by its normal coordinate ([26], [40]). is called the quadrilateral coordinate of .
For a normal disk , let be the number of normal arcs in . If is a normal triangle in meeting a particular tetrahedra at edges with edge valence , , then its contribution to the Euler characteristic of is taken to be
If is a normal quadrilateral in meeting a particular tetrahedra at edges with edge valence , , then its contribution to the Euler characteristic of is taken to be
Then the generalized Euler characteristic function is defined as
| (2.1) |
where and are the normal quadrilaterals and normal triangles in respectively. The generalized Euler characteristic function is linear, and coincides with the classical Euler characteristic for any embedded or immersed normal surface in . See Section 2.6, [26] for details.
There are some linear constraints between the normal coordinate of a normal surface . Let be an internal face shared by two tetrahedra, say and . Let be a normal isotopy class of a normal arc in . There are two types of normal disks in , one is type for normal triangles, the other is type for normal quadrilaterals, such that when restricted to , the corresponding normal arcs are of the same type as . Similarly, there are two types of normal disks in , one is type for normal triangles, the other is type for normal quadrilaterals with similar properties. Thus, the normal coordinate satisfies a linear equation at the face as follows, which is called the compatibility equation:
| (2.2) |
Denote by the set of all vectors satisfying (2.2) at any internal face. For this linear space, Kang-Rubinstein [19] once introduced a basis
where is the number of -simplex in and is the number of internal edges in . For concrete meanings of and , see [19] and [26]. Then for any , there exists a unique coordinate such that
| (2.3) |
Given a normal disk in some , if is a -sided polygon, and intersects the internal edges of some particular , then its combinatorial area is defined to be
| (2.4) |
Definition 2.12.
If , then define
| (2.5) |
where is the set of all the normal triangles of , and is the corresponding normal triangle coordinate of .
Remark 2.13.
For any function defined on the internal edges of , which is called “angle” and may not satisfy the conditions for defining an angle structure, one can define the combinatorial area without any difference. By definition, for an internal edge , its combinatorial curvature is minus the sum of the angles surrounding it. For the area-curvature function , one may define [26] its Euler characteristic function as
where is expressed in Definition 2.12. However, only case is used in our paper.
Luo-Tillmann ([26], Lemma 15) got the following relationship between and :
Lemma 2.14.
Suppose admits an angle (or semi-angle) structure with . If , then
| (2.6) |
where is the set of all the normal quadrilaterals of and is the combinatorial area of induced by the angle (or semi-angle) structure .
2.5 Farkas’s lemma
If , we use (, , resp.) to mean that all components of are positive (non-negative, negative, non-positive resp.). To approach our main results, we need the following duality result from linear programming, which is known as Farkas’s lemma, and can be found, for instance, in [42]. In the following lemma, vectors in and are considered to be column vectors.
Lemma 2.15.
Let be a real matrix, , and be the inner product on .
-
1.
if and only if for all such that , one has .
-
2.
if and only if for all such that , one has .
-
3.
if and only if for all such that and , one has .
3 The proof of Proposition 1.2
It must be pointed out that in the proof of our main theorems, in addition to ideal ones, we only use truncated type 1-3 tetrahedra and type 1- polyhedra. Therefore, whenever a hyperideal polyhedron (or partially truncated polyhedron, hyperideal tetrahedron, partially truncated tetrahedron resp.) appears later, it always refers to a hyperideal polyhedron of 1- type (partially truncated polyhedron of 1- type, hyperideal tetrahedron of 1-3 type, partially truncated tetrahedron of 1-3 type resp.). And from now on, always refers to a hyperbolic 3-manifold with both cusps and totally geodesic boundaries.
3.1 The ideal triangulation of
Definition 3.1.
Let be an ideal quadrilateral with four ideal vertices , , , in turn. We connect the two pairs of vertices, and , and , with geodesic segments and , respectively. Then the ideal quadrilateral with diagonals and is called a flat ideal tetrahedron, see Figure 4.
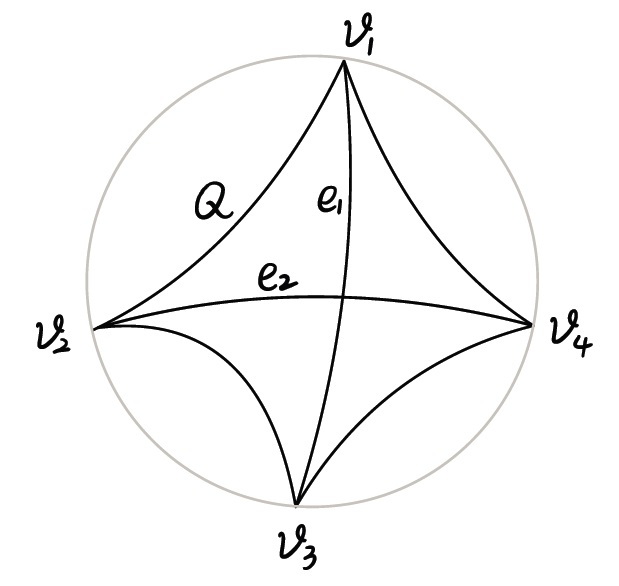
By Theorem 2.7, we obtain the following (topological) ideal triangulation of :
Corollary 3.2.
Let be a volume finite, non-compact, complete hyperbolic -manifold with totally geodesic boundary. Then admits an ideal triangulation such that each cell is either an (may be flat) ideal tetrahedron or a partially truncated tetrahedron.
Proof.
Using Theorem 2.7, we get a mixed ideal polyhedra decomposition such that each cell is either an ideal polyhedron or a partially truncated polyhedron with only one truncated hyperideal vertex.
To obtain the ideal triangulation of , two more steps are required. The first step is to triangulate eacn polyhedron as follows, and there are two cases to consider:
Case , assume is a partially truncated polyhedron induced by a convex polyhedron in . Recall a pyramid is a polyhedron with one face (known as the “base”) a -polygon and all the other faces triangles meeting at a common polygon vertex (known as the “tip”) . Consider the polyhedron , by taking cones at the unique hyperideal vertex , which is called the cone vertex, with each face of disjoint from , we get a decomposition of into pyramids. These pyramids have a common tip , and each face of disjoint from is the base of a pyramid. For any base polygon in a pyramid, we arbitrarily pick a vertex of and decompose into triangles by taking cones at . The triangulation of extends to a triangulation of the pyramid into tetrahedra, and no vertices are added throughout the process. In this way, is decomposed into a union of convex tetrahedra, each of which has only one common hyperideal vertex in . Then after the truncation at the hyperideal vertex from the intersection of with , has a triangulation whose cells are all partially truncated tetrahedron.
Case , assume is an ideal polyhedron. By taking cones at any ideal vertex , which is also called cone vertex, we get a decomposition of into pyramids with tips and bases the faces of disjoint from . Similar to case , for any base polygon in a pyramid, we arbitrarily pick a vertex of and decompose into ideal triangles by taking cones at . The ideal triangulation of extends to a decomposition of the pyramid into ideal tetrahedra. In this way, is decomposed into a union of ideal tetrahedra with no vertices are added throughout the process.
Consider a common face of two adjacent polyhedra and . If both and are partially truncated, by the constructions in case 1, the triangulation of in matches perfectly with the triangulation of in . For the remaining possibilities, at least one of and is an ideal polyhedron, the decompositions of the ideal polygon from and are not always match together to get a triangulation. Such face is called a pillow.
The second step is to insert flat tetrahedra into these pillows to get a layered triangulation as follows.
Let and be the vertices of a face where the cone is taken at separately from and . Let and be the remaining vertices of which are arranged sequentially along the boundaries of from to , see Figure 5 for example. For each diagonal switch from to , , and each diagonal switch from to , , we insert a flat tetrahedron with vertices and a flat tetrahedron with vertices respectively.
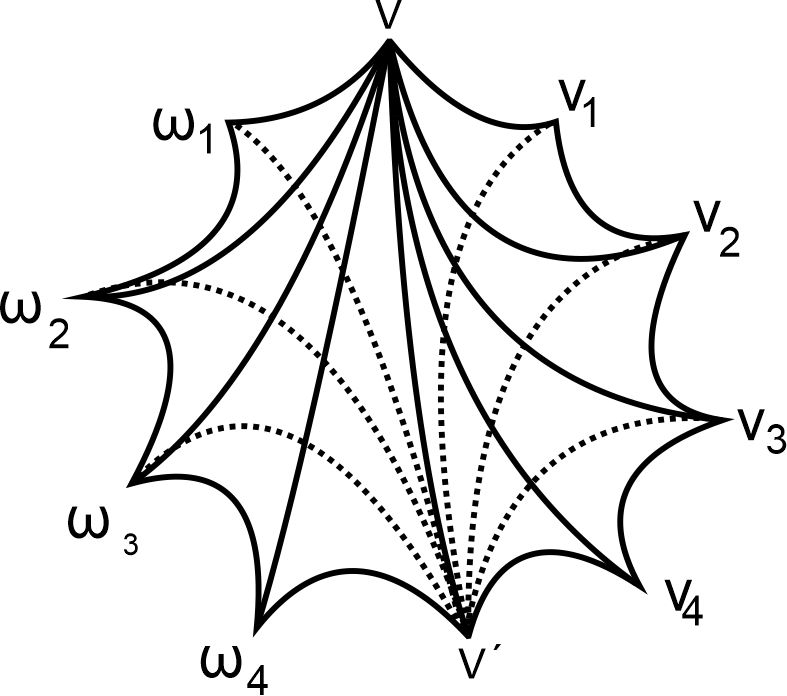
After the above two steps, we finally get an ideal triangulation of such that each cell is an (may be flat) ideal tetrahedron or a partially truncated tetrahedron. ∎
Note at each internal edge in the ideal triangulation , the value of its dihedral angle is in , hence we obtain a naturally semi-angle structure on .
3.2 Sufficient conditions for the existence of angle structures
Let be the ideal triangulation derived in the previous section, and all its (flat) ideal or partially truncated tetrahedra are . Suppose is an angle structure on . For each and each internal edge in , consider the dihedral angle at as a variable of the equations in Farkas’ Lemma 2.15, see Figure 6.
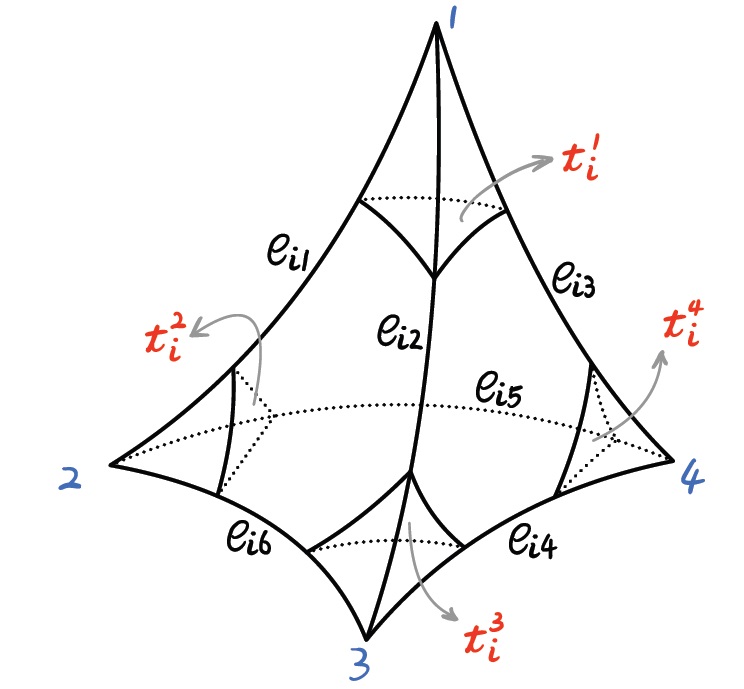
At the four normal triangles , , of , we have the following equations:
| (3.1) |
If is a partially truncated tetrahedron, then only one of its is less then , and the the remaining three are equal to . If is an (flat) ideal tetrahedron, then all its are equal to . The elements of are divided into two classes, one of them satisfies with the corresponding normal triangles denoted by , the other satisfies with the corresponding normal triangles denoted by .
Recall is the number of -simplex in and is the number of internal edges in . At each internal edge of , where , there holds:
| (3.2) |
where the sum traverses all the tetrahedra surround the edge .
Consider the vector
| (3.3) |
where (, ) comes from (3.1) and () comes from (3.2). Writing the system of equations (3.1) and (3.2) in a matrix form as
Consider the transpose of , which is also the dual of . It has one variable for each normal triangle type and one variable for each internal edge . If we denote the variables corresponding to by , where , and , then .
The following useful formula (i.e., Formula (4.9) in [26]) belongs to Luo-Tillmann:
| (3.4) | ||||
where , and the summation runs over all internal edges in the whole triangulation .
Note the vector looks like this
where . In order to obtain an angle structure on , we only need to prove that there exists a vector such that
| (3.5) |
Further using the third part of Farkas’s lemma, i.e., Lemma 2.15, we just need to show that for all with and , one has .
Claim 3.3.
There exists a vector with such that
for all with and .
Proof.
By Corollary 3.2, is an ideal triangulation of . Then admits a semi-angle structure according to the decomposition operation in Section 3.1 (when inserting a flat polyhedron, a angle or angle may occur). Then by the second part of Farkas’s Lemma 2.15, there exists a such that for all , where .
Next, we use the continuity method to prove the above, and for this, we introduce a function defined for all :
Here are the variables corresponding to , and is the variable corresponding to in the equation (3.1).
Thus we have , and by Equation (3.2), for all and .
Lemma 3.4.
for any , and for any variable .
Proof.
We prove it by contradiction. Assume there is a and such that
On the one hand , derived from the seme-angle structure on (), and on the other hand, as a function of is monotonic because of the linearity of . Then , which contradicts the fact that . Then we proved the above lemma.
∎
4 The proof of Theorem 1.1
Let be a cusped hyperbolic -manifold with totally geodesic boundary and be the ideal triangulation of as in Corollary 3.2. Recall that there exists a natural semi-angle structure on by the analysis in Section 3. For a quadrilateral type normal disk in , the combinatorial area of by definition is
where are the dihedral angles assigned by in the vertices (which are the intersections of with the four edges of a particular tetrahedron ) of .
Definition 4.1.
A quadrilateral type normal disk is called vertical if .
Proposition 4.2.
If there is no such , all of its quadrilateral coordinates are non-negative, all non-vertical quadrilateral coordinates are zero, and at least one quadrilateral coordinate is positive, then admits an angle structure.
Proof.
Let be the semi-angle structure on , and be a quadrilateral type normal disk in a particular tetrahedron of .
If is a flat tetrahedron, then . Hence is vertical.
If is an ideal or partially truncated tetrahedron, in this case it is not flat, then the combinatorial area
where is the angle of the edge in which faces , and is positive as a real dihedral angle induced from the hyperbolic structure.
According to the conditions in the proposition, for any with all quadrilateral coordinates non-negative and at least one quadrilateral coordinate positive, there exist quadrilateral type normal disk such that is non-vertical and . Note , hence by Lemma 2.14,
Then by Theorem 1.2, we get an angle structure on . ∎
Recall is the solution space of the compatibility equations (2.2). Denote by a subset of whose element has all non-negative integer coordinates. With a similar argument of Hodgson-Rubinstein-Segerman [17], we have:
Proposition 4.3.
If there is no such , all of its quadrilateral coordinates are non-negative, all non-vertical quadrilateral coordinates are zero, and at least one quadrilateral coordinate is positive, then admits an angle structure.
Proof.
If there is a satisfying the properties assumed in Proposition 4.2, then the coordinates of are all rational numbers since the coefficients in the compatibility equations (2.2) are all integers. So there is a positive integer such that , i.e., has integer coordinates. Because all the quadrilateral coordinates of are non-negative, so is . If all the triangle coordinates of are non-negative, we are done. If some triangle coordinates of are negative, we can always add enough normal copies of peripheral , tori or Klein bottles. Then we can get a whose triangle coordinates are all none-negative. Hence , we are done.
∎
According to Proposition 4.3, to get an angle structure on , we should exclude the cases that “ with all its quadrilateral coordinates non-negative, all non-vertical quadrilateral coordinates zero, and at least one quadrilateral coordinate positive”.
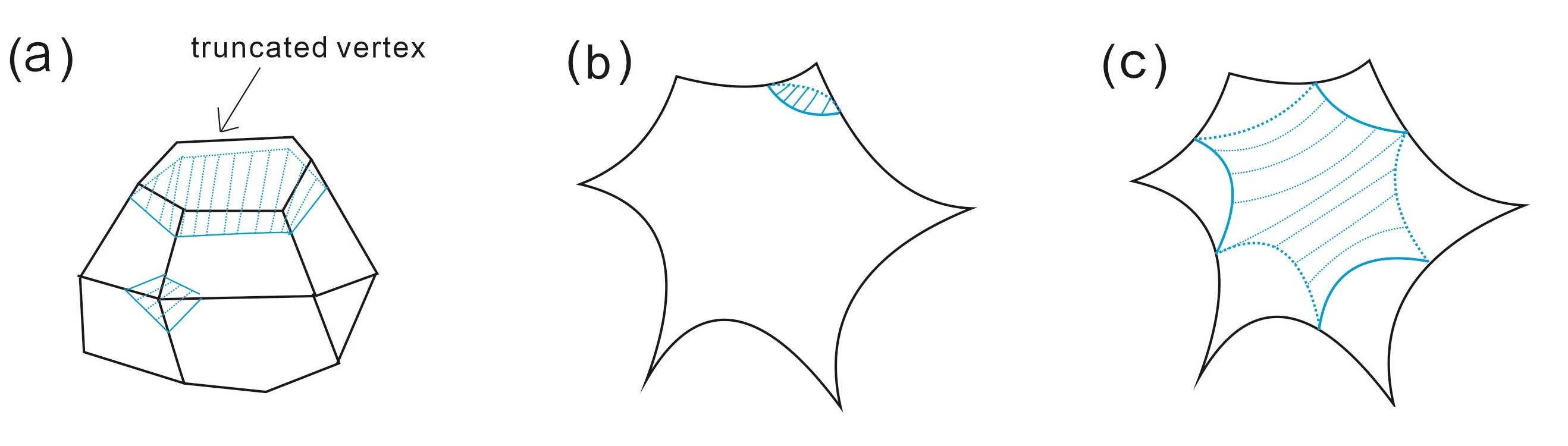
Let be the mixed polyhedron decomposition described in Theorem 2.7. Let be the decomposition synthesized by with the ideal polyhedra pillows defined in the proof of Corollary 3.2. Let and be the ideal polyhedra (including partially truncated polyhedra) and polygonal pillows respectively in , and let and be the non-planar 3-simplices and planar tetrahedra respectively in . Notably, according to Lemma 7.4 of Hodgson-Rubinstein-Segerman [17], each polygonal pillow represented by can only be a quadrilateral or a hexagon.
Consider the normal surface corresponds to a . If does not contain any normal quadrilaterals for each , and contains at least one normal quadrilateral for some , then
-
1.
for each so that , then are vertex-linking polygons;
-
2.
for each so that , then are either twisted surfaces or vertex-linking bigons.
See Figure 7 for example.
The following are the proof of Theorem 1.1:
Proof.
Let be a non-compact, volume-finite hyperbolic three-dimensional manifold. Denote by the compact -manifold with boundary, with each torus (or Klein bottle) boundary component corresponds to a cusp of . After subtracting the torus (or Klein bottle) boundary components, is homeomorphic to , and each boundary of is a torus or Klein bottle or a closed surface of high genus. Consider the mixed polyhedral decomposition of described in Theorem 2.7. It determines a graph with one vertex for each polyhedron and an edge joining two vertices for each face incident to the two corresponding polyhedra
Lemma 4.4.
There exists an ideal triangulation of , which is a subdivision of , such that contains a maximal tree with the property that the gluing faces corresponding to the edges of are not polygon pillows in .
Proof.
For each vertex of degree in the maximal tree , if the corresponding polyhedron is a truncated one, take the hyperideal vertex as the cone vertex; if the corresponding polyhedron is an ideal one, take the ideal vertex which is not on the face and is represented by an edge of as the cone vertex. Then remove these vertices and the corresponding edges from , and continue the above operation in the remaining tree until either there is an empty set left, or a single point set left.
If there is an empty set left, then the proof is complete. If there is a single point set left, there are two scenarios to consider:
Case , if the corresponding polyhedron is ideal, then any triangulation of this polyhedron satisfies the condition.
Case , if the corresponding polyhedron is truncated, then take the unique hyperideal vertex of this truncated polyhedron as the cone vertex, and take any triangulation at the other ideal faces. Since each truncated face is shared by two truncated polyhedra, the inherited triangulations of the truncated faces match perfectly. Hence the final triangulation of this truncated polyhedron also satisfies the condition. ∎
Note that the construction of and is consistent as in Corollary 3.2. Hence also satisfies Proposition 1.2.
For the ideal triangulation , denote by the union of and polygon pillows generated by . Now assume that there exists a , and without loss of generality, further assume that the corresponding normal surface (of ) is not a Haken sum and contains some twisted disks. By the conditions of Theorem 1.1 and the construction of , does not intersect the maximal tree .
Next we show the number of twisted disks in is even. If there is an odd number of twisted disks of at some polygon pillow in . Denote the edge on corresponding to the polygon pillow by . Then contains a closed curve whose intersection with is odd. Thus, represents a nontrivial element in the homology group .
Consider the following long exact sequence:
Since the closed curve representing any non-trivial element in must have an even geometric intersection number with any closed surface in , is not in the image of the map , and therefore not in the kernel of the map , contradicting the known conditions in Theorem 1.1. Therefore, the number of twisted disks in is even at all polygon pillows.
If the number of all vertex-linking disks and vertex-linking bigons are even, then is a double of some surface, contradicting the assumption that is not a Haken sum. Hence, there must be at least one vertex-linking bigons or vertex-linking disks whose number is odd. Let be a copy of all such odd-count vertex-linking bigons or vertex-linking disks.
Claim 4.5.
is a solution to the compatibility equations.
Proof.
Consider the normal arc type at a face in the triangulation .
Case : Both tetrahedra , adjacent to are ideal, or truncated. If has a normal disk at , it must be a vertex-linking disk in some ideal polyhedron or partially truncated polyhedron of . Since the contributions of , to are the same, it satisfies the compatibility equations.
Case : Both tetrahedra , adjacent to are flat ideal. If has a normal disk at , it must be a vertex-linking bigon in some polygonal pillows of . Again, the contributions of , to are the same, satisfying the compatibility equations.
Case : One tetrahedron is ideal or truncated, and the other is flat ideal. Since the possible twisted disks on at are even, the parity of bigons and linking disks at is the same. If has a normal disk at , it must be a bigon and a linking disk in some polygonal pillows of . The contributions of , to are the same, also satisfying the compatibility equations. ∎
Therefore, is the Haken sum of and some surface which contains at least one twisted disk. This contradicts with the assumption that is not a Haken sum. Therefore Theorem 1.1 is proved. ∎
References
- [1] H. Akiyoshi, On the Ford domains of once-punctured torus groups, from: “Hyperbolic spaces and related topics (Japanese) (Kyoto, 1998)”, Sūrikaisekikenkyūsho Kōkyūroku 1104 (1999), 109-121.
- [2] H. Akiyoshi, M. Sakuma, M. Wada, Y. Yamashita, Jørgensen’s picture of punctured torus groups and its refinement, from: “Kleinian groups and hyperbolic 3-manifolds (Warwick, 2001)”, (Y. Komori, V. Markovic, C. Series, editors), London Math. Soc. Lecture Note Ser. 299, Cambridge Univ. Press (2003), 247-273.
- [3] H. Akiyoshi, M. Sakuma, M. Wada, Y. Yamashita, Punctured torus groups and 2-bridge knot groups. I, Lecture Notes in Math. 1909, Springer, Berlin (2007).
- [4] X. Bao, F. Bonahon, Hyperideal polyhedra in hyperbolic 3-space, Bull. Soc. Math. France 130 (2002), no. 3, 457-491.
- [5] R. Benedetti, C. Petronio, Lectures on hyperbolic geometry, Springer, Berlin, 1992.
- [6] H. Cao, X. Zhu, A complete proof of the Poincaré and geometrization conjectures-application of the Hamilton-Perelman theory of the Ricci flow, Asian J. Math. 10 (2006), 165-492, Erratum in Asian J. Math. 10 (2006), 663-664.
- [7] D. Epstein, R. Penner, Euclidean decomposition of non-compact hyperbolic manifolds, J. Differential Geom. 27 (1988), 67-80.
- [8] K. Feng, H. Ge, B. Hua, Combinatorial Ricci flows and the hyperbolization of a class of compact 3-manifolds, Geom. Topol. 26 (2022), no. 3, 1349-1384.
- [9] D. Futer, F. Guéritaud, From angled triangulations to hyperbolic structures, Contemp. Math., 541 American Mathematical Society, Providence, RI, 2011, 159-182.
- [10] D. Futer, E. Hamilton, N. R. Hoffman, Infinitely many virtual geometric triangulations, J. Topol. 15 (2022), no. 4, 2352-2388.
- [11] S. Garoufalidis, C. D. Hodgson, J. H. Rubinstein, H. Segerman, 1-efficient triangulations and the index of a cusped hyperbolic 3-manifold, Geom. Topol. 19 (2015), 2619-2689.
- [12] H. Ge, L. Jia, F. Zhang, The polyhedral decomposition of cusped hyperbolic -manifolds with totally geodesic boundary, arxiv, 2024.
- [13] F. Guéritaud, On canonical triangulations of once-punctured torus bundles and two-bridge link complements, Geom. Topol. 10 (2006), 1239-1284, With an appendix by D. Futer.
- [14] F. Guéritaud, Triangulated cores of punctured-torus groups, J. Differential Geom. 81 (2009), 91-142.
- [15] F. Guéritaud, S. Schleimer, Canonical triangulations of Dehn fillings, Geom. Topol. 14 (2010), no. 1, 193-242.
- [16] S. L. Ham, J. S. Purcell, Geometric triangulations and highly twisted links, Algebr. Geom. Topol. 23 (2023), 1399-1462.
- [17] C. D. Hodgson, J. H. Rubinstein, H. Segerman, Triangulations of hyperbolic 3-manifolds admitting strict angle structures, J. Topol. 5 (2012), no. 4, 887-908.
- [18] T. Jørgensen, On pairs of once-punctured tori, from: “Kleinian groups and hyperbolic 3-manifolds (Warwick, 2001)”, (Y Komori, V Markovic, C Series, editors), London Math. Soc. Lecture Note Ser. 299, Cambridge Univ. Press (2003), 183-207.
- [19] E. Kang, J. H. Rubinstein, Ideal triangulations of -manifolds. II. Taut and angle structures, Algebr. Geom. Topol.5 (2005), 1505-1533.
- [20] B. Kleiner, J. Lott, Notes on Perelman’s papers, Geom. Topol. 12 (2008), no.5, 2587-2855.
- [21] M. Lackenby, Word hyperbolic Dehn surgery, Invent. Math. 140 (2000), 243-282.
- [22] M. Lackenby, The canonical decomposition of once-punctured torus bundles, Comment. Math. Helv. 78 (2003), 363-384.
- [23] M. Lackenby, Taut ideal triangulations of 3-manifolds, Geom. Topol. 4 (2000), 369-395.
- [24] F. Luo, A combinatorial curvature flow for compact 3-manifolds with boundary, Electron. Res. Announc. Amer. Math. Soc. 11 (2005) 12-20.
- [25] F. Luo, S. Schleimer, S. Tillmann, Geodesic ideal triangulations exist virtually, Proc. Amer. Math. Soc. 136 (2008), no. 7, 2625-2630.
- [26] F. Luo, S. Tillmann, Angle structures and normal surfaces, Trans. Amer. Math. Soc. 360 (2008), no. 6, 2849-2866.
- [27] F. Luo, T. Yang, Volume and rigidity of hyperbolic polyhedral 3-manifolds, J. Topol. 11 (2018) 1-29.
- [28] S. Kojima, Polyhedral decomposition of hyperbolic 3-manifolds with totally geodesic boundary, Aspects of low-dimensional manifolds, 93-112, Adv. Stud. Pure Math., 20 (1992), 93-112.
- [29] B. Martelli, An Introduction to Geometric Topology, eprint arXiv:1610.02592.
- [30] E. E. Moise, Affine structures in 3-Manifolds. V. The triangulation theorem and hauptvermutung, Ann. Math. 56 (1952), 96-114.
- [31] J. Morgan, G. Tian, Ricci flow and the Poincaré conjecture, Clay Mathematics Monographs 3, Amer. Math. Soc. (2007).
- [32] B. Nimershiem, Geometric triangulations of a family of hyperbolic 3-braids, Algebr. Geom. Topol. 23 (2023), no.9, 4309-4348.
- [33] G. Perelman, The entropy formula for the Ricci flow and its geometric applications, arXiv:math/0211159.
- [34] G. Perelman, Ricci flow with surgery on three-manifolds, arXiv:math/0303109.
- [35] G. Perelman, Finite extinction time for the solutions to the Ricci flow on certain three-manifolds, arXiv:math/0307245.
- [36] C. Petronio, J. Porti, Negatively oriented ideal triangulations and a proof of Thurston’s hyperbolic Dehn filling theorem, Expo. Math. 18 (2000), no. 1, 1-35.
- [37] R. Qiu, F. Zhang, T. Yang, Angle structures and hyperbolic -manifolds with totally geodesic boundary, arXiv:1405.1545v2, 2014.
- [38] I. Rivin, Euclidean structures on simplicial surfaces and hyperbolic volume, Ann. of Math. 139 (1994), 553-580.
- [39] J. M. Schlenker, Hyperideal polyhedra in hyperbolic manifolds, preprint (2002) arXiv math/0212355.
- [40] S. Tillmann, Normal surfaces in topologically finite 3-manifolds, Enseign. Math. 54(3-4) (2008), 329-380.
- [41] W. P. Thurston, The geometry and topology of three-manifolds, lecture notes, Princeton Univ. (1980), available at http://library.msri.org/books/gt3m/.
- [42] G. M. Ziegler, Lectures on polytopes, Springer-Verlag, New York, 1995.
Huabin Ge, [email protected]
School of Mathematics, Renmin University of China, Beijing 100872, P. R. China
Longsong Jia, [email protected]
School of Mathematical Sciences, Peking University, Beijing, 100871, P.R. China
Faze Zhang, [email protected]
School of Mathematics and Statistics, Northeast Normal University, Changchun, Jilin, 130024, P.R.China