Analysis of the L3 BEC at Z0-pole
– Comparison of the conventional formula against the -model –
Abstract
The L3 Collaboration reported data on 2-jet and 3-jet Bose–Einstein correlations (BECs) with the results obtained through the -model in 2011. In this study, we analyze these correlations using the conventional formula with the Gaussian long-range correlation (). The estimated ranges of interactions for 2-jet and 3-jet, and , are almost the same magnitude as those by -model: (stat) fm and (stat) fm. The anticorrelation in BEC (less than 1.0) observed by the L3 Collaboration is related to the partially negative density profile ( in space) in the -model and the in , respectively. Remarkably, the probability calculated from the Levy canonical form exhibits partially negative behavior.
1 Introduction
The L3 Collaboration reported their data on 2-jet and 3-jet Bose–Einstein correlation (BEC) in collisions at Z0-pole in 2011 [1]. The BEC is described in terms of the four momentum transfer ,
| (1) |
where the numerator is the two-particle (mainly pions) distribution including the BE effect and the denominator is the two-particle distribution without the BE effect which is the mixture procedure. That means the distribution made from different events.
Furthermore, introducing various corrections, L3 Collaboration adopted the following ratio expressed by Eq. (1),
| (2) |
In Eq. (2), the suffixes data, gen, det, and gen-noBE mean the following ensembles, respectively:
- 1) data:
-
the data sample.
- 2) gen:
-
a generator-level Monte Carlo (MC) sample.
- 3) det:
-
the same MC sample passed through detector simulation and subject to the same selection procedure as the data.
- and 4) gen-noBE:
-
a generator-level sample of a MC generated without BEC simulation.
Finally, data are analyzed by the following -model based on the Levy canonical form to explain the anticorrelation (BEC: less than 1.0) observed in the interval GeV:
| (3) |
where denotes the magnitude of the interaction region and does a constrain expressed by . The long-range correlation () is expressed as . The parameter denotes the degree of coherence, and represents the characteristic index introduced in the Levy canonical form in the stochastic theory [2, 3].
In contrast, OPAL [4], DELPHI [5] and ALEPH Collaborations [6] reported their data on BEC at Z0-pole in 1991 and 1992, using the double ratio (DR) described with the single ratios and ,
| (4) |
where denotes the number of events. The suffixes and indicate charge combinations.
It should be remarked that the reported data on BEC at Z0-pole [4, 5, 6] were analyzed by the conventional formula with and ,
| (5) |
where is the exchange function due to Bose–Einstein statistics for the identical pions.
Thus, to compare fit parameters by L3 Collaboration and those by OPAL, DELPHI and ALEPH Collaborations, we have to analyze data on by Eq. (5). This is one of the aims of the present study.
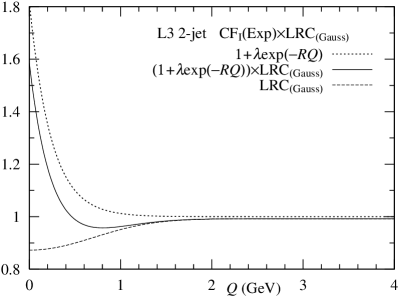
First, to know the role of , we examine data measured as by L3 Collaboration [1] using Eq. (3). Table 1 and Fig. 1 present the results estimated using Eq. (3). As seen in Table 1, the role of is considerably important because /dof’s are improved. In other words, the term of cannot sufficiently explain the anticorrelation. To show the role of , we present our calculation with the constraint in § 4.
| event | (fm) | (GeV-1) | /dof | |||
| 2-jet | — | 119.7/96 | ||||
| 3-jet | — | 226.8/96 | ||||
| 2-jet | 94.6/95 | |||||
| 3-jet | 113/95 | |||||
| 2-jet | 91.5/94 | |||||
| GeV-2 | ||||||
| 3-jet | 92.6/94 | |||||
| GeV-2 | ||||||
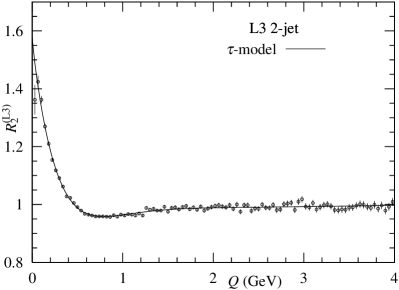
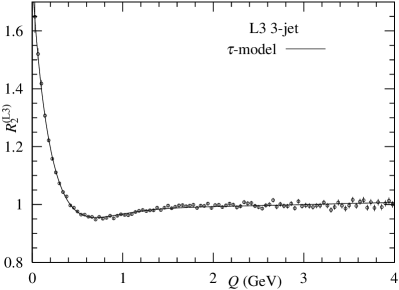
Second, to know the role of , we analyze the 2-jet and 3-jet BECs using Eq. (5) and the conventional formula with which is expressed as follows:
| (6) | |||
where was derived by us in Ref. [7] via analysis of CMS MC events at 13 TeV in LHC reported in Ref. [2]. On the contrary, it should be noted that L3 Collaboration did not report their MC data. Thus we assume in the present study. See Ref. [8], for the sake of reference. Nevertheless, it should be stressed that the Gauss distribution is stable distribution in the sense of the Levy canonical form. See Appendix B.
We consider the following four functions based on our previous study [9]:
The remainder of this paper is organized as follows. In Section 2, we analyze the data for 2-jet and 3-jet using Eqs. (5) and (6). In Section 3, we analyze the same data by -model. The second aim of this paper is to examine connections in -space between the quantum optics (QO) and the -model in the stochastic approach. In Section 4, introducing the Fourier transformation in the 4-dimensional Euclidean space-time (see Eq. (18)), we can study the profiles of the exchange function of 2-jet and 3-jet in -space, where . Finally, Section 5 presents the concluding remarks.
In Appendix A, data on at -pole by DELPHI Collaboration [5] are presented, because of no-information by L3 Collaboration. Therein we analyze DELPHI data by and . In Appendix B, the Levy canonical form and several formulations calculated using the inverse Fourier transformation are presented. In Appendix C, first, the systematic error and uncertainties are investigated using of BEC at Z0-pole by OPAL Collaboration [4], where and are used. Second, the same quantities on BEC by L3 Collaboration are concisely mentioned.
2 Analysis of data on 2-jet and 3-jet using with and
I: Application of Eqs. (5) and (6)
Using Eqs. (5) and (6), we analyze data on the 2-jet and 3-jet with and . Our results are presented in Table 2.
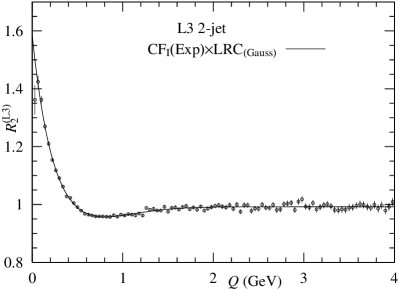
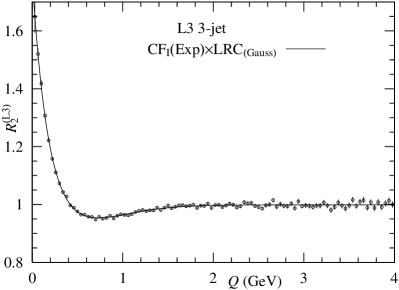
| (fm) | (GeV-1) | /dof | ||||
| 2-jet | ||||||
| Gauss | 247/96 | |||||
| Exp. | 255/96 | |||||
| IP2.0 | 247/96 | |||||
| IP2.5 | 231/96 | |||||
| 3-jet | ||||||
| Gauss | 455/96 | |||||
| Exp. | 438/96 | |||||
| IP2.0 | 472/96 | |||||
| IP2.5 | 436/96 | |||||
| (fm) | (GeV-2) | /dof | ||||
| 2-jet | ||||||
| Gauss | 199/95 | |||||
| Exp. | 90.0/95 | |||||
| IP2 | 118/95 | |||||
| IP2.5 | 126/95 | |||||
| 3-jet | ||||||
| Gauss | 310/95 | |||||
| Exp. | 83.9/95 | |||||
| IP2.0 | 140/95 | |||||
| IP2.5 | 157/95 | |||||
As shown in Tables 1 and 2, our results from Eq. (6) and are compatible with those presented in Table 1. However, the degree of coherence ’s presented in Table 1 are somewhat smaller than those presented in Table 2.
Moreover, we would like to add the following: For 2-jet, as we assume the Levy distribution () times , we obtain the similar figures as , because of the Levy index (). For 3-jet, there is no coincidence with the result by , because of and .
II: Analysis of 2-jet and 3-jet events using the quantum optics approach
As shown in Table 2, the degree of coherence in is observed. To consider its meaning, we use the following formula with QO [11, 12, 13].
| (8) |
where represents the ratio of the chaotic component to the total multiplicity. denotes the ratio of the coherent component to the total one. For the 2-jet event, as shown in Table 3, , the coherent component is approximately 30%. Moreover, fm is larger than those in Table 2. This is attributed to the third term .
| event | (fm) | (GeV-1) | (GeV-2) | /dof | ||
|---|---|---|---|---|---|---|
| 2-jet | — | 314/96 | ||||
| 3-jet | — | 447/96 | ||||
| 2-jet | 156/95 | |||||
| 3-jet | 167/95 | |||||
| event | (fm) | (GeV-2) | /dof | |||
| 2-jet | 90.4/95 | |||||
| 3-jet | 83.6/95 |
3 Analysis of 2-jet and 3-jet events using the -model including
To examine the role of in Eq. (3), we propose the following formula,
| (9) |
Using of sets of six random variables and the CERN MINUIT program, we can estimate the fit parameters shown in Table 4.
| event | (fm) | (GeV-2) | /dof | ||||
|---|---|---|---|---|---|---|---|
| 2-jet | 91.2/94 | ||||||
| 3-jet | 83.5/94 |
The differences concerning /dof’s in Tables 1 and 4 are obvious. It is worthwhile to stress that the degree of coherence s is larger than those by in Table 1. Moreover, the magnitudes of s are almost the same as those by the exponential function in Table 2. For 3-jet, (stat) fm estimated using Eq. (8) in Table 3 is compatible with (stat) fm obtained using Eq. (9) in Table 4.
4 Mechanism of anticorrelation and profiles of the source functions of 2-jet and 3-jet BECs in the -space
I: Explanation of the anticorrelation
The anticorrelation in the 2-jet and 3-jet events, i.e., is observed in the region GeV. These values in BEC are smaller than 1.0. These behaviors can be explained in two ways.
In the conventional formula with the function, , the anticorrelation is explained by the Gaussian function with . Second, the cross term which is a product of the exponential function and ): . For reference, we present data on at -ploe by DELPHI Collaboration [5] in Appendix A because we have no-information on them (, and ) by L3 Collaboration at present.
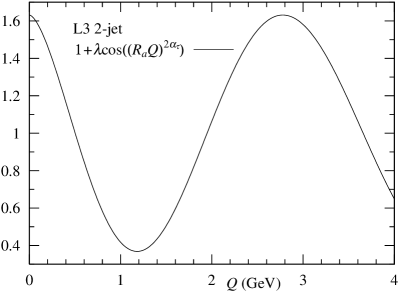
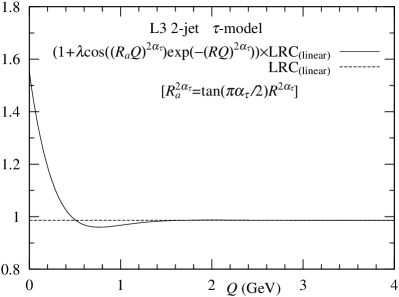
Alternatively, in the -model, the anticorrelation is described by the cosine in the exchange function. Indeed, this mechanism is shown in Fig. 3. The behavior of is oscillating. By multiplying , the anticorrelation is created. Moreover, when was replaced by in -model, we observe more significant anticorrelation. See Fig. 4.
II: Source functions of BEC in the -space
Using the Fourier transform of ’s and , we calculate the profiles of and the -model in the -space, which are expressed as the density s.
We use the following expansion to study the profile of in the -space. Before concrete computation, we add the physical meaning. is interpreted as dimensional Lorentz distribution because (see Ref. [16] 111The chapter 7, “multivariate stable laws” is useful for the calculation of the general systematical distributions (). The results in Ref. [9] are consistent with those in Ref. [16] for . See also Ref. [17]). is connected to in the [9].
| (12) |
The source function of the is calculated as follows:
| (15) |
The contribution from the cross term, , is computed by the inverse Fourier transformation () and the numerical integration.
For the stochastic density of the exchange function in the -model, we first employ the following numerical calculation:
| (18) |
where is the Bessel function [9]. Note that in Eq. (18). The Wick rotation is necessary [10]. Fig. 4 shows the numerical calculation of Eq. (18).
Second, concerning with the analytic expansion of Eq. (18), we obtain the following formula,
| (19) |
where , and (see Table 1). However, it is regretful that we cannot obtain the full numerical values, because of the mathematical limit of serious expansion of the Bessel function. Note that fm is the applicable limit of Eq. (19).
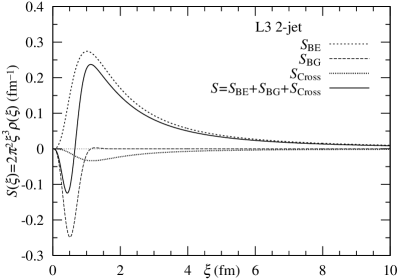
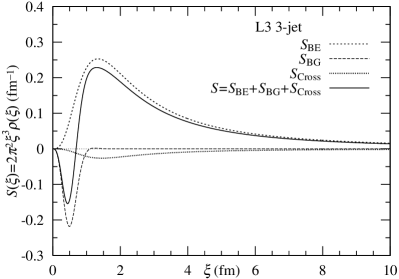
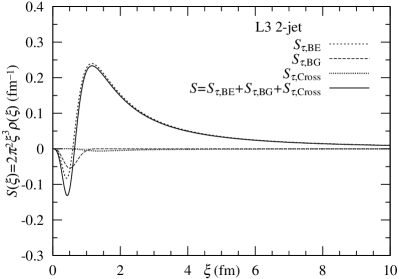
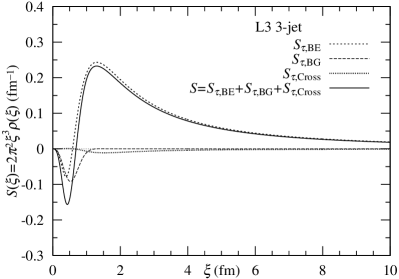
Third, we calculate profiles of Eqs (6) and (9) in -space. Fig. 4 shows the two types of behaviors for the 2-jet and 3-jet events. The dip structures at fm are observed. The dip structures in the 3-jet (right) are somewhat deeper than those in the 2-jet (left).
It can be said that, the negative profile of the density in originates from the denominator. In other words, the Monte Carlo calculation in the denominator in L3 BEC at Z0-pole implies the extent of the clustering effect expressed by the Gaussian distribution as well as in the for LHC CMS BEC at 13 TeV [2, 7].
| -space | Momentum ()-space | |
| Our approach | The numerator: | |
| ( | . | |
| ) | where . means | |
| 4-dimension. | ||
| The denominator of LRC: | ||
| . | . | |
| See Ref. [9]. | which is reflecting the clustering effect | |
| observed in [7, 2]. See Ref. [5]. | ||
| -model | The probability density and source function | Levy canonical form () |
| are calculated from in the right column. | , | |
| . | ||
| See Appendix B. . | ||
| cf. The probability of the Levy canonical form ( dimension) is expressed as | ||
| , | ||
| where Re[ ] means the real part. The Lorentz (or Cauchy) distribution is obtained by | ||
| . The Gaussian one is obtained by . The formulas | ||
| with are calculated by the following replacement in above: and | ||
| . and are obtained. | ||
Concerning the Levy canonical form and the inverse Fourier transformation ( and ), several formulations are shown in Appendix B.
5 Concluding remarks
C1)
From our analysis of L3 BEC by , we have known that the anticorrelation (observed in GeV) in related to the denominator of the DR. In the , cooperates with (see Fig. 4). Provided that the MC events at Z0-pole by L3 Collaboration were reported, we are able to know whether or not the statement mentioned above is correct.
C2)
On the other hand, in the -model, the anticorrelation is explained by the imaginary part in the Levy canonical form. Indeed, through the analytic form of the exchange function in the -space, we understand that the anticorrelation in BEC is related to the negative behavior therein.
C3)
In the -model, we obtain the analytic formula, i.e., the series expansion of (see Eq. (19)). We can understand the partially negative behavior ( fm) in the Levy canonical form in Fig. 4.
The profile of source function in the -model is described as a product of the phase factor and . The source function (with fm and ) is shown in Fig. 5. We observe the partially negative behavior in the range fm, because of .
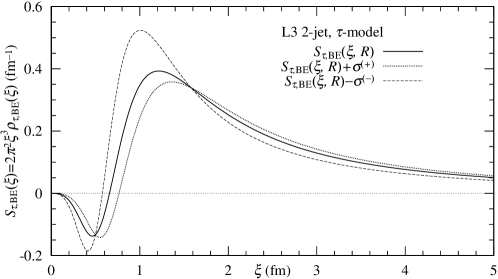
C4)
Two estimated values (stat) fm (2-jet) and (stat) fm (3-jet) by (see Table 6) are compared with (stat) fm (2-jet) and (stat) fm (3-jet) estimated by -model, respectively. It is remarked that the fitting parameters for the and -model with are almost coincident with each other.
| 2-jet | (-value %) | |||||
|---|---|---|---|---|---|---|
| /dof | 255/96 | 90.0/95 | (62.6) | |||
| (fm) | ||||||
| -model | /dof | 94.6/95 | 91.2/94 | (56.3) | ||
| (fm) | ||||||
| 3-jet | (-value %) | |||||
| /dof | 438/96 | 83.9/95 | (78.5) | |||
| (fm) | ||||||
| -model | /dof | 113/95 | 83.5/94 | (77.3) | ||
| (fm) | ||||||
From values in Table 4, we can estimate the values of full width of half maximum (FWHM) for 2-jet and 3-jet. The estimated FWHMs and HWHM (fm)s are presented in Table 7. It can be stressed that HWHM’s in the -model are coincident with ’s in Table 6. In , the HWHM’s increase about 10% than ’s in Table 6.
| (fm) | FWHM (fm) | HWHM (fm) | ||
|---|---|---|---|---|
| 2-jet | ||||
| -model | ||||
| 3-jet | ||||
| -model |
C5)
As is seen in Table 5, the Lorentz and Gaussian distributions are calculated from the Levy canonical form and , respectively. Moreover, the asymptotic behavior in the -space in our approach is calculated as follows:
| (20) |
However, in the -model, by use of the linear regression method, we have confirmed in the following:
| (21) |
This behavior (: 2-jet) is exactly expected in the Levy canonical form.
C6)
D1)
L3 Collaboration did not report the single ratios, and . Thus, in the present study we cannot analyze them. In the future, as DELPHI Collaboration did, L3 Collaboration would publish data on , and , we could examine the role of in BEC. See Appendix A.
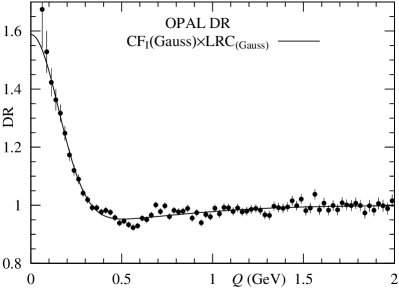
Moreover, concerning the systematic errors and uncertainties, we present calculation based on OPAL BEC at Z0-pole [4], because of no data on [5, 23], in Appendix C. According to the calculations using OPAL BEC data [4], we are able to understand the magnitude of the systematic error of estimated values with .
Acknowledgments. One of the authors (M.B.) would like to thank the colleagues of the Center for General Education at Shinshu University.
Appendix A Data on at -pole by DELPHI Collaboration
DELPHI Collaboration reported the data on at -pole by making use of JETSET 7.2 with DELSIM [5, 22, 23]. The data are analyzed by and in Fig. 6. seems to be better than . About data in the interval GeV, because of resonance effect from decays of and mesons, we do not use them in the present analysis. See also Ref. [5].
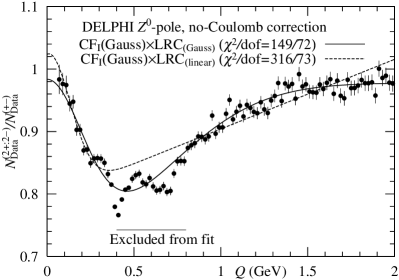
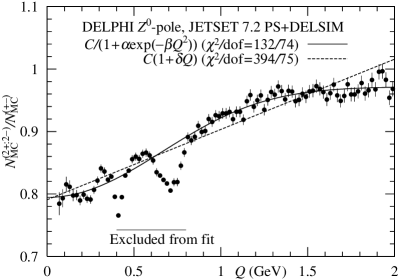
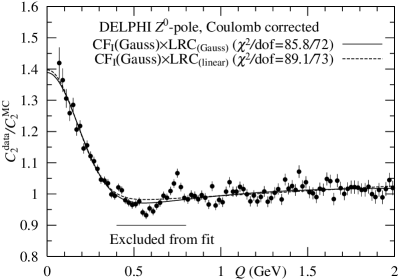
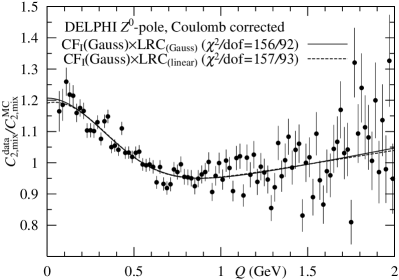
The present results as shown in Figs. 6 imply that the is preferable to the , except for . To confirm this statement, dof values (156/92 and 157/93) should be smaller.
In conclusion, we obtain the following results from analyses of and :
They are consistent with results shown in Ref. [5]. When we assume the for two DR’s, the following results are obtained:
| LRC | (fm) | (GeV-1)/(, (GeV-2)) | /dof | ||
| linear | 316/73 | ||||
| no-Coulomb correction | Gauss | (, ) | 149/72 | ||
| linear | — | — | 394/75 | ||
| Gauss | — | — | (, ) | 131/74 | |
| linear | 89.1/73 | ||||
| Coulomb correction | Gauss | (, ) | 85.8/72 | ||
| linear | 157/93 | ||||
| Coulomb correction | Gauss | (, ) | 156/92 | ||
| LRC | (fm) | (GeV-1) | /dof | ||
| linear | 107/73 | ||||
| linear | 161/93 |
Appendix B Levy canonical form and formulation obtained by the inverse Fourier transformation ( and )
1)
First, we show the proper time function calculated by L3 Collaboration [1]. According to the notation in Ref. [1], the Levy canonical form with is expressed as
| (22) |
The function is calculated by the inverse Fourier transformation as
| (23) | |||||
where cc and ss represent the products of and respectively. Using fm and , , and are calculated (Fig. 7). The magnitudes of area presented in Fig. 7 are and in the range of fm.
Combining the transverse and the rapidity distributions and , L3 Collaboration calculated their emitting source functions.
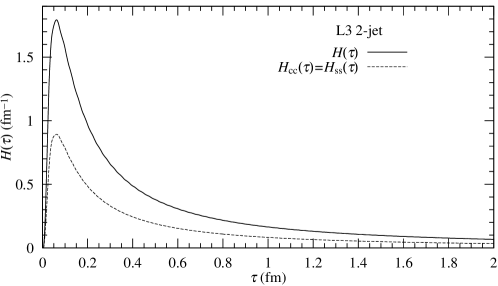
2)
Second, to analyze the 2-jet events, they introduced the transverse mass . With the following identification, , they started with the following Levy canonical form ():
| (24) |
By making use the inverse Fourier transformation, the probability () is calculated as
| (25) |
The results ( fm, ) are shown in Fig. 8. Two figures in Fig. 7 and Fig. 8 are different each other, because of difference between and .
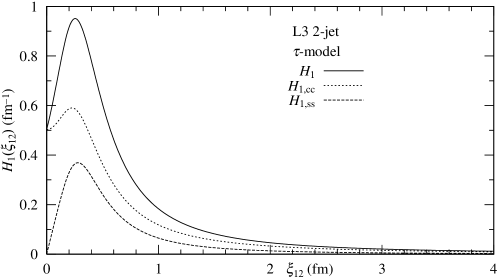
The magnitude of , is computed in the range fm. Because its magnitude, the name of probability for seems to be unsuitable. Note that present calculation is based on .
3)
Third, L3 Collaboration adopted the following effective Levy form (),
| (26) |
From Eq. (26), we calculate the probability as
| (29) |
where is used.
The probability ( fm, ) is shown in Fig. 9. That the magnitude of is computed. However, it is very strange that shows the partially negative behavior in the range of fm: and , which mean the positive and the negative magnitudes, respectively [19, 18].
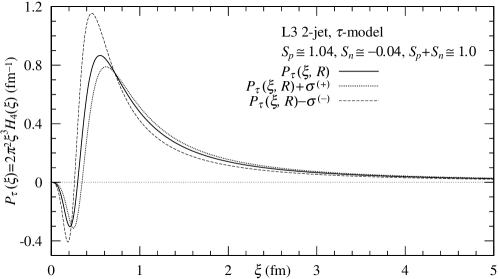
The exchange function in the -model is calculated as follows,
| (30) | |||||
Introducing the degree of coherence and , we obtain Eq. (2).
The stochastic density of exchange function in the -model is calculated by the inverse Fourier transformation () as
| (33) |
Appendix C Systematic errors and uncertainties
I) BEC at Z0-pole by OPAL Collaboration
To explain the systematic errors, we need the various SRs and DRs in BEC by L3 Collaboration. However, because of no-information on various distributions by L3 Collaboration, we treat the SR and DR by OPAL Collaboration. Using estimated values in Table 9, and the definition given in Ref. [4], we are able to calculate the systematic errors as
Finally, we obtain the following values:
Those values are compared with , and fm as is used [4]. The absolute value fm is larger than 0.150 fm [4].
by OPAL Collaboration. Notice that we have no-distribution with conditions “different data selection” and “use 0.05 GeV binning”.
| data | (fm) | /ndf | |
|---|---|---|---|
| (a) SR excluding and decay effect | 97.6/59 | ||
| (b) SR full data | 287/73 | ||
| (c) SR GeV | 273/53 | ||
| (d) DR full data | 98.1/73 |
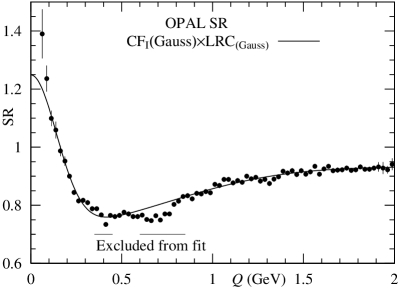
When we use the different definition with the largest positive and negative differences among ’s and , and among ’s and , where the suffix (a) means the first line (a) in Table 9, we obtain the following values and fm for the systematic uncertainties.
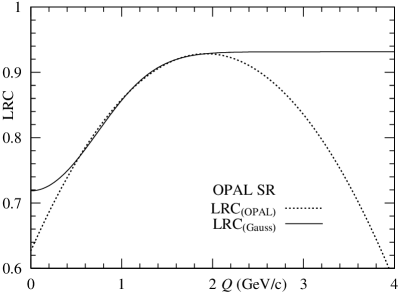
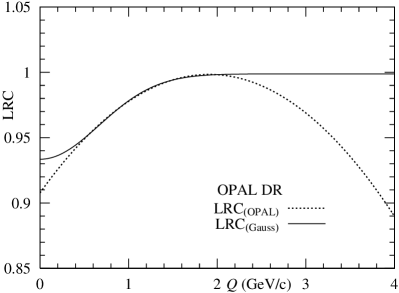
In Fig. 11, we show two behaviors related to and in SR and DR. The difference is observed in the range of GeV. On the contrary, in the range of GeV, the coincidences are seen.
II) BEC at Z0-pole by L3 Collaboration
References
- [1] P. Achard et al. [L3], Eur. Phys. J. C 71 (2011), 1648.
- [2] A. M. Sirunyan et al. [CMS], JHEP 03 (2020), 014.
- [3] V. Khachatryan et al. [CMS], JHEP 05 (2011), 029.
- [4] P. D. Acton et al. [OPAL], Phys. Lett. B 267 (1991) 143.
- [5] P. Abreu et al. [DELPHI], Phys. Lett. B 286 (1992), 201-210.
- [6] D. Decamp et al. [ALEPH], Z. Phys. C 54 (1992), 75-86.
- [7] T. Mizoguchi, S. Matsumoto and M. Biyajima, Phys. Rev. D 108 (2023) 5, 056014.
- [8] T. Mizoguchi, S. Matsumoto and M. Biyajima, Int. J. Mod. Phys. A 37 (2022) 25, 2250148.
- [9] R. Shimoda, M. Biyajima and N. Suzuki, Prog. Theor. Phys. 89 (1993), 697-708.
- [10] G. C. Wick, Phys. Rev. 96 (1954), 1124-1134.
- [11] M. Biyajima, Phys. Lett. B 92 (1980), 193.
- [12] M. Biyajima, A. Bartl, T. Mizoguchi, O. Terazawa and N. Suzuki, Prog. Theor. Phys. 84 (1990), 931-940.
- [13] G. A. Kozlov, O. V. Utyuzh, G. Wilk and Z. Wlodarczyk, Phys. Atom. Nucl. 71 (2008), 1502-1504.
- [14] R. Hanbury Brown and R. Q. Twiss, Nature 178 (1956), 1046-1048.
- [15] G. Goldhaber, S. Goldhaber, W. Y. Lee and A. Pais, Phys. Rev. 120 (1960), 300-312
- [16] V. V. Uchaikin, and V. M. Zolotarev, “Chance and stability: Stable distributions and their applications,” VSP, Utrecht, Netherlands, 1999:
- [17] V. M. Zolotarev, “Integral Transformation of Distributions and Estimates of Parameters of Multidimensional Spherically Symmetric Stable Laws” in “Contributions to Probability” (Academic Press, New York 1981), pp. 283-305.
- [18] V. M. Zolotarev, “One-dimensional stable distributions,” Translations of Mathematical Monographs Vol. 65, American Mathematical Society, Providence, 1986.
- [19] J. P. Nolan, “Univariate Stable Distributions: Models for Heavy Tailed Data,” Springer Nature, Switzerland, 2020.
- [20] F. Oberhettinger, “Tables of Fourier Transforms and Fourier Transforms of Distributions,” Springer, Berlin/Heidelberg, 1990.
- [21] I. S. Gradshteyn and I. ,M. Ryzhik, “Table of Integrals, Series, and Products,” 8th edition, Academic Press, Waltham, 2014.
- [22] T. Sjostrand and M. Bengtsson, Comput. Phys. Commun. 43 (1987), 367.
- [23] DELPHI Collaboration, “Comparison of data with QCD models,” contributed paper to the LP-EPS conference, Geneva, August 1991.