Analysis of flux-integrated semi-exclusive cross sections for charged current quasi-elastic neutrino scattering off 40Ar at energies available at the MicroBooNE experiment
Abstract
Flux-integrated semi-exclusive differential and integral cross sections for quasi-elastic neutrino charged-current scattering on argon are analyzed. We calculate these cross sections using the relativistic distorted-wave impulse approximation and compare with recent MicroBooNE data. We found that the measured cross sections can be described well within the experimental uncertainties with value of the nucleon axial mass GeV. The contribution of the exclusive channel to the flux-integrated inclusive cross sections is about 50%.
1 Introduction
Current Acero:2019ksn ; Abe:2020vdv and future Acciarri:2016crz ; Abe:2018uyc neutrino oscillation experiments use high-intensity muon-(anti)neutrino beams that are not monoenergetic and peak in the energy range from tens of MeV to a few GeV. The goal of these experiments is to measure oscillation features in the neutrino energy spectrum reconstructed at far detectors. To evaluate the oscillation parameters, the probabilities of neutrino oscillations as functions of neutrino energy are measured. The accuracy to which they can extract neutrino oscillation parameters depends on their ability to determine the individual energy of detected neutrino. This requires detailed understanding of neutrino interactions with nuclei.
In the energy range – 5 GeV charged-current (CC) quasielastic (QE) scattering and scattering induced by two-body meson exchange current (MEC), resonance production and deep inelastic process yield the main contributions to the neutrino-nucleus interaction. The understanding of these interactions comes through cross sections measurements on various channels. The incident neutrino energy can be reconstructed using the calorimetric method, which rely not only on the lepton and hadron energies visible in the final state after the neutrino has interacted but also on models of the neutrino-nucleus interactions that are implement in neutrino events generators.
The CCQE interaction forms a significant contribution in many accelerator-based neutrino experiments Aguilar-Arevalo:2010zc ; Abe:2014iza ; Fiorentini:2013ezn ; Walton:2014esl ; Betancourt:2017uso ; Abe:2018pwo ; Abratenko:2019jqo ; Abratenko:2020acr ; Abratenko:2020sga . Because the CCQE interaction represents a two particle scattering process, its final state topology is simple with an easy identifiable lepton, and neutrino energy may be estimated using the outgoing lepton kinematics, i.e. applying kinematical methods. However, as neutrino beams have broad energy distributions, various contributions to the inclusive cross section, where only final lepton is detected, can significantly overlap with each other making it difficult to identify the channels of neutrino interaction. The interpretation of the inclusive CCQE data is complicated because of the presence of other interactions such as MEC and pion production, where the pion is absorbed in the residual nucleus. So, when only the muon is detected, the event can easily be mistaken as a CCQE interaction and application of the kinematic method will lead to a bias in the neutrino energy estimation.
Compared to inclusive experiments, semi-exclusive scattering provides additional information about hadrons in the final state. In this process the neutrino removes a single intact nucleon from the nucleus without production of any additional particles. For these CC1p0 events the experimental signature requires the identification of a neutrino interaction vertex with an outgoing lepton, exactly one outgoing proton, and no additional particles, which is relatively straight forward to measure. The information about hadrons will improve the accuracy of reconstruction of the incoming neutrino energy. Understanding the interaction of neutrino with argon nuclei is of particular importance, since neutrino oscillation experiments such as DUNE Acciarri:2016crz and SBN Antonello:2015lea employ neutrino detectors using liquid argon time projector chamber (LArTPs).
Weak interactions of neutrinos probe the nucleus in a similar way as electromagnetic electron interactions. Of course, there are a number of differences with neutrino scattering, the most important one being the absence of the axial current contribution. Nevertheless the influence of the nuclear medium is the same as in neutrino-nucleus scattering data. Precise electron-scattering data gives a unique opportunity to validate the nuclear model employed in neutrino physics. Therefore, the detailed comparison with data is a necessary test for any theoretical model used to describe the CC1p0 cross sections.
Systematic measurements of cross sections were performed at Saclay Frullani:1984nn , NIKHEF Dieperink:1990uk , and JLab Fissum:2004we ; Dutta:2003yt ; Gu:2020shc . The impact of the MEC on the nuclear response functions and differential cross section for the knockout of protons from 16O was studied in Ref. Fissum:2004we . It was shown that explicit inclusion of the two-body current contribution does not markedly improve the overall agreement between the data and calculated cross sections. Unfortunately, the cross section data for the semi-exclusive lepton scattering on argon in the relevant energy range are rather scare. There are only experimental data for GeV electron scattering of 40Ar Gu:2020shc and flux-integrated differential CC1p0 cross sections for Ar scattering, measured with the MicroBooNE detector Abratenko:2020sga . On the other hand the structure of 40Ca and 40Ar nuclei are almost identical, and for calcium high resolution exclusive experiments were carried out at Tokyo Nakamura:1974zz ; Nakamura:1976kn , Saclay Mougey:1976sc , and NIKHEF Kramer:1990 ; Kramer:1989uiu ; Kramer:2000kc .
The data analysis of and processes was performed in Refs. Fissum:2004we ; Kelly:1996hd ; Udias:2001tc ; Kelly:2005is ; Maieron:2003df ; Meucci:2003cv ; Martinez:2005xe within the relativistic distorted-wave impulse approximation (RDWIA) Picklesimer:1985ey ; Picklesimer:1986wj ; Kelly:1998ti , using a relativistic shell model approach. The implementation of the final state interaction (FSI) of the ejected nucleon has been done differently. The RDWIA approach describes with high degree of accuracy the experimental shape of the outgoing particle momentum distributions. In order to reproduce experimental cross sections, normalizations of the bound-state wave functions were fit to the data and identified with the spectroscopic factors. The semi-inclusive process for CCQE reactions was recently discussed in Refs. Gonzalez-Jimenez:2021ohu ; Amaro:2021sec .
In this work we calculated the flux-integrated differential cross sections of 40Ar interactions with the RDWIA approach, using the Booster Neutrino Beam (BNB) at Fermilab Aguilar-Arevalo:2008yp . This approach was successfully applied in Refs. Butkevich:2007gm ; Butkevich:2009cp ; Butkevich:2010cr ; Butkevich:2012zr ; Butkevich:2020ysf for calculation of the CCQE semi-exclusive and inclusive cross sections for the electron and neutrino scattering on 12C, 16O, 40Ca, and 40Ar nuclei. The aim of this work is to test the RDWIA predictions against the MicroBooNE data Abratenko:2020sga . Within this model we estimated the range of the values of nucleon axial mass from the measured CC1p0 flux-integrated differential cross sections.
The outline of this article is as follows. In Sec.II we present briefly the formalism for the CCQE semi-inclusive scattering process and basic aspects of the RDWIA approach, used for the calculation. The results are presented and discussed in Sec.III. Our conclusions are summarized in Sec.IV.
2 Formalism of quasi-elastic scattering and RDWIA
In this section we consider shortly the formalism used to describe electron and neutrino quasi-elastic exclusive
| (2.1) |
and inclusive
| (2.2) |
scattering off nuclei in the one-photon (W-boson) exchange approximation. Here labels the incident lepton [electron or muon (anti)neutrino], and represents the scattered lepton (electron or muon), and are the initial and final lepton momenta, , and are the initial and final target momenta, is the ejectile nucleon momentum, is the momentum transfer carried by the virtual photon (W-boson), and is the photon (W-boson) virtuality.
2.1 CCQE lepton-nucleus cross sections
In the laboratory frame the differential cross section for exclusive electron () and (anti)neutrino () CC scattering can be written as
| (2.3a) | ||||
| (2.3b) | ||||
where is the solid angle for the lepton momentum, is the solid angle for the ejectile nucleon momentum, is the fine-structure constant, 1.16639 MeV-2 is the Fermi constant, is the Cabbibo angle ( 0.9749), is the lepton tensor, and and are correspondingly the electromagnetic and weak CC nuclear tensors.
For exclusive reactions in which only a single discrete state or narrow resonance of the target is excited, it is possible to integrate over the peak in missing energy and obtain a fivefold differential cross section of the form
| (2.4a) | ||||
| (2.4b) | ||||
where is a recoil factor
| (2.5) |
is solution to equation where , and and are masses of the target and recoil nucleus, respectively. Note, that missing momentum is and missing energy is defined by . The differential cross sections ( can be obtained by integrating the exclusive cross sections (2.4a) and (2.4b) over solid angle for the ejectile nucleon.
All information about the nuclear structure and FSI effects is contained in the electromagnetic and weak CC hadronic tensors, and , which are given by the bilinear products of the transition matrix elements of the nuclear electromagnetic or CC operator between the initial nucleus state and the final state as
| (2.6) |
where the sum is taken over undetected states.
In the inclusive reaction (2.2) only the outgoing lepton is detected and lepton scattering cross sections in term of nuclear response functions can be written as
| (2.7a) | ||||
| (2.7b) | ||||
where
| (2.8) |
is the Mott cross section. The coupling coefficient and , the expression of which are given in Ref. Butkevich:2007gm are kinematic factors depending on the lepton’s kinematics. The response functions are given in terms of components of the inclusive hadronic tensors (Butkevich:2007gm ) and depend on the variables or .
The experimental data of the reaction are usually presented in terms of the reduced cross section
| (2.9) |
where and are phase-space factors for electron and neutrino scattering and is the corresponding elementary cross section for the lepton scattering from the moving free nucleon. The reduced cross section is an interesting quantity that can be regarded as the nucleon momentum distribution modified by FSI. Therefore these cross sections for (anti)neutrino scattering off nuclei are similar to the electron scattering apart from small differences at low beam energy due to effects of Coulomb distortion of the incoming electron wave function. Precise electron reduced cross section data can be used to validate the neutrino reduced cross sections employed in neutrino generators.
2.2 Model
We describe genuine QE electron-nuclear scattering within the RDWIA approach. This formalism is based on the impulse approximation (IA), assuming that the incoming lepton interacts with only one nucleon of the target, which is subsequently emitted. In this approximation the nuclear current is written as a sum of single-nucleon currents and the nuclear matrix element in Eq. (2.6) takes the form
| (2.10) |
where is the vertex function, is the recoil-corrected momentum transfer, is the invariant mass and and are relativistic bound-state and outgoing wave functions.
For electron scattering, we use the CC2 electromagnetic vertex function for a free nucleon DeForest:1983ahx
| (2.11) |
where , and are the Dirac and Pauli nucleon form factors. The single-nucleon charged current has structure . For a free-nucleon vertex function we use the CC2 vector current vertex function
| (2.12) |
and the axial current vertex function
| (2.13) |
The weak vector form factors and are related to the corresponding electromagnetic form factors and for protons and neutrons by the hypothesis of the conserved vector current. We use the approximation of Ref. Mergell:1995bf for the Dirac and Pauli nucleon form factors. Because the bound nucleons are off-shell we employ the de Forest prescription DeForest:1983ahx and Coulomb gauge for the off-shell vector current vertex . The vector-axial and pseudoscalar form factors are parametrized using a dipole approximation:
| (2.14) |
where , is the axial mass that controls -dependence of , and is the pion mass.
In the RDWIA calculations the independent particle shell model (IPSM) is assumed for the nuclear structure. In Eq.(2.10) the relativistic bound-state wave functions for nucleons are obtained as the self-consistent solutions of a Dirac equation, derived within a relativistic mean-field approach from a Lagrangian containing , , and mesons Horowitz:1981xw . These functions were calculated by the TIMORA code Horowitz:1991 with the normalization factors relative to full occupancy of the IPSM orbital of 40Ca. For 40Ca and 40Ar an average factor . This estimation of depletion of hole states follows from the RDWIA analysis of 40Ca data Butkevich:2012zr . The source of the reduction of the spectroscopic factors with respect to the mean field values are the short-range and tensor correlations in the ground state, leading to the appearance of the high-momentum and high-energy component in the nucleon distribution in the target. Mean values of the proton and neutron binding energies and occupancies of shells are given also in Ref. Butkevich:2012zr .

In the RDWIA model, final state interaction effects for the outgoing nucleon are taken into account. The system of two coupled first-order Dirac equations is reduced to a single second-order Schrödinger-like equation for the upper component of the Dirac wave function . This equation contains equivalent nonrelativistic central and spin-orbit potentials which are functions of the relativistic, energy dependent, scalar, and vector optical potentials. The optical potential consists of areal part, which describes the rescattering of the ejected nucleon and an imaginary part which account for its absorption into unobserved channels. We use the LEA program Kelly:1996 for the numerical calculation of the distorted wave functions with the EDAD1 parametrization Cooper:1993nx of the relativistic optical potential for calcium. This code was successfully tested in Ref. Butkevich:2012zr against data for electron scattering off 40Ca. In Ref. Butkevich:2012zr the reduced cross sections as functions of missing momentum calculated in the RDWIA approach for the 40Ca reaction are shown in figures 1 and 2 with NIKHEF data and provide a good description of the measured distributions. Neutrino and antineutrino cross sections are also shown in figure 1 for comparison.

The inclusive cross sections with the FSI effects, taking into account short-range nucleon-nucleon () correlations were calculated using the method proposed in Ref. Butkevich:2007gm with the nucleon high-momentum and high-energy distribution from Ref. CiofidegliAtti:1995qe that was renormalized to value of 13% for calcium and argon. The contribution of the -correlated pairs is evaluated in impulse approximation, i.e., the virtual photon couples to only one member of the -pair.

In Ref. Butkevich:2020ysf was shown that this approach describes well the electron scattering data for carbon, calcium, and argon at different kinematics. The calculated and measured cross sections are in agreement within the experimental uncertainties.
3 Results and analysis
The first measurement of exclusive CCQE-like neutrino-argon interaction cross sections, performed using the MicroBooNE liquid argon time projector chamber (LArTPC) neutrino detector was presented in Ref. Abratenko:2020sga . A specific subset of CCQE-like interactions (CC1p0 interactions), includes CC scattering events with a detected muon and exactly one proton, with momenta greater than 100 and 300 MeV/c, respectively. The data were taken in a phase-space region that corresponds to GeV/c, GeV/c, , and . After the application of the event selection requirement only 410 CC1p0 candidate events were retained.
3.1 Semi-exclusive CCQE double differential cross section
For these CC1p0 events were measured the flux-integrated differential cross sections in muon and proton momentum and angle, and as a function of the calorimetric measured energy and reconstructed momentum transfer. The statistical uncertainty of the integrated measured CC1p0 cross section is 15.9% and the systematic uncertainty sums to 26.2%. The MicroBooNE detector is located along the Booster Neutrino Beam at Fermilab. The BNB energy spectrum extends to 2 GeV and peaks around 0.7 GeV Aguilar-Arevalo:2008yp . In this work we calculate within the RDWIA model with GeV and 1.2 GeV the flux-integrated CCQE semi-exclusive cross sections, taking into account the MicroBooNE momentum thresholds for muons and protons. Thus, we do not consider MEC nor the process where charged pions may be produced in the final state.
The flux-integrated double-differential cross section of the semi-exclusive CCQE scattering is presented in figure 1, which shows the cross section as a function of muon momentum and muon scattering angle . Here the result was obtained in the RDWIA approach with the value of the nucleon axial mass GeV. The maximum of the calculated cross section is in the range GeV/c and . So, neutrino interactions with energy higher than 1 GeV and high values of that corresponds to low momentum transfer, yield the main contribution to the measured cross sections.
Figures 2 and 3 show the flux-integrated cross sections as functions of for several bins of the muon scattering angle. On can observe that within the RDWIA model with GeV the cross sections in the region of the QE peak are predicted to be on about 20% higher than cross sections calculated with GeV.

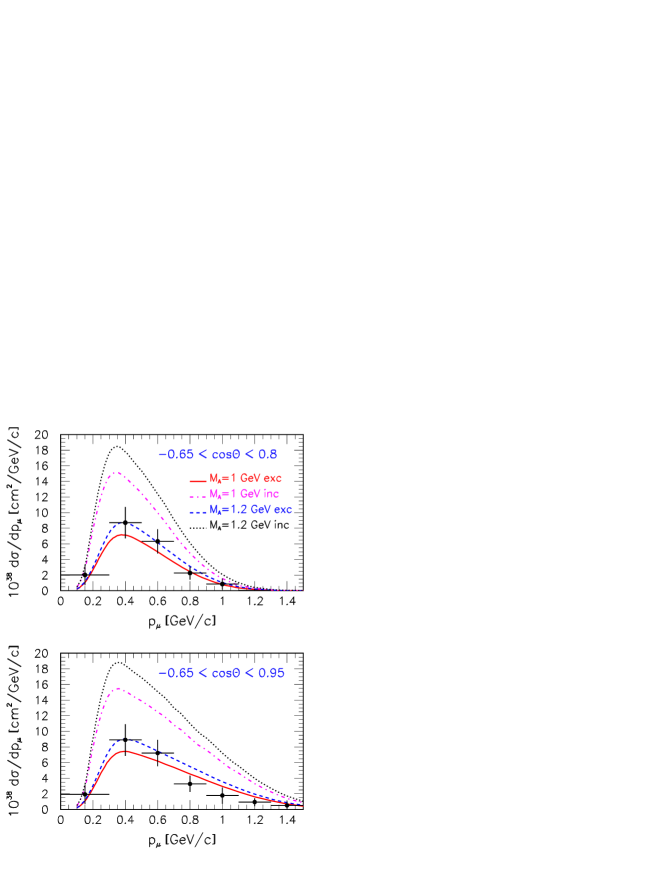
3.2 Semi-exclusive CCQE single differential cross section
Figure 4 shows the flux-integrated differential cross section as a function of the cosine of the measured muon scattering angle. In Ref. Abratenko:2020sga was shown that the bin migration effects on this measurement are small and within the assessed uncertainties. The data are compared to the RDWIA calculations.

As can be seen in figure, calculated cross sections are in overall agreement with data, except for the highest bin, where the measured cross section is lower than the theoretical predictions. We note that this bin corresponds to low-momentum transfer ( (GeV/c)2), where the nuclear effects are significant and the neutrino interactions with energy GeV (high energy range of the BNB neutrino flux) give the main contribution to the measured cross section.
As the differential , , and cross sections include contributions from all muon scattering angles, their agreement with the theoretical calculations is effected by these inclusions. In Ref. Abratenko:2020sga the relevant cross sections in the case where events with are excluded and in the full available phase space are presented. Figure 5 shows measured differential cross section as a function of muon momentum for and compared to the RDWIA calculations. Removing events with significantly improves the agreement between data and theory at GeV/c. The calculated flux-integrated cross sections for inclusive reaction are shown as well in figure 5 for the full measured phase space and for events with . The contribution of channel with MeV/c to the inclusive cross section increases slowly from 35% at GeV/c to 50% at GeV/c. The value of muon momentum where the maximum of cross sections appears is about 0.4 GeV/c.
The differential cross sections as functions of proton momentum are shown in Figure 6 with and without events with . Also shown are the results obtained in the RDWIA. Overall, agreement is observed between data and calculations, even for the full event sample without the requirement. Figure 6 demonstrates that the measured proton momentum distribution is wider than the muon momentum distribution and the maximum in the cross section is located at GeV/c.
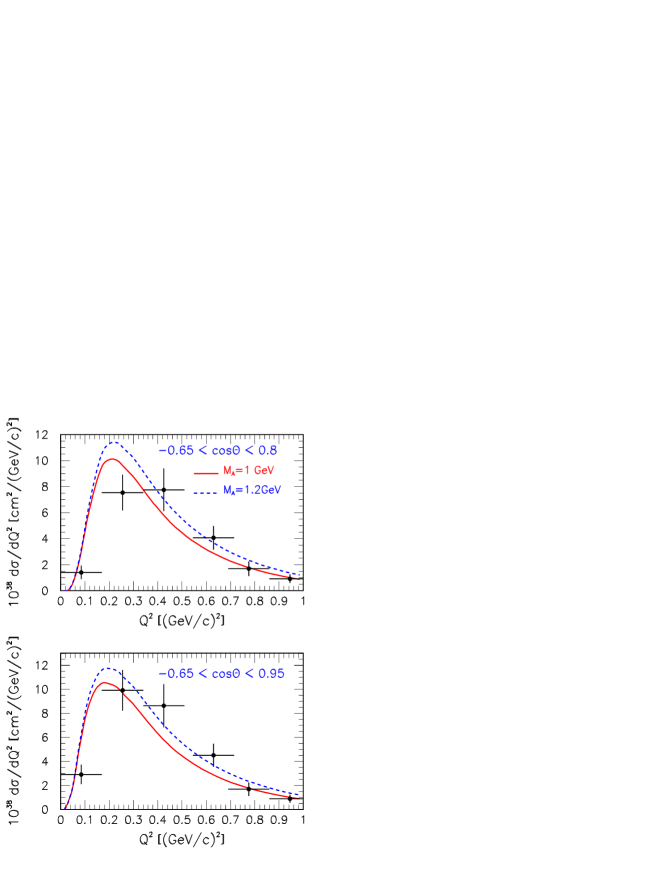
Finally, figure 7 shows the flux-integrated differential cross sections as functions of for and . The data are compared to the RDWIA calculations. Note, that in the bin (GeV/c)2 the agreement between data and theoretical result for the full phase space is better than for event sample with the requirement. As can be seen in figure 7 at (GeV/c)2, the measured cross section is significantly lower than the theoretical prediction. Note, that at low the cross section depends weakly on the value of axial mass and distributions are controled by nuclear effects.
We calculated the value for the agreement of the RDWIA prediction with data as simple sum of those values obtained for , , and distributions separately. As follows from this analysis the values of /degree of freedom (d.o.f.) for GeV are (1.36) for and (2.22) for . The measured integrated cross sections obtained by integrating cross section over and are equal to cm2 and cm2, correspondingly Abratenko:2020sga . The calculated with GeV cross section values of cm2 for and cm2 for the full measured phase space agree also with data. On the other hand the statistical and systematic precision of the MicroBooNE data are insufficient for current needs. Thus, within the RDWIA approach the measured flux-integrated CC1p0 differential and integral cross sections can be described well within the experimental errors with GeV. These values of are in agreement with the best fit values GeV and GeV obtained from the CCQE-like fit of the MiniBooNE and MINERvA data in Refs. Wilkinson:2016wmz ; Butkevich:2018hll .
4 Conclusions
In this work we study the semi-exclusive CCQE Ar scattering. Within the RDWIA approach the flux-integrated CC1p0 differential and integral cross sections were calculated with GeV and 1.2 GeV. It was shown that the maximum of the double differential cross sections is in the range GeV and . The calculated single differential cross sections were tested against the MicroBooNE data. We found that the muon angular distribution is in overall agreement with measured one except at small muon scattering angle, where the measured cross section is about lower than the theoretical predictions.
The differential cross sections calculated in the RDWIA approach with GeV and 1.2 GeV for , and with GeV for full phase space are in agreement with data. The calculated integral CC1p0 cross sections also agree with data even for the full event sample without the requirement. The contribution of the exclusive channel with MeV/c to the inclusive cross sections is about 50% at GeV/c. The measurements of the double and single differential exclusive CC1p0 cross sections on 40Ar with statistical and systematical uncertainty better than 20% allow to constrains models of the CCQE interaction and values of that use in precision neutrino oscillation analysis.
Acknowledgments
The author greatly acknowledges A. Habig for fruitful discussions and a critical reading of the manuscript.
References
- (1) NOvA collaboration, M. A. Acero et al., First Measurement of Neutrino Oscillation Parameters using Neutrinos and Antineutrinos by NOvA, Phys. Rev. Lett. 123 (2019) 151803, [1906.04907].
- (2) T2K collaboration, K. Abe et al., T2K measurements of muon neutrino and antineutrino disappearance using protons on target, Phys. Rev. D. 103 (2021) L011101, [2008.07921].
- (3) DUNE collaboration, R. Acciarri et al., Long-Baseline Neutrino Facility (LBNF) and Deep Underground Neutrino Experiment (DUNE): Conceptual Design Report, Volume 1: The LBNF and DUNE Projects, [1601.05471].
- (4) Hyper-Kamiokande collaboration, K. Abe et al., Hyper-Kamiokande Design Report, [1805.04163].
- (5) MiniBooNE collaboration, A. A. Aguilar-Arevalo et al., First Measurement of the Muon Neutrino Charged Current Quasielastic Double Differential Cross Section, Phys. Rev. D. 81 (2010) 092005, [1002.2680].
- (6) T2K collaboration, K. Abe et al., Measurement of the charged-current quasielastic cross section on carbon with the ND280 detector at T2K, Phys. Rev. D. 92 (2015) 112003, [1411.6264].
- (7) MINERvA collaboration, G. A. Fiorentini et al., Measurement of Muon Neutrino Quasielastic Scattering on a Hydrocarbon Target at GeV, Phys. Rev. Lett. 111 (2013) 022502, [1305.2243].
- (8) MINERvA collaboration, T. Walton et al., Measurement of muon plus proton final states in interactions on hydrocarbon at 4.2 GeV, Phys. Rev. D. 111 (2015) 071301, [1409.4497].
- (9) MINERvA collaboration, M. Betancourt et al., Direct Measurement of Nuclear Dependence of Charged Current Quasielasticlike Neutrino Interactions Using MINERA, Phys. Rev. Lett. 119 (2017) 082001, [1705.03791].
- (10) T2K collaboration, K. Abe et al., Characterization of nuclear effects in muon-neutrino scattering on hydrocarbon with a measurement of final-state kinematics and correlations in charged-current pionless interactions, Phys. Rev. D. 98 (2018) 032003, [1802.05078].
- (11) MicroBooNE collaboration, P. Abratenko et al., First Measurement of Inclusive Muon Neutrino Charged Current Differential Cross Sections on Argon at 0.8 GeV with the MicroBooNE Detector, Phys. Rev. Lett.123 (2019) 131801, [1905.09694].
- (12) MicroBooNE collaboration, P. Abratenko et al., First Measurement of Differential Charged Current Quasielastic-like -Argon Scattering Cross Sections with the MicroBooNE Detector, Phys. Rev. Lett.125 (2020) 201803, [2006.00108].
- (13) MicroBooNE collaboration, P. Abratenko et al., Measurement of differential cross sections for -Ar charged-current interactions with protons and no pions in the final state with the MicroBooNE detector, Phys. Rev. D.102 (2020) 112013, [2010.02390].
- (14) MicroBooNe, LAr1-ND, ICARUS-WA104 collaboration, M. Antonello et al., A Proposal for a Three Detector Short-Baseline Neutrino Oscillation Program in the Fermilab Booster Neutrino Beam, [1503.01520].
- (15) S. Frullani and J. Mougey, Single Particle Properties of Nuclei Through (e, e′ p) Reactions, Adv. Nucl. Phys. 14 (1984) 1–283.
- (16) A. E. L. Dieperink, P. K. A. Huberts, On high resolution (e,e′,p) reactions, Ann. Rev. Nucl. Part. Sci. 40 (1990) 239–284.
- (17) Jefferson Lab Hall A collaboration, K. G. Fissum et al., The Dynamics of the quasielastic 16O(e, e′ p) reaction at =~ 0.8 (GeV/c)2, Phys. Rev. C.70 (2004) 034606, [nucl-ex/0401021].
- (18) JLab E91013 collaboration, D. Dutta et al., A Study of the quasielastic (e,e′ p) reaction on 12C, 56Fe and 97Au, Phys. Rev. C.68 (2003) 064603, [nucl-ex/0303011].
- (19) Jefferson Lab Hall A collaboration, L. Gu et al., Measurement of the Ar(e,e′ p) and Ti(e,e′ p) cross sections in Jefferson Lab Hall A, Phys. Rev. C.103 (2021) 034604, [2012.11466].
- (20) K. Nakamura, S. Hiramatsu, T Kamae, H. Muramatsu, H. Izutsu, Y. Watase Reaction 40Ca(e, e’ p) and Observation of the 1s Proton State, Phys. Rev. Lett. 33 (1974) 853–855.
- (21) K. Nakamura, S. Hiramatsu, T Kamae, H. Muramatsu, H. Izutsu, Y. Watase, The 27Al, 40Ca and 51V(e, e′ p) Reactions and Observation of Deep Hole States, Nucl. Phys. A 271 (1976) 221–234.
- (22) J. Mougey, M. Bernheim, A. Bussiere, A. Gillibert, Xuan Ho Phan, M. Priou, D. Royer, I. Sick, G. J. Wagner, Quasifree (e, e′ p) Scattering on 12C, 28Si, 40Ca and 58Ni, Nucl. Phys. A 262 (1976) 461–492.
- (23) G. J. Kramer, The proton spectral function of 40Ca and 48Ca studing with the (e, e′ p) reaction. An investigation of ground-state correlations. PhD thesis, Amsterdam U., 1990 (unpublished).
- (24) G. J. Kramer et al., Proton ground-state correlations in 40Ca studied with the reaction Ca(e, e′ p) 49K, Phys. Lett. B. 227 (1989) 199–203.
- (25) G. J. Kramer, H. P. Blok, Louk Lapikas, A Consistent analysis of (e,e′ p) and (d,3H) experiments, Nucl. Phys. A 679 (2001) 267–286, [nucl-ex/0007014].
- (26) J. J. Kelly, Nucleon knockout by intermediate-energy electrons, Adv. Nucl. Phys. 23 (1996) 75–294.
- (27) J. M. Udias and J. A. Caballero and E. Moya de Guerra and Javier R. Vignote and A. Escuderos, Relativistic mean field approximation to the analysis of 160(e, e′ p) 15N data at less than 0.4(GeV/c)2, Phys. Rev. C 64 (2001) 024614, [nucl-ex/0101038].
- (28) J. J. Kelly, RDWIA analysis of 12C(e, e′ p) for 2 (GeV/c)2, Phys. Rev. C 71 (2005) 064610, [nucl-ex/0501079].
- (29) C. Maieron, M. C. Martinez, J. A. Caballero, J. M. Udias, Nuclear model effects in charged current neutrino nucleus quasielastic scattering, Phys. Rev. C 68 (2003) 048501. [nucl-ex/0303075].
- (30) Andrea Meucci, Carlotta Giusti, Franco Davide Pacati, Relativistic Green’s function approach to charged current neutrino nucleus quasielastic scattering, Nucl. Phys. A 739 (2004) 277–290, [nucl-ex/0311081].
- (31) M. C. Martinez, P. Lava, N. Jachowicz, J. Ryckebusch, K. Vantournhout, J. M. Udias, Relativistic models for quasi-elastic neutrino scattering, Phys. Rev. C 73 (2006) 024607, [nucl-ex/0505008].
- (32) A. Picklesimer, J. W. Van Orden, Stephen J. Wallace, Final State Interactions and Relativistic Effects in the (Polarized), Reaction, Phys. Rev. C 32 (1985) 1312–1326.
- (33) A. Picklesimer, J. W. Van Orden, A Formal Framework for the Electroproduction of Polarized Nucleons From Nuclei, Phys. Rev. C 35 (1987) 266–279.
- (34) J. J. Kelly, Channel coupling in A(polarized e, e′ polarized N)B reactions, Phys. Rev. C 59 (1999) 3256–3274, [nucl-ex/9809090].
- (35) R. Gonzalez-Jimenez, M. B. Barbaro, J. A. Caballero, T. W. Donnelly, N. Jachowicz, G. D. Megias, K. Niewczas, A. Nikolakopoulos, J. W. Van Orden, J. M. Udias, Neutrino energy reconstruction from semi-inclusive samples [2104.01701].
- (36) J. E. Amaro, M. B. Barbaro, J. A. Caballero, T. W. Donnelly, R. Gonzalez-Jimenez, G. D. Megias, and I. Ruiz Simo Neutrino-Nucleus scattering in the SuSA model [2106.02857].
- (37) MiniBooNE collaboration, A. A. Aguilar-Arevalo et al., The Neutrino Flux prediction at MiniBooNE, Phys. Rev. D. 79 (2009) 072002, [0806.1449].
- (38) A. V. Butkevich, Sergey. A. Kulagin, Quasi-elastic neutrino charged-current scattering cross sections on oxygen, Phys. Rev. C 76 (2007) 045502, [0705.1051].
- (39) A. V. Butkevich, Quasi-elastic neutrino charged-current scattering off C-12, Phys. Rev. C 80 (2009) 014610, [0904.1472].
- (40) A. V. Butkevich, Analysis of flux-integrated cross sections for quasi-elastic neutrino charged-current scattering off 12C at MiniBooNE energies, Phys. Rev. C 82 (2010) 055501, [1006.1595].
- (41) A. V. Butkevich, Quasi-elastic neutrino charged-current scattering off medium-heavy nuclei: 40Ca and 40Ar, Phys. Rev. C 85 (2012) 065501, [1204.3160].
- (42) A. V. Butkevich, S. V. Luchuk, Inclusive electron scattering off 12C, 40Ca , and 40Ar : Effects of the meson exchange currents, Phys. Rev. C 102 (2020) 024602, [2004.04780].
- (43) T. De Forest, Off-Shell electron Nucleon Cross-Sections. The Impulse Approximation, Nucl. Phys. A. 392 (1983) 232–248.
- (44) P. Mergell, Ulf G. Meissner, D. Drechsel, Dispersion theoretical analysis of the nucleon electromagnetic form-factors, Nucl. Phys. A. 596 (1996) 367–396, [hep-ph/9506375].
- (45) C. J. Horowitz, Brian D. Serot, Selfconsistent Hartree Description of Finite Nuclei in a Relativistic Quantum Field Theory, Nucl. Phys. A. 368 (1981) 503–528.
- (46) C. J. Horowitz, D. P. Murdock, B D. Serot, The Relativistic Impulse Approximation, In: K. Langanke, J. A. Maruhn, S. E. Koonin (eds) Computation Nuclear. Physics. 1: , Springer, Berlin, Heidelberg (1991), pg. 129, .
- (47) E. D. Cooper, S. Hama, B. C. Clark, R. L. Mercer, Global Dirac phenomenology for proton nucleus elastic scattering, Phys. Rev. C 47 (1993) 297–311.
- (48) J. J. Kelly, [http://www.physics.umd.edu/enp/jjkelly/LEA].
- (49) C. Ciofi degli Atti, S. Simula, Realistic model of the nucleon spectral function in few and many nucleon systems, Phys. Rev. C 53 (1996) 1689. [nucl-th/9507024].
- (50) C. Wilkinson et al., Testing charged current quasi-elastic and multinucleon interaction models in the NEUT neutrino interaction generator with published datasets from the MiniBooNE and MINERA experiments, Phys. Rev. D. 93 (2016) 072010, [1601.05592].
- (51) A. V. Butkevich, and S. V. Luchuk, Testing of quasi-elastic neutrino charged-current and two-body meson exchange current models with the MiniBooNE neutrino data and analysis of these processes at energies available at the NOvA experiment Phys. Rev. D. 99 (2019) 093001, [1812.11073].