Analysis and Design of Thompson Sampling
for Stochastic Partial Monitoring
Abstract
We investigate finite stochastic partial monitoring, which is a general model for sequential learning with limited feedback. While Thompson sampling is one of the most promising algorithms on a variety of online decision-making problems, its properties for stochastic partial monitoring have not been theoretically investigated, and the existing algorithm relies on a heuristic approximation of the posterior distribution. To mitigate these problems, we present a novel Thompson-sampling-based algorithm, which enables us to exactly sample the target parameter from the posterior distribution. Besides, we prove that the new algorithm achieves the logarithmic problem-dependent expected pseudo-regret for a linearized variant of the problem with local observability. This result is the first regret bound of Thompson sampling for partial monitoring, which also becomes the first logarithmic regret bound of Thompson sampling for linear bandits.
1 Introduction
Partial monitoring (PM) is a general sequential decision-making problem with limited feedback (Rustichini, 1999; Piccolboni and Schindelhauer, 2001). PM is attracting broad interest because it includes a wide range of problems such as the multi-armed bandit problem (Lai and Robbins, 1985), a linear optimization problem with full or bandit feedback (Zinkevich, 2003; Dani et al., 2008), dynamic pricing (Kleinberg and Leighton, 2003), and label efficient prediction (Cesa-Bianchi et al., 2005).
A PM game can be seen as a sequential game that is played by two players: a learner and an opponent. At every round, the learner chooses an action, while the opponent chooses an outcome. Then, the learner suffers an unobserved loss and receives a feedback symbol, both of which are determined from the selected action and outcome. The main characteristic of this game is that the learner cannot directly observe the outcome and loss. The goal of the learner is to minimize his/her cumulative loss over all rounds. The performance of the learner is evaluated by the regret, which is defined as the difference between the cumulative losses of the learner and the optimal action (i.e., the action whose expected loss is the smallest).
There are mainly two types of PM games, which are the stochastic and adversarial settings (Piccolboni and Schindelhauer, 2001; Bartók et al., 2011). In the stochastic setting, the outcome at each round is determined from the opponent’s strategy, which is a probability vector over the opponent’s possible choices. On the other hand, in the adversarial setting, the outcomes are arbitrarily decided by the opponent. We refer to the PM game with finite actions and finite outcomes as a finite PM game. In this paper, we focus on the stochastic finite game.
One of the first algorithms for PM was considered by Piccolboni and Schindelhauer (2001). They proposed the FeedExp3 algorithm, the key idea of which is to use an unbiased estimator of the losses. They showed that the FeedExp3 algorithm attains minimax regret for a certain class of PM games, and showed that any algorithm suffers linear minimax regret for the other class. Here is the time horizon and the notation hides polylogarithmic factors. The upper bound is later improved by Cesa-Bianchi et al. (2006) to , and they also provided a game with a matching lower bound.
In the seminal paper by Bartók et al. (2011), they classified PM games into four classes based on their minimax regrets. To be more specific, they classified games into trivial, easy, hard, and hopeless games, where their minimax regrets are , , , and , respectively. Note that the easy game is also called a locally observable game. After their work, several algorithms have been proposed for the finite PM problem (Bartók et al., 2012; Vanchinathan et al., 2014; Komiyama et al., 2015). For the problem-dependent regret analysis, Komiyama et al. (2015) proposed an algorithm that achieves regret with the optimal constant factor. However, it requires to solve a time-consuming optimization problem with infinitely many constraints at each round. In addition, this algorithm relies on the forced exploration to achieve the optimality, which makes the empirical performance near-optimal only after prohibitively many rounds, say, or .
Thompson sampling (TS, Thompson, 1933) is one of the most promising algorithms on a variety of online decision-making problems such as the multi-armed bandit (Lai and Robbins, 1985) and the linear bandit (Agrawal and Goyal, 2013b), and the effectiveness of TS has been investigated both empirically (Chapelle and Li, 2011) and theoretically (Kaufmann et al., 2012; Agrawal and Goyal, 2013a; Honda and Takemura, 2014). In the literature on PM, Vanchinathan et al. (2014) proposed a TS-based algorithm called BPM-TS (Bayes-update for PM based on TS) for stochastic PM, which empirically achieved state-of-the-art performance. Their algorithm uses Gaussian approximation to handle the complicated posterior distribution of the opponent’s strategy. However, this approximation is somewhat heuristic and can degrade the empirical performance due to the discrepancy from the exact posterior distribution. Furthermore, no theoretical guarantee is provided for BPM-TS.
Our goals are to establish a new TS-based algorithm for stochastic PM, which allows us to sample the opponent’s strategy parameter from the exact posterior distribution, and investigate whether the TS-based algorithm can achive sub-linear regret in stochastic PM. Using the accept-reject sampling, we propose a new TS-based algorithm for PM (TSPM), which is equipped with a numerical scheme to obtain a posterior sample from the complicated posterior distribution. We derive a logarithmic regret upper bound for the proposed algorithm on the locally observable game under a linearized variant of the problem. This is the first regret bound for TS on the locally observable game. Moreover, our setting includes the linear bandit problem and our result is also the first logarithmic expected regret bound of TS for the linear bandit, whereas a high-probability bound was provided, for example, in Agrawal and Goyal (2013b). Finally, we compare the performance of TSPM with existing algorithms in numerical experiments, and show that TSPM outperforms existing algorithms.
2 Preliminaries
This paper studies finite stochastic PM games (Bartók et al., 2011). A PM game with actions and outcomes is defined by a pair of a loss matrix and feedback matrix , where is the number of feedback symbols and .
A PM game can be seen as a sequential game that is played by two players: the learner and the opponent. At each round , the learner selects action , and at the same time the opponent selects an outcome based on the opponent’s strategy , where is the -dimensional probability simplex. The outcome of each round is an independent and identically distributed sample from , and then, the learner suffers loss at time . The learner cannot directly observe the value of this loss, but instead observes the feedback symbol . The setting explained above has been widely studied in the literature of stochastic PM (Bartók et al., 2011; Komiyama et al., 2015), and we call this the discrete setting. In Section 4, we also introduce a linear setting for theoretical analysis, which is a slightly different setting from the discrete one.
The learner aims to minimize the cumulative loss over rounds. The expected loss of action is given by , where is the -th column of . We say action is optimal under strategy if for any . We assume that the optimal action is unique, and without loss of generality that the optimal action is action . Let for and be the number of times action is selected before the -th round. When the time step is clear from the context, we use instead of . We adopt the pseudo-regret to measure the performance: . This is the relative performance of the algorithm against the oracle, which knows the optimal action before the game starts.
We introduce the following definitions to clarify the class of PM games, for which we develop an algorithm and derive a regret upper bound. The following cell decomposition is the concept to divide the simplex based on the loss matrix to identify the optimal action, which depends on the opponent’s strategy .
Definition 1 (Cell decomposition and Pareto-optimality (Bartók et al., 2011)).
For every action , cell is the set of opponent’s strategies for which action is optimal. Action is Pareto-optimal if there exists an opponent’s strategy under which action is optimal.
Each cell is a convex closed polytope. Next, we define neighbors between two Pareto-optimal actions, which intuitively means that the two actions “touch” each other in their surfaces.
Definition 2 (Neighbors and neighborhood action (Bartók et al., 2011)).
Two Pareto-optimal actions and are neighbors if is an -dimensional polytope. For two neighboring actions , the neighborhood action set is defined as .
Note that the neighborhood action set includes actions and from its definition. Next, we define the signal matrix, which encodes the information of the feedback matrix so that we can utilize the feedback information.
Definition 3 (Signal matrix (Komiyama et al., 2015)).
The signal matrix of action is defined as , where if the event is true and otherwise.
Note that if we define the signal matrix as above, is a probability vector over feedback symbols of action . The following local observability condition separates easy and hard games, this condition intuitively means that the information obtained by taking actions in the neighborhood action set is sufficient to distinguish the loss difference between actions and .
Definition 4 (Local observability (Bartók et al., 2011)).
A partial monitoring game is said to be locally observable if for all pairs of neighboring actions, , where is the image of the linear map , and is the direct sum between the vector spaces and .
We also consider the concept of the strong local observability condition, which implies the above local observability condition.
Definition 5 (Strong local observability).
A partial monitoring game is said to be strongly locally observable if for all pairs , .
This condition was assumed in the theoretical analysis in Vanchinathan et al. (2014), and we also assume this condition in theoretical analysis in Section 4. Note that the strong local observability means that, for any , there exists such that .
Notation. Let and be the Euclidian norm and -norm, and let be the norm induced by the positive semidefinite matrix . Let be the Kullback-Leibler divergence of from . The vector is the -th orthonormal basis of , and is the -dimensional all-one vector. Let be the empirical feedback distribution of action at time , i.e., , where and . The notation is summarized in Appendix A.
Methods for Sampling from Posterior Distribution. We briefly review the methods to draw a sample from the posterior distribution. While TS is one of the most promising algorithms, the posterior distribution can be in a quite complicated form, which makes obtaining a sample from it computationally hard. To overcome this issue, a variety of approximate posterior sampling methods have been considered, such as Gibbs sampling, Langevin Monte Carlo, Laplace approximation, and the bootstrap (Russo et al., 2018, Section 5). Recent work (Lu and Van Roy, 2017) proposed a flexible approximation method, which can even efficiently be applied to quite complex models such as neural networks. However, more recent work revealed that algorithms based on such an approximation procedure can suffer a linear regret (Phan et al., 2019), even if the approximation error in terms of the -divergence is small enough.
Although BPM-TS is one of the best methods for stochastic PM, it approximates the posterior by a Gaussian distribution in a heuristic way, which can degrade the empirical performance due to the distributional discrepancy from the exact posterior distribution. Furthermore, no theoretical guarantee is provided for BPM-TS. In this paper, we mitigate these problems by providing a new algorithm for stochastic PM, which allows us to exactly draw samples from the posterior distribution. We also give theoretical analysis for the proposed algorithm.
3 Thompson-sampling-based Algorithm for Partial Monitoring
In this section, we present a new algorithm for stochastic PM games, where we name the algorithm TSPM (TS-based algorithm for PM). The algorithm is given in Algorithm 1, and we will explain the subroutines in the following.
3.1 Accept-Reject Sampling
We adopt the accept-reject sampling (Casella et al., 2004) to exactly draw samples from the posterior distribution. The accept-reject sampling is a technique to draw samples from a specific distribution , and a key feature is to use a proposal distribution , from which we can easily draw a sample and whose ratio to , that is , is bounded by a constant value . To obtain samples from , (i) we generate samples ; (ii) accept with probability . Note that and do not have to be normalized when the acceptance probability is calculated.
Let be a prior distribution for . Then an unnormalized density of the posterior distribution for can be expressed as
| (1) |
the detailed derivation of which is given in Appendix B. We use the proposal distribution with unnormalized density
| (2) |
Based on these distributions, we use Algorithm 2 for exact sampling from the posterior distribution, where is the uniform distribution over and is the distribution corresponding to the unnormalized density in (2). The following proposition shows that setting realizes the exact sampling.
Proposition 1.
This proposition can easily be proved by Pinsker’s inequality, which is detailed in Appendix B.
In practice, is a parameter to balance the amount of over-exploration and the computational efficiency. As decreases from 1, the algorithm tends to accept a point far from the mode. The case corresponds the TSPM algorithm where the proposal distribution is used without the accept-reject sampling, which we call TSPM-Gaussian. As we will see in Section 4, TSPM-Gaussian corresponds to exact sampling of the posterior distribution when the feedback follows a Gaussian distribution rather than a multinomial distribution.
TSPM-Gaussian can be related to BPM-TS (Vanchinathan et al., 2014) in the sense that both of them use samples from Gaussian distributions. Nevertheless, they use different Gaussians and TSPM-Gaussian performs much better than BPM-TS as we will see in the experiments. Details on the relation between TSPM-Gaussian and BPM-TS are described in Appendix D.
In general, we can realize efficient sampling with a small number of rejections if the proposal distribution and the target distribution are close to each other. On the other hand, in our problem, the densities in (1) and (2) for each fixed point exponentially decay with the number of samples if the empirical feedback distribution converges. This means that and have an exponentially large relative gap in most rounds. Nevertheless, the number of rejections does not increase with as we will see in the experiments, which suggests that the proposal distribution approximates the target distribution well with high probability.
3.2 Sampling from Proposal Distribution
When we consider Gaussian density truncated over as a prior, the proposal distribution also has the Gaussian density over , where
| (3) |
Here note that the probability simplex is in an -dimensional space and a sample from is not contained in with probability one. In the literature, e.g., Altmann et al. (2014), sampling methods for Gaussian distributions truncated on a simplex have been discussed. We use one of these procedures summarized in Algorithm 3, where we first sample elements of from another Gaussian distribution and determine the remaining element by the constraint .
Proposition 2.
We give the proof of this proposition for self-containedness in Appendix C.
4 Theoretical Analysis
This section considers a regret upper bound of the TSPM algorithm.
In the theoretical analysis, we consider a linear setting of PM. In the linear PM, the learner suffers the expected loss as in the discrete setting, and receives feedback vector for whereas the one-hot representation of is distributed by the probability vector in the discrete setting. Therefore, if can be regarded as a sub-Gaussian random variable as in Kirschner et al. (2020) then the linear PM includes the discrete PM, though our theoretical analysis requires to be Gaussian. The relation between discrete and linear settings can also be seen from the observation that bandit problems with Bernoulli and Gaussian rewards can be expressed as discrete and linear PM, respectively. The linear PM also includes the linear bandit problem, where the feedback vector is expressed as .
In the linear PM, in (2) becomes the exact posterior distribution rather than a proposal distribution. The definition of the cell decomposition for this setting is largely the same as that of discrete setting and detailed in Appendix F. Therefore, TS with exact posterior sampling in the linear PM corresponds to TSPM-Gaussian. In the linear PM, the unknown parameter is in rather than in , and therefore we consider the prior over , where the posterior distribution becomes .
There are a few works that analyze TS for the PM because of its difficulty. For example in Vanchinathan et al. (2014), an analysis of the TS-based algorithm (BPM-TS) is not given despite the fact that its performance is better than the algorithm based on a confidence ellipsoid (BPM-LEAST). Zimmert and Lattimore (2019) considered the theoretical aspect of a variant of TS for the linear PM in view of the Bayes regret, but this algorithm is based on the knowledge on the time horizon and different from the family of TS used in practice. More specifically, their algorithm considers the posterior distribution for regret (not pseudo-regret), and an action is chosen according to the posterior probability that each arm minimizes the cumulative regret. Thus, the time horizon also needs to be known.
Types of Regret Bounds. We focus on the (a) problem-dependent (b) expected pseudo-regret. (a) In the literature, a minimax (or problem-independent) regret bound has mainly been considered, for example, to classify difficulties of the PM problem (Bartók et al., 2010, 2011). On the other hand, a problem-dependent regret bound often reflects the empirical performance more clearly than the minimax regret (Bartók et al., 2012; Vanchinathan et al., 2014; Komiyama et al., 2015). For this reason, we consider this problem-dependent regret bound. (b) In complicated settings of bandit problems, a high-probability regret bound has mainly been considered (Abbasi-Yadkori et al., 2011; Agrawal and Goyal, 2013b), which bounds the pseudo-regret with high probability . Though such a bound can be transformed to an expected regret bound, this type of analysis often sacrifices the tightness since a linear regret might be suffered with small probability . This is why the analysis in Vanchinathan et al. (2014) for BPM-LEAST finally yielded an expected regret bound whereas their high-probability bound is .
4.1 Regret Upper Bound
In the following theorem, we show that logarithmic problem-dependent expected regret is achievable by the TSPM-Gaussian algorithm.
Theorem 3 (Regret upper bound).
Consider any finite stochastic linear partial monitoring game. Assume that the game is strongly locally observable and for any . Then, the regret of TSPM-Gaussian satisfies for sufficiently large that
| (4) |
where for with defined after Definition 5.
Remark.
In the proof of Theorem 3, it is sufficient to assume that for , which is weaker than the strong local observability, though it is still sometimes stronger than the local observability condition.
The proof of Theorem 3 is given in Appendix F. This result is the first problem-dependent bound of TS for PM, which also becomes the first logarithmic regret bound of TS for linear bandits.
The norm of in intuitively indicates the difficulty of the problem. Whereas we can estimate with noise through taking actions and , the actual interest is the gap of the losses . Thus, if is large, the gap estimation becomes difficult since the noise is enhanced through .
Unfortunately, the derived bound in Theorem 3 has quadratic dependence on , which seems to be not tight. This quadratic dependence comes from the difficulty of the expected regret analysis. In general, we evaluate the regret before and after the convergence of the statistics separately. Whereas the latter one usually becomes dominant, the main difficulty comes from the analysis of the former one, which might become large with low probability (Agrawal and Goyal, 2012; Kaufmann et al., 2012; Agrawal and Goyal, 2013a).
In our analysis, we were not able to bound the former one within a non-dominant order, though it is still logarithmic in . In fact, our analysis shows that the regret after convergence is as shown in Lemma 18 in Appendix F, which will become the regret with high probability. In particular, if we consider the classic bandit problem as a PM game, we can confirm that the derived bound after convergence becomes the best possible bound
by considering depending on each suboptimal arm as the difficulty measure instead of . Still, deriving a regret bound for the term before convergence within an non-dominant order is an important future work.
4.2 Technical Difficulties of the Analysis
The main difficulty of this regret analysis is that PM requires to consider the statistics of all actions when the number of selections of some action is evaluated. This is in stark contrast to the analysis of the classic bandit problems, where it becomes sufficient to evaluate statistics of action and the best action 1. This makes the analysis remarkably complicated in TS, where we need to separately consider the randomness caused by the feedback and TS.
To overcome this difficulty, we handle the effect of actions of no interest in two different novel ways depending on each decomposed regret. The first one is to evaluate the worst-case effect of these actions based on an argument (Lemma 10) related to the law of the iterated logarithm (LIL), which is sometimes used in the best-arm identification literature to improve the performance (Jamieson et al., 2014). The second one is to bound the action-selection probability of TS using an argument of (super-)martingale (Theorem 16), which is of independent interest. Whereas such a technique is often used for the construction of confidence bounds (Abbasi-Yadkori et al., 2011), we reveal that it is also useful for evaluation of the regret of TS.
We only focused on the Gaussian noise , rather than the more general sub-Gaussian noise. This restriction to the Gaussian noise comes from the essential difficulty of the problem-dependent analysis of TS, where lower bounds for some probabilities are needed whereas the sub-Gaussian assumption is suited for obtaining upper bounds. To the best of our knowledge, the problem-dependent regret analysis for TS on the sub-Gaussian case has never been investigated even for the multi-armed bandit setting, which is quite simple compared to that of PM. In the literature of the problem-dependent regret analysis, the noise distribution is restricted to distributions with explicitly given forms, e.g., Bernoulli, Gaussian, or more generally a one-dimensional canonical exponential family (Kaufmann et al., 2012; Agrawal and Goyal, 2013a; Korda et al., 2013). Their analysis relies on the specific characteristic of the distribution to bound the problem-dependent regret.
5 Experiments
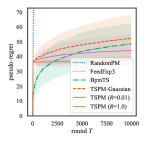
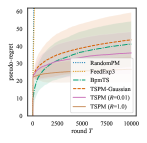
In this section, we numerically compare the performance of TSPM and TSPM-Gaussian against existing methods, which are RandomPM (the algorithm which selects action randomly), FeedExp3 (Piccolboni and Schindelhauer, 2001), and BPM-TS (Vanchinathan et al., 2014). Recently, Lattimore and Szepesvári (2019) considered the sampling-based algorithm called Mario sampling for easy games. Mario sampling coincides with TS (except for the difference between pseudo-regret and regret with known time horizon) mentioned in the last section when any pair of actions is a neighbor. As shown in Appendix G, this property is indeed satisfied for dp-easy games defined in the following. Therefore, the performance is essentially the same between TSPM with and Mario sampling. To compare the performance, we consider a dynamic pricing problem, which is a typical example of PM games. We conducted experiments on the discrete setting because the experiments for PM has been mainly focused on the discrete setting.
In the dynamic pricing game, the player corresponds to a seller, and the opponent corresponds to a buyer. At each round, the seller sells an item for a specific price , and the buyer comes with an evaluation price for the item, where the selling price and the evaluation price correspond to the action and outcome, respectively. The buyer buys the item if the selling price is smaller than or equal to and not otherwise. The seller can only know if the buyer bought the item (denoted as feedback ) or did not buy the item (denoted as ). The seller aims to minimize the cumulative “loss”, and there are two types of definitions for the loss, where each induced game falls into the easy and hard games. We call them dp-easy and dp-hard games, respectively.
In both cases, the seller incurs the constant loss when the item is not bought due to the loss of opportunity to sell the item. In contrast, when the item is not bought, the loss incurred to the seller is different between these settings. The seller in the dp-easy game does not take the buyer’s evaluation price into account. In other words, the seller gains the selling price as a reward (equivalently incurs as a loss). Therefore, the loss for the selling price and the evaluation is
This setting can be regarded as a generalized version of the online posted price mechanism, which was addressed in, e.g., Blum et al. (2004) and Cesa-Bianchi et al. (2006), and an example of strongly locally observable games.
On the other hand, the seller in dp-hard game does take the buyer’s evaluation price into account when the item is bought. In other words, the seller incurs the difference between the opponent evaluation and the selling price as a loss because the seller could have made more profit if the seller had sold at the price . Therefore, the loss incurred at time is
This setting is also addressed in Cesa-Bianchi et al. (2006), and belongs to the class of hard games. Note that our algorithm can also be applied to a hard game, though there is no theoretical guarantee.









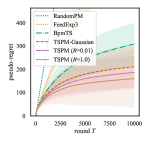
Setup. In the both dp-easy and dp-hard games, we fixed and . We fixed the time horizon to and simulated times. For FeedExp3 and BPM-TS, the setup of hyperparameters follows their original papers. For TSPM, we set , and was selected from . Here, recall that TSPM with and correspond to the exact sampling and TSPM-Gaussian, respectively, and a smaller value of gives the higher acceptance probability in the accept-reject sampling. Therefore, using small makes the algorithm time-efficient, although it can worsen the performance since it over-explores the tail of the posterior distributions. To stabilize sampling from the proposal distribution in Algorithm 3, we used an initialization that takes each action times. The detailed settings of the experiments with more results are given in Appendix H.
Results. Figure 1 is the empirical comparison of the proposed algorithms against the benchmark methods. This result shows that, in all cases, the TSPM with exact sampling gives the best performance. TSPM-Gaussian also outperforms BPM-TS even though both of them use Gaussian distributions as posteriors. Besides, the experimental results suggest that our algorithm performs reasonably well even for a hard game. It can be observed that the proposed methods outperform BPM-TS more significantly for a larger number of outcomes. Further discussion for this observation is given in Appendix D.
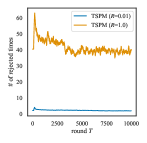
Figure 2 shows the number of rejections at each time step in the accept-reject sampling. We counted the number of times that either Line 2 in Algorithm 2 or Line 3 in Algorithm 3 was not satisfied. In the accept-reject sampling, it is desirable that the frequency of rejection does not increase as the time-step and does not increase rapidly with the number of outcomes. We can see that the former one is indeed satisfied. For the latter property, the frequency of rejection becomes unfortunately large when exact sampling () is conducted. Still, we can substantially improve this frequency by setting to be a small value or zero, which still keeps regret tremendously better than that of BPM with almost the same time-efficiency as BPM-TS.
6 Conclusion and Discussion
This paper investigated Thompson sampling (TS) for stochastic partial monitoring from the algorithmic and theoretical viewpoints. We provided a new algorithm that enables exact sampling from the posterior distribution, and numerically showed that the proposed algorithm outperforms existing methods. Besides, we provided an upper bound for the problem-dependent logarithmic expected pseudo-regret for the linearized version of the partial monitoring. To our knowledge, this bound is the first logarithmic problem-dependent expected pseudo-regret bound of a TS-based algorithm for linear bandit problems and strongly locally observable partial monitoring games.
There are several remaining questions. As mentioned in Section 4, Kirschner et al. (2020) considered linear partial monitoring with the feedback structure , where is a sequence of independent sub-Gaussian noise vector in . This setting is the generalization of our linear setting, where are i.i.d. Gaussian vectors. Therefore, a natural question that arises is whether we can extend our analysis on TSPM-Gaussian to the sub-Gaussian case, although we believe it would be not straightforward as discussed in Section 4. It is also an important open problem to derive a regret bound on TSPM using the exact posterior sampling for the discrete partial monitoring. Although we conjecture that the algorithm also achieves logarithmic regret for the setting, there still remain some difficulties in the analysis. In particular, we have to handle the KL divergence in and consider the restriction of the support of the opponent’s strategy to , which make the analysis much more complicated. Besides, it is worth noting that the theoretical analysis of TS for hard games has never been theoretically investigated. We believe that in general TS suffers linear regret in the minimax sense due to its greediness. However, we conjecture that TS can achieve the sub-linear regret for some specific instances of hard games in the sense of the problem-dependent regret, as empirically observed in the experiments. Finally, it is an important open problem to derive the minimax regret for anytime TS-based algorithms. This needs more detailed analysis on terms in the regret bound, which were dropped in our main result.
Broader Impact
Application. Partial monitoring (PM) includes various online decision-making problems such as multi-armed bandits, linear bandits, dynamic pricing, and label efficient prediction. Not only can PM handles them, the dueling bandits, combinatorial bandits, transductive bandits, and many other problems can be seen as a partial monitoring game, as discussed in Kirschner et al. (2020). Therefore, our analysis of Thompson sampling (TS) for PM games pushes the application of TS to a more wide range of online decision-making problems forward. Moreover, PM has the potential that novel online-decision making problems are newly discovered, where we have to handle the limited feedback in an online fashion.
Practical Use. The obvious advantage of using TS is that the users can easily apply the algorithm to their problems. They do not have to solve mathematical optimization problems, which are often required to solve when using non-sampling-based algorithms (Bartók et al., 2012; Komiyama et al., 2015). For the negative side, the theoretical analysis for the regret upper bound might make the users become overconfident when the users use their algorithms. For example, they might use the TSPM algorithm to the linear PM game with heavy-tailed noise, such as sub-exponential noise, without noticing it. Nevertheless, this is not an TS-specific problem, but one that can be found in many theoretical studies, and TS is still one of the most promising policies.
Acknowledgements
The authors would like to thank the meta-reviewer and reviewers for a lot of helpful comments. The authors would like to thank Kento Nozawa and Ikko Yamane for maintaining servers for our experiments, and Kenny Song for helpful discussion on the writing. TT was supported by Toyota-Dwango AI Scholarship, and RIKEN Junior Research Associate Program for the final part of the project. JH was supported by KAKENHI 18K17998, and MS was supported by KAKENHI 17H00757.
References
- Abbasi-Yadkori et al. (2011) Yasin Abbasi-Yadkori, Dávid Pál, and Csaba Szepesvári. Improved algorithms for linear stochastic bandits. In Advances in Neural Information Processing Systems 24, pages 2312–2320, 2011.
- Agrawal and Goyal (2012) Shipra Agrawal and Navin Goyal. Analysis of Thompson sampling for the multi-armed bandit problem. In the 25th Annual Conference on Learning Theory, volume 23, pages 39.1–39.26, 2012.
- Agrawal and Goyal (2013a) Shipra Agrawal and Navin Goyal. Further optimal regret bounds for Thompson sampling. In the Sixteenth International Conference on Artificial Intelligence and Statistics, volume 31, pages 99–107, 2013a.
- Agrawal and Goyal (2013b) Shipra Agrawal and Navin Goyal. Thompson sampling for contextual bandits with linear payoffs. In the 30th International Conference on Machine Learning, pages 127–135, 2013b.
- Altmann et al. (2014) Yoann Altmann, Steve McLaughlin, and Nicolas Dobigeon. Sampling from a multivariate gaussian distribution truncated on a simplex: A review. In 2014 IEEE Workshop on Statistical Signal Processing (SSP), pages 113–116, 2014.
- Bartók et al. (2010) Gábor Bartók, Dávid Pál, and Csaba Szepesvári. Toward a classification of finite partial-monitoring games. In Algorithmic Learning Theory, pages 224–238, 2010.
- Bartók et al. (2012) Gábor Bartók, Navid Zolghadr, and Csaba Szepesvári. An adaptive algorithm for finite stochastic partial monitoring. In the 29th International Conference on Machine Learning, pages 1–20, 2012.
- Bartók et al. (2011) Gábor Bartók, Dávid Pál, and Csaba Szepesvári. Minimax regret of finite partial-monitoring games in stochastic environments. In the 24th Annual Conference on Learning Theory, volume 19, pages 133–154, 2011.
- Blum et al. (2004) Avrim Blum, Vijay Kumar, Atri Rudra, and Felix Wu. Online learning in online auctions. Theoretical Computer Science, 324(2):137–146, 2004.
- Casella et al. (2004) George Casella, Christian P. Robert, and Martin T. Wells. Generalized accept-reject sampling schemes, volume 45 of Lecture Notes–Monograph Series, pages 342–347. Institute of Mathematical Statistics, 2004.
- Cesa-Bianchi et al. (2005) Nicolò Cesa-Bianchi, Gábor Lugosi, and Gilles Stoltz. Minimizing regret with label efficient prediction. IEEE Transactions on Information Theory, 51(6):2152–2162, 2005.
- Cesa-Bianchi et al. (2006) Nicolò Cesa-Bianchi, Gábor Lugosi, and Gilles Stoltz. Regret minimization under partial monitoring. Mathematics of Operations Research, 31(3):562–580, 2006.
- Chapelle and Li (2011) Olivier Chapelle and Lihong Li. An empirical evaluation of Thompson sampling. In Advances in Neural Information Processing Systems 24, pages 2249–2257, 2011.
- Dani et al. (2008) Varsha Dani, Thomas P. Hayes, and Sham M. Kakade. Stochastic linear optimization under bandit feedback. In 21st Annual Conference on Learning Theory, pages 355–366, 2008.
- Honda and Takemura (2014) Junya Honda and Akimichi Takemura. Optimality of Thompson sampling for Gaussian bandits depends on priors. In the Seventeenth International Conference on Artificial Intelligence and Statistics, volume 33, pages 375–383, 2014.
- Jamieson et al. (2014) Kevin Jamieson, Matthew Malloy, Robert Nowak, and Sébastien Bubeck. lil’ ucb : An optimal exploration algorithm for multi-armed bandits. In The 27th Conference on Learning Theory, pages 423–439, 2014.
- Kaufmann et al. (2012) Emilie Kaufmann, Nathaniel Korda, and Rémi Munos. Thompson sampling: An asymptotically optimal finite-time analysis. In Algorithmic Learning Theory, pages 199–213, 2012.
- Kirschner et al. (2020) Johannes Kirschner, Tor Lattimore, and Andreas Krause. Information directed sampling for linear partial monitoring. arXiv preprint arXiv:2002.11182, 2020.
- Kleinberg and Leighton (2003) Robert Kleinberg and Tom Leighton. The value of knowing a demand curve: Bounds on regret for online posted-price auctions. In the 44th Annual IEEE Symposium on Foundations of Computer Science, pages 594–605, 2003.
- Komiyama et al. (2015) Junpei Komiyama, Junya Honda, and Hiroshi Nakagawa. Regret lower bound and optimal algorithm in finite stochastic partial monitoring. In Advances in Neural Information Processing Systems 28, pages 1792–1800, 2015.
- Korda et al. (2013) Nathaniel Korda, Emilie Kaufmann, and Remi Munos. Thompson sampling for 1-dimensional exponential family bandits. In Advances in Neural Information Processing Systems 26, pages 1448–1456, 2013.
- Lai and Robbins (1985) T. L. Lai and Herbert Robbins. Asymptotically efficient adaptive allocation rules. Advances in Applied Mathematics, 6(1):4–22, 1985.
- Lattimore and Szepesvári (2019) Tor Lattimore and Csaba Szepesvári. An information-theoretic approach to minimax regret in partial monitoring. In the 32nd Annual Conference on Learning Theory, volume 99, pages 2111–2139, 2019.
- Lu and Van Roy (2017) Xiuyuan Lu and Benjamin Van Roy. Ensemble sampling. In Advances in Neural Information Processing Systems 30, pages 3258–3266, 2017.
- Phan et al. (2019) My Phan, Yasin Abbasi Yadkori, and Justin Domke. Thompson sampling and approximate inference. In Advances in Neural Information Processing Systems 32, pages 8804–8813, 2019.
- Piccolboni and Schindelhauer (2001) Antonio Piccolboni and Christian Schindelhauer. Discrete prediction games with arbitrary feedback and loss. In COLT/EuroCOLT, pages 208–223, 2001.
- Russo et al. (2018) Daniel J. Russo, Benjamin Van Roy, Abbas Kazerouni, Ian Osband, and Zheng Wen. A tutorial on Thompson sampling. Foundations and Trends in Machine Learning, 11(1):1–96, 2018.
- Rustichini (1999) Aldo Rustichini. Minimizing regret: The general case. Games and Economic Behavior, 29(1):224–243, 1999.
- Thompson (1933) William R Thompson. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika, 25(3-4):285–294, 12 1933.
- Vanchinathan et al. (2014) Hastagiri P Vanchinathan, Gábor Bartók, and Andreas Krause. Efficient partial monitoring with prior information. In Advances in Neural Information Processing Systems 27, pages 1691–1699, 2014.
- Zimmert and Lattimore (2019) Julian Zimmert and Tor Lattimore. Connections between mirror descent, thompson sampling and the information ratio. In Advances in Neural Information Processing Systems 32, pages 11973–11982, 2019.
- Zinkevich (2003) Martin Zinkevich. Online convex programming and generalized infinitesimal gradient ascent. In the Twentieth International Conference on Machine Learning, pages 928–935. AAAI Press, 2003.
Appendix A Notation
Table 1 summarizes the symbols used in this paper.
| Symbol | Meaning |
|---|---|
| -dimensional probability simplex | |
| Euclidian norm for vector and operator norm for matrix | |
| -norm | |
| norm induced by positive semidefinite matrix | |
| KL divergence from to | |
| -dimensional Euclidian ball of radius at point | |
| the number of actions and outcomes | |
| set of feedback symbols | |
| the number of feedback symbols | |
| opponent’s strategy | |
| time horizon | |
| loss matrix | |
| feedback matrix | |
| signal matrix | |
| action taken at time | |
| the number of times the action is taken before time | |
| outcome taken by opponent at time | |
| feedback observed at time | |
| unnormalized posterior distribution in (1) | |
| probability density function corresponding to | |
| unnormalized proposal distribution for in (2) | |
| probability density function corresponding to | |
| empirical feedback distribution of action by time | |
| empirical feedback distribution of action after the action is taken times | |
| cell of action |
Appendix B Posterior Distribution and Proposal Distribution in Section 3
In this appendix, we discuss representation of the posterior distribution and its relation with the proposal distribution.
Proposition 4.
in (1) is proportional to the posterior distribution of the opponent’s strategy, and for all .
Proof.
The posterior distribution of the opponent’s strategy parameter is rewritten as
| (5) |
where is the -th row of the signal matrix , and note that is the empirical feedback distribution of action at time , that is, for and .
Next, we show that holds for all . Using the Pinsker’s inequality, the unnormalized posterior distribution can be bounded from above as
| (6) |
∎
Remark.
The unnormalized density is indeed Gaussian. Recalling that and are defined in (3) as
| (7) |
we have
| (8) |
Therefore, we have
| (9) |
Appendix C Proof of Proposition 2
We will see that the the procedure sampling from and Algorithm 3 are equivalent. First, we derive the Gaussian density of projected onto .
For simplicity, we omit the subscript and write, e.g., instead of . We define . Let , and define . Let , where , and . Also, let .
Using the decomposition
| (10) |
we rewrite each term by restricting the domain of so that it satisfies the condition . Now the first term (a) is rewritten as
| (a) | ||||
| (11) |
The term (a1) is rewritten as
| (a1) | ||||
| (12) |
and the term (a2) is rewritten as
| (a2) | ||||
| (13) |
Therefore,
| (a) | (14) |
With regard to the term (b), we have
| (b) | ||||
| (15) |
Therefore,
| (16) |
From the above argument, the density is the Gaussian distribution of on . Therefore, the for is supported over .
If the sample from is in , then we can obtain the last element by . Otherwise, the probability that is the first elements of the sample from is zero, and hence, cannot be a sample from . Therefore, sampling from and Algorithm 3 are equivalent.
Appendix D Relation between TSPM-Gaussian and BPM-TS
In this appendix, we discuss the relation between TSPM-Gaussian and BPM-TS (Vanchinathan et al., 2014).
Underlying Feedback Structure. Here, we discuss the underlying feedback structure behind TSPM-Gaussian and BPM-TS.
We first consider the underlying feedback structure behind BPM-TS. In the following, we see that the feedback structure
| (17) |
induces the posterior distribution in BPM-TS. Under this feedback structure, we have .
When we take the prior distribution as , the posterior distribution for the opponent’s strategy parameter can be written as
| (18) |
where
| (19) | ||||
| (20) |
Therefore, the posterior distribution is
| (21) |
and this distribution indeed corresponds to the posterior distribution in BPM-TS (Vanchinathan et al., 2014) with .
Using the same argument, we can confirm that the feedback structure
| (22) |
induces
| (23) |
which corresponds to the posterior distribution for TSPM in linear partial monitoring.
Covariances in TSPM-Gaussian and BPM-TS. In the linear partial monitoring, TSPM assumes noise with covariance , which is compatible with the fact that the discrete setting can be regarded as linear PM with -sub-Gaussian noise. On the other hand, BPM-TS assumes covariance , and in general holds. Therefore, BPM-TS assumes unnecessarily larger covariance, which makes learning slow down.
Appendix E Preliminaries for Regret Analysis
In this appendix, we give some technical lemmas, which are used for the derivation of the regret bound in Appendix F. Here, we write to denote . For , let be if otherwise , and be if otherwise . We use to evaluate the behavior of the posterior samples, where is the chi-squared distribution with degree of freedom.
E.1 Basic Lemmas
Fact 5 (Moment generating function of squared-Gaussian distribution).
Let be the random variable following the standard normal distribution. Then, the moment generating function of is for .
Lemma 6 (Chernoff bound for chi-squared random variable).
Let be the random variable following the chi-squared distribution with degree of freedom. Then, for any and ,
| (24) |
Proof.
By Markov’s inequality, the LHS can be bounded as
| (25) |
which completes the proof. ∎
E.2 Property of Strong Local Observability
Recall that for , which is the difference of the expected loss of actions and . For this define
| (26) |
which is used throughout the proof of this appendix and Appendix F. The following lemma provides the key property of the strong local observability condition.
Lemma 7.
For any partial monitoring game with strong local observability and , any of the conditions 1–3 in the following is not satisfied:
-
1.
(Worse action looks better under .)
-
2.
-
3.
.
Proof.
We prove by contradiction. Assume that there exists such that conditions 1–3 are simultaneously satisfied.
Now, by the conditions 2 and 3, we have
| (27) | ||||
Here, is the element-wise absolute value, and means that the inequality holds for each element. Therefore,
| (30) |
On the other hand, by the strong local observability condition, for any , there exists such that
| (33) |
Now, we have
| (36) | |||
| (39) | |||
| (40) |
and
| (43) | |||
| (44) |
Therefore, from (40) and (44), we have
| (45) |
This inequality does not hold for all for the predefined value of , since we have
| (46) |
Therefore, the proof is completed by contradiction. ∎
Remark.
The similar result holds when the optimal action is replaced with action such that by taking satisfying
| (47) |
From Lemma 7, we have the following corollary.
Corollary 8.
For any satisfying and , we have
| (48) |
Proof.
Note that is equivalent to for any . Therefore, the result directly follows from Lemma 7. ∎
The next lemma is the property of Mahalanobis distance corresponding to .
Lemma 9.
Define . Assume that , . Then, for any
| (49) |
Proof.
To bound the LHS of the above inequality, we bound from below for . Using the triangle inequality and the assumptions, we have
| (50) |
Therefore, we have
| (51) |
By the Chernoff bound for a chi-squared random variable in Lemma 6, we now have
| (52) |
for any and . Hence, using the fact that follows the chi-squared distribution with degree of freedom, we have
| (53) |
which completes the proof. ∎
E.3 Statistics of Uninterested Actions
For any and , define
| (54) | ||||
| (55) |
In this section, we bound from above. Note that is independent of the randomness of Thompson sampling.
Lemma 10 (Upper bound for the expectation of ).
| (56) |
Proof.
Recall that in linear partial monitoring, the feedback for action is given as
| (57) |
at round , Therefore, . Since for any , we have
| (58) |
Therefore,
| (59) |
and thus
| (60) |
Therefore, for any ,
| (61) |
where . Therefore, taking , we have
| (62) |
which completes the proof. ∎
E.4 Mahalanobis Distance Process
Discussions in this section are essentially very similar to Abbasi-Yadkori et al. (2011, Lemma 11), but their results are not directly applicable and we give the full derivation for self-containedness. To maximize the applicability here we only assume sub-Gaussian noise rather than a Gaussian one.
Let be zero-mean -sub-Gaussian random variable, which satisfies
| (63) |
for any .
Lemma 11.
For any vector and positive definite matrix such that ,
| (64) |
Proof.
For any
| (65) |
Therefore, by letting we see that
| (66) |
As a result, by the definition of sub-Gaussian random variables, we have
| (67) |
∎
Lemma 12.
| (68) |
Proof.
Let , and we have
-
•
,
-
•
,
-
•
.
In the following we omit the conditioning on for notational simplicity.
Let us define and . Then, using the Sherman-Morrison-Woodbury formula we have
| (69) | ||||
E.5 Norms under Perturbations
In the following two lemmas, we give some analysis of norms under perturbations.
Lemma 13.
Let be a positive definite matrix. Let and be such that . Then
| (71) |
Proof.
By considering the Lagrangian multiplier we see that any stationary point of the function over satisfies
| (72) |
and therefore . Considering the last two conditions of (72) we have , implying that
| (73) |
or
| (74) |
for satisfying .
Note that it holds for any positive definite matrix that
| (75) |
which is positive almost everywhere, meaning that is strictly convex with respect to . Therefore, there exists at most two ’s satisfying (73) and , and there exists at most two ’s satisfying (74) and . In summary, there at most four stationary points of over .
On the other hand, two optimization problems
| (76) |
and
| (77) |
can be easily solved by an elementary calculation and the optimal values are equal to those corresponding to (73).
Therefore, the optimal solutions of the two minimax problems
| (78) |
and
| (79) |
correspond to two points corresponding to (74).
Lemma 14.
Let be a positive-definite matrix with minimum eigenvalue at least . Then, for any and satisfying ,
| (81) |
Proof.
Let . By Lemma 13, we have
| (82) | ||||
Now define . Then, we see that . Therefore, an elementary calculation using the Lagrange multiplier technique shows
| (83) |
As a result, we see that
| (84) |
∎
For the subsets of , and , let be the Minkowski sum, and let be the -dimensional Euclidian ball of radius at point (the superscript can be omitted when it is clear from context). We also let be
| (85) |
which is also used throughout the proof of this appendix and Appendix F as in (26).
Theorem 15.
Let be a constant for defined in (26). Let be satisfying . Then, there exists satisfying for any and that
| (86) |
Proof.
We prove by contradiction and the proof is basically same as that of Lemma 7 but more general in the sense that the condition on is not but . Assume that , that is, there exists satisfying and . Note that implies . Therefore, we now have following conditions on :
-
•
-
•
-
•
.
Following the same argument as the proof of Lemma 7, we have
| (90) |
On the other hand, since we can take such that . Hence,
| (93) | ||||
| (94) |
| (95) |
Now, the left hand side of (95) is bounded from below as
| (96) |
On the other hand, using the definition of , the right hand side of (95) is bounded from above as
| (97) |
Therefore, the proof is completed by contradiction. ∎
E.6 Exit Time Analysis
We next consider the exit time. Let be an event deterministic given , and be a random event such that if occurred then never occurs for . Let , be a stochastic process satisfying a.s. and is a supermartingale with respect to the filtration induced by .
Theorem 16.
Let be the stopping time defined as
| (98) |
Then we almost surely have
| (99) |
We prove this theorem based on the following lemma.
Lemma 17.
Let be an arbitrary stochastic process such that is a supermartingale with respect to a filtration . Then, for any ,
| (100) |
Proof.
Let
| (101) |
We show a.s. for any , and by induction. First, for the statement holds since
| (102) |
Next, assume that the statement holds for all , and . Then, we almost surely have
| (103) |
We obtain the lemma from
| (104) |
∎
Proof of Theorem 16.
The statement is obvious for the case and we consider the other case in the following.
Let be the time of the -th occurrence of . More formally, we define as the stopping time and
| (105) |
Then is a stochastic process measurable by the filtration induced by . By Lemma 17 we obtain
| (106) |
∎
Appendix F Regret Analysis of TSPM Algorithm
In this appendix, we give the proof of Theorem 3. Note that the cells are defined for the decomposition of , not . In other words, the cell is here defined as . For the linear setting, the empirical feedback distribution and are defined as
| (107) | ||||
| (108) |
Recall that , which is the mode of .
F.1 Regret Decomposition
Here, we break the regret into several terms. For any , we define events
| (109) | ||||
| (110) |
We first decompose the regret as
| (111) |
To decompose the last term, we define the following notation. We define for any
| (112) |
We also define
| (113) |
where is defined in (85), and
| (114) |
We define as an arbitrary point in . Then, we define
| (115) |
F.2 Analysis for Case (A)
Lemma 18.
For any ,
| (118) |
Lemma 19.
For any ,
| (119) |
where .
Proof.
Since for , the squared Mahalanobis distance follows the chi-squared distribution with degree of freedom. Therefore, we have
| (120) |
where . To use Lemma 9, we check the condition of Lemma 9 is indeed satisfied. First, it is obvious that the assumptions and are satisfied. Besides, implies from Corollary 8. Thus, applying Lemma 9 concludes the proof. ∎
F.3 Analysis for Case (B)
Lemma 20.
For any ,
| (124) |
The regret in this case can intuitively be bounded because as the round proceeds the event makes close to , which implies that the expected number of times the event occurs is not large.
Before going to the analysis of Lemma 20, we prove useful inequalities between , , and .
Lemma 21.
Assume . Then,
| (125) |
Proof.
Recall that is the maximizer of , and we have
| (126) |
Using this and the definition of , we have
| (127) |
Dividing by on the both sides completes the proof. ∎
Lemma 22.
Assume that and hold. Then,
| (128) |
Proof.
Proof of Lemma 20.
F.4 Analysis for Case (C)
Before going to the analysis of cases (C), (D), and (E), we recall some notations. Recall that
| (132) |
, , and is an arbitrary point in . Also recall that
| (133) |
Lemma 23.
For any ,
| (134) |
Before proving the above lemma, we give two lemmas.
Lemma 24.
| (135) |
where .
Proof.
First, we prove
| (136) |
This follows from
| (137) |
Using the definition of completes the proof. ∎
Lemma 25.
For any , the event implies .
Proof.
Using the triangle inequality, we have
| (138) |
∎
Proof of Lemma 23.
For any , which is specified later, we have
| (139) |
The first term can be bounded by from Lemma 24. The rigorous proof can be obtained by the almost same argument as the following analysis of the second term using Theorem 16.
Then, we will bound the second term. Specifically, we will prove that for ,
| (140) |
First we have
| (141) | ||||
Let
| (142) |
be the first time such that and occur. Letting , and in Theorem 16, we have
| (143) |
Here implies that
| (144) |
where the last inequality follows from Lemma 25. Therefore we have
| (145) |
Note that for by Lemma 10 of Abbasi-Yadkori et al. (2011), where is the Frobenius norm. Therefore we have
| (146) | ||||
| (147) |
where (146) holds since is a supermartingale from Lemma 12. Combining (143), (145), and (147), we obtain
| (148) |
By choosing we obtain the lemma. ∎
F.5 Analysis for Case (D)
Lemma 26.
For any ,
| (149) |
Remark.
To prove the regret upper bound, it is enough to prove Lemma 26 only for . However, for the sake of generality, we prove the lemma for any .
Before proving Lemma 26, we give two following lemmas.
Lemma 27.
For any , the event implies .
Proof.
Using the triangle inequality, we have
| (150) |
which completes the proof. ∎
Now, Lemma 26 can be intuitively proven because from Lemma 27, implies , and the events and does not simultaneously occur many times.
Let be the time of the first times that the event occurred (not ). In other words, we define
-
•
: the first time that and occurred
-
•
: the second time that and occurred
-
•
… .
Now we prove the following lemma using Lemma 9.
Lemma 28.
For any ,
| (151) |
Proof.
F.6 Analysis for Case (E)
Lemma 29.
Remark.
The upper bound in (156) goes to infinite when we set , that is, a flat prior is used. However, this is not the essential effect of the prior but just comes from the minimum eigenvalue of . In fact, we can see from the proof that a similar bound can be obtained for if we run some deterministic initialization until becomes positive definite.
Proof.
We evaluate each term in the summation using Theorem 16 with
| (158) |
for . Recall that
| (159) |
is the probability density function of given . Using defined in (98), it holds for any that
| (160) | ||||
| (161) |
where (160) follows since for any such that , and the last inequality follows from Theorem 15. To apply Theorem 15, we used Lemma 27.
Now we define a stochastic process corresponds to (161) as
| (162) |
Then, by Lemma 12,
| (163) |
which means that is a supermartingale. Therefore we can apply Theorem 16 and obtain
| (164) |
Finally we have
| (165) | ||||
which completes the proof. ∎
Appendix G Property of Dynamic Pricing Games
In this appendix, we will see a property of dp-easy games.
Proposition 30.
Consider any dp-easy games with . Then, any two actions in the game are neighbors.
Remark.
Proof.
Take any two different actions such that . From the definition of the loss matrix in dp-easy games, we have and .
First, we will find such that
| (166) |
From the definition of the loss matrix, the -th element of is
| (167) |
It is easy to see that the indices which give the minimum value in (167) is or . Thus, to achieve the condition (166), the following should be satisfied,
| (168) |
which is equivalent to
| (169) |
Note that we have for any .
Next, we introduce the following definitions.
| (170) | ||||
| (171) | ||||
| (172) |
To prove the proposition, it is enough to prove the following: there exists , .
To prove this, it is enough to prove that, there exists ,
| (173) |
We will prove (173) in the following. Take any and
| (174) |
Note that the used here is different from the one used in the proof of the regret upper bounds.
Case (A): When , using Cauchy–Schwarz inequality, we have
| (175) |
The arguments for cases (B) and (C) follow in the similar manner as case (A).
Case (B): When , we have
| (176) |
Case (C): When , we have
| (177) |
Summing up the argument for cases (A) to (C), the proof is completed. ∎
Appendix H Details and Additional Results of Experiments
Here we give the specific values of the opponent’s strategy used in Section 5 and show the extended experimental results for performance comparison. Table 2 summarizes the values of opponent’s strategy used in this appendix and Section 5. Figure 3 shows the empirical comparison of the proposed algorithms against the benchmark methods, and Figure 4 shows the number of the rejected times. We can see the same tendency as Section 5, that is, TSPM performs the best and the number of rejections does not increase with the time step .
| # of outcomes | opponent’s strategy |
|---|---|