An origin of narrow extended structure in the interstellar medium:
an interstellar contrail created by a fast-moving massive object
Abstract
We investigate the thermal condensation caused by a massive object that passes through the interstellar medium with high velocity, and propose a mechanism for creating a filamentary gaseous object, or interstellar contrail. Our main result shows that a long interstellar contrail can form with a certain parameter; a compact object more massive than can make a filament whose length is larger than . Observation of interstellar contrails may provide information on the number, masses, and velocities of fast-moving massive objects, and can be a new method for probing invisible gravitating sources such as intermediate-mass black holes.
1 Introduction
A sizable fraction of interstellar gas is in approximate thermal equilibrium where heating and cooling are balanced (e.g., Ferrière, 1998). The stable phases are classified as the cold neutral medium (CNM) and the warm neutral medium (WNM) (e.g., Field et al., 1969; Cox, 2005). When a shock wave propagates through such a stable gas, it is compressed by thermal condensation (e.g., Field, 1965; Falle et al., 2020). Supernovae are supposed to be the main cause of those shock waves, and their interactions with the interstellar medium (ISM) have been extensively studied (e.g., Koyama & Inutsuka, 2000, 2002; Audit & Hennebelle, 2005; Inoue & Inutsuka, 2008, 2009; Kupilas et al., 2021).
We propose that a massive compact object that moves fast creates a filamentary structure (interstellar contrail). This is because by gravitational focusing due to the massive compact object moving fast, a shock wave is driven and thermal condensation occurs. Although it has been suggested that trajectories of celestial objects create structure in interstellar space (e.g., Wallin et al., 1996; Martinez-Medina et al., 2016; Li & Shi, 2021), quantitative analysis of the resultant thermal structure has not been studied. This paper analyzes the cloud formation quantitatively. Note that the structure analyzed in this paper is very different from the bow shock and cocoon generated by a supersonically moving object that has a surface (e.g., Wilkin, 1996).
In the next section, we explain our model and the details of our analysis. Results are presented in §3. In §4, we discuss approximate formulates of an interstellar contrail and the possibility of observation. §5 presents a summary. The symbols and their definitions that we use in this paper are compiled in Tab.1.
| Symbol | Definition |
|---|---|
| Particle number accretion rate per unit length of filament | |
| Impact parameter | |
| Nondimensionalized with | |
| Impact parameter corresponding to | |
| Speed of sound in front of the shock wave | |
| Mass accretion rate per unit length | |
| Filament length | |
| Largest coordinate where the gas density reaches high enough to be observed by thermal condensation | |
| Largest coordinate where the gas density reaches high enough to be observed by thermal condensation | |
| obtained without considering the condition for shock wave generation | |
| Largest coordinate where a shock wave is generated | |
| Mass of proton | |
| Number density of gas in the filament | |
| Number density of gas in front of the shock surface | |
| Number density of gas in the ambient medium | |
| Critical pressure of thermal condensation | |
| Pressure of HI gas in thermal equilibrium | |
| Mass of the gravitating object | |
| Mass accretion rate to the gravitating object | |
| Total mass of filament | |
| Mass accretion rate on the filament | |
| Radius of a fluid element in units of | |
| Hoyle–Lyttleton accretion radius | |
| Position of filament surface | |
| Filament radius in units of | |
| Radius at the end of the filament | |
| Position of the stagnation point | |
| Gas temperature in thermal equilibrium | |
| Gas temperature in the post shock region | |
| The minimum velocity of a gravitating object to form a contrail | |
| Velocity component in the filament in the -axis direction | |
| Vertical velocity component at the shock wave front | |
| Velocity in the direction | |
| Velocity in the direction | |
| Velocity of the gravitating object | |
| Filament width | |
| The coordinate of the filament surface | |
| The coordinate of the filament surface in units of | |
| The ratio of specific heats | |
| Heating function | |
| Velocity dispersion inside filament | |
| Filament formation timescale | |
| Filament dispersal timescale | |
| Mean molecular weight | |
| Density enhancement due to orbital compression | |
| Density enhancement due to orbital compression at the filament surface | |
| Density enhancement by shock compression at the filament surface | |
| Cooling function | |
| Mass density of the ambient medium |
2 Methods
2.1 Orbit of Gas Fragments
Turbulent structures are ubiquitously observed in the ISM (e.g., Miville-Deschênes et al., 2016, 2017). To form a linear gaseous structure, it must be formed in a shorter time than eddy turnover time. In this paper we consider a gravitating object moving at supersonic speeds relative to the ISM. For simplicity, we consider the gravitating object moving at a constant velocity through an interstellar gas of uniform density. We describe the hydrodynamical equations in the comoving frame of the gravitating object. In this frame, we expect that the solution is in a steady state. In this section, we neglect the effect of the gas pressure prior to the formation of a shock wave. The effect of the pre-shock pressure will be discussed in §2.3.
2.1.1 Characteristic Length Scale
A characteristic length scale for the accretion onto a gravitating object is called the Hoyle–Lyttleton accretion radius (Hoyle & Lyttleton, 1939, 1941; Bondi & Hoyle, 1944) and is defined as follows:
| (1) |
where , , and are the velocity of the gravitating object, the gravitational constant, and the mass of the gravitating object.
2.1.2 Orbit’s Equation

First, we derive the gas streamline in the rest frame of the gravitating object. Since we are considering uniform background density, the solution should be symmetric with respect to the straight path of the gravitating object. We choose a polar coordinate plane , and the resultant structure is uniform in the direction. If we neglect pressure, gas elements with the same impact parameter intersect at a single point and we choose the z-axis as the line connecting the center of the gravitation object to that point. We consider the geometry shown in Fig.1. If the pressure gradient force can be neglected as described above, the streamline is a freefall solution. The derivation of the orbit of the motion is straightforward (e.g., Binney & Tremaine, 2008). Taking the gravitating object as the origin of the coordinates, the gas equation of motion and the boundary condition are given as
| (2) | |||
| (3) | |||
| (4) | |||
| (5) |
and the streamlines are obtained as follows:
| (6) |
where is the impact parameter of the gas fragments. Also, the velocity in the direction and the direction are defined as follows:
| (7) | |||||
| (8) |
where for and for .
Nondimensionalizing the stream equation using yields
| (9) |
where and . This nondimensional formula is convenient because it does not depend on or .
2.1.3 Compressibility
By the law of conservation of mass and Eq.(6), the compressibility due to accretion can be obtained as follows:
| (10) |
where and are the number density at in the streamlines and the number density of the gas far upstream. If the gas falls onto the -axis, will diverge. In reality, the density does not diverge because the shock wave is generated before the gravitationally accelerated gas falls onto the -axis and the flow is bent to be more in the direction of the -axis. We define as the shock surface. From , the compressibility on the surface as follows:
| (11) |
where .
2.1.4 Accretion Rate per Unit Length of the Filament
Now we consider the accretion rate per unit length of the filament. For simplicity, we neglect the shock surface and the filament width. Thereby, the gas falls onto the -axes and holds (substitute in Eq.(6)). In this approximation, the mass accretion rate per unit length is as follows:
| (12) |
where
| (13) |
Moreover, and are the average molecular weight and the proton mass; is used in this study. This equation indicates that the accretion rate on the filament is independent of .
2.2 Shock Surface
The location of the shock is estimated from the law of conservation of mass along the -axis. We assume a steady state for simplicity, the mass conservation law in the -axis direction is as follows:
| (14) |
where and are the macroscopic number density inside the shock surface and the velocity along the -axis. This yields
| (15) |
where is a stagnation point. Although it is difficult to determine accurately the location of the stagnation point, it is known to be (e.g., Matsuda et al., 2015).
As we are interested in the length of the filament, we seek a solution at . Since the effect of the gravitating object has almost no effect at , is the same as and then the solution is as follows:
| (16) |
We define the density compression ratio by the shock . In the limit of a weak shock, the compressibility is close to 1, and in the limit of a strong shock wave, it is 4, so . Since holds, we have
| (17) |
where is the value of the intersection of streamline and shock surface.
As in the case of streamlines, the nondimensionalization is as follows:
| (18) |
where .
Considering that the shock is not so strong far from the gravitating object and the post-shock region is actually supported by magnetic pressure in the magnetized ISM (e.g., Inoue & Inutsuka, 2009), can be used in an approximate calculation.
For the sake of later discussion, we derive the vertical velocity component at the shock wave front as follows:
| (19) |
2.3 Dimensionless Quantities
By Eqs.(9),(11), and (18), the relation between and is as follows:
| (20) |
The solution is obviously in . As mentioned in §2.2, is used in this study. From this, we can derive the relationship between dimensionless quantities.
Now, we are interested in the behavior at the point far from the stagnation point. In this case, Eq.(20) is approximated as
| (21) |
From this equation and , the values of , , and in the region far from the stagnation point are as follows:
| (22) | |||||
| (23) | |||||
| (24) | |||||
| (25) |
From this result, in the region far from the stagnation point (see ). Since does not depend on , the pressure gradient force can be neglected. The calculation results are shown in Fig.2.




2.4 Length of the Filament
2.4.1 Condition of Thermal Condensation
It is known that the evolution of HI gas after the shock compression is almost isobaric and if the post-shock pressure is sufficiently high, the resultant density increases by orders of magnitudes by thermal condensation (Koyama & Inutsuka, 2000). In reality, the resultant structure is not a one-phase but a multiphase medium where cold high-density material moves turbulently in a warm low-density medium by the nonlinear development of thermal instability (Koyama & Inutsuka, 2002; Audit & Hennebelle, 2005; Inoue & Inutsuka, 2008, 2009). We expect that such a multiphase medium corresponds to an interstellar contrail. In this study, we assume that if the gas pressure at the post-shock region exceeds the critical pressure , the resultant density increases sufficiently to be observed as a filament after thermal condensation. We consider that the filament is observed when its density is 10 times denser than the background gas density, and for the critical pressure , we adopt the following:
| (26) |
where is Boltzmann’s constant. is the pressure of HI gas with a number density of in thermal equilibrium, which is approximated as
| (27) |
where , , , and are a heating function, a cooling function, the HI gas temperature, and the HI gas temperature in thermal equilibrium (Inoue & Inutsuka, 2008). The relation between and is shown in Fig.3.

2.4.2 Critical Distance for Shock Wave Generation
We assume that a shock wave is generated if ; is the speed of sound in front of the shock wave. Assuming that the pre-shock state is in radiative equilibrium, we calculate as follows:
| (28) |
where , and is the specific heat ratio; is used in this study. From these, , the coordinate of the furthest position where a shock wave is generated, is obtained as
| (29) |
2.4.3 Length Limit from Thermal Condensation Condition
We estimate the largest coordinate where the gas density reaches high enough to be observed by thermal condensation. First, assuming a shock wave is generated, we derive the distance from this condition . The pressure inside the filament can be obtained using the momentum conservation law. Because of the angular momentum conservation law, the velocity in the direction is very small far from the gravitating object. Assuming that the vertical velocity component in the post-shock region (i.e., in the filament) is negligible and noting that , the post-shock pressure balances the combination of the ram pressure and pre-shock pressure as
| (30) |
where and is the pressure at the shock wave front.
Assuming thermal equilibrium conditions, is as follows:
| (31) |
is obtained from the following relation:
| (32) |
From these, is obtained from the following relation:
| (33) |
Although we adopt a thermal radiative equilibrium value for the pre-shock temperature in Eq.(28) and pressure in Eq.(31), the resulting value of does not change much even if we adopt the pressure value of adiabatic compression. This is because is not very large.
2.4.4 Filament Length
If gases become thermally unstable by shock compression, they grow into a mixture of CNM and WNM in a turbulent state (Koyama & Inutsuka, 2002). In this study, we model the resultant shocked gas flowing in the -axis direction as a multiphase filamentary structure that will diffuse out in the region far away from the gravitating object.
We estimate the dispersal timescale . After the shock compression, a fraction of the gas becomes a cold dense phase by thermal instability, but the low-density warm gas tends to be supported by the interstellar magnetic field. As a result, the average density does not increase much. Thus, we approximately use as the overall macroscopic number density of the gas after the shock compression. We assume that the gas expands by turbulence while flowing at in the -axis direction and we define the dispersal time at which the overall decreasing density reaches . From the law of conservation of mass, the following equation is obtained:
| (34) |
where is the radius at the end of the filament. From this, can be estimated as follows:
| (35) |
where is the dispersion velocity inside the filament, and we estimate as follows:
| (36) |
where is the temperature in thermal equilibrium in the post-shock region, and . Using the dispersal time scale we define the filament length in the following:
| (37) |
2.5 Basic Dimensions of the Filament
We estimate other basic dimensions of the filament such as the width and the total mass. Since the filament boundary surface depends on the value of , a representative value is taken as the filament width. This study estimates the filament width as follows:
| (38) |
Next, we approximate the total filament mass . We denote , and the accretion rate on the filament is as follows:
| (39) |
Since the filament formation timescale , is obtained as follows:
| (40) |
3 Overall Result
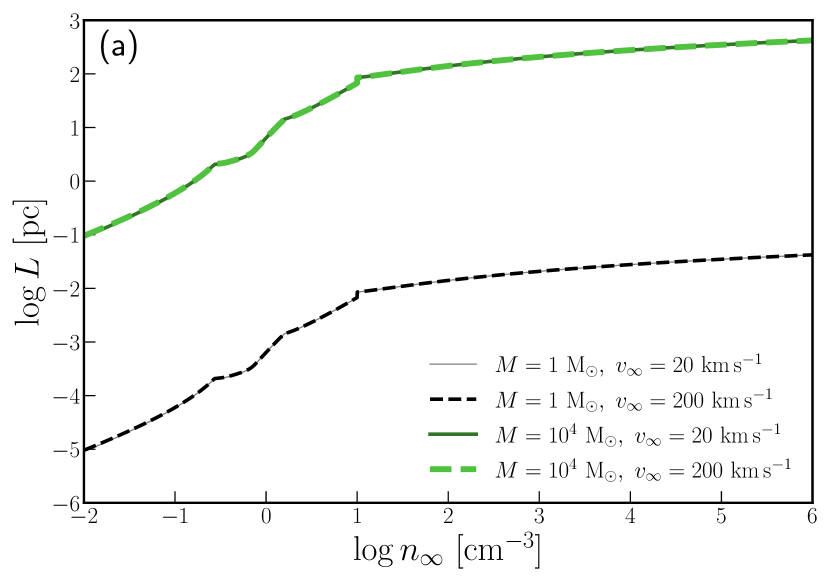
We calculate the length , the width , and the total mass from with , , and . We consider a stellar-mass and an intermediate-mass black hole as a gravitating object. For the velocity of those objects relative to the ambient ISM, we consider the range from the speed of sound of WNM () and the virial velocity in our galaxy ( a few ). The background gas is assumed to be WNM or CNM. A range of densities including WNM and CNM was employed as the density of the background gas (e.g., Cox, 2005; Hennebelle & Inutsuka, 2019). Fig.4 shows the result of the calculation. We find that various filaments are formed depending on the parameters such as mass and velocity of the gravitating object, and background density. Especially notable is that a compact object more massive than can make a filament whose length is larger than .
This section describes the qualitative behavior. Quantitative estimates are provided in §4.1.
The length is an increasing function of and as shown in Fig.4(a) because the momentum flux increases with and as can be seen in Eq.(13). Moreover, the filament length does not depend on if is sufficiently large (; will be discussed in §4.2) because for increasing , the effect of increasing the momentum flux and decreasing the mass accretion rate per unit length (see Eqs.(1) and (13)) cancel each other. The filament width is an increasing function of and and decreasing function of as shown in Fig.4(b). The reason for an increasing function of and is the same as the reason for the length’s behavior (see Eq.(38)). The reason for the filament width is a decreasing function of where the total mass becomes smaller as becomes larger as will be explained later and the filament length does not depend on .
The impact parameter that corresponds to is also an increasing function of and and decreasing function of as shown in Fig.4(c). The reason for an increasing function of and is the same as the reason for the length’s behavior. The reason for the decreasing function of is derived from , which is also a decreasing function of and holds (substitute in Eq.(6)).
The total filament mass is also an increasing function of and and decreasing function of as shown in Fig.4(d). The reason for this behavior can be understood from the behavior of and (see Eq.(40)). The reason for this behavior can also be understood as follows. If is larger, the filament formation timescale is shorter and the accretion rate on the filament is also small.



4 Discussion
4.1 Approximate Expressions for Various Physical Quantities of the Filaments
We derive expressions for various physical quantities of filaments. For simplicity, we ignore and use the approximation . In this approximation, the length follows from Eqs.(23), (25) , (30), and (32) so that
| (41) |
Thus, it is shown that does not depend on .
Using the approximation , the filament width , and total mass can be estimated similarly as follows:
| (42) | |||||
| (43) | |||||
| (44) |
4.2 Conditions for Contrail Formation
First, the radius of the gravitating object should be much larger than for creating a contrail. Second, if a massive compact object moves at a very low velocity, the object only absorbs surrounding gases and obviously does not create a contrail. In such situations, the stagnation point () is located far away from the massive object in our framework and the gravitational focusing is negligible. If the relative speed satisfies , the interstellar contrail is expected to form. We denote such condition by where is estimated from the approximation as follows:
| (45) |
The ratio of and is shown in Fig.5.

4.3 Filament Formation Site
The Galactic midplane is supposed to be occupied mostly by WNM except in bubbles due to supernova explosions. The estimation in §4.1 corresponds to the case when a massive compact object moves in WNM. This process is very different from the formation of filamentary molecular clouds in a shock-compressed layer (e.g., Abe et al., 2021).
On the other hand, a limited volume of the Galactic disk corresponds to CNM (i.e., cold HI clouds and molecular clouds). If the CNM size is large enough, a massive object of may create a long filament as large as , which should be compared to those observed in Zucker et al. (2018). If the CNM size is smaller than , the filament length is smaller than that estimated in this study. If the CNM is distributed intermittently on the trajectory of the gravitating source, the resulting filament might have spatially disconnected (see Fig.6).
Recent line observations (e.g., HI4PI Collaboration et al., 2016) have revealed the existence of numerous linear structures along the interstellar magnetic fields in HI clouds (e.g., Clark et al., 2014; Jelić et al., 2018; Turić et al., 2021). It is difficult to determine the distance to those filaments, which is one of the difficulties in understanding their property. Although such filamentary structures seem to be ubiquitous on the celestial plane, the cause of those structures is not fully understood. Thus, it is interesting to consider the possibility of creating filamentary structures by multiple gravitating sources passing through the shell of the Local Bubble. The typical length of observed HI filaments is roughly estimated as if they are located on the surface of the Local Bubble whose radius is about (e.g., Zucker et al., 2022). With Eqs. (41) – (44) we can estimate the condition for a gravitating object to form these filaments. For example, we consider a gravitating object passing through the Local Bubble’s shell. If the number density of ambient gas is , gravitating objects of , , and create filaments with lengths of approximately , , and , respectively. Whereas the number density is , gravitating objects of , , and create approximately , , and , respectively. Note that is not a simple linear function of so the filament length (Eq. (41)) has a nonlinear dependence on . We should note, however, that the thermal condensation is hindered by the interstellar magnetic field (e.g., Inoue & Inutsuka, 2008, 2009), and the length of the interstellar contrail becomes shorter than our model if the strength of the magnetic field is significantly large. It is difficult to treat the effects of magnetic fields in the present analytical framework and we will study them by numerical simulation in the future.

4.4 Accretion to Gravitating Source
Accretion onto a moving gravitating source is called Bondi–Hoyle–Littleton accretion (Hoyle & Lyttleton, 1939, 1941; Bondi & Hoyle, 1944), and the mass accretion rate to the gravitating source can be estimated by
| (46) | |||||
| (47) |
This value seems to be too small to be observed. A detailed discussion on observability is beyond the scope of this paper (see, e.g., Fukue & Ioroi, 1999; Ogata et al., 2021).
5 Conclusions
We propose a new mechanism for creating an interstellar contrail formed by the thermal condensation of HI gas or molecular gas in the trajectory of a fast-moving gravitating source in the ISM, and estimate the characteristics of the interstellar contrail analytically. The results show that the filament length is independent of the relative velocity of the gas and the gravitating object if the formation conditions are satisfied. It is also found that filaments with a variety of lengths, widths, and masses can be formed depending on the mass of the gravitating source, relative velocity, and the density of ambient gas. The resulting filament is expected to be in thermal equilibrium and the average number density depends on . Roughly speaking, if the gravitating object passes through in WNM, the number density of the filament is on the order of 100 and if the gravitating object passes through in the dense region such as CNM or molecular cloud, the number density of the filament is about 1000 or more. For example, when a object passes through the dense region () in the shell of the Local Bubble, it creates a filament whose length is about . In particular, if a compact object more massive than such as an intermediate-mass black hole goes through a large region of mostly cold atomic or molecular gas, it can form a filament whose length is larger than a hundred parsecs. If we observationally identify such phenomena in multiple regions, we will be able to estimate the frequency of intermediate-mass black holes that are not luminous enough to be visible. This line of work is expected to provide an important step toward understanding the formation process of massive black holes.
References
- Abe et al. (2021) Abe, D., Inoue, T., Inutsuka, S.-i., & Matsumoto, T. 2021, ApJ, 916, 83, doi: 10.3847/1538-4357/ac07a1
- Audit & Hennebelle (2005) Audit, E., & Hennebelle, P. 2005, A&A, 433, 1, doi: 10.1051/0004-6361:20041474
- Binney & Tremaine (2008) Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton University Press)
- Bondi & Hoyle (1944) Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273, doi: 10.1093/mnras/104.5.273
- Clark et al. (2014) Clark, S. E., Peek, J. E. G., & Putman, M. E. 2014, ApJ, 789, 82, doi: 10.1088/0004-637X/789/1/82
- Cox (2005) Cox, D. P. 2005, ARA&A, 43, 337, doi: 10.1146/annurev.astro.43.072103.150615
- Falle et al. (2020) Falle, S. A. E. G., Wareing, C. J., & Pittard, J. M. 2020, MNRAS, 492, 4484, doi: 10.1093/mnras/staa131
- Ferrière (1998) Ferrière, K. 1998, ApJ, 497, 759, doi: 10.1086/305469
- Field (1965) Field, G. B. 1965, ApJ, 142, 531, doi: 10.1086/148317
- Field et al. (1969) Field, G. B., Goldsmith, D. W., & Habing, H. J. 1969, ApJ, 155, L149, doi: 10.1086/180324
- Fukue & Ioroi (1999) Fukue, J., & Ioroi, M. 1999, PASJ, 51, 151, doi: 10.1093/pasj/51.1.151
- Hennebelle & Inutsuka (2019) Hennebelle, P., & Inutsuka, S.-i. 2019, Frontiers in Astronomy and Space Sciences, 6, 5, doi: 10.3389/fspas.2019.00005
- HI4PI Collaboration et al. (2016) HI4PI Collaboration, Ben Bekhti, N., Flöer, L., et al. 2016, A&A, 594, A116, doi: 10.1051/0004-6361/201629178
- Hoyle & Lyttleton (1939) Hoyle, F., & Lyttleton, R. A. 1939, Proceedings of the Cambridge Philosophical Society, 35, 405, doi: 10.1017/S0305004100021150
- Hoyle & Lyttleton (1941) —. 1941, MNRAS, 101, 227, doi: 10.1093/mnras/101.4.227
- Inoue & Inutsuka (2008) Inoue, T., & Inutsuka, S.-i. 2008, ApJ, 687, 303, doi: 10.1086/590528
- Inoue & Inutsuka (2009) —. 2009, ApJ, 704, 161, doi: 10.1088/0004-637X/704/1/161
- Jelić et al. (2018) Jelić, V., Prelogović, D., Haverkorn, M., Remeijn, J., & Klindžić, D. 2018, A&A, 615, L3, doi: 10.1051/0004-6361/201833291
- Koyama & Inutsuka (2000) Koyama, H., & Inutsuka, S.-I. 2000, ApJ, 532, 980, doi: 10.1086/308594
- Koyama & Inutsuka (2002) Koyama, H., & Inutsuka, S.-i. 2002, ApJ, 564, L97, doi: 10.1086/338978
- Kupilas et al. (2021) Kupilas, M. M., Wareing, C. J., Pittard, J. M., & Falle, S. A. E. G. 2021, MNRAS, 501, 3137, doi: 10.1093/mnras/staa3889
- Li & Shi (2021) Li, G.-X., & Shi, X. 2021, MNRAS, 503, 4466, doi: 10.1093/mnras/stab735
- Martinez-Medina et al. (2016) Martinez-Medina, L. A., Pichardo, B., Moreno, E., Peimbert, A., & Velazquez, H. 2016, ApJ, 817, L3, doi: 10.3847/2041-8205/817/1/L3
- Matsuda et al. (2015) Matsuda, T., Isaka, H., & Ohsugi, Y. 2015, Progress of Theoretical and Experimental Physics, 2015, 113E01, doi: 10.1093/ptep/ptv148
- Miville-Deschênes et al. (2016) Miville-Deschênes, M. A., Duc, P. A., Marleau, F., et al. 2016, A&A, 593, A4, doi: 10.1051/0004-6361/201628503
- Miville-Deschênes et al. (2017) Miville-Deschênes, M.-A., Murray, N., & Lee, E. J. 2017, ApJ, 834, 57, doi: 10.3847/1538-4357/834/1/57
- Ogata et al. (2021) Ogata, E., Ohsuga, K., & Yajima, H. 2021, PASJ, 73, 929, doi: 10.1093/pasj/psab055
- Turić et al. (2021) Turić, L., Jelić, V., Jaspers, R., et al. 2021, A&A, 654, A5, doi: 10.1051/0004-6361/202141071
- Wallin et al. (1996) Wallin, J. F., Higdon, J. L., & Staveley-Smith, L. 1996, ApJ, 459, 555, doi: 10.1086/176920
- Wilkin (1996) Wilkin, F. P. 1996, ApJ, 459, L31, doi: 10.1086/309939
- Zucker et al. (2018) Zucker, C., Battersby, C., & Goodman, A. 2018, ApJ, 864, 153, doi: 10.3847/1538-4357/aacc66
- Zucker et al. (2022) Zucker, C., Goodman, A. A., Alves, J., et al. 2022, Nature, 601, 334, doi: 10.1038/s41586-021-04286-5