An Observed Transition of Galaxy Spins on the Void Surfaces
Abstract
In the linear theory, the galaxy angular momentum vectors which originate from the initial tidal interactions with surrounding matter distribution intrinsically develop perpendicular alignments with the directions of maximum matter compression, regardless of galaxy mass. In simulations, however, the galaxy spins exhibit parallel alignments in the mass-range lower than a certain threshold, which depends on redshift, web type, and background cosmology. We show that the observed three dimensional spins of the spiral galaxies located on the void surfaces from the Sloan Digital Sky Survey indeed transit from the perpendicular to the parallel alignments with the directions toward the nearest void centers at the threshold zone, . This study presents a first direct observational evidence for the occurrence of the mass-dependent spin transition of the real galaxies with respect to the non-filamentary structures of the cosmic web, opening a way to constrain the initial conditions of the early universe by measuring the spin transition threshold.
1 Introduction
What is conventionally denominated the galaxy spin transition is a phenomenon that the angular momentum vectors (spins) of low-mass galaxies exhibit parallel alignments with the directions of maximum compression of surrounding matter, while those of high-mass counterparts manifest perpendicular alignments. The occurrence of the galaxy spin transition was witnessed by numerous N-body simulations (e.g., Aragón-Calvo et al., 2007; Hahn et al., 2007; Paz et al., 2008; Codis et al., 2012; Trowland et al., 2013; Aragon-Calvo & Yang, 2014; Dubois et al., 2014; Forero-Romero et al., 2014; Codis et al., 2015a, 2018; Ganeshaiah Veena et al., 2018; Wang et al., 2018; Ganeshaiah Veena et al., 2019; Kraljic et al., 2020; Lee et al., 2020), which in turn propelled a flurry of theoretical and observational exertions to find a physical explanation and a practical evidence for it (Libeskind et al., 2013; Tempel et al., 2013; Tempel & Libeskind, 2013; Codis et al., 2015b; Zhang et al., 2015; Pahwa et al., 2016; Wang & Kang, 2017; Krolewski et al., 2019; Welker et al., 2020; Barsanti et al., 2022; Tudorache et al., 2022; Moon & Lee, 2023).
In spite of these endeavors, no established theoretical model for its mechanism nor highly significant detection of the galaxy spin transition from observations have so far been made. On the theoretical side, the main difficulty is to coherently explain the complex behavior of the threshold mass, , at which the galaxy spin transition occurs. The value of was shown by numerical experiments to sensitively depend on such various factors as redshift, environment, scale, web type and background cosmology (Aragón-Calvo et al., 2007; Hahn et al., 2007; Codis et al., 2012; Trowland et al., 2013; Zhang et al., 2015; Codis et al., 2018; Lee et al., 2020; Lee & Libeskind, 2020; Ganeshaiah Veena et al., 2021). The conventional scenario which attributed the galaxy spin transition to the effect of hierarchical merging along anisotropic cosmic web (Aragón-Calvo et al., 2007; Hahn et al., 2007; Pichon et al., 2011; Codis et al., 2012; Trowland et al., 2013; Dubois et al., 2014; Codis et al., 2018; Ganeshaiah Veena et al., 2018; Krolewski et al., 2019) failed to provide a coherent physical explanation for the variation of with these factors. Furthermore, this conventional scenario was shown to be inconsistent with the recent numerical finding of Lee & Moon (2022) that the alignment strengths of the galaxy spins with the directions of maximum matter compression do not show any strong variation with the latest merging epochs.
On the observational side, the most challenging task is to measure the galaxy spins () and directions of maximal matter compression () as accurately as possible in practice. Although several authors reported possible observational detections of the mass dependent spin transition of the real galaxies, the low statistical significance of their signals as well as relatively low accuracy in the measurements of beleaguered their results with cautions. For example, Welker et al. (2020) claimed a first direct detection of the mass dependent spin transition of the field galaxies with respect to the nearby filaments from the Sydney–AAO Multi-object Integral-field spectrograph (SAMI) survey (Croom et al., 2012), under the assumption that is perpendicular to the elongated filament axes. Their analysis, however, relied on the simple approximation of the three dimensional spins of the SAMI galaxies by the position angles alone as well as on the measurements of the filament axes in the two dimensional projected space.
Barsanti et al. (2022) analyzed the same SAMI data but with an improved methodology to detect a signal of the mass dependent spin transition of the galaxies. They improved the measurement of the galaxy spins by employing the scheme proposed by Lee & Erdogdu (2007) which basically reckons the shape of a galaxy as a circular thin disk, and properly took into account the two-fold ambiguity that the sign of the radial component of a galaxy spin along the line-of-sight direction cannot be determined by the scheme based on the circular thin disk approximation (Lee, 2011; Kraljic et al., 2021). They also improved the measurement of by efficiently eliminating the Finger-of-God (FoG) effect (Jackson, 1972) caused by the peculiar motions of group/cluster galaxies embedded in the filaments (see also Kraljic et al., 2018).
Barsanti et al. (2022) assumed that the spins of the elliptical galaxies should be in the direction of their minor shape axes and thus could be obtained by the same scheme applied to the spiral galaxies. Yet, recent N-body simulations disproved this assumption, demonstrating that the galaxy spins are not perfectly aligned with their minor shape axes and that the shape axes do not show any mass-dependent spin transition (Lee & Moon, 2022), which implies that the scheme of Lee & Erdogdu (2007) is invalid for the measurements of the elliptical galaxy spins. Since the - alignments are expected to be quite a weak signal vulnerable to systematic contaminations, it is essentially important to diminish all known systematics to the lowest levels for a detection of the galaxy spin transition and for the measurement of .
Besides, the previous observational works determined as a direction perpendicular to a thin straight filament nearest to a given galaxy. However, the real filaments in the universe have much more complex shapes, whose geometrical properties have been found to severely affect the strengths and tendencies of the alignments with the galaxy spins (see Ganeshaiah Veena et al., 2021, and references therein). In other words, the systematic errors in the measurement of are likely to be produced not only by the FoG effect but also by the deviation of the filament shapes from thin straight lines. Given these simple approximations and assumptions made in the previous works, it was not a surprise that the solidity of their claimed detections have been protested by several counter-evidences against the occurrence of the galaxy spin transitions (e.g., Zhang et al., 2015; Chen et al., 2019; Krolewski et al., 2019; Tudorache et al., 2022). Henceforth, it is still inconclusive whether or not the mass-dependent galaxy spin transition indeed occurs in reality.
Here, we suggest that the cosmic voids, large empty regions devoid of galaxies in the universe, be the most optimal web-type from which a signal of the occurrence of the galaxy spin transition could be detectable with high significance. The logic behind this suggestion can be found in the context of the linear tidal torque theory (White, 1984; Lee & Pen, 2000, 2001). In this theory, the protogalaxies acquire angular momentum at first order and develop preferential spin alignments with the principal axes of the local tidal tensors, only if the principal axes of their inertia momentum tensor are not perfectly aligned with those of the local tidal tensor. It turned out, however, that the principal axes of the two tensors are quite strongly aligned with one another with alignment strengths sensitively dependent on the environmental density (Lee, 2006). The lower density the environment has, the less strong alignment the principal axes of the two tensors exhibit. Therefore, it may be more probable to find a statistically significant signal of the spin alignment and its transition with respect to the principal axes of the local tidal field from the galaxies located in the neighborhood of cosmic voids – the web-type with lowest environmental densities.
For the galaxies at the void outskirts, can be determined as a direction toward the void centers without making any simplified assumption about the void shapes nor concerning about the FoG effect. Analyzing the most updated catalogs of the observed voids, we attempt here to explore how the three dimensional spins of the spiral galaxies are aligned with the directions toward the nearest void centers and to investigate if a significant signal of the mass-dependent galaxy spin transition can be found. We will focus only on the spiral galaxies whose three dimensional spins can be rather accurately determined by the circular thin disk approximation up to the aforementioned sign ambiguity. Throughout this paper, we will assume a flat universe with dominant cosmological constant () and cold dark matter (CDM).
2 Physical Analysis
From the Seventh Data Release of the Sloan Digital Sky Survey (SDSS DR7, Abazajian et al., 2009), Douglass et al. (2023) produced three different catalogs of cosmic voids in the redshift range of for the Planck and and the Wilkinson Microwave Anisotropy Probe 5 year (WMAP5) cosmologies. The three catalogs correspond to three different void-identification algorithms, namely, the VIDE (Sutter et al., 2015), REVOLVER (Nadathur et al., 2019), and VoidFinder (Hoyle & Vogeley, 2002). The former two implement the same ZOBOV scheme (Neyrinck, 2008) based on the Voronoi tessellation density estimator, but differ in the pruning steps through which the linked zones of local density minima are selectively divided into individual voids (Sutter et al., 2015; Nadathur et al., 2019). Meanwhile, the VoidFinder finds the voids as merged volumes of maximum empty spheres in the spatial galaxy distributions (Hoyle & Vogeley, 2002). For more information on the void finding process, we refer the readers to Douglass et al. (2023) and references therein. A total of , and (, and ) voids were identified via the , , and algorithms, respectively, from a volumed limited sample of the SDSS DR7 galaxies for the planck (WMAP5) cosmology, whose median radii turned out to be in the range of (Douglass et al., 2023).
To be statistically consistent with the void catalogs of Douglass et al. (2023), we utilize a spectroscopic galaxy catalog from the SDSS DR7 compiled by Huertas-Company et al. (2011), which contains information on how probable it is for a given galaxy to be classified as a certain morphological type. To each galaxy in the catalog is assigned four different probabilities, , , , and , of its morphology being elliptical, lenticular, early type spiral, and late-type spiral, respectively. To the galaxy catalog of Huertas-Company et al. (2011), we apply the following three cuts for the selection of only large spiral galaxies: (size-cut), (morphology cut), and (redshift cut), where denotes the number of pixels that the apparent size of a given galaxy occupies in the SDSS frame. As we are going to use information on the isophotal quantities like position angles ( and axial ratios () of the selected spirals for the determination of their spins, we exclude those galaxies whose isophotal images are not large enough to guarantee reliable measurements of and (Singh & Mandelbaum, 2016).
For each of the selected spiral galaxies, we determine its spin, , from information on and , with the help of the scheme devised by Lee (2011) based on the circular thin disk approximation (see also Lee & Erdogdu, 2007). We first estimate its inclination angle, , as
| (1) |
where is the ”intrinsic flatness parameter” introduced by Haynes & Giovanelli (1984) to take into account non-negligible thickness of a spiral disk due to the presence of a central bulge. To the and galaxies are conventionally assigned the and , respectively (Haynes & Giovanelli, 1984). If the spiral arms of a given spiral galaxy viewed face-on are spinning in a clockwise manner, then can be determined in the spherical-polar coordinate system as
| (2) | |||||
| (3) | |||||
| (4) |
Since it is usually very hard in practice to determine whether a spiral galaxy is spinning in a clock-wise or counterclock-wise manner, the true sign of a galaxy spin along the line of sight direction cannot be readily determined, so called the two-fold ambiguity of the spin measurement (Lee, 2011). Accepting this sign ambiguity, we will consider both of the possibilities, i.e., clockwise and counter clockwise spinning as in Lee (2011). Rotating the frame to the equatorial Cartesian system, we end up having two different spin realizations, and , for each selected spiral galaxy as
| (5) | |||||
| (6) | |||||
| (7) |
| (8) | |||||
| (9) | |||||
| (10) |
where and with declination and right ascension .
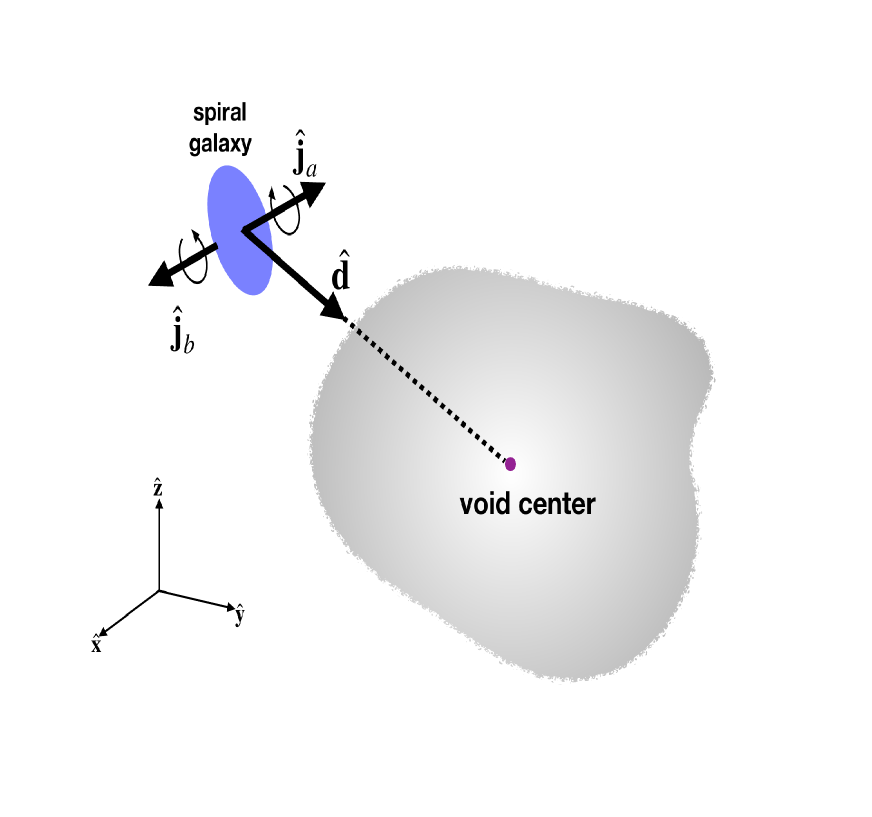
Using information on the equatorial Cartesian coordinates of each selected spiral galaxy, we first measure its separation distances from all of the voids to search for the nearest one. The unit direction vector, , from a given spiral galaxy located at toward the center of its nearest void, , is calculated as . Then, two realizations of the alignment between the spiral galaxy spin and the direction to its nearest void are computed as and . Figure 1 illustrates a schematic view of , and for a SDSS spiral galaxy in the neighborhood of a cosmic void.
Obtaining information on the stellar masses, , of the selected spiral galaxies from the estimates made by Mendel et al. (2014) with the help of the broadband spectral energy distributions, we also apply two additional cuts to the selected spirals: and , where denotes the effective radius of a nearest void. The first condition is required to exclude those few spirals located inside the nearest voids, while the second condition excludes those spirals for which no information on the stellar mass is available. The selected spirals are then split into six samples of equal sizes according to ( in a -increasing order). The first six rows of Table 1 list the numbers of the selected spiral galaxies, , belonging to for the six different cases (three different void-identification algorithms and two different cosmologies). The dependence of on the void-identification algorithm comes from the fact that the numbers of the excluded galaxies depend on the void abundance.
The ensemble average of the alignments between the galaxy spins and the directions to the nearest void centers is taken separately over each of as
| (11) |
where and are the two spin realizations of the th spiral galaxy whose unit direction toward its nearest void is denoted by . The errors in are obtained with the help of the bootstrap method. A significantly higher (lower) value of than will in principle signal a parallel (perpendicular) alignment of the spiral galaxy spins with the directions to the nearest void centers, where the reference value of comes from the theoretical expectation of the ensemble average in case of no - alignments under the assumption that there is no systematic errors, either.
In reality, however, some unknown systematics could always exist, which would deviate the reference value from even in case of no true alignments between and . To statistically deal with this unknown systematics, we create resamples by repeatedly and randomly shuffling the positions of the selected spiral galaxies but with fixing their spins. Then, we redo the whole analysis with each of the resamples to determine one standard deviation scatters () of averaged over the resamples (see Tempel & Libeskind, 2013; Kraljic et al., 2021; Barsanti et al., 2022, and references therein). Figure 2 plots from the original samples (purple colored filled circles) with the bootstrap errorbars along with the scatters among the resamples (violet colored dotted lines), for the six different cases. As can be clearly seen, for all of the cases, the values show an overall trend of diminishing with the increment of from above down to below . But only for the case, we note that both of the parallel and perpendicular spin alignments found at the lowest and highest mass bins (corresponding to and , respectively), are statistically significant (), which implies the occurrence of the spin transition somewhere in between mass ranges.
To rigorously determine the threshold stellar mass range, (spin transition zone), at which the transition from parallel to perpendicular spin alignments really occurs, we employ a statistical methodology similar to the one suggested by Lee & Libeskind (2020). Basically, this methodology first sets up a null hypothesis, , of no - alignment at a given mass bin and performs a KS test of . For a given mass bin to be determined as , the following two conditions must be satisfied: First, the KS test rejects at the confidence level, , in the given mass bin. Second, the KS test rejects at in the adjacent mass bins both higher and lower than the given one.
Under , the probability density of is statistically equivalent to a uniform distribution provided that systematic contamination is negligible. For each of the six mass-selected sample, we compute the maximum difference between and , which are the cumulative versions of the probability density of and the uniform probability density corresponding to , respectively. Then, we evaluate whose value is expected to be higher (lower) than the critical value of (Lee & Libeskind, 2020) if the KS test rejects at (). If the spin transition occurs in a certain mass bin, we expect from the corresponding sample but from the other samples.
We also apply this method repeatedly to each of the resamples created by the random shuffling, and calculate scatters from the average over the resamples. As can be seen in Figure 3, the randomly shuffled resamples yield almost constant values of lower than within in the whole mass range (violet colored dotted lines). This result implies that the probability density function of from the randomly shuffled resamples is statistically equivalent to the uniform probability density and thus that no signal of the spin transition can be found from the resamples. Meanwhile, the values from the original samples (purple colored filled circles) exhibit fluctuating behaviors, higher or lower than , depending on . For the VoidFinder case, we find only from while the other samples yield , which implies the occurrence of the spin transition in the mass range of , i.e., . Whereas, the VIDE and REVOLVER cases yield from two non-adjacent samples, failing in satisfying the aforementioned two conditions.
We also redo the whole analysis but at a fixed morphological type by separately treating the and galaxies, whose numbers are listed in Table 1. Figure 4 shows with Bootstrap errorbars from the original six samples of the and galaxies (blue and red colored filled circles, respectively) along with the scatters from the average over the randomly shuffled resamples of the two types (sky blue and pink colored dotted lines, respectively). Note that each of the six selected samples composed of the galaxies has a different mass range from that of the ones, although the same notations, , are used for both of the cases. As can be seen, neither nor galaxy samples show a spin transition behavior for any of the six cases. From the galaxies, we find only perpendicular alignments between and in the almost entire mass range except for in the lowest mass bin corresponding to from which no signal of any alignment is found. In contrast, the galaxies yield only parallel alignments in the entire mass range, albeit statistically significant only in the high mass bins (corresponding to and ).
Recalling the claim of Barsanti et al. (2022) that the bulge mass is most strongly linked with the occurrence of the galaxy spin transitions as well as the well known fact that the galaxies have much lower bulge masses than the counterparts at a fixed total stellar mass, we recalculate and scatters from the and galaxies separately as a function of their bulge masses, , which are also obtained from the estimates of Mendel et al. (2014). Figure 5 plots the same as Figure 4 but as a function of . As can be seen, we still fail to find any indication of the mass dependent spin transition at fixed morphology. Note that a significant difference exists in their alignment tendency between the and galaxies even at the same bulge masses, which implies the transition from parallel to perpendicular spin alignments may not be triggered mainly by the growth of central bulges but by some evolutionary process through which the late-type spirals are segregated from the early-type ones.
3 Summary and Discussion
We have observationally detected a statistically significant signal of mass dependent galaxy spin transition by investigating the alignments between the spin axes of the spiral galaxies located at the void outskirts and the directions toward the centers of the nearest voids as a function of the galaxy stellar mass. For this investigation, we have considered only the SDSS spiral galaxies whose three dimensional spin axes can be calibrated from the photometric position angles and axial ratios up to the two-fold ambiguity via the scheme based on the circular thin disk approximation (Lee & Erdogdu, 2007; Lee, 2011). We have also analyzed the most updated catalogs of the voids identified by Douglass et al. (2023) via three different algorithms (VIDE, REVOLVER, and VoidFinder), assuming that the direction from a given galaxy to its nearest void center is parallel to the direction of maximum matter compression in the galaxy neighborhood.
It has been found that the spiral galaxy spins indeed gradually transit from parallel to perpendicular orientations with respect to the directions of maximum matter compression as the galaxy stellar mass increases, regardless of the void-identification algorithms. However, the coexistence of the statistically significant signals () of the parallel and perpendicular spin alignments in the smallest and largest mass bins, respectively, has been detected only for the VoidFinder case, where has been obtained from the resamples created by random shuffling of the galaxy positions. For this case, the threshold stellar mass, , at which the galaxy spin transition occurs has been efficiently constrained to the range of (spin transition zone) for both of the Planck and WMAP5 cosmologies by employing the KS-test based methodology developed by Lee & Libeskind (2020).
At a fixed morphological type, however, has been witnessed disappearance of the spin transition signals. The galaxies exhibit only perpendicular spin alignments in an almost mass independent manner, in contrast to the galaxies whose spins yield only insignificant parallel alignments in the entire stellar mass range. Even when the alignments are measured as a function of the bulge masses, a similar result has been found, which implies that disappearance of the spin transition signals at fixed morphology cannot be ascribed to the difference between the and galaxies in the bulge masses.
Yet, the high statistical significance of the spin transition signal we have been able to attain here is owing to the large size of our sample, which has in turn been possible to obtain because we have determined the spiral galaxy spins by using the photometric position angles and axial ratios. Although a higher accuracy in the determination of the spiral galaxy spins could have be achieved by using more reliable kinematic position angles rather than the photometric counterparts as in Kraljic et al. (2021) and Barsanti et al. (2022), we have chosen the latter to avoid a poor number statistics, since information on kinematic position angles from well resolved data is available only for a limited number of the spiral galaxies. Furthermore, for the case of the spiral galaxies located at the outskirts of cosmic voids characterized by the lowest environmental densities, the offsets between their photometric and kinematic position angles were observationally known to be as low as (e.g., Barnes & Sellwood, 2003; Barrera-Ballesteros et al., 2014, 2015; Graham et al., 2018), which justifies our choice in some degree.
Providing an observational evidence for the occurrence of the galaxy spin transition phenomenon in the non-filamentary environments, our results bear three physical implications. First, the filamentary merging of the galaxies may not be the most crucial mechanism that drives the spiral galaxies to transit their spin orientations with respect to the directions of maximum matter compression. Second, the most decisive factor that triggers the occurrence of the spin transition should be linked not with the growth of total or bulge stellar masses of the spiral galaxies but with some other mechanism responsible for the morphology segregation. Third, it becomes quite feasible to use the observed spin transition zone as a discriminator of cosmology, since we have found no difference in the spin transition zone between the Planck and WMAP5 cosmologies, while it was previously found that it significantly differs between the standard and non-standard cosmologies (Lee et al., 2020; Lee & Libeskind, 2020).
It is also worth listing two crucial questions raised by the current work. The first one is why the mass-dependent spin transition threshold for the spiral galaxies on the void surfaces can be efficiently constrained only when the voids are identified by the VoidFinder algorithm. The second one is why the mass-dependent spin transition signal disappears at fixed morphology, and what factor plays the most decisive role for the spiral galaxy spin transition, if it is not the growth of total/bulge stellar masses. Our future work will be in the direction of finding answers to these questions by performing a comprehensive numerical and observational analysis.
References
- Abazajian et al. (2009) Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543. doi:10.1088/0067-0049/182/2/543
- Aragón-Calvo et al. (2007) Aragón-Calvo, M. A., van de Weygaert, R., Jones, B. J. T., et al. 2007, ApJ, 655, L5. doi:10.1086/511633
- Aragon-Calvo & Yang (2014) Aragon-Calvo, M. A. & Yang, L. F. 2014, MNRAS, 440, L46. doi:10.1093/mnrasl/slu009
- Barrera-Ballesteros et al. (2014) Barrera-Ballesteros, J. K., Falcón-Barroso, J., García-Lorenzo, B., et al. 2014, A&A, 568, A70. doi:10.1051/0004-6361/201423488
- Barrera-Ballesteros et al. (2015) Barrera-Ballesteros, J. K., García-Lorenzo, B., Falcón-Barroso, J., et al. 2015, A&A, 582, A21. doi:10.1051/0004-6361/201424935
- Barsanti et al. (2022) Barsanti, S., Colless, M., Welker, C., et al. 2022, MNRAS, 516, 3569. doi:10.1093/mnras/stac2405
- Blue Bird et al. (2020) Blue Bird, J., Davis, J., Luber, N., et al. 2020, MNRAS, 492, 153. doi:10.1093/mnras/stz3357
- Chen et al. (2019) Chen, Y.-C., Ho, S., Blazek, J., et al. 2019, MNRAS, 485, 2492. doi:10.1093/mnras/stz539
- Codis et al. (2012) Codis, S., Pichon, C., Devriendt, J., et al. 2012, MNRAS, 427, 3320. doi:10.1111/j.1365-2966.2012.21636.x
- Codis et al. (2015a) Codis, S., Gavazzi, R., Dubois, Y., et al. 2015, MNRAS, 448, 3391. doi:10.1093/mnras/stv231
- Codis et al. (2015b) Codis, S., Pichon, C., & Pogosyan, D. 2015, MNRAS, 452, 3369. doi:10.1093/mnras/stv1570
- Codis et al. (2018) Codis, S., Jindal, A., Chisari, N. E., et al. 2018, MNRAS, 481, 4753. doi:10.1093/mnras/sty2567
- Croom et al. (2012) Croom, S. M., Lawrence, J. S., Bland-Hawthorn, J., et al. 2012, MNRAS, 421, 872. doi:10.1111/j.1365-2966.2011.20365.x
- Douglass et al. (2023) Douglass, K. A., Veyrat, D., & BenZvi, S. 2023, ApJS, 265, 7. doi:10.3847/1538-4365/acabcf
- Dubois et al. (2014) Dubois, Y., Pichon, C., Welker, C., et al. 2014, MNRAS, 444, 1453. doi:10.1093/mnras/stu1227
- Barnes & Sellwood (2003) Barnes, E. I. & Sellwood, J. A. 2003, AJ, 125, 1164. doi:10.1086/346142
- Forero-Romero et al. (2014) Forero-Romero, J. E., Contreras, S., & Padilla, N. 2014, MNRAS, 443, 1090. doi:10.1093/mnras/stu1150
- Ganeshaiah Veena et al. (2018) Ganeshaiah Veena, P., Cautun, M., van de Weygaert, R., et al. 2018, MNRAS, 481, 414. doi:10.1093/mnras/sty2270
- Ganeshaiah Veena et al. (2019) Ganeshaiah Veena, P., Cautun, M., Tempel, E., et al. 2019, MNRAS, 487, 1607. doi:10.1093/mnras/stz1343
- Ganeshaiah Veena et al. (2021) Ganeshaiah Veena, P., Cautun, M., van de Weygaert, R., et al. 2021, MNRAS, 503, 2280. doi:10.1093/mnras/stab411
- Graham et al. (2018) Graham, M. T., Cappellari, M., Li, H., et al. 2018, MNRAS, 477, 4711. doi:10.1093/mnras/sty504
- Hahn et al. (2007) Hahn, O., Carollo, C. M., Porciani, C., et al. 2007, MNRAS, 381, 41. doi:10.1111/j.1365-2966.2007.12249.x
- Haynes & Giovanelli (1984) Haynes, M. P. & Giovanelli, R. 1984, AJ, 89, 758. doi:10.1086/113573
- Hirv et al. (2017) Hirv, A., Pelt, J., Saar, E., et al. 2017, A&A, 599, A31. doi:10.1051/0004-6361/201629248
- Hoyle & Vogeley (2002) Hoyle, F. & Vogeley, M. S. 2002, ApJ, 566, 641. doi:10.1086/338340
- Huertas-Company et al. (2011) Huertas-Company, M., Aguerri, J. A. L., Bernardi, M., et al. 2011, A&A, 525, A157. doi:10.1051/0004-6361/201015735
- Jackson (1972) Jackson, J. C. 1972, MNRAS, 156, 1P. doi:10.1093/mnras/156.1.1P
- Kraljic et al. (2018) Kraljic, K., Arnouts, S., Pichon, C., et al. 2018, MNRAS, 474, 547. doi:10.1093/mnras/stx2638
- Kraljic et al. (2020) Kraljic, K., Davé, R., & Pichon, C. 2020, MNRAS, 493, 362. doi:10.1093/mnras/staa250
- Kraljic et al. (2021) Kraljic, K., Duckworth, C., Tojeiro, R., et al. 2021, MNRAS, 504, 4626. doi:10.1093/mnras/stab1109
- Krolewski et al. (2019) Krolewski, A., Ho, S., Chen, Y.-C., et al. 2019, ApJ, 876, 52. doi:10.3847/1538-4357/ab1010
- Lee & Pen (2000) Lee, J. & Pen, U.-L. 2000, ApJ, 532, L5. doi:10.1086/312556
- Lee & Pen (2001) Lee, J. & Pen, U.-L. 2001, ApJ, 555, 106. doi:10.1086/321472
- Lee (2006) Lee, J. 2006, ApJ, 644, L5. doi:10.1086/505389
- Lee & Erdogdu (2007) Lee, J. & Erdogdu, P. 2007, ApJ, 671, 1248. doi:10.1086/523351
- Lee (2011) Lee, J. 2011, ApJ, 732, 99. doi:10.1088/0004-637X/732/2/99
- Lee et al. (2020) Lee, J., Libeskind, N. I., & Ryu, S. 2020, ApJ, 898, L27. doi:10.3847/2041-8213/aba2ee
- Lee & Libeskind (2020) Lee, J. & Libeskind, N. I. 2020, ApJ, 902, 22. doi:10.3847/1538-4357/abb314
- Libeskind et al. (2013) Libeskind, N. I., Hoffman, Y., Forero-Romero, J., et al. 2013, MNRAS, 428, 2489. doi:10.1093/mnras/sts216
- Mendel et al. (2014) Mendel, J. T., Simard, L., Palmer, M., et al. 2014, ApJS, 210, 3. doi:10.1088/0067-0049/210/1/3
- Lee & Moon (2022) Lee, J. & Moon, J.-S. 2022, ApJ, 936, 119. doi:10.3847/1538-4357/ac879d
- Moon & Lee (2023) Moon, J.-S. & Lee, J. 2023, arXiv:2302.00679. doi:10.48550/arXiv.2302.00679
- Nadathur et al. (2019) Nadathur, S., Carter, P. M., Percival, W. J., et al. 2019, Phys. Rev. D, 100, 023504. doi:10.1103/PhysRevD.100.023504
- Neyrinck (2008) Neyrinck, M. C. 2008, MNRAS, 386, 2101. doi:10.1111/j.1365-2966.2008.13180.x
- Pahwa et al. (2016) Pahwa, I., Libeskind, N. I., Tempel, E., et al. 2016, MNRAS, 457, 695. doi:10.1093/mnras/stv2930
- Paz et al. (2008) Paz, D. J., Stasyszyn, F., & Padilla, N. D. 2008, MNRAS, 389, 1127. doi:10.1111/j.1365-2966.2008.13655.x
- Pichon et al. (2011) Pichon, C., Pogosyan, D., Kimm, T., et al. 2011, MNRAS, 418, 2493. doi:10.1111/j.1365-2966.2011.19640.x
- Singh & Mandelbaum (2016) Singh, S. & Mandelbaum, R. 2016, MNRAS, 457, 2301. doi:10.1093/mnras/stw144
- Sutter et al. (2015) Sutter, P. M., Lavaux, G., Hamaus, N., et al. 2015, Astronomy and Computing, 9, 1. doi:10.1016/j.ascom.2014.10.002
- Tempel et al. (2013) Tempel, E., Stoica, R. S., & Saar, E. 2013, MNRAS, 428, 1827. doi:10.1093/mnras/sts162
- Tempel & Libeskind (2013) Tempel, E. & Libeskind, N. I. 2013, ApJ, 775, L42. doi:10.1088/2041-8205/775/2/L42
- Trowland et al. (2013) Trowland, H. E., Lewis, G. F., & Bland-Hawthorn, J. 2013, ApJ, 762, 72. doi:10.1088/0004-637X/762/2/72
- Tudorache et al. (2022) Tudorache, M. N., Jarvis, M. J., Heywood, I., et al. 2022, MNRAS, 513, 2168. doi:10.1093/mnras/stac996
- Wang & Kang (2017) Wang, P. & Kang, X. 2017, MNRAS, 468, L123. doi:10.1093/mnrasl/slx038
- Wang et al. (2018) Wang, P., Guo, Q., Kang, X., et al. 2018, ApJ, 866, 138. doi:10.3847/1538-4357/aae20f
- Welker et al. (2020) Welker, C., Bland-Hawthorn, J., van de Sande, J., et al. 2020, MNRAS, 491, 2864. doi:10.1093/mnras/stz2860
- White (1984) White, S. D. M. 1984, ApJ, 286, 38. doi:10.1086/162573
- Zhang et al. (2015) Zhang, Y., Yang, X., Wang, H., et al. 2015, ApJ, 798, 17. doi:10.1088/0004-637X/798/1/17




| Type | Model | Algorithm | ||||||
|---|---|---|---|---|---|---|---|---|
| VIDE | ||||||||
| All | Planck | REVOLVER | ||||||
| VoidFinder | ||||||||
| VIDE | ||||||||
| All | WMAP5 | REVOLVER | ||||||
| VoidFinder | ||||||||
| VIDE | ||||||||
| Planck | REVOLVER | |||||||
| VoidFinder | ||||||||
| VIDE | ||||||||
| WMAP5 | REVOLVER | |||||||
| VoidFinder | ||||||||
| VIDE | ||||||||
| Planck | REVOLVER | |||||||
| VoidFinder | ||||||||
| VIDE | ||||||||
| WMAP5 | REVOLVER | |||||||
| VoidFinder |