An Integral-Based Technique (IBT) to Accelerate the Monte-Carlo Radiative Transfer Computation for Supernovae
Abstract
We present an integral-based technique (IBT) algorithm to accelerate supernova (SN) radiative transfer calculations. The algorithm utilizes “integral packets”, which are calculated by the path integral of the Monte-Carlo energy packets, to synthesize the observed spectropolarimetric signal at a given viewing direction in a 3-D time-dependent radiative transfer program. Compared to the event-based technique (EBT) proposed by Bulla et al. (2015), our algorithm significantly reduces the computation time and increases the Monte-Carlo signal-to-noise ratio. Using a 1-D spherical symmetric type Ia supernova (SN Ia) ejecta model DDC10 and its derived 3-D model, the IBT algorithm has successfully passed the verification of: (1) spherical symmetry; (2) mirror symmetry; (3) cross comparison on a 3-D SN model with direct-counting technique (DCT) and EBT. Notably, with our algorithm implemented in the 3-D Monte-Carlo radiative transfer code SEDONA, the computation time is faster than EBT by a factor of , and the signal-to-noise (S/N) ratio is better by a factor of , with the same number of Monte-Carlo quanta.
1 Introduction
Type Ia supernovae (SNe Ia) have been widely applied in cosmological studies (e.g. Abbott et al. (2019); Brout et al. (2022)) based on the empirical relation between the light curve properties and the luminosities (e.g. Phillips (1993)). However, the explosion mechanism of SNe Ia is still a mystery; studies of the ejecta structure rely on simulations that include hydrodynamics, nucleosynthesis, and radiative transfer.
Radiative transfer simulations of supernovae calculate the specific intensity and plasma excitation states to obtain spectra that can be compared to optical spectroscopic and photometric observations. Many radiative transfer codes assume that SNe Ia are spherical symmetric and reasonable agreement have been found among the simulation results of different codes (Blondin et al., 2022).
However, imaging of nearby SN Ia remnants (e.g. Ferrazzoli et al. (2023)) and hydrodynamic simulations (e.g. Gamezo et al. (2004); Kromer et al. (2013)) suggest that SNe Ia have an asymmetric 3-D structure. Given the distance to most SNe Ia, this 3-D structure cannot be resolved, but can be probed by spectropolarimetric observations (e.g., Wang et al., 2003; Cikota et al., 2019; Yang et al., 2022). The polarization from SN Ia is primarily due to Thomson scattering of photons, and a non-zero linear polarization signal can arise in asymmetric SN ejecta due to the incomplete cancellation of polarization from photons scattered from different geometrical structures (Wang & Wheeler, 2008).
Monte-Carlo methods, which use energy packets to emulate the propagation of photons in the SN plasma, provide a flexible way to treat complicated physical processes (Lucy, 2002, 2003) and have been applied in 3-D time-dependent radiative transfer codes such as SEDONA (Kasen et al., 2006), and ARTIS (Kromer & Sim, 2009). 3-D Monte-Carlo radiative transfer (MCRT) simulations can be computationally expensive, as many photon packets must be propagated to reduce the statistical noise in the synthesized observables. This especially poses a challenge for modeling SN polarization, as the expected signals are typically only at the 1% level or less. To reduce the noise in SN MCRT simulations, Bulla et al. (2015) introduced an “event-based technique” (EBT) for spectropolarimetry synthesis, which has been applied to simulations of SNe Ia (Bulla et al., 2016a, b), superluminous SNe (Inserra et al., 2016), and kilonovae (Bulla et al., 2021).
In this paper, we introduce a new integral-based technique (IBT), which is implemented in the MCRT code SEDONA, to efficiently construct observable spectra from a 3-D MCRT computation. We find that IBT is times faster and times less Monte-Carlo noise than EBT, with the same number of Monte-Carlo quanta. Moreover, IBT can be applied to the ultraviolet and infrared wavelength, and early phase of SNe, which was not calculated with EBT (Bulla et al., 2015). Section 2 reviews the direct-counting technique (DCT) and event-based technique (EBT) that have been used in previous MCRT codes. Section 3 presents the IBT method. Section 4 uses several toy models to verify the spectropolarimetry results from IBT. Section 5 compares the Monte-Carlo simulation error and computation time of the three algorithms: DCT, EBT, and IBT. Section 6 summarizes our main conclusions.
2 Polarized Spectrum Extraction
In the SEDONA code, an optical photon packet (OP) represents a collection of photons with the same frequency, spatial coordinate, and propagation direction. The OPs undergo interaction events due to Thomson scattering, bound-bound transitions, bound-free transitions, and free-free transitions which can change their frequency and direction.
The polarization information of an OP is stored as a dimensionless Stokes vector
| (1) |
and the Stokes vector can be constructed with and the energy of the OP .
Typically, OPs are generated with zero initial polarization as expected for thermal emission. During the propagation of an OP, the linear polarization state changes in a Thomson scattering event according to the Rayleigh scattering phase matrix (Section 1.17, equation 217 of (Chandrasekhar, 1960)). In bound-bound, bound-free, and free-free interactions, the OPs are typically assumed to be fully depolarized. The current version of SEDONA does not include magnetic fields, and the parameter in the Stokes vector, which represents the circular polarization, is set to zero.
2.1 Direct Counting Technique
A straightforward method of spectral synthesis in MCRT is the direct counting technique (DCT), which sums the energy of OPs that escape the simulation domain within a certain frequency, time, and viewing angle bin. The observed flux is then calculated as
| (2) |
where is dimensionless Stokes vector of the -th OP, is the lab frame energy of the -th OP, is the size of the arrival time bin, is the size of the frequency bin, is the distance to the SN center, is the viewing direction bin size. The summation is over all the OPs in the arrival time interval , the frequency interval , and the viewing direction interval ; .
In the DCT method, the signal-to-noise ratio (S/N) values of the synthetic spectra depend on the number of OPs simulated and the choice of the bins of arrival time, frequency, and viewing direction. Therefore, a higher resolution in viewing angle results in fewer OPs per bin and a lower S/N. The DCT has been the default implementation in the SEDONA code.
2.2 Virtual Packets
Several techniques have been suggested to improve the S/N in MCRT simulations. The idea of a “virtual packet” (VP) in the SN simulation context is discussed by Kerzendorf & Sim (2014) and implemented in the 3-D simulation by Bulla et al. (2015). Generally, VPs are used as follows
-
•
An observer viewing direction is specified at the start of the MCRT simulation.
-
•
VPs are created in the SN plasma to represent the emitted and the scattered photons at the corresponding volume-time-frequency bin pointing to the viewing direction.
-
•
The energy of each VP is reduced by the optical depth along the path to the observer.
-
•
Finally, the escaped VPs are used to synthesize the spectrum for the specified observer viewing angle.
Event-based techinque (EBT), proposed by Bulla et al. (2015), utilizes VPs to increase the S/N relative to DCT. In the EBT calculation, when an OP has undergone a physical event, a VP is created at the same coordinate and time with the same co-moving frame frequency. If the interaction event is Thomson scattering, then the co-moving frame Stokes vector of the VP is calculated from the Rayleigh scattering rule (Chandrasekhar, 1960):
| (3) |
where is the Stokes vector of the OP in the co-moving frame, is the OP propagating direction in the co-moving frame, is the viewing direction in the co-moving frame, is the combination of the rotation matrix and the scattering matrix (See Equation 10 in Bulla et al. (2015)). In the following, co-moving frame quantities are denoted with a bar, whereas non-bar quantities refer to the lab frame. A detailed expression of the matrix is given in Appendix A.
If the interaction event is a bound-bound transition, bound-free transition, or free-free transition, then an depolarized VP propagating towards the viewing direction is created. The energy of the VP is
| (4) |
After creation, the VPs propagate along the viewing direction with the speed of light, and are not considered in the subsequent computation of the plasma excitation and ionization states. The total optical depth along the VP trajectory is integrated as
| (5) |
where is the length of the -th line segment of the VP trajectory, is the total extinction coefficient at the -th line segment. The lab frame extinction coefficient is calculated from the co-moving frame value
| (6) |
where and are the co-moving frame frequency and the rest-frame frequency respectively.
The VP is moved in small line segments, the length of which are determined by finding the minimum distance among the following
-
•
The VP reaches the boundary of a volume cell.
-
•
The VP reaches the end of a time step.
-
•
The co-moving frame frequency of the VP reaches the boundary of the frequency grid of .
The final spectrum is constructed by summing the VPs
| (7) |
the summation is over all the VPs in the frequency bin , and arrival time interval .
The EBT can be accelerated by only emitting VPs with frequencies within a desired spectral range (e.g., ) for the synthetic observables, and by removing the VP once the integrated optical depth reaches a critical value . We do not apply these optimizations in the present calculations, but Bulla et al. (2015) find that they can decrease the computational time by a factor of while not affecting accuracy.
3 The Integral-Based Technique
Our proposed IBT uses integrated packets (IPs), which are an improved version of VPs that can be used to more efficiently construct spectra. Compared to VP, the major changes of IP are: (1) A VP stores the energy and polarization at a single frequency with a four-vector , while an IP stores the energy and polarization at multiple frequency bins with a tensor of cell radiance ; (2) The creation of a VP is based on the physical interactions of OPs, whereas an IP is created in each volume cell for each time step.
3.1 The Integrated Packets
The IP computation is based on a universal logarithmically spaced frequency grid . The frequency ratio between the adjacent pixels is a constant , satisfying
| (8) |
Using this frequency grid, the Doppler shift of the variables could be simplified to the shifting of the index of the frequency bin, which saves computation time.
We define the cell radiance in the lab frame for a cell located at coordinate and time as the energy radiated per frequency bin at frequency toward the viewing direction, the units of is . The formal solution of the cell radiance is:
| (9) | |||
| (10) | |||
| (11) |
where is the specific intensity as a four-vector of the Stokes parameters; is the size of the simulation time step; and are the four-vectors of the emission terms due to depolarized isotropic emission and scattered light from Thomson scattering, respectively; the function is the depolarized isotropic emission term, which includes all the emission from bound-bound, bound-free, and free-free transitions; the function is a combination of the Rayleigh scattering phase matrix and rotation matrix discussed in Appendix A; is the extinction coefficient for Thomson scattering; the integral is over all the incident directions (); the term is the correction of the Doppler effect (Castor e.g., 1972, eq. (1–3); see also Mihalas 1978, p. 31,33,495–496).
For each IP, the cell radiance is calculated on the universal frequency grid and stored as a vector. During the propagation of an IP, is reduced by the extinction coefficient on the trajectory. The spectral synthesis is the summation of over the IPs at a specific arrival time. Section 3.2 and Section 3.3 illustrate the computation of in a MCRT simulation during the creation of an IP. Section 3.4 illustrates the update of during the propagation of IP and spectral synthesis.
3.2 Isotropic Emission
The isotropic emission term, including bound-bound, bound-free, and free-free interactions, can be calculated by the summation of the OPs from the same physical events
| (12) |
where the summation is over all the OPs within the frequency bin , the volume cell , and the time step bin . Only OPs that are newly created or undergone the same physical events are taken into account.
In the present SEDONA calculation, we include bound-free and free-free transitions and adopt the line expansion opacity approximation (Kasen et al. 2006, eq. (8)) for bound-bound transitions which are treated as purely absorptive. Therefore, the isotropic emission term is calculated from the current plasma state as , where is the blackbody spectrum and is the total extinction coefficient including bound-bound, bound-free, and free-free transitions (Thomson scattering is not included in this term).
3.3 The Path Integral
The cell radiance from Thomson scattering is calculated from the path integral of the OPs
| (13) |
where is the co-moving frame length of the -th line segment of the -th OP trajectory in the volume cell and in the time step, the summation is over all the trajectories within the frequency bin , the volume cell , the time step bin .
For each volume cell and at each time step, an IP is created. The initial coordinate of the IP is randomly chosen in the volume cell, and the initial time of the IP is randomly chosen in the time step. The cell radiance is calculated on the universal frequency grid and stored in IP as a tensor.
3.4 The Propagation of Integral Packets
After creation, the IPs propagate toward the viewer with the speed of light, and the cell radiance is reduced during propagation. Similar to the propagation of the VPs, the trajectory of an IP is split into line segments by the edges of time steps and volume cells. Moreover, the trajectory is further split to satisfy the criterion:
| (14) |
where is the co-moving frame frequency at the beginning of the line segment, is the co-moving frame frequency of the same lab frame frequency at the ending of the line segment, the constant is defined in Equation 8.
In the calculation of VP in Equation 5 and 7, the total opacity is accumulated over the trajectory, which computationally requires one more double precision floating point number per VP to store the opacity. This process reduces the computation time on exponentials at the cost of memory space. While in the propagation of IPs, the cell radiance is updated at every line segment on the trajectory without accumulating the total opacity over the trajectory
| (15) |
where is the length of the -th IP at the -th line segment over the trajectory, is the total extinction coefficient of the -th IP at the -th line segment and at lab frame frequency . The final spectrum is the sum of the IPs:
| (16) |
where is the final cell radiance when the -th IP escapes the simulation domain. The summation is over all IPs in the arrival time interval . Note that the grid size of arrival time should be much larger than the time step size to avoid grid mismatch issue, while this issue is not significant in DCT or EBT calculations.
4 Model Validation

In this section, we prepare two toy models to validate the IBT computation results. The first model is the SN Ia delayed-detonation model DDC10. DDC10 is calculated from hydrodynamic simulations in Blondin et al. (2013) and adopted as a benchmark in Blondin et al. (2022) to evaluate the differences between radiative transfer codes. We remap the 1-D model into a 3-D Cartesian grid. retaining the spherical symmetry and with the outer boundary velocity limited to 25,000 km/s. Figure 1 shows the abundance of several elements and the density profile of the DDC10 model. The second model is an ellipsoidal model based on the DDC10 model; the y and z coordinates are reprojected with and , in order to introduce asphericity. This model is also realized on a Cartesian grid, with a boundary velocity of 32,500 km/s. The geometry of the model is shown in the right panel of Figure 1.
In the following text, the spherical symmetric DDC10 model is denoted as D1D, and the modified ellipsoidal 3-D model is denoted as D3D. Both the models are treated with 3-D time-dependent radiative transfer calculations in SEDONA starting from 0.976 days after the explosion. Before 6.6 days, the simulation time step is a logarithmic with . After 6.6 days, the simulation time step is days. The arrival time bin size is day, which satisfies . The frequency grid ranges from Hz to Hz (30,000 to 600 ) with .
4.1 Spherical Symmetry
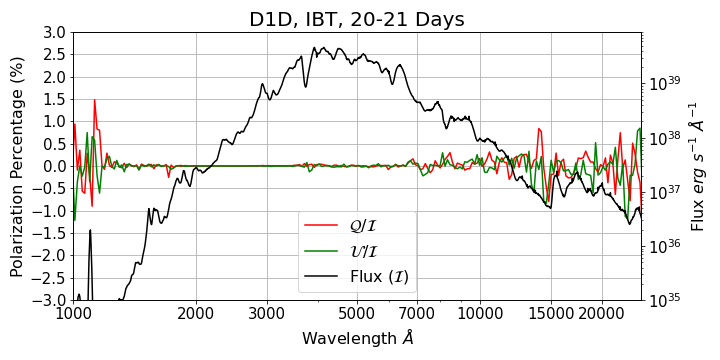
Because the linear polarization components cancel out, a spherical symmetric model should produce zero polarization. Using IBT, we calculate the spectropolarimetry of the D1D model to test if the algorithm recovers zero polarization. Figure 2 shows the spectra and the polarization percentage at different times after the explosion. At each time step, OPs are generated to represent the energy release from radioactive decay and gamma-ray scattering. We find that the polarization signal at all times and wavelengths is consistent with the expected zero polarization. Moreover, the simulation error between 7 days and 31 days and between 2000 and 10000 wavelength range (within which most SNe Ia spectropolarimetry observations are made (Cikota et al., 2019)) is as low as . Notably, the spectra in the ultraviolet wavelength between 7 days and 21 days also show high S/N, despite the emergent flux being low in this band. In the early phase of SNe Ia, most of the OPs are generated below the photosphere, therefore the cell radiance above the photosphere has low S/N. As a result, the spectrum shows low S/N at 3-4 days after the explosion. Moreover, the S/N in the infrared wavelength is lower than that in the optical wavelength, because most of the OPs are in the optical wavelength. Due to the limited number of OPs in the ultraviolet wavelength at late phase, the ultraviolet spectrum at 30-31 days and after is dominated by Monte-Carlo noise. In the IBT simulation of this paper, this phenomenon is only observed below 2000 and can be alleviated by increasing the number of OPs.





4.2 Mirror Symmetry
In this section, we use IBT to calculate the spectropolarimetry at two mirror symmetric viewing directions of the D3D model. At each time step we generate OPs. Based on the mirror symmetry of the D3D model in the X-Z, Y-Z, and X-Y planes, spectropolarimetry in the viewing directions and should have the same Stokes terms and inverted terms. Figure 3 shows the spectropolarimetry at the two symmetric viewing directions. We notice the simulation results are consistent with the theoretical expectations of the symmetry at above 2000 wavelength from early phase (7-8 days after the explosion) to late phase (50-51 days after explosion). Similar to the spherical symmetric validation results in Figure 2, the ultraviolet spectropolarimetry below 2000 after 25 days are dominated by Monte-Carlo noise. Moreover, ultraviolet spectropolarimetry at 7-8 days and 15-16 days shows an exceptional high S/N.




4.3 Cross Comparison
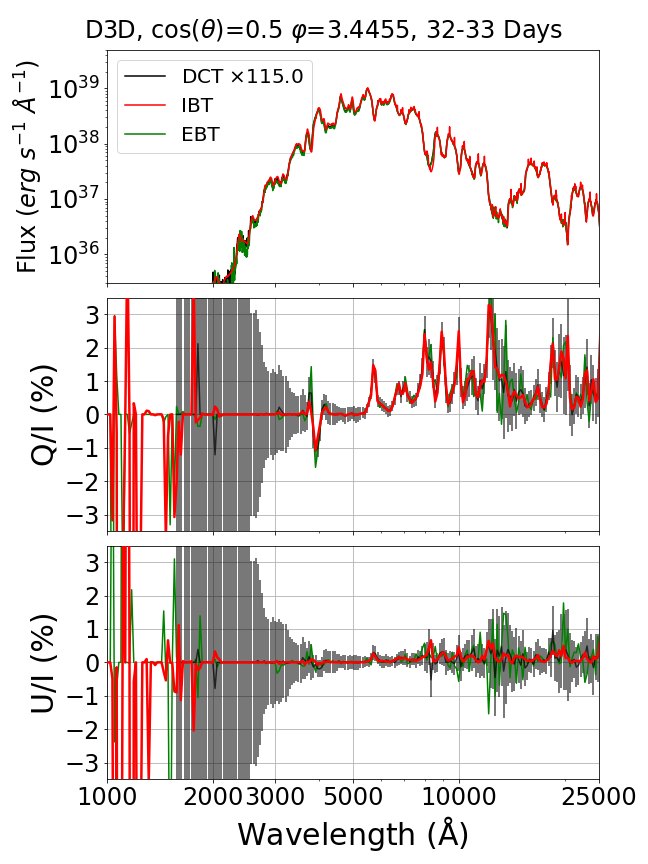
In this section, we compare the simulation results from the EBT, IBT, and DCT methods using the D3D model. Figure 4 shows the spectra and linear polarization time sequence calculated by the three methods. In the DCT calculation, the viewing direction is split into a bin and OPs are generated per time step to achieve a reasonable S/N. For the EBT and IBT calculations, we only generate OPs per time step. Figure 4 shows that the IBT calculation produced spectra and polarization with a S/N comparable to a DCT calculation that used times more OPs. This noise reduction holds from 6 days to 33 days after the explosion and from ultraviolet to infrared wavelengths.
Due to the high opacity at the early phase of SN, the OPs undergo multiple scattering events near the core of SN, which results in a rapidly growing number of VPs in the EBT calculation and an increasing memory usage expense. Therefore, in this example EBT calculation we started the calculation at 25 days after the explosion due to the limit of hardware.


5 Computational Performance
5.1 Computational Speed Comparison
The computational speed of the three methods is measured on one 48-core compute node of Grace supercomputer in TAMU HPRC 111https://hprc.tamu.edu/. Each node has 2 sockets of Intel Xeon 6248R CPUs, in total 48 cores, and has 384 GBs of RAM memory. The majority of the computation time in a 3-D time-dependent radiative transfer computation consists of two components: (1) the computation of the plasma state, level population, and opacity of the grid; (2) the propagation of energy packets including OPs, VPs, or IPs. The choice of spectral synthesis methods only affects the propagation time of the energy packets.

Figure 5 shows the computation time of particle propagation at each time step as a function of the time after explosion using the EBT and IBT methods as described in Section 4.3, and the corresponding DCT computation time with OPs per time step, the same number of OPs as the EBT and IBT results. The time needed to compute the plasma state and opacity does not change drastically at different time steps. In contrast, the computation time for packet propagation increases in the first 3 days, because the optical depth is high and the OPs cannot easily escape the SN ejecta and undergo repeated interaction events. With the expansion of the SN ejecta, the optical depth decreases, and the accumulated OPs escape the SN ejecta, therefore the computation time decreases. In particular, the computation time for EBT is a factor of 30 higher than DCT around 25 days after the explosion, and is a factor of 10 higher than DCT around 60 days. In contrast, the introduction of IBT only increases the computation time by a factor of 0.3-0.5 of the DCT computation time, throughout the time after the SN explosion, to reach a comparable S/N as EBT.
5.2 Signal to Noise Ratio
In an MCRT simulation, the output spectral flux error scales roughly as , where is the number of photon packets. We therefore use the simulation results on the D1D model to measure the simulation error of the three spectral retrieval methods. First, we split the output spectra into ultraviolet wavelength range (1000-2000 ), optical wavelength range (2000-10000 ), and infrared wavelength range (10000-25000 ). Second, we measure the simulation root mean squared error (RMSE) of the Stokes parameters and using the following equation:
| (17) |
where is the number of frequency indicies in the selected wavelength range, the summation is over all frequency indicies in the selected wavelength range. Note that the theoretical solution of the D1D model is no polarization which results in the zero term in the equation. The RMSE observes the inverse square root relation with the number of packets, .






Figure 6 shows the relationship between the number of OPs per time step and the resulting RMSE at 10-11 days after the explosion using DCT or IBT, and at 37-38 days after the explosion using DCT, EBT, or IBT. We notice the result from IBT could reproduce the relation in most of the time and wavelength ranges. The DCT result also reproduces the relation in the optical and infrared wavelength ranges when the number of packets is large enough. However, in the ultraviolet wavelength, and in the optical wavelength with the number of packets per step smaller than , the inverse square root relation is not observed due to the large simulation error. The result from EBT also reproduces the relation in optical ind infrared wavelength ranges at 37-38 days after the explosion. In the ultraviolet wavelength range at 37-38 days after the explosion, none of the methods could simulate good S/N spectra to reproduce the relation.
A direct comparison of the computation efficiency of the three methods could be made using the RMSE values measured in the optical and infrared wavelength range. The RMSE of IBT is smaller than that of DCT by a factor of , leading to a factor of less packets needed to calculate to reach similar S/N. The RMSE of EBT is smaller than that of DCT by a factor of , resulting in a factor of less packets to calculate to achieve a comparable S/N. The accuracy comparison between EBT and IBT is consistent with the reports in Table 1 of Bulla et al. (2015).
6 Conclusion
We present IBT, an algorithm to efficiently synthesize the spectropolarimetry signal from 3-D MCRT simulations. Comparing to EBT (Bulla et al., 2015), the present IBT method is upgraded in the following aspects:
-
•
In EBT, a VP is created at each scattering event of an OP, which could lead to an uncontrolled number of VPs and limit the application of EBT on high-opacity plasma models (i.e. SNe Ia at 3 days after the explosion). However, IBT uses the cell radiance as a proxy of all VPs in a volume cell of the plasma model, and limits the number of IPs to save memory and computation time in tracing the particles.
- •
In the tests on the D3D model, both IBT and EBT have successfully reproduced the spectral time sequence with spectropolarimetry from 1000Å to 25000Å, and the S/N is comparable to DCT with 115 more Monte-Carlo OPs. The computation time for IBT is 0.3 of DCT with the same number of OPs per viewing direction, while the computation time for EBT is a factor of of DCT per viewing direction. With an opacity limit and wavelength limit to accelerate the computation, the EBT computation time is still about a factor of two of DCT per viewing direction(Bulla et al., 2015). Moreover, IBT has successfully calculated the spectral time sequence from 1 day to 60 days after the explosion, while EBT failed before day 25 due to the limited memory space of the computing facility.
In the tests on the D1D model, IBT has successfully reproduced the zero polarization signal as the theoretical predictions from the spherical symmetry. Using the same number of Monte-Carlo OPs, the S/N of the IBT spectrum is 30 times higher than the DCT spectrum S/N and times higher than the EBT spectrum.
Chen et al. (2020, 2024) developed the Artificial Intelligence Assisted Inversion (AIAI) method which enables theoretical models of SNe Ia to be derived using the observational data as input constraints. The published AIAI is based on 1-D models. The studies demonstrate that it is possible to combine empirical models of SNe Ia with detailed radiative transfer code to improve the use of SNe Ia as cosmological probes. In the future, we will extend the 1-D models to 3-D time-dependent models. The proposed IBT is the ideal algorithm to efficiently generate a time sequence of spectrophotometric and spectropolarimetric data bases which can be used to train AI models, this can be an important step in assimilating the extensive observational data of SNe Ia into studies of the physics of thermonuclear explosions and the use of SNe Ia as cosmological distance candles.
Appendix A Rayleigh Scattering
The Thomson scattering between free electron and photon is calculated by the Rayleigh scattering phase matrix:
| (A1) |
where is the angle between the incident light and the emergent light. Before the calculation of Rayleigh scattering phase matrix, the reference axis of the incident light should be rotated into the scattering plane, and the polarization state is changed by the rotation matrix:
| (A2) |
where is the rotation angle between the observer’s reference axis and the scattering plane reference axis. A similar rotation matrix of is also applied to the emergent light, in order to convert the polarization state to the observer’s reference axis.
We define as the multiplication of the packet energy and the dimensionless Stokes vector:
| (A3) |
Therefore, the full Rayleigh scattering formula in the SN radiative transfer simulation is written as:
| (A4) |
Note that the Rayleigh scattering happens in the co-moving frame, and all the variables in the above equation are measured in the co-moving frame. In Equation 3, Equation 9, and Equation 13, the operator is defined as .
Replacing the axis rotation angles and scatter angle (, , ) with the propagating direction of the incident OP (, ) and the propagating direction of the emergent VP/IP (, ), the expression of the operator becomes (Chandrasekhar, 1960):
| (A5) | |||||
| (A6) | |||||
| (A7) | |||||
| (A8) |
where , , , are:
| (A9) | |||||
| (A10) | |||||
| (A11) | |||||
| (A12) |
References
- Abbott et al. (2019) Abbott, T. M. C., Allam, S., Andersen, P., et al. 2019, ApJ, 872, L30, doi: 10.3847/2041-8213/ab04fa
- Blondin et al. (2013) Blondin, S., Dessart, L., Hillier, D. J., & Khokhlov, A. M. 2013, MNRAS, 429, 2127, doi: 10.1093/mnras/sts484
- Blondin et al. (2022) Blondin, S., Blinnikov, S., Callan, F. P., et al. 2022, A&A, 668, A163, doi: 10.1051/0004-6361/202244134
- Boerner et al. (2023) Boerner, T. J., Deems, S., Furlani, T. R., Knuth, S. L., & Towns, J. 2023, in Practice and Experience in Advanced Research Computing, 173–176
- Brout et al. (2022) Brout, D., Scolnic, D., Popovic, B., et al. 2022, ApJ, 938, 110, doi: 10.3847/1538-4357/ac8e04
- Bulla et al. (2015) Bulla, M., Sim, S. A., & Kromer, M. 2015, MNRAS, 450, 967, doi: 10.1093/mnras/stv657
- Bulla et al. (2016a) Bulla, M., Sim, S. A., Pakmor, R., et al. 2016a, MNRAS, 455, 1060, doi: 10.1093/mnras/stv2402
- Bulla et al. (2016b) Bulla, M., Sim, S. A., Kromer, M., et al. 2016b, MNRAS, 462, 1039, doi: 10.1093/mnras/stw1733
- Bulla et al. (2021) Bulla, M., Kyutoku, K., Tanaka, M., et al. 2021, MNRAS, 501, 1891, doi: 10.1093/mnras/staa3796
- Castor (1972) Castor, J. I. 1972, ApJ, 178, 779, doi: 10.1086/151834
- Chandrasekhar (1960) Chandrasekhar, S. 1960, Radiative transfer
- Chen et al. (2020) Chen, X., Hu, L., & Wang, L. 2020, ApJS, 250, 12, doi: 10.3847/1538-4365/ab9a3b
- Chen et al. (2024) Chen, X., Wang, L., Hu, L., & Brown, P. J. 2024, ApJ, 962, 125, doi: 10.3847/1538-4357/ad0a33
- Cikota et al. (2019) Cikota, A., Patat, F., Wang, L., et al. 2019, MNRAS, 490, 578, doi: 10.1093/mnras/stz2322
- Ferrazzoli et al. (2023) Ferrazzoli, R., Slane, P., Prokhorov, D., et al. 2023, ApJ, 945, 52, doi: 10.3847/1538-4357/acb496
- Gamezo et al. (2004) Gamezo, V. N., Khokhlov, A. M., & Oran, E. S. 2004, Phys. Rev. Lett., 92, 211102, doi: 10.1103/PhysRevLett.92.211102
- Inserra et al. (2016) Inserra, C., Bulla, M., Sim, S. A., & Smartt, S. J. 2016, ApJ, 831, 79, doi: 10.3847/0004-637X/831/1/79
- Kasen et al. (2006) Kasen, D., Thomas, R. C., & Nugent, P. 2006, ApJ, 651, 366, doi: 10.1086/506190
- Kerzendorf & Sim (2014) Kerzendorf, W. E., & Sim, S. A. 2014, MNRAS, 440, 387, doi: 10.1093/mnras/stu055
- Kromer & Sim (2009) Kromer, M., & Sim, S. A. 2009, MNRAS, 398, 1809, doi: 10.1111/j.1365-2966.2009.15256.x
- Kromer et al. (2013) Kromer, M., Fink, M., Stanishev, V., et al. 2013, MNRAS, 429, 2287, doi: 10.1093/mnras/sts498
- Lucy (2002) Lucy, L. B. 2002, A&A, 384, 725, doi: 10.1051/0004-6361:20011756
- Lucy (2003) —. 2003, A&A, 403, 261, doi: 10.1051/0004-6361:20030357
- Mihalas (1978) Mihalas, D. 1978, Stellar atmospheres (San Francisco: W.H. Freeman and Company)
- Phillips (1993) Phillips, M. M. 1993, ApJ, 413, L105, doi: 10.1086/186970
- Wang & Wheeler (2008) Wang, L., & Wheeler, J. C. 2008, ARA&A, 46, 433, doi: 10.1146/annurev.astro.46.060407.145139
- Wang et al. (2003) Wang, L., Baade, D., Höflich, P., et al. 2003, The Astrophysical Journal, 591, 1110, doi: 10.1086/375444
- Yang et al. (2022) Yang, Y., Yan, H., Wang, L., et al. 2022, The Astrophysical Journal, 939, 18, doi: 10.3847/1538-4357/ac8d5f