An improved bound on the chromatic number of the Pancake graphs
Abstract
In this paper an improved bound on the chromatic number of the Pancake graph , is presented. The bound is obtained using a subadditivity property of the chromatic number of the Pancake graph. We also investigate an equitable coloring of . An equitable -coloring based on efficient dominating sets is given and optimal equitable -colorings are considered for small . It is conjectured that the chromatic number of coincides with its equitable chromatic number for any .
keywords:
Pancake graph; chromatic number; equitable coloringMSC:
[2010] 05C15, 05C25, 05C691 Introduction
The Pancake graph , is defined as the Cayley graph over the symmetric group with the generating set of all prefix–reversals , inverting the order of any substring of a permutation when multiplied on the right. It is a connected vertex–transitive -regular graph without loops and multiple edges of order . It contains all cycles of length , where [14, 23].
A mapping is called a proper –coloring of a graph if whenever the vertices and are adjacent. The chromatic number of a graph is the least number of colors needed to properly color vertices of . A subset of vertices assigned to the same color forms an independent set, i.e. a proper –coloring is the same as a partition of the vertex set into independent sets. The trivial lower and upper bounds on the chromatic number of the Pancake graphs are given as follows:
| (1) |
Indeed, the graph is –regular, hence by Brooks’ theorem [4] we have the upper bound. Moreover, since , and since there are –cycles in for any [19] which gives us the lower bound. The Brooks’ bound is improved by for graphs with , where and are the size of the maximum clique and the maximum degree of the graph (see [5, 6]). Since , then for any . Moreover, there is a proper –coloring of [18]. Thus, we have:
| (2) |
Catlin’s bound for –free graphs [7], that is , gives one more bound for any :
| (3) |
Using structural properties of , the following bounds were obtained in [18]:
| (4) |
| (5) |
| (6) |
These bounds improve (2) for , however Catlin’s bound (3) is still better for all and some smaller (for example, ). Thus, they are far from good. Meanwhile, the asymptotic bound holds for the Pancake graphs which follows from the results for –free graphs [10, 15].
In this paper in Section 2 we present a new upper bound which improves Catlin’s bound (3). The new bound is obtained using a subadditivity property of the chromatic number of and known chromatic numbers for . We have since , and since there are –cycles in . An example of a proper –coloring for was given in [18]. An optimal -coloring for was computed by Tomaž Pisanski, University of Primorska, Koper, Slovenia, and Jernej Azarija, University of Ljubljana, Slovenia, so . Since is an induced subgraph of , then is at least , and from (4) we have . Optimal -colorings for and were computed by A. H. Ghodrati, Sharif University, Tehran, Iran. By (5), , where , however, proper -colorings in these cases are unknown. The known chromatic numbers are presented in the Table 1.
In Section 3 an equitable coloring is considered. A graph is said to be equitably -colorable if has a proper -coloring such that the sizes of any two color classes differ by at most one. The equitable chromatic number is the smallest integer such that is equitably -colorable. Equitable coloring was introduced by W. Meyer in due to scheduling problems [21]. Moreover, it was conjectured that every connected graph with maximum degree has an equitable coloring with or fewer colors, with the exceptions of complete graphs and odd cycles. A strengthened version [8] of the conjecture states that each such graph has an equitable coloring with exactly colors, with one additional exception, a complete bipartite graph in which both sides of the bipartition have the same odd number of vertices. A survey on equitable colorings can be found in [20].
In Section 3.1 an equitable -coloring based on efficient dominating sets in the Pancake graphs , is presented. Moreover, in Section 3.2 simple optimal equitable -colorings for and are described.
Let us note that any equitable coloring of with at most colors has the property that the sizes of all color classes are equal since every integer at most divides . Thus, we have a strongly equitable coloring [12].
Since equitable coloring is a proper coloring with an additional condition, the inequality holds for any . However, since all above optimal colorings are strongly equitable we have conjectured.
Conjecture 1
For any ,
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 2 | 2 | 3 | 3 | 4 | 4 | 4 | 4 |
2 Improved upper bound
Our main result is given by the following theorem.
Theorem 1
For any the following holds for the Pancake graph :
| (7) |
To prove this result we need more notation. Let . We consider a permutation written as a string in one-line notation, where for any . For , let be the induced subgraph of whose vertex set consists of all permutations with . By the symmetry of , for any -element subset of , the induced subgraph is isomorphic to , which is abbreviated to .
We define a map by removing the elements that are not in . For example, for and , the vertex of is mapped to the vertex of . It is clear that this mapping is a graph homomorphism. Note that is surjective, but not necessarily an isomorphism. In fact, is not even connected unless or .
Since an -coloring of a graph is equivalent to a graph homomorphism from to the complete graph , this property implies that
| (8) |
Since always contains a subgraph isomorphic to (e. g. the subgraph of all vertices that end with ) it even follows that .
One more useful property says that all fibers are of size , which means that for every . Indeed, for any permutation of length one can insert at different positions: the first position is forbidden since the vertices of start with an element from .
The following theorem immediately gives the general upper bound of (7) with taking into account .
Theorem 2
The chromatic number of the Pancake graph is subadditive, i. e.
| (9) |
for all positive integers and .
Proof. Let the vertices of be partitioned into sets and such that contains permutations whose first element is in and contains permutations whose first element is in . The subgraphs and are isomorphic to and , respectively. Hence, by (8) the graph is -colorable, and is -colorable. Using disjoint color sets on both subgraphs proves the desired inequality.
3 Equitable coloring and optimal colorings
It was shown in Introduction that there are optimal colorings of the Pancake graphs found by computer experiments. Such computations do not provide us any structural insight. In this section we consider colorings of the Pancake graphs , using their structural properties. More precisely, we present equitable colorings of in colors.
An equitable coloring is not the same as a perfect coloring for which the multiset of colors of all neighbors of a vertex depends only on its own color [11]. This type of coloring gives a partition known as an equitable partition [13] which are used in algebraic combinatorics, graph theory and coding theory. In coding theory such kind of partitions are known as perfect codes [1, 16]. Some general information about equitable partitions can be found in [2].
The notion of perfect codes was generalized to the Pancake graphs in a natural way in [9]. An independent set of vertices in a graph is an efficient dominating set (or -perfect code) if each vertex not in is adjacent to exactly one vertex in . There are efficient dominating sets in [9, 22] given by:
| (10) |
where . It is obvious that , , which immediately gives a proper -coloring. Moreover, this coloring is perfect and equitable.
To present a proper -coloring of the Pancake graphs based on efficient dominating sets we need to define such sets for induced subgraphs of .
Due to the hierarchical structure, for any the graph has copies of with the vertex set , where , . Any two copies , are connected by edges , where . Prefix–reversals , define internal edges in all copies , and the prefix–reversal defines external edges between copies.
Efficient dominating sets of , contain all permutations with the last element fixed to and the first element fixed [17], namely:
| (11) |
where , . For any , the sets (10) and (11) are given by the following obvious relationship:
| (12) |
3.1 Equitable -coloring
We now present an equitable -coloring based on efficient dominating sets. Let
| (13) |
and
| (14) |
where
| (15) |
Note that partitions the vertices of , and partitions the vertices of that end with . We now define a graph whose vertices are the elements of , and are adjacent in if and only if a vertex of is adjacent to a vertex of in . From the properties of the Pancake graphs we immediately see that vertices and are adjacent in if and only if one of the following statements is true:
-
(A1)
and .
-
(A2)
and .
It is obvious that a proper coloring of trivially extends to a proper coloring of in such a way that any vertex of belongs to exactly one efficient dominating set and we give it the color .
We now have reduced the problem to finding a proper ()-coloring for . First let us show an idea of such colorings for the graphs and . The graphs are presented on Figures 1 and 2 such that the vertices corresponding to the set , are denoted by labels . The vertices are arranged in a hamiltonian cycle such that all vertices with the same last element are grouped together and form - and -cliques, respectively. Within each clique the first element of labeling is cyclically incremented. Obviously, the elements of each clique must all have different colors, but the pictures suggest that we can ‘almost’ cyclically repeat a color pattern chosen on the first clique. The only collisions occur with the ‘long’ chords that connect antipodal vertices. We see that if we exchange the color of one end of each long chord with the color of the vertex counterclockwise next to it on the cycle, we obtain a proper coloring. It is clear that the proper colorings of and are equitable. Indeed, by (13)-(15) and from the construction has color classes of cardinality each, and has color classes of cardinality each. However, they are not perfect since the multisets of colors of all neighbors are different for different vertices having the same color. For example, in the red vertex has two green and one blue neighbors, while the red vertex has two blue and one green neighbors. Similar, in despite the red and the purple vertices have the same multiset of colors of their neighbors, the green, the blue and the dark blue vertices do not meet this condition to be perfect.
Note that this coloring is exactly the greedy coloring for the vertex sequence that starts with and then counterclockwise follows the cycle.

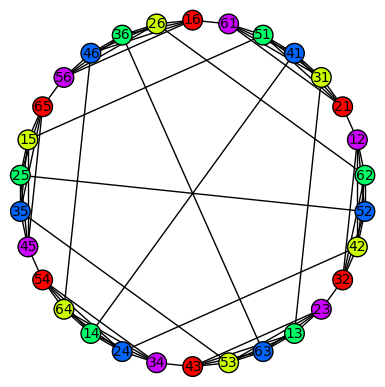
Now we formalize and prove this observation. First we define a map:
| (16) |
such that
| (17) |
Note that indeed has all its values in , and that the restriction of to is injective, i.e.
Next we let and define a coloring
| (18) |
by
| (19) |
where
| (20) |
If is odd, the first two cases cannot occur, since is an integer, but is not. The restriction of to is still injective, since it is either equal to for or it is equal to with at most two adjacent function values exchanged.
In terms of the intuitive approach above, is the coloring that cyclically repeats along the cycle, and is the coloring that exchanges the colors near the ends of long chords.
Theorem 3
The coloring is proper and equitable for .
Proof. Indeed, suppose that and are adjacent. If , then by (A1). By the injectivity of for fixed , and must have different colors. By (A2) the only other possibility is that . Without loss of generality we assume that .
First we handle the case that is odd. Then , and . The equality implies , so is even. There is a contradiction.
In the last part of the proof we assume that is even, so is an integer. We do a case analysis based on the position of .
If then , and . The equality implies , so , and this gives a contradiction.
If then , and . The equality implies , so . Then must be even, hence , and or . Since we have by (20) which gives a contradiction.
If then and . The equality implies , so , and hence and have the same parity. There are the following possibilities.
(i) If then . Since we have which gives a contradiction.
(ii) If , . As in case (i), we have which leads to a contradiction.
(iii) If , then . Again, since , this is only possible if and . Then , so by (20), and we have a contradiction.
3.2 Optimal colorings
It is obvious that above equitable -coloring produces an optimal coloring for and (see Table 1). However, for a proper coloring of can never produce an optimal coloring for . Indeed, by (2) for we have and since contains an ()-clique.
Now we give a simple optimal -coloring of , or . We define an even (odd) prefix–reversal , if it corresponds to an even (odd) permutation. By [18, Lemma 4], if then is an even prefix–reversal. Similar, is an odd prefix–reversal if . By [18, Lemma 6], the Pancake graph , has independent even –cycles where .
Let be one of , , . Then the subgraph generated by the even prefix–reversals and is a spanning subgraph of consisting of disjoint -cycles . Since even prefix–reversals preserve parity, all vertices of that are on the same cycle have the same parity. Since all other edges of correspond to odd permutations, they have one endpoint on an ‘even’ -cycle and the other endpoint on an ‘odd’ -cycle. Thus, we can -color the even cycles and -color the odd cycles using two other colors. This results in an equitable -coloring of where each of the color classes has vertices. Since this coloring is optimal for and .
4 Discussion
There are trivial examples of graphs for which Conjecture holds such as even cycles, bipartite graphs with equal parts. Any Cayley graph over the symmetric group generated by a set of transpositions gives a bipartite graph with two equal color classes. The statement holds for the Hamming graphs whose (equitable) chromatic number is . A regular graph with a Hoffman coloring always gives a strongly equitable coloring [3]. Hoffman’s lower bound is known as , where and are the largest and the smallest eigenvalues of . If equality holds, an optimal coloring of is called a Hoffman coloring.
Acknowledgements
The research work of the second author is supported by Mathematical Center in Akademgorodok, the agreement with Ministry of Science and High Education of the Russian Federation number 075-15-2019-1613. The authors thank Alexander Kostochka and Sergey Avgustinovich for useful discussions on equitable colorings.
References
- [1] R. Ahlswede, H. Aydinian, L. Khachatrian, On Perfect Codes and Related Concepts, Designs, Codes and Cryptography, 22 (2001) 221-–237.
- [2] R. A. Bailey, P. J. Cameron, A. L. Gavrilyuk, S. V. Goryainov, Equitable partitions of Latin-square graphs, Journal of Combinatorial Designs, 27 (2019) 142–160.
- [3] A. Blokhuis, A. E. Brouwer, W. H. Haemers, On -chromatic distance-regular graphs, Designs, Codes and Cryptography, 44 (2007) 293–305.
- [4] R. L. Brooks, On colouring the nodes of a network, Proc. Cambridge Phil. Soc., 37 (1941) 194–197.
- [5] O. V. Borodin, A. V. Kostochka, On an upper bound of a graph’s chromatic number depending on the graph’s degree and destiny, J. Combin. Theory. Ser. B., 23 (1977) 247–250.
- [6] P. A. Catlin, A bound on the chromatic number of a graph, Discrete Math., 22 (1978) 81–84.
- [7] P. A. Catlin, Another bound on the chromatic number of a graph, Discrete Math., 24 (1978) 1–6.
- [8] B. L. Chen, K. W. Lih, P. L Wu, Equitable coloring and the maximum degree, European Journal of Combinatorics, 15 (1994) 443–447.
- [9] I. J. Dejter, O. Serra, Efficient dominating sets in Cayley graphs, Discrete Applied Mathematics, 129 (2003) 319–328.
- [10] A. Johansson, Asymptotic choice number for triangle free graphs, DIMACS Technical Report, (1996) 91–95.
- [11] D. G. Fon-Der-Flaass, Perfect -colorings of a hypercube, Siberian Mathematical Journal, 48 (2007) 740-–745.
- [12] H. Furmaňczyk, M. Kubale, V. V. Mkrtchyan, Equitable colorings of corona multiproducts of graphs, Discussiones Mathematicae Graph Theory, 37 (2017) 1079–1094.
- [13] C. Godsil, Compact graphs and equitable partitions, Linear Algebra and its Applications, 255 (1997) 259-–266.
- [14] A. Kanevsky, C. Feng, On the embedding of cycles in pancake graphs, Parallel Computing, 21 (1995) 923–936.
- [15] J. H. Kim, On Brooks’ theorem for sparse graphs, Combinatorics, Probability and Computing, 4 (1995) 97-–132.
- [16] S. Klavžar, U. Milutinović, C. Petr, -perfect codes in Sierpinski graphs, Bulletin of the Australian Mathematical Society, 66 (2002) 369–384.
- [17] E. Konstantinova, On some structural properties of Star and Pancake graphs, LNCS, 7777 (2013) 472–487.
- [18] E. V. Konstantinova, Chromatic properties of the Pancake graphs, Discussiones Mathematicae Graph Theory, 37 (2017) 777–787.
- [19] E. V. Konstantinova, A. N. Medvedev, Cycles of length seven in the Pancake graph, Diskretnyi Analiz i Issledovanie Operatsii, 17 (2010) 46–55. (in Russian)
- [20] K. W. Lih, Equitable Coloring of Graphs, In: P. Pardalos, D. Z. Du, R. Graham (Eds), Handbook of Combinatorial Optimization, Springer, New York, NY, (2013) 1199–1248.
- [21] W. Meyer, Equitable coloring, American Mathematical Monthly, 80 (1973) 920-–922.
- [22] Ke Qiu, Optimal broadcasting algorithms for multiple messages on the star and pancake graphs using minimum dominating sets, Congress. Numerantium, 181 (2006) 33–39.
- [23] J. J. Sheu, J. J. M. Tan, K. T. Chu, Cycle embedding in pancake interconnection networks, In.: Proc. 23rd Workshop on Combinatorial Mathematics and Computation Theory, Taiwan, (2006) 85–92.