An implementation of the density functional perturbation theory
in the PAW framework

The td DFT offers an efficient description of the dynamics of an interacting many-electron system in the presence of external fields. [3] As a self-consistent perturbation theory of td DFT, DFPT is introduced in this section, wherein the Sternheimer equations are specialized to crystalline systems under a monochromatic, periodic external electromagnetic field.

In td DFT, to account for both charge and spin degrees of freedom, the generalized density is given by

where $\theta_{n}$ is the occupancy of the spinor single-particle state $\psi_{n}$, and the four-vector spin $\sigma=(\sigma_{0},\sigma_{1},\sigma_{2},\sigma_{3})$ ($\sigma_{0}$ is the identity matrix and $\sigma_{\alpha}$ with $\alpha=1,2,3$ are the Pauli matrices). The atomic units ¹¹1$e=\hbar=m_{e}=1$ are adopted in this paper, so $\rho_{0}$ is the total charge density, and $\bm{m}$ is magnetization density. The dynamics of $\psi_{n}$ is prescribed by the td Kohn-Sham equations [3]

The ground state Kohn-Sham Hamiltonian [2] in Eq. (2) is $H=-\frac{1}{2}\nabla^{2}+v[\rho^{(0)}](\bm{r})$ where the self-consistent potential is a functional of the ground state density $\rho^{(0)}$, composed of ionic, Hartree and exchange-correlation (xc) potentials, namely, $v^{\text{i}}$, $v^{\text{H}}$ and $v^{\text{xc}}$. Though the xc potential $v^{\text{xc}}$ as a functional of density is in principle nonlocal in space and time, [29, 30, 31, 32, 33] the commonly adopted local and adiabatic approximation (ALDA) is assumed in this work. [34, 35, 36]

The first-order Hamiltonian $\delta H$ comprises two contributions. The first arises from the coupling of the four-vector spin $\sigma$ with external fields

where the four-vector electromagnetic field $B(\bm{r},t)=(-\phi,\frac{1}{2}\bm{B})$. ²²2Here, $\bm{B}$ is the Zeeman field. We ignore the nonlocal coupling between the magnetic field and orbitals, which requires the current density functional theory and is beyond the scope of the present work. The indices $\alpha,\beta=0,1,2,3$ are implicitly summed over when repeated, but we will keep other summations explicit. The self-consistent inclusion of the density dependence in the Hartree and xc potentials means that $\delta H$ also includes a second contribution from induced density $\delta\rho(\bm{r},t)$ that screens $v^{\text{ext}}$. In the adiabatic linear response theory, this can be formulated in terms of a dressed spin $\tau_{\alpha}$

Here $\chi_{\alpha\beta}(\bm{r},\bm{r}^{\prime},t)$ is the linear susceptibility that we pursue in this work, defined via

The interaction kernel has two components, $f_{\alpha\beta}=f^{\text{H}}_{\alpha\beta}+f^{\text{xc}}_{\alpha\beta}$, namely, the Hartree and xc kernels in the ALDA

In terms of the dressed spin, the first-order Hamiltonian in unscreened external fields is written

Now with the first-order Hamiltonian, the first-order wavefunctions can be obtained by solving the Sternheimer equations [38, 39, 9, 8, 40, 12]

in which $\psi_{n}^{(\ell)}(t)$ is the $\ell$th-order wavefunction, with $|\psi_{n}^{(0)}(t)\rangle=e^{-\text{i}\varepsilon_{n}t}|\psi_{n}\rangle$. With the first-order wavefunctions, we will be able to compute the induced density via the variation of Eq. (1), from which the first-order Hamiltonian will be updated.

With the above introduction, a DFPT calculation can then be performed in a nested iterative process depicted in Fig. 1. In the initializing step, $\delta H$ is constructed from the external electromagnetic fields, whence the Sternheimer equations are solved in the inner iteration. This produces a set of first-order wavefunctions, from which the induced density is calculated. A charge mixing strategy [41, 42] is employed to revise the induced density, with the linear susceptibility and dressed spin computed subsequently. Then a new $\delta H$ is constructed from the updated spin to enter a second round of the outer iteration. The above process is repeated till convergence.

Now we will explain how the Sternheimer equations are solved in a crystalline solid. For electrons in a crystal, the initial Kohn-Sham states are Bloch functions such that $|\psi_{n}\rangle\mapsto|\psi_{n\bm{k}}\rangle=e^{\text{i}\bm{k}\cdot r}|u_{n\bm{k}}\rangle,$ where $n$ is the band index and $\bm{k}$ is the crystal momentum, and $u_{n\bm{k}}$ is the cell-periodic part of the Bloch function. The system is subject to spatially periodic and monochromatic external electromagnetic fields

where $\bm{p}=\bm{q}+\bm{g}$ with $\bm{g}$ being a reciprocal lattice vector for $\bm{q}$ to in the first Brillouin zone. In this case, the following expansion is useful

for $\zeta=\delta H,\delta\rho_{\alpha}$, in which $\zeta(\bm{r},l)$ is a cell-periodic function with

Then the first-order Hamiltonian in the $l$ channel is

where $\mathcal{B}_{\alpha}(\omega,\bm{q})=\mathcal{B}_{\alpha}$, $\mathcal{B}_{\alpha}(-\omega,-\bm{q})=(\mathcal{B}_{\alpha})^{*}$, and

The first-order wavefunction is expanded as

For the fields in Eq. (9), $|\psi^{(1)}_{n\bm{k}}(\nu)\rangle$ is nonzero only when $\nu=\pm\omega$ and can be written as

Then the Sternheimer equations become

in which $H_{\bm{k}}=e^{-\mathrm{i}\bm{k}\cdot\bm{r}}He^{\mathrm{i}\bm{k}\cdot\bm{r}}$ is the Bloch Hamiltonian. A positive infinitesimal $\eta$ is introduced on the left-hand side as a convergence factor to embody the causality structure of the linear susceptibility. In actual calculations, $\eta$ takes finite values to ensure convergence with finite $\bm{k}$-mesh especially for metals and bestows finite broadening on spectral peaks.

From the first-order wavefunctions, we compute the first-order induced density as

The linear susceptibility can be extracted from the Fourier components of $\delta\rho_{\alpha}(\bm{r},l)$

whence

It is worth mentioning that the Sternheimer equations in (15) admit the following formal solutions in the $l$ channel

in which the dressed spin matrix element is

Because it requires the summation over a large number of empty states, this formal solution is not used in practice. ³³3As will be explained later, in our implementation the exact solution is used to quickly correct the contributions of occupied and a small number of low-lying particle states in the iterative solution of the Sternheimer equations. The screened susceptibility then has the same expression as the (bare) Kohn-Sham susceptibility, except that the (unscreened) external fields are now coupled to the dressed spin; that is,

In arriving at the last expression, we have used the fact that $\tau_{\alpha}(\bm{k},l)_{n^{\prime}n}=\tau_{\alpha}(\bm{k}+\bm{l},-l)^{*}_{nn^{\prime}}$.

The previous Subsection presents a sketch of the DFPT for periodic systems without recourse to computational details. In practical calculations, however, various technologies have been developed such that one can perform DFT (and therefore DFPT) calculations on valence electrons only for crystalline materials using planewave bases with the aid of pseudopotentials, to yield satisfactory accuracy with high efficiencies. It is well known that the norm-conserving pseudopotential [21] requires large planewave bases particularly for localized orbitals in transition elements, while the application of ultrasoft pseudopotential [22] is partly limited by the rather laborious construction. In contrast, the PAW method, combining the pseudopotential and linearized augmented-plane-wave methods, is free from the above difficulties and has been used widely. Thus, performing DFPT within the PAW framework [23, 24] for inhomogeneous and td electromagnetic fields is evidently useful though notably nontrivial. DFPT with the PAW method has been implemented within the Vienna ab initio simulation package (VASP) [25] for atomic displacements in the static and long-wavelength limit to calculate zone-center phonon energies. The extension to inhomogeneous and td electromagnetic fields is accomplished in this work based on VASP 5.4.4, and a few implementation details warrant further clarification. Here, we will briefly review the PAW method and describe how it is used in our DFPT calculations. Although the formalism for the ground state quantities is identical to those in the literature and notationally notorious, we feel compelled to provide some of these details, particularly in view of the time- and position-dependent external fields involved in our implementation.

The PAW method is based on a linear transformation between the all-electron (AE) Hilbert space orthogonal to core states and pseudo (PS) Hilbert space. The AE and PS wavefunctions are related by

with the linear operator defined as

The index $i$ is a shorthand encapsulating the atomic site located at $\bm{R}_{i}$ as well as the quantum numbers $(nlm)$ of the local orbitals and spin. $\phi$, $\tilde{\phi}$ and $\tilde{p}$ are AE partial waves, PS partial waves and projector functions, respectively, and should all be understood as spinors. In order to perform the DFPT calculations on a crystalline solid in the electromagnetic fields in Eq. (9), the key is to find the cell-periodic part of each PAW-pseudized quantity, especially the nonlocal ones.

Upon application of the time-independent transformation $T$ to the first-order wavefunctions the pseudized Sternheimer equations read

with $S=T^{\dagger}T$, $\tilde{H}=T^{\dagger}HT$ and $\delta\tilde{H}(t)=T^{\dagger}\delta{H}(t)T$.

According to the implementation of PAW method in VASP, [24] we have

in which the nonlocal potential $D_{ij}=\hat{D}_{ij}+\tilde{D}_{ij}$ with $\tilde{D}_{ij}=D^{1}_{ij}-\tilde{D}^{1}_{ij}$. The quantities $q_{ij}$, $D^{1}_{ij}$ and $\tilde{D}^{1}_{ij}$ are defined in reference. [24] Apparently, the local potential $\tilde{v}^{\mathrm{eff}}(\bm{r})$ is a functional of pseudo density $\tilde{n}(\bm{r})$ and compensation density $\hat{n}(\bm{r})$, while $\tilde{D}_{ij}$ is a function of density matrix $\varrho$, i.e.

We have hidden the functional dependence on the pseudized core densities in $\tilde{v}^{\mathrm{eff}}(\bm{r})$, which are kept frozen during the DFPT calculations. $\tilde{n}(\bm{r})$, $\hat{n}(\bm{r})$ and $\varrho_{ij}$ are given by, respectively,

Here $Q_{ij}(\bm{r})=\sum_{L}\operatorname{tr}\{\sigma\hat{Q}_{ij}^{L}(\bm{r})\}$ with $\hat{Q}_{ij}^{L}(\bm{r})$ defined to construct the compensation density $\hat{n}(\bm{r})$ in the reference. [24] It should be noticed that for $\varrho_{ij}$, only elements with $\bm{R}_{i}=\bm{R}_{j}$ are useful in our calculations, while $D_{ij}$ are nonzero only when $\bm{R}_{i}=\bm{R}_{j}$.

Now we derive the expression for the first-order Hamiltonian $\delta\tilde{H}(t)$. For the fields in Eq. (9), the first-order local densities and potentials follow the same expansion as in Eq. (10), while the first-order density matrix $\delta\varrho_{ij}$ and nonlocal potential $\delta D_{ij}$ can be expanded as

Here, the factor $e^{\mathrm{i}\bm{l}\cdot\bm{R}_{i}}$ in the $l$ channel is introduced such that $\delta\zeta_{ij}(l)$ is cell-periodic, i.e., $\delta\zeta_{ij}(l)=\delta\zeta_{i^{\prime}j^{\prime}}(l)$ if the positions of atomic site for $i,j$ and $i^{\prime},j^{\prime}$ differ by a lattice vector.

The contribution of external electromagnetic fields in $\delta\tilde{H}(t)$ can be calculated directly

with

The contribution to $\delta\tilde{H}(t)$ from the induced densities has a similar expression as in Eq. (28) and can be calculated via an explicit finite difference, as $\tilde{H}$ is a functional of $\tilde{n}$, $\hat{n}$ and $\rho_{ij}$. The first-order densities are found to be

where we define $|\tilde{p}_{i\bm{k}}\rangle=e^{-\mathrm{i}\bm{k}\cdot(\bm{r}-\bm{R}_{i})}|\tilde{p}_{i}\rangle$. To linear order in external fields, the first order effective local potential is given by

Similarly, the first-order nonlocal potentials can be approximated as

Though introduced as forward differences in Eq.(31) and (32), these quantities are evaluated using 4th-order centered finite differences, with a step length of a thousandth the density variables.

With the above results, the final Sternheimer equations become

with

Here $\tilde{u}_{n\bm{k}}$ and $\tilde{u}_{n\bm{k}}^{(1)}(l)$ are the cell-periodic parts of corresponding pseudo wavefunctions, respectively.

The pseudized Sternheimer equations in $\pm(\omega,\bm{q})$ channels are solved separately in each iteration using a variant of residual minimization method with a direct inversion in the iterative subspace (RMM-DIIS), [44, 45] which is already implemented in VASP 5.4.4. The Löwdin perturbation theory is also performed to correct the first-order wavefunctions in the subspace of occupied states and low-lying excitations to speed up convergence

In the last equation above, the summations on $n^{\prime}$ run over the occupied bands plus a few empty bands.

Apparently, solving Eq. (33) requires a $\bm{k}$-grid supplemented by two additional grids shifted by $\pm\bm{q}$ when $\bm{q}$ itself is not on the $\bm{k}$-grid. Doing so, however, not only increases the computational burden but also, more seriously, obliterates the exact cancellation of the contribution of the occupied manifold to the density change due to a $\bm{k}$-grid discretization error. The latter can be easily avoided by employing a pair of grids with a $\bm{q}$ shift, which also reduces the calculation partly. Then Eq. (33) is solved on the $\bm{k}$-grid in $+\bm{q}$ channel, and on the $\bm{k}+\bm{q}$ grid in $-\bm{q}$ channel. It is observed that in this dual grid setup, the above cancellation is well preserved.

The xc potentials in ALDA are functionals of real-valued densities. Thus, calculating $\delta\tilde{v}^{\mathrm{eff}}(l)$ like in Eq. (31) requires caution as $\delta\tilde{n}(l)$ and $\delta\hat{n}(l)$ are usually complex. In fact, the real and imaginary part of $\delta\tilde{v}^{\mathrm{eff}}(l)$ are calculated separately,

where $\mathfrak{F}=\operatorname{Re},\operatorname{Im}$ takes the real or imaginary part, respectively. In the case of nonlocal potential, $\delta\tilde{D}_{ij}(l)$ and $\delta\varrho_{ij}(l)$ are first decomposed into two independent Hermitian matrices (i.e. Hermitian part and anti-Hermitian part multiplied by $-\mathrm{i}$), and then finite differenced separately in an analogous fashion.

Symmetry reduction is also performed in our implementation, where the summation over $\bm{k}$ points in Eq. (30) is restricted to the symmetry-irreducible part of the Brillouin zone. The symmetry group here is the subgroup of the magnetic group of the studied crystal in which the external electromagnetic fields in Eq. (9) is invariant.

As shown in the inset in Fig. 2, chromium dioxide, CrO₂, is a ferromagnetic half-metallic oxide with a rutile crystal structure, where each Cr atom is situated at the center of an octahedral cage formed by oxygen atoms. [49, 50] Widely used as a magnetic recording material, CrO₂ also has various potential applications in spintronics and magnetoelectronics [51, 52] due to its half-metallic properties.

The experimental lattice parameters $a=b=4.4218~{}$Å and $c=2.9182~{}$Å [50] are used in our calculations. The planewave energy cutoff is set to be $500$ eV and a $13\times 13\times 20$ $\Gamma$-centered mesh of $\bm{k}$-points is used. The spin-resolved density of states of CrO₂ is computed from the collinear spin-polarized calculation and shown in Fig. 2, where the half-metallic band structure is clearly seen. The magnetic moment of Cr is found to be 2 $\mu_{\mathrm{B}}$. We then turn to the noncollinear calculations, and compute the transverse spin susceptibility $\chi_{\scriptscriptstyle+-}(\bm{p},\omega)$ along [100] and [001] directions for $\omega\leq 400$ meV on 10 meV intervals. The broadening parameter $\eta$ introduced in Eq. (15) is set to be 50 meV in the calculations in this subsection.

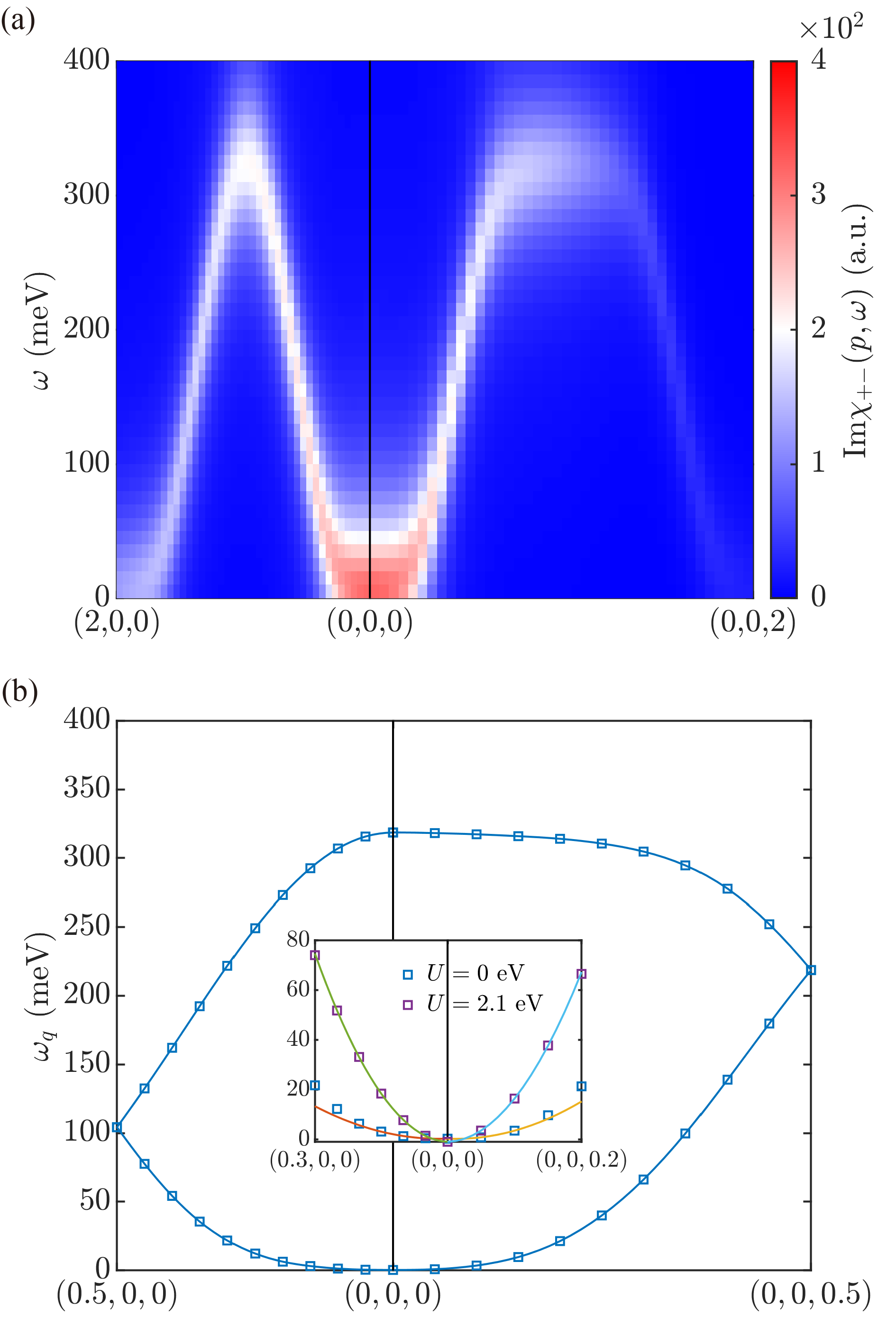
Fig. 3(a) shows the computed Im$\chi_{\scriptscriptstyle+-}(\bm{p},\omega)$, without spin-orbit interaction, along two $\bm{p}$ paths. In general, $\chi_{\scriptscriptstyle+-}(\bm{p},\omega)$ is not periodic in $\bm{p}$. Then the branch in the first Brillouin Zone is composed of acoustic magnon modes, while the branch in the second Brillouin zone optical modes. The profile of the magnon peak at a given $\bm{p}$ is nearly perfect Lorentzian over the entire energy range. The extracted half width at half maximum $\eta_{\bm{p}}$ are almost a constant and equal to the artificial broadening parameter $\eta$, indicating that the Landau damping in CrO₂ is negligible. This is expected given that half-metallic CrO₂ has a large spin-flip gap around 310 meV, as shown in Fig. 2.

The location of the maxima of magnon peaks, $\omega_{\bm{p}}$, are then recorded and folded to the first Brillouin zone ($\omega_{\bm{q}}$). As shown in Fig. 3(b), we find one acoustic magnon branch and one optical branch, consistent with the fact that the unit cell in CrO₂ contains two magnetic Cr atoms. There is no magnon gap at the Brillouin zone boundaries, which is result of the $n$ glide symmetry. The energy of long-wavelength acoustic magnons is quadratic in $q$ with a gapless Goldstone mode, $\omega_{\bm{q}}=D_{\parallel}(q_{x}^{2}+q_{y}^{2})+D_{z}q_{z}^{2}$, as expected for a ferromagnet with spin rotation symmetry. The spin stiffness coefficients are found to be $D_{\parallel}=82$ meV$\cdot$Ų along [100] and $D_{z}=92$ meV$\cdot$Ų along [001] directions, respectively. From this, we can estimate the average spin stiffness coefficient to be 85 meV$\cdot$Ų, which is close to the experimental measured result ($\sim 112.5$ meV$\cdot$Ų [53]).

For comparison, additional electron correlation is included statically within the LSDA+U formalism [54] in both the ground state calculation and subsequent DFPT calculations, with $U^{\mathrm{eff}}=2.1$ eV. [55] As shown in the inset of Fig. 3(b), the gapless Goldstone mode is obtained again, accompanied by an average spin stiffness coefficient $D=391$ meV$\cdot$Ų, almost five times as large as the one without Hubbard $U$ correction. The energy of magnon in CrO₂ seems to be highly overestimated in LSDA+U calculations.

As a further test, we examine the Goldstone gap as a result of breaking the spin rotation symmetry by introducing spin-orbit interaction. The atomic spin-orbit interaction for Cr is fairly weak (on the order of tens of meV). Since the gap in the Goldstone magnon is second order in the spin-orbit coupling, it is small for CrO₂. In order to visualize the effect of spin-orbit coupling, we introduce a parameter $\lambda$ to artificially tune its strength (or speed of light), as in $H=H^{0}+\lambda H^{\mathrm{soc}},$ where $\lambda=1$ corresponds to the actual strength of spin-orbit coupling in CrO₂. The calculated Im$\chi_{\scriptscriptstyle+-}(p=0,\omega)$ as a function of $\omega$ for different $\lambda$ values are shown in Fig. 4(a). Apparently there is blue shift of the Goldstone mode with increasing $\lambda$, indicating the emergence of a Goldstone gap. The Goldstone gap indeed shows a quadratic dependence on $\lambda$, as demonstrated by the gap-vs-$\lambda^{2}$ plot in Fig. 4(b). The extrapolated Goldstone gap in CrO₂ is about 0.1 meV.

The ternary intermetallic Cu₂MnAl is a Mn-based full-Heusler alloy with the $L2_{1}$ structure type (see inset in Fig. 5). The experimental lattice parameter for the conventional cubic cell (space group $Fm\bar{3}m$) is $a=5.968$ Å. [56] Cu₂MnAl is ferromagnetic below the relatively high Curie temperature (603 K). [56] Apart from being regarded as a prototype for understanding the electronic correlations in Heusler intermetallics, [57] Cu₂MnAl is also being used as a neutron polarizer and monochromator material. [58, 59]

A planewave energy cutoff of $350$ eV and a $15\times 15\times 15$ $\Gamma$-centered $\bm{k}$-grid are used in our calculations. Spin-orbit coupling is not included. The spin-resolved densities of states of Cu₂MnAl computed from the collinear spin-polarized calculation confirms the ferromagnetism of Cu₂MnAl, as shown in Fig. 5. The magnetic moment is carried primarily by Mn atoms and computed to be 3.4 $\mu_{\mathrm{B}}$/Mn. The transverse spin susceptibility $\chi_{\scriptscriptstyle+-}(\bm{p},\omega)$ along [100], [110] and [111] crystallographic directions is then computed in noncollinear calculations for $\omega\leq 300$ meV on 5 meV intervals, with a broadening parameter $\eta$ of 50 meV.

Fig. 6(a) shows the computed magnon spectral function Im$\chi_{\scriptscriptstyle+-}(\bm{p},\omega)$ along the three principal directions. The acoustic magnon branch is seen clearly only at low energies near the Brillouin zone center. The spectral peaks of these low-energy modes can be adequately fitted with the Lorentzian lineshape as in the CrO₂ case. The dispersion of the long-wavelength modes is quadratic and isotropic, as demonstrated in the inset of Fig. 7 (a). A spin stiffness coefficient $D=268$ meV$\cdot$Ų is procured from the quadratic fit, which is about 1.5 times larger than the experimental value of 175 meV$\cdot$Ų. [60]

Notably, at higher energies and near Brillouin zone boundaries, the magnon peaks become fuzzier and broader, attesting to substantial Landau damping in this material. In stark contrast to the CrO₂ case with almost no Landau damping, the coupling to the Stoner continuum in Cu₂MnAl bestows a magnon peak at a given $\bm{p}$ an asymmetric profile that defies a Lorentzian fit, as shown in Fig. 6(b). The stronger Landau damping in this system is consistent with the absence of the spin-flip gap as shown in Fig.5. Viewing the coupling to the Stoner continuum as a Fano-type resonance, we superimpose a linear function on the Lorentzian to describe the asymmetric line shape, as

with $\omega_{\bm{p}},a_{\bm{p}},\eta_{\bm{p}}$ and $\xi_{\bm{p}}$ as fitting parameters.

As it turns out, this simple modification leads to satisfactory fitting for the entire spectrum, as evidenced in Fig.6(c). The extracted magnon dispersion is then shown in Fig. 7(a), which coincides with the calculated results of Buczek et al. [10, 61] and agrees well with the experimental observations along [100] direction. [60] Along the [110] and [111] directions where the Landau damping seems more pronounced, our computed dispersion shows significant discrepancy from the experimental one. For low-energy modes, $\eta_{\bm{p}}$ is dominated by the artificial broadening parameter $\eta$ and the asymmetry is small, as shown in Fig. 7(b). With increasing energies, however, the broadening quickly exceeds $\eta$ and the asymmetry becomes pronounced, especially near Brillouin zone boundaries, both providing quantitative characterization of the Landau damping.