An explicit formula for the $A$ -polynomial of the knot with Conway’s notation $C(2n,4)$

Ji-Young Ham¹¹1This work was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (No. NRF-2018R1A2B6005847). School of Liberal Arts, Seoul National University of Science and Technology, 232 Gongneung-ro, Nowon-gu, Seoul, korea 01811
Department of Architecture, Konkuk University, 120 Neungdong-ro, Gwangjin-gu, Seoul, Korea 05029 [email protected] Joongul Lee²²2The author was supported by 2018 Hongik University Research Fund. Department of Mathematics Education, Hongik University, 94 Wausan-ro, Mapo-gu, Seoul, Korea 04066 [email protected]

Abstract

An explicit formula for the $A$ -polynomial of the knot having Conway’s notation $C(2n,4)$ is computed up to repeated factors. Our polynomial contains exactly the same irreducible factors as the $A$ -polynomial defined in [1].

keywords:

A

-polynomial, explicit formula, knot with Conway’s notation

C(2n,4)

, Riley-Mednykh polynomial

^†^†journal: Journal of LaTeX Templates

1 Introduction

In 1994, Cooper, Culler, Gillet, Long, and Shalen introduced the $A$ -polynomial, $A(L,M)\in Z[L,M]$ , of a compact 3-manifold $N$ with a single torus boundary [1]. A-polynomials are related to the following invariants: incompressible surfaces [1], the Culler-Shalen seminorm [2, 3], cusp shapes [4], the volumes [1, 5, 6] and Chern-Simons invariants [7, 8, 9, 10, 11] of the deformed orbifolds, Mahler measure [12], Alexander polynomials [1], $AJ$ conjecture [13, 14], etc. The $AJ$ conjecture has been proved for some knots. For example, our knot, the knot with Conway’s notation $C(2n,4)$ has been proved to satisfy the $AJ$ conjecture [15] except $C(-4,4)$ .

$A$ -polynomials are known only for a few due to the difficulty of computations. Among them some are not full ones. A-polynomials were obtained using triangulation in [16, 17, 18, 19, 20]. In [21], Culler presented $A$ -polynomials up to $8$ crossings and most $9$ crossings and many $10$ crossings, and all knots that can be triangulated with up to seven ideal tetrahedra. $A$ -polynomials are known for twist knots [22], $(-2,3,1+2n)$ pretzel knots [23, 24], $J[m,2n]$ [22, for $m$ between $2$ and $3$ ] [25, for $m$ between $2$ and $5$ and for $m=2n$ ], recursively. Explicit formulas for the A-polynomials were computed for two-bridge torus knots [1, 22, 26], iterated torus knots [27], twist knots [8, 28, 29, 30], knots with Conway’s notation $C(2n,3)$ [31], and the twisted torus knots $T(5,1-5n,2,2)$ [30]. We recall here that $J[4,-2n]$ is the mirror image of $C(2n,4)$ .

The main purpose of the paper is to find the explicit formula for the $A$ -polynomial of the knot having Conway’s notation $C(2n,4)$ up to repeated factors. Let us denote the $A$ -polynomial of the knot having Conway’s notation $C(2n,4)$ by $A_{2n}$ . The following theorem gives the explicit formula for the $A$ -polynomial of $C(2n,4)$ .

Theorem 1.1

The $A$ -polynomial $A_{2n}=A_{2n}(L,M)$ is given explicitly by

		$\displaystyle\qquad\qquad\qquad A_{2n}=p_{2n}(u)p_{2n}(-u)$
	where
	$\displaystyle p_{2n}(z)=$	$\displaystyle\begin{cases}\sum_{i=0}^{2n}\binom{\left\lfloor\frac{i}{2}\right\rfloor+n}{i}2^{-2\left\lfloor\frac{i+1}{2}\right\rfloor-i}\left(M^{2}\right)^{-\left\lfloor\frac{i}{2}\right\rfloor-2\left\lfloor\frac{i+1}{2}\right\rfloor+i+n}\left(LM^{2}+1\right)^{-2\left\lfloor\frac{i+1}{2}\right\rfloor-i+2n}\\ \times\left(-2LM^{6}+LM^{4}-LM^{2}-M^{4}+M^{2}z+M^{2}-2\right)^{\left\lfloor\frac{i+1}{2}\right\rfloor}\\ \times\left(LM^{2}+L+M^{2}+z+1\right)^{i}\left(-3LM^{2}+L+M^{2}+z-3\right)^{\left\lfloor\frac{i-1}{2}\right\rfloor}\\ \times\left((-1)^{i+1}\left(LM^{2}+1\right)-2LM^{2}+L+M^{2}+z-2\right)\qquad\qquad\text{if $n\geq 0$,}\\ \sum_{i=0}^{-2n}\binom{\left\lfloor\frac{i-1}{2}\right\rfloor-n}{i}2^{-2\left\lfloor\frac{i+1}{2}\right\rfloor-i}\left(M^{2}\right)^{-\left\lfloor\frac{i}{2}\right\rfloor-2\left\lfloor\frac{i+1}{2}\right\rfloor+i-n}\left(LM^{2}+1\right)^{-\frac{1}{2}-2\left\lfloor\frac{i+1}{2}\right\rfloor-i-2n}\\ \times\left(-2LM^{6}+LM^{4}-LM^{2}-M^{4}+M^{2}z+M^{2}-2\right)^{\left\lfloor\frac{i+1}{2}\right\rfloor}\\ \times\left(LM^{2}+L+M^{2}+z+1\right)^{i}\left(-3LM^{2}+L+M^{2}+z-3\right)^{\left\lfloor\frac{i-1}{2}\right\rfloor}\\ \times\left((-1)^{i}\left(-2LM^{2}+L+M^{2}+z-2\right)-LM^{2}-1\right)\qquad\qquad\text{if $n<0$,}\end{cases}$
	and
	$\displaystyle u$	$\displaystyle=\sqrt{5L^{2}M^{4}-2L^{2}M^{2}+L^{2}-2LM^{4}+12LM^{2}-2L+M^{4}-2M^{2}+5}.$

Our writing is parallel with that in [31] which is based on [8, 22, 29]. The $A$ -polynomial of $C(2n,4)$ can be obtained from the Riley-Mednykh polynomial in [32]. With our theorem, we can easily get $A$ -polynomials for $C(2n,4)$ having more than 12 crossings.

2 Proof of Theorem 1.1

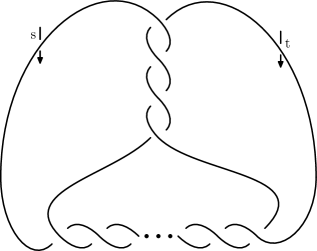
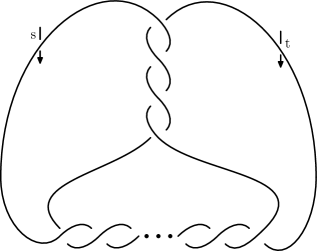
Refer to caption — Figure 1: A two bridge knot having Conway’s notation $C(2n,4)$ for $n>0$ (left) and for $n<0$ (right)

A knot $K$ is a two bridge knot with Conway’s notation $C(2n,4)$ if $K$ has a regular two-dimensional projection of the form in Figure 1. Let us denote the exterior of $C(2n,4)$ by $X_{2n}$ . The following proposition gives the fundamental group of $X_{2n}$ [22, 32, 33].

Proposition 2.1

\pi_{1}(X_{2n})=\left\langle s,t\ |\ swt^{-1}w^{-1}=1\right\rangle,

where $w=(ts^{-1}ts^{-1}t^{-1}st^{-1}s)^{n}$ .

Given a set of generators, $\{s,t\}$ , of the fundamental group for $\pi_{1}(X_{2n})$ , we define a representation $\rho\ :\ \pi_{1}(X_{2n})\rightarrow\text{SL}(2,\mathbb{C})$ by

\begin{array}[]{ccccc}\rho(s)=\left[\begin{array}[]{cc}M&1\\ 0&M^{-1}\end{array}\right]\text{,}\ \ \ \rho(t)=\left[\begin{array}[]{cc}M&0\\ 2-M^{2}-M^{-2}-x&M^{-1}\end{array}\right].\end{array}

Then $\rho$ can be identified with the point $(M,x)\in\mathbb{C}^{2}$ . When $M$ varies we have an algebraic set whose defining equation is the following explicit Riley-Mednykh polynomial $P_{2n}=P_{2n}(M,x)$ defined recursively by the following form:

\displaystyle P_{2n}=\begin{cases}QP_{2(n-1)}-M^{12}P_{2(n-2)}\ \text{if $n>1$},\\ QP_{2(n+1)}-M^{12}P_{2(n+2)}\ \text{if $n<-1$},\end{cases}

(1)

with initial conditions

	$\displaystyle P_{-2}$	$\displaystyle=-M^{4}x^{3}-\left(2M^{6}-M^{4}+2M^{2}\right)x^{2}-\left(M^{8}-M^{6}+2M^{4}-M^{2}+1\right)x+M^{4},$
	$\displaystyle P_{0}$	$\displaystyle=M^{-2}\ \text{{for}}\ n<0\qquad\text{{and}}\qquad P_{0}=1\ \text{{for}}\ n\geq 0,$
	$\displaystyle P_{2}$	$\displaystyle=M^{6}x^{4}+\left(3M^{8}-M^{6}+3M^{4}\right)x^{3}+\left(3M^{10}-2M^{8}+5M^{6}-2M^{4}+3M^{2}\right)x^{2}$
		$\displaystyle+\left(M^{12}-M^{10}+2M^{8}-2M^{6}+2M^{4}-M^{2}+1\right)x+M^{6},$

and

	$\displaystyle Q$	$\displaystyle=M^{6}x^{4}+\left(3M^{8}-2M^{6}+3M^{4}\right)x^{3}+\left(3M^{10}-4M^{8}+6M^{6}-4M^{4}+3M^{2}\right)x^{2}$
		$\displaystyle+\left(M^{12}-2M^{10}+3M^{8}-4M^{6}+3M^{4}-2M^{2}+1\right)x+2M^{6}.$

It is known in [32] that $\rho$ is a representation of $\pi_{1}(X_{2n})$ if and only if $x$ is a root of $P_{2n}$ . We use different initial conditions $P_{0}$ for $P_{2n}(n>1)$ and $P_{2n}(n<-1)$ , but the same $P$ for both series for simplicity.

Lemma 2.2

The Riley-Mednykh polynomial $P_{2n}=P_{2n}(x,M)$ is described explicitly by

\displaystyle\footnotesize P_{2n}=\begin{cases}\sum_{i=0}^{2n}\binom{\left\lfloor\frac{i}{2}\right\rfloor+n}{i}\left(M^{2}\right)^{-\left\lfloor\frac{i}{2}\right\rfloor-2\left\lfloor\frac{i+1}{2}\right\rfloor+3n}x^{\left\lfloor\frac{i+1}{2}\right\rfloor}\left(M^{4}+M^{2}x-2M^{2}+1\right)^{\left\lfloor\frac{i-1}{2}\right\rfloor}\\ \times\left(M^{4}+M^{2}x+1\right)^{i}\left(\left((-1)^{i+1}+1\right)M^{2}/2+M^{4}+M^{2}x-2M^{2}+1\right)\qquad\ \ \\ \text{if $n\geq 0$},\\ \sum_{i=0}^{-2n}\binom{\left\lfloor\frac{i-1}{2}\right\rfloor-n}{i}\left(M^{2}\right)^{-\left\lfloor\frac{i}{2}\right\rfloor-2\left\lfloor\frac{i+1}{2}\right\rfloor-3n-1}x^{\left\lfloor\frac{i+1}{2}\right\rfloor}\left(M^{4}+M^{2}x-2M^{2}+1\right)^{\left\lfloor\frac{i-1}{2}\right\rfloor}\\ \times\left(M^{4}+M^{2}x+1\right)^{i}\left(\left((-1)^{i}-1\right)M^{2}/2+(-1)^{i}\left(M^{4}+M^{2}x-2M^{2}+1\right)\right)\ \\ \text{if $n<0$}.\end{cases}

Proof 1

Write $f_{2n}$ for the claimed formula and show that $f_{2n}=P_{2n}$ .

Case I: $n\geq 0$ . When $i>2n$ or $i<0$ , $\binom{\left\lfloor\frac{i}{2}\right\rfloor+n}{i}$ is undefined and can be considered as zero. Hence the finite sum can be regarded as an infinite sum. Direct computation shows that $f_{0}=P_{0}$ and $f_{2}=P_{2}$ . Now, we only need to show that $f_{2n}$ satisfies the recursive relation. Note that $Q$ can be written as $x\left(M^{4}+M^{2}x+1\right)^{2}\left(M^{4}+M^{2}x-2M^{2}+1\right)+2M^{6}$ .

	$\displaystyle Qf_{2(n-1)}-M^{12}f_{2(n-2)}$
	$\displaystyle=\left(x\left(M^{4}+M^{2}x+1\right)^{2}\left(M^{4}+M^{2}x-2M^{2}+1\right)+2M^{6}\right)$
	$\displaystyle\times\sum_{i}\binom{\left\lfloor\frac{i}{2}\right\rfloor+n-1}{i}\left(M^{2}\right)^{-\left\lfloor\frac{i}{2}\right\rfloor-2\left\lfloor\frac{i+1}{2}\right\rfloor+3(n-1)}x^{\left\lfloor\frac{i+1}{2}\right\rfloor}\left(M^{4}+M^{2}x-2M^{2}+1\right)^{\left\lfloor\frac{i-1}{2}\right\rfloor}$
	$\displaystyle\times\left(M^{4}+M^{2}x+1\right)^{i}\left(\left((-1)^{i+1}+1\right)M^{2}/2+M^{4}+M^{2}x-2M^{2}+1\right)$
	$\displaystyle-M^{12}\sum_{i}\binom{\left\lfloor\frac{i}{2}\right\rfloor+n-2}{i}\left(M^{2}\right)^{-\left\lfloor\frac{i}{2}\right\rfloor-2\left\lfloor\frac{i+1}{2}\right\rfloor+3(n-2)}x^{\left\lfloor\frac{i+1}{2}\right\rfloor}\left(M^{4}+M^{2}x-2M^{2}+1\right)^{\left\lfloor\frac{i-1}{2}\right\rfloor}$
	$\displaystyle\times\left(M^{4}+M^{2}x+1\right)^{i}\left(\left((-1)^{i+1}+1\right)M^{2}/2+M^{4}+M^{2}x-2M^{2}+1\right)$
	$\displaystyle=\sum_{i}\left[\binom{\left\lfloor\frac{i}{2}\right\rfloor+n-2}{i-2}+2\binom{\left\lfloor\frac{i}{2}\right\rfloor+n-1}{i}-\binom{\left\lfloor\frac{i}{2}\right\rfloor+n-2}{i}\right]$
	$\displaystyle\left(M^{2}\right)^{-\left\lfloor\frac{i}{2}\right\rfloor-2\left\lfloor\frac{i+1}{2}\right\rfloor+3n}x^{\left\lfloor\frac{i+1}{2}\right\rfloor}\left(M^{4}+M^{2}x-2M^{2}+1\right)^{\left\lfloor\frac{i-1}{2}\right\rfloor}$
	$\displaystyle\times\left(M^{4}+M^{2}x+1\right)^{i}\left(\left((-1)^{i+1}+1\right)M^{2}/2+M^{4}+M^{2}x-2M^{2}+1\right)$
	$\displaystyle=\sum_{i}\binom{\left\lfloor\frac{i}{2}\right\rfloor+n}{i}\left(M^{2}\right)^{-\left\lfloor\frac{i}{2}\right\rfloor-2\left\lfloor\frac{i+1}{2}\right\rfloor+3n}x^{\left\lfloor\frac{i+1}{2}\right\rfloor}\left(M^{4}+M^{2}x-2M^{2}+1\right)^{\left\lfloor\frac{i-1}{2}\right\rfloor}$
	$\displaystyle\times\left(M^{4}+M^{2}x+1\right)^{i}\left(\left((-1)^{i+1}+1\right)M^{2}/2+M^{4}+M^{2}x-2M^{2}+1\right)$
	$\displaystyle=f_{2n}$

In the last equality we use the binomial relation

\binom{a}{b}=\binom{a-1}{b-1}+\binom{a-1}{b}

three times.

Case II: $n<0$ . When $i>-2n-1$ or $i<0$ , $\binom{\left\lfloor\frac{i-1}{2}\right\rfloor-n}{i}$ is undefined and can be considered as zero. Hence the finite sum can be regarded as an infinite sum. Direct computation shows that $f_{0}=P_{0}$ and $f_{-2}=P_{-2}$ . As in Case I, one can easily show that $f_{2n}$ satisfies the recursive relation. \qed

Let $l=ww^{*}$ [1, 22], where $w^{*}$ is the word obtained by reversing $w$ (by reading words in $w$ from right to left). Let $L=\rho(l)_{11}$ (the left upper entry of $\rho(l)$ , [32, lemma 7.9]). Then $l$ is the longitude which is null-homologous in $X_{2n}$ (you can read a twisted longitude $ww^{*}$ from the Schubert normal form of the knot $C(2n,4)$ ), and we have

Lemma 2.3

[32, Theorem 7.10]

	$\displaystyle L$	$\displaystyle=-M^{-2}\frac{M^{-4}-M^{-2}+(2M^{-2}+M^{2}-1)x+x^{2}}{M^{4}-M^{2}+(M^{-2}+2M^{2}-1)x+x^{2}},$
	$\displaystyle x$	$\displaystyle=\frac{-2LM^{8}+LM^{6}-LM^{4}-M^{6}+M^{4}z+M^{4}-2M^{2}}{2\left(LM^{6}+M^{4}\right)}$
	where
	$\displaystyle z=u$	$\displaystyle=\sqrt{5L^{2}M^{4}-2L^{2}M^{2}+L^{2}-2LM^{4}+12LM^{2}-2L+M^{4}-2M^{2}+5}$
	$\displaystyle\text{ or }z=-u.$

Now substituting $\frac{-2LM^{8}+LM^{6}-LM^{4}-M^{6}+M^{4}z+M^{4}-2M^{2}}{2\left(LM^{6}+M^{4}\right)}$ for $x$ into $P_{2n}$ , for $n>0$ , gives

	$\displaystyle\sum_{i=0}^{2n}\binom{\left\lfloor\frac{i}{2}\right\rfloor+n}{i}\left(M^{2}\right)^{-\left\lfloor\frac{i}{2}\right\rfloor-2\left\lfloor\frac{i+1}{2}\right\rfloor+3n}\left(\frac{-2LM^{8}+LM^{6}-LM^{4}-M^{6}+M^{4}z+M^{4}-2M^{2}}{2\left(LM^{6}+M^{4}\right)}\right)^{\left\lfloor\frac{i+1}{2}\right\rfloor}$
	$\displaystyle\times\left(M^{4}+M^{2}\frac{-2LM^{8}+LM^{6}-LM^{4}-M^{6}+M^{4}z+M^{4}-2M^{2}}{2\left(LM^{6}+M^{4}\right)}-2M^{2}+1\right)^{\left\lfloor\frac{i-1}{2}\right\rfloor}$
	$\displaystyle\times\left(M^{4}+M^{2}\frac{-2LM^{8}+LM^{6}-LM^{4}-M^{6}+M^{4}z+M^{4}-2M^{2}}{2\left(LM^{6}+M^{4}\right)}+1\right)^{i}$
	$\displaystyle\times\left(\left((-1)^{i+1}+1\right)M^{2}/2+M^{4}+M^{2}\frac{-2LM^{8}+LM^{6}-LM^{4}-M^{6}+M^{4}z+M^{4}-2M^{2}}{2\left(LM^{6}+M^{4}\right)}-2M^{2}+1\right)$

We observe that

	$\displaystyle\frac{-2LM^{8}+LM^{6}-LM^{4}-M^{6}+M^{4}z+M^{4}-2M^{2}}{2\left(LM^{6}+M^{4}\right)}=\frac{M^{2}\left(-2LM^{6}+LM^{4}-LM^{2}-M^{4}+M^{2}z+M^{2}-2\right)}{2M^{4}\left(LM^{2}+1\right)},$
	$\displaystyle M^{4}+M^{2}\frac{-2LM^{8}+LM^{6}-LM^{4}-M^{6}+M^{4}z+M^{4}-2M^{2}}{2\left(LM^{6}+M^{4}\right)}-2M^{2}+1=\frac{M^{6}\left(-3LM^{2}+L+M^{2}+z-3\right)}{2M^{4}\left(LM^{2}+1\right)},$
	$\displaystyle M^{4}+M^{2}\frac{-2LM^{8}+LM^{6}-LM^{4}-M^{6}+M^{4}z+M^{4}-2M^{2}}{2\left(LM^{6}+M^{4}\right)}+1=\frac{M^{6}\left(LM^{2}+L+M^{2}+z+1\right)}{2M^{4}\left(LM^{2}+1\right)},$

and

	$\displaystyle\left((-1)^{i+1}+1\right)M^{2}/2+M^{4}+M^{2}\frac{-2LM^{8}+LM^{6}-LM^{4}-M^{6}+M^{4}z+M^{4}-2M^{2}}{2\left(LM^{6}+M^{4}\right)}-2M^{2}+1$
	$\displaystyle=\frac{M^{6}\left((-1)^{i+1}\left(LM^{2}+1\right)-2LM^{2}+L+M^{2}+z-2\right)}{2M^{4}\left(LM^{2}+1\right)}.$

The resulting expression is

	$\displaystyle q_{2n}(z)$	$\displaystyle=\sum_{i=0}^{2n}\binom{\left\lfloor\frac{i}{2}\right\rfloor+n}{i}\left(M^{2}\right)^{-\left\lfloor\frac{i}{2}\right\rfloor-2\left\lfloor\frac{i+1}{2}\right\rfloor+3n}\left(\frac{-2LM^{6}+LM^{4}-LM^{2}-M^{4}+M^{2}z+M^{2}-2}{2M^{2}\left(LM^{2}+1\right)}\right)^{\left\lfloor\frac{i+1}{2}\right\rfloor}$
		$\displaystyle\times\left(\frac{M^{2}\left(-3LM^{2}+L+M^{2}+z-3\right)}{2\left(LM^{2}+1\right)}\right)^{\left\lfloor\frac{i-1}{2}\right\rfloor}\left(\frac{M^{2}\left(LM^{2}+L+M^{2}+z+1\right)}{2\left(LM^{2}+1\right)}\right)^{i}$
		$\displaystyle\times\left(\frac{M^{2}\left((-1)^{i+1}\left(LM^{2}+1\right)-2LM^{2}+L+M^{2}+z-2\right)}{2\left(LM^{2}+1\right)}\right).$

Since $q_{2n}(u)$ is a non-polynomial factor of the $A$ -polynomial, we multiply it by its Galois conjugate $q_{2n}(-u)$ to obtain the entire $A$ -polynomial [1, 22]. This is actually another method of defining the resultant of two polynomials [34, p.209-p.210]. We multiply $q_{2n}(u)q_{2n}(-u)$ by $M^{-8n}\left(LM^{2}+1\right)^{4n}$ to clear the denominators and factor out some power of $M$ so that we have the $A$ -polynomial $A_{2n}(L,M)=p_{2n}(u)p_{2n}(-u)$ in Theorem 1.1. Formally, it can be done by multiplying $q_{2n}(z)$ by $M^{-4n}\left(LM^{2}+1\right)^{2n}$ . Notice that $p_{2n}(z)=M^{-4n}\left(LM^{2}+1\right)^{2n}q_{2n}(z)$ and recall that

u=\sqrt{5L^{2}M^{4}-2L^{2}M^{2}+L^{2}-2LM^{4}+12LM^{2}-2L+M^{4}-2M^{2}+5}.

Now we want to show that the claimed formula does not have fractions. Direct computation shows that $A_{0}(L,M)=1$ , $A_{2}(L,M)$ , and $A_{4}(L,M)$ (see, Appendix B) are polynomials in $\mathbb{Z}[L,M]$ . From now on a polynomial means a polynomial in $\mathbb{Z}[L,M]$ . Let us assume that $A_{2k}$ for $k\leq n$ is a polynomial. From the equation (1), we have $P_{2n}=QP_{2(n-1)}-M^{12}P_{2(n-2)}$ for $n>1$ . Hence $q_{2n}=Qq_{2(n-1)}-M^{12}q_{2(n-2)}$ and

\displaystyle p_{2n}(z)=M^{-4}\left(LM^{2}+1\right)^{2}Qp_{2(n-1)}(z)-\left(LM^{2}+1\right)^{4}M^{4}p_{2(n-2)}(z).

(2)

Now, we have

Proposition 2.4

	$\displaystyle A_{2n}=p_{2n}(u)p_{2n}(-u)$
	$\displaystyle=M^{-8}\left(LM^{2}+1\right)^{4}Q(u)Q(-u)p_{2(n-1)}(u)p_{2(n-1)}(-u)$		(3)
	$\displaystyle-\left(LM^{2}+1\right)^{6}\left(Q(u)p_{2(n-1)}(u)p_{2(n-2)}(-u)+Q(-u)p_{2(n-1)}(-u)p_{2(n-2)}(u)\right)$		(4)
	$\displaystyle+M^{8}\left(LM^{2}+1\right)^{8}p_{2(n-2)}(u)p_{2(n-2)}(-u).$		(5)

By direct computations,

$\displaystyle Q(u)$	$\displaystyle=2^{-1}M^{4}\left(LM^{2}+1\right)^{-4}\left(a(L,M)+Lb(L,M)u\right)$	(6)
$\displaystyle Q(-u)$	$\displaystyle=2^{-1}M^{4}\left(LM^{2}+1\right)^{-4}\left(a(L,M)-Lb(L,M)u\right)$	(7)
$\displaystyle Q(u)Q(-u)$	$\displaystyle=M^{8}\left(LM^{2}+1\right)^{-4}f(L,M)$	(8)
$\displaystyle Q(u)Q(u)$	$\displaystyle=2^{-1}M^{8}\left(LM^{2}+1\right)^{-8}\left(g(L,M)+h(L,M)u\right)$	(9)
$\displaystyle Q(-u)Q(-u)$	$\displaystyle=2^{-1}M^{8}\left(LM^{2}+1\right)^{-8}\left(g(L,M)-h(L,M)u\right)$	(10)

where $a(L,M)$ , $b(L,M)$ , $f(L,M)$ , $g(L,M)$ and $h(L,M)$ are some polynomials (see Appendix A). Since $A_{2n}=p_{2n}(u)p_{2n}(-u)$ , $A_{2(n-1)}=p_{2(n-1)}(u)p_{2(n-1)}(-u)$ , and

A_{2(n-2)}=p_{2(n-2)}(u)p_{2(n-2)}(-u)

are polynomials and since $M^{-8}\left(LM^{2}+1\right)^{4}Q(u)Q(-u)$ is a polynomial by Equation (8), the terms in Proposition 2.4-(3) and Proposition 2.4-(5) are polynomials and hence the term

-\left(LM^{2}+1\right)^{6}\left(Q(u)p_{2(n-1)}(u)p_{2(n-2)}(-u)+Q(-u)p_{2(n-1)}(-u)p_{2(n-2)}(u)\right)

in Proposition 2.4-(4) is a polynomial. Now we only need to show that $A_{2(n+1)}=p_{2(n+1)}(u)p_{2(n+1)}(-u)$ is a polynomial. By Proposition 2.4, we have

	$\displaystyle A_{2(n+1)}=p_{2(n+1)}(u)p_{2(n+1)}(-u)$
	$\displaystyle=M^{-8}\left(LM^{2}+1\right)^{4}Q(u)Q(-u)p_{2n}(u)p_{2n}(-u)$		(11)
	$\displaystyle-\left(LM^{2}+1\right)^{6}\left(Q(u)p_{2n}(u)p_{2(n-1)}(-u)+Q(-u)p_{2n}(-u)p_{2(n-1)}(u)\right)$		(12)
	$\displaystyle+M^{8}\left(LM^{2}+1\right)^{8}p_{2(n-1)}(u)p_{2(n-1)}(-u).$		(13)

Since the terms in (11) and (13) are polynomials by the induction hypothesis and Equation (8), we only need to show the term in (12) is a polynomial. Now $-1$ times the term in (12) becomes

	$\displaystyle M^{-4}\left(LM^{2}+1\right)^{8}\left(Q(u)Q(u)+Q(-u)Q(-u)\right)p_{2(n-1)}(u)p_{2(n-1)}(-u)$		(14)
	$\displaystyle-M^{4}\left(LM^{2}+1\right)^{10}(Q(u)p_{2(n-1)}(-u)p_{2(n-2)}(u)+Q(-u)p_{2(n-1)}(u)p_{2(n-2)}(-u))$		(15)

by using Equation (2). The term in (14) is a polynomial because of Equations (9), (10), and the induction hypothesis. We will show that the term in (15) is a polynomial. By using Equation (2) again, $-1$ times the term in (15) becomes

	$\displaystyle 2\left(LM^{2}+1\right)^{12}Q(u)Q(-u)p_{2(n-2)}(-u)p_{2(n-2)}(u)$
	$\displaystyle-M^{8}\left(LM^{2}+1\right)^{14}\left(Q(u)p_{2(n-2)}(u)p_{2(n-3)}(-u)+Q(-u)p_{2(n-2)}(-u)p_{2(n-3)}(u)\right).$

It is a polynomial by (4), (8), and the induction hypothesis. Therefore, for all $n>0$ , by induction, $A_{2n}(L,M)=p_{2n}(u)p_{2n}(-u)$ is a polynomial.

Now, we are going to show that $A_{2n}(L,M)$ for $n>0$ has $L^{2}$ and $M^{8n}$ as terms so that it does not have any redundant $L$ or $M$ factors. Let us consider $p_{2n}$ and $Q$ as functions of $L$ , $M$ and $z$ and $u$ as a function of $L$ and $M$ . Let $(\beta_{1})=(L,0,u(L,0))$ and $(\bar{\beta_{1}})=(L,0,-u(L,0))$ . When $M$ is equal to zero, Proposition 2.4 simplifies to

Proposition 2.5

	$\displaystyle p_{2n}(\beta_{1})p_{2n}(\bar{\beta_{1}})$
	$\displaystyle=f(L,0)p_{2(n-1)}(\beta_{1})p_{2(n-1)}(\bar{\beta_{1}})$
	$\displaystyle=(1-3L+3L^{2}-L^{3})p_{2(n-1)}(\beta_{1})p_{2(n-1)}(\bar{\beta_{1}}).$

Since

\displaystyle p_{2}(\beta_{1})p_{2}(\bar{\beta_{1}})=L^{2}-L^{3},

(16)

for all $n>0$ , by induction, $A_{2n}(L,M)=p_{2n}(u)p_{2n}(-u)$ has $L^{2}$ as a term. Let $(\beta_{2})=\left(0,M,u(0,M)\right)$ and $(\bar{\beta_{2}})=\left(0,M,-u(0,M)\right)$ . Since $Q(\beta_{2})=Q(\bar{\beta_{2}})=M^{4}(1+M^{4})$ , we have the following equations from Equation (2):

	$\displaystyle p_{2n}(\beta_{2})$	$\displaystyle=(1+M^{4})p_{2(n-1)}(\beta_{2})-M^{4}p_{2(n-2)}(\beta_{2})$
	$\displaystyle p_{2n}(\bar{\beta_{2}})$	$\displaystyle=(1+M^{4})p_{2(n-1)}(\bar{\beta_{2}})-M^{4}p_{2(n-2)}(\bar{\beta_{2}}).$

Since $p_{0}=1$ , $p_{2}(\beta_{2})=p_{2}(\bar{\beta_{2}})=M^{4}$ , by induction, we have $p_{2n}(\beta_{2})=p_{2n}(\bar{\beta_{2}})=M^{4n}$ and $A_{2n}(0,M)=M^{8n}$ . Therefore $A_{2n}(L,M)$ for $n>0$ has $M^{8n}$ as a term. Now, we are going to show that $A_{2n}(L,M)$ for $n>0$ has $L^{3n}$ as a term and does not have a constant (nonzero) times $L^{3n+1}M^{2}$ as a term so that it does not have any redundant $LM^{2}+1$ factors. By Proposition 2.5 and Equation (16), $A_{2n}(L,M)$ for $n>0$ has $L^{3n}$ as a term. Since $p_{0}=1$ and $p_{2}(\pm u)$ (see Appendix C) is a polynomial up to $\left(2\left(LM^{2}+1\right)\right)^{2}$ , by Equations (2), (6) and (7), $p_{2n}(\pm u)$ for $n>0$ is a polynomial up to $\left(2\left(LM^{2}+1\right)\right)^{2n}$ . Hence, all the terms in (5) have at least 8th power of $M$ , and, by using Equations (6), (7) again, all the terms in (4) have at least 4th power of $M$ because we know that factoring out $\left(2\left(LM^{2}+1\right)\right)^{*}$ from a polynomial won’t affect $M^{**}$ factor of it and formulae in (4) and (5) are polynomials. Therefore if there were a constant (nonzero) times $L^{3n+1}M^{2}$ in $A_{2n}(L,M)$ for $n>0$ , it would be in the terms in (3). By using Equation (8), the terms in (3) can be rewritten as

\displaystyle f(L,M)p_{2(n-1)}(u)p_{2(n-1)}(-u).

(17)

The terms in $f(L,M)$ whose power of $M$ is less than or equal to $2$ are

-L^{3}+3L^{2}-3L+1+\left(2L^{3}-8L^{2}+6L\right)M^{2}.

The terms in $A_{2}(L,M)=p_{2}(u)p_{2}(-u)$ whose power of $M$ is less than or equal to $2$ are

L^{3}+L^{2}+\left(L^{3}+L^{2}\right)M^{2}.

Now, one can easily prove that the terms in 17 do not include a constant (nonzero) times $L^{3n+1}M^{2}$ .

From now on, we will deal with the case for $n<0$ .

Substituting $\frac{-2LM^{8}+LM^{6}-LM^{4}-M^{6}+M^{4}z+M^{4}-2M^{2}}{2\left(LM^{6}+M^{4}\right)}$ for $x$ into $P_{2n}$ , for $n<0$ , gives

	$\displaystyle q_{2n}(z)$	$\displaystyle=\sum_{i=0}^{-2n}\binom{\left\lfloor\frac{i-1}{2}\right\rfloor-n}{i}\left(M^{2}\right)^{-\left\lfloor\frac{i}{2}\right\rfloor-2\left\lfloor\frac{i+1}{2}\right\rfloor-3n-1}\left(\frac{-2LM^{6}+LM^{4}-LM^{2}-M^{4}+M^{2}z+M^{2}-2}{2M^{2}\left(LM^{2}+1\right)}\right)^{\left\lfloor\frac{i+1}{2}\right\rfloor}$
		$\displaystyle\times\left(\frac{M^{2}\left(-3LM^{2}+L+M^{2}+z-3\right)}{2\left(LM^{2}+1\right)}\right)^{\left\lfloor\frac{i-1}{2}\right\rfloor}\left(\frac{M^{2}\left(LM^{2}+L+M^{2}+z+1\right)}{2\left(LM^{2}+1\right)}\right)^{i}$
		$\displaystyle\times\left(\frac{M^{2}\left((-1)^{i}\left(-2LM^{2}+L+M^{2}+z-2\right)-LM^{2}-1\right)}{2\left(LM^{2}+1\right)}\right).$

As in case $n>0$ , we multiply it by its Galois conjugate $q_{2n}(-u)$ to obtain the entire $A$ -polynomial. We multiply $q_{2n}(u)q_{2n}(-u)$ by $M^{8n+4}\left(LM^{2}+1\right)^{-4n+1}$ to clear the denominators and factor out some power of $M$ so that we have the $A$ -polynomial $A_{2n}(L,M)=p_{2n}(u)p_{2n}(-u)$ in Theorem 1.1. Similarly as in case $n>0$ , we can show that $A_{2n}(L,M)$ for $n<0$ does not have any redundant $L$ , $M$ or $LM^{2}+1$ factors. It can be done by showing that it has $1$ and $L^{3(n-1)+1}$ as terms and does not have a constant times $L^{3(n-1)+2}M^{2}$ as a term.

3 Appendix A

	$\displaystyle a(L,M)=2L^{4}\left(M^{12}+M^{8}\right)+L^{3}\left(-3M^{12}+10M^{10}+5M^{8}+4M^{6}-M^{4}+2M^{2}-1\right)+2\left(M^{4}+1\right)$
	$\displaystyle+2L^{2}\left(M^{12}-4M^{10}+5M^{8}+8M^{6}+5M^{4}-4M^{2}+1\right)-L\left(M^{12}-2M^{10}+M^{8}-4M^{6}-5M^{4}-10M^{2}+3\right)$
	$\displaystyle b(L,M)=(L-1)(M-1)^{3}(M+1)^{3}\left(M^{2}+1\right)^{2}$
	$\displaystyle f(L,M)=-L^{3}+3L^{2}-3L+1+\left(6L^{3}-8L^{2}+2L\right)M^{14}+\left(6L^{3}+8L^{2}+2L\right)M^{10}+\left(2L^{3}+8L^{2}+6L\right)M^{6}$
	$\displaystyle+\left(-2L^{3}+2L^{2}+2L+2\right)M^{4}+\left(2L^{3}-8L^{2}+6L\right)M^{2}+\left(L^{4}-3L^{3}+3L^{2}-L\right)M^{16}$
	$\displaystyle+\left(2L^{4}+2L^{3}+2L^{2}-2L\right)M^{12}+\left(L^{4}+4L^{3}+14L^{2}+4L+1\right)M^{8}.$
	$\displaystyle g(L,M)=2L^{8}\left(M^{4}+1\right)^{2}M^{16}+2L^{7}\left(-3M^{16}+10M^{14}+2M^{12}+14M^{10}+4M^{8}+6M^{6}-2M^{4}+2M^{2}-1\right)M^{8}$
	$\displaystyle+L^{6}\left(11M^{24}-52M^{22}+54M^{20}+76M^{18}+91M^{16}-8M^{14}+68M^{12}-8M^{10}-7M^{8}-4M^{6}+6M^{4}-4M^{2}+1\right)$
	$\displaystyle-2L^{5}\left(7M^{24}-34M^{22}+52M^{20}+18M^{18}-106M^{16}-178M^{14}+54M^{12}-22M^{10}-31M^{8}+4M^{6}+22M^{4}-12M^{2}+2\right)$
	$\displaystyle+2L^{4}\left(5M^{24}-28M^{22}+44M^{20}+4M^{18}-71M^{16}+24M^{14}+324M^{12}+24M^{10}-71M^{8}+4M^{6}+44M^{4}-28M^{2}+5\right)$
	$\displaystyle-2L^{3}\left(2M^{24}-12M^{22}+22M^{20}+4M^{18}-31M^{16}-22M^{14}+54M^{12}-178M^{10}-106M^{8}+18M^{6}+52M^{4}-34M^{2}+7\right)$
	$\displaystyle+L^{2}\left(M^{24}-4M^{22}+6M^{20}-4M^{18}-7M^{16}-8M^{14}+68M^{12}-8M^{10}+91M^{8}+76M^{6}+54M^{4}-52M^{2}+11\right)$
	$\displaystyle+L\left(-2M^{16}+4M^{14}-4M^{12}+12M^{10}+8M^{8}+28M^{6}+4M^{4}+20M^{2}-6\right)+2\left(M^{4}+1\right)^{2}$
	$\displaystyle h(L,M)=L\left(L-1\right)\left(M^{2}-1\right)^{3}\left(M^{2}+1\right)^{2}h_{1}(L,M)$
	$\displaystyle h_{1}(L,M)=L^{4}\left(2M^{12}+2M^{8}\right)+L^{3}\left(-3M^{12}+10M^{10}+5M^{8}+4M^{6}-M^{4}+2M^{2}-1\right)$
	$\displaystyle+L^{2}\left(2M^{12}-8M^{10}+10M^{8}+16M^{6}+10M^{4}-8M^{2}+2\right)$
	$\displaystyle+L\left(-M^{12}+2M^{10}-M^{8}+4M^{6}+5M^{4}+10M^{2}-3\right)+2M^{4}+2$

4 Appendix B

	$\displaystyle A_{2}(L,M)=L^{4}M^{8}+L^{3}\left(-2M^{12}+3M^{10}+3M^{8}+M^{2}-1\right)+L^{2}\left(M^{16}-3M^{14}-M^{12}+3M^{10}+6M^{8}+3M^{6}-M^{4}-3M^{2}+1\right)$
	$\displaystyle+L\left(-M^{16}+M^{14}+3M^{8}+3M^{6}-2M^{4}\right)+M^{8}$

	$\displaystyle A_{4}(L,M)=L^{8}M^{16}+L^{7}\left(-2M^{24}+3M^{22}-2M^{20}+M^{18}+8M^{16}+M^{14}-2M^{12}+3M^{10}-2M^{8}\right)\qquad\qquad\qquad\qquad\qquad$
	$\displaystyle+L^{6}\left(M^{32}-3M^{30}+3M^{28}-M^{26}-4M^{24}-9M^{22}+15M^{20}+13M^{18}-2M^{16}+13M^{14}\right.$
	$\displaystyle\left.+15M^{12}-9M^{10}-4M^{8}-M^{6}+3M^{4}-3M^{2}+1\right)$
	$\displaystyle+L^{5}\left(-4M^{32}+16M^{30}-14M^{28}-21M^{26}+24M^{24}+16M^{22}-56M^{20}\right.$
	$\displaystyle\left.+17M^{18}+100M^{16}+17M^{14}-56M^{12}+16M^{10}+24M^{8}-21M^{6}-14M^{4}+16M^{2}-4\right)$
	$\displaystyle+L^{4}\left(6M^{32}-26M^{30}+22M^{28}+40M^{26}-59M^{24}-64M^{22}+82M^{20}\right.$
	$\displaystyle\left.+50M^{18}-32M^{16}+50M^{14}+82M^{12}-64M^{10}-59M^{8}+40M^{6}+22M^{4}-26M^{2}+6\right)$
	$\displaystyle+L^{3}\left(-4M^{32}+16M^{30}-14M^{28}-21M^{26}+24M^{24}+16M^{22}-56M^{20}+17M^{18}+100M^{16}\right.$
	$\displaystyle\left.+17M^{14}-56M^{12}+16M^{10}+24M^{8}-21M^{6}-14M^{4}+16M^{2}-4\right)$
	$\displaystyle+L^{2}\left(M^{32}-3M^{30}+3M^{28}-M^{26}-4M^{24}-9M^{22}+15M^{20}+13M^{18}-2M^{16}+13M^{14}+15M^{12}-9M^{10}\right.$
	$\displaystyle\left.-4M^{8}-M^{6}+3M^{4}-3M^{2}+1\right)$
	$\displaystyle+L\left(-2M^{24}+3M^{22}-2M^{20}+M^{18}+8M^{16}+M^{14}-2M^{12}+3M^{10}-2M^{8}\right)+M^{16}$

5 Appendix C

	$\displaystyle p_{2}(\pm u)=\left(2\left(LM^{2}+1\right)\right)^{-2}\left[\mp L\left(M^{4}-1\right)^{2}\left(L+M^{2}\right)u\right.$
	$\displaystyle\left.+2L^{4}M^{8}+L^{3}\left(-2M^{12}+3M^{10}+3M^{8}+4M^{6}+M^{2}-1\right)+L^{2}\left(M^{12}-6M^{10}+5M^{8}+12M^{6}+5M^{4}-6M^{2}+1\right)\right.\qquad\qquad\qquad\qquad\qquad$
	$\displaystyle\left.+L\left(-M^{12}+M^{10}+4M^{6}+3M^{4}+3M^{2}-2\right)+2M^{4}\right]$

	$\displaystyle p_{-2}(\pm u)=(2\left(LM^{2}+1\right))^{-\frac{3}{2}}\left[\pm L\left(M^{4}-1\right)^{2}u\right.$
	$\displaystyle\left.+2L^{3}M^{10}-L^{2}\left(M^{10}-5M^{8}-2M^{6}+M^{2}-1\right)+L\left(M^{10}-M^{8}+2M^{4}+5M^{2}-1\right)+2\right]\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad$

	$\displaystyle p_{-4}(\pm u)=\left(2\left(LM^{2}+1\right)\right)^{-7/2}\left[\pm L\left(M^{4}-1\right)^{2}\left(L^{4}\left(2M^{4}-M^{2}+1\right)M^{8}+L^{3}\left(-3M^{12}+9M^{10}+M^{8}+M^{6}-M^{4}+2M^{2}-1\right)\right.\right.$
	$\displaystyle\left.\left.+L^{2}\left(2M^{12}-8M^{10}+7M^{8}+10M^{6}+7M^{4}-8M^{2}+2\right)+L\left(-M^{12}+2M^{10}-M^{8}+M^{6}+M^{4}+9M^{2}-3\right)+M^{4}-M^{2}+2\right)u\right.$
	$\displaystyle\left.+2L^{7}M^{22}+L^{6}\left(-4M^{14}+15M^{12}+6M^{10}-5M^{8}+3M^{4}-2M^{2}+1\right)M^{8}\right.$
	$\displaystyle\left.+L^{5}\left(7M^{22}-25M^{20}+22M^{18}+51M^{16}-M^{14}-32M^{12}+13M^{10}+10M^{8}-2M^{6}-3M^{4}+3M^{2}-1\right)\right.$
	$\displaystyle\left.+L^{4}\left(-7M^{22}+28M^{20}-21M^{18}-31M^{16}+62M^{14}+82M^{12}-50M^{10}-30M^{8}+33M^{6}+18M^{4}-17M^{2}+3\right)\right.$
	$\displaystyle\left.+L^{3}\left(3M^{22}-17M^{20}+18M^{18}+33M^{16}-30M^{14}-50M^{12}+82M^{10}+62M^{8}-31M^{6}-21M^{4}+28M^{2}-7\right)\right.$
	$\displaystyle\left.-L^{2}\left(M^{22}-3M^{20}+3M^{18}+2M^{16}-10M^{14}-13M^{12}+32M^{10}+M^{8}-51M^{6}-22M^{4}+25M^{2}-7\right)\right.$
	$\displaystyle\left.+L\left(M^{14}-2M^{12}+3M^{10}-5M^{6}+6M^{4}+15M^{2}-4\right)+2\right]$

Acknowledgement

This work was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (No. NRF-2018R1A2B6005847). The second author was supported by 2018 Hongik University Research Fund.

References

[1] D. Cooper, M. Culler, H. Gillet, D. D. Long, P. B. Shalen, Plane curves associated to character varieties of $3$ -manifolds, Invent. Math. 118 (1) (1994) 47–84. doi:10.1007/BF01231526.
URL http://dx.doi.org/10.1007/BF01231526
[2] S. Boyer, X. Zhang, A proof of the finite filling conjecture, J. Differential Geom. 59 (1) (2001) 87–176.
URL http://projecteuclid.org/euclid.jdg/1090349281
[3] M. Culler, C. M. Gordon, J. Luecke, P. B. Shalen, Dehn surgery on knots, Ann. of Math. (2) 125 (2) (1987) 237–300. doi:10.2307/1971311.
URL http://dx.doi.org/10.2307/1971311
[4] D. Cooper, D. D. Long, Remarks on the $A$ -polynomial of a knot, J. Knot Theory Ramifications 5 (5) (1996) 609–628. doi:10.1142/S0218216596000357.
URL http://dx.doi.org/10.1142/S0218216596000357
[5] J.-Y. Ham, J. Lee, The volume of hyperbolic cone-manifolds of the knot with Conway’s notation $C(2n,3)$ , J. Knot Theory Ramifications 25 (6) (2016) 1650030, 9. doi:10.1142/S0218216516500309.
URL http://dx.doi.org/10.1142/S0218216516500309
[6] J.-Y. Ham, A. Mednykh, V. Petrov, Trigonometric identities and volumes of the hyperbolic twist knot cone-manifolds, J. Knot Theory Ramifications 23 (12) (2014) 1450064, 16. doi:10.1142/S0218216514500643.
URL http://dx.doi.org/10.1142/S0218216514500643
[7] S.-s. Chern, J. Simons, Some cohomology classes in principal fiber bundles and their application to Riemannian geometry, Proc. Nat. Acad. Sci. U.S.A. 68 (1971) 791–794.
[8] J.-Y. Ham, J. Lee, Explicit formulae for Chern-Simons invariants of the twist-knot orbifolds and edge polynomials of twist knots, Mat. Sb. 207 (9) (2016) 144–160. doi:10.4213/sm8610.
URL http://dx.doi.org/10.4213/sm8610
[9] J.-Y. Ham, J. Lee, Explicit formulae for Chern-Simons invariants of the hyperbolic orbifolds of the knot with Conway’s notation $C(2n,3)$ , Lett. Math. Phys. 107 (3) (2017) 427–437. doi:10.1007/s11005-016-0904-0.
URL http://dx.doi.org/10.1007/s11005-016-0904-0
[10] J.-Y. Ham, J. Lee, Explicit formulae for chern-simons invariants of the hyperbolic ${J}(2n,-2m)$ knot orbifolds, arXiv:1703.10984, preprint (2017).
[11] H. M. Hilden, M. T. Lozano, J. M. Montesinos-Amilibia, On volumes and Chern-Simons invariants of geometric $3$ -manifolds, J. Math. Sci. Univ. Tokyo 3 (3) (1996) 723–744.
[12] D. W. Boyd, Mahler’s measure and invariants of hyperbolic manifolds, in: Number theory for the millennium, I (Urbana, IL, 2000), A K Peters, Natick, MA, 2002, pp. 127–143.
[13] C. Frohman, R. Gelca, W. Lofaro, The A-polynomial from the noncommutative viewpoint, Trans. Amer. Math. Soc. 354 (2) (2002) 735–747. doi:10.1090/S0002-9947-01-02889-6.
URL https://doi.org/10.1090/S0002-9947-01-02889-6
[14] S. Garoufalidis, Knots and tropical curves, in: Interactions between hyperbolic geometry, quantum topology and number theory, Vol. 541 of Contemp. Math., Amer. Math. Soc., Providence, RI, 2011, pp. 83–101. doi:10.1090/conm/541/10680.
URL http://dx.doi.org/10.1090/conm/541/10680
[15] T. T. Q. Le, A. T. Tran, On the AJ conjecture for knots, Indiana Univ. Math. J. 64 (4) (2015) 1103–1151, with an appendix written jointly with Vu Q. Huynh. doi:10.1512/iumj.2015.64.5602.
URL http://dx.doi.org/10.1512/iumj.2015.64.5602
[16] A. A. Champanerkar, A-polynomial and Bloch invariants of hyperbolic 3-manifolds, ProQuest LLC, Ann Arbor, MI, 2003, thesis (Ph.D.)–Columbia University.
[17] J. Howie, D. Mathews, J. Purcell, A-polynomials, ptolemy equations and dehn filling, arXiv:2002.10356, preprint (2021).
[18] J. Howie, D. Mathews, J. Purcell, A-polynomials of fillings of the whitehead sister, arXiv:2106.13462, preprint (2021).
[19] C. K. Zickert, Ptolemy coordinates, Dehn invariant and the $A$ -polynomial, Math. Z. 283 (1-2) (2016) 515–537. doi:10.1007/s00209-015-1608-3.
URL https://doi.org/10.1007/s00209-015-1608-3
[20] M. Goerner, C. K. Zickert, Triangulation independent Ptolemy varieties, Math. Z. 289 (1-2) (2018) 663–693. doi:10.1007/s00209-017-1970-4.
URL https://doi.org/10.1007/s00209-017-1970-4
[21] M. Culler, A-polynomials, http://homepages.math.uic.edu/culler/Apolynomials.
[22] J. Hoste, P. D. Shanahan, A formula for the A-polynomial of twist knots, J. Knot Theory Ramifications 13 (2) (2004) 193–209. doi:10.1142/S0218216504003081.
URL http://dx.doi.org/10.1142/S0218216504003081
[23] S. Garoufalidis, T. W. Mattman, The $A$ -polynomial of the $(-2,3,3+2n)$ pretzel knots, New York J. Math. 17 (2011) 269–279.
URL http://nyjm.albany.edu:8000/j/2011/17_269.html
[24] N. Tamura, Y. Yokota, A formula for the $A$ -polynomials of $(-2,3,1+2n)$ -pretzel knots, Tokyo J. Math. 27 (1) (2004) 263–273. doi:10.3836/tjm/1244208490.
URL http://dx.doi.org/10.3836/tjm/1244208490
[25] K. Petersen, The $A$ -polynomial of a family of two-bridge knots, New York J. Math. 21 (2015) 847–881.
[26] F. Nagasato, Computing the A-polynomial using noncommutative methods, J. Knot Theory Ramifications 14 (6) (2005) 735–749. doi:10.1142/S0218216505004068.
URL https://doi.org/10.1142/S0218216505004068
[27] Y. Ni, X. Zhang, Detection of knots and a cabling formula for A-polynomials, arXiv:1411.0353, preprint (2014).
[28] D. V. Mathews, Erratum: An explicit formula for the A-polynomial of twist knots [mr3268980], J. Knot Theory Ramifications 23 (11) (2014) 1492001, 1. doi:10.1142/S0218216514920011.
URL http://dx.doi.org/10.1142/S0218216514920011
[29] D. V. Mathews, An explicit formula for the A-polynomial of twist knots, J. Knot Theory Ramifications 23 (9).
[30] E. Thompson, Twisting, ladder graphs and A-polynomials, arXiv:2107.11028, preprint (2021).
[31] J.-Y. Ham, J. Lee, An explicit formula for the $A$ -polynomial of the knot with Conway’s notation $C(2n,3)$ , J. Knot Theory Ramifications 25 (10) (2016) 1650057, 9. doi:10.1142/S0218216516500577.
URL http://dx.doi.org/10.1142/S0218216516500577
[32] J.-Y. Ham, J. Lee, A. Mednykh, A. Rasskazov, On the volume and Chern-Simons invariant for 2-bridge knot orbifolds, J. Knot Theory Ramifications 26 (12) (2017) 1750082, 22. doi:10.1142/S0218216517500821.
URL https://doi.org/10.1142/S0218216517500821
[33] R. Riley, Parabolic representations of knot groups. I, Proc. London Math. Soc. (3) 24 (1972) 217–242.
[34] S. Lang, Algebra, 2nd Edition, Addison-Wesley Publishing Company, Advanced Book Program, Reading, MA, 1984.

An explicit formula for the AA-polynomial of the knot with Conway’s notation C​(2​n,4)C(2n,4)

Abstract

keywords:

1 Introduction

Theorem 1.1

2 Proof of Theorem 1.1

Proposition 2.1

Lemma 2.2

Proof 1

Lemma 2.3

Proposition 2.4

Proposition 2.5

3 Appendix A

4 Appendix B

5 Appendix C

Acknowledgement

References

References

An explicit formula for the $A$ -polynomial of the knot with Conway’s notation $C(2n,4)$