An EPTAS for Budgeted Matroid Independent Set
Abstract
We consider the budgeted matroid independent set problem. The input is a ground set, where each element has a cost and a non-negative profit, along with a matroid over the elements and a budget. The goal is to select a subset of elements which maximizes the total profit subject to the matroid and budget constraints. Several well known special cases, where we have, e.g., a uniform matroid and a budget, or no matroid constraint (i.e., the classic knapsack problem), admit a fully polynomial-time approximation scheme (FPTAS). In contrast, already a slight generalization to the multi-budgeted matroid independent set problem has a PTAS but does not admit an efficient polynomial-time approximation scheme (EPTAS). This implies a PTAS for our problem, which is the best known result prior to this work.
Our main contribution is an EPTAS for the budgeted matroid independent set problem. A key idea of the scheme is to find a representative set for the instance, whose cardinality depends solely on , where is the accuracy parameter of the scheme. The representative set is identified via matroid basis minimization, which can be solved by a simple greedy algorithm. Our scheme enumerates over subsets of the representative set and extends each subset using a linear program. The notion of representative sets may be useful in solving other variants of the budgeted matroid independent set problem.
1 Introduction
We consider the budgeted matroid independent set (BMI) problem, defined as follows. We are given a set of elements , a membership oracle for a collection of independent sets , where is a matroid, a budget , a cost function , and a profit function . A solution for the problem is an independent set of total cost at most (i.e., ). The profit of a solution is , and the objective is to find a solution of maximal profit.
BMI is a generalization of the classic -knapsack problem, which is NP-hard and therefore unlikely to admit an exact polynomial-time algorithm. Thus, there is a long line of work on finding efficient approximations for knapsack and its variants (for comprehensive surveys see, e.g., [20, 17]).
Let be the value of an optimal solution for an instance of a maximization problem . For , we say that is an -approximation algorithm for if, for any instance of , outputs a solution of value at least . A polynomial-time approximation scheme (PTAS) for a maximization problem is a family of algorithms such that, for any , is a polynomial-time -approximation algorithm for ; is an EPTAS if the running time of is of the form , where is an arbitrary function, and is the bit-length encoding size of the input instance; is an FPTAS if the running time of is of the form .
Polynomial-time approximation schemes allow us to obtain almost optimal solutions for NP-hard optimization problems via a speed-accuracy trade-off. However, the strong dependency of run-times on the error parameter, , often renders these schemes highly impractical. Thus, a natural goal is to seek the fastest scheme for a given problem, assuming one exists. Having obtained a PTAS, the next step is to consider possible improvements to an EPTAS, or even to an FPTAS. This is the focus of our work.
For the classic knapsack problem, a very efficient FPTAS exists since the 1970’s. Lawler’s scheme [19], based on ideas from [12], achieves a running time of for a -approximation. In contrast, already the two-dimensional knapsack problem has a PTAS but does not admit an EPTAS [18]. For the well known multiple knapsack problem, Chekuri and Khanna [3] derived the first PTAS, which was later improved by Jansen to an EPTAS [13, 14]. The existence of an FPTAS is ruled out by a simple reduction from Partition [3]. More generally, resolving the complexity status of NP-hard optimization problem with respect to approximation schemes has been the focus of much research relating to resource allocation and scheduling (see, e.g., [24, 6, 8, 15, 16] and the surveys [22, 23]).
For BMI, FPTASs are known for instances in which the matroid belongs to a restricted family. One notable example is multiple choice knapsack [19], where the elements are partitioned into groups, and a set is independent if it contains at most one element from each group. Another example is -dimensional knapsack [2], in which a set is independent if it contains at most elements for some (i.e., a uniform matroid constraint).
There are known results also for generalizations of BMI which involve multiple budget constraints or an additional matroid constraint. Specifically, Grandoni and Zenklusen developed in [9] a PTAS for multi-budgeted matroid independent set (MBMI), a generalization of BMI in which the costs are -dimensional (for some constant ). The PTAS of [9] is based on integrality properties of a linear programming relaxation of the problem. As MBMI generalizes the two-dimensional knapsack problem, it does not admit an EPTAS unless [18].
The budgeted matroid intersection problem is a generalization of BMI in which the input includes membership oracles for independent sets of two different matroids, and the solution must be an independent set of both matroids. A PTAS for budgeted matroid intersection was developed in [1]. The algorithm of [1] uses a Lagrangian relaxation along with some combinatorial properties of the problem to patch two solutions (i.e., a feasible solution with sub-optimal profit, and a non-feasible solution with high profit) into the final solution. The existence of an EPTAS (or an FPTAS) for budgeted matroid intersection is still open.
The multi-budgeted matroid intersection problem is a generalization of both multi-budgeted matroid independent set and budgeted matroid intersection, in which the cost function is -dimensional, and the input contains two matroids. In [4] the authors developed a PTAS for multi-budgeted matroid intersection, based on randomized rounding of a solution for a linear programming (LP) relaxation of the problem.
The budgeted matroid independent set problem is also a special case of multiple knapsack with a matroid, a variant of BMI in which the input contains budgets . A solution consists of sets , where the cost of the th set is at most the th budget (), and the union of the sets is an independent set of the matroid. A PTAS for the problem (based on randomized rounding) was given in [7]. The existence of an FPTAS is ruled out, as multiple knapsack is a special case [3].
To the best of our knowledge, BMI is studied here for the first time. A PTAS for the problem follows from known results for any of the above generalizations. In all cases, the running time of the scheme is dominated by an enumeration phase which guesses the most profitable elements in an optimal solution.
Our main result is an EPTAS for BMI, thus substantially improving the running times of existing schemes for the problem. Let denote a BMI instance, the profit of an optimal solution for , and the bit-length encoding of the instance .
Theorem 1.1.
Given an instance of BMI and , there is an algorithm that outputs a solution of profit at least in time .
Main Technique. Our algorithm builds upon a framework of Grandoni and Zenklusen [9] for multi-budgeted matroid independent set. In [9] the authors show that a basic solution for a linear programming relaxation of the problem has only a few non-integral entries. Thus, a solution for MBMI is constructed by solving the LP relaxation and adding all the elements with non-zero integral entries to the MBMI solution. An exhaustive enumeration phase which guesses the most profitable elements in an optimal solution is used to mitigate the profit loss caused by discarding the (few) elements with non-integral entries in the solution for the LP. The running time of the algorithm is dominated by the operations required for exhaustive enumeration.
The improved running time of our algorithm is obtained by reducing the time complexity of the enumeration phase. Consider a BMI instance . Given some , we say that an element is profitable if . Our algorithm identifies a representative set of elements satisfying , for a computable function . Furthermore, we show that the BMI instance has a solution where all elements in are non-profitable and . Thus, we can use enumeration to guess and then extend the solution using an LP relaxation similar to [9]. Crucial to our construction of is the notion of profit gap, used for identifying elements that may be added to by solving the LP (see Section 3). Since all the elements in are non-profitable, the profit loss caused by the few non-integral entries is negligible. Moreover, since , guessing can be done in steps (in fact, we obtain a slightly better running time), eliminating the dependency of enumeration on the input size. The representative set is identified via matroid basis minimization, which can be solved by a simple greedy algorithm (see Section 3).
Organization. In Section 2 we give some definitions and notation. Section 3 presents our approximation scheme, EPTAS, and its analysis. In Section 4 we give a proof of correctness for algorithm FindRep that is used as a subroutine by the scheme. We conclude in Section 5 with a summary and open problems.
2 Preliminaries
For simplicity of the notation, for any set and an element , we use and to denote and , respectively. Also, for any let . Finally, for a function and a subset of elements , we define .
2.1 Matroids
Let be a finite ground set and a non-empty set containing subsets of called the independent sets of . Then, is a matroid if the following hold:
-
1.
(Hereditary Property) For all and , it holds that .
-
2.
(Exchange Property) For any where , there is such that .
The next observation follows by repeatedly applying the exchange property.
Observation 2.1.
Given a matroid and , there is , such that .
A basis of a matroid is an independent set such that for all it holds that . Given a cost function , we say that a basis of is a minimum basis of w.r.t. if, for any basis of it holds that . A minimum basis of w.r.t. can be easily constructed in polynomial-time using the greedy approach (see, e.g., [5]). In the following we define several operations on matroids that will be useful for deriving our results.
Definition 2.2.
Let be a matroid.
-
1.
(restriction) For every define and .
-
2.
(contraction) For every define and .
-
3.
(truncation) For every define and .
-
4.
(union) Let be matroids; define , where
and .
The next lemma gathers known results which follow directly from the definition of a matroid (see, e.g., [21]).
Lemma 2.3.
Let be a matroid.
-
1.
For any , the restriction of to (i.e., ) is a matroid.
-
2.
For any , the contraction of by (i.e., ) is a matroid.
-
3.
For any , the truncation of (i.e., ) is a matroid.
-
4.
Given matroids , the union of (i.e., ) is a matroid.
2.2 Matroid polytope
Let be a matroid. Given , the indicator vector of is the vector , where for all and we have and , respectively. Then the matroid polytope of is the convex hull of the set of indicator vectors of all independent sets of : . The next observation will be used in the analysis of our scheme.
Observation 2.4.
Let be a matroid, and . Then .
3 The Algorithm
In this section we present an EPTAS for BMI. Our scheme initially handles elements of high profits. This is done by finding a small representative set out of which the scheme selects the most profitable elements in the solution. More elements, of lower profits, are then added to the solution using a linear program. For the remainder of this section, fix a BMI instance and a parameter . W.l.o.g., for all we assume that (otherwise cannot belong to any solution for ).
Let be the set of profitable elements in , and the set of non-profitable elements; when understood from the context, we simply use . We can easily obtain a PTAS by enumerating over all subsets of at most profitable elements to find the profitable elements in the solution. However, such exhaustive search is done in time , which cannot lead to an EPTAS. Thus, we take a different approach.
A key observation is that efficient solution can be obtained without enumerating over all subsets of profitable elements. Instead, we limit our scheme to a smaller search space using the notions of replacements and representative sets. Let be an independent set having a bounded number of elements. A replacement of is a subset of elements which can replace the profitable elements in , resulting with an independent set of lower cost and almost the same profit. A representative set is a subset of elements which contains a replacement within for any independent set with bounded number of elements. Definitions 3.1 and 3.2 give the formal properties of replacements and representative sets, respectively. Let , and recall that (the selection of value for becomes clear in the proof of Lemma 3.3).
Definition 3.1.
Given a BMI instance , , and , we say that is a replacement of for and if the following holds:
-
1.
.
-
2.
.
-
3.
.
-
4.
.
Definition 3.2.
Given a BMI instance and , we say that is a representative set of and if, for any , there is a replacement of for and .
In particular, observe that for any solution of we have that is a replacement of ; also, is a representative set. In the next lemma we show that there exists an almost optimal solution in which all profitable elements belong to a given representative set. Hence, guessing the profitable elements only requires enumerating over subsets of a representative set.
Lemma 3.3.
Let be a BMI instance and . Also, let be a representatives set of and . Then, there is a solution of such that the following holds.
-
1.
.
-
2.
.
We give a brief outline of the proof of Lemma 3.3. Informally, we consider the elements in some optimal solution, OPT, in non-increasing order by profit. We then partition these elements into three sets: and , such that the maximal profit in is at most times the minimum profit in . This is the profit gap of and . In addition, , and . Thus, we can use as a replacement of , i.e., will be replaced by elements in (note that is not necessarily a subset of the profitable elements). We now discard , and define . As may not be an independent set, we use Observation 2.1 to construct such that . An illustration of the proof is given in Figure 1.
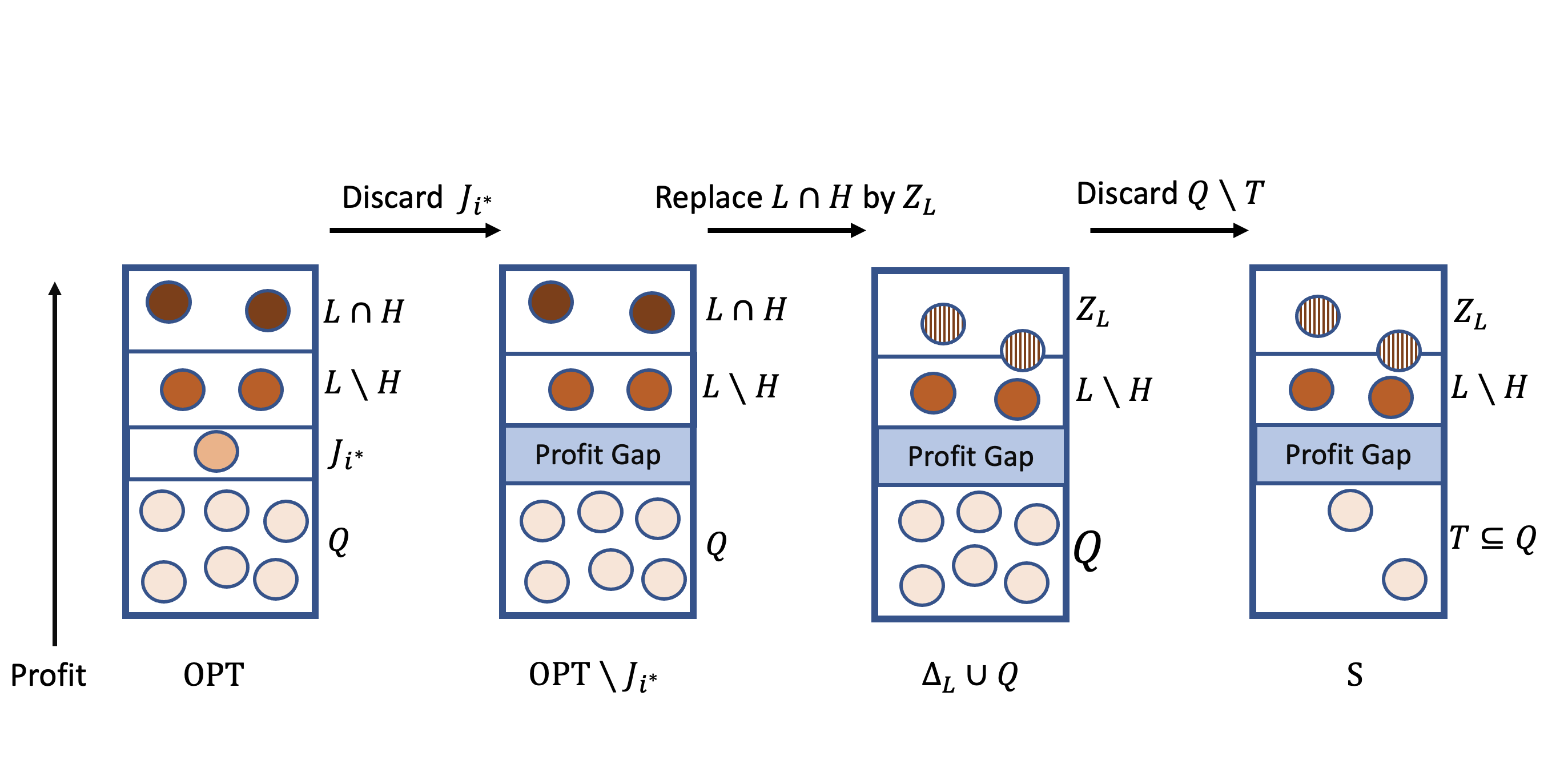
Proof of Lemma 3.3: With a slight abuse of notation, we use OPT also to denote the profit of an optimal solution for . Given an optimal solution, we partition a subset of the elements in the solution into disjoint sets (some sets may be empty). Specifically, let ; for all define
| (1) |
Let . By (1) we have at least disjoint sets; thus, . Now, let be the subset of all elements in OPT of profits greater than , and . To complete the proof of the lemma, we need several claims.
Claim 3.4.
.
Proof.
Since , by the hereditary property of we have that . Also,
The first inequality holds since
for all . For the second inequality, we note that is a solution for . By the above and Definition 2.2, it follows that .
By Claim 3.4 and as is a representative set,
it follows that has a replacement .
Let . By Property 1 of Definition 3.1, we have that , and
by Definition 2.2 it holds that .
Hence, . Furthermore, as , by the
hereditary property for we have that . Therefore, by Observation 2.1, there is a subset , where , such that .
Let . We show that satisfies the conditions of the lemma.
Claim 3.5.
is a solution for .
Proof.
By the definition of it holds that . Moreover,
The second inequality holds since (see Property 2 of Definition 3.1). For the third inequality, recall that . The last inequality holds since OPT is a solution for .
The proof of the next claim relies on the profit gap between the elements in and .
Claim 3.6.
.
Proof.
Observe that
| (2) |
The first inequality follows from the definition of . For the third inequality, we use Property 4 of Definition 3.1. Hence,
The first inequality holds since for all .
The second inequality is by (2). The third inequality holds since for all .
Claim 3.7.
.
Proof.
The last inequality holds since . Observe that and . Therefore,
Finally, we note that, by (1) and the definition of , . Consequently, by the definition of , we have that .
As (by Definition 3.2), it follows that . Hence, using Claims 3.5 and 3.7,
we have the statement of the lemma. ∎
Our scheme for BMI constructs a representative set whose cardinality depends solely on . To this end, we first partition the profitable elements (and possibly some more elements) into a small number of profit classes, where elements from the same profit class have similar profits. The profit classes are derived from a -approximation for , which can be easily computed in polynomial time. specifically, for all define the -profit class as
| (5) |
For each , we define , the corresponding matroid for the -profit class. We construct a representative set by computing a minimum basis w.r.t. the cost function , for the matroid defined as the union of the corresponding matroids of all profit classes. Note that by Lemma 2.3 the latter is a matroid. The pseudocode of algorithm FindRep, which outputs a representative set, is given in Algorithm 1.
Lemma 3.8.
Given a BMI instance and , Algorithm 1 returns in time a representative set of and , such that .
In the following we outline the main ideas of the proof. Let , and consider some and . By (5) the element belongs to some profit class . Since is a minimum basis w.r.t. , we can use matroid properties to show that there is some of cost such that . We now keep replacing elements in in a similar manner, until no such element exists. Thus, we have a replacement of within , i.e., is a representative set. A formal proof of Lemma 3.8 is given in Section 4.
Our scheme uses the representative set to select profitable elements for the solution. Using a linear program, the solution is extended to include also non-profitable elements. As the exact set of non-profitable elements is unknown, we use an approximation for the optimal profit. Specifically, let , and denote by the set including the non-profitable elements, and possibly also profitable elements such that .
The LP is based on the matroid polytope of the following matroid. Given a solution for , we define ; in other words, , where . Note that is indeed a matroid, by Properties 1 and 2 of Lemma 2.3. The LP formulation is given by
| (6) | ||||
| s.t. | ||||
The linear program maximizes the total profit of a point in the matroid polytope of (i.e., ), such that the total cost of elements is at most ; that is, the residual budget after selecting for the solution the elements in .
Observation 3.9.
Let be a BMI instance, , a solution for , and an optimal basic solution for . Then, .
It is folklore that a linear program such as can be solved in polynomial-time in . As we could not find a proper reference, we include the proof of the next lemma in the appendix.
Lemma 3.10.
For any BMI instance , , and a solution of , a basic optimal solution of can be found in time .
The next lemma will be useful for deriving a solution of high profit using . The proof follows as a special case of a result of [9].
Lemma 3.11.
Let be a BMI instance, , a solution of , and a basic solution for . Then has at most two non-integral entries.
Using the above, we have the required components for an EPTAS for BMI. Let be the representative set returned by . For all solutions with , we find a basic optimal solution for and define as the solution of . Our scheme iterates over the solutions for all such subsets and chooses a solution of maximal total profit. The pseudocode of the scheme is given in Algorithm 2.
Lemma 3.12.
Given a BMI instance and , Algorithm 2 returns a solution for of profit at least .
Proof.
By Lemma 3.3, there is a solution for such that , and . As for all we have , and is a solution for , it follows that . We note that there is an iteration of Step 2 in which ; thus, in Step 2 we construct a basic optimal solution of . We use for every basic solution computed in Step 2 for . Then,
| (7) | ||||
The first inequality holds since, by Lemma 3.11, , and for all , . The second inequality follows from Observation 3.9. Now,
| (8) |
Claim 3.13.
is a solution of .
Proof.
If the claim trivially follows since is a solution of . Otherwise, by Step 2 of Algorithm 2, there is a solution of such that . By Observation 2.4, is an independent set in the matroid . Also, recall that . Hence, by Definition 2.2, we have that . Additionally,
The inequality follows from (6). By the above, we conclude that is a solution for .
By Claim 3.13, Steps 2, 2 and 2 of Algorithm 2 and (8), we have that is a solution for satisfying . This completes the proof.
∎
Lemma 3.14.
Given a BMI instance and , Algorithm 2 runs in time .
Proof.
By Lemma 3.8, the time complexity of Step 2 is . Step 2 can be computed in time , by using a PTAS for BMI taking (see, e.g., [9]). Now, using logarithm rules we have
| (9) |
The second inequality follows from , and . Therefore,
| (10) |
The first inequality is by Lemma 3.8. The second inequality is by (9). Let
be the set of solutions considered in Step 2 of Algorithm 2. Then,
| (11) |
The second inequality is by (10). Hence, by (11), the number of iterations of the for loop in Step 2 is bounded by . In addition, by Lemma 3.10, the running time of each iteration is . By the above, the running time of Algorithm 2 is . ∎
4 Correctness of FindRep
In this section we give the proof of Lemma 3.8. The proof is based on substitution of subsets by profit classes. A substitution is closely related to replacement (see Definition 3.1); indeed, we can construct replacements for independent sets (and therefore a representative set) by specific substitutions. We start by stating several lemmas that will be used in the proof of Lemma 3.8. The first lemma refers to a generalized exchange property of matroids.
Lemma 4.1.
Let be a matroid, , and such that . Then there is such that .
Proof.
By Observation 2.1, there is such that . Then,
| (12) |
The first inequality holds since and . Recall that ; also, by the hereditary property of , . Therefore, by (12) and the exchange property of , there is such that . As , it follows that , thus . Now, assume towards contradiction that ; then, since and . As , by the hereditary property of it follows that . Contradiction. Hence, and it follows that and . ∎
The next lemma gives a general property of minimum bases of matroids.
Lemma 4.2.
Given a matroid and a weight function , let be a minimum basis of w.r.t. . Then, for any it holds that .
Proof.
Let . Assume towards contradiction that . Then, by Observation 2.1 there is such that ; let . Note that . Hence, as and is a basis of , we have that is a basis of (since all bases have the same cardinality; see, e.g., (39.2) in [21]). Noting that , and , there is such that . As and it holds that , and it follows that . Therefore,
| (13) |
By (13), we have that is a basis of satisfying . Contradiction (to the minimality of w.r.t. ). ∎
In the next lemma we consider a simple property of bases of union matroids.
Lemma 4.3.
Let be matroids such that ; also, let be a weight function, and a minimum basis of w.r.t. . Then, for all , is a minimum basis of w.r.t. .111With a slight abuse of notation we use also for the restriction of on .
Proof.
Let . For all , it holds that is not an independent set of since otherwise is an independent set of by Definition 2.2, contradicting that is a basis of ; we conclude that is a basis of . Assume towards contradiction that there is a basis of the matroid such that . As , by Definition 2.2 it follows that is a basis of the matroid . In addition,
We reach a contradiction since is a minimum basis w.r.t. of . ∎
We now prove Lemma 3.8 using several auxiliary lemmas. For the remainder of this section, let be a BMI instance, , , and the value from Step 1 of Algorithm 1. For the next lemma, recall the sets for were defined in (5).
Lemma 4.4.
For all it holds that is a minimum basis w.r.t. of the matroid , where .
Proof.
Lemma 4.5.
For all there is exactly one such that .
Proof.
Let . Observe that:
| (14) |
The first inequality holds since . The second and third inequalities are because is the value of a -approximation for the optimum of ; thus, . The last inequality is because is a solution of . In addition, observe that for it holds that and that for it holds that . Hence, because , by (14), there is exactly one such that ; thus, by (5) it holds that and for . ∎
For the proof of Lemma 3.8, we define a substitution of some independent set. The first two properties of substitution of some are identical to the first two properties in the definition of a replacement of . However, we require that a substitution preserves the number of profitable elements in from each profit class, and that a substitution must be disjoint to the set of non-profitable elements in .
Definition 4.6.
For and , we say that is a substitution of if the following holds.
-
1.
.
-
2.
.
-
3.
For all it holds that .
-
4.
.
Lemma 4.7.
For all there is a substitution of such that .
In the proof of Lemma 4.7, we assume towards a contradiction that there is no substitution for some which is a subset of . To reach a contradiction, we take a substitution of with maximal number of elements from and show that using Lemma 4.1 and Lemma 4.2 we can create a substitution with more elements from by replacing an element from by an element from .
Proof of Lemma 4.7.
Let and let be a substitution of such that is maximal among all substitutions of ; formally, let be all substitutions of and let . Since is in particular a substitution of it follows that , and thus is well defined. Assume towards a contradiction that there is ; then, by Definition 4.6 there is such that . Let .
Claim 4.8.
There is such that and .
Proof.
Let and . By Lemma 4.4 it holds that is a minimum basis w.r.t. of . Define . Then, since , it holds that by Lemma 4.2. In addition, by Definition 2.2 it holds that . Hence, . Therefore, by Lemma 4.1 there is such that . The claim follows since because .
Using Claim 4.8, let such that and . Then, the properties of Definition 4.6 are satisfied for by the following.
-
1.
by the definition of .
-
2.
because .
-
3.
for all it holds that because .
-
4.
where the inequality follows because and the equality is since is a substitution of .
By the above and Definition 4.6, it follows that is a substitution of ; that is, . Moreover,
| (15) |
The first inequality is because and . By (15) we reach a contradiction since we found a replacement of with more elements in than , which is defined as a replacement of with maximal number of elements in . Therefore, as required. ∎
We are now ready to prove Lemma 3.8. The proof follows by showing that for any a substitution of which is a subset of is in fact a replacement of .
Proof of Lemma 3.8: Let . By Lemma 4.7, has a substitution . Then,
| (16) | ||||
The third inequality is by (5) and Property 3 of Definition 4.6. The last inequality follows from Lemma 4.5. Therefore,
| (17) | ||||
The first equality follows by Property 4 of Definition 4.6. The first inequality is by (16). Now, satisfies Property 1 and 2 of Definition 3.1 by Properties 1, 2 of Definition 4.6, respectively. In addition, satisfies Property 3 of Definition 3.1 by (17). Finally, satisfies Property 4 of Definition 3.1 by
The first inequality holds since is a substitution of . The last equality follows from Lemma 4.5. We conclude that is a replacement of such that ; thus, is a representative set by Definition 3.2. By Step 1 of Algorithm 1 and Definition 2.2, it holds that ; thus, it follows that .
We now bound the time complexity of Algorithm FindRep. Step 1 can be computed in time using a PTAS for BMI with an error parameter (see, e.g., [9]). In addition, a membership oracle for the matroid in Step 1 can be implemented in time by Definition 2.2. Finally, the basis in Step 1 can be computed in time using a greedy matroid basis minimization algorithm [5]. Hence, the running time of the algorithm is . ∎
5 Discussion
In this paper we showed that the budgeted matroid independent set problem admits an EPTAS, thus improving upon the previously known schemes for the problem. The speed-up is achieved by replacing the exhaustive enumeration used by existing algorithms [9, 1, 4, 7] with efficient enumeration over subsets of a representative set whose size depends only on .
The representative set found by our algorithm is a minimum cost matroid basis for a union matroid. The union matroid is a union of a matroid for each profit class in the given instance. The basis itself can be easily found using a simple greedy procedure. The correctness relies on matroid exchange properties, optimality properties of minimal cost bases and a “profit gap” obtained by discarding a subset of elements from an optimal solution.
We note that our EPTAS, which directly exploits structural properties of our problem, already achieves substantial improvement over schemes developed for generalizations of BMI. Furthemore, we almost resolve the complexity status of the problem w.r.t approximation schemes. The existence of an FPTAS remains open.
The notion of representative sets can potentially be used to replace exhaustive enumeration in the PTASs for multiple knapsack with matroid constraint [7] and budgeted matroid intersection [1], leading to EPTASs for both problems. It seems that the construction of a representative set, as well as the ideas behind the main lemmas, can be adapted to the setting of the multiple knapsack with matroid problem. However, to derive an EPTAS for budgted matroid intersection, one needs to generalize first the concept of representative set, so it can be applied to matroid intersection. We leave this generalization as an interesting direction for follow-up work.
References
- [1] Berger, A., Bonifaci, V., Grandoni, F., Schäfer, G.: Budgeted matching and budgeted matroid intersection via the gasoline puzzle. Mathematical Programming 128(1), 355–372 (2011)
- [2] Caprara, A., Kellerer, H., Pferschy, U., Pisinger, D.: Approximation algorithms for knapsack problems with cardinality constraints. European Journal of Operational Research 123(2), 333–345 (2000)
- [3] Chekuri, C., Khanna, S.: A polynomial time approximation scheme for the multiple knapsack problem. SIAM Journal on Computing 35(3), 713–728 (2005)
- [4] Chekuri, C., Vondrák, J., Zenklusen, R.: Multi-budgeted matchings and matroid intersection via dependent rounding. In: Proceedings of the twenty-second annual ACM-SIAM symposium on Discrete Algorithms. pp. 1080–1097. SIAM (2011)
- [5] Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C.: Introduction to algorithms. MIT press (2022)
- [6] Das, S., Wiese, A.: On minimizing the makespan when some jobs cannot be assigned on the same machine. In: 25th Annual European Symposium on Algorithms, ESA. pp. 31:1–31:14 (2017)
- [7] Fairstein, Y., Kulik, A., Shachnai, H.: Modular and submodular optimization with multiple knapsack constraints via fractional grouping. In: 29th Annual European Symposium on Algorithms, ESA 2021, September 6-8, 2021, Lisbon, Portugal (Virtual Conference). pp. 41:1–41:16 (2021)
- [8] Grage, K., Jansen, K., Klein, K.M.: An EPTAS for machine scheduling with bag-constraints. In: The 31st ACM Symposium on Parallelism in Algorithms and Architectures. pp. 135–144 (2019)
- [9] Grandoni, F., Zenklusen, R.: Approximation schemes for multi-budgeted independence systems. In: European Symposium on Algorithms. pp. 536–548. Springer (2010)
- [10] Grötschel, M., Lovász, L., Schrijver, A.: Geometric algorithms and combinatorial optimization, vol. 2. Springer Science & Business Media (1993)
- [11] Heydrich, S., Wiese, A.: Faster approximation schemes for the two-dimensional knapsack problem. ACM Trans. Algorithms 15(4), 47:1–47:28 (2019)
- [12] Ibarra, O.H., Kim, C.E.: Fast approximation algorithms for the knapsack and sum of subset problems. Journal of the ACM (JACM) 22(4), 463–468 (1975)
- [13] Jansen, K.: Parameterized approximation scheme for the multiple knapsack problem. SIAM Journal on Computing 39(4), 1392–1412 (2010)
- [14] Jansen, K.: A fast approximation scheme for the multiple knapsack problem. In: SOFSEM 2012: Theory and Practice of Computer Science - 38th Conference on Current Trends in Theory and Practice of Computer Science, Špindlerův Mlýn, Czech Republic, January 21-27, 2012. Proceedings. pp. 313–324 (2012])
- [15] Jansen, K., Maack, M.: An EPTAS for scheduling on unrelated machines of few different types. Algorithmica 81(10), 4134–4164 (2019)
- [16] Jansen, K., Sinnen, O., Wang, H.: An EPTAS for scheduling fork-join graphs with communication delay. Theor. Comput. Sci. 861, 66–79 (2021)
- [17] Kellerer, H., Pferschy, U., Pisinger, D.: Knapsack problems. Springer (2004)
- [18] Kulik, A., Shachnai, H.: There is no EPTAS for two-dimensional knapsack. Information Processing Letters 110(16), 707–710 (2010)
- [19] Lawler, E.L.: Fast approximation algorithms for knapsack problems. Math. Oper. Res. 4(4), 339–356 (1979)
- [20] Pisinger, D., Toth, P.: Knapsack problems. In: Handbook of combinatorial optimization, pp. 299–428 (1998)
- [21] Schrijver, A.: Combinatorial optimization: polyhedra and efficiency, vol. 24. Springer (2003)
- [22] Schuurman, P., Woeginger, G.J.: Approximation schemes-a tutorial. Lectures on Scheduling (to appear) (2001)
- [23] Shachnai, H., Tamir, T.: Polynomial time approximation schemes. In: Handbook of Approximation Algorithms and Metaheuristics, Second Edition, Volume 1: Methologies and Traditional Applications, pp. 125–156 (2018)
- [24] Woeginger, G.J.: When does a dynamic programming formulation guarantee the existence of an FPTAS? In: Proceedings of the Tenth Annual ACM-SIAM Symposium on Discrete Algorithms, 17-19 January 1999, Baltimore, Maryland, USA. pp. 820–829 (1999)
Appendix A Solving the Linear Program
In this section we show how can be solved in polynomial time, thus proving Lemma 3.10.
The main idea is to show that the feasibility domain of is a well described polytope, and that a separation oracle for it can be implemented in polynomial time. Thus, using a known connection between separation and optimization, we obtain a polynomial-time algorithm which solves . Our initial goal, however, is to show that is indeed a linear program, for which we need a characterization of the matroid polytope via linear inequalities.
Let be a matroid. The matroid rank function of , , is defined by . That is, is the maximal size of an independent set which is also a subset of . The rank function is used in a characterization of a matroid polytope via a system of linear inequalities.
Theorem A.1 (Corollary 40.2b in [21]).
For any matroid , it holds that
Let be a BMI instance, and . By Theorem A.1 it holds that (6) is equivalent to the following linear program.
| s.t. | (18) | ||||
| (19) | |||||
| (20) | |||||
We follow the definitions and techniques presented in [10]. We say a polytope is of facet complexity if it is the solution set of a system of linear inequalities with rational coefficients, and the encoding length of each inequality in the system is at most . The following is an immediate consequence of the representation of as a linear program.
Observation A.2.
The feasibility region of is of facet complexity polynomial in .
A separating hyperplane between a polytope and is vector such that , where is the inner product of and . With a slight abuse of notation, we say that the constraint , where and , is a separation hyperplane between and if and for every . A separation oracle for a polytope is an oracle which receives as input, and either determines that or returns a separating hyperplane between and . We use the following known connection between separation and optimization.
Theorem A.3 (Thm 6.4.9 and Remark 6.5.2 in [10]).
There is an algorithm which given , and a separation oracle for a non-empty polytope of facet complexity , returns a vertex of such that in time polynomial in and .
Thus, to show can be solved in polynomial time, we need to show that a separation oracle for can be implemented in polymomial time. To this end, we use a known result for matroid polytopes.
Theorem A.4 (Thm 40.4 in [21]).
There is a polynomial time algorithm MatroidSeparator which given a subset of elements , a membership oracle for a matroid and either determines that or returns such that .
A polynomial-time implementation of a separation oracle for is now straightforward.
Lemma A.5.
There is an algorithm which given a BMI instance , , and implements a separation oracle for the feasibility region of in polynomial time.
Proof.
To implement a separation oracle, the algorithm first checks if the input satisfies constraints (18) and (20). If one of the constraints is violated, the algorithm returns the constraint as a separating hyperplane.
Next, the algorithm invokes MatroidSeparator (Theorem A.4) with the matroid and the point . If MatroidSeparator returns that then the algorithm returns that is in the feasibility region. Otherwise, the MatroidSeparator returns such that ; that is, a set for which (19) is violated. In this case, the algorithm returns as a separating hyperplane. Observe that for every in the feasibility region of , it holds that
where the first inequality is by (19). Thus, is indeed a separating hyperplane.
Clearly, the separating hyperplanes returned by the algorithm are indeed separating hyperplanes. Furthermore, if the algorithm asserts that is in the feasibility region then constraints (18) and (20) hold as those were explicitly checked, and (19) holds by (Theorem A.4 and Theorem A.1). That is, is indeed in the feasibility region of . The algorithm runs in polynomial-time as each of its steps can be implemented in polynomial-time. ∎
Proof of Lemma 3.10.
Observe that the vector is in the feasibility region of , and thus the feasibility region is not empty. By Theorem A.3 and Observation A.2, there is an algorithm which finds an optimal basic solution for using a polynomial number of operations and calls for a separation oracle. By Lemma A.5, the separation oracle can be implemented in polynomial time as well. Thus, an optimal basic solution for can be found in time polynomial in . ∎