An efficient descent method for locally Lipschitz multiobjective optimization problems

Bennet Gebken Department of Mathematics, Paderborn University, Germany Sebastian Peitz Department of Mathematics, Paderborn University, Germany

Abstract

In this article, we present an efficient descent method for locally Lipschitz continuous multiobjective optimization problems (MOPs). The method is realized by combining a theoretical result regarding the computation of descent directions for nonsmooth MOPs with a practical method to approximate the subdifferentials of the objective functions. We show convergence to points which satisfy a necessary condition for Pareto optimality. Using a set of test problems, we compare our method to the multiobjective proximal bundle method by Mäkelä. The results indicate that our method is competitive while being easier to implement. While the number of objective function evaluations is larger, the overall number of subgradient evaluations is lower. Finally, we show that our method can be combined with a subdivision algorithm to compute entire Pareto sets of nonsmooth MOPs.

1 Introduction

In many scenarios in real life, the problem of optimizing multiple objectives at the same time arises. In engineering for example, one often wants to steer a physical system as close as possible to a desired state while minimizing the required energy cost at the same time. These problems are called multiobjective optimization problems (MOPs) and generally do not possess a single optimal solution. Instead, the solution is the set of all optimal compromises, the so-called Pareto set containing all Pareto optimal points. Due to this, the numerical computation of solutions to MOPs is more challenging than to single-objective problems. On top of that, there are numerous applications where the objectives are nonsmooth, for example contact problems in mechanics, which adds to the difficulty. In this article, we will address both difficulties combined by considering nonsmooth MOPs.

When addressing the above-mentioned difficulties, i.e., multiple objectives and nonsmoothness, separately, there exists a large number solution methods. For smooth MOPs, the most popular methods include evolutionary [9, 10] and scalarization methods [27]. Additionally, some methods from single-objective optimization have been generalized, like gradient descent methods [13, 30, 14] and Newton’s method [12]. For the nonsmooth single-objective case, commonly used methods include subgradient methods [31], bundle methods [20] and gradient sampling methods [3]. More recently, in [22], a generalization of the steepest descent method to the nonsmooth case was proposed, which is based on an efficient approximation of the subdifferential of the objective function. For nonsmooth multiobjective optimization, the literature is a lot more scarce. Since classical scalarization approaches do not require the existence of gradients, they can still be used. In [1], a generalization of the steepest descent method was proposed for the case when the full subdifferentials of the objectives are known, which is rarely the case in practice. In [2, 7], the subgradient method was generalized to the multiobjective case, but both articles report that their method is not suitable for real life application due to inefficiency. In [25] (see also [18, 23]), a multiobjective version of the proximal bundle method was proposed, which currently appears to be the most efficient solver.

In this article, we develop a new descent method for locally Lipschitz continuous MOPs by combining the descent direction from [1] with the approximation of the subdifferentials from [22]. In [1] it was shown that the element with the smallest norm in the negative convex hull of the subdifferentials of the objective functions is a common descent direction for all objectives. In [22], the subdifferential of the objective function was approximated by starting with a single subgradient and then systematically computing new subgradients until the element with the smallest norm in the convex hull of all subgradients is a direction of (sufficient) descent. Combining both approaches yields a descent direction for locally Lipschitz MOPs and together with an Armijo step length, we obtain a descent method. We show convergence to points which satisfy a necessary condition for Pareto optimality. Using a set of test problems, we compare the performance of our method to the multiobjective proximal bundle method from [25]. The results indicate that our method is inferior in terms of function evaluations, but superior in terms of subgradient evaluations.

The structure of this article is as follows: we start with a short introduction to nonsmooth and multiobjective optimization in Section 2. In Section 3, we derive our descent method by replacing the Clarke subdifferential for the computation of the descent direction by the Goldstein $\varepsilon$ -subdifferential and then showing how the latter can be efficiently approximated. In Section 4, we apply our descent method to numerical examples. We first visualize and discuss the typical behavior of our method before comparing it to the multiobjective proximal bundle method from [25] using a set of test problems. Afterwards, we show how our method can be combined with a subdivision algorithm to approximate entire Pareto sets. Finally, in Section 5, we draw a conclusion and discuss possible future work.

2 Nonsmooth multiobjective optimization

We consider the nonsmooth multiobjective optimization problem

\displaystyle\min_{x\in\mathbb{R}^{n}}f(x)=\min_{x\in\mathbb{R}^{n}}\begin{pmatrix}f_{1}(x)\\ \vdots\\ f_{k}(x)\end{pmatrix},

(MOP)

where $f:\mathbb{R}^{n}\rightarrow\mathbb{R}^{k}$ is the objective vector with components $f_{i}:\mathbb{R}^{n}\rightarrow\mathbb{R}$ , $i\in\{1,...,k\}$ , called objective functions. We assume the objective functions to be locally Lipschitz continuous, i.e., for each $i\in\{1,...,k\}$ and $x\in\mathbb{R}^{n}$ , there is some $L_{i}>0$ and $\varepsilon>0$ with

\displaystyle|f_{i}(y)-f_{i}(z)|\leq L_{i}\|y-z\|\quad\forall y,z\in\{y\in\mathbb{R}^{n}:\|x-y\|<\varepsilon\},

where $\|\cdot\|$ denotes the Euclidean norm in $\mathbb{R}^{n}$ . Since (MOP) is an optimization problem with a vector-valued objective function, the classical concept of optimality from the scalar case can not directly be conveyed. Instead, we are looking for the Pareto set, which is defined in the following way:

Definition 2.1.

A point $x\in\mathbb{R}^{n}$ is called Pareto optimal, if there is no $y\in\mathbb{R}^{n}$ such that

	$\displaystyle f_{i}(y)$	$\displaystyle\leq f_{i}(x)\quad\forall i\in\{1,...,k\},$
	$\displaystyle f_{j}(y)$	$\displaystyle<f_{j}(x)\quad\text{for some }j\in\{1,...,k\}.$

The set of all Pareto optimal points is the Pareto set.

In practice, to check if a given point is Pareto optimal, we need optimality conditions. In the smooth case, there are the well-known KKT conditions (cf. [27]), which are based on the gradients of the objective functions. In case the objective functions are merely locally Lipschitz, the KKT conditions can be generalized using the concept of subdifferentials. In the following, we will recall the required definitions and results from nonsmooth analysis. For a more detailed introduction, we refer to [6].

Definition 2.2.

Let $\Omega_{i}\subseteq\mathbb{R}^{n}$ be the set of points where $f_{i}$ is not differentiable. Then

	$\displaystyle\partial f_{i}(x)=\operatorname*{conv}(\{\xi\in\mathbb{R}^{n}:$	$\displaystyle\exists(x_{j})_{j}\in\mathbb{R}^{n}\setminus\Omega_{i}\text{ with }x_{j}\rightarrow x\text{ and }$
		$\displaystyle\nabla f_{i}(x_{j})\rightarrow\xi\text{ for }j\rightarrow\infty\})$

is the (Clarke) subdifferential of $f_{i}$ in $x$ . $\xi\in\partial f_{i}(x)$ is a subgradient.

It is easy to see that if $f_{i}$ is continuously differentiable, then the Clarke subdifferential is the set containing only the gradient of $f_{i}$ . We will later use the following technical result on some properties of the Clarke subdifferential (cf. [6], Prop. 2.1.2).

Lemma 2.3.

$\partial f_{i}(x)$ is nonempty, convex and compact.

Using the subdifferential, we can state a necessary optimality condition for locally Lipschitz MOPs (cf. [24], Thm. 12).

Theorem 2.4.

Let $x\in\mathbb{R}^{n}$ be Pareto optimal. Then

\displaystyle 0\in\operatorname*{conv}\left(\bigcup_{i=1}^{k}\partial f_{i}(x)\right).

(1)

In the smooth case, (1) reduces to the classical multiobjective KKT conditions. Note that in contrast to the smooth case, the optimality condition (1) is numerically challenging to work with, as subdifferentials are difficult to compute. Thus, in numerical methods, (1) is only used implicitly.

The method we are presenting in this paper is a descent method, which means that, starting from a point $x_{1}\in\mathbb{R}^{n}$ , we want to generate a sequence $(x_{j})_{j}\in\mathbb{R}^{n}$ in which each point is an improvement over the previous point. This is done by computing directions $v_{j}\in\mathbb{R}^{n}$ and step lengths $t_{j}\in\mathbb{R}^{>0}$ such that $x_{j+1}=x_{j}+t_{j}v_{j}$ and

\displaystyle f_{i}(x_{j+1})<f_{i}(x_{j})\quad\forall j\in\mathbb{N},\ i\in\{1,...,k\}.

For the computation of $v_{j}$ , we recall the following basic result from convex analysis that forms the theoretical foundation for descent methods in the presence of multiple (sub)gradients. Let $\|.\|$ be the Euclidean norm in $\mathbb{R}^{n}$ .

Theorem 2.5.

Let $W\subseteq\mathbb{R}^{n}$ be convex and compact and

\displaystyle\bar{v}:=\operatorname*{arg\,min}_{\xi\in-W}\|\xi\|^{2}.

(2)

Then either $\bar{v}\neq 0$ and

\displaystyle\langle\bar{v},\xi\rangle\leq-\|\bar{v}\|^{2}<0\quad\forall\xi\in W,

(3)

or $\bar{v}=0$ and there is no $v\in\mathbb{R}^{n}$ with $\langle v,\xi\rangle<0$ for all $\xi\in W$ .

Proof.

Since $\bar{v}$ is the projection of the origin onto the closed and convex set $-W$ , we have

		$\displaystyle 0\leq\langle-\xi-\bar{v},\bar{v}-0\rangle=-\langle\bar{v},\xi\rangle-\\|\bar{v}\\|^{2}$
	$\displaystyle\Leftrightarrow\quad$	$\displaystyle\langle\bar{v},\xi\rangle\leq-\\|\bar{v}\\|^{2}$

for all $\xi\in W$ (cf. [4], Lem.). In particular, if $\bar{v}\neq 0$ then $\langle\bar{v},\xi\rangle\leq-\|\bar{v}\|^{2}<0$ .

Conversely, $\bar{v}=0$ implies $0\in W$ , so in this case there can not be any $v\in\mathbb{R}^{n}$ with $\langle v,\xi\rangle<0$ for all $\xi\in W$ . ∎

Roughly speaking, Theorem 2.5 states that the element of minimal norm in the convex and compact set $-W$ is directionally opposed to all elements of $W$ . To be more precise, $\bar{v}$ is contained in the intersection of all half-spaces induced by elements of $-W$ . In the context of optimization, this result has several applications:

(i)

In the smooth, single-objective case, $W=\{\nabla f(x)\}$ trivially yields the classical steepest descent method.
(ii)

In the smooth, multiobjective case, $W=\operatorname*{conv}(\{\nabla f_{1}(x),...,\nabla f_{k}(x)\})$ yields the descent direction from [13] (after dualization) and [30].
(iii)

In the nonsmooth, single-objective case, $W=\partial f(x)$ yields the descent direction from [6], Prop. 6.2.4.
(iv)

In the nonsmooth, multiobjective case, $W=\operatorname*{conv}\left(\bigcup_{i=1}^{k}\partial f_{i}(x)\right)$ yields the descent direction from [1].

In (i) and (ii), the solution of problem (2) is straightforward, since $W$ is a convex polytope with the gradients as vertices. In (iii), the solution of (2) is non-trivial due to the difficulty of computing the subdifferential. In subgradient methods [31], the solution is approximated by using a single subgradient instead of the entire subdifferential. As a result, it can not be guaranteed that the solution is a descent direction and in particular, (2) can not be used as a stopping criterion. In gradient sampling methods [3], the subdifferential is approximated by the convex hull of gradients of the objective function in randomly sampled points around the current point. Due to the randomness, it can not be guaranteed that the resulting direction yields sufficient descent. Additionally, a check for differentiability of the objective is required, which can pose a problem [17]. In (iv), the solution of (2) gets even more complicated due to the presence of multiple subdifferentials. So far, the only methods that deal with (2) in this case are multiobjective versions of the subgradient method [2, 7], which were reported unsuitable for real life applications.

In the following section, we will describe a new way to compute descent directions for nonsmooth MOPs by systematically computing an approximation of $\operatorname*{conv}\left(\cup_{i=1}^{k}\partial f_{i}(x)\right)$ that is sufficient to obtain a ”good enough” descent direction from (2).

3 Descent method for nonsmooth MOPs

In this section, we will present a method to compute descent directions of nonsmooth MOPs that generalizes the method from [22] to the multiobjective case. As described in the previous section, when computing descent directions via Theorem 2.5, one has the problem of having to compute subdifferentials. Since these are difficult to come by in practice, we will instead replace $W$ in Theorem 2.5 by an approximation of $\operatorname*{conv}\left(\cup_{i=1}^{k}\partial f_{i}(x)\right)$ such that the resulting direction is guaranteed to have sufficient descent. To this end, we will first replace the Clarke subdifferential by the so-called $\varepsilon$ -subdifferential, and then take a finite approximation of the latter.

3.1 The epsilon-subdifferential

By definition, $\partial f_{i}(x)$ is the convex hull of the limits of the gradient of $f_{i}$ in all sequences near $x$ that converge to $x$ . Thus, if we evaluate $\nabla f_{i}$ in a number of points close to $x$ (where it is defined) and take the convex hull, we expect the resulting set to be an approximation of $\partial f_{i}(x)$ . To formalize this, we introduce the following definition [16, 21].

Definition 3.1.

Let $\varepsilon\geq 0$ , $x\in\mathbb{R}^{n}$ and $B_{\varepsilon}(x):=\{y\in\mathbb{R}^{n}:\|x-y\|\leq\varepsilon\}$ . Then

\displaystyle\partial_{\varepsilon}f_{i}(x):=\operatorname*{conv}\left(\bigcup_{y\in B_{\varepsilon}(x)}\partial f_{i}(y)\right)

is the (Goldstein) $\varepsilon$ -subdifferential of $f_{i}$ in $x$ . $\xi\in\partial_{\varepsilon}f_{i}(x)$ is an $\varepsilon$ -subgradient.

Note that $\partial_{0}f_{i}(x)=\partial f_{i}(x)$ and $\partial f_{i}(x)\subseteq\partial_{\varepsilon}f_{i}(x)$ . For $\varepsilon\geq 0$ we define for the multiobjective setting

\displaystyle F_{\varepsilon}(x):=\operatorname*{conv}\left(\bigcup_{i=1}^{k}\partial_{\varepsilon}f_{i}(x)\right).

To be able to choose $W=F_{\varepsilon}(x)$ in Theorem 2.5, we first need to establish some properties of $F_{\varepsilon}(x)$ .

Lemma 3.2.

$\partial_{\varepsilon}f_{i}(x)$ is nonempty, convex and compact. In particular, the same holds for $F_{\varepsilon}(x)$ .

Proof.

For $\partial_{\varepsilon}f_{i}(x)$ , this was shown in [16], Prop. 2.3. For $F_{\varepsilon}(x)$ , it then follows directly from the definition. ∎

We immediately get the following corollary from Theorems 2.4 and 2.5.

Corollary 3.3.

Let $\varepsilon\geq 0$ .

a)

If $x$ is Pareto optimal, then

$\displaystyle 0\in F_{\varepsilon}(x).$ (4)
b)

Let $x\in\mathbb{R}^{n}$ and

$\displaystyle\bar{v}:=\operatorname*{arg\,min}_{\xi\in-F_{\varepsilon}(x)}\|\xi\|^{2}.$ (5)

Then either $\bar{v}\neq 0$ and

$\displaystyle\langle\bar{v},\xi\rangle\leq-\|\bar{v}\|^{2}<0\quad\forall\xi\in F_{\varepsilon}(x),$ (6)

or $\bar{v}=0$ and there is no $v\in\mathbb{R}^{n}$ with $\langle v,\xi\rangle<0$ for all $\xi\in F_{\varepsilon}(x)$ .

The previous corollary states that when working with the $\varepsilon$ -subdifferential instead of the Clarke subdifferential, we still have a necessary optimality condition and a way to compute descent directions, although the optimality conditions are weaker and the descent direction has a less strong descent. This is illustrated in the following example.

Example 3.4.

Consider the locally Lipschitz function

\displaystyle f:\mathbb{R}^{2}\rightarrow\mathbb{R}^{2},\quad x\mapsto\begin{pmatrix}(x_{1}-1)^{2}+(x_{2}-1)^{2}\\ x_{1}^{2}+|x_{2}|\end{pmatrix}.

The set of nondifferentiable points of $f$ is $\mathbb{R}\times\{0\}$ . For $\varepsilon>0$ and $x\in\mathbb{R}^{2}$ we have

\displaystyle\nabla f_{1}(x)=\begin{pmatrix}2(x_{1}-1)\\ 2(x_{2}-1)\end{pmatrix}\quad\text{and}\quad\partial_{\varepsilon}f_{1}(x)=2B_{\varepsilon}(x)-\begin{pmatrix}2\\ 2\end{pmatrix}.

For $x\in\mathbb{R}\times\{0\}$ we have

\displaystyle\partial f_{2}(x)=\{2x_{1}\}\times[-1,1]\quad\text{and}\quad\partial_{\varepsilon}f_{2}(x)=\{2x_{1}+[-2\varepsilon,2\varepsilon]\}\times[-1,1].

Figure 1 shows the Clarke subdifferential (a), the $\varepsilon$ -subdifferential (b) for $\varepsilon=0.2$ and the corresponding sets $F_{\varepsilon}(x)$ for $x=(1.5,0)^{\top}$ .

Refer to caption — Figure 1: Clarke subdifferentials (a), $\varepsilon$ -subdifferentials (b) for $\varepsilon=0.2$ and the corresponding sets $F_{\varepsilon}(x)$ for $x=(1.5,0)^{\top}$ in Example 3.4.

Additionally, the corresponding solutions of (5) are shown. In this case, the predicted descent $-\|\bar{v}\|^{2}$ (cf. (3)) is approximately $-3.7692$ in (a) and $-2.4433$ in (b).

Figure 2 shows the same scenario for $x=(0.5,0)^{\top}$ .

Here, the Clarke subdifferential still yields a descent, while $\bar{v}=0$ for the $\varepsilon$ -subdifferential. In other words, $x$ satisfies the necessary optimality condition (4) but not (1).

The following lemma shows that for the direction from (5), there is a lower bound for a step size up to which we have guaranteed descent in each objective function $f_{i}$ .

Lemma 3.5.

Let $\varepsilon\geq 0$ and $\bar{v}$ be the solution of (5). Then

\displaystyle f_{i}(x+t\bar{v})\leq f_{i}(x)-t\|\bar{v}\|^{2}\quad\forall t\leq\frac{\varepsilon}{\|\bar{v}\|}.

Proof.

Let $t\leq\frac{\varepsilon}{\|\bar{v}\|}$ . Since $f_{i}$ is locally Lipschitz continuous on $\mathbb{R}^{n}$ , it is in particular Lipschitz continuous on an open set containing $x+[0,t]\bar{v}$ . By applying the mean value theorem (cf. [6], Thm. 2.3.7), we obtain

\displaystyle f_{i}(x+t\bar{v})-f_{i}(x)\in\langle\partial f_{i}(x+r\bar{v}),t\bar{v}\rangle

for some $r\in(0,t)$ . Since $\|x-(x+r\bar{v})\|=r\|\bar{v}\|<\varepsilon$ we have $\partial f_{i}(x+r\bar{v})\subseteq\partial_{\varepsilon}f_{i}(x)$ . This means that there is some $\xi\in\partial_{\varepsilon}f_{i}(x)$ such that

\displaystyle f_{i}(x+t\bar{v})-f_{i}(x)=t\langle\xi,\bar{v}\rangle.

Combined with (6) we obtain

		$\displaystyle f_{i}(x+t\bar{v})-f_{i}(x)\leq-t\\|\bar{v}\\|^{2}$
	$\displaystyle\Leftrightarrow\quad$	$\displaystyle f_{i}(x+t\bar{v})\leq f_{i}(x)-t\\|\bar{v}\\|^{2}.$

∎

In the following, we will describe how we can obtain a good approximation of (5) without requiring full knowledge of the $\varepsilon$ -subdifferentials.

3.2 Efficient computation of descent directions

In this part, we will describe how the solution of (5) can be approximated when only a single subgradient can be computed at every $x\in\mathbb{R}^{n}$ . Similar to the gradient sampling approach, the idea behind our method is to replace $F_{\varepsilon}(x)$ in (5) by the convex hull of a finite number of $\varepsilon$ -subgradients $\xi_{1},...,\xi_{m}\in F_{\varepsilon}(x)$ , $m\in\mathbb{N}$ . Since it is impossible to know a priori how many and which $\varepsilon$ -subgradients are required to obtain a good descent direction, we solve (5) multiple times in an iterative approach to enrich our approximation until a satisfying direction has been found. To this end, we have to specify how to enrich our current approximation $\operatorname*{conv}(\{\xi_{1},...,\xi_{m}\})$ and how to characterize an acceptable descent direction.

Let $W=\{\xi_{1},...,\xi_{m}\}\subseteq F_{\varepsilon}(x)$ and

\displaystyle\tilde{v}:=\operatorname*{arg\,min}_{v\in-\operatorname*{conv}(W)}\|v\|^{2}.

(7)

Let $c\in(0,1)$ . Motivated by Lemma 3.5, we regard $\tilde{v}$ as an acceptable descent direction, if

\displaystyle f_{i}\left(x+\frac{\varepsilon}{\|\tilde{v}\|}\tilde{v}\right)\leq f_{i}(x)-c\varepsilon\|\tilde{v}\|\quad\forall i\in\{1,...,k\}.

(8)

If the set $I\subseteq\{1,...,k\}$ for which (8) is violated is non-empty then we have to find a new $\varepsilon$ -subgradient $\xi^{\prime}\in F_{\varepsilon}(x)$ such that $W\cup\{\xi^{\prime}\}$ yields a better descent direction. Intuitively, (8) being violated means that the local behavior of $f_{i}$ , $i\in I$ , in $x$ in the direction $\tilde{v}$ is not sufficiently captured in $W$ . Thus, for each $i\in I$ , we expect that there exists some $t^{\prime}\in(0,\frac{\varepsilon}{\|\tilde{v}\|}]$ such that $\xi^{\prime}\in\partial f_{i}(x+t^{\prime}\tilde{v})$ improves the approximation of $F_{\varepsilon}(x)$ . This is proven in the following lemma.

Lemma 3.6.

Let $c\in(0,1)$ , $W=\{\xi_{1},...,\xi_{m}\}\subseteq F_{\varepsilon}(x)$ and $\tilde{v}$ be the solution of (7). If

\displaystyle f_{i}\left(x+\frac{\varepsilon}{\|\tilde{v}\|}\tilde{v}\right)>f_{i}(x)-c\varepsilon\|\tilde{v}\|,

then there is some $t^{\prime}\in(0,\frac{\varepsilon}{\|\tilde{v}\|}]$ and $\xi^{\prime}\in\partial f_{i}(x+t^{\prime}\tilde{v})$ such that

\displaystyle\langle\tilde{v},\xi^{\prime}\rangle>-c\|\tilde{v}\|^{2}.

(9)

In particular, $\xi^{\prime}\in F_{\varepsilon}(x)\setminus\operatorname*{conv}(W)$ .

Proof.

Assume that for all $t^{\prime}\in(0,\frac{\varepsilon}{\|\tilde{v}\|}]$ and $\xi^{\prime}\in\partial f_{i}(x+t^{\prime}\tilde{v})$ we have

\displaystyle\langle\tilde{v},\xi^{\prime}\rangle\leq-c\|\tilde{v}\|^{2}.

(10)

By applying the mean value theorem as in Lemma 3.5, we obtain

\displaystyle f_{i}\left(x+\frac{\varepsilon}{\|\tilde{v}\|}\tilde{v}\right)-f_{i}(x)\in\langle\partial f_{i}(x+r\tilde{v}),\frac{\varepsilon}{\|\tilde{v}\|}\tilde{v}\rangle

for some $r\in(0,\frac{\varepsilon}{\|\tilde{v}\|})$ . This means that there is some $\xi^{\prime}\in\partial f_{i}(x+r\tilde{v})$ such that

\displaystyle f_{i}\left(x+\frac{\varepsilon}{\|\tilde{v}\|}\tilde{v}\right)-f_{i}(x)=\langle\xi^{\prime},\frac{\varepsilon}{\|\tilde{v}\|}\tilde{v}\rangle=\frac{\varepsilon}{\|\tilde{v}\|}\langle\xi^{\prime},\tilde{v}\rangle.

By (10) it follows that

		$\displaystyle f_{i}\left(x+\frac{\varepsilon}{\\|\tilde{v}\\|}\tilde{v}\right)-f_{i}(x)\leq-c\varepsilon\\|\tilde{v}\\|$
	$\displaystyle\Leftrightarrow\quad$	$\displaystyle f_{i}\left(x+\frac{\varepsilon}{\\|\tilde{v}\\|}\tilde{v}\right)\leq f_{i}(x)-c\varepsilon\\|\tilde{v}\\|,$

which is a contradiction. In particular, (3) yields $\xi^{\prime}\in F_{\varepsilon}(x)\setminus\operatorname*{conv}(W)$ . ∎

The following example visualizes the previous lemma.

Example 3.7.

Consider $f$ as in Example 3.4, $\varepsilon=0.2$ and $x=(0.75,0)^{\top}$ . The dashed lines in Figure 3 show the $\varepsilon$ -subdifferentials, $F_{\varepsilon}(x)$ and the resulting descent direction (cf. Figure 1 and 2).

Let $y=(0.94,-0.02)^{\top}$ . Then $\|x-y\|\approx 0.191\leq\varepsilon$ , so $y\in B_{\varepsilon}(x)$ and

	$\displaystyle\partial_{\varepsilon}f_{1}(x)$	$\displaystyle\supseteq\partial f_{1}(y)=\left\{\begin{pmatrix}-0.12\\ -2.04\end{pmatrix}\right\}=:\{\xi_{1}\},$
	$\displaystyle\partial_{\varepsilon}f_{2}(x)$	$\displaystyle\supseteq\partial f_{2}(y)=\left\{\begin{pmatrix}1.88\\ -1\end{pmatrix}\right\}=:\{\xi_{2}\}.$

Let $W:=\{\xi_{1},\xi_{2}\}$ and $\operatorname*{conv}(W)$ be the approximation of $F_{\varepsilon}(x)$ , shown as the solid line in Figure 3(a). Let $\tilde{v}$ be the solution of (7) for this $W$ and choose $c=0.25$ . Checking (8), we have

\displaystyle f_{2}\left(x+\frac{\varepsilon}{\|\tilde{v}\|}\tilde{v}\right)

\displaystyle\approx 0.6101>0.4748\approx f_{2}(x)-c\varepsilon\|\tilde{v}\|.

By Lemma 3.6, this means that there is some $t^{\prime}\in(0,\frac{\varepsilon}{\|\tilde{v}\|}]$ and $\xi^{\prime}\in\partial f_{2}(x+t^{\prime}\tilde{v})$ such that

\displaystyle\langle\tilde{v},\xi^{\prime}\rangle>-c\|\tilde{v}\|^{2}.

In this case, we can take for example $t^{\prime}=\frac{1}{2}\frac{\varepsilon}{\|\tilde{v}\|}$ , resulting in

	$\displaystyle\partial f_{2}(x+t^{\prime}v)\approx\left\{\begin{pmatrix}1.4077\\ 1\end{pmatrix}\right\}=:\{\xi^{\prime}\},$
	$\displaystyle\langle\tilde{v},\xi^{\prime}\rangle\approx 0.4172>-0.7696\approx-c\\|\tilde{v}\\|^{2}.$

Figure 3(b) shows the improved approximation $W\cup\{\xi^{\prime}\}$ and the resulting descent direction $\tilde{v}$ . By checking (8) for this new descent direction, we see that $\tilde{v}$ is acceptable. (Note that in general, a single improvement step like this will not be sufficient to reach an acceptable direction.)

Note that Lemma 3.6 only shows the existence of $t^{\prime}$ and $\xi^{\prime}$ without stating a way how to actually compute them. To this end, let $i$ be the index of an objective function for which (8) is not satisfied, define

\displaystyle h_{i}:\mathbb{R}\rightarrow\mathbb{R},\quad t\mapsto f_{i}(x+t\tilde{v})-f_{i}(x)+ct\|\tilde{v}\|^{2}

(11)

(cf. [22]) and consider Algorithm 1. If $f_{i}$ is continuously differentiable around $x$ , then (9) is equivalent to $h_{i}^{\prime}(t^{\prime})>0$ , i.e., $h_{i}$ being monotonically increasing around $t^{\prime}$ . Thus, the idea of Algorithm 1 is to find some $t$ such that $h_{i}$ is monotonically increasing around $t$ , while checking if (9) is satisfied for a subgradient $\xi\in f_{i}(x+t\tilde{v})$ .

Algorithm 1 Compute new subgradient

0: Current point

x\in\mathbb{R}^{n}

, direction

\tilde{v}

, tolerance

\varepsilon

, Armijo parameter

c\in(0,1)

1: Set

a=0

b=\frac{\varepsilon}{\|\tilde{v}\|}

and

t=\frac{a+b}{2}

2: Compute

\xi^{\prime}\in\partial f_{i}(x+t\tilde{v})

3: If

\langle\tilde{v},\xi^{\prime}\rangle>-c\|\tilde{v}\|^{2}

then stop.

4: If

h_{i}(b)>h_{i}(t)

then set

a=t

. Otherwise set

b=t

5: Set

t=\frac{a+b}{2}

and go to step 2.

Although in the general setting, we can not guarantee that Algorithm 1 yields a subgradient satisfying (9), we can at least show that after finitely many iterations, a factor $t$ is found such that $\partial f_{i}(x+t\tilde{v})$ contains a subgradient that satisfies (9).

Lemma 3.8.

Let $(t_{k})_{k}$ be the sequence generated in Algorithm 1. If $(t_{k})_{k}$ is finite, then some $\xi^{\prime}$ was found such that (9) is satisfied. If $(t_{k})_{k}$ is infinite, then it converges to some $\bar{t}\in[0,\frac{\varepsilon}{\|\tilde{v}\|}]$ such that there is some $\xi^{\prime}\in\partial f_{i}(x+\bar{t}\tilde{v})$ which satisfies (9). Additionally, there is some $N\in\mathbb{N}$ such that for all $k>N$ there is some $\xi^{\prime}\in\partial f_{i}(x+t_{k}\tilde{v})$ satisfying (9).

Proof.

Let $(t_{k})_{k}$ be finite with last element $\bar{t}\in(0,\frac{\varepsilon}{\|\tilde{v}\|})$ . Then Algorithm 1 must have stopped in step 3, i.e., some $\xi^{\prime}\in\partial f_{i}(x+\bar{t}\tilde{v})$ satisfying (9) was found.
Now let $(t_{k})_{k}$ be infinite. By construction, $(t_{k})_{k}$ is a Cauchy sequence in the compact set $[0,\frac{\varepsilon}{\|\tilde{v}\|}]$ , so it has to converge to some $\bar{t}\in[0,\frac{\varepsilon}{\|\tilde{v}\|}]$ . Additionally, since (8) is violated for the index $i$ by assumption, we have

\displaystyle h_{i}(0)=0\quad\text{and}\quad h_{i}\left(\frac{\varepsilon}{\|\tilde{v}\|}\right)>0.

Let $(a_{k})_{k}$ and $(b_{k})_{k}$ be the sequences corresponding to $a$ and $b$ in Algorithm 1 (at the start of each iteration). Then $h_{i}(a_{k})<h_{i}(b_{k})$ for all $k\in\mathbb{N}$ . Thus, by the mean value theorem, there has to be some $r_{k}\in(a_{k},b_{k})$ such that

\displaystyle 0<h_{i}(b_{k})-h_{i}(a_{k})\in\langle\partial h_{i}(r_{k}),b_{k}-a_{k}\rangle=\partial h_{i}(r_{k})(b_{k}-a_{k}).

In particular, $\lim_{k\rightarrow\infty}r_{k}=\bar{t}$ and since $a_{k}<b_{k}$ , $\partial h_{i}(r_{k})\cap\mathbb{R}^{>0}\neq\emptyset$ for all $k\in\mathbb{N}$ . By upper semicontinuity of $\partial h$ there must be some $\theta\in\partial h_{i}(\bar{t})$ with $\theta>0$ . By the chain rule, we have

\displaystyle 0<\theta\in\partial h_{i}(\bar{t})\subseteq\langle\tilde{v},\partial f_{i}(x+\bar{t}\tilde{v})\rangle+c\|\tilde{v}\|^{2}.

(12)

Thus, there must be some $\xi^{\prime}\in\partial f_{i}(x+\bar{t}\tilde{v})$ with

		$\displaystyle 0<\langle\tilde{v},\xi^{\prime}\rangle+c\\|\tilde{v}\\|^{2}$
	$\displaystyle\Leftrightarrow\quad$	$\displaystyle\langle\tilde{v},\xi^{\prime}\rangle>-c\\|\tilde{v}\\|^{2}.$

By upper semicontinuity of $\partial h$ it also follows that there is some $N\in\mathbb{N}$ such that $\partial h_{i}(t_{k})\cap\mathbb{R}^{>0}\neq\emptyset$ for all $k>N$ . Applying the same argument as above completes the proof. ∎

In the following remark, we will briefly discuss the implication of Lemma 3.8 for practical use of Algorithm 1.

Remark 3.9.

Let $N\in\mathbb{N}$ be as in Lemma 3.8.

a)

Note that if $k>N$ and $h$ is differentiable in $t_{k}$ , then we have

$\displaystyle 0<\nabla h_{i}(t_{k})=\langle\tilde{v},\nabla f_{i}(x+t_{k}\tilde{v})\rangle+c\|\tilde{v}\|^{2},$

i.e., the stopping criterion in step 3 is satisfied. Thus, if Algorithm 1 generates an infinite sequence, $h$ must be nonsmooth in $t_{k}$ for all $k>N$ . In particular, $f_{i}$ must be nonsmooth in $x+t_{k}\tilde{v}$ for all $k>N$ .
b)

If $f$ is regular (cf. [6], Def. 2.3.4), then equality holds when applying the chain rule to $h$ (cf. [6], Thm. 2.3.10), i.e.,

$\displaystyle\partial h_{i}(t_{k})=\langle\tilde{v},\partial f_{i}(x+t_{k}\tilde{v})\rangle+c\|\tilde{v}\|^{2}.$

Thus, if Algorithm 1 generates an infinite sequence, then for all $k>N$ there must be both positive and negative elements in $\partial h_{i}(t_{k})$ . By convexity of $\partial h_{i}(t_{k})$ , this implies that $0\in\partial h_{i}(t_{k})$ for all $k>N$ , i.e., $h$ must have infinitely many (nonsmooth) stationary points in $[0,\frac{\varepsilon}{\|\tilde{v}\|}]$ .

Motivated by the previous remark, we will from now on assume that Algorithm 1 stops after finitely many iterations and thus yields a new subgradient satisfying (9). We can use this method of finding new subgradients to construct an algorithm that computes descent directions of nonsmooth MOPs, namely Algorithm 2.

Algorithm 2 Compute descent direction

0: Current point

x\in\mathbb{R}^{n}

, tolerances

\varepsilon,\delta>0

, Armijo parameter

c\in(0,1)

1: Compute

\xi^{i}_{1}\in\partial_{\varepsilon}f_{i}(x)

for all

i\in\{1,...,k\}

. Set

W_{1}=\{\xi^{1}_{1},...,\xi^{k}_{1}\}

and

l=1

2: Compute

v_{l}=\operatorname*{arg\,min}_{v\in-\operatorname*{conv}(W_{l})}\|v\|^{2}

3: If

\|v_{l}\|\leq\delta

then stop.

4: Find all objective functions for which there is insufficient descent:

\displaystyle I_{l}=\left\{j\in\{1,...,k\}:f_{j}\left(x+\frac{\varepsilon}{\|v_{l}\|}v_{l}\right)>f_{j}(x)-c\varepsilon\|v_{l}\|\right\}.

I_{l}=\emptyset

then stop.

5: For each

j\in I_{l}

, compute

t\in(0,\frac{\varepsilon}{\|v_{l}\|}]

and

\xi^{j}_{l}\in\partial f_{j}(x+tv_{l})

such that

\displaystyle\langle v_{l},\xi^{j}_{l}\rangle>-c\|v_{l}\|^{2}

via Algorithm 1.

6: Set

W_{l+1}=W_{l}\cup\{\xi^{j}_{l}:j\in I_{l}\}

l=l+1

and go to step 2.

The following theorem shows that Algorithm 2 stops after a finite number of iterations and produces an acceptable descent direction (cf. (8)).

Theorem 3.10.

Algorithm 2 terminates. In particular, if $\tilde{v}$ is the last element of $(v_{l})_{l}$ , then either $\|\tilde{v}\|\leq\delta$ or $\tilde{v}$ is an acceptable descent direction, i.e.,

\displaystyle f_{i}\left(x+\frac{\varepsilon}{\|\tilde{v}\|}\tilde{v}\right)\leq f_{i}(x)-c\varepsilon\|\tilde{v}\|\quad\forall i\in\{1,...,k\}.

Proof.

Assume that Algorithm 2 does not terminate, i.e., $(v_{l})_{l\in\mathbb{N}}$ is an infinite sequence. Let $l>1$ and $j\in I_{l-1}$ . Since $\xi^{j}_{l-1}\in W_{l}$ and $-v_{l-1}\in W_{l-1}\subseteq W_{l}$ we have

$\displaystyle\\|v_{l}\\|^{2}$	$\displaystyle\leq\\|-v_{l-1}+s(\xi^{j}_{l-1}+v_{l-1})\\|^{2}$
	$\displaystyle=\\|v_{l-1}\\|^{2}-2s\langle v_{l-1},\xi^{j}_{l-1}+v_{l-1}\rangle+s^{2}\\|\xi^{j}_{l-1}+v_{l-1}\\|^{2}$
	$\displaystyle=\\|v_{l-1}\\|^{2}-2s\langle v_{l-1},\xi^{j}_{l-1}\rangle-2s\\|v_{l-1}\\|^{2}+s^{2}\\|\xi^{j}_{l-1}+v_{l-1}\\|^{2}$	(13)

for all $s\in[0,1]$ . Since $j\in I_{l-1}$ we must have

\displaystyle\langle v_{l-1},\xi^{j}_{l-1}\rangle>-c\|v_{l-1}\|^{2}

(14)

by step 5. Let $L$ be a common Lipschitz constant of all $f_{i}$ , $i\in\{1,...,k\}$ , on the closed $\varepsilon$ -ball $B_{\varepsilon}(x)$ around $x$ . Then by [6], Prop. 2.1.2, and the definition of the $\varepsilon$ -subdifferential, we must have $\|\xi\|\leq L$ for all $\xi\in F_{\varepsilon}(x)$ . So in particular,

\displaystyle\|\xi^{j}_{l-1}+v_{l-1}\|\leq 2L.

(15)

Combining (3.2) with (14) and (15) yields

	$\displaystyle\\|v_{l}\\|^{2}$	$\displaystyle<\\|v_{l-1}\\|^{2}-2sc\\|v_{l-1}\\|^{2}-2s\\|v_{l-1}\\|^{2}+4s^{2}L^{2}$
		$\displaystyle=\\|v_{l-1}\\|^{2}-2s(c+1)\\|v_{l-1}\\|^{2}+4s^{2}L^{2}.$

Let $s:=\frac{c+1}{4L^{2}}\|v_{l-1}\|^{2}$ . Since $c+1\in(1,2)$ and $\|v_{l-1}\|\leq L$ we have $s\in(0,1)$ . We obtain

	$\displaystyle\\|v_{l}\\|^{2}$	$\displaystyle<\\|v_{l-1}\\|^{2}-2\frac{(c+1)^{2}}{4L^{2}}\\|v_{l-1}\\|^{4}+\frac{(c+1)^{2}}{4L^{2}}\\|v_{l-1}\\|^{4}$
		$\displaystyle=\left(1-\frac{(c+1)^{2}}{4L^{2}}\\|v_{l-1}\\|^{2}\right)\\|v_{l-1}\\|^{2}.$

Since Algorithm 2 did not terminate, it holds $\|v_{l-1}\|>\delta$ . It follows that

\displaystyle\|v_{l}\|^{2}<\left(1-\left(\frac{c+1}{2L}\delta\right)^{2}\right)\|v_{l-1}\|^{2}.

Let $r=1-\left(\frac{c+1}{2L}\delta\right)^{2}$ . Note that we have $\delta<\|v_{l}\|\leq L$ for all $l\in\mathbb{N}$ , so $r\in(0,1)$ . Additionally, $r$ does not depend on $l$ , so we have

\displaystyle\|v_{l}\|^{2}<r\|v_{l-1}\|^{2}<r^{2}\|v_{l-1}\|^{2}<...<r^{l-1}\|v_{1}\|^{2}\leq r^{l-1}L^{2}.

In particular, there is some $l$ such that $\|v_{l}\|\leq\delta$ , which is a contradiction. ∎

Remark 3.11.

The proof of Theorem 3.10 shows that for convergence of Algorithm 2, it would be sufficient to consider only a single $j\in I_{j}$ in step 5. Similarly, for the initial approximation $W_{1}$ , a single element from $\partial_{\varepsilon}f_{i}(x)$ for any $i\in\{1,...,k\}$ would be enough. A modification of either step can potentially reduce the number of executions of step 5 (i.e., Algorithm 1) in Algorithm 2 in case the $\varepsilon$ -subdifferentials of multiple objective functions are similar. Nonetheless, we will restrain the discussion in this article to Algorithm 2 as it is, since both modifications also introduce a bias towards certain objective functions, which we want to avoid.

To highlight the strengths of Algorithm 2, we will consider an example where standard gradient sampling approaches can fail to obtain a useful descent direction.

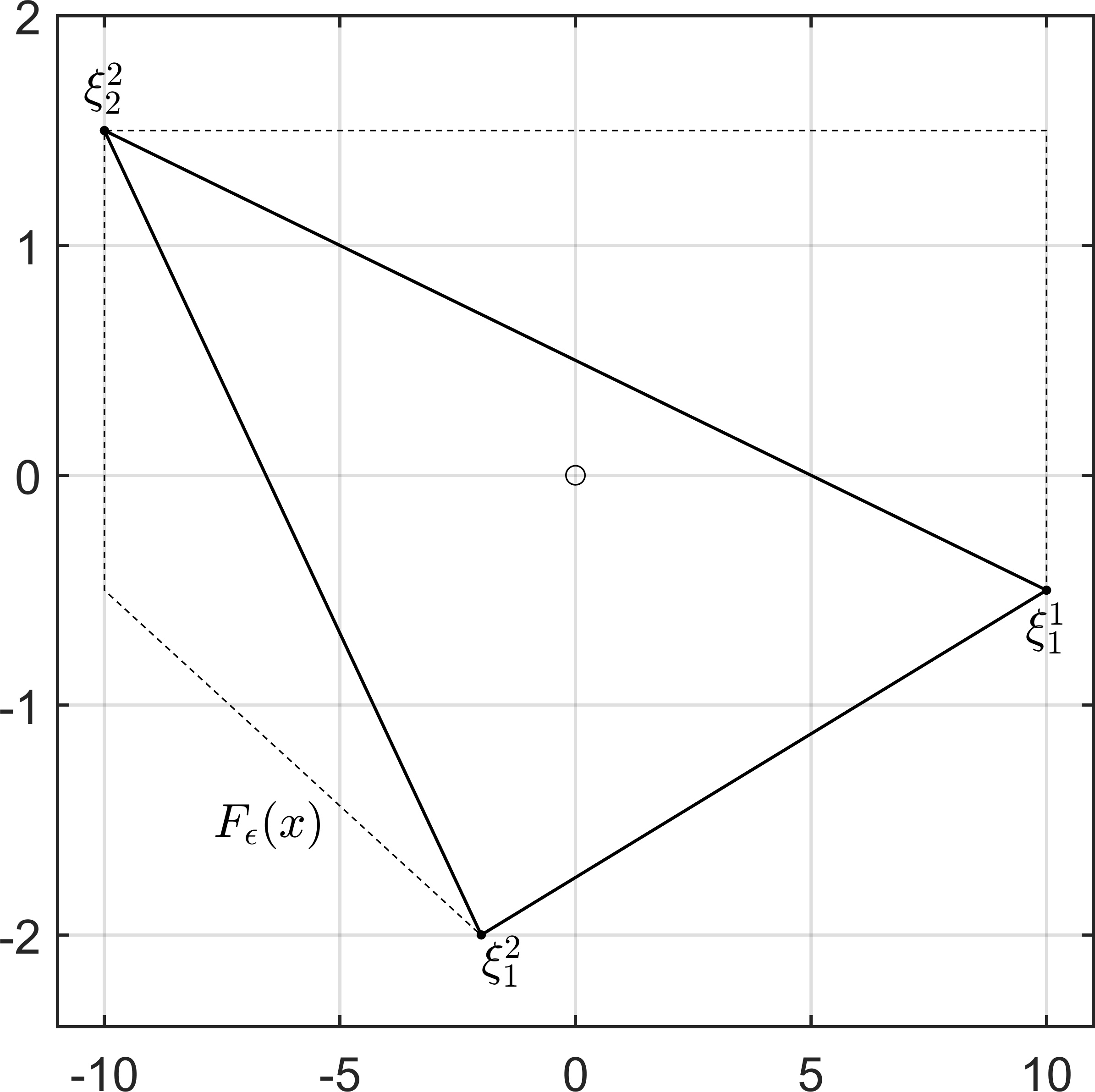
Example 3.12.

For $a,b\in\mathbb{R}\setminus\{0\}$ consider the locally Lipschitz function

\displaystyle f:\mathbb{R}^{2}\rightarrow\mathbb{R}^{2},\quad x\mapsto\begin{pmatrix}(x_{1}-1)^{2}+(x_{2}-1)^{2}\\ |x_{2}-a|x_{1}||+bx_{2}\end{pmatrix}.

The set of nondifferentiable points is

\displaystyle\Omega_{f}=(\{0\}\times\mathbb{R})\cup\{(\lambda,a|\lambda|)^{\top}:\lambda\in\mathbb{R}\},

separating $\mathbb{R}^{2}$ into four smooth areas (cf. Figure 4(a)). For large $a>0$ , the two areas above the graph of $\lambda\mapsto a|\lambda|$ become small, making it difficult to compute the subdifferential close to $(0,0)^{\top}$ .

Let $a=10$ , $b=0.5$ , $\varepsilon=10^{-3}$ and $x=(10^{-4},10^{-4})^{\top}$ . In this case, $(0,0)^{\top}$ is the minimal point of $f_{2}$ and

	$\displaystyle\partial_{\varepsilon}f_{2}(x)$	$\displaystyle=\operatorname*{conv}\left\{\begin{pmatrix}-a\\ b-1\end{pmatrix},\begin{pmatrix}a\\ b+1\end{pmatrix},\begin{pmatrix}a\\ b-1\end{pmatrix},\begin{pmatrix}-a\\ b+1\end{pmatrix}\right\}$
		$\displaystyle=\operatorname*{conv}\left\{\begin{pmatrix}-10\\ -0.5\end{pmatrix},\begin{pmatrix}10\\ 1.5\end{pmatrix},\begin{pmatrix}10\\ -0.5\end{pmatrix},\begin{pmatrix}-10\\ 1.5\end{pmatrix}\right\}.$

In particular, $0\in\partial_{\varepsilon}f_{2}(x)$ , so the descent direction with the exact $\varepsilon$ -subdifferentials from (5) is zero. When applying Algorithm 2 in $x$ , after two iterations we obtain

\displaystyle\tilde{v}=v_{2}\approx(0.118,1.185)\cdot 10^{-9},

i.e., $\|\tilde{v}\|\approx 1.191\cdot 10^{-11}$ . Thus, $x$ is correctly identified as (potentially) Pareto optimal. The final approximation $W_{2}$ of $F_{\varepsilon}(x)$ is

\displaystyle W_{2}=\left\{\xi^{1}_{1},\xi^{2}_{1},\xi^{2}_{2}\right\}=\left\{\begin{pmatrix}10\\ -0.5\end{pmatrix},\begin{pmatrix}-1.9998\\ -1.9998\end{pmatrix},\begin{pmatrix}-10\\ 1.5\end{pmatrix}\right\}.

The first two elements of $W_{2}$ are the gradients of $f_{1}$ and $f_{2}$ in $x$ from the first iteration of Algorithm 2, and the last element is the gradient of $f_{2}$ in $x^{\prime}=x+tv_{1}=(0.038,0.596)^{\top}\cdot 10^{-3}\in B_{\varepsilon}(x)$ from the second iteration. The result is visualized in Figure 4.

Building on Algorithm 2, it is now straightforward to construct the descent method for locally Lipschitz continuous MOPs given in Algorithm 3. In step 4, the classical Armijo backtracking line search was used (cf. [13]) for the sake of simplicity. Note that it is well defined due to step 4 in Algorithm 2.

Algorithm 3 Nonsmooth descent method

0: Initial point

x_{1}\in\mathbb{R}^{n}

, tolerances

\varepsilon,\delta>0

, Armijo parameters

c\in(0,1),t_{0}>0

1: Set

j=1

2: Compute a descent direction

v_{j}

via Algorithm 2.

3: If

\|v_{j}\|\leq\delta

then stop.

4: Compute

\displaystyle\bar{s}=\inf(\{s\in\mathbb{N}\cup\{0\}:f_{i}(x_{j}+2^{-s}t_{0}v_{j})\leq f_{i}(x_{j})-2^{-s}t_{0}c\|v_{j}\|^{2}\ \forall i\in\{1,...,k\}\})

and set

\bar{t}=\max(\{2^{-\bar{s}}t_{0},\frac{\varepsilon}{\|v_{j}\|}\})

5: Set

x_{j+1}=x_{j}+\bar{t}v_{j}

j=j+1

and go to step 2.

Since we introduced the two tolerances $\varepsilon$ (for the $\varepsilon$ -subdifferential) and $\delta$ (as a threshold for when we consider $\varepsilon$ -subgradients to be zero), we can not expect that Algorithm 3 computes points which satisfy the optimality condition (1). This is why we introduce the following definition, similar to the definition of $\varepsilon$ -stationarity from [3].

Definition 3.13.

Let $x\in\mathbb{R}^{n}$ , $\varepsilon>0$ and $\delta>0$ . Then $x$ is called $(\varepsilon,\delta)$ -critical, if

\displaystyle\min_{v\in-F_{\varepsilon}(\bar{x})}\|v\|\leq\delta.

It is easy to see that $(\varepsilon,\delta)$ -criticality is a necessary optimality condition for Pareto optimality, but a weaker one than (1). The following theorem shows that convergence in the sense of $(\varepsilon,\delta)$ -criticality is what we can expect from our descent method.

Theorem 3.14.

Let $(x_{j})_{j}$ be the sequence generated by Algorithm 3. Then either $(f_{i}(x_{j}))_{j}$ is unbounded below for each $i\in\{1,...,k\}$ , or $(x_{j})_{j}$ is finite with the last element being $(\varepsilon,\delta)$ -critical.

Proof.

Assume that $(x_{j})_{j}$ is infinite. Then $\|v_{j}\|>\delta$ for all $j\in\mathbb{N}$ . By step 4 and Lemma 3.5 we have

\displaystyle f_{i}(x_{j}+\bar{t}v_{j})-f_{i}(x_{j})\leq-\bar{t}\|v_{j}\|^{2}\leq-\varepsilon\|v_{j}\|<-\varepsilon\delta<0

for all $i\in\{1,...,k\}$ . This implies that $(f_{i}(x_{j}))_{j}$ is unbounded below for each $i\in\{1,...,k\}$ .
Now assume that $(x_{j})_{j}$ is finite, with $\bar{x}$ and $\bar{v}$ being the last elements of $(x_{j})_{j}$ and $(v_{j})_{j}$ , respectively. Since the algorithm stopped, we must have $\|\bar{v}\|\leq\delta$ . From the application of Algorithm 2 in step 2, we know that there must be some $\overline{W}\subseteq F_{\varepsilon}(\bar{x})$ such that $\bar{v}=\operatorname*{arg\,min}_{v\in-\overline{W}}\|v\|^{2}$ . This implies

\displaystyle\min_{v\in-F_{\varepsilon}(\bar{x})}\|v\|\leq\min_{v\in-\operatorname*{conv}(\overline{W})}\|v\|=\|\bar{v}\|\leq\delta.

∎

4 Numerical examples

In this section we will apply our nonsmooth descent method (Algorithm 3) to several examples. We will begin by discussing its typical behavior before comparing its performance to the multiobjective proximal bundle method [25]. Finally, we will combine our method with the subdivision algorithm [11] in order to approximate the entire Pareto set of nonsmooth MOPs.

4.1 Typical behavior

In smooth areas, the behavior of Algorithm 3 is almost identical to the behavior of the multiobjective steepest descent method [13]. The only difference stems from the fact that, unlike the Clarke subdifferential, the $\varepsilon$ -subdifferential does not reduce to the gradient when $f$ is continuously differentiable. As a result, Algorithm 3 may behave differently in points $x\in\mathbb{R}^{n}$ where

\displaystyle\max\{\|\nabla f_{i}(x)-\nabla f_{i}(y)\|:y\in B_{\varepsilon}(x),\ i\in\{1,...,k\}\}

is large. (If $f$ is twice differentiable, this can obviously be characterized in terms of second order derivatives.) Nevertheless, if $\varepsilon$ is chosen small enough, this difference can be neglected. Thus, in the following, we will focus on the behavior with respect to the nonsmoothness of $f$ .

To show the typical behavior of Algorithm 3, we consider the objective function

\displaystyle f:\mathbb{R}^{2}\rightarrow\mathbb{R}^{2},\quad x\mapsto\begin{pmatrix}\max\{x_{1}^{2}+(x_{2}-1)^{2}+x_{2}-1,-x_{1}^{2}-(x_{2}-1)^{2}+x_{2}+1\}\\ -x_{1}+2(x_{1}^{2}+x_{2}^{2}-1)+1.75|x_{1}^{2}+x_{2}^{2}-1|\end{pmatrix}

(16)

from [25] (combining Crescent from [19] and Mifflin 2 from [26]). The set of nondifferentiable points is $\Omega_{f}=S^{1}\cup(S^{1}+(0,1)^{\top})$ . We consider the starting points

\displaystyle x^{1}=(0,-0.3)^{\top},\quad x^{2}=(0.6,1.0)^{\top},\quad x^{3}=(-1,-0.2)^{\top},

the tolerances $\varepsilon=10^{-3}$ , $\delta=10^{-3}$ and the Armijo parameters $c=0.25$ , $t_{0}=1$ . The results are shown in Figure 5.

We will briefly go over the result for each starting point:

•

For $x^{1}$ , the sequence moves through the smooth area like the steepest descent method until a point is found with a distance less or equal $\varepsilon$ to the set of nondifferentiable points $\Omega_{f}$ . In that point, more than one $\varepsilon$ -subgradient is required to obtain a sufficient approximation of the $\varepsilon$ -subdifferentials. Since this part of $\Omega_{f}$ is Pareto optimal, no acceptable descent direction (cf. (8)) is found and the algorithm stops (in a $(\varepsilon,\delta)$ -critical point).
•

For $x^{2}$ , the sequence starts zig-zagging around the non-optimal part of $\Omega_{f}$ , since the points are too far away from $\Omega_{f}$ for the algorithm to notice the nondifferentiability. When a point is found with distance less or equal $\varepsilon$ to $\Omega_{f}$ , a better descent direction is found, breaking the zig-zagging motion.
•

For $x^{3}$ , the sequence has a similar zig-zagging motion to the previous case. The difference is that this time, the sequence moves along $\Omega_{f}$ until a Pareto optimal point in $\Omega_{f}$ is found.

As described above, the zig-zagging behavior when starting in $x^{2}$ is caused by the fact that $\varepsilon$ was too small for the method to notice the nondifferentiability. To circumvent problems like this and quickly move through problematic areas, it is possible to apply Algorithm 3 consecutively with decreasing values of $\varepsilon$ . The result is Algorithm 4. (A similar idea was implemented in [22].)

Algorithm 4

\varepsilon

-decreasing nonsmooth descent method

0: Initial point

x_{1}\in\mathbb{R}^{n}

, tolerances

\delta,\varepsilon_{1},...,\varepsilon_{K}>0

, Armijo parameters

c\in(0,1),t_{0}>0

1: Set

y_{1}=x_{1}

2: for

i=1,...,K

3: Apply Algorithm 3 with initial point

y_{i}

and tolerance

\varepsilon=\varepsilon_{i}

. Let

y_{i+1}

be the final element in the generated sequence.

4: end for

4.2 Comparison to the multiobjective proximal bundle method

We will now compare Algorithms 3 and 4 to the multiobjective proximal bundle method (MPB) by Mäkelä, Karmitsa and Wilppu from [25] (see also [23]). As test problems, we consider the 18 MOPs in Table 1, which are created on the basis of the scalar problems from [25]. Problems 1 to 15 are convex (and were also considered in [28]) and problems 16 to 18 are nonconvex. Due to their simplicity, we are able to differentiate all test problems by hand to obtain explicit formulas for the subgradients. For each test problem, we choose 100 starting points on a 10 $\times$ 10 grid in the corresponding area given in Table 1.

Table 1: Test problems (using objectives from [25])

Nr.	$f_{i}$	Area	Nr.	$f_{i}$	Area
1.	CB3, DEM	$[-3,3]^{2}$	10.	QL, LQ	$[-3,3]^{2}$
2.	CB3, QL	$[-3,3]^{2}$	11.	QL, Mifflin 1	$[-3,3]^{2}$
3.	CB3, LQ	$[0.5,1.5]^{2}$	12.	QL, Wolfe	$[-3,3]^{2}$
4.	CB3, Mifflin 1	$[-3,3]^{2}$	13.	LQ, Mifflin 1	$[0.5,1.5]\times[-0.5,1]$
5.	CB3, Wolfe	$[-3,3]^{2}$	14.	LQ, Wolfe	$[-3,3]^{2}$
6.	DEM, QL	$[-3,3]^{2}$	15.	Mifflin 1, Wolfe	$[-3,3]^{2}$
7.	DEM, LQ	$[-3,3]^{2}$	16.	Crescent, Mifflin 2	$[-0.5,1.5]^{2}$
8.	DEM, Mifflin 1	$[-3,3]^{2}$	17.	Mifflin 2, WF	$[-3,3]^{2}$
9.	DEM, Wolfe	$[-3,3]^{2}$	18.	Mifflin 2, SPIRAL	$[-3,3]^{2}$

For the MPB, we use the Fortran implementation from [23] with the default parameters. For Algorithm 3, we use $\varepsilon=10^{-3}$ , $\delta=10^{-3}$ , $c=0.25$ and $t_{0}=\max\{\|v_{j}\|^{-1},1\}$ (i.e., the initial step size $t_{0}$ is chosen depending on the norm of the descent direction $v_{j}$ in the current iteration). For Algorithm 4, we additionally use $\varepsilon_{1}=10^{-1}$ , $\varepsilon_{2}=10^{-2}$ , $\varepsilon_{3}=10^{-3}$ . By this choice of parameters, all three methods produce results of similar approximation quality.

To compare the performance of the three methods, we count the number of evaluations of objectives $f_{i}$ , their subgradients $\xi\in\partial f_{i}$ and the number of iterations (i.e., descent steps) needed. (This means that one call of $f$ will account for $k$ evaluations of objectives.) Since the MPB always evaluates all objectives and subgradients in a point, the value for the objectives and the subgradients are the same here. The results are shown in Table 2 and are discussed in the following.

Table 2: Performance of MPB, Algorithm 3 and Algorithm 4 for the test problems in Table 1 for

100

starting points

	# $f_{i}$			# $\partial f_{i}$			# Iter
Nr.	MPB	Alg. 3	Alg. 4	MPB	Alg. 3	Alg. 4	MPB	Alg. 3	Alg. 4
1.	1780	6924	7801	1780	1102	1751	761	492	695
2.	2522	14688	12263	2522	1906	2351	1151	842	914
3.	880	5625	6447	880	921	1534	340	448	662
4.	4416	103826	17664	4416	11774	3415	1832	4644	1242
5.	2956	30457	16877	2956	3479	3037	1377	1616	1161
6.	1640	8357	8684	1640	1209	1802	706	552	736
7.	1702	8736	8483	1702	1307	1832	723	595	739
8.	4226	8283	8620	4226	1318	1914	1204	582	759
9.	1828	8201	8794	1828	1194	1805	793	536	732
10.	1782	6799	7201	1782	1101	1722	684	543	733
11.	4426	52096	17594	4426	6311	3189	1964	2442	1206
12.	2482	15146	12446	2482	1992	2401	1140	967	1010
13.	2662	36570	9513	2662	4958	2247	1221	1692	787
14.	4264	95303	12227	4264	9524	2571	1774	4379	921
15.	3594	85936	15669	3594	9329	3124	1444	3963	1125
16.	2206	20372	11094	2206	2596	2400	884	1194	947
17.	2388	7920	5852	2388	1272	1556	868	626	706
18.	11430	166707	31528	11430	16676	6902	2789	8291	2412
Avg.	3176.9	37885.9	12153.2	3176.9	4331.6	2530.7	1203.1	1911.3	971.5
	100%	1192.5%	382.5%	100%	136.3%	79.7%	100%	158.9%	80.8%

•

Function evaluations: When considering the number of function evaluations, it is clear that the MPB requires far less evaluations than both of our algorithms. In our methods, these evaluations are used to check if a descent direction is acceptable (cf. (8)) and for the computation of the Armijo step length. One reason for the larger total amount is the fact that unlike the MPB, our methods are autonomous in the sense that they do not reuse information from previous iterations, so some information is potentially gathered multiple times. Additionally, the step length we use is fairly simple, so it might be possible to lower the number of evaluations by using a more sophisticated step length. When comparing our methods to each other, we see that Algorithm 4 is a lot more efficient than Algorithm 3 when the number of evaluations is high and is slightly less efficient when the number of evaluations is low. The reason for this is that for simple problems (i.e., where the number of evaluations is low), some of the iterations of Algorithm 4 will be redundant, because the $(\varepsilon_{i-1},\delta)$ -critical point of the previous iteration is already $(\varepsilon_{i},\delta)$ -critical.
•

Subgradient evaluations: For the subgradient evaluations, we see that MPB is slightly superior to our methods on problems 3, 5 and 16, but inferior on the rest. Regarding the comparison of Algorithms 3 and 4, we observe the same pattern as for the function evaluations: Algorithm 3 is superior for simple and Algorithm 4 for complex problems.
•

Iterations: For the number of iterations, besides problem 5, we see the exact same pattern as for the number of subgradient evaluations. Note that the MPB can perform null steps, which are iterations where only the bundle is enriched, while the current point in the descent sequence stays the same.

For our set of test problems, this leads us to the overall conclusion that in terms of function evaluations, the MPB seems to be superior to our methods, while in terms of subgradient evaluations, our methods seem to be (almost always) more efficient. Furthermore, we remark that the implementation of the MPB is somewhat challenging, whereas our method can be implemented relatively quickly.

4.3 Combination with the subdivision algorithm

Note that so far, we have a method where we can put in some initial point from $\mathbb{R}^{n}$ and obtain a single $(\varepsilon,\delta)$ -critical point (close to an actual Pareto optimal point) as a result. But ultimately, we are not interested in one, but all Pareto optimal points. The intuitive and straightforward approach to extend our method would be to just take a large set of well-spread initial points and apply our method to each of them. The problem with this is that we have no guarantee that this results in a good approximation of the Pareto set. To solve this issue, we combine our method with the subdivision algorithm which was developed for smooth problems in [11]. Since we only have to do minor adjustments for the nonsmooth case, we will only sketch the method here and refer to [11] for the details.

The idea is to interpret the nonsmooth descent method as a discrete dynamical system

\displaystyle x_{j+1}=g(x_{j}),\quad j=0,1,2,...,\quad x_{0}\in\mathbb{R}^{n},

(17)

where $g:\mathbb{R}^{n}\rightarrow\mathbb{R}^{n}$ is the map that applies one iteration of Algorithm 3 to a point in $\mathbb{R}^{n}$ . (For the sake of brevity, we have omitted the rest of the input of the algorithm here.) Since no information is carried over between iterations of the algorithm, the trajectory (i.e., the sequence) generated by the system (17) is the same as the one generated by Algorithm 3. In particular, this means that the Pareto set of the MOP is contained in the set of fixed points of the system (17). Thus, the subdivision algorithm (which was originally designed to compute attractors of dynamical systems) can be used to compute (a superset of) the Pareto set.

The subdivision algorithm starts with a large hypercube (or box) in $\mathbb{R}^{n}$ that contains the Pareto set and mainly consists of two steps:

1.

Subdivision: Divide each box in the current set of boxes into smaller boxes.
2.

Selection: Compute the image of the union of the current set of boxes under $g$ and remove all boxes that have an empty intersection with this image. Go to step 1.

In practice, we realize step 1 by evenly dividing each box into $2^{n}$ smaller boxes and step 2 by using the image of a set of sample points. The algorithm is visualized in Figure 6.

Unfortunately, the convergence results of the subdivison algorithm only apply if $g$ is a diffeomorphism. If the objective function $f$ is smooth, then the descent direction is at least continuous (cf. [13]) and the resulting dynamical system $g$ , while not being a diffeomorphism, still behaves well enough for the subdivision algorithm to work. If $f$ is nonsmooth, then our descent direction is inherently discontinuous close to the nonsmooth points. Thus, the subdivision algorithm applied to (17) will (usually) fail to work. In practice, we were able to solve this issue by applying multiple iterations of Algorithm 3 in $g$ at once instead of just one. Roughly speaking, this smoothes $g$ by pushing the influence of the discontinuity further away from the Pareto set and was sufficient for convergence (in our tests).

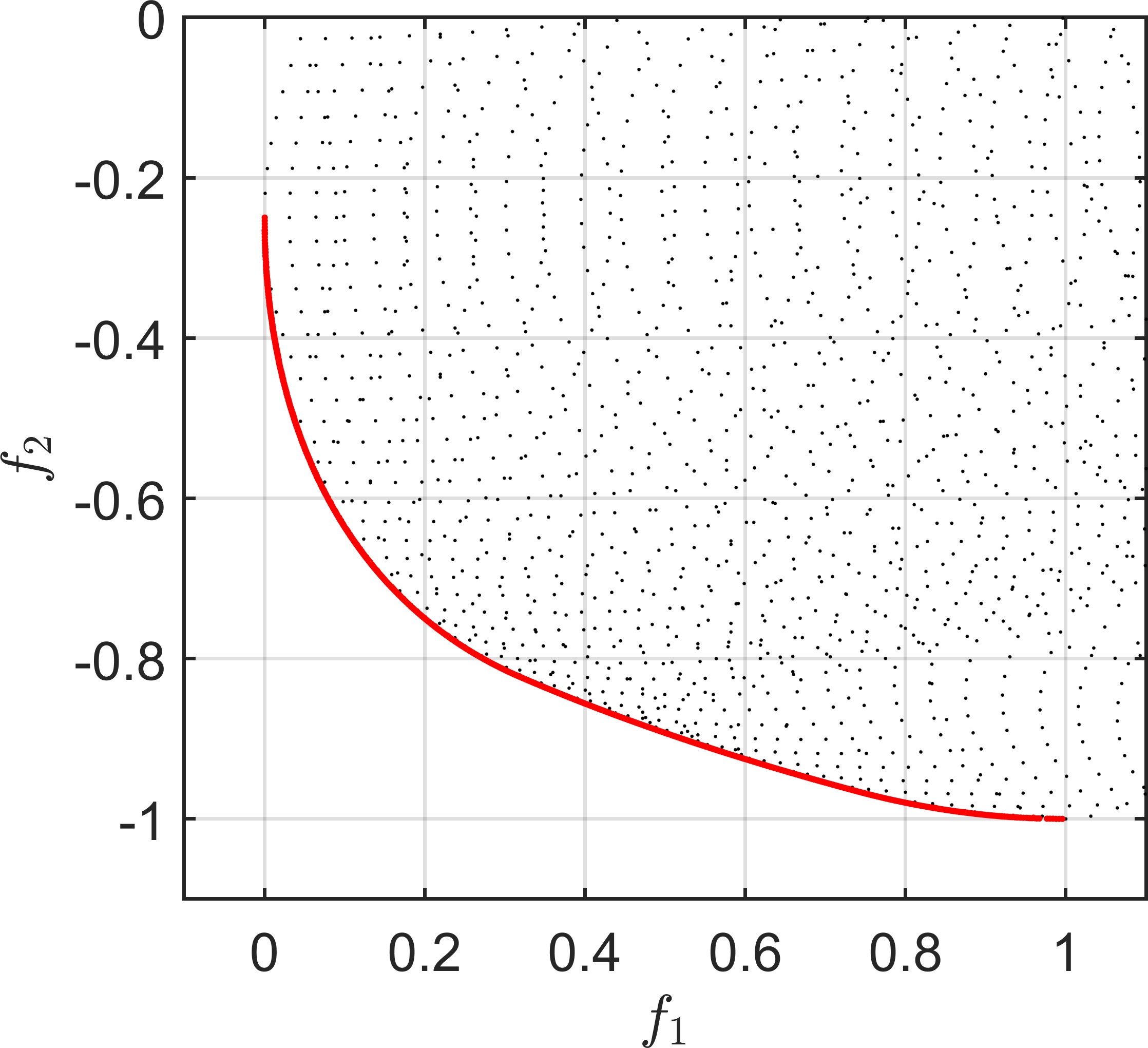
Figures 7 to 9 show the result of the subdivision algorithm for some of the problems from Table 1. For each problem, we used $15$ iterations of Algorithm 3 in $g$ , $[-3.1,3]^{2}$ as the starting box and applied $9$ iterations of the subdivision algorithm. For the approximation of the Pareto front (i.e., the image of the Pareto set), we evaluated $f$ in all points of the image of $g$ of the last selection step in the subdivision algorithm. In all of these examples, the algorithm produced a tight approximation of the Pareto set.

5 Conclusion and outlook

In this article, we have developed a new descent method for locally Lipschitz continuous multiobjective optimization problems, which is based on the efficient approximation of the Clarke subdifferentials of the objective functions from [22]. In [1], it was shown that the element with the smallest norm in the negative convex hull of the union of the subdifferentials is a descent direction for all objectives at the same time. In practice, the entire subdifferentials which are required to compute this direction are rarely known and only single subgradients can be computed. To solve this issue, we presented a method to obtain an approximation of the subdifferentials which is sufficient to obtain a descent direction. The idea is to start with a rough approximation of the subdifferentials by only a few subgradients and then systematically enrich the approximation with new subgradients until a direction of sufficient descent is found. By combining the descent direction with an Armijo step length, we obtained a descent method for nonsmooth MOPs and showed convergence to points which satisfy a necessary condition for Pareto optimality. We then compared the performance to the multiobjective proximal bundle method from [25]. For the 18 test problems we considered, the MPB was superior in terms of objective function evaluations, but our method required less subgradient evaluations and iterations. Finally, we showed that our descent method can be combined with the subdivision algorithm from [11] to compute approximations of entire Pareto sets.

For future work, we believe that it is straightforward to extend our method to constrained MOPs by adding constraints to the problem (7) that ensure that the descent direction maintains the feasibility of the descent sequence (similar to [14] for smooth problems). Additionally, in [8], the classical gradient sampling method for scalar nonsmooth optimization was generalized by allowing variable norms in the direction finding problem, increasing its efficiency. We expect that a similar generalization can be performed for problem (7), which potentially yields a similar increase in efficiency. Additional potential for increased performance lies in more advanced step length schemes as well as descent directions with memory (for instance, conjugate-gradient-like). Furthermore, it might be possible to extend our method to infinite-dimensional nonsmooth MOPs [29, 5]. Finally, in the context of nonsmooth many-objective optimization, we believe that considering subsets of objectives is a very promising and efficient approach (cf. [15] for smooth problems). However, theoretical advances are required for locally Lipschitz continuous problems.

Acknowledgement

This research was funded by the DFG Priority Programme 1962 ”Non-smooth and Complement-arity-based Distributed Parameter Systems”.

References

[1] H. Attouch, G. Garrigos, and X. Goudou. A dynamic gradient approach to pareto optimization with nonsmooth convex objective functions. Journal of Mathematical Analysis and Applications, 422(1):741 – 771, 2015.
[2] Y. Bello-Cruz. A Subgradient Method for Vector Optimization Problems. SIAM Journal on Optimization, Nov 2013.
[3] J. Burke, A. Lewis, and M. Overton. A Robust Gradient Sampling Algorithm for Nonsmooth, Nonconvex Optimization. SIAM Journal on Optimization, 15:751–779, Jan 2005.
[4] W. Cheney and A. A. Goldstein. Proximity maps for convex sets. Proceedings of the American Mathematical Society, 10(3):448–450, 1959.
[5] C. Christof and G. Müller. Multiobjective Optimal Control of a Non-Smooth Semilinear Elliptic Partial Differential Equation. European Series in Applied and Industrial Mathematics (ESAIM) : Control, Optimisation and Calculus of Variations, 2020.
[6] F. Clarke. Optimization and Nonsmooth Analysis. Society for Industrial and Applied Mathematics, 1983.
[7] J. Cruz Neto, G. Silva, O. Ferreira, and J. Lopes. A subgradient method for multiobjective optimization. Computational Optimization and Applications, 54:461–472, Apr 2013.
[8] F. E. Curtis and X. Que. An adaptive gradient sampling algorithm for non-smooth optimization. Optimization Methods and Software, 28(6):1302–1324, 2013.
[9] K. Deb. Multi-objective optimization using evolutionary algorithms, volume 16. John Wiley & Sons, 2001.
[10] K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2):182–197, Apr 2002.
[11] M. Dellnitz, O. Schütze, and T. Hestermeyer. Covering Pareto Sets by Multilevel Subdivision Techniques. Journal of Optimization Theory and Applications, 124(1):113–136, 2005.
[12] J. Fliege, L. Graña, and B. F. Svaiter. Newton’s Method for Multiobjective Optimization. SIAM Journal on Optimization, 20, Mar 2008.
[13] J. Fliege and B. F. Svaiter. Steepest descent methods for multicriteria optimization. Mathematical Methods of Operations Research, 51(3):479–494, Aug 2000.
[14] B. Gebken, S. Peitz, and M. Dellnitz. A Descent Method for Equality and Inequality Constrained Multiobjective Optimization Problems. In L. Trujillo, O. Schütze, Y. Maldonado, and P. Valle, editors, Numerical and Evolutionary Optimization – NEO 2017, pages 29–61. Springer, Cham, 2019.
[15] B. Gebken, S. Peitz, and M. Dellnitz. On the hierarchical structure of Pareto critical sets. Journal of Global Optimization, 73(4):891–913, 2019.
[16] A. Goldstein. Optimization of Lipschitz continuous functions. Mathematical Programming, 13:14–22, 12 1977.
[17] E. S. Helou, S. A. Santos, and L. E. A. Simões. On the differentiability check in gradient sampling methods. Optimization Methods and Software, 31(5):983–1007, 2016.
[18] K. C. Kiwiel. A descent method for nonsmooth convex multiobjective minimization. Large scale systems, 8(2):119–129, 1985.
[19] K. C. Kiwiel. Methods of Descent for Nondifferentiable Optimization. Springer-Verlag Berlin Heidelberg, 1985.
[20] K. C. Kiwiel. Proximity Control in Bundle Methods for Convex Nondifferentiable Minimization. Mathematical Programming, 46:105–122, Jan 1990.
[21] K. C. Kiwiel. A Nonderivative Version of the Gradient Sampling Algorithm for Nonsmooth Nonconvex Optimization. SIAM Journal on Optimization, 20(4):1983–1994, 2010.
[22] N. Mahdavi-Amiri and R. Yousefpour. An Effective Nonsmooth Optimization Algorithm for Locally Lipschitz Functions. Journal of Optimization Theory and Applications, 155(1):180–195, Oct 2012.
[23] M. M. Mäkelä. Multiobjective proximal bundle method for nonconvex nonsmooth optimization: Fortran subroutine mpbngc 2.0. Reports of the Department of Mathematical Information Technology, Series B. Scientific Computing, B, 13:2003, 2003.
[24] M. M. Mäkelä, V.-P. Eronen, and N. Karmitsa. On Nonsmooth Multiobjective Optimality Conditions with Generalized Convexities, pages 333–357. Springer New York, New York, NY, 2014.
[25] M. M. Mäkelä, N. Karmitsa, and O. Wilppu. Multiobjective proximal bundle method for nonsmooth optimization. TUCS technical report No 1120, Turku Centre for Computer Science, Turku, 2014.
[26] M. M. Mäkelä and P. Neittaanmäki. Nonsmooth Optimization: Analysis and Algorithms with Applications to Optimal Control. World Scientific, 1992.
[27] K. Miettinen. Nonlinear Multiobjective Optimization. Springer US, 1998.
[28] O. Montonen, N. Karmitsa, and M. M. Mäkelä. Multiple subgradient descent bundle method for convex nonsmooth multiobjective optimization. Optimization, 67(1):139–158, 2018.
[29] B. Mordukhovich. Multiobjective optimization problems with equilibrium constraints. Optimization Methods and Software, 117:331–354, Jul 2008.
[30] S. Schäffler, R. Schultz, and K. Weinzierl. Stochastic Method for the Solution of Unconstrained Vector Optimization Problems. J. Optim. Theory Appl., 114(1):209–222, 2002.
[31] N. Shor. Minimization Methods for Non-Differentiable Function. Springer-Verlag Berlin Heidelberg, 1985.

$\displaystyle\\|v_{l}\\|^{2}$	$\displaystyle\leq\\|-v_{l-1}+s(\xi^{j}_{l-1}+v_{l-1})\\|^{2}$
	$\displaystyle=\\|v_{l-1}\\|^{2}-2s\langle v_{l-1},\xi^{j}_{l-1}+v_{l-1}\rangle+s^{2}\\|\xi^{j}_{l-1}+v_{l-1}\\|^{2}$
	$\displaystyle=\\|v_{l-1}\\|^{2}-2s\langle v_{l-1},\xi^{j}_{l-1}\rangle-2s\\|v_{l-1}\\|^{2}+s^{2}\\|\xi^{j}_{l-1}+v_{l-1}\\|^{2}$	(13)