An asymmetric dust ring around a very low mass star ZZ Tau IRS
Abstract
We present Atacama Large Millimeter/submillimeter Array (ALMA) gas and dust observations at band 7 (339 GHz: 0.89 mm) of the protoplanetary disk around a very low mass star ZZ Tau IRS with a spatial resolution of 025. The 12CO position–velocity diagram suggests a dynamical mass of ZZ Tau IRS of 0.1–0.3 . The disk has a total flux density of 273.9 mJy, corresponding to an estimated mass of 24–50 in dust. The dust emission map shows a ring at 58 au and an azimuthal asymmetry at 45 au with a position angle of 135°. The properties of the asymmetry, including radial width, aspect ratio, contrast, and contribution to the total flux, were found to be similar to the asymmetries around intermediate mass stars (2 ) such as MWC 758 and IRS 48. This implies that the asymmetry in the ZZ Tau IRS disk shares a similar origin with others, despite the star being 10 times less massive. Our observations also suggest that the inner and outer parts of the disk may be misaligned. Overall, the ZZ Tau IRS disk shows evidence of giant planet formation at 10 au scale at a few Myr. If confirmed, it will challenge existing core accretion models, in which such planets have been predicted to be extremely hard to form around very low mass stars.
1 Introduction
Core accretion planet formation theories predict that only terrestrial and icy planets can form around very low mass (VLM) stars (0.1–0.2 ), and the formation of gas giant planets is essentially prohibited (e.g., Liu et al., 2019, 2020; Matsumoto et al., 2020; Miguel et al., 2020). The reasons are multifold. First, a low stellar mass results in longer dynamical timescale and longer growth timescale of dust, delaying the formation of planetary cores. Secondly, the mass of dust in protoplanetary disks, the building blocks of planets, is correlated with stellar mass (e.g., Ansdell et al., 2017). A low dust mass in disks around VLM stars leads to low mass of protoplanets, suppressing pebble accretion (Ormel & Liu, 2018) and preventing cores from ever reaching the critical mass to trigger runaway gas accretion. Last but not least, observed stellar accretion rates suggest that disks around VLM stars evolve faster than those around higher mass stars, further daunting the task of planet formation (Manara et al., 2012; Liu et al., 2020). In addition, water snowline has been proposed to be the preferred site of planetesimal and planet formation due to its enhanced local dust-to-gas ratio (Ormel, 2017). Around VLM stars, snowline is close to the star at 0.1 au. Therefore compact systems with rocky planets like the TRAPPIST-1 (Gillon et al., 2016) are expected, while planet formation at 1 au is not (Miguel et al., 2020).
Indeed, statistical studies show that at small orbital separations rocky and icy planets are common around M dwarfs (e.g., Dressing & Charbonneau, 2015), while the occurrence rate of gas giant planets dives from 14% around 2 M☉ stars to 3% around 0.5 M☉ stars (Johnson et al., 2010). Around VLM stars, only a handful of gas giant planets have ever been found (e.g., GJ 3512; Morales et al., 2019), and their formation mechanism is a mystery. Since their host stars are mature mean sequence stars that have finished planet formation long before, it is unclear where and when do those planets form. Protoplanetary disks around VLM stars serve as excellent laboratories for investigating planet formation in these extreme environments.
The Atacama Large Millimeter/submillimeter Array (ALMA) has revealed a variety of sub-structures in protoplanetary disks, such as rings, gaps, cavities, spirals, and crescent structures. While rings/gaps are the most common (e.g., Andrews et al., 2018; Long et al., 2018; Cieza et al., 2020), roughly 10 disks show azimuthal asymmetries (e.g., Francis & van der Marel, 2020; van der Marel et al., 2020; Tsukagoshi et al., 2019; Pérez et al., 2018; Dong et al., 2018b; Cieza et al., 2017). Disks around VLM stars also harbor rings and gaps (e.g., Kurtovic et al., 2020); however, azimuthal asymmetries have not yet been reported. Asymmetric dust crescents may be local dust traps at gas pressure maxima (e.g., Raettig et al., 2015; Ragusa et al., 2017), thus ideal locations of planet formation (e.g., Chang & Oishi, 2010). Three possible origins of asymmetries have been discussed by van der Marel et al. (2020): (a) long-lived anticyclonic vortices at gap edges, possibly opened by companions (e.g., Raettig et al., 2015), (b) gas horseshoes at the edge of eccentric cavities curved by massive companions (e.g., Ragusa et al., 2017), and (c) part of spiral arms (van der Marel et al., 2016) triggered by companions. The main difference between the former two is in the mass of the companions: a vortex can be produced at the edges of gaps opened by planets as low mass as super-Earths (Dong et al., 2018a), whereas a horseshoe needs to be triggered by a much more massive companion, i.e., a brown dwarf. Overall, all three mechanisms suggest the presence of companions (planets) inside the cavity or gap.
In this paper, we report a ring and an asymmetric structure around the VLM star ZZ Tau IRS (spectral type: M4.5 to M5, : 3015 to 3125 K, : 0.02 to 0.13 , : 0.09 to 0.16 , White & Hillenbrand, 2004; Andrews et al., 2013; Herczeg & Hillenbrand, 2014) in the Taurus star forming region at an assumed distance of 130.7 pc111We do not use the GAIA distance of 105.7 pc because the astrometric solution is poor with a value of the renormalized unit weight error (RUWE) of 2.490 (GAIA EDR3; Gaia Collaboration et al., 2020). taken from Akeson et al. (2019). The stellar luminosity is 0.017 to 0.113 (White & Hillenbrand, 2004; Andrews et al., 2013; Herczeg & Hillenbrand, 2014, scaled by the updated distance), with the large uncertainty mainly due to factors including flux calibration and extinction (see the discussions in Herczeg & Hillenbrand, 2014). With these and , the Baraffe et al. (2015) isochrone yields a stellar mass around 0.1 at an age of 1 to 12 Myr consistently. ZZ Tau IRS is a single star (i.e., not identified as a spectroscopic binary; Kounkel et al., 2019) while its companion ZZ Tau is 35′′ away. Its spectral energy distribution (SED; Figure 5 in Appendix A) does not show any deficits at IR wavelengths 10 m, and thus ZZ Tau IRS was not classified as having a cavity/gap structure in its disk. The large IR excess relative to the stellar flux in the SED (Figure 5) was interpreted as an edge-on disk (Furlan et al., 2011), and high-resolution optical spectroscopy of ZZ Tau IRS also suggested the existence of a close to edge-on disk based on its narrow emission lines from the optical jet (White & Hillenbrand, 2004). The total disk mass (gas dust) was estimated to be 0.014 by observations at millimeter wavelengths using the Submillimeter Array (Andrews et al., 2013; Akeson et al., 2019).
2 ALMA archive data
We used the ALMA archive data at band 7 (program ID: 2016.1.01511.S, PI: J. Patience), summarized in Table 1. The data were calibrated by the Common Astronomy Software Applications (CASA) package (McMullin et al., 2007), following the calibration scripts provided by ALMA. We performed a self-calibration of the visibilities. The phases were self-calibrated once, with fairly long solution intervals (solint = ‘inf’) that combined all spectral windows. To facilitate analyses later (§ 4), we shifted the observed dust continuum images to minimize the asymmetry relative to the phase center using the procedure described in Appendix B.
| Observations | ||||
|---|---|---|---|---|
| Observing date (UT) | 2017.Jul.6 | |||
| Project code | 2016.1.01511.S (PI: J. Patience) | |||
| Time on source (min) | 4.5 | |||
| Number of antennas | 42 | |||
| Baseline lengths | 16.7 m to 2.6 km | |||
| Baseband Freqs. (GHz) | 331.9 (cont.) | 333.8 (cont.) | 343.9 (cont.) | 345.8 (12CO ) |
| Channel width (MHz) | 15.6 | 15.6 | 15.6 | 0.488 |
| Continuum band width (GHz) | 7.5 | |||
| Bandpass calibrator | J05101800 | |||
| Flux calibrator | J05101800 | |||
| Phase calibrator | J04383004 | |||
| Typical PWV (mm) | 0.60 | |||
| Imaging | Dust continuum | 12CO | ||
| Robust clean parameter | 2.0 | |||
| Outer -taper parameter | 0.4 500.0 M with 48.0 | |||
| Beam shape | 254 248 mas at PA of 61.7 | 283 156 mas at PA of 50.2 | ||
| r.m.s. noise (mJy/beam) | 0.268 | 9.56 at 0.5 km/s bin | ||
The final synthesized dust continuum image of the combined data is shown in Figure 1. In the CLEAN task, we set the -taper (0.4 500.0 M at PA of 48°) with a robust parameter of 2.0 to obtain a nearly circular beam, and we did not use the ‘multi-scale’ option. The r.m.s. noise in the region far from the source is 268 Jy/beam with a beam size of 254 248 mas at a position angle (PA) of 61.7°.
The 12CO line data (Table 1) were extracted by subtracting the continuum in the plane using the uvcontsub task in the CASA tools. A line image cube with a channel width of 0.5 km/s was produced by the CLEAN task. The integrated line flux map (moment 0) and the intensity-weighted velocity map (moment 1) are shown in Figure 2. The channel maps at 1.0 to 13.0 km/s are shown in Figure 7 in the Appendix C. The r.m.s. noise in the moment 0 map is 61.4 mJy/beamkm/s with a beam size of 283 156 mas at a PA of 50.2, and the r.m.s. noise in the moment 1 map is 9.56 mJy/beam at 0.5 km/s bin. The peak signal-to-noise ratio (SNR) is 24.1 in the channel map of 4.0 km/s.
3 Results
3.1 Dust continuum emission
Figure 1 shows dust continuum images of the ZZ Tau IRS disk in band 7, as well as its radial and azimuthal profiles. We found two structures: a ring at 50 au (hereafter we refer to the ZZ Tau IRS disk as a ‘ring’) in Figure 1(b) and an azimuthal asymmetry with a contrast ratio of 1.39 0.05 between its peak and the opposite side on the ring in Figure 1(c). The peak SNR in the ring is 78.4. The dust continuum image synthesized with only the imaginary part (which efficiently detects asymmetric structures) indicates that the asymmetric structure in the ring is significant with a peak SNR of 34.3 in the central panel in Figure 6 in the Appendix B. In the azimuthal profile (Figure 1c), we found two peaks at PAs of 130 and 310. Such a two-peak structure along a disk major axis is commonly found in low spatial resolution images of rings (02–04; e.g., Ansdell et al., 2016). Our visibility analyses in § 4 suggest that the peak at a PA of 310 is caused by beam effects. Hereafter we refer to the peak at a PA of 130 as the asymmetry.
The total flux density of the dust continuum derived from visibility analyses in § 4 is 273.9 27.4 mJy (Table 2), assuming a 10 % uncertainty in the absolute flux calibration, consistent with previous single-disk observations (300 40 mJy, Di Francesco et al., 2008). The peak brightness temperature in the ring calculated from the best-fit model in the visibility analyses (§ 4) is 14.9 0.9 K assuming a 10 % uncertainty in the absolute flux calibration.
We now estimate the physical properties of the dust ring. The optical depth is calculated as:
| (1) |
where , , and are the intensity, the Planck function, and the midplane temperature, respectively. We use the midplane temperature profile with a simplified expression for a passively heated, flared disk in radiative equilibrium (e.g., Dullemond et al., 2001):
| (2) |
where is the stellar luminosity (0.017 to 0.113 ), is the flaring angle, and is the Stefan–Boltzmann constant. If the starlight-absorbing small dust grains (sub-micron-sized) have a similar spatial distribution to the large dust grains (millimeter-sized) traced by millimeter emission (similar to the PDS 70 disk; Hashimoto et al. 2012; Keppler et al. 2019), the inner wall of the ring is directly exposed to stellar radiation, and reaches unity. In this case, at 45 au where the asymmetry is located (see visibility analyses in § 4), Equation (2) yields – K (uncertainty due to the stellar luminosity). The corresponding optical depth is 0.5–1.4 based on Equation (1). Therefore, the asymmetry is marginally optically thin. The rest of the ring is expected to be optically thinner. Approximating the entire disk as an optically thin structure, the total flux corresponds to a total mass (gas dust) of 7.6–15.7 assuming the dust temperature of – K, an opacity per unit dust mass of 3.45 cm2 g-1 at 345 GHz (Beckwith & Sargent, 1991), and a gas-to-dust mass ratio of 100. We note that the dust mass estimate is a lower limit since the actual dust temperature can be lower. The large dust grains are expected to concentrate at the pressure peak outside the cavity wall and reach a temperature lower than that estimated using Equation 2 with unity. In the extreme case, the observed cavity in large dust grains may even be filled with small dust grains (e.g., “missing cavities”; Dong et al. 2012), resulting in substantially lower temperature at the ALMA ring location.

3.2 Gas emission
The integrated line flux map of 12CO in Figure 2(a) shows a single-peak structure with a peak flux of 1.0 0.1 Jy/beamkm/s at 16.3 and a total flux above 3 of 1.9 0.19 Jykm/s assuming a 10 % uncertainty in the absolute flux calibration. As shown in the channel maps in Figure 7 in the Appendix C, the 12CO emission is absorbed at 6.5–7.0 km/s, and thus the total flux could be a lower limit. The brightness temperature map of 12CO converted from the moment 8 map (maximum values of the spectrum) is shown in Figure 2(b). Since 12CO could be generally optically thick, it could be a good tracer for the gas temperature in the emitting region. At the location of the asymmetry, the brightness temperature of 12CO is 35 K, higher than the 17.8–28.6 K estimated by Equation (2). This could be because the emitting surface of 12CO is in the upper hotter layer of the disk. Figure 2(d) shows the 12CO position–velocity (PV) diagram (channel maps: Figure 7 in the Appendix C) along PA 135. We overplotted the loci of the peak emission of a Keplerian disk with an inclination of 60 (see § 4) around a central star with masses of 0.1, 0.2, and 0.3 , and found that the dynamical mass of ZZ Tau IRS is 0.1–0.3 . This value is consistent with the spectroscopically determined mass (0.1–0.2 ; Andrews et al., 2013; Herczeg & Hillenbrand, 2014). Note that we assume that the systemic velocity of ZZ Tau IRS is 6.5 km/s in the PV diagram.

4 Visibility analyses
Since the contrast of the asymmetry in the ZZ Tau IRS ring is of order unity, an imaging artifact such as a sidelobe of the bright ring could generate an apparent asymmetry. To characterize the disk structure, we performed forward modelling in which the observed visibilities are reproduced with a parametric model of the ring in the visibility domain.
The ZZ Tau IRS disk is assumed to consist of a ring and an asymmetry. The model ring consists of a narrow Gaussian ring (ring A) superposed on a wide Gaussian ring (ring B) as shown in Figure 3(a), and is described as follows:
| (3) |
where , , , , and are the radial peak positions and standard deviations of two Gaussian rings and a scaling factor between the two, respectively. The width of the ring (FWHM) is calculated as 2.355.
The asymmetry is defined as an elliptical Gaussian function in polar coordinates as follows:
| (4) |
where , , , and are the radial peak position, azimuthal peak position, radial standard deviation, and azimuthal standard deviation, respectively. The flux for the asymmetry is normalized to . The combined model image is magnified and rotated with an inclination () and a PA. The total flux for the combined model image is normalized to . The radial and azimuthal widths (FWHM) of the asymmetry are 2.355 and 2.355, respectively. In total, there are 13 free parameters in our model (, , , , , , , , , , , , PA).
The model image was converted to complex visibilities with the public Python code vis_sample (Loomis et al., 2017), in which model visibilities are samples with the same (, ) grid points as the observations. The model visibilities are deprojected222Visibilities are deprojected in the -plane using the following equations (e.g., Zhang et al., 2016):
where and PA are free parameters in our visibility analyses in § 4. with the system PA and as free parameters. The fitting is performed with a Markov chain Monte Carlo (MCMC) method in the emcee package (Foreman-Mackey et al., 2013). The log-likelihood function ln in visibility analyses is
| (5) |
where the subscript represents the -th data. , , and are observed and model visibilities and weights corresponding to 1/ ( is the rms noise of a given visibility. See details in CASA Guides333https://casaguides.nrao.edu/index.php/DataWeightsAndCombination.), respectively. The values of and (i.e., 1/) are provided in the measurement set of ALMA data. Our calculations used flat priors with the parameter ranges summarized in Table 2. We ran 3,000 steps with 100 walkers, and discarded the initial 1,000 steps as the burn-in phase based on trace plots in Figure 8 in Appendix D.
The fitting results with uncertainties computed from the 16th and 84th percentiles, the radial profile of best-fit surface brightness for the ring with a raw resolution, the best-fit model image, and the probability distributions for the MCMC posteriors are shown in Table 2, Figure 3(a), Figure 3(d), and Figure 9 in the Appendix E, respectively. We subtracted modeled visibilities from observed visibilities (Figure 10 in Appendix F), and made a CLEANed image (Figure 3e) in which we did not find significant residuals. To calculate the value of the reduced-, we derived a factor between the weights and standard deviations (referred to as stddev) in the visibilities by calculating the standard deviations of the real and imaginary parts in 2 k bins along the azimuthal direction in the visibility domain. The values of weights are provided in the measurement set of ALMA data while the standard deviations (stddev) are calculated in our fitting. The visibilities were deprojected with 60 and PA 135. Figure 11 in Appendix G shows a comparison between the weights and standard deviations (stddev-2). We found that the weights are typically 4.0 higher than the standard deviations. Finally, we calculated a reduced- of 1.91. We also conducted visibility analyses using a model with one Gaussian ring one asymmetry (i.e., 0), and found significant residuals. Thus, the model with two Gaussian rings one asymmetry is necessary to reproduce the observed dust continuum image.
| FWHMringA | FWHMringB | PA | FWHMr,asym | FWHMθ,asym | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (au) | (au) | (au) | (au) | (deg) | (deg) | (mJy) | (mJy) | (au) | (deg) | (au) | (deg) | |
| 57.51 | 41.08 | 83.62 | 133.65 | 0.34 | 60.16 | 134.73 | 14.51 | 45.15 | 18.17 | 11.31 | 103.07 | |
| {0.0 .. 117.6} | {0.0 .. 78.4} | {0.0 .. 117.6} | {78.4 .. 196.1} | {0.0 .. 1.0} | {50.0 .. 70.0} | {125.0 .. 145.0} | {0.0 .. 100.0} | {0.0 .. 117.6} | {45.0 .. 45.0} | {0.0 .. 117.6} | {0.0 .. 360.0} |
Note. — Parentheses describe parameter ranges in our MCMC calculations.

Though the observed dust continuum image in Figure 1(a) shows two peaks along the ring major axis, our visibility analyses suggest that only the one at PA 130 is real.
The radial ring position (i.e., the peak position) and its FWHM (Ring A Ring B) in the model image were measured to be 58 and 49 au in Figure 3(a). The contrast in the asymmetry, which is the ratio between the peak brightness at the asymmetry and that at its opposite side on the ring, is measured to be 3.0 in Figure 3(d).
5 Discussion
5.1 Azimuthal asymmetry
Azimuthal asymmetries in rings have been identified in roughly ten protoplanetary disks (e.g., van der Marel et al., 2020). At band 7, their shape parameters (e.g., the radial FWHM and the aspect ratio defined as the azimuthal FWHM divided by the radial FWHM) are summarized in Table 3444The physical quantities of other asymmetries are taken from van der Marel et al. (2020). V1247 Ori shows a crescent structure in ALMA band 7 (Kraus et al., 2017). However, we do not include V1247 Ori because the structure does not have a Gaussian profile (Kraus et al., 2017). Though HD 142527 also shows a crescent structure in ALMA band 7 (Fukagawa et al., 2013), the visibility analyses in van der Marel et al. (2020) did not find convergence; thus, we do not include HD 142527.. All but ZZ Tau IRS are intermediate mass stars (2 ). In Figure 4 we compare various properties of these asymmetries as a function of the peak radial location. Though ZZ Tau IRS is a VLM star, its asymmetry has similar properties to other asymmetries around more massive stars, implying a similar origin.
We explore the correlation in Figure 4 by calculating Pearson’s correlation coefficient for logarithmic numbers except the aspect ratio. The 5% significance values for Pearson’s with 7 and 8 are 0.75 and 0.71, respectively (Pugh & Winslow, 1966). We found two (marginally) statistically significant relations: radial location v.s. radial FWHM (0.89), and radial location v.s. azimuthal FWHM (0.69; top panels in Figure 4). Asymmetric structures have been interpreted as dust traps at pressure maxima in gas vortices (e.g., Raettig et al., 2015) or horseshoes (e.g., Ragusa et al., 2017). The radial width of a gas pressure bump is expected to be comparable to the gas scale height (e.g., Dullemond et al., 2018), typically prescribed as with unity (e.g., assuming , ). The most significant correlation we see in Figure 4, radial location v.s. radial FWHM, may simply trace the dependence of the radial size of gas pressure structure on .
Another interpretation of asymmetries is that they are part of spiral arms induced by companions (e.g., van der Marel et al., 2016). One way to distinguish these mechanisms is to derive the spectral index from multi-wavelength observations, which may constrain the size of the dust grains (e.g., Testi et al., 2014). Dust trapping in gas vortices and horseshoes results in a bigger dust size, while spiral arms are not expected to trap dust particles as they deferentially rotate with respect to the local disk material (Papaloizou et al., 2007; Li et al., 2020). Measuring the pattern speed of asymmetries may also shed light on their origin, as vortices and horseshoes are expected to move at the local Keplerian velocity while spirals corotate with their drivers.
| Object | Stellar mass | Radial location | Radial FWHM | Azimuthal FWHM | Aspect ratio | Contrast | Flux ratio | Refs |
|---|---|---|---|---|---|---|---|---|
| () | (au) | (au) | (deg; au) | (%) | ||||
| ZZ Tau IRS | 0.2 | 45 | 11.3 | 103; 80.9 | 7.2 | 3.0 | 5.3 | a,a |
| MWC 758 | 1.9 | 50 | 7.5 | 49; 42.7 | 5.7 | 4.4 | 6.4 | b,c |
| 90 | 15 | 47; 73.8 | 4.9 | 11.7 | 20.0 | b,c | ||
| HD 34282 | 2.0 | 137 | 110 | 52; 124.3 | 1.1 | 1.7 | 4.8 | b,d |
| SR 21 | 2.1 | 55 | 19 | 82; 78.7 | 4.1 | 2.1 | 12.5 | b,c |
| 58 | 19 | 165; 166.9 | 8.8 | 2.0 | 26.0 | b,c | ||
| AB Aur | 2.3 | 170 | 96 | 122; 361.8 | 3.8 | 2.7 | 39.5 | b,c |
| IRS 48 | 2.2 | 70 | 29 | 58; 70.8 | 2.4 | — | — | b,c |
Note. — (1) Object name. MWC 758 and SR 21 have two asymmetries (van der Marel et al., 2020). (2) Stellar mass. (3) Radial location. (4) Radial FWHM calculated by 2.355. The radial FWHM of the IRS 48 asymmetry is calculated with 2.17 because the radial profile for IRS 48 was found to be best fit with a 4th power in 2D Gaussian in van der Marel et al. (2020). (5) Azimuthal FWHM. (6) The aspect ratio defined as the azimuthal FWHM divided by the radial FWHM. (7) Contrast measured in the model between the peak brightness and the opposite side of the ring. The model images are constructed with the parameters from the literature in column (9). For SR 21, since the azimuthal positions of the two asymmetries are located at almost opposite sides, the contrast of the each asymmetry was measured for a model containing only one asymmetry and the ring. For IRS 48, the contrast is not measured because the model contains only the asymmetry without the ring (van der Marel et al., 2020). (8) Ratio of the asymmetry to total flux in the model. For IRS 48, this value is not measured because the model contains only the asymmetry without the ring (van der Marel et al., 2020). (9) References for information of stellar masses and properties of asymmetries: a) this work, b) Garufi et al. (2018), c) van der Marel et al. (2020), d) van der Plas et al. (2017).

5.2 Gravitational stability
ZZ Tau IRS’ disk is one of the most massive among VLM stars (cf., Kurtovic et al., 2020). We examine its gravitational stability. Theoretical studies (e.g., Durisen et al., 2007) suggest that if the Toomre (1964) Q-parameter, defined as
| (6) |
where , , and are the sound speed, the Keplerian angular velocity, and the disk (gas) surface density, respectively, is of order of unity, the disk may be subject to gravitational instability (GI). With the scale height of , Toomre’s -parameter can be described as , where . Therefore, if the disk’s aspect ratio is , GI occurs in massive disks with 0.1. The disk-to-star mass ratio is 0.04–0.08 in ZZ Tau IRS (§ 3.1), and thus the disk may be globally gravitationally stable. Meanwhile the Q-value at the asymmetry is 1.7–6.2 assuming a local surface density / 7–20 g/cm2 ( and 0.5–1.4, § 3.1), an opacity per unit dust mass of 3.45 cm2 g-1 at 345 GHz (Beckwith & Sargent, 1991), a temperature of 17.8–28.6 K (§ 3.1), and a gas-to-dust mass ratio of 100. Hence, the asymmetry may also be marginally stable.
5.3 Possible warped inner disk
ZZ Tau IRS has been suggestsed to have an edge-on inner disk (White & Hillenbrand, 2004; Furlan et al., 2011), because the IR excess is larger than the optical stellar flux due to partial disk obscuration of the star (Figure 5 in the Appendix A). Our visibility analyses suggest that the outer ring at 50 au has an inclination () of 60 (§ 4). Radiative transfer calculations for protoplanetary disks (full disks) show that typically the central star starts to be significantly obscured by the disk once the inclination is larger than 70 (e.g., see Figure 2 in Whitney et al., 2013). Hence ZZ Tau IRS could possess an inner disk misaligned with the outer ring. Such warped inner disks have been discovered in twisted gas flow patterns (e.g., Rosenfeld et al., 2014; Mayama et al., 2018) and shadows on the outer disk in NIR scattering images (e.g., Marino et al., 2015). For ZZ Tau IRS, current ALMA gas observations in Figure 2 are insufficient to confirm a twisted gas flow due to low spatial & spectral resolution. Furthermore, high spatial resolution observations of NIR scattering images have not yet been carried out. Another possible explanation of the observed SED is that the source is a “flat spectrum” young stellar object surrounded by an infalling dusty envelope (Calvet et al., 1994). In this case, an extended reflection nebulae around the source is expected in NIR scattered light observations (e.g., similar to T Tau, Whitney & Hartmann, 1993). Future observations are necessary to test these hypotheses.
A few possible mechanisms have been proposed to explain warped disks. An exciting one is disk–companion interactions (e.g., Zhu, 2019), in which a massive companion with a companion-star mass ratio (or around a 0.1 star) on an inclined orbit induces both a deep wide gap and a misaligned inner disk. Such a system with a massive companion and a misaligned inner disk has been reported in HD 142527 (Biller et al., 2012; Marino et al., 2015). Future detection of massive companions in the gap would serve as a test for the planet origin hypothesis.
6 Conclusion
We analyzed ALMA band 7 archive data (dust continuum and 12CO emission) of ZZ Tau IRS. The source has been classified as a VLM star with a mass of 0.1–0.2 in the literature. The observed 12CO kinematics suggest a dynamical mass of 0.1–0.3 , consistent with previous estimates. The ALMA dust continuum image at a spatial resolution of 025 shows a ring and an asymmetric structures around ZZ Tau IRS. Our visibility analysis confirmed that the observed asymmetry is real rather than apparent.
Our best-fit model of the ALMA dust observations shows that the asymmetry has a radial FWHM of 11.3 au, an aspect ratio of 7.2 (ratio of azimuthal FWHM to azimuthal FWHM), a brightness contrast of 3.0, and the asymmetry contributes 5% of the total disk flux. These metrics are comparable with asymmetries seen around intermediate mass stars (2 ), implying a similar origin, despite ZZ Tau IRS being 10 times less massive. While future high spatial resolution observations in multiple wavelengths with ALMA and JVLA are needed to determine the exact origin of the asymmetry, the three leading hypotheses all invoke companions inside the gap.
The inner disk around ZZ Tau IRS, not visible in our observations, has been inferred to be edge-on based on the SED. Our observations showed that the inclination of the outer disk at 50 au is 60°. These results imply that the ZZ Tau IRS inner disk may be misaligned relative to the outer ring, and it is possible that the misalignment (and the gap) is produced by a giant planet with on an inclined orbit inside the gap. Future scattered light observations may test this hypothesis by searching for shadows on the outer disk cast by the inner disk.
Overall, the structures found in the ZZ Tau IRS disk suggest the presence of massive companions including gas giant planets at au. This is surprising as the core accretion theories have generally prohibited the formation of such planets around VLM stars (Miguel et al., 2020; Liu et al., 2020, § 1). Hence, ZZ Tau IRS will be a prime target in the investigation of planet formation around VLM stars.
vis_sample (Loomis et al., 2017),
CASA (McMullin et al., 2007),
emcee (Foreman-Mackey et al., 2013)
Appendix A SED of ZZ Tau IRS
Figure 5 shows the SED of ZZ Tau IRS. Extinction correction is not applied to show the large IR excess relative to the stellar flux. The photometric data without extinction correction are summarized in Table 4.
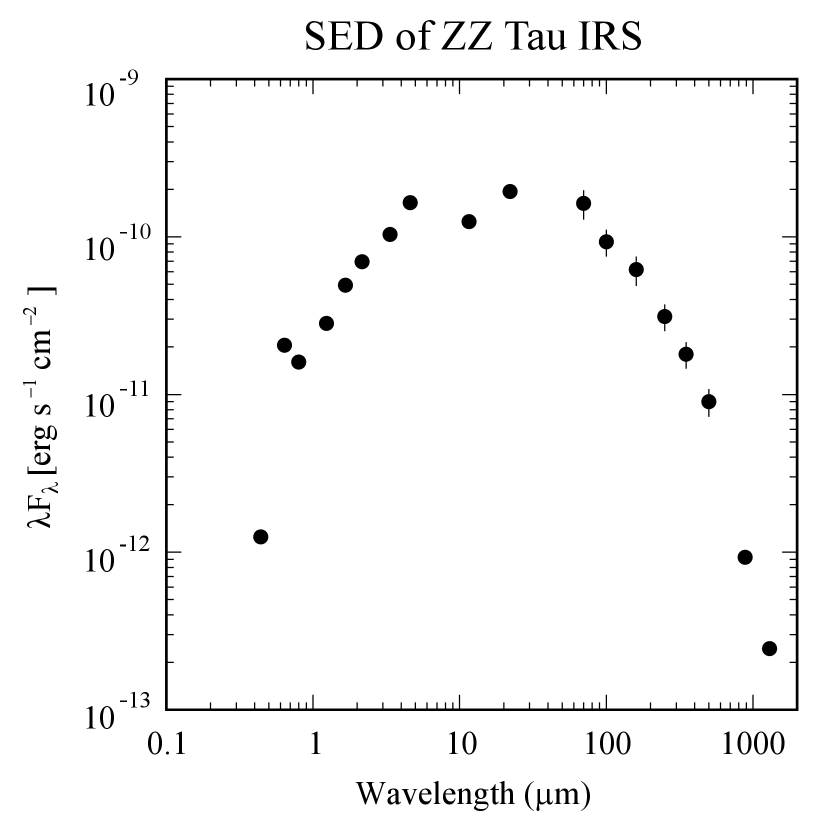
| Wavelength | Reference | |
|---|---|---|
| (m) | (10-12 erg s-1 cm-2) | |
| 0.44 | 1.25 | USNO-B1.0 (Monet et al., 2003) |
| 0.64 | 20.5 | USNO-B1.0 (Monet et al., 2003) |
| 0.80 | 16.1 | USNO-B1.0 (Monet et al., 2003) |
| 1.23 | 28.3 0.6 | 2MASS (Cutri et al., 2003) |
| 1.66 | 49.2 1.0 | 2MASS (Cutri et al., 2003) |
| 2.16 | 69.4 1.5 | 2MASS (Cutri et al., 2003) |
| 3.35 | 100.4 2.0 | WISE (Cutri & et al., 2014) |
| 4.60 | 164.5 3.2 | WISE (Cutri & et al., 2014) |
| 11.6 | 124.8 1.6 | WISE (Cutri & et al., 2014) |
| 22.1 | 193.8 2.9 | WISE (Cutri & et al., 2014) |
| 70 | 162.9 34.3 | Herschel (Ribas et al., 2017) |
| 100 | 93.0 18.0 | Herschel (Ribas et al., 2017) |
| 160 | 61.9 13.1 | Herschel (Ribas et al., 2017) |
| 250 | 31.2 6.0 | Herschel (Ribas et al., 2017) |
| 350 | 18.0 3.4 | Herschel (Ribas et al., 2017) |
| 500 | 9.0 1.8 | Herschel (Ribas et al., 2017) |
| 885 | 0.928 0.093 | ALMA (this work) |
| 1300 | 0.244 0.003 | SMA (Andrews et al., 2013) |
Note. — Extinction correction is not applied here.
Appendix B Dust continuum images synthesized with only the imaginary part
We shifted the observed dust continuum images to minimize the asymmetry relative to the phase center as follows. First, the proper motions of ZZ Tau IRS were calculated with the function EPOCH_PROP in GAIA ADQL (Astronomical Data Query Language555https://gea.esac.esa.int/archive/). The phase centers were corrected to (4h30m51.7346s, 24d41m47.175s) in ICRS using fixvis in the CASA tools. Next, in order to make the analyses of the disk structure more effective, we further shift the center of the image by searching for the location where the disk asymmetry is minimized. We subtracted the 180°-rotated image in the visibility domain. This procedure corresponds to producing a synthesized image with only the imaginary part of the visibilities.
This method has been utilized in the analyses of DM Tau (Hashimoto et al., 2021) and WW Cha (Kanagawa et al., 2021). Since the visibility is a Fourier transform of the surface brightness distribution of the sky, which is a real quantity, the visibility at in the -plane is a complex conjugate of that at ,
| (B1) |
The 180°-rotation of the image with respect to the origin on sky corresponds to flipping the signs of both coordinates, i.e., . In the visibility domain, this is mathematically equivalent to flipping the signs of . Therefore, the visibility of 180°-rotated image is
| (B2) |
Thus, subtracting the 180°-rotated image is mathematically equivalent to setting the real part to zero and doubling the value of the imaginary part as follows
| (B3) |
In other words, the real part contains information on both the symmetric and asymmetric structures of objects, whereas the imaginary part contains only information on the asymmetries. Therefore, by synthesizing the image with only the imaginary part, we selectively remove symmetric structures and reveal only asymmetric structures. We determined the minimum r.m.s. in the central region of the images by shifting the images relative to the new GAIA phase center in the visibility domain by a phase shift of , where and are the spatial frequencies and R.A. and DEC are the shift values. Figure 6 shows dust continuum images synthesized with only the imaginary part, including the image with the minimum r.m.s. We found shift values for the minimum r.m.s. (RA, DEC) of (28 mas, 23 mas) relative to the phase center determined by GAIA. The final phase center in the ICRS coordinate is (4h30m51.7325, 24d41m47.152).

Appendix C 12CO channel maps
Figure 7 shows the 12CO channel maps at 1.0 to 13.0 km/s.

Appendix D Trace plots in MCMC calculations
Figure 8 shows trace plots for 100 walkers for 13 parameters in the model in our visibility analyses (§ 4). The burn-in phase is set as the initial 1,000 steps.

Appendix E Histogram of the marginal distributions for the MCMC posteriors

Appendix F Observed and modeled visibilities

Appendix G Weight values and standard deviations in the real and imaginary parts
Figure 11 shows a comparison of the values of weights and standard deviations in the real and imaginary parts. The values of weights () are provided in the measurement set of ALMA data while the standard deviations (stddev) are calculated in each 2 k bin in the deprojected visibilities of the real and imaginary parts with 60 and PA 135. We found that the weights are typically 4.0 higher than 1/stddev2 of the real and imaginary parts at 100–600 k.

References
- Akeson et al. (2019) Akeson, R. L., Jensen, E. L. N., Carpenter, J., et al. 2019, ApJ, 872, 158, doi: 10.3847/1538-4357/aaff6a
- Andrews et al. (2013) Andrews, S. M., Rosenfeld, K. A., Kraus, A. L., & Wilner, D. J. 2013, ApJ, 771, 129, doi: 10.1088/0004-637X/771/2/129
- Andrews et al. (2018) Andrews, S. M., Huang, J., Pérez, L. M., et al. 2018, ApJ, 869, L41, doi: 10.3847/2041-8213/aaf741
- Ansdell et al. (2017) Ansdell, M., Williams, J. P., Manara, C. F., et al. 2017, AJ, 153, 240, doi: 10.3847/1538-3881/aa69c0
- Ansdell et al. (2016) Ansdell, M., Williams, J. P., van der Marel, N., et al. 2016, ApJ, 828, 46, doi: 10.3847/0004-637X/828/1/46
- Baraffe et al. (2015) Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42, doi: 10.1051/0004-6361/201425481
- Beckwith & Sargent (1991) Beckwith, S. V. W., & Sargent, A. I. 1991, ApJ, 381, 250, doi: 10.1086/170646
- Biller et al. (2012) Biller, B., Lacour, S., Juhász, A., et al. 2012, ApJ, 753, L38, doi: 10.1088/2041-8205/753/2/L38
- Calvet et al. (1994) Calvet, N., Hartmann, L., Kenyon, S. J., & Whitney, B. A. 1994, ApJ, 434, 330, doi: 10.1086/174731
- Chang & Oishi (2010) Chang, P., & Oishi, J. S. 2010, ApJ, 721, 1593, doi: 10.1088/0004-637X/721/2/1593
- Cieza et al. (2017) Cieza, L. A., Casassus, S., Pérez, S., et al. 2017, ApJ, 851, L23, doi: 10.3847/2041-8213/aa9b7b
- Cieza et al. (2020) Cieza, L. A., González-Ruilova, C., Hales, A. S., et al. 2020, MNRAS, doi: 10.1093/mnras/staa3787
- Cutri & et al. (2014) Cutri, R. M., & et al. 2014, VizieR Online Data Catalog, II/328
- Cutri et al. (2003) Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog, II/246
- Di Francesco et al. (2008) Di Francesco, J., Johnstone, D., Kirk, H., MacKenzie, T., & Ledwosinska, E. 2008, ApJS, 175, 277, doi: 10.1086/523645
- Dong et al. (2018a) Dong, R., Li, S., Chiang, E., & Li, H. 2018a, ApJ, 866, 110, doi: 10.3847/1538-4357/aadadd
- Dong et al. (2012) Dong, R., Rafikov, R., Zhu, Z., et al. 2012, ApJ, 750, 161, doi: 10.1088/0004-637X/750/2/161
- Dong et al. (2018b) Dong, R., Liu, S.-y., Eisner, J., et al. 2018b, ApJ, 860, 124, doi: 10.3847/1538-4357/aac6cb
- Dressing & Charbonneau (2015) Dressing, C. D., & Charbonneau, D. 2015, ApJ, 807, 45, doi: 10.1088/0004-637X/807/1/45
- Dullemond et al. (2001) Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957, doi: 10.1086/323057
- Dullemond et al. (2018) Dullemond, C. P., Birnstiel, T., Huang, J., et al. 2018, ApJ, 869, L46, doi: 10.3847/2041-8213/aaf742
- Durisen et al. (2007) Durisen, R. H., Boss, A. P., Mayer, L., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 607. https://arxiv.org/abs/astro-ph/0603179
- Foreman-Mackey et al. (2013) Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306, doi: 10.1086/670067
- Francis & van der Marel (2020) Francis, L., & van der Marel, N. 2020, arXiv e-prints, arXiv:2003.00079. https://arxiv.org/abs/2003.00079
- Fukagawa et al. (2013) Fukagawa, M., Tsukagoshi, T., Momose, M., et al. 2013, PASJ, 65, L14, doi: 10.1093/pasj/65.6.L14
- Furlan et al. (2011) Furlan, E., Luhman, K. L., Espaillat, C., et al. 2011, ApJS, 195, 3, doi: 10.1088/0067-0049/195/1/3
- Gaia Collaboration et al. (2020) Gaia Collaboration, Brown, A. G. A., Vallenari, A., et al. 2020, arXiv e-prints, arXiv:2012.01533. https://arxiv.org/abs/2012.01533
- Garufi et al. (2018) Garufi, A., Benisty, M., Pinilla, P., et al. 2018, A&A, 620, A94, doi: 10.1051/0004-6361/201833872
- Gillon et al. (2016) Gillon, M., Jehin, E., Lederer, S. M., et al. 2016, Nature, 533, 221, doi: 10.1038/nature17448
- Hashimoto et al. (2021) Hashimoto, J., Muto, T., Dong, R., et al. 2021, arXiv e-prints, arXiv:2102.05905. https://arxiv.org/abs/2102.05905
- Hashimoto et al. (2012) Hashimoto, J., Dong, R., Kudo, T., et al. 2012, ApJ, 758, L19, doi: 10.1088/2041-8205/758/1/L19
- Herczeg & Hillenbrand (2014) Herczeg, G. J., & Hillenbrand, L. A. 2014, ApJ, 786, 97, doi: 10.1088/0004-637X/786/2/97
- Johnson et al. (2010) Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010, PASP, 122, 905, doi: 10.1086/655775
- Kanagawa et al. (2021) Kanagawa, K. D., Hashimoto, J., Muto, T., et al. 2021, arXiv e-prints, arXiv:2101.10550. https://arxiv.org/abs/2101.10550
- Keppler et al. (2019) Keppler, M., Teague, R., Bae, J., et al. 2019, A&A, 625, A118, doi: 10.1051/0004-6361/201935034
- Kounkel et al. (2019) Kounkel, M., Covey, K., Moe, M., et al. 2019, AJ, 157, 196, doi: 10.3847/1538-3881/ab13b1
- Kraus et al. (2017) Kraus, S., Kreplin, A., Fukugawa, M., et al. 2017, ApJ, 848, L11, doi: 10.3847/2041-8213/aa8edc
- Kurtovic et al. (2020) Kurtovic, N. T., Pinilla, P., Long, F., et al. 2020, arXiv e-prints, arXiv:2012.02225. https://arxiv.org/abs/2012.02225
- Li et al. (2020) Li, Y.-P., Li, H., Li, S., et al. 2020, ApJ, 892, L19, doi: 10.3847/2041-8213/ab7fb2
- Liu et al. (2019) Liu, B., Lambrechts, M., Johansen, A., & Liu, F. 2019, A&A, 632, A7, doi: 10.1051/0004-6361/201936309
- Liu et al. (2020) Liu, B., Lambrechts, M., Johansen, A., Pascucci, I., & Henning, T. 2020, A&A, 638, A88, doi: 10.1051/0004-6361/202037720
- Long et al. (2018) Long, F., Pinilla, P., Herczeg, G. J., et al. 2018, ApJ, 869, 17, doi: 10.3847/1538-4357/aae8e1
- Loomis et al. (2017) Loomis, R. A., Öberg, K. I., Andrews, S. M., & MacGregor, M. A. 2017, ApJ, 840, 23, doi: 10.3847/1538-4357/aa6c63
- Manara et al. (2012) Manara, C. F., Robberto, M., Da Rio, N., et al. 2012, ApJ, 755, 154, doi: 10.1088/0004-637X/755/2/154
- Marino et al. (2015) Marino, S., Perez, S., & Casassus, S. 2015, ApJ, 798, L44, doi: 10.1088/2041-8205/798/2/L44
- Matsumoto et al. (2020) Matsumoto, Y., Gu, P.-G., Kokubo, E., Oshino, S., & Omiya, M. 2020, A&A, 642, A23, doi: 10.1051/0004-6361/202038332
- Mayama et al. (2018) Mayama, S., Akiyama, E., Panić, O., et al. 2018, ApJ, 868, L3, doi: 10.3847/2041-8213/aae88b
- McMullin et al. (2007) McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Society of the Pacific Conference Series, Vol. 376, Astronomical Data Analysis Software and Systems XVI, ed. R. A. Shaw, F. Hill, & D. J. Bell, 127
- Miguel et al. (2020) Miguel, Y., Cridland, A., Ormel, C. W., Fortney, J. J., & Ida, S. 2020, MNRAS, 491, 1998, doi: 10.1093/mnras/stz3007
- Monet et al. (2003) Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984, doi: 10.1086/345888
- Morales et al. (2019) Morales, J. C., Mustill, A. J., Ribas, I., et al. 2019, Science, 365, 1441, doi: 10.1126/science.aax3198
- Ormel (2017) Ormel, C. 2017, in 10th RESCEU/Planet2 Symposium Planet Formation around Snowline, E5
- Ormel & Liu (2018) Ormel, C. W., & Liu, B. 2018, A&A, 615, A178, doi: 10.1051/0004-6361/201732562
- Papaloizou et al. (2007) Papaloizou, J. C. B., Nelson, R. P., Kley, W., Masset, F. S., & Artymowicz, P. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 655. https://arxiv.org/abs/astro-ph/0603196
- Pérez et al. (2018) Pérez, L. M., Benisty, M., Andrews, S. M., et al. 2018, ApJ, 869, L50, doi: 10.3847/2041-8213/aaf745
- Pugh & Winslow (1966) Pugh, E. M., & Winslow, G. H. 1966, The analysis of physical measurements (Reading, MA: Addison-Wesley)
- Raettig et al. (2015) Raettig, N., Klahr, H., & Lyra, W. 2015, ApJ, 804, 35, doi: 10.1088/0004-637X/804/1/35
- Ragusa et al. (2017) Ragusa, E., Dipierro, G., Lodato, G., Laibe, G., & Price, D. J. 2017, MNRAS, 464, 1449, doi: 10.1093/mnras/stw2456
- Ribas et al. (2017) Ribas, Á., Espaillat, C. C., Macías, E., et al. 2017, ApJ, 849, 63, doi: 10.3847/1538-4357/aa8e99
- Rosenfeld et al. (2014) Rosenfeld, K. A., Chiang, E., & Andrews, S. M. 2014, ApJ, 782, 62, doi: 10.1088/0004-637X/782/2/62
- Testi et al. (2014) Testi, L., Birnstiel, T., Ricci, L., et al. 2014, in Protostars and Planets VI, ed. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 339, doi: 10.2458/azu_uapress_9780816531240-ch015
- Toomre (1964) Toomre, A. 1964, ApJ, 139, 1217, doi: 10.1086/147861
- Tsukagoshi et al. (2019) Tsukagoshi, T., Muto, T., Nomura, H., et al. 2019, ApJ, 878, L8, doi: 10.3847/2041-8213/ab224c
- van der Marel et al. (2016) van der Marel, N., Cazzoletti, P., Pinilla, P., & Garufi, A. 2016, ApJ, 832, 178, doi: 10.3847/0004-637X/832/2/178
- van der Marel et al. (2020) van der Marel, N., Birnstiel, T., Garufi, A., et al. 2020, arXiv e-prints, arXiv:2010.10568. https://arxiv.org/abs/2010.10568
- van der Plas et al. (2017) van der Plas, G., Wright, C. M., Ménard, F., et al. 2017, A&A, 597, A32, doi: 10.1051/0004-6361/201629523
- White & Hillenbrand (2004) White, R. J., & Hillenbrand, L. A. 2004, ApJ, 616, 998, doi: 10.1086/425115
- Whitney & Hartmann (1993) Whitney, B. A., & Hartmann, L. 1993, ApJ, 402, 605, doi: 10.1086/172163
- Whitney et al. (2013) Whitney, B. A., Robitaille, T. P., Bjorkman, J. E., et al. 2013, ApJS, 207, 30, doi: 10.1088/0067-0049/207/2/30
- Zhang et al. (2016) Zhang, K., Bergin, E. A., Blake, G. A., et al. 2016, ApJ, 818, L16, doi: 10.3847/2041-8205/818/1/L16
- Zhu (2019) Zhu, Z. 2019, MNRAS, 483, 4221, doi: 10.1093/mnras/sty3358