date912017
An approximate randomization test for high-dimensional two-sample Behrens-Fisher problem under arbitrary covariances
Abstract
This paper is concerned with the problem of comparing the population means of two groups of independent observations. An approximate randomization test procedure based on the test statistic of Chen and Qin, (2010) is proposed. The asymptotic behavior of the test statistic as well as the randomized statistic is studied under weak conditions. In our theoretical framework, observations are not assumed to be identically distributed even within groups. No condition on the eigenstructure of the covariance matrices is imposed. And the sample sizes of the two groups are allowed to be unbalanced. Under general conditions, all possible asymptotic distributions of the test statistic are obtained. We derive the asymptotic level and local power of the approximate randomization test procedure. Our theoretical results show that the proposed test procedure can adapt to all possible asymptotic distributions of the test statistic and always has correct test level asymptotically. Also, the proposed test procedure has good power behavior. Our numerical experiments show that the proposed test procedure has favorable performance compared with several alternative test procedures.
Key words: Behrens-Fisher problem; High-dimensional data; Randomization test; Lindeberg principle.
1 Introduction
Two-sample mean testing is a fundamental problem in statistics with an enormous range of applications. In modern statistical applications, high-dimensional data, where the data dimension may be much larger than the sample size, is ubiquitous. However, most classical two-sample mean tests are designed for low-dimensional data, and may not be feasible, or may have suboptimal power, for high-dimensional data; see, e.g., Bai and Saranadasa, (1996). In recent years, the study of high-dimensional two-sample mean tests has attracted increasing attention.
Suppose that , , , are independent -dimensional random vectors with , . The hypothesis of interest is
| (1) |
Denote by the average covariance matrix within group , . Most existing methods on two-sample mean tests assumed that the observations within groups are identically distributed. In this case, , , , and the considered testing problem reduces to the well-known Behrens-Fisher problem. In this paper, we consider the more general setting where the observations are allowed to have different distributions even within groups. Also, we consider the case where the data is possibly high-dimensional, that is, the data dimension may be much larger than the sample size , .
Let and denote the sample mean vector and the sample covariance matrix of group , respectively, . Denote . A classical test statistic for hypothesis (1) is Hotelling’s statistic, defined as
where is the pooled sample covariance matrix. When , the matrix is not invertible, and consequently Hotelling’s statistic is not well-defined. In a seminal work, Bai and Saranadasa, (1996) proposed the test statistic
where is the data matrix of group , . The test statistic is well-defined for arbitrary . Bai and Saranadasa, (1996) assumed that the observations within groups are identically distributed and . The main term of is . Chen and Qin, (2010) removed terms from and proposed the test statistic
The test method of Chen and Qin, (2010) can be applied when . Both Bai and Saranadasa, (1996) and Chen and Qin, (2010) used the asymptotical normality of the statistics to determine the critical value of the test. However, the asymptotical normality only holds for a restricted class of covariance structures. For example, Chen and Qin, (2010) assumed that
| (2) |
However, (2) may not hold when has a few eigenvalues significantly larger than the others, excluding some important senarios in practice. For example, (2) is often violated when the variables are affected by some common factors; see, e.g., Fan et al., (2021) and the references therein. If the condition (2) is violated, the test procedures of Bai and Saranadasa, (1996) and Chen and Qin, (2010) may have incorrect test level; see, e.g., Wang and Xu, (2019). For years, how to construct test procedures that are valid under general covariances has been an important open problem in the field of high-dimensional hypothesis testing; see the review paper of Hu and Bai, (2016).
Intuitively, one may resort to the bootstrap method to control the test level under general covariances. Surprisingly, as shown by our numerical experiments, the empirical bootstrap method does not work well for . Also, the wild bootstrap method, which is popular in high-dimensional statistics, does not work well either. We will give heuristic arguments to understand this phenomenon in Section 3. Recently, several methods were proposed to give a better control of the test level of and related test statistics. In the setting of , Zhang et al., (2020) considered the statistic and proposed to use the Welch-Satterthwaite -approximation to determine the critical value. Subsequently, Zhang et al., (2021) extended the test procedure of Zhang et al., (2020) to the two-sample Behrens-Fisher problem, and Zhang and Zhu, (2021) considered a -approximation of . However, the test methods of Zhang et al., (2020), Zhang et al., (2021) and Zhang and Zhu, (2021) still require certain conditions on the eigenstructure of , . In another work, Wu et al., (2018) investigated the general distributional behavior of for one-sample mean testing problem. They proposed a half-sampling procedure to determine the critical value of the test statistic. A generalization of the method of Wu et al., (2018) to the statistc for the two-sample Behrens-Fisher problem when both and are even numbers was presented in Chapter 2 of Lou, (2020). Unfortunately, Wu et al., (2018) and Lou, (2020) did not include detailed proofs of their theoretical results. Recently, Wang and Xu, (2019) considered a randomization test based on the test statistic of Chen and Qin, (2010) for the one-sample mean testing problem. Their randomization test has exact test level if the distributions of the observations are symmetric and has asymptotically correct level in the general setting. Although many efforts have been made, no existing test procedure based on is valid for arbitrary with rigorous theoretical guarantees.
The statistics and are based on sum-of-squares. Some researchers investigated variants of sum-of-squares statistics that are scalar-invariant; see, e.g., Srivastava and Du, (2008), Srivastava et al., (2013) and Feng et al., (2015). These test methods also impose some nontrivial assumptions on the eigenstructure of the covariance matrices. There is another line of research initiated by Cai et al., (2013) which utilizes extreme value type statistics to test hypothesis (1). Chang et al., (2017) considered a parametric bootstrap method to determine the critical value of the extreme value type statistics. The method of Chang et al., (2017) allows for general covariance structures. Recently, Xue and Yao, (2020) investigated a wild bootstrap method. The test procedure in Xue and Yao, (2020) does not require that the observations within groups are identically distributed. The theoretical analyses in Chang et al., (2017) and Xue and Yao, (2020) are based on recent results about high-dimensional bootstrap methods developed by Chernozhukov et al., (2013) and Chernozhukov et al., (2017). While their theoretical framework can be applied to extreme value type statistics, it can not be applied to sum-of-squares type statistics like . Indeed, we shall see that the wild bootstrap method does not work well for .
In the present paper, we propose a new test procedure based on . In the proposed test procedure, we use a new randomization method to determine the critical value of the test statistic. The proposed randomization method is motivated by the randomization method proposed in Fisher, (1935), Section 21. While this randomization method is widely used in one-sample mean testing problem, it can not be directly applied to two-sample Behrens-Fisher problem. In comparison, the proposed randomization method has satisfactory performance for two-sample Behrens-Fisher problem. We investigate the asymptotic properties of the proposed test procedure and rigorously prove that it has correct test level asymptotically under fairly weak conditions. Compared with existing test procedures based on sum-of-squares, the present work has the following favorable features. First, the proposed test procedure has correct test level asymptotically without any restriction on , . As a consequence, the proposed test procedure serves as a rigorous solution to the open problem that how to construct a valid test based on under general covariances. Second, the proposed test procedure is valid even if the observations within groups are not identically distributed. To the best of our knowledge, the only existing method that can work in such a general setting is the test procedure in Xue and Yao, (2020). However, the test procedure in Xue and Yao, (2020) is based on extreme value statistic, which is different from the present work. Third, our theoretical results are valid for arbitrary and as long as . In comparison, all the above mentioned methods only considered the balanced data, that is, the sample sizes and are of the same order. We also derive the asymptotic local power of the proposed method. It shows that the asymptotic local power of the proposed test procedure is the same as that of the oracle test procedure where the distribution of the test statistic is known. A key tool for the proofs of our theoretical results is a universality property of the generalized quadratic forms. This result may be of independent interest. We also conduct numerical experiments to compare the proposed test procedure with some existing methods. Our theoretical and numerical results show that the proposed test procedure has good performance in both level and power.
2 Asymptotics of
In this section, we investigate the asymptotic behavior of under general conditions. We begin with some notations. For two random variables and , let denote the distribution of , and denote the conditional distribution of given . For two probability measures and on , let be the signed measure such that for any Borel set , . Let denote the class of bounded functions with bounded and continuous derivatives up to order . It is known that a sequence of random variables converges weakly to a random variable if and only if for every , ; see, e.g., Pollard, (1984), Chapter III, Theorem 12. We use this property to give a metrization of the weak convergence in . For a function , let denote the th derivative of , . For a finite signed measure on , we define the norm as , where the supremum is taken over all such that and , . It is straightforward to verify that is indeed a norm for finite signed measures. Also, a sequence of probability measures converges weakly to a probability measure if and only if ; see, e.g., Dudley, (2002), Corollary 11.3.4.
The test procedure of Chen and Qin, (2010) determines the critical value based on the asymptotic normality of under the null hypothesis. Define , , . Then . Under the null hypothesis, we have where , . Denote by the variance of . Under certain conditions, Chen and Qin, (2010) proved that converges weakly to . They reject the null hypothesis if is greater than the quantile of where is an estimate of and is the test level. However, we shall see that normal distribution is just one of the possible asymptotic distributions of in the general setting.
Now we list the main conditions imposed by Chen and Qin, (2010) to prove the asymptotic normality of . First, Chen and Qin, (2010) imposed the condition (2) on the eigenstructure of , . Second, Chen and Qin, (2010) assumed that as ,
| (3) |
That is, Chen and Qin, (2010) assumed the sample sizes in two groups are balanced. This condition is commonly adopted by existing test procedures for hypothesis (1). Third, Chen and Qin, (2010) assumed the general multivariate model
| (4) |
where is a matrix for some , , and are -dimensional independent and identically distributed random vectors such that , , and the elements of satisfy , and for a positive integer such that and distinct . We note that the general multivariate model (4) assumes that the observations within group are identically distributed, . Also, the elements of have finite moments up to order and behave as if they are independent.
As we have noted, the condition (2) can be violated when the variables are affected by some common factors. The condition (3) is assumed by most existing test methods. However, this condition is not reasonable if the sample sizes are unbalanced. The general multivariate model (4) is commonly adopted by many high-dimensional test methods; see, e.g., Chen and Qin, (2010), Zhang et al., (2020) and Zhang et al., (2021). However, the conditions on may be difficult to verify and are not generally satisfied by the elliptical symmetric distributions. Also, the model (4) is not valid if the observations within groups are not identically distributed. Thus, we would like to investigate the asymptotic behavior of beyond the conditions (2), (3) and (4). We consider the asymptotic setting where and all quantities except for absolute constants are indexed by , a subscript we often suppress. We make the following assumption on and .
Assumption 1.
Suppose as , .
Assumption 1 only requires that both and tend to infinity, which allows for the unbalanced sample sizes. This relaxes the condition (3). We make the following assumption on the distributions of , , .
Assumption 2.
Assume there exists an absolute constant such that for any positive semi-definite matrix ,
Intuitively, Assumption 2 requires that the fourth moments of are of the same order as the squared second moments of . We shall see that this assumption is fairly weak. However, the above inequality is required to be satisfied for all positive semi-definite matrix , which may not be straightforward to check in some cases. The following lemma gives a sufficient condition of Assumption 2.
Lemma 1.
Suppose , , , where is an arbitrary matrix and is an arbitrary positive integer. Suppose , , and the elements of satisfy where is an absolute constant. Suppose for any distinct ,
| (5) |
Then Assumption 2 holds with .
It can be seen that the conditions of Lemma 1 is strictly weaker than the multivariate model (4). In fact, Lemma 1 does not require , nor does it require the finiteness of th moments of . Also, the moment conditions in (5) are much weaker than that required by the multivariate model (4). In addition to the multivariate model (4), the conditions of Lemma 1 also allow for an important class of elliptical symmetric distributions. In fact, if has an elliptical symmetric distribution, then can be written as , where is a matrix, is a random vector distributed uniformly on the unit sphere in , and is a nonnegative random variable which is independent of ; see, e.g., Fang et al., (1990), Theorem 2.5. Suppose there is an absolute constant such that . Then from the symmetric property of and the independence of and , the conditions of Lemma 1 hold. In comparison, the multivariate model (4) does not allow for elliptical symmetric distributions in general.
Most existing test methods for the hypothesis (1) assume that the observations within groups are identically distributed. In this case, Assumptions 1 and 2 are all we need, and we completely avoid an assumption on the eigenstucture of like (2). In the general setting, may be different within groups, and we make the following assumption to avoid the case in which there exist certain observations with significantly larger variance than the others.
Assumption 3.
Suppose that as ,
If the covariance matrices within groups are equal, i.e., , , , then Assumption 3 holds for arbitrary , , provided as . In this view, Assumption 3 imposes no restriction on , .
Define . Let be a -dimensional standard normal random vector. We have the following theorem.
Theorem 1 characterizes the general distributional behavior of . It implies that the distributions of and are equivalent asymptotically. To gain further insights on the distributional behavior of , we would like to derive the asymptotic distributions of . However, Theorem 1 implies that may not converge weakly in general. Nevertheless, is uniformly tight and we can use Theorem 1 to derive all possible asympotitc distributions of .
Corollary 1.
Suppose the conditions of Theorem 1 hold. Then is uniformly tight and all possible asymptotic distributions of are give by
| (6) |
where is a sequence of independent standard normal random variables, is a sequence of positive numbers such that and is the almost sure limit of as .
Remark 1.
Corollary 1 gives a full characteristic of the possible asymptotic distributions of . In general, these possible asymptotic distributions are weighted sums of an independent normal random variable and centered random variables. From the proof of Corollary 1, the parameters are in fact the limit of the eigenvalues of the matrix along a subsequence of . If , then (6) becomes the standard normal distribution, and the test procedure of Chen and Qin, (2010) has correct level asymptotically. On the other hand, if , then (6) becomes the distribution of a weighted sum of independent centered random variables. This case was considered in Zhang et al., (2021). However, these two settings are just special cases among all possible asymptotic distributions where . In general, the distribution (6) relies on the nuisance paramters . To construct a test procedure based on the asymptotic distributions, one needs to estimate these nuisance parameters consistently. Unfortunately, the estimation of the eigenvalues of high-dimensional covariance matrices may be a highly nontrivial task; see, e.g., Kong and Valiant, (2017) and the references therein. Hence in general, it may not be a good choice to construct test procedures based on the asymptotic distributions.
3 Test procedure
An intuitive idea to control the test level of in the general setting is to use the bootstrap method. Surprisingly, the empirical bootstrap method and wild bootstrap method may not work for . This phenomenon will be shown by our numerical experiments. For now, we give a heuristic argument to understand this phenomenon. First we consider the empirical bootstrap method. Suppose the resampled observations are uniformly sampled from with replacement, . Denote , . The empirical bootstrap method uses the conditional distribution to approximate the null distribution of . If this bootstrap method can work, one may expect that the first two moments of can approximately match the first two moments of under the null hypothesis. Under the null hypothesis, we have . Lemma S.5 implies that under Assumptions 1 and 3 and under the null hypothesis,
On the othen hand, it is straightforward to show that . Also, under Assumptions 1 and 3,
Unfortunately, is not a ratio-consistent estimator of even in the settings where is normally distributed, the covariance matrices , , , are all equal and ; see, e.g., Bai and Saranadasa, (1996) and Zhou and Guo, (2017). Consequently, the empirical bootstrap method may not be valid for .
We turn to the wild bootstrap method. Recently, the wild bootstrap method has been widely used for extreme value type statistics in the high-dimensional setting; see, e.g., Chernozhukov et al., (2013), Chernozhukov et al., (2017), Xue and Yao, (2020) and Deng and Zhang, (2020). For the wild bootstrap method, the resampled observations are defined as , , , where are independent and identically distributed random variables with and , and are independent of the original data , . We have . With some tedious but straightforward derivations, it can be seen that under Assumptions 1 and 3,
where is the bias term and satisfies
The above inequality implies that the bias term may not be negligible compared with . For example, if , , , then we have and . In this case, the bias term is not negligible provided . Thus, the wild bootstrap method may not be valid for either.
We have seen that the methods based on asymptotic distributions and the bootstrap methods may not work well for the test statistic . These phenomenons imply that it is highly nontrivial to construct a valid test procedure based on . To construct a valid test procedure, we resort to the idea of the randomization test, a powerful tool in statistical hypothesis testing. The randomization test is an old idea and can at least date back to Fisher, (1935), Section 21; see Hoeffding, (1952), Lehmann and Romano, (2005), Section 15.2, Zhu, (2005) and Hemerik and Goeman, (2018) for general frameworks and extensions of the randomization tests. The original randomization method considered in Fisher, (1935), Section 21 can be abstracted into the following general form. Suppose are independent -dimensional random vectors such that . Let be any statistics taking values in . Suppose are independent and identically distributed Rademacher random variables, i.e., , and are independent of . Define the conditional cumulative distribution function as . Then from the theory of randomization test (see, e.g., Lehmann and Romano, (2005), Section 15.2), for any ,
where for any right continuous cumulative distribution function on , for . Also, under mild conditions, the difference between the above probability and is negligible.
To apply Fisher’s randomization method to specific problems, the key is to construct random variables such that under the null hypothesis. This randomization method can be directly applied to one-sample mean testing problem, as did in Wang and Xu, (2019). However, it can not be readily applied to the testing problem (1). In fact, the mean vector of is unknown under the null hypothesis, and consequently, one can not expect that holds under the null hypothesis. As a result, can not serve as in Fisher’s randomization method.
We observe that the difference has zero means and hence is free of the mean vector . Also, if , then . These facts imply that Fisher’s randomization method may be applied to the random vectors , , where , . Define
where , . Let where are independent and identically distributed Rademacher random variables which are independent of , . Define randomized statistic
Define the conditional distribution function . From Fisher’s randomization method, if , then for , . It can be seen that and take a similar form. Also, under the null hypothesis, and . Thus, it may be expected that under the null hypothesis. On the other hand, the classical results of Hoeffding, (1952) on randomization tests give the insight that the randomness of may be negligible for large samples. From the above insights, it can be expected that under the null hypothesis, for ,
Motivated by the above heuristics, we propose a new test procedure which rejects the null hypothesis if
While the assumption is used in the above heuristic arguments, it will not be assumed in our theoretical analysis. This generality may not be surprising. Indeed, for low-dimensional testing problems, it is known that such symmetry conditions can often be relaxed for randomization tests; see, e.g., Romano, (1990), Chung and Romano, (2013) and Canay et al., (2017). In the proposed procedure, the conditional distribution is used to approximate the null distribution of . We have . From Lemma S.10, under Assumptions 1-3, we have
That is, the first two moments of can match those of . As we have seen, this favorable property is not shared by the empirical bootstrap method and wild bootstrap method.
We should emphasis that the proposed test procedure is only inspired by the randomization test, and is not a randomization test in itself. As a consequence, it can not be expected that the proposed test can have an exact control of the test level. In fact, even if the observations are -dimensional and normally distributed, the exact control of the test level for Behrens-Fisher problem is not trivial; see Linnik, (1966) and the references therein. Nevertheless, we shall show that the proposed test procedure can control the test level asymptotically under Assumptions 1-3.
The conditional distribution is a discrete distribution uniformly distributed on values. Hence it is not feasible to compute the exact quantile of . In practice, one can use a finite sample from to approximate the -value of the proposed test procedure; see, e.g., Lehmann and Romano, (2005), Chapter 15. More specifically, given data, we can independently sample and compute , , where is a sufficiently large number. Then the null hypothesis is rejected if
In the above procedure, one needs to compute the original statistic and the randomized statistics . The direct computation of the original statistic costs time. During the computation of , we can cache the inner products , , , and , , . Then the computation of only requires time. In total, the computation of the proposed test procedure can be completed within time.
Now we rigorously investigate the theoretical properties of the proposed test procedure. From Theorem 1, the distribution of is asymptotically equivalent to the distribution of a quadratic form in normal random variables. Now we show that the conditional distribution is equivalent to the same quadratic form. In fact, our result is more general and includes the case that the elements of are generated from the standard normal distribution.
Theorem 2.
Suppose the conditions of Theorem 1 hold. Let , where are independent and identically distributed random variables, and is a standard normal random variable or a Rademacher random variable. Then as ,
From Theorems 1 and 2, the conditional distribution is asymptotically equivalent to the distribution of under the null hypothesis. These two theorems allow us to derive the asymptotic level and local power of the proposed test procedure. Let denote the cumulative distribution function of .
Corollary 2.
Suppose the conditions of Theorem 1 hold, is an absolute constant and as , . Then as ,
Corollary 2 implies that under the conditions of Theorem 1, the proposed test procedure has correct test level asymptotically. In particular, Corollary 2 provides a rigorous theoretical guarantee of the validity of the proposed test procedure for two-sample Behrens-Fisher problem with arbitrary , . Furthermore, the proposed test procedure is still valid when the observations are not identically distributed within groups and the sample sizes are unbalanced. To the best of our knowledge, the proposed test procedure is the only one that is guaranteed to be valid in such a general setting. Corollary 2 also gives the asymptotic power of the proposed test procedure under the local alternative hypotheses. If is asymptotically normally distributed, that is, converges weakly to the cumulative distribution function of the standard normal distribution, then the proposed test procedure has the same local asymptotic power as the test procedure of Chen and Qin, (2010). In general, the proposed test procedure has the same local asymptotic power as the oracle test procedure which rejects the null hypothesis when is greater than the quantile of . Thus, the proposed test procedure has good power behavior.
4 Simulations
In this section, we conduct simulations to examine the performance of the proposed test procedure and compare it with alternative test procedures. The first competing test procedures are based on , including the original test procedure of Chen and Qin, (2010) which is based on the asymptotic normality of , the test procedure based on the empirical bootstrap method, the wild bootstrap method described in Section 3 where are Rademacher random variables, and the -approximation method in Zhang and Zhu, (2021). The next competing test procedures are based on the statistic , including the -approximation method in Zhang et al., (2021) and the half-sampling method in Lou, (2020). The last competing test procedures are scalar-invariant tests of Srivastava and Du, (2008), Srivastava et al., (2013) and Feng et al., (2015).
In our simulations, the nominal test level is . For the proposed method and competing resampling methods, the resampling number is . The reported empirical sizes and powers are computed based on independent replications. We consider the following data generation models for .
-
•
Model I: , , .
-
•
Model II: , , , where with
-
•
Model III: , , , where , and are independent standardized random variables with degree of freedom, that is, . For , , and for , .
-
•
Model IV: The th element of is , , , , where are independent standardized random variables with degree of freedom.
For Model I, observations are simply normal random vectors with identity covariance matrix. For Model II, the variables are correlated, and the condition (2) is not satisfied. For Model III, are not equal and the observations have skewed distributions. For Model IV, the variables are correlated and their variances are different.
| Model | NEW | CQ | EB | WB | ZZ | ZZGZ | LOU | SD | SKK | FZWZ | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 8 | 12 | 300 | 4.95 | 5.42 | 0.00 | 1.32 | 4.92 | 5.46 | 6.13 | 3.77 | 32.8 | 3.20 |
| 16 | 24 | 300 | 5.19 | 5.94 | 0.00 | 3.88 | 5.41 | 5.72 | 5.98 | 4.37 | 14.4 | 5.08 | |
| 32 | 48 | 300 | 5.00 | 5.65 | 0.00 | 4.79 | 5.21 | 5.33 | 5.42 | 4.21 | 8.36 | 5.11 | |
| 8 | 12 | 600 | 5.07 | 5.52 | 0.00 | 0.45 | 4.99 | 5.73 | 6.22 | 2.62 | 48.2 | 2.55 | |
| 16 | 24 | 600 | 4.85 | 5.44 | 0.00 | 2.25 | 5.07 | 5.40 | 5.57 | 3.05 | 17.5 | 4.21 | |
| 32 | 48 | 600 | 5.23 | 5.50 | 0.00 | 4.22 | 5.21 | 5.35 | 5.40 | 3.94 | 9.48 | 5.14 | |
| II | 8 | 12 | 300 | 8.99 | 10.1 | 5.91 | 8.56 | 8.23 | 9.87 | 9.14 | 3.31 | 5.94 | 7.78 |
| 16 | 24 | 300 | 6.65 | 8.15 | 5.54 | 6.70 | 6.41 | 7.39 | 6.70 | 2.12 | 3.52 | 7.37 | |
| 32 | 48 | 300 | 5.46 | 7.45 | 5.14 | 5.56 | 5.34 | 6.25 | 5.57 | 1.85 | 2.52 | 7.04 | |
| 8 | 12 | 600 | 9.02 | 10.4 | 6.10 | 8.80 | 8.44 | 9.85 | 9.48 | 2.64 | 4.77 | 8.02 | |
| 16 | 24 | 600 | 6.10 | 7.83 | 4.79 | 5.95 | 5.60 | 6.84 | 6.06 | 1.64 | 2.60 | 6.72 | |
| 32 | 48 | 600 | 5.27 | 7.09 | 4.71 | 5.20 | 5.07 | 5.87 | 5.20 | 1.18 | 1.78 | 6.65 | |
| III | 8 | 12 | 300 | 5.23 | 5.50 | 0.00 | 1.30 | 1.63 | 2.18 | 6.14 | 0.17 | 14.1 | 0.00 |
| 16 | 24 | 300 | 5.31 | 5.63 | 0.00 | 3.78 | 2.89 | 3.22 | 5.71 | 0.22 | 8.30 | 0.00 | |
| 32 | 48 | 300 | 5.56 | 6.09 | 0.01 | 5.10 | 3.94 | 4.16 | 5.81 | 0.16 | 6.79 | 0.13 | |
| 8 | 12 | 600 | 5.58 | 5.77 | 0.00 | 0.58 | 2.04 | 2.46 | 6.38 | 0.00 | 19.5 | 0.00 | |
| 16 | 24 | 600 | 5.01 | 5.28 | 0.00 | 2.39 | 2.64 | 2.94 | 5.46 | 0.00 | 10.5 | 0.00 | |
| 32 | 48 | 600 | 5.00 | 5.32 | 0.00 | 4.20 | 3.64 | 3.82 | 5.12 | 0.02 | 7.11 | 0.03 | |
| IV | 8 | 12 | 300 | 5.90 | 7.27 | 1.33 | 5.92 | 5.22 | 6.15 | 6.64 | 3.05 | 11.2 | 2.05 |
| 16 | 24 | 300 | 5.21 | 6.73 | 2.29 | 5.49 | 4.63 | 5.35 | 5.48 | 3.25 | 6.90 | 3.53 | |
| 32 | 48 | 300 | 5.03 | 6.76 | 3.17 | 5.58 | 4.92 | 5.50 | 5.38 | 4.02 | 5.82 | 5.21 | |
| 8 | 12 | 600 | 5.97 | 7.49 | 1.29 | 6.03 | 5.20 | 6.17 | 6.75 | 2.24 | 14.4 | 1.48 | |
| 16 | 24 | 600 | 5.60 | 7.19 | 2.37 | 5.99 | 5.06 | 5.91 | 5.94 | 2.52 | 7.62 | 3.13 | |
| 32 | 48 | 600 | 5.50 | 7.11 | 3.59 | 5.90 | 5.16 | 5.90 | 5.85 | 3.66 | 5.86 | 4.46 |
NEW, the proposed test procedure; CQ, the test of Chen and Qin, (2010); EB, the empirical bootstrap method based on ; WB, the wild bootstrap method based on ; ZZ, the test of Zhang and Zhu, (2021); ZZGZ, the test of Zhang et al., (2021); LOU, the test of Lou, (2020); SD, the test of Srivastava and Du, (2008); SKK, the test of Srivastava et al., (2013); FZWZ, the test of Feng et al., (2015).
In Section S.1, we give quantile-quantile plots to examine the correctness of Theorem 1 and Corollary 1 of the proposed test statistic. The results show that the distribution approximation in Theorem 1 is quite accurate, and the asymptotic distributions in Corollary 1 are reasonable even for finite sample size.
Now we consider the simulations of empirical sizes. We take . Table 1 lists the empirical sizes of various test procedures. It can be seen that the test procedure of Chen and Qin, (2010) tends to have inflated empirical sizes, especially for Models II and IV. The empirical bootstrap method does not work well for Models I, III and IV. While the wild bootstrap method has a better performance than the empirical bootstrap method, it is overly conservative for Models I and III when is small. The performance of bootstrap methods confirm our heuristic arguments in Section 3. It is interesting that the empirical bootstrap method has relatively good performance for Model II. In fact, in Model II, has a low-rank structure, and therefore, the test statistic may have a similar behavior as in the low-dimensional setting. It is known that the empirical bootstrap method has good performance in the low-dimensional setting. Hence it is reasonable that the empirical bootstrap method works well for Model II. The -approximation methods of Zhang et al., (2021) and Zhang and Zhu, (2021) have reasonable performance under Model I, II and IV, but are overly conservative for Model III. The half-sampling method of Lou, (2020) has inflated empirical sizes, especially for small . Compared with the test procedures based on or , the scalar-invariant tests of Srivastava and Du, (2008), Srivastava et al., (2013) and Feng et al., (2015) have relatively poor performance, especially when is small. For Models I, III and IV, the empirical sizes of the proposed test procedure are quite close to the nominal test level. For Model II, all test procedures based on or have inflated empirical sizes. For this model, the proposed test procedure outperforms the test procedure of Chen and Qin, (2010). Also, as increases, the empirical sizes of the proposed test procedure tends to the nominal test level. For , , the proposed test procedure has reasonable performance in all settings. Overall, the proposed test procedure has reasonably good performance in terms of empirical sizes, which confirms our theoretical results.
| Model | NEW | CQ | EB | WB | ZZ | ZZGZ | LOU | SD | SKK | FZWZ | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 8 | 12 | 1 | 24.4 | 26.4 | 0.00 | 10.6 | 23.5 | 26.7 | 28.0 | 19.9 | 65.9 | 16.7 |
| 16 | 24 | 1 | 25.3 | 27.1 | 0.01 | 20.7 | 26.0 | 26.7 | 27.2 | 21.5 | 43.7 | 23.2 | |
| 32 | 48 | 1 | 25.3 | 27.2 | 0.37 | 24.2 | 25.8 | 26.2 | 26.5 | 22.8 | 33.7 | 25.6 | |
| 8 | 12 | 2 | 55.5 | 59.1 | 0.0 | 35.1 | 53.8 | 59.6 | 61.0 | 48.2 | 88.7 | 43.4 | |
| 16 | 24 | 2 | 57.7 | 60.5 | 0.22 | 51.5 | 58.9 | 59.9 | 60.7 | 52.1 | 75.5 | 54.5 | |
| 32 | 48 | 2 | 58.5 | 60.5 | 3.88 | 57.3 | 58.8 | 59.3 | 59.6 | 55.5 | 66.3 | 58.2 | |
| II | 8 | 12 | 1 | 28.1 | 31.7 | 24.0 | 28.3 | 27.8 | 31.0 | 29.5 | 16.4 | 21.8 | 26.4 |
| 16 | 24 | 1 | 25.5 | 30.0 | 24.2 | 26.6 | 26.0 | 28.0 | 26.6 | 14.9 | 17.9 | 27.8 | |
| 32 | 48 | 1 | 24.5 | 29.3 | 23.7 | 25.0 | 24.5 | 26.7 | 25.3 | 13.7 | 16.1 | 28.4 | |
| 8 | 12 | 2 | 46.7 | 50.9 | 42.4 | 47.5 | 46.8 | 50.3 | 48.7 | 31.8 | 38.7 | 45.0 | |
| 16 | 24 | 2 | 44.3 | 50.6 | 43.1 | 46.2 | 45.4 | 48.5 | 46.5 | 29.6 | 34.6 | 48.1 | |
| 32 | 48 | 2 | 44.0 | 50.0 | 43.1 | 44.6 | 44.2 | 46.6 | 44.9 | 29.4 | 32.9 | 48.8 | |
| III | 8 | 12 | 1 | 24.8 | 25.9 | 0.00 | 11.1 | 12.7 | 14.7 | 27.3 | 0.01 | 34.0 | 0.00 |
| 16 | 24 | 1 | 25.5 | 27.2 | 0.02 | 20.8 | 17.5 | 18.7 | 27.1 | 0.00 | 28.2 | 0.01 | |
| 32 | 48 | 1 | 25.1 | 26.8 | 0.49 | 24.2 | 20.7 | 21.3 | 26.0 | 0.03 | 24.4 | 1.22 | |
| 8 | 12 | 2 | 57.9 | 60.7 | 0.00 | 36.9 | 39.4 | 43.9 | 62.0 | 0.00 | 80.1 | 0.00 | |
| 16 | 24 | 2 | 57.9 | 60.2 | 0.29 | 52.5 | 47.8 | 49.6 | 60.0 | 0.10 | 69.3 | 0.87 | |
| 32 | 48 | 2 | 59.7 | 61.7 | 5.37 | 58.6 | 54.0 | 54.8 | 60.6 | 0.36 | 63.2 | 12.4 | |
| IV | 8 | 12 | 1 | 22.3 | 26.9 | 7.83 | 22.6 | 20.6 | 23.3 | 25.1 | 100 | 100 | 100 |
| 16 | 24 | 1 | 21.4 | 25.9 | 12.2 | 22.8 | 20.2 | 22.3 | 22.7 | 100 | 100 | 100 | |
| 32 | 48 | 1 | 21.3 | 26.4 | 15.7 | 22.5 | 20.8 | 22.6 | 22.2 | 100 | 100 | 100 | |
| 8 | 12 | 2 | 49.9 | 57.0 | 24.2 | 51.2 | 47.7 | 51.6 | 54.3 | 100 | 100 | 100 | |
| 16 | 24 | 2 | 49.5 | 56.5 | 33.1 | 51.7 | 47.7 | 51.2 | 51.9 | 100 | 100 | 100 | |
| 32 | 48 | 2 | 49.4 | 56.5 | 39.6 | 51.1 | 48.4 | 51.0 | 50.5 | 100 | 100 | 100 |
NEW, the proposed test procedure; CQ, the test of Chen and Qin, (2010); EB, the empirical bootstrap method based on ; WB, the wild bootstrap method based on ; ZZ, the test of Zhang and Zhu, (2021); ZZGZ, the test of Zhang et al., (2021); LOU, the test of Lou, (2020); SD, the test of Srivastava and Du, (2008); SKK, the test of Srivastava et al., (2013); FZWZ, the test of Feng et al., (2015).
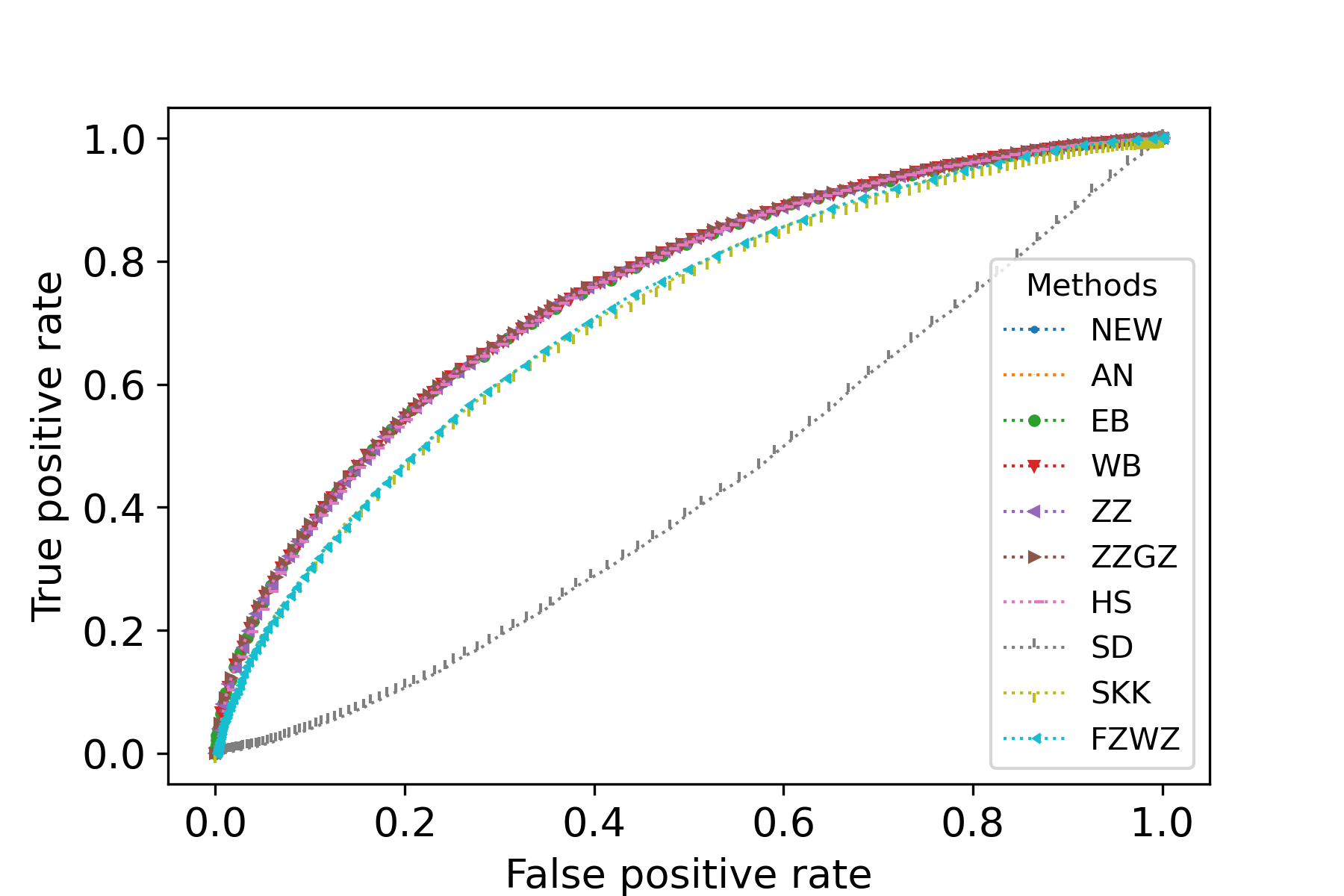
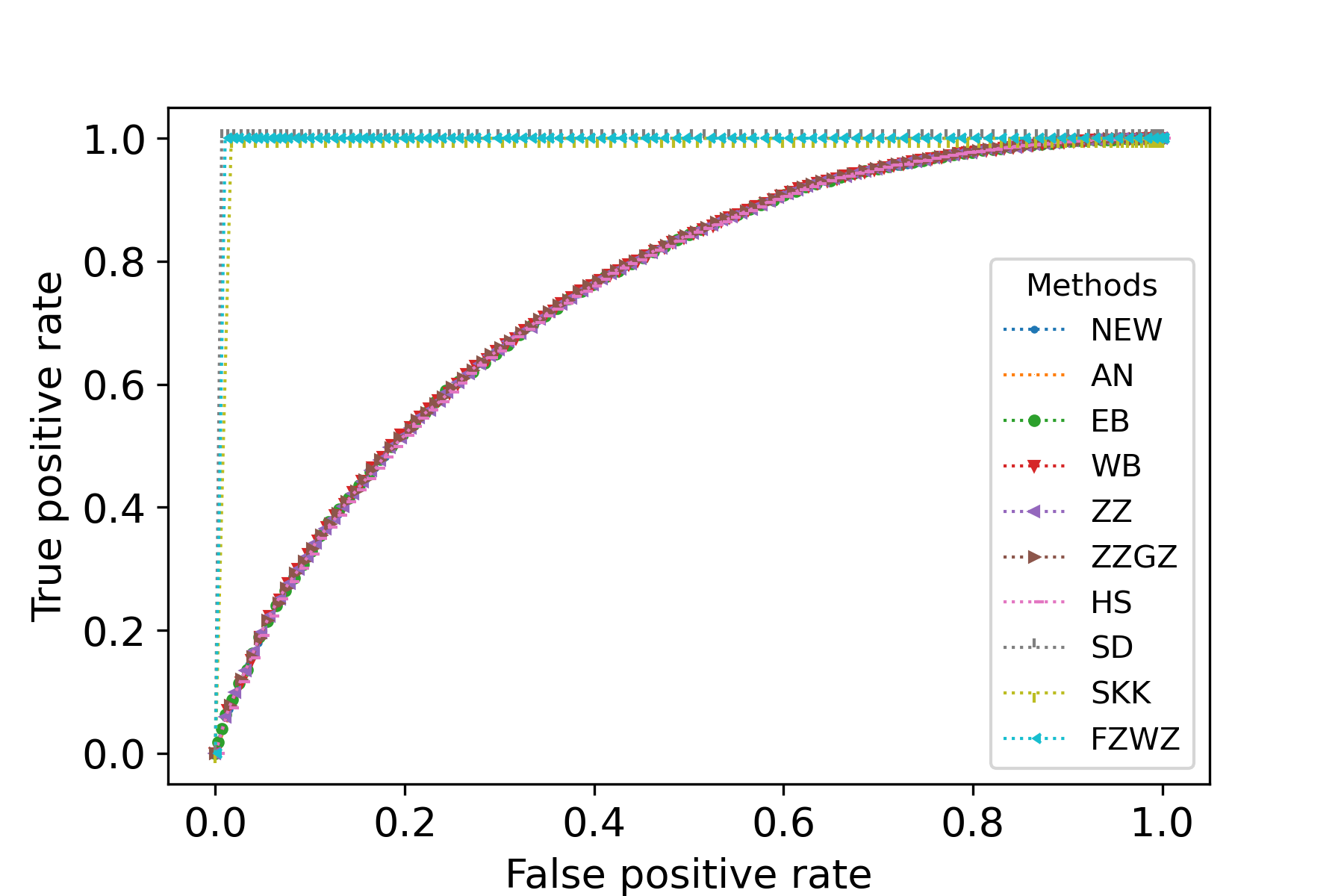
Now we consider the empirical powers of various test procedures. In view of the expression of the asymptotic power given in Corollary 2, we define the signal-to-noise ratio . We take and where is chosen such that reaches given values of signal-to-noise ratio. Table 2 lists the empirical powers of various test procedures when . It can be seen that for Model IV where the variables have different variance scale, the scalar-invariant tests have better performance than other tests. However, for Model III where are not identical and the observations have skewed distributions, the scalar-invariant tests have relatively low powers. The proposed test procedure has a reasonable power behavior among the test procedures based on or . We have seen that some competing tests do not have a good control of test level. To get rid of the effect of distorted test level on the power, we present the receiver operating characteristic curves of the test procedures in Section S.1. It shows that for a given test level, all test procedures based on or have quite similar power behavior. In summary, the proposed test procedure has promising performance of empirical sizes, and has no power loss compared with existing tests based on or .
| NEW | CQ | EB | WB | ZZ | ZZGZ | LOU | SD | SKK | FZWZ |
|---|---|---|---|---|---|---|---|---|---|
| 9.99e-4 | 1.89e-10 | 9.99e-4 | 9.99e-4 | 7.74e-4 | 7.47e-5 | 0 | 0.27 | 0.18 | 4.78e-3 |
NEW, the proposed test procedure; CQ, the test of Chen and Qin, (2010); EB, the empirical bootstrap method based on ; WB, the wild bootstrap method based on ; ZZ, the test of Zhang and Zhu, (2021); ZZGZ, the test of Zhang et al., (2021); LOU, the test of Lou, (2020); SD, the test of Srivastava and Du, (2008); SKK, the test of Srivastava et al., (2013); FZWZ, the test of Feng et al., (2015).
5 Real-data example
In this section, we apply the proposed test procedure to the gene expression dataset released by Alon et al., (1999). This dataset consists of the gene expression levels of normal and tumor colon tissue samples. It contains the expression of genes with highest minimal intensity across the tissues. We would like to test if the normal and tumor colon tissue samples have the same average gene expression levels. Table 3 lists the -values of various test procedures. With , all but the test procedures of Srivastava and Du, (2008) and Srivastava et al., (2013) reject the null hypothesis, claiming that the average gene expression levels of normal and tumor colon tissue samples are significantly different.
We would also like to examine the empirical sizes of various test procedures on the gene expression data. To mimick the null distribution of the gene expression data, we generate resampled datasets as follows: the resampled observations are uniformly sampled from with replacement, and are uniformly sampled from with replacement. We conduct various test procedures with on the resampled observations . The above procedure is independently replicated for times to compute the empirical sizes. The results are listed in Table 4. It can be seen that the test procedures of Srivastava and Du, (2008) and Srivastava et al., (2013) are overly conservative. Hence the -values of these two test procedures for gene expression data may not be reliable. The test procedures of Chen and Qin, (2010) and Feng et al., (2015) are a little inflated. In comparison, the remaining test procedures, including the proposed test procedure, have a good control of the test level for the resampled gene expression data. This implies that the -value of the proposed test procedure for the gene expression data is reliable.
| NEW | CQ | EB | WB | ZZ | ZZGZ | LOU | SD | SKK | FZWZ |
| 5.43 | 7.28 | 5.22 | 5.84 | 5.19 | 5.98 | 5.71 | 0.60 | 0.79 | 7.03 |
NEW, the proposed test procedure; CQ, the test of Chen and Qin, (2010); EB, the empirical bootstrap method based on ; WB, the wild bootstrap method based on ; ZZ, the test of Zhang and Zhu, (2021); ZZGZ, the test of Zhang et al., (2021); LOU, the test of Lou, (2020); SD, the test of Srivastava and Du, (2008); SKK, the test of Srivastava et al., (2013); FZWZ, the test of Feng et al., (2015).
Acknowledgements
The authors thank the editor, associate editor and three reviewers for their valuable comments and suggestions. This work was supported by Beijing Natural Science Foundation (No Z200001), National Natural Science Foundation of China (No 11971478). Wangli Xu serves as the corresponding author of the present paper.
References
- Alon et al., (1999) Alon, U., Barkai, N., Notterman, D. A., Gish, K., Ybarra, S., Mack, D., and Levine, A. J. (1999). Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proceedings of the National Academy of Sciences, 96(12):6745–6750.
- Bai and Saranadasa, (1996) Bai, Z. and Saranadasa, H. (1996). Effect of high dimension: by an example of a two sample problem. Statistica Sinica, 6(2):311–329.
- Cai et al., (2013) Cai, T., Liu, W., and Xia, Y. (2013). Two-sample test of high dimensional means under dependence. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 76(2):349–372.
- Canay et al., (2017) Canay, I. A., Romano, J. P., and Shaikh, A. M. (2017). Randomization tests under an approximate symmetry assumption. Econometrica, 85(3):1013–1030.
- Chang et al., (2017) Chang, J., Zheng, C., Zhou, W.-X., and Zhou, W. (2017). Simulation-based hypothesis testing of high dimensional means under covariance heterogeneity. Biometrics, 73(4):1300–1310.
- Chatterjee, (2006) Chatterjee, S. (2006). A generalization of the lindeberg principle. The Annals of Probability, 34(6):2061–2076.
- Chen and Qin, (2010) Chen, S. X. and Qin, Y. L. (2010). A two-sample test for high-dimensional data with applications to gene-set testing. The Annals of Statistics, 38(2):808–835.
- Chernozhukov et al., (2013) Chernozhukov, V., Chetverikov, D., and Kato, K. (2013). Gaussian approximations and multiplier bootstrap for maxima of sums of high-dimensional random vectors. The Annals of Statistics, 41(6):2786–2819.
- Chernozhukov et al., (2017) Chernozhukov, V., Chetverikov, D., and Kato, K. (2017). Central limit theorems and bootstrap in high dimensions. The Annals of Probability, 45(4):2309–2352.
- Chung and Romano, (2013) Chung, E. and Romano, J. P. (2013). Exact and asymptotically robust permutation tests. The Annals of Statistics, 41(2):484–507.
- Cohn, (2013) Cohn, D. L. (2013). Measure Theory. Birkhäuser, New York, 2nd edition.
- de Jong, (1987) de Jong, P. (1987). A central limit theorem for generalized quadratic forms. Probability Theory & Related Fields, 75(2):261–277.
- Deng and Zhang, (2020) Deng, H. and Zhang, C.-H. (2020). Beyond Gaussian approximation: bootstrap for maxima of sums of independent random vectors. The Annals of Statistics, 48(6):3643–3671.
- Döbler and Peccati, (2017) Döbler, C. and Peccati, G. (2017). Quantitative de jong theorems in any dimension. Electronic Journal of Probability, 22(0).
- Dudley, (2002) Dudley, R. M. (2002). Real Analysis and Probability. Cambridge University Press.
- Fan et al., (2021) Fan, J., Wang, K., Zhong, Y., and Zhu, Z. (2021). Robust high-dimensional factor models with applications to statistical machine learning. Statistical Science, 36(2):303–327.
- Fang et al., (1990) Fang, K. T., Kotz, S., and Ng, K. W. (1990). Symmetric multivariate and related distributions. Chapman and Hall, Ltd., London.
- Feng et al., (2015) Feng, L., Zou, C., Wang, Z., and Zhu, L. (2015). Two-sample Behrens-Fisher problem for high-dimensional data. Statistica Sinica, 25(4):1297–1312.
- Fisher, (1935) Fisher, R. A. (1935). The design of experiments. Oliver and Boyd, Edinburgh, 1 edition.
- Hemerik and Goeman, (2018) Hemerik, J. and Goeman, J. (2018). Exact testing with random permutations. TEST, 27(4):811–825.
- Hoeffding, (1952) Hoeffding, W. (1952). The large-sample power of tests based on permutations of observations. The Annals of Mathematical Statistics, 23(2):169–192.
- Hu and Bai, (2016) Hu, J. and Bai, Z. (2016). A review of 20 years of naive tests of significance for high-dimensional mean vectors and covariance matrices. Science China. Mathematics, 59(12):2281–2300.
- Kong and Valiant, (2017) Kong, W. and Valiant, G. (2017). Spectrum estimation from samples. The Annals of Statistics, 45(5):2218–2247.
- Lehmann and Romano, (2005) Lehmann, E. L. and Romano, J. P. (2005). Testing Statistical Hypotheses. Springer, New York, 3rd edition.
- Linnik, (1966) Linnik, J. V. (1966). Latest investigations on Behrens-Fisher problem. Sankhyā. Series A, 28:15–24.
- Lou, (2020) Lou, Z. (2020). High Dimensional Inference Based on Quadratic Forms. Thesis (Ph.D.)–The University of Chicago.
- Mossel et al., (2010) Mossel, E., O’Donnell, R., and Oleszkiewicz, K. (2010). Noise stability of functions with low influences: invariance and optimality. Annals of Mathematics. Second Series, 171(1):295–341.
- Nourdin et al., (2010) Nourdin, I., Peccati, G., and Reinert, G. (2010). Invariance principles for homogeneous sums: universality of Gaussian Wiener chaos. The Annals of Probability, 38(5):1947–1985.
- Pollard, (1984) Pollard, D. (1984). Convergence of stochastic processes. Springer, New York, 1st edition.
- Romano, (1990) Romano, J. P. (1990). On the behavior of randomization tests without a group invariance assumption. Journal of the American Statistical Association, 85(411):686–692.
- Simon, (2015) Simon, B. (2015). Real analysis. A Comprehensive Course in Analysis, Part 1. American Mathematical Society, Providence, RI. With a 68 page companion booklet.
- Srivastava and Du, (2008) Srivastava, M. S. and Du, M. (2008). A test for the mean vector with fewer observations than the dimension. Journal of Multivariate Analysis, 99(3):386–402.
- Srivastava et al., (2013) Srivastava, M. S., Katayama, S., and Kano, Y. (2013). A two sample test in high dimensional data. Journal of Multivariate Analysis, 114(Supplement C):349–358.
- Tao, (2012) Tao, T. (2012). Topics in random matrix theory, volume 132 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI.
- Tropp, (2015) Tropp, J. A. (2015). An introduction to matrix concentration inequalities. Foundations and Trends® in Machine Learning, 8(1-2):1–230.
- Wang and Xu, (2019) Wang, R. and Xu, X. (2019). A feasible high dimensional randomization test for the mean vector. Journal of Statistical Planning and Inference, 199:160–178.
- Wu et al., (2018) Wu, W. B., Lou, Z., and Han, Y. (2018). Hypothesis testing for high-dimensional data. In Handbook of big data analytics, pages 203–224.
- Xu et al., (2019) Xu, M., Zhang, D., and Wu, W. B. (2019). Pearson’s chi-squared statistics: approximation theory and beyond. Biometrika, 106(3):716–723.
- Xue and Yao, (2020) Xue, K. and Yao, F. (2020). Distribution and correlation-free two-sample test of high-dimensional means. The Annals of Statistics, 48(3):1304–1328.
- Zhang et al., (2020) Zhang, J.-T., Guo, J., Zhou, B., and Cheng, M.-Y. (2020). A simple two-sample test in high dimensions based on -norm. Journal of the American Statistical Association, 115(530):1011–1027.
- Zhang et al., (2021) Zhang, J.-T., Zhou, B., Guo, J., and Zhu, T. (2021). Two-sample Behrens-Fisher problems for high-dimensional data: a normal reference approach. Journal of Statistical Planning and Inference, 213:142–161.
- Zhang and Zhu, (2021) Zhang, J.-T. and Zhu, T. (2021). A further study on chen-qin’s test for two-sample behrens-fisher problems for high-dimensional data. Department of Statistics and Applied Probability, National University of Singapore.
- Zhou and Guo, (2017) Zhou, B. and Guo, J. (2017). A note on the unbiased estimator of . Statistics & Probability Letters, 129:141–146.
- Zhu, (2005) Zhu, L. (2005). Nonparametric Monte Carlo tests and their applications. Springer, New York.
Appendix S.1 Additional numerical results
In this section, we present additional numerical results. The experimental setting is as described in the main text.
We would like to use quantile-quantile plots to examine the correctness of Theorem 1 and Corollary 1. First we consider the correctness of Theorem 1. Theorem 1 implies that the distribution of can be approximated by that of . Fig. 1 illustrates the plots of the empirical quantiles of against that of under Models I-IV described in the main text with , , . The empirical quantiles of are obtained by replications. The results imply that the distribution approximation in Theorem 1 is quite accurate for finite sample size.
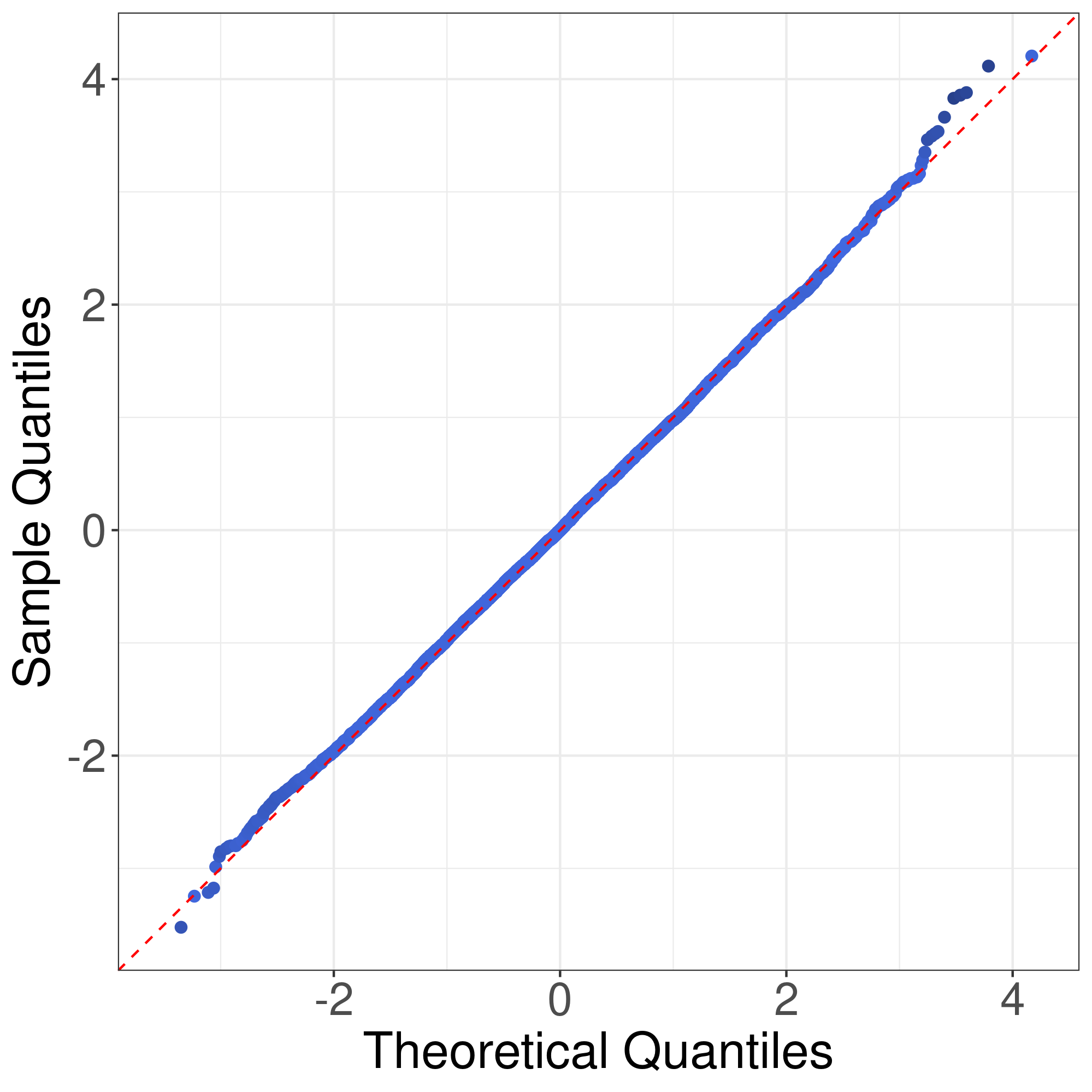
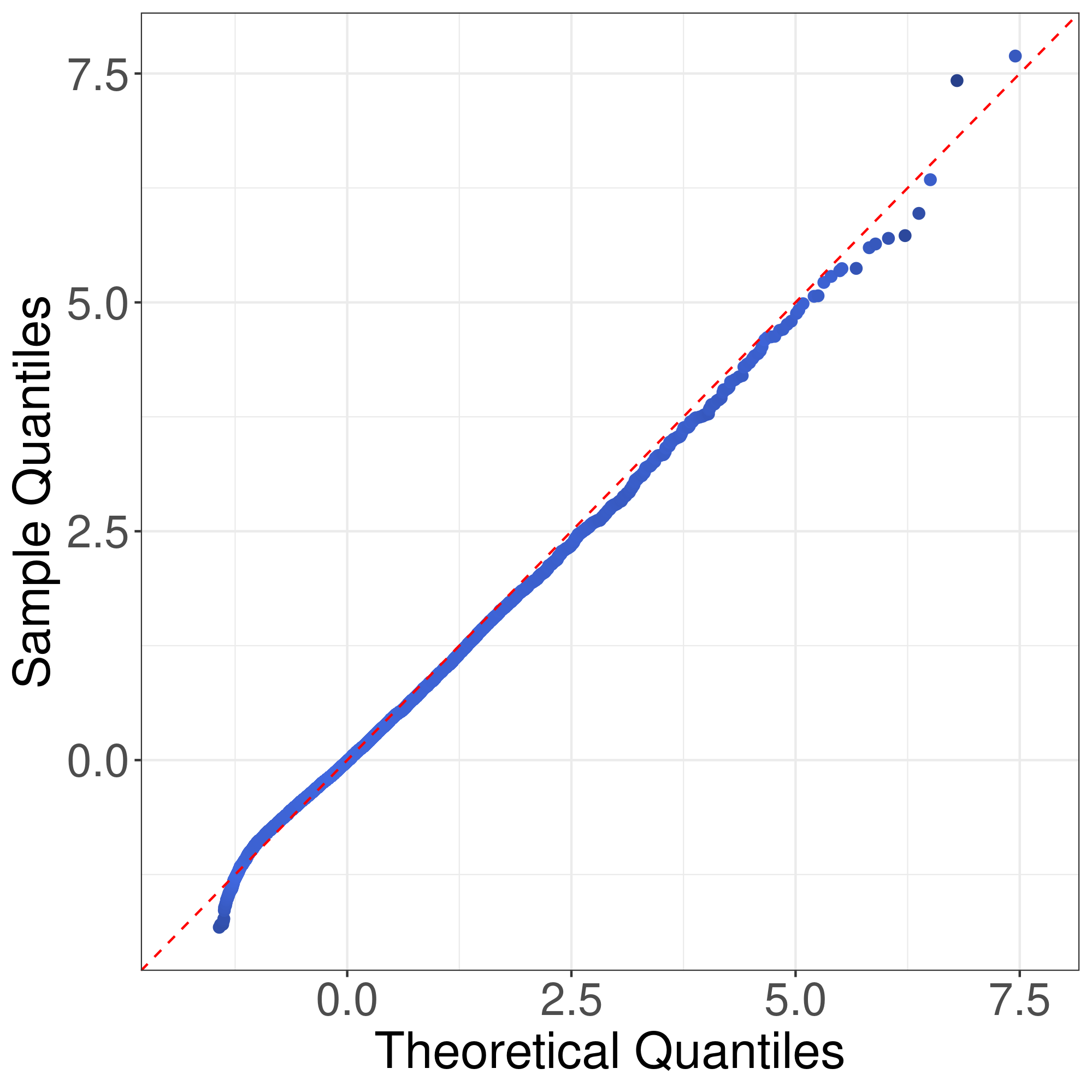
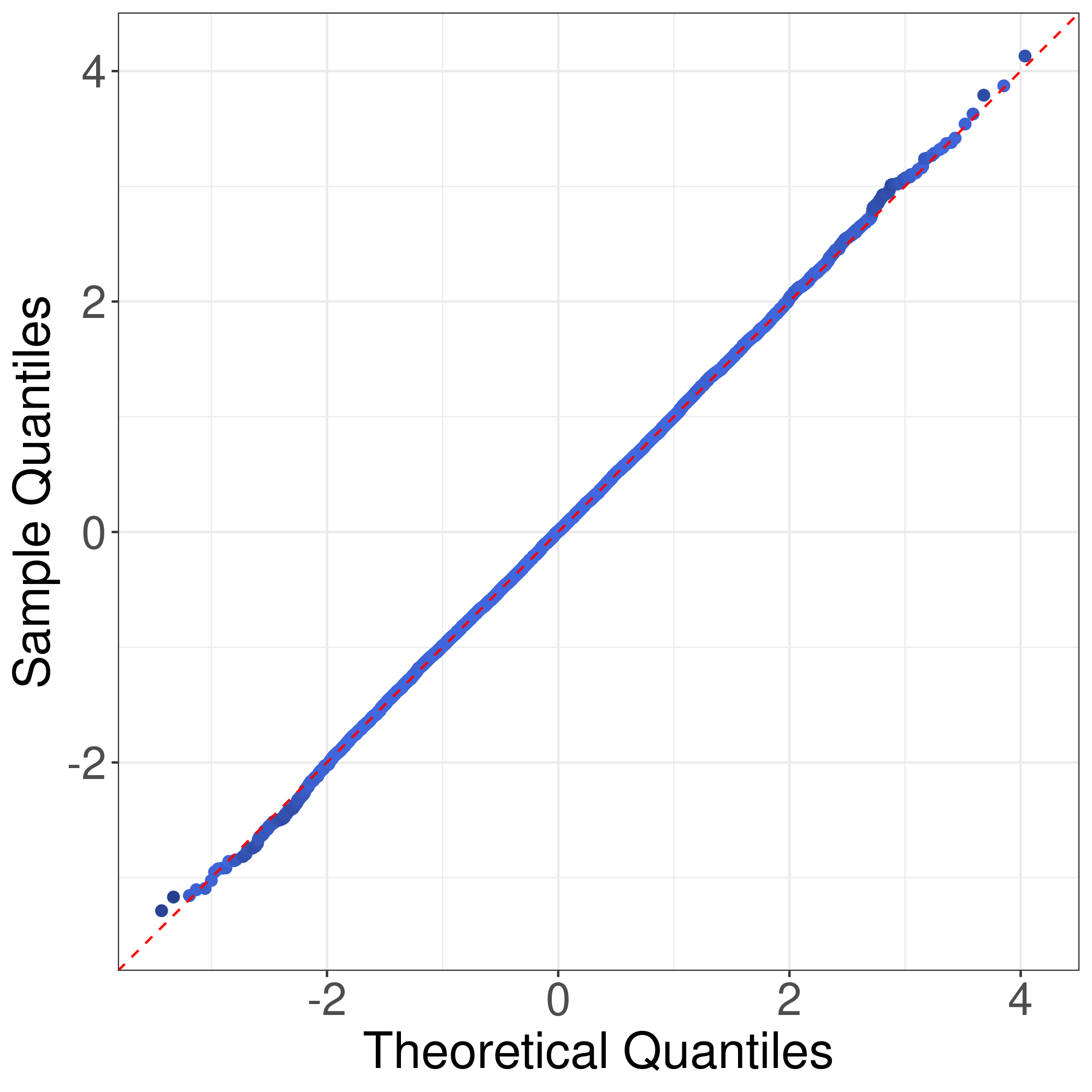
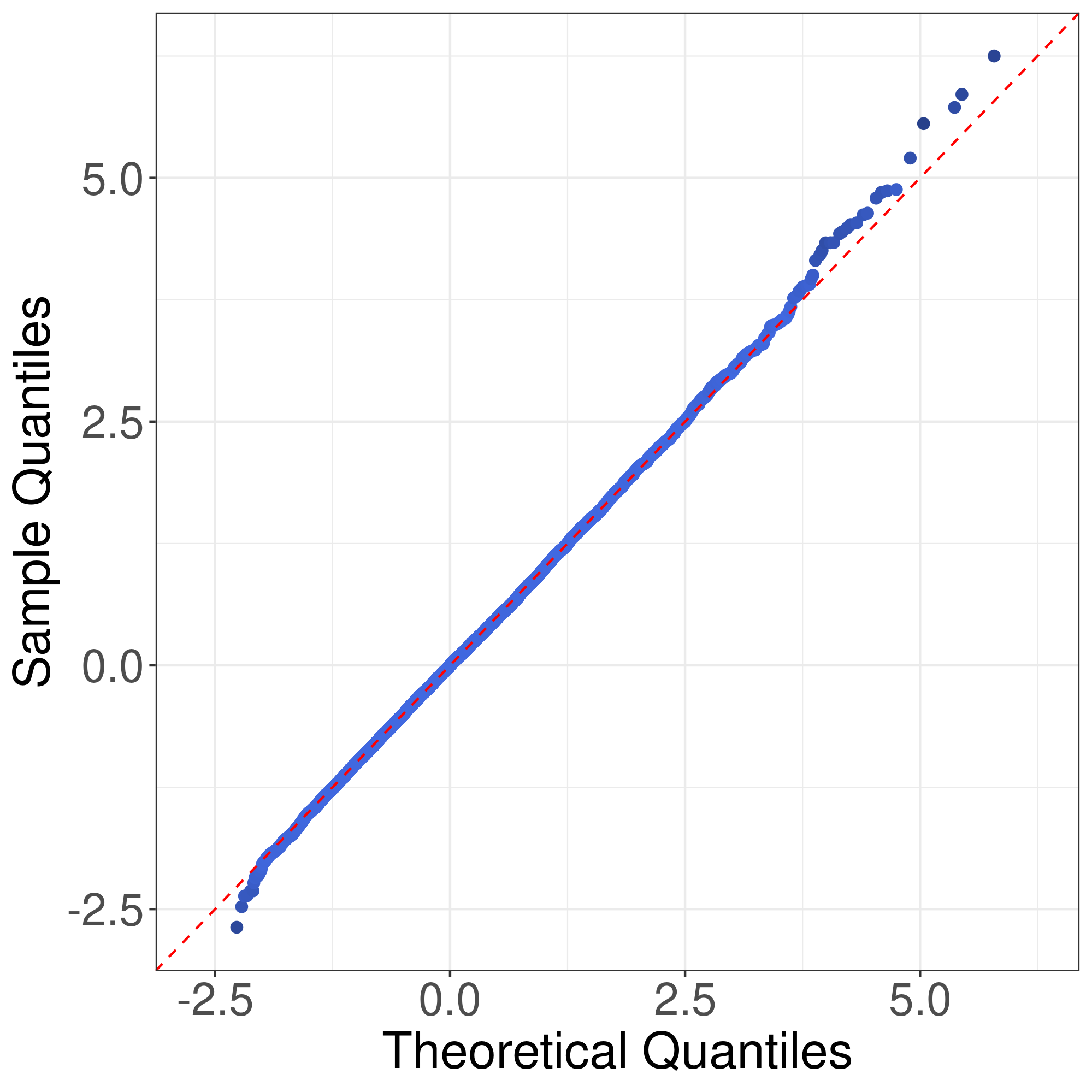
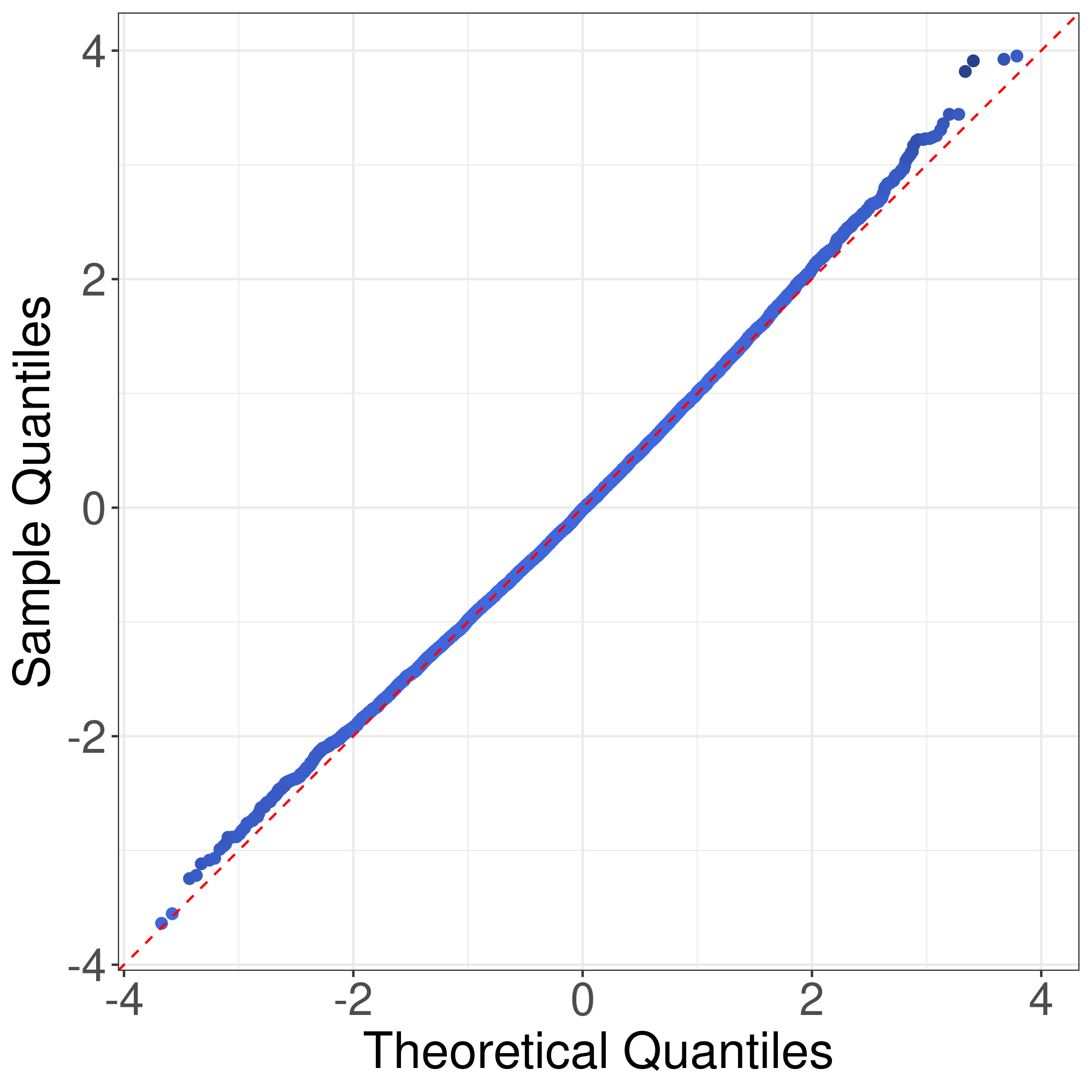
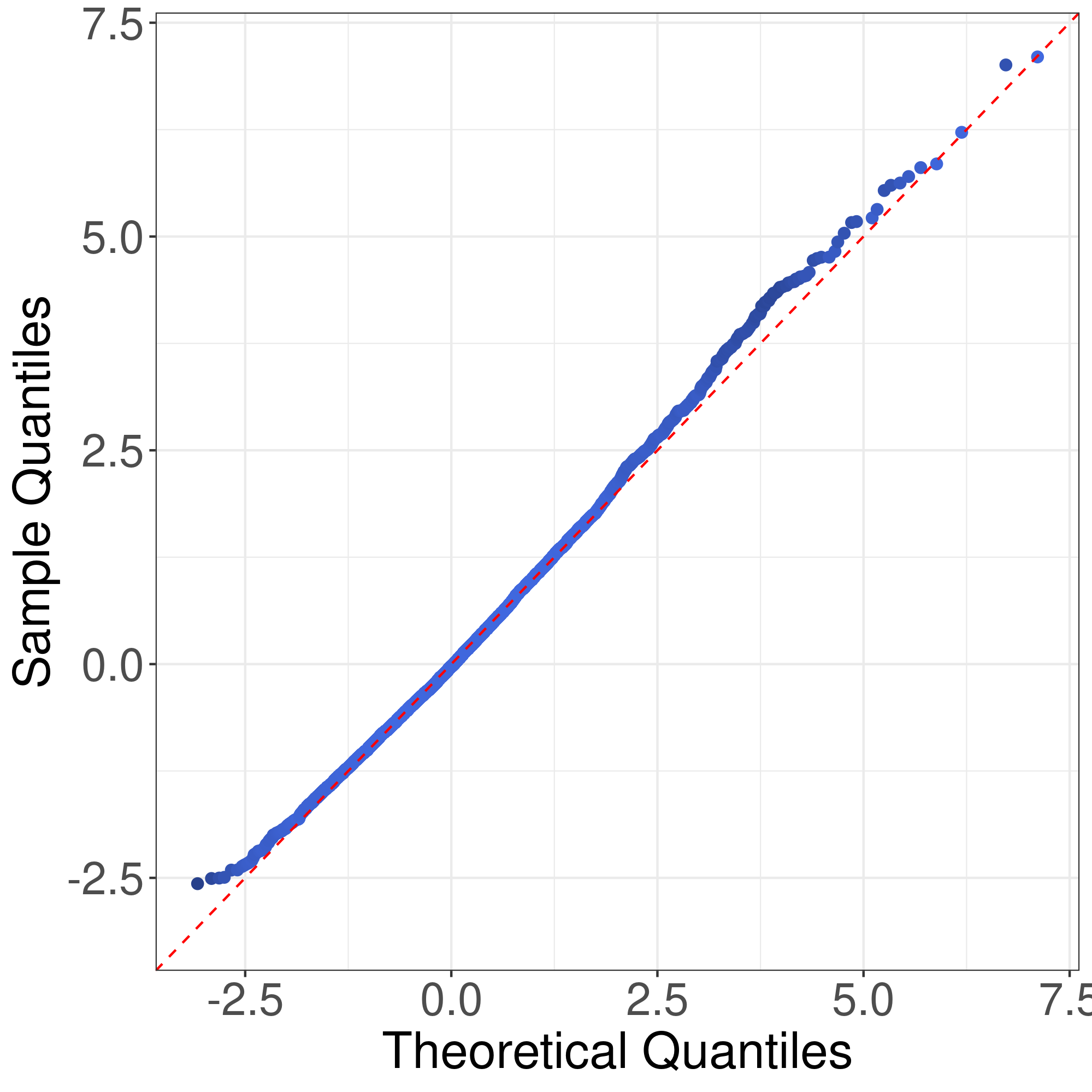
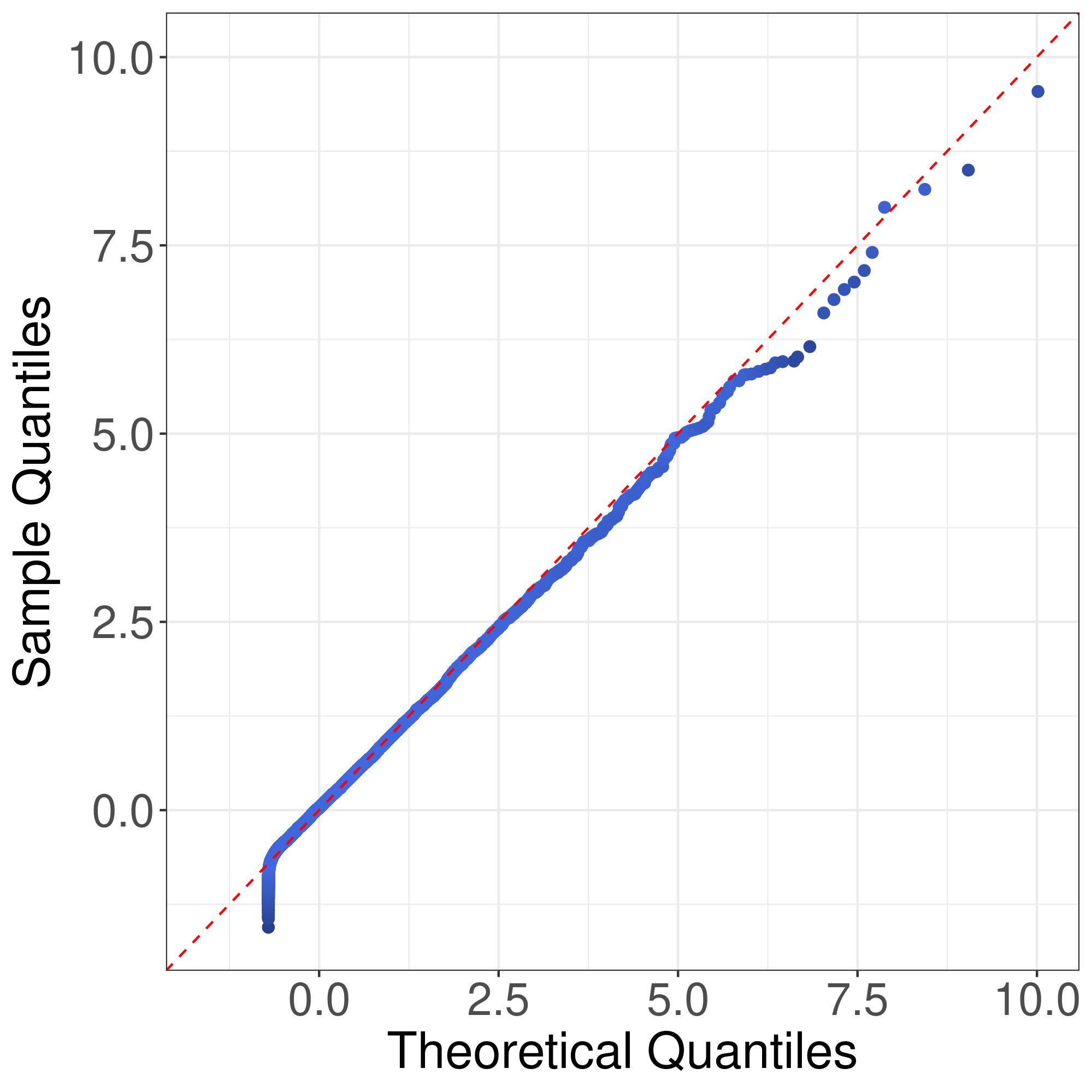
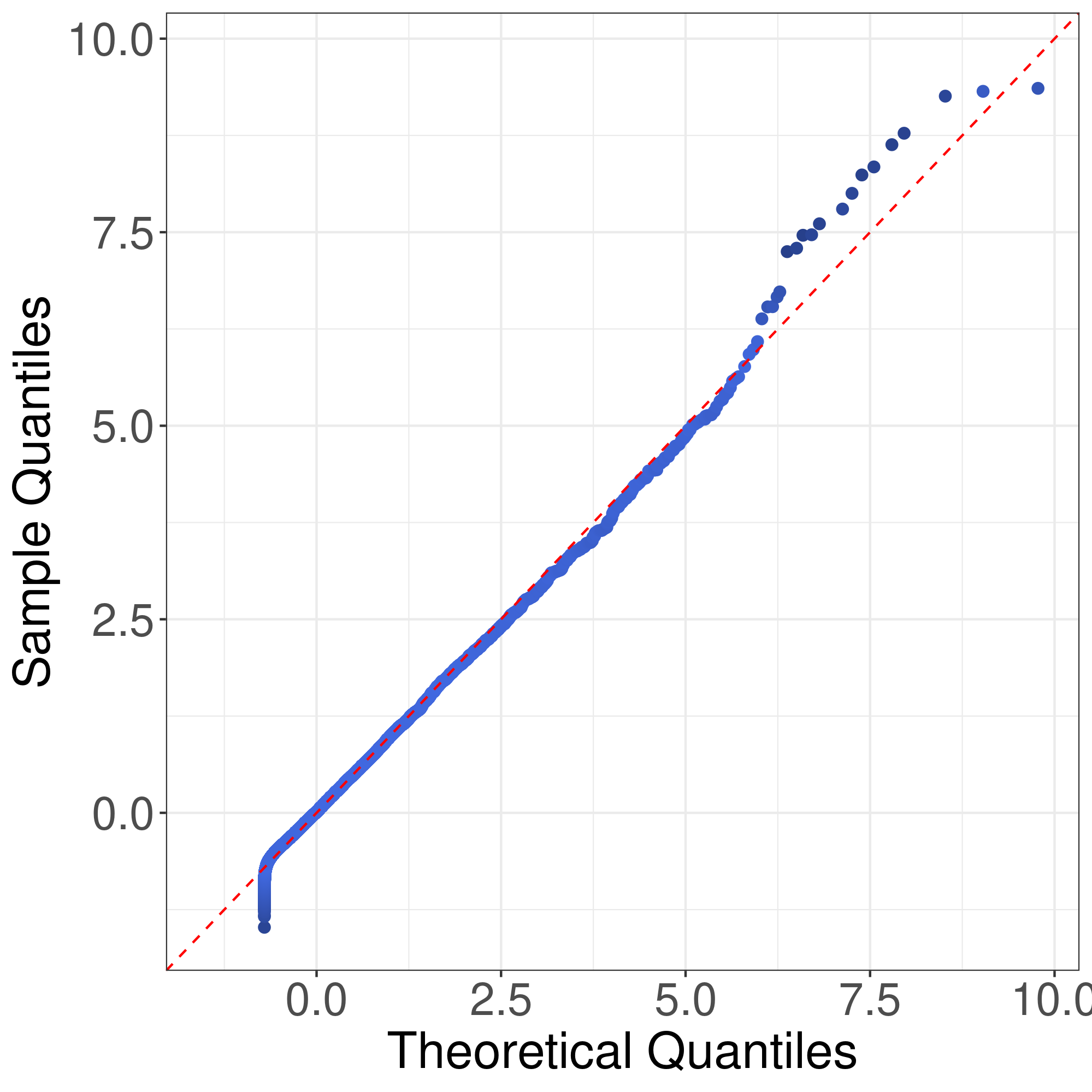
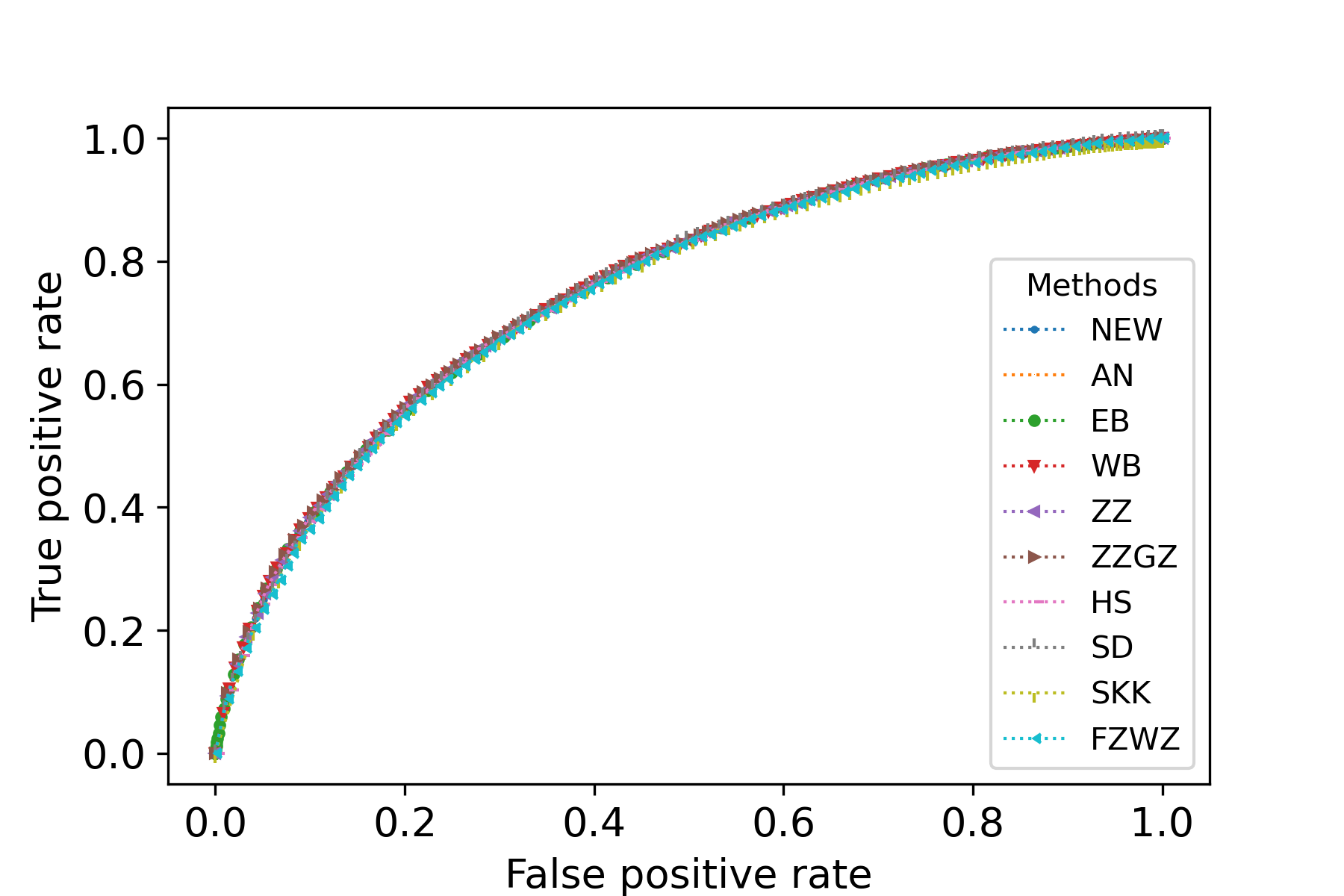
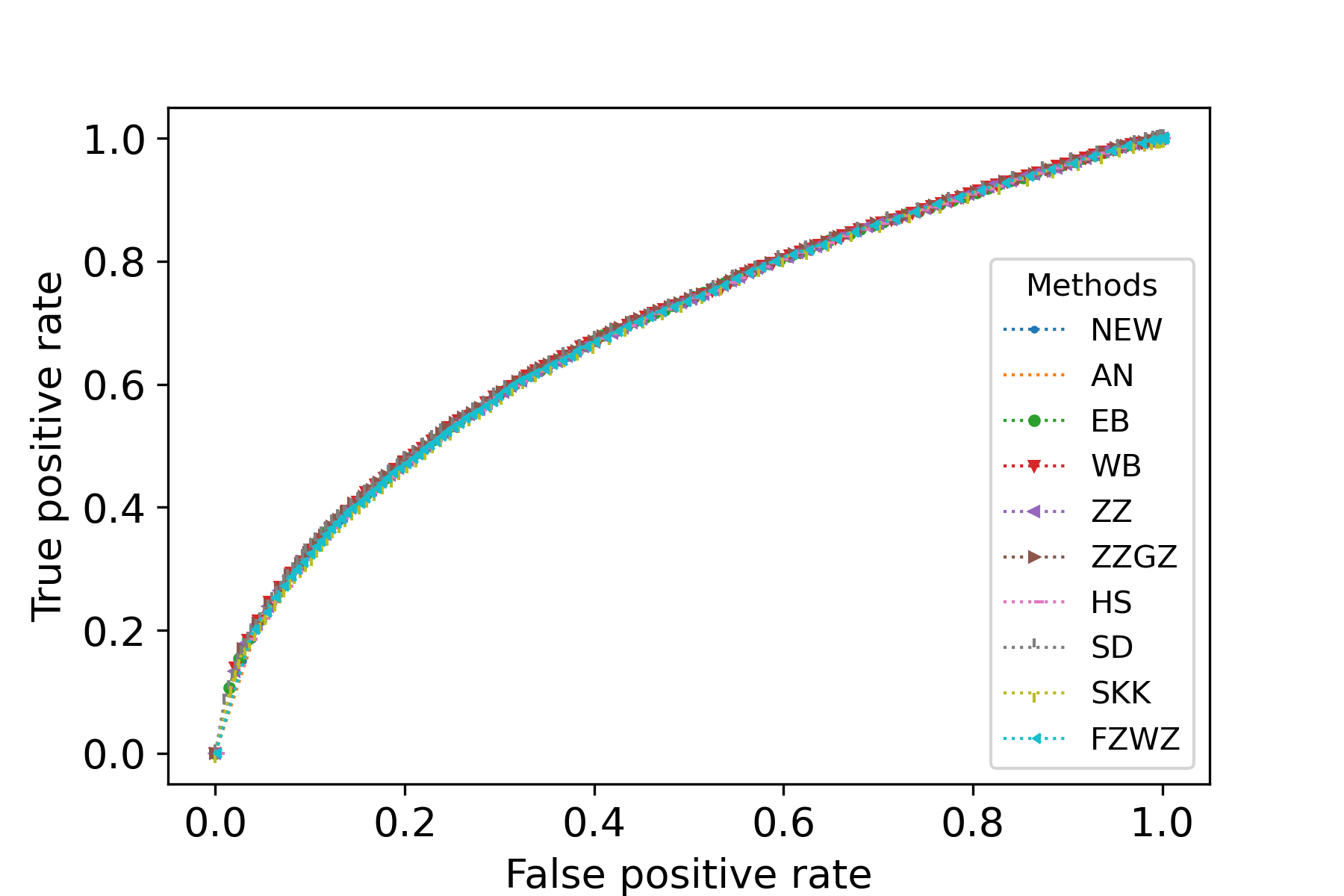
Now we consider the correctness of Corollary 1. Corollary 1 claims that the general asymptotic distributions of are weighted sums of independent normal random variable and centered random variables. In Corollay 1, the parameters relies on the limits of the eigenvalues of along a subsequence of . To cover different senarios of asymptotic distributions, we consider the following model. Suppose , , , where . In this case, the eigenvalues of are
with multiplicities and , respectively. We assume as . We consider four choices of . First, we consider . In this case, , , and the asymptotic distribution of is the standard normal distribution. Second, we consider . In this case, , and , , and the asymptotic distribution of is . In the third and fourth cases, we consider and , respectively. In these two cases, , and , , and the asymptotic distribution of is the standardized distribution with degree of freedom. Fig. 2 illustrates the plots of the empirical quantiles of against that of the asymptotic distribution in (6) for various values of . The empirical quantiles of are obtained by replications. It can be seen that the distribution of can be well approximated by the asymptotic distributions given in Corollary 1. This verifies the conclusion of Corollary 1. We note that the approximation in Theorem 1 is slightly better than the distribution approximations in Corollary 1. This phenomenon is reasonable since the distributions in Corollary 1 are in fact the asymptotic distributions of in Theorem 1, and hence may have larger approximation error than .
We have seen that many competing test procedures do not have a good control of test level. To get rid of the effect of distorted test level, we plot the receiver operating characteristic curve of the test procedures. Fig. 3 illustrates the receiver operating characteristic curve of various test procedures with , and . It can be seen that for Models I and II, all test procedures have similar power behavior. For Model III, the scalar-invariant tests are less powerful than other tests. For Model IV, the scalar-invariant tests are more powerful than other tests. These results show that various test procedures based on or may not have essential difference in power, and their performances are largely driven by the test level.
Appendix S.2 Universality of generalized quadratic forms
In this section, we investigate the universality property of generalized quadratic forms, which is the key tool to study the distributional behavior of the proposed test procedure. The result in this section is also interesting in its own right.
Suppose are independent random elements taking values in a Polish space . We consider the generalized quadratic form
where is measurable with respect to the product -algebra on , . The generalized quadratic form includes the statistic as a special case. To see this, consider , and , . Let
In this case, the generalized quadratic form becomes the statistic . Similarly, conditioning on and , the randomized statistic is a special case of the generalized quadratic form with , and , . Hence it is meaningful to investigate the general behavior of the generalized quadratic form.
The asymptotic normality of the generalized quadratic forms was studied by de Jong, (1987) via martingale central limit theorem and by Döbler and Peccati, (2017) via Stein’s method. However, we are interested in the general setting in which may not be asymptotically normally distributed. Therefore, compared with the asymptotic normality, we are more interested in the universality property of ; i.e., the distributional behavior of does not rely on the particular distribution of asymptotically. In this regard, many achievements have been made for the universality of for special form of ; see, e.g., Mossel et al., (2010), Nourdin et al., (2010), Xu et al., (2019) and the references therein. However, these results can not be used to deal with in our setting. In fact, the results in Mossel et al., (2010) and Nourdin et al., (2010) can not be readily applied to while the result in Xu et al., (2019) can only be applied to identically distributed observations. To the best of our knowledge, the universality of the generalized quadratic forms was never considered in the literature. We shall derive a universality property of the generalized quadratic forms using Lindeberg principle, an old and powerful technique; see, e.g., Chatterjee, (2006), Mossel et al., (2010) for more about Lindeberg principle.
Assumption S.1.
Suppose are independent random elements taking values in a Polish space . Assume the following conditions hold for all :
-
(a)
.
-
(b)
For all , .
Define . Under Assumption S.1, we have and . We would like to give explicit bound for the difference between the distributions of and for a general class of random vectors . We impose the following conditions on .
Assumption S.2.
Suppose are independent random elements taking values in and are independent of . Assume the following conditions hold for all :
-
(a)
, and .
-
(b)
For all , .
-
(c)
For any ,
We claim that under Assumptions S.1 and S.2, there exists a nonnegative (which possibly depends on ) such that for all ,
| (S.1) |
In fact, by Assumption S.1, (a) and Assumption S.2, (a), the left hand side of (S.1) is finite. Also, if , that is, , then from (c) of Assumption S.2,
It follows that almost surely. In this case, the left hand side of (S.1) is also . Hence our claim is valid. Let denote the minimum nonnegative such that (S.1) holds for all , It will turn out that the difference between the distributions of and relies on .
The following theorem provides a universality property of .
From Theorem S.1, the distance between and is bounded by a function of and the influences. Suppose as , is bounded and tends to . Then Theorem S.1 implies that and share the same possible asymptotic dsitribution. That is, the distribution of enjoys a universality property. In the proof of Theorem 1 and Theorem 2, we apply Theorem S.1 to and , respectively, and consider normally distributed , . With this technique, the distributional behaviors of and are reduced to the circumstances where the observations are normally distributed.
of Theorem S.1.
For , define
Then and . Fix an . We have
| (S.2) |
Define
Note that only relies on . It can be seen that
From Taylor’s theorem,
| (S.3) | ||||
| (S.4) |
Now we show that
| (S.5) |
By conditioning on , it can be seen that (S.5) holds provided that for and ,
For the case of , we have
which equals by (b) of Assumption S.1. Similarly, we have
Now we deal with the case of . From (c) of Assumption S.2, we have
Therefore, (S.5) holds. It follows from (S.3), (S.4) and (S.5) that
Combining (S.2) and the above inequality leads to
Now we derive upper bounds for and . We have
From the above equality and the definition of , we have
Similarly, . Thus,
This completes the proof. ∎
Appendix S.3 Technical results
We begin with some notations that will be used throughout our proofs of main results. For a matrix , let denote the Frobenious norm of . For a matrix , let denote the th largest eigenvalue of . We adopt the convention that for .
The following lemma collects some trace inequalities that will be used in our proofs of main results. To make our proofs of main results concise, the application of these trace inequalities are often tacit.
Lemma S.1.
The following trace inequalities hold:
-
(i)
For any matrices , , .
-
(ii)
For any positive semi-definite matrices , .
-
(iii)
Suppose is an increasing function from to , and are symmetric. Then .
-
(iv)
For any symmetric matrices , .
Remark 2.
Lemma S.2.
Suppose are positive semi-definite matrices. Let . Then
Proof.
For distinct , we have . Hence
Similarly, we have
And
And
It follows that
Thus, we have
This completes the proof.
∎
Lemma S.3.
Suppose and are positive semi-definite matrices. Let and . Then
Proof.
Note that
Hence we have
It follows that
This completes the proof. ∎
Lemma S.4.
Suppose and are two random variables. Then
Proof.
For , Taylor’s theorem implies that
Then the conclusion follows from the definition of the norm . ∎
Proof.
Lemma S.6.
Suppose is a -dimensional standard normal random vector where is an arbitrary sequence of positive integers. Suppose is a symmetric matrix and is an matrix where is a fixed positive integer. Furthermore, suppose
Let be a sequence of positive numbers such that . Let be a sequence of matrices such that . Then
where is an -dimensional standard normal random vector and is a standard normal random variable which is independent of .
Proof.
The conclusion holds if and only if for any subsequence of , there is a further subsequence along which the conclusion holds. Using this subsequence trick, we only need to prove that the conclusion holds for a subsequence of . By taking a subsequence, we can assume without loss of generality that
where and is an positive semi-definite matrix. Then we have and . Consequently, converges weakly to . Hence we only need to prove that
To prove this, it suffices to prove that
where “” means weak convergence.
Denote by the spectral decomposition of where and is an orthogonal matrix. Define . Then is also a -dimensional standard normal random vector and , where .
Fix and . Let be the th element of , . The characteristic function of the random vector at is
where the last equality can be obtained from the characteristic function of noncentral random variable, and for functions, we put the cut along , that is, with .
The condition implies that . Consequently, Taylor’s theorem implies that
where . It follows that
On the other hand,
Thus,
where is the characteristic function of the distribution
This completes the proof. ∎
Lemma S.7.
Suppose is a symmetric matrix where is a function of .
Let be a -dimensional standard normal random vector and a sequence of independent standard normal random variables. Then as ,
Proof.
Let . Then we have
where is a sequence of independent standard normal random variables which are independent of . From Fatou’s lemma, we have . It follows from Lévy’s equivalence theorem and three-series theorem (see, e.g., Dudley, (2002), Theorem 9.7.1 and Theorem 9.7.3) that converges weakly to as . Hence for any , there is a positive integer such that
| (S.6) |
By taking a possibly larger , we can also assume that . Now we fix such an and apply Lindeberg principle. For , define
Then we have , , and
For , we have
| (S.7) |
For , we have
But
Thus, for , we have
| (S.8) |
where the last inequality holds since and . Note that . Hence we have
| (S.9) |
Note that has the same distribution as . Then from Lemma S.4,
| (S.10) |
where the right hand side tends to as . From (S.6), (S.9) and (S.10), we have
But is an arbitrary positive real number. Hence the above limit must be . This completes the proof. ∎
Appendix S.4 Proof of Lemma 1
In this section, we provide the proof of Lemma 1.
Fix an arbitrary positive semi-definite matrix . Let . We only need to show that
Let denote the th element of . Then
From the condition (5), the expectation of the cross term is zero, and
where the last inequality holds since is positive semi-definite. On the other hand
Hence the conclusion holds.
Appendix S.5 Proof of Theorem 1
In this section, we provide the proof of Theorem 1.
Let , , , be independent -dimensional random vectors with . Let , . First we apply Theorem S.1 to prove that
| (S.11) |
It follows from Assumption 2 and the fact that has the same first two moments as that Assumptions S.1 and S.2 hold. By direct calculation, we have
Consequently,
We have
It can be seen that . On the other hand, from Assumption 3,
It follows that .
On the other hand, from Assumption 2, for all ,
Hence is upper bounded by the absolute constant . Thus, (S.11) holds.
Appendix S.6 Proof of Corollary 1
In this section, we provide the proof of Corollary 1.
Since has zero mean and unit variance, the distribution of is uniformly tight. From Theorem 1, and share the same possible asymptotic distributions. Hence we only need to find all possible asymptotic distributions of .
Let be a possible asymptotic distribution of . We show that can be represented in the form of (6). Note that there is a subsequence of along which converges weakly to . Denote , . By Cantor’s diagonalization trick (see, e.g., Simon, (2015), Section 1.5), there exists a further subsequence along which , , where are real numbers in . Then Lemma S.7 implies that along this further subsequence,
Thus, .
Now we prove that for any sequence of positve numbers such that , there exits a sequence such that is the asymptotic distribution of . To construct the sequence , we take and let , where for and for . Then and , . It is straightforward to show that converges weakly to . This completes the proof.
Appendix S.7 Proof of Theorem 2
In this section, we provide the proof of Theorem 2.
If the conclusion holds for the case that is a standard normal random variable, then Lemma S.11 implies that it also holds for the case of Rademacher random variable. Hence without loss of generality, we assume that is a standard normal random variable.
We begin with some basic notations and facts that are useful for our proof. Denote by the spectral decomposition of where and is an orthogonal matrix. Let be the first columns of and be the last columns of . Then we have and . For , we have
| (S.14) |
To prove the conclusion, we apply the subsequence trick. That is, for any subsequence of , we prove that there is a further subsequence along which the conclusion holds. For any subsequence of , by Cantor’s diagonalization trick (see, e.g., Simon, (2015), Section 1.5), there exists a further subsequence along which
| (S.15) |
Thus, we only need to prove the conclusion with the additional condition (S.15). Without loss of generality, we assume that (S.15) holds for the full sequence .
From Fatou’s lemma, we have . Now we claim that there exists a sequence of non-decreasing integers which tends to infinity such that
| (S.16) |
We defer the proof of this fact to Lemma S.8 in Section S.9.
Fix a positive integer . Then for large , we have . Let be the th to the th columns of . Then is a column orthogonal matrix such that . We can decompose the identity matrix into the sum of three mutually orthogonal projection matrices as . Then we have , where
Let be a sequence of independent standard normal random variables. We claim that
| (S.17) |
The above quantity is a continuous function of and and is thus measurable. We defer the proof of (S.17) to Lemma S.12 in Section S.9. It is known that for random variables in , convergence in probability is metrizable; see, e.g., Dudley, (2002), Section 9.2. As a standard property of metric space, (S.17) also holds when is replaced by certain with and . Also note that Lévy’s equivalence theorem and three-series theorem (see, e.g., Dudley, (2002), Theorem 9.7.1 and Theorem 9.7.3) implies that converges weakly to . Thus,
| (S.18) |
Appendix S.8 Proof of Corollary 2
Using the subsequence trick, it suffices to prove the conclusion for a subsequence of . Then from Corollary 1, we can assume without loss of generality that
| (S.20) |
where is a sequence of independent standard normal random variables, is a sequence of positive numbers such that . Let denote the cumulative distribution function of . We claim that is continuous and strictly increasing on the interval . We defer the proof of this fact to Lemma S.13 in Section S.9. This fact, combined with (S.20), leads to
| (S.21) |
Furthermore, in view of Theorem 2 and (S.20), we have
| (S.22) |
Appendix S.9 Deferred proofs
In this section, we provide proofs of some intermediate results in our proofs of main results. Some results in this section are also used in the main text.
Lemma S.8.
Proof.
For any fixed positive integer , we have
Therefore, there exists an such that for any ,
We can without loss of generality and assume since otherwise we can enlarge some . Define for , and for . By definition, is non-decreasing and . Also, for any ,
Thus,
The conclusion follows from the above limit and the fact that . ∎
Lemma S.9.
Suppose Assumption 2 holds. Then for any positive semi-definite matrix and ,
Proof.
We have
where the last inequality follows from Assumption 2. Note that
It follows from the above two inequalities and the condition that
This completes the proof. ∎
Lemma S.10.
Proof.
We have
Now we compute the variance of . Note that
We denote the above terms by . On the other hand,
We denote the above terms by . It can be seen that for , . Thus,
Note that for and ,
Consequently,
From Lemma S.9, for and distinct ,
Thus,
where the last equality follows from Assumption 3. Combining the above bound and (S.23) leads to
| (S.24) |
Lemma S.11.
Suppose the conditions of Theorem 2 hold. Let , where , , , are independent Rademacher random variables. Let , where , , , are independent standard normal random variables. Then as ,
Proof.
We apply Theorem S.1 conditioning on and . Define
Define
With the above definitions, we have and . It can be easily seen that Assumptions S.1 and S.2 hold. By direct calculation, we have
Hence
It can be easily seen that for the above defined random variables. From Theorem S.1, it suffices to prove that . We have
But
where the last equality follows from Lemma S.10. Hence it suffices to prove that . We have
We have
where the second inequality follows from Lemma S.9 and the last equality follows from Assumption 3. On the other hand,
Thus,
Similarly,
This completes the proof. ∎
Lemma S.12.
Proof.
To prove (S.25), we only need to show that where the expectation is unconditional. It is straightforward to show that
For , we have
But
| (S.27) |
where the first inequality follows from Lemma S.9 and the second inequality follows from Cauchy-Schwarz inequality. Note that . Thus,
where the second equality follows from Assumption 3. On the other hand, for , we have
But
where the first inequality follows from (S.27). It follows that
Thus, (S.25) holds.
From Lemma S.10,
| (S.28) |
where the last equality follows from (S.16). On the other hand,
For , let . We have
We split the above sum into the following four cases: ; ; ; . The second and the third cases result in the same sum. Then we have
| (S.29) |
First we deal with the first two terms of (S.29). For distinct , two applications of Lemma S.9 yield
Consequently,
| (S.30) |
where the last equality follows from Assumption 3. Now we deal with the third term of (S.29). For distinct , we have
Then from Lemma S.2, we have
where the last equality follows from (S.14) and Assumption 3. It follows from (S.30) and the above bound that
Similarly, we have .
Now we deal with . For , , let . Then
| (S.31) |
First we deal with the first three terms of (S.31). From Lemma S.9, for and ,
Consequently,
| (S.32) |
where the second last equality follows from Assumption 3. Now we deal with the fourth term of (S.31). For distinct and distinct , we have
Then from Lemma S.3, we have
where the last equality follows from (S.14) and Assumption 3. It follows from the above inequality and (S.32) that
Thus, we have
| (S.33) |
Now we deal with . We have
For , we have
Consequently,
where the third inequality follows from (S.27) and the last equality follows from Assumption 3. Thus,
It follows that
| (S.34) |
Note that we have proved that (S.28), (S.33) and (S.34) hold in probability. Then for every subsequence of , there is a further subsequence along which these three equalities hold almost surely, and consequently (S.26) holds almost surely by Lemma S.6. That is, (S.26) holds in probability. This completes the proof. ∎
Lemma S.13.
Suppose is a sequence of independent standard normal random variables and is a sequence of positive numbers such that . Then the cumulative distribution function of is continuous and strictly increasing on the interval .
Proof.
If , , then the conclusion holds since is a standard normal random variable. Otherwise, we can assume ithout loss of generality that . Let . Then . Let denote the probability density function of . Let denote the cumulative distribution function of . Then has density function
As a result, is continuous.
Now we prove that is strictly increasing on the interval . Let be a point in the support of . For any real number such that and for any ,
Since is in the support of , we have ; see, e.g., Cohn, (2013), Section 7.4. Thus, . Therefore, is strictly increasing on the interval . Then the conclusion follows from the fact that is an arbitrary point in the support of . ∎