An Analysis of Quality Indicators Using Approximated Optimal Distributions in a Three-dimensional Objective Space

We suppose a multi-objective minimization problem in this paper. A continuous MOP is to find a solution $\mbox{\boldmath$x$}\in\mathbb{S}$ that minimizes a given objective function vector $\mbox{\boldmath$f$}:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$. Here, $\mathbb{S}\subseteq\mathbb{R}^{n}$ is the $n$-dimensional solution space, and $\mathbb{R}^{m}$ is the $m$-dimensional objective space. Thus, $n$ is the number of decision variables, and $m$ is the number of objective functions.

A solution $\mbox{\boldmath$x$}_{1}$ is said to dominate $\mbox{\boldmath$x$}_{2}$ iff $f_{i}(\mbox{\boldmath$x$}_{1})\leq f_{i}(\mbox{\boldmath$x$}_{2})$ for all $i\in\{1,...,m\}$ and $f_{i}(\mbox{\boldmath$x$}_{1})<f_{i}(\mbox{\boldmath$x$}_{2})$ for at least one index $i$. In addition, $\mbox{\boldmath$x$}_{1}$ is said to weakly dominate $\mbox{\boldmath$x$}_{2}$ iff $f_{i}(\mbox{\boldmath$x$}_{1})\leq f_{i}(\mbox{\boldmath$x$}_{2})$ for all $i\in\{1,...,m\}$. If $\mbox{\boldmath$x$}^{*}$ is not dominated by any other solutions in $\mathbb{S}$, $\mbox{\boldmath$x$}^{*}$ is a Pareto optimal solution. The set of all $\mbox{\boldmath$x$}^{*}$ is the Pareto optimal solution set. The set of all $\mbox{\boldmath$f$}(\mbox{\boldmath$x$}^{*})$ is the Pareto front. The goal of MOPs for the “a posteriori” decision making is to find a non-dominated solution set that approximates the Pareto front in the objective space.

For the sake of simplicity, we denote the objective vector $\mbox{\boldmath$f$}(\mbox{\boldmath$x$})=\bigl{(}f_{1}(\mbox{\boldmath$x$}),...,f_{m}(\mbox{\boldmath$x$})\bigr{)}^{\rm T}$ as $\mbox{\boldmath$a$}=(a_{1},...,a_{m})^{\rm T}$, where $a_{i}=f_{i}(\mbox{\boldmath$x$})$ for $i\in\{1,...,m\}$. Let $\mbox{\boldmath$A$}=\{\mbox{\boldmath$a$}_{1},...,\mbox{\boldmath$a$}_{\mu}\}$ be a set of $\mu$ objective vectors, where $\mu$ is the population size.

Let $\Omega$ be a set of all possible objective vector sets. A unary quality indicator $I:\Omega\rightarrow\mathbb{R}$ evaluates the quality of $A$ in terms of at least one of the convergence, the uniformity, and the spread. $I$ is said to be Pareto-compliant iff the ranking of all objective vector sets in $\Omega$ by $I$ is consistent with the Pareto dominance relation (for details, see [26]). In this paper, we define the convergence, the uniformity, and the spread as follows. The convergence of $A$ means how close objective vectors in $A$ are to the Pareto front. The uniformity of $A$ means how uniform the distribution of objective vectors in $A$ is. The spread of $A$ means how well objective vectors in $A$ cover the entire Pareto front. As pointed out in [5], the spread is not equal to the extensity, which represents the length of the boundaries of $A$. A combination of the uniformity and the spread is referred to as “diversity” in the evolutionary multi-objective optimization (EMO) community. Fig. S.1 in the supplementary file shows examples of distributions of objective vectors in the three cases on the linear Pareto front with $m=2$.

Below, we explain the following nine quality indicators used in this paper: HV, IGD, IGD⁺, R2, NR2, $I_{\epsilon+}$, SE, $\Delta$, and PD. We do not consider convergence-based quality indicators, such as generational distance (GD) [27], which evaluate the quality of an objective vector set $A$ in terms only of the convergence. This is because the optimal $\mu$-distribution for such a quality indicator is obvious. $A$ is optimal for convergence-based quality indicators if all elements in $A$ are on the Pareto front regardless of their distribution. For the same reason, we do not consider cardinality-based quality indicators, such as overall non-dominated vector generation (ONVG) [28], which evaluate the quality of $A$ based on the number of non-dominated solutions. For example, all of $\mbox{\boldmath$A$}_{1}$, $\mbox{\boldmath$A$}_{2}$, and $\mbox{\boldmath$A$}_{3}$ in Fig. S.1 are optimal for both GD and ONVG.

Below, $R$ is a set of $m$-dimensional reference vectors that approximate the Pareto front in the objective space. The reference point $\mbox{\boldmath$q$}=(q_{1},...,q_{m})^{\rm T}\in\mathbb{R}^{m}$ is used for the HV and NR2 calculations. It should be noted that $\mbox{\boldmath$q$}\not\in\mbox{\boldmath$R$}$.

Okabe et al. [8] analyzed 15 quality indicators using objective vector sets artificially generated on the linear Pareto front and objective vector sets found by EMOAs on the convex Pareto front. The results show that some quality indicators can generate misleading results. Jiang et al. [15] examined six quality indicators using a pair of objective vector sets on the linear, convex, and concave Pareto fronts. The results show that $I_{\epsilon+}$, IGD, and HV are consistent with each other on the convex Pareto front, but IGD is inconsistent with HV on the concave Pareto front. Ravber et al. [36] investigated 11 quality indicators using a chess rating system. They used objective vector sets found by EMOAs on some test problems. The results show the robustness of HV, $I_{\epsilon+}$, and IGD⁺. However, the results also show that the three quality indicators do not equally evaluate the quality of objective vector sets in terms of the convergence, the uniformity, and the spread.

Wessing and Naujoks [37] analyzed the correlation between HV, R2, and $I_{\epsilon+}$. Their analysis was based on objective vector sets randomly generated on two- and three-objective problems. The results based on Pearson’s correlation coefficient show that HV is highly consistent with R2. Liefooghe and Derbel [38] examined the correlation between six quality indicators. They used objective vector sets found by the random search and NSGA-II [13] on test problems with $m\in\{2,3\}$. The results based on the Kendall rank correlation show that HV is consistent with R2 and R3. In contrast, $I_{\epsilon+}$ and its multiplicative version are inconsistent with other quality indicators. Ishibuchi et al. [39] compared IGD⁺ with IGD on various objective vector sets found by NSGA-II on problems with up to 10 objectives. The results show that IGD⁺ can evaluate objective vector sets more accurately than IGD in terms of the Pareto compliance. In addition to IGD⁺ and IGD, three quality indicators (GD, $I_{\epsilon+}$, and D1 [32]) were examined. Bezerra et al. [40] analyzed the relation between IGD⁺ and IGD on the linear Pareto front. Various objective vector sets were used in their analysis. The results show that IGD and IGD⁺ are consistent with each other in most cases. The results also show that IGD may favor objective vectors with a poor spread.

It is difficult to obtain the optimal $\mu$-distributions in an exact manner. Thus, the optimal $\mu$-distributions are generally approximated by analytical or empirical methods. For the differences between the two methods, see Section I.

Auger et al. [12] formulated finding the optimal $\mu$-distribution for HV on two-objective problems as a single-objective continuous optimization problem. Below, we describe its problem formulation in a general manner. Our description significantly differs from the original one.

Let $\mbox{\boldmath$A$}=\{\mbox{\boldmath$a$}_{1},...,\mbox{\boldmath$a$}_{\mu}\}$ be a set of $\mu$ objective vectors on the Pareto front. Also, let $\theta_{i}$ be a real value that determines the first element (i.e., the value of the first objective $f_{1}$) of the $i$-th objective vector $\mbox{\boldmath$a$}_{i}$ ($i\in\{1,...,\mu\}$) in $A$. All objective vectors in the optimal $\mu$-distributions must always be on the Pareto front. For this restriction, the position of $\mbox{\boldmath$a$}_{i}$ for $f_{1}$ specifies that for the second objective $f_{2}$. In [12], a front shape function $F:\mathbb{R}\rightarrow\mathbb{R}$ is used to determine the position of $\mbox{\boldmath$a$}_{i}$ for $f_{2}$ as follows: $\mbox{\boldmath$a$}_{i}=\bigl{(}\theta_{i},F(\theta_{i})\bigr{)}^{\rm T}$. For all $i\in\{1,...,\mu\}$, $\theta_{i}$ is in the range $[\theta^{\rm min},\theta^{\rm max}]$, where $\theta^{\rm min}$ and $\theta^{\rm max}$ are the lower and upper bounds for $\theta_{i}$. Here, $\theta^{\rm min}$ and $\theta^{\rm max}$ correspond to the minimum and maximum values of $f_{1}$ in the Pareto front, respectively. In this manner, the distribution of $\mu$ objective vectors in $A$ is determined by a vector $\mbox{\boldmath$\theta$}=(\theta_{1},...,\theta_{\mu})^{\rm T}$.

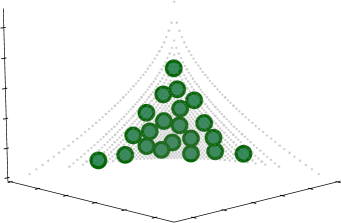
Fig. 1 shows examples of five objective vectors. In Fig. 1, the Pareto front is shown by

where $F_{\rm DTLZ1}$, $F_{\rm DTLZ2}$, and $F_{\rm ZDT1}$ represent the Pareto front shapes of DTLZ1 [41], DTLZ2 [41], and ZDT1 [42], respectively. In Fig. 1, $\mu=5$, $\mbox{\boldmath$\theta$}=(0,0.125,0.25,0.375,0.5)^{\rm T}$ for $F_{\rm DTLZ1}$, and $\mbox{\boldmath$\theta$}=(0,0.25,0.5,0.75,1)^{\rm T}$ for $F_{\rm DTLZ2}$ and $F_{\rm ZDT1}$. As shown in Fig. 1, distributions of objective vectors on various Pareto fronts can be examined by changing $F$.

In summary, finding $A$ that minimizes a quality indicator $I$ is the same as finding $\theta$ that indirectly minimizes $I$ as follows:

where $\theta$ is a solution of the problem defined in (19). $I$ that needs to be maximized (e.g., HV, NR2, and PD) can be translated as $-I$ without loss of generality. Any derivative-free optimizer can be used to minimize $I$ in (19).

Auger et al. [12] proposed analytical and empirical methods of approximating optimal $\mu$-distributions for HV. Details of the analytical method for each $F$ can be found in the supplementary website of [12] (https://sop.tik.ee.ethz.ch/download/supplementary/testproblems/). The proposed problem-specific local search algorithm in [12] for (19) uses variable-wise perturbation. For each iteration, each $\theta_{i}$ is perturbed by a value selected randomly from a normal distribution. Brockhoff et al. [17] applied CMA-ES [20] to (19) to find the optimal $\mu$-distributions for R2. Their results show that objective vectors in the optimal $\mu$-distributions for R2 are densely distributed in the center of the Pareto front. They also examined the contribution of each objective vector in the optimal $\mu$-distribution for R2 to HV (and that for HV to R2).

In contrast to the above-mentioned studies [12, 17], the following studies do not use (19). Bringmann et al. [19] proposed the analytical method for finding the optimal $\mu$-distributions for $I_{\epsilon+}$ on the Pareto front with $m=2$. The proposed method explicitly exploits the properties of $I_{\epsilon+}$ presented in [43]. The results show that the optimal $\mu$-distributions for $I_{\epsilon+}$ on most Pareto fronts with $m=2$ are uniform. Glasmachers [18] proposed a gradient-based analytical method for approximating the optimal $\mu$-distributions for HV on $m\in\{2,3\}$. For $m=3$, the proposed method in [18] decomposes the three-dimensional objective space into cuboids. Then, the proposed method in [18] uses the gradient of HV based on the cuboids.

Ishibuchi et al. [4] used SMS-EMOA [44] to approximate the optimal $\mu$-distributions for HV on Pareto fronts of three-objective problems. SMS-EMOA uses the HV contribution in the steady-state selection. For each iteration, the worst individual in terms of the HV contribution is removed from the last non-domination level. In [4], SMS-EMOA was applied to the DTLZ and inverted-DTLZ problems whose number of distance variables is zero. Then, the influence of the reference vector on the optimal $\mu$-distributions for HV is examined. Ishibuchi et al. [3] also investigated the optimal $\mu$-distributions for IGD approximated by a similar approach. The HV contribution-based selection in SMS-EMOA was replaced by the IGD contribution-based selection. The optimal $\mu$-distributions for HV, IGD, and IGD⁺ approximated by SMS-EMOA in a similar manner were analyzed in [31]. The results show that the optimal $\mu$-distributions for IGD are almost uniform in all problems. The results also show that the optimal $\mu$-distributions for HV and IGD⁺ are similar in all problems when the reference vector for HV is set appropriately.

Below, we explain the proposed formulation for general cases. Only a disconnected front shape function $F_{\rm disconnected}$ explained in Subsection IV-C requires an alternative formulation. For details, see Subsection S.1-D in the supplementary file. Finding the optimal $\mu$-distribution for a quality indicator $I$ on the Pareto front with $m$ objectives is formulated as follows:

where $G$ is a constraint function for constrained front shape functions (e.g., $F_{\rm c\mathchar 45\relax concave}$ explained in Subsection IV-C). In contrast to (19), $G$ is added to (20). If a given front shape function has no constraint, $G$ is eliminated from (20). An objective vector set $\mbox{\boldmath$A$}=\{\mbox{\boldmath$a$}_{1},...,\mbox{\boldmath$a$}_{\mu}\}$ is a translated version of a solution $\theta$ of this problem in a two-phase manner as follows:

where $\mbox{\boldmath$\theta$}=(\theta_{1},...,\theta_{d})^{\rm T}$ is a $d$-dimensional vector, and $d=\mu(m-1)$. Any single-objective black-box optimizer can be used to find $\theta$ that minimizes $I$. While the size of $\theta$ is $\mu$ in (19), that is $d$ in (21). For all $i\in\{1,...,d\}$, $\theta_{i}$ is in $[0,1]$.

The function “${\rm translate}$” in (22) translates a $d$-dimensional vector $\theta$ into a set $\mbox{\boldmath$B$}=\{\mbox{\boldmath$b$}_{1},...,\mbox{\boldmath$b$}_{\mu}\}$ that consists of $\mu$ $m$-dimensional vectors. For each $i\in\{1,...,\mu\}$, $\mbox{\boldmath$b$}_{i}=(b_{i,1},...,b_{i,m})^{\rm T}$, and $\sum^{m}_{j=1}b_{i,j}=1$. Although $\mbox{\boldmath$b$}_{i}$ is an $m$-dimensional vector, it is not an objective vector. Subsection IV-B explains the translation operator in detail.

After translating $\theta$ into $B$ in (22), $B$ is further mapped to the objective vector set $A$ by a front shape function $F$ in (21). For each $i\in\{1,...,\mu\}$, an element $\mbox{\boldmath$b$}_{i}$ in $B$ corresponds to an objective vector $\mbox{\boldmath$a$}_{i}$ in $A$. All objective values are normalized into $[0,1]$ in our study by using the ideal point $\mbox{\boldmath$z$}^{*}$ and the nadir point $\mbox{\boldmath$z$}^{\rm nadir}=(z^{\rm nadir}_{1},...,z^{\rm nadir}_{m})^{\rm T}$ of each $F$ as follows: $a_{i}:=(a_{i}-z^{*}_{i})/(z^{\rm nadir}_{i}-z^{*}_{i})$ for each $i\in\{1,...,m\}$. Here, $z^{\rm nadir}_{i}$ is the maximum value of the $i$-th objective function of the Pareto front. We use the normalization in order to examine the approximated optimal $\mu$-distributions for the quality indicators without worrying about the influence of differently-scaled objective values. Subsection IV-C specifies how to map $B$ to $A$ by the front shape function $F$.

We explain how the translation operator in (22) maps $\theta$ to $B$. First, all $d$ elements in $\theta$ are divided into $\mu$ vector groups as $(\theta_{1},...,\theta_{1+m-2})^{\rm T}$, …, $(\theta_{d-m+2},...,\theta_{d})^{\rm T}$. For example, when $\mu=2$, $m=3$, $d=\mu(m-1)=4$, and $\mbox{\boldmath$\theta$}=(0.1,0.2,0.3,0.4)^{\rm T}$, 4 elements in $\theta$ are divided as follows: $(0.1,0.2)^{\rm T}$ and $(0.3,0.4)^{\rm T}$. For the sake of simplicity, we denote $(\theta_{i},...,\theta_{i+m-2})^{\rm T}$ as $\mbox{\boldmath$y$}=(y_{1},...,y_{m-1})^{\rm T}$ for each $i\in\{1,1(m-1),2(m-1),...,(d-m+2)\}$.

Below, we describe how the $(m-1)$-dimensional vector $y$ is translated into an $m$-dimensional vector $b$ in $B$. To obtain all $\mu$ vectors in $B$, the same operation is repeatedly applied to $y$ for each $i\in\{1,1(m-1),2(m-1),...,(d-m+2)\}$. Each element in $b$ is obtained using the Jaszkiewicz’s method of generating random weight vectors [46] as follows:

where $j\in\{2,...,m-1\}$ in (23). It should be noted that $b$ obtained by (23) satisfies the condition $\sum^{m}_{k=1}b_{k}=1$. Although the Jaszkiewicz’s method was originally proposed for the weight vector generation in decomposition-based EMOAs, it can be used to translate $y$ into $b$ in a straightforward manner.

The proposed formulation can be applied to any Pareto front when its front shape function $F$ is available. In other words, the proposed formulation cannot be applied to the Pareto front whose analytical expression (i.e., its front shape function) is unavailable such as WFG3 [47]. Although various front shape functions were presented in the previous study [12], they are only for $m=2$. We design front shape functions for $m\geq 3$ based on a method of generating uniformly distributed reference vectors in representative test problems (e.g., DTLZ and WFG) presented in [48].

We use eight front shape functions shown in Table I. The name of the original problems and the shape of the Pareto fronts are also shown in Table I. $F_{\rm linear}$, $F_{\rm concave}$, and $F_{\rm convex}$ are the most basic front shape functions. $F_{\rm i\mathchar 45\relax linear}$, $F_{\rm i\mathchar 45\relax concave}$, and $F_{\rm i\mathchar 45\relax convex}$ are inverted versions of $F_{\rm linear}$, $F_{\rm convex}$, and $F_{\rm concave}$, respectively. It should be noted that an inverted version of the convex Pareto front is concave, and vice versa. $F_{\rm disconnected}$ has the disconnected and mixed Pareto front. Some parts of the Pareto front of $F_{\rm c\mathchar 45\relax concave}$ are infeasible due to the constraint. We select $F_{\rm c\mathchar 45\relax concave}$ to demonstrate that the proposed formulation can handle the constrained Pareto front. In our preliminary experiments, we used the degenerate front shape function $F_{\rm degenerate}$ whose original problem is DTLZ5. $F_{\rm degenerate}$ is not a surface but a curve since it is degenerate. Because the shape of $F_{\rm degenerate}$ is concave, the optimal $\mu$-distribution on $F_{\rm degenerate}$ is similar to that for a two-objective problem with $F_{\rm concave}$. For this reason, we omit $F_{\rm degenerate}$.

Due to the paper length limitation, we explain only $F_{\rm concave}$ in this paper. We describe other front shape functions in Section S.1 in the supplementary file. In $F_{\rm concave}$, the $i$-th element $b_{i}$ of $b$ in $B$ is translated into the $i$-th element $a_{i}$ of $a$ in $A$ on the concave Pareto front as follows:

where $t=\sqrt{\sum^{m}_{j=1}b_{j}^{2}}$. This translation is based on the method of generating reference vectors in DTLZ2 described in [48]. All objective vectors obtained by (24) satisfy the following relation of the Pareto front of DTLZ2: $\sum^{m}_{i=1}(f_{i}(\mbox{\boldmath$x$}^{*}))^{2}=1$. In addition to the eight front shape functions in Table I, we believe that it is possible to design other front shape functions using [48] as reference.

Figs. 4–9 show approximated optimal $\mu$-distributions with $\mu=21$ obtained by the proposed approach for the nine quality indicators on the eight Pareto fronts. In Figs. 4–9, $x$, $y$, and $z$ axes represent $f_{1}$, $f_{2}$, and $f_{3}$, respectively. Figs. 4–9 show the best objective vector set found by L-SHADE among 31 runs for each quality indicator on each front shape function $F$. Below, we denote the best $\mu$-distribution for a quality indicator $I$ as $\mbox{\boldmath$A$}_{I}$ (e.g., $\mbox{\boldmath$A$}_{\rm HV}$). Figs. S.3–S.50 in the supplementary file show approximated optimal $\mu$-distributions with the other $\mu$ values. All reference vectors in $R$ are shown in each figure.

For the sake of comparison, Figs. 4–7 (j) show a set of $\mu$ objective vectors generated by simplex-lattice design, denoted as $\mbox{\boldmath$A$}_{\rm SLD}$. We generated $\mbox{\boldmath$A$}_{\rm SLD}$ using the same method as for generating the reference vector set $R$ described in Section V. Since the number of objective vectors generated by simplex-lattice design on $F_{\rm disconnected}$ and $F_{\rm c\mathchar 45\relax concave}$ cannot be specified arbitrarily due to their characteristics, we do not show $\mbox{\boldmath$A$}_{\rm SLD}$ in Figs. 9 and 9. $\mbox{\boldmath$A$}_{\rm SLD}$ can be viewed as an “ideal” objective vector set found by decomposition-based EMOAs (e.g., NSGA-III [49]). Although the distribution of objective vectors in $\mbox{\boldmath$A$}_{\rm SLD}$ is uniform, $\mbox{\boldmath$A$}_{\rm SLD}$ is not optimal for all the nine quality indicators (see Subsection VI-B).

Since the distribution of objective vectors in some objective vector sets is not uniform, one may think that the approximated objective vector sets are far from optimal. However, as demonstrated in Subsection VI-B using Table II, some quality indicators do not prefer uniformly distributed objective vectors. For example, as shown in Figs. 4 (j) and (h), $\mbox{\boldmath$A$}_{\rm SLD}$ clearly has a better uniformity than $\mbox{\boldmath$A$}_{\Delta}$ on $F_{\rm concave}$. Nevertheless, Table II shows that $\Delta$ evaluates $\mbox{\boldmath$A$}_{\Delta}$ as better than $\mbox{\boldmath$A$}_{\rm SLD}$ (details are discussed later). Such an unintuitive result may be due to a hidden property of each quality indicator. We reemphasize that a theoretical analysis of the optimal $\mu$-distribution for $m\geq 3$ is difficult. For this reason, the (true and approximated) optimal $\mu$-distributions for almost all quality indicators have not been investigated on the Pareto front with $m\geq 3$.

Below, we individually discuss the optimal $\mu$-distribution for each of the nine quality indicators ($\mbox{\boldmath$A$}_{\rm HV}$, $\mbox{\boldmath$A$}_{\rm IGD}$, $\mbox{\boldmath$A$}_{\rm IGD^{+}}$, $\mbox{\boldmath$A$}_{\rm R2}$, $\mbox{\boldmath$A$}_{\rm NR2}$, $\mbox{\boldmath$A$}_{I_{\epsilon+}}$, $\mbox{\boldmath$A$}_{\rm SE}$, $\mbox{\boldmath$A$}_{\Delta}$, and $\mbox{\boldmath$A$}_{\rm PD}$). Although results of HV, IGD, and IGD⁺ are consistent with the previous studies, some results of other quality indicators provide insightful information. Our findings are summarized in Section VII.

In Subsection VI-A, we analyzed the nine quality indicators using the optimal $\mu$-distributions. Here, we examine the nine quality indicators using the ranking information.

Table II shows the rankings of the nine approximated optimal $\mu$-distributions ($\mbox{\boldmath$A$}_{\rm HV}$, …, $\mbox{\boldmath$A$}_{\rm PD}$) and $\mbox{\boldmath$A$}_{\rm SLD}$ by each quality indicator on $F_{\rm concave}$. The average ranking values are reported at the bottom of Table II. Tables S.2–S.6 in the supplementary file show the rankings on $F_{\rm linear}$, $F_{\rm convex}$, $F_{\rm i\mathchar 45\relax linear}$, $F_{\rm i\mathchar 45\relax concave}$, and $F_{\rm i\mathchar 45\relax convex}$, respectively. Since $\mbox{\boldmath$A$}_{\rm SLD}$ cannot be generated on $F_{\rm disconnected}$ and $F_{\rm c\mathchar 45\relax concave}$, the rankings for $F_{\rm disconnected}$ and $F_{\rm c\mathchar 45\relax concave}$ are not shown. Note that the quality indicator called “SLD” does not exist. Recall that $\mbox{\boldmath$A$}_{\rm SLD}$ is generated by simplex-lattice design. Due to the paper length limitation, we mainly explain the results on $F_{\rm concave}$.

On the one hand, from each row in Table II, we can read the ranking of the ten objective vector sets by the corresponding quality indicator on $F_{\rm concave}$. For example, HV evaluates $\mbox{\boldmath$A$}_{\rm HV}$ and $\mbox{\boldmath$A$}_{\rm IGD}$ as the best and the worst, respectively. On the other hand, from each column in Table II, we can read the ranking of the corresponding objective vector set by the nine indicators. For example, $\mbox{\boldmath$A$}_{\rm SE}$ is ranked at fourth by HV, IGD, and NR2.

The average ranking value of each objective vector set in the bottom row of Table II (i.e., average value of each column) means how highly the corresponding objective vector set is evaluated by all the nine quality indicators. $\mbox{\boldmath$A$}_{\rm R2}$ performs the best among the 10 objective vector sets on $F_{\rm concave}$ in terms of the average ranking values. Thus, a good objective vector set with respect to R2 may be highly evaluated by the other quality indicators on $F_{\rm concave}$. In contrast, $\mbox{\boldmath$A$}_{\rm PD}$ performs the worst in terms of the average ranking values. This result indicates that a good objective vector set with respect to PD may be evaluated as inferior to other objective vector sets by the other quality indicators on $F_{\rm concave}$. These results are useful for selecting a quality indicator used in indicator-based EMOAs. Note that the best objective vector set in terms of the average ranking values depends on the choice of $F$. For example, Table S.4 shows that $\mbox{\boldmath$A$}_{\rm R2}$ performs the second worst on $F_{\rm i\mathchar 45\relax linear}$.

Each quality indicator $I$ evaluates its optimal $\mu$-distribution $\mbox{\boldmath$A$}_{I}$ as the best. For this reason, all diagonal elements in Table II are “1”. The same results can be found in the rankings on the other front shape functions, except for the ranking of $\mbox{\boldmath$A$}_{\rm IGD^{+}}$ by IGD⁺ on $F_{\rm linear}$ in Table S.2 and $\mbox{\boldmath$A$}_{\rm NR2}$ by NR2 on $F_{\rm i\mathchar 45\relax concave}$ in Table S.5. IGD⁺ and NR2 evaluate $\mbox{\boldmath$A$}_{\rm IGD}$ and $\mbox{\boldmath$A$}_{\rm HV}$ as the best in Tables S.2 and S.5, respectively. These exceptional results are due to the similarity between IGD and IGD⁺, and the similarity between HV and NR2.