An Algorithm for Streaming Differentially Private Data

A large body of work has explored privacy-preserving techniques for spatial datasets. The methods can be broadly classified into two categories based on whether or not the curator is a trusted entity. If the curator is not-trusted, more strict privacy guarantees such as Local Differential Privacy and Geo-Indistinguishability are used and action is taken at the user level before the data reaches the server. We focus on the case where data is stored in a trusted server and the curator has access to the true data of all users. This setup is more suited for publishing privacy-preserving microdata and aggregate statistics. Most methods in this domain rely on Private Spatial Decomposition (PSD) to create a histogram-type density estimation of the spatial data domain. PrivTree (Zhang et al., 2016) is perhaps the most popular algorithm of this type and we refer the reader to (loc, 2021) for a survey of some other related methods. However, these offline algorithms assume we have access to the entire dataset at once so they do not apply directly to our use case.

We use a notion of differential privacy that accepts stream as input and guarantees privacy over the entire time horizon, sometimes referred to as continual DP. Early work such as (Dwork et al., 2010) and (Chan et al., 2010) explores the release of bit count over an infinite stream of bits and introduce various effective algorithms, including the Binary Tree mechanism. We refer to these mechanisms here as Counters and use them as a subroutine of our algorithm. In (Dwork et al., 2015), the authors build upon the work in (Dwork et al., 2010) and use the Binary Tree mechanism together with an online partitioning algorithm to answer range queries. However, the problem considered is answering queries on offline datasets. In (Wang et al., 2021; Chen et al., 2017) authors further build upon the task of privately releasing a stream of bits or integers under user and event-level privacy. A recent work (Jain et al., 2023) addresses deletion when observing a stream under differential privacy. They approach the problem of releasing a count of distinct elements in a stream. Since these works approach the task of counting a stream of one-dimensional data, they are different from our use case of multi-dimensional density estimation and synthetic data generation. The Binary Tree Mechanism has also been used in other problems such as online convex learning (Guha Thakurta & Smith, 2013) and deep learning (Kairouz et al., 2021), under the name tree-based aggregation trick. Many works with streaming input have also explored the use of local differential privacy for the collection and release of time series data such as telemetry (Joseph et al., 2018; Ding et al., 2017).

To the best of our knowledge a very recent work (Bun et al., 2023) is the only other to approach the task of releasing a synthetic stream with differential privacy. However, they approach a very different problem where the universe consists of a fixed set of users, each contributing to the dataset at all times. Moreover, a user’s contribution is limited to one bit at a time, and the generated synthetic data is derived to answer a fixed set of queries. In contrast, we allow multi-dimensional continuous value input from an arbitrary number of users and demonstrate the utility over randomly generated range queries.

The classical definition of differential privacy of a randomized differential algorithm $\mathcal{A}$ demands that for any pair of input data $f$, $\tilde{f}$ that differ by a single data point, the outputs $\mathcal{A}(f)$ and $\mathcal{A}(\tilde{f})$ be statistically indistinguishable. Here is a version of this definition, which is very naturally adaptable to problems about data streams.

To keep track of the change of data stream $f$ over time, it is natural to consider the differential stream

where we set $f(x,0)=0$. The total change of $f$ over all times and locations is the quantity

which defines a seminorm on the space of data streams. A moment’s thought reveals that two data streams satisfy

if and only if $\tilde{f}$ can be obtained from $f$ by changing a single data point: either one data point is added at some time and is never removed later, or one data point is removed and is never added back later. This makes it natural to consider DP of streaming algorithms wrt. the $\mathinner{\!\left\lVert\cdot\right\rVert}_{\nabla}$ norm.

The algorithm we are about to describe produces synthetic data: it converts an input stream $f(x,t)$ into an output stream $g(x,t)$. The algorithm is streaming: at each time $t_{0}$, it can only see the part of the input stream $f(x,t)$ for all $x\in\Omega$ and $t\leq t_{0}$, and at that time the algorithm outputs $g(x,t_{0})$ for all $x\in\Omega$.

Now that we quantified the effect of the change of a single input data point, we can change any number of input data points. If two data streams satisfy $\mathinner{\lVert f-\tilde{f}\rVert}_{\nabla}=k$, then applying Definition 2.1 $k$ times and using the triangle inequality, we conclude that

For example, suppose that a patient who gets sick and spends a week at some hospital; then she recovers, but after some time she gets sick again and spends another week at another hospital and finally recovers completely. If the data stream $\tilde{f}$ is obtained from $f$ by removing such a patient, then, due to the four events described above, $\mathinner{\lVert f-\tilde{f}\rVert}_{\nabla}=4$. Hence, we conclude that $\mathbb{P}\{\mathcal{A}(\tilde{f})\in S\}\leq e^{4\varepsilon}\cdot\mathbb{P}\{\mathcal{A}(f)\in S\}.$ In other words, the privacy of patients who contribute four events to the data stream is automatically protected as well, although the protection guarantee is four times weaker than for patients who contribute a single event.

First, we convert the problem of differentially private streaming of a function $f(x,t)$ on a set $\Omega$ to a problem of differentially private streaming of a function $F(x,t)$ on a tree. To this end, fix some hierarchical partition of the domain $\Omega$. Thus, assume that $\Omega$ is partitioned into some $\beta>1$ subsets $\Omega_{1},\ldots,\Omega_{\beta}$, and each of these subsets $\Omega_{i}$ is partitioned into $\beta$ further subsets, and so on. A hierarchical partition can be equivalently represented by a tree $T$ whose vertices are subsets of $\Omega$ and the children of each vertex form a partition of that vertex. Thus, the tree $T$ has root $\Omega$; the root is connected to the $\beta$ vertices $\Omega_{1},\ldots,\Omega_{\beta}$, and so on. We refer to $\beta$ as the fanout number of the tree.

In practice, there often exists a natural hierarchical decomposition of $\Omega$. For example, if $\Omega=\{0,1\}^{d}$ a binary partition obtained by fixing a coordinate is natural such as $\Omega_{1}=\{0\}\times\{0,1\}^{d-1}$ and $\Omega_{2}=\{1\}\times\{0,1\}^{d-1}$. Each of $\Omega_{1}$ and $\Omega_{2}$ can be further partitioned by fixing another coordinate. As another example, if $\Omega=[0,1]^{d}$ and fanout $\beta=2$, a similar natural partition can be obtained by splitting a particular dimension’s region into halves such that $\Omega_{1}=[0,\frac{1}{2})\times[0,1]^{d-1}$ and $\Omega_{2}=[\frac{1}{2},1]\times[0,1]^{d-1}$. Each of $\Omega_{1}$ and $\Omega_{2}$ can be further partitioned by splitting another coordinate’s region into halves.

We can convert any function on the set $\Omega$ into a function on the vertices of the tree $T$ by summing the values in each vertex. I.e., to convert $f\in\mathbb{R}^{\Omega}$ into $F\in\mathbb{R}^{V(T)}$, we set

Vice versa, we can convert any function $G$ on the vertices of the tree $T$ into a function $g$ on the set $\Omega$ by assigning value $G(v)$ to one arbitrarily chosen point in each leaf $v$. In practice, however, the following variant of this rule works better if $G(v)>0$. Assign value $1$ to $\lceil G(v)\rceil$ random points in $v$, i.e. set

where $x_{i}(v)$ are independent random points in $v$ and ${\textbf{1}}_{x}$ denotes the indicator function of the set $\{x\}$. The points $x_{i}(v)$ can be sampled from any probability measure on $v$, and in practice we often choose the uniform measure on $v$.

Summarizing, we reduced our original problem to constructing an algorithm that transforms any given stream $F(x,t)\mathrel{\mathop{\mathchar 58\relax}}V(T)\times\mathbb{N}\to\{0,1,2,\ldots\}$ into a differentially private stream $G(x,t)\mathrel{\mathop{\mathchar 58\relax}}V(T)\times\mathbb{N}\to\{0,1,2,\ldots\}$ where $V(T)$ is the vertex set of a fixed, known tree $T$.

Let $C(T)$ denote the set of all functions $F\in\mathbb{R}^{V(T)}$ that can be obtained from functions $f\in\mathbb{R}^{\Omega}$ using transformation (4). The transformation is linear, so $C(T)$ must be a linear subspace of $\mathbb{R}^{V(T)}$. A moment’s thought reveals that $C(T)$ is comprised of all consistent functions – the functions $F$ that satisfy the equations

Any function on $V(T)$ can be transformed into a consistent function by pushing the values up the tree and spreading them uniformly down the tree. More specifically, this can be achieved by the linear transformation

that we call the consistent extension. Suppose that a function $F$ takes value $1$ on some vertex $v\in V(T)$ and value $0$ on all other vertices. To define $G=\operatorname{Ext}_{T}(F)$, we let $G(u)$ equal $1$ for any ancestor of $v$ including $v$ itself, $1/\beta$ for any child of $v$, $1/\beta^{2}$ for any grandchild of $v$, and so on. In other words, we set $G(u)=\beta^{-\max(0,d(v,u))}$ where $d(v,u)$ denotes the directed distance on the tree $T$, which equals the usual graph distance (the number of edges in the path from $v$ to $u$) if $u$ is a descendant of $v$, and minus the graph distance otherwise. Extending this rule by linearity, we arrive at the explicit definition of the consistent extension operator:

By definition (6), a consistent function is uniquely determined by its values on the leaves of the tree $T$. Thus a natural norm of $C(T)$ is

A key subroutine of our method is a version of the remarkable algorithm $\operatorname{PrivTree}$ due to (Zhang et al., 2016). In the absence of noise addition, one can think of $\operatorname{PrivTree}$ as a deterministic algorithm that inputs a tree $T$ and a function $F\in\mathbb{R}^{V(T)}$ and outputs a subtree of $T$. The algorithm grows the subtree iteratively: for every vertex $v$, if $F(v)$ is larger than a certain threshold $\theta$, the children of vertex $v$ are added to the subtree.

In Appendix A, we give the $\operatorname{PrivTree}$ algorithm and proof of its delicate privacy guarantees in detail.

We present our method PHDStream (Private Hierarchical Decomposition of Stream) in Algorithm 2. Algorithm 1 transforms an input stream $F(\cdot,t)\in V(T)\times\mathbb{N}\to\mathbb{R}$ into a stream $G(\cdot,t)\in V(T)\times\mathbb{N}\to\mathbb{R}$. In the algorithm, $\mathcal{L}(T)$ denotes the set of leaves of tree $T$, and $\operatorname{Lap}(\cdot,t,2/\varepsilon)$ denote independent Laplacian random variables. Using Algorithm 1 as a subroutine, Algorithm 2 transforms a stream $f(x,t)\in\Omega\times\mathbb{N}\to\mathbb{R}$ into a stream $g(x,t)\in\Omega\times\mathbb{N}\to\mathbb{R}$:

In the first step of this algorithm, we consider the previously released synthetic stream $G(\cdot,t-1)$, update it with the newly received real data $\nabla F(\cdot,t)$, and feed it into $\operatorname{PrivTree}_{T}$, which produces a differentially private subtree $T(t)$ of $T$.

In the next two steps, we compute the updated stream on the tree. It is tempting to choose for $G(\cdot,t)$ a stream computed by a simple random perturbation as, $G(\cdot,t)=G(\cdot,t-1)+\nabla F(\cdot,t)+\operatorname{Lap}(\cdot,t,2/\varepsilon)$. The problem, however, is that such randomly perturbed stream would not be differentially private. Indeed, imagine we make a stream $\tilde{f}$ by changing the value of the input stream $f$ at some time $t\in\mathbb{N}$ and point $x\in\Omega$ by $1$. Then the sensitivity condition (3) holds. But when we convert $f$ into a consistent function $F$ on the tree, using (4), that little change propagates up the tree. It affects the values of $F$ not just at one leaf $v\ni x$ but all of the ancestors of $v$ as well, and this could be too many changes to protect. In other words, consistency on the tree makes sensitivity too high, which in turn jeopardizes privacy.

To halt the propagation of small changes up the tree, the last two steps of the algorithm restrict the function only on the leaves of the subtree. This restriction controls sensitivity: a change to $F(v)$ made in one leaf $v$ does not propagate anymore, and the resulting function $d(v,t)$ is differentially private. In the last step, we extend the function $d(v,t)$ from the leaves to the whole tree–an operation that preserves privacy–and use it as an update to the previous, already differentially private, synthetic stream $G(\cdot,t-1)$.

These considerations lead to the following privacy guarantee as announced in Section 2.1, i.e. in the sense of Definition 2.1, for the $\mathinner{\!\left\lVert\cdot\right\rVert}_{\nabla}$ norm.

A formal proof of Theorem 3.2 is given in Appendix B.

Furthermore, we are interested in counters that satisfy differential privacy guarantees as per Definition 2.1 with respect to the norm $\mathinner{\!\left\lVert f\right\rVert}\coloneqq\sum_{t\in\mathbb{N}}\mathinner{\!\left\lvert f(t)\right\rvert}$. Note that we have not used the norm $\mathinner{\!\left\lVert\cdot\right\rVert}_{\nabla}$ here as the input to the counter algorithm will already be the differential stream $\nabla f$. The foundational work of (Chan et al., 2010) and (Dwork et al., 2010) introduced private counters for the sum of bit-streams but the same algorithms can be applied to real-valued streams as well. In particular, we will be using the Simple II, Two-Level, and Binary Tree algorithms from (Chan et al., 2010), hereafter referred to as Simple, Block, and Binary Tree Counters respectively. The counter algorithms are included in Appendix D for completeness. We also discuss there how the Binary Tree counter is only useful if the input stream to the counter has a large time horizon and thus we limit our experiments in Section 5 to Simple and Block counters.

Algorithm 3 is a version of Algorithm 1 with counters. Here, we create an instance of some counter algorithm for each node $v\in V(T)$. Algorithm 3 is agnostic to the counter algorithm used, and we can even use different counter algorithms for different nodes of the tree. Since at any time $t\in\mathbb{N}$, we only count at the leaf nodes of the tree $T(t)$, the counter $C_{v}$ is updated for any node $v\in V(T)$ if and only if $v\in\mathcal{L}(T(t))$. Hence the input to the counter $C_{v}$ is the restriction of the stream $\nabla F$ on the set of times in $N_{v}$, that is ${\left.\kern-1.2pt{\nabla F(v,\cdot)}\right|_{N_{v}}}$, where $N_{v}=\{t\in\mathbb{N}\mid v\in\mathcal{L}(T(t))\}$. In the subsequent sections, we discuss a few general ideas about the use of multiple counters and selectively updating some of them. We use these discussions to prove the privacy of Algorithm 3 in Subsection 4.5.

To efficiently prove the privacy guarantees of our algorithm, which utilizes many counters, we introduce the notion of a multi-dimensional counter. A $d$-dimensional counter $\mathcal{C}$ is a randomized streaming algorithm consisting of $d$ independent counters $\mathcal{C}_{1},\mathcal{C}_{2},\ldots,\mathcal{C}_{d}$ such that it maps an input stream $f\mathrel{\mathop{\mathchar 58\relax}}\mathbb{N}\to\mathbb{R}^{d}$ to an output stream $g\mathrel{\mathop{\mathchar 58\relax}}\mathbb{N}\to\mathbb{R}^{d}$ with $g(t)=\left(\mathcal{C}_{1}(f(t)_{1}),\mathcal{C}_{2}(f(t)_{2}),\ldots,\mathcal{C}_{d}(f(t)_{d})\right)$ for all $t\in\mathbb{N}$. For differential privacy of such counters, we will still use Definition 2.1 but with the extension of the norm to streams with multi-dimensional output as $\mathinner{\!\left\lVert f\right\rVert}\coloneqq\sum_{t\in\mathbb{N}}\mathinner{\!\left\lVert f(t)\right\rVert}_{\ell_{1}}$.

Let us assume that we have a set of $k$ counters $\mathinner{\left\{\mathcal{C}_{1},\mathcal{C}_{2},\dots,\mathcal{C}_{k}\right\}}$. At any time $t\in\mathbb{N}$, we want to activate exactly one of these counters as selected by a randomized streaming algorithm $\mathcal{M}$. The algorithm $\mathcal{M}$ depends on the input stream $f$ and optionally on the entire previous output history, that is the time indices when each of the counters was selected and their corresponding outputs at those times. We present this idea formally as Algorithm 4.

The proof of Theorem 4.2 is given in Appendix E. Note the following about Algorithm 4 and Theorem 4.2: (1) each individual counter can be of any finite dimensionality, (2) we do not assume anything about the relation among the counters, (3) the privacy guarantees are independent of the number of counters, and (4) the algorithm can be easily extended to the case when the input streams to all sub-routines $\mathcal{C}_{1},\mathcal{C}_{2},\ldots,\mathcal{C}_{k}$, and $\mathcal{M}$ may be different.

We first show that Algorithm 3 is a version of the selective counting algorithm (Algorithm 4). Let $\mathcal{P}(T)$ be a set of all possible subtrees of the tree $T$. Since each node $v\in T$ is associated with a counter, the collection of counters in $\mathcal{L}(S)$ for any $S\in\mathcal{P}(T)$ is a multi-dimensional counter. Moreover, for any neighboring input streams $F$ and $\tilde{F}$ with $\mathinner{\!\left\lVert F-\tilde{F}\right\rVert}_{\nabla}=1$, at most one leaf node will differ in the count. Hence $\mathcal{L}(S)$ is a counter with $\varepsilon/2$-DP. $\mathcal{P}(T)$ is thus a set of multi-dimensional counters, each satisfying $\varepsilon/2$-DP. $\operatorname{PrivTree}_{T}$ at time $t$ selects one counter as $\mathcal{L}(T(t))$ from $\mathcal{P}(T)$ and performs counting. Hence, by Theorem 4.2, Algorithm 3 is $\varepsilon$-DP.

We conducted experiments on datasets with the location (latitude and longitude coordinates) of users collected over time. We analyzed the performance of our method on two real-world and three artificially constructed datasets.

Real-world Datasets: We use two real-world datasets: Gowalla (Cho et al., 2011) and NY Taxi (Donovan & Work, 2016). The Gowalla dataset contains location check-ins by a user on the social media app Gowalla. The NY Taxi dataset (Donovan & Work, 2016) contains the pickup and drop-off locations and times of Yellow Taxis in NY.

Simulated Datasets: Our first simulated dataset is derived from the Gowalla dataset. Motivated by the problem of releasing the location of active coronavirus infection cases, we consider each check-in as a report of infection and remove this check-in after $30$ days indicating that the reported individual has recovered. This creates a version of Gowalla with deletion. The second dataset contains points sampled on two concentric circles but the points first appear on one circle and then gradually move to the other circle. This creates a dataset where the underlying distribution changes dramatically. We also wanted to explore the performance of our algorithm based on the number of data points it observes in initialization and then at each batch. Thus for this dataset, we first fix a constant batch size for the experiment and then index time accordingly. Additionally, we keep initialization time $t_{0}$ as a value in $[0,1]$ denoting the proportion of total data the algorithm uses for initialization.

Many real-world datasets such as Gowalla have a slow growth at the beginning of time. In practice, we can hold the processing of such streams until some time $t_{0}\in\mathbb{N}$, which we refer to as initialization time, until sufficient data has been collected. Thus for any input data stream $f\mathrel{\mathop{\mathchar 58\relax}}\Omega\times\mathbb{N}\to\mathbb{R}$ and initialization time $t_{0}\in\mathbb{N}$, we use a modified stream $\hat{f}\mathrel{\mathop{\mathchar 58\relax}}\Omega\times\mathbb{N}\to\mathbb{R}$ such that $\hat{f}(\cdot,t)=f(\cdot,t+t_{0}-1)$ for all $t\in\mathbb{N}$. We discuss the effects of initialization time $t_{0}$ on the algorithm performance in detail in Section 5.5

Let $\varepsilon$ be our privacy budget. Consider the offline synthetic data generation algorithm as per (Zhang et al., 2016), which is to use $\operatorname{PrivTree}_{T}$ with privacy budget $\varepsilon/2$ to obtain a subtree $S$ of $T$, generate the synthetic count of each node $v\in\mathcal{L}(S)$ by adding Laplace noise with scale $2/\varepsilon$, and sample points in each node $v\in\mathcal{L}(S)$ equal to their synthetic count. Let us denote this algorithm as $\operatorname{PrivTree}_{T}+\operatorname{Counting}$. A basic approach to convert an offline algorithm to a streaming algorithm is to simply run independent instances of the algorithm at each time $t\in\mathbb{N}$. We use this idea to create the following three baselines and compare our algorithm with them.

Baseline 1) Offline PrivTree on stream: At any time $t\in\mathbb{N}$, we run an independent version of the offline $\operatorname{PrivTree}_{T}+\operatorname{Counting}$ on $f(\cdot,t)$, that is the stream data at time $t$. We want to emphasize that to be differentially private, this baseline requires a privacy parameter that scales with time $t$ and it does NOT satisfy differential privacy with the parameter $\varepsilon$. Thus we expect it to perform much better with an algorithm that is $\varepsilon$-DP. We still use this method as a baseline since, due to a lack of DP algorithms for streaming data, industry applications sometimes naively re-run DP algorithms as more data is collected. However, we show that PHDStream performs competitively close to this baseline.

Baseline 2) Offline PrivTree on differential stream Similar to Baseline 1, at any time $t\in\mathbb{N}$, we run an independent version of the offline $\operatorname{PrivTree}_{T}+\operatorname{Counting}$ algorithm, but with the input data $\nabla f(\cdot,t)$, that is the differential data observed at $t$. This baseline satisfies $\varepsilon$-DP. For a fair comparison, at time $t$, any previous output is discarded and the current synthetic data is scaled by the factor ${|f(\cdot,t)|}/{|\nabla f(\cdot,t)|}$.

Baseline 3) Initialization with PrivTree, followed by counting with counters: We first use the offline $\operatorname{PrivTree}_{T}+\operatorname{Counting}$ algorithm at only the initialization time $t_{0}$ and get a subtree $S$ of $T$ as selected by PrivTree. We then create a counter for all nodes $v\in\mathcal{L}(S)$ with privacy budget $\varepsilon$. At any time $t>t_{0}$, $S$ is not updated, and only the counter for each of the nodes in $\mathcal{L}(S)$ is updated using the differential stream $\nabla f(\cdot,t)$. This baseline also satisfies $\varepsilon$-DP. Note that this algorithm has twice the privacy budget for counting at each time $t>t_{0}$ as we do not update $S$. We only have results for this baseline if $t_{0}>0$. We show that PHDStream outperforms this baseline if the underlying density of points changes sufficiently with time.

We evaluate the performance of our algorithm against range counting queries, that count the number of points in a subset of the space $\Omega$. For $\Omega^{\prime}\subseteq\Omega$, the associated range counting query $q_{\Omega^{\prime}}$ over a function $h\mathrel{\mathop{\mathchar 58\relax}}\Omega\to\mathbb{R}$ is defined as $q_{\Omega^{\prime}}(h)\coloneqq\sum_{x\in\Omega^{\prime}}h(x)$. In our experiments, we use random rectangular subsets of $\Omega$ as the subregion for a query. Similar to (Zhang et al., 2016), we generate three sets of queries: $10,000$ small, $5000$ medium, and $1000$ large with area in $[0.01\%,0.1\%)$, $[0.1\%,1\%)$, and $[1\%,10\%)$ of the space $\Omega$ respectively. We use average relative error over a query set as our metric. At time $t$, given query set $Q$, the relative error of a synthetic stream $g\mathrel{\mathop{\mathchar 58\relax}}\Omega\times\mathbb{N}\to\mathbb{R}$ as compared to the input stream $f\mathrel{\mathop{\mathchar 58\relax}}\Omega\times\mathbb{N}\to\mathbb{R}$ is thus defined as,

where $0.001|f(\cdot,t)|$ or $1\%$ of $|f(\cdot,t)|$ is a small additive term to avoid division by $0$. We evaluate the metric for each query set at a regular time interval and report our findings.

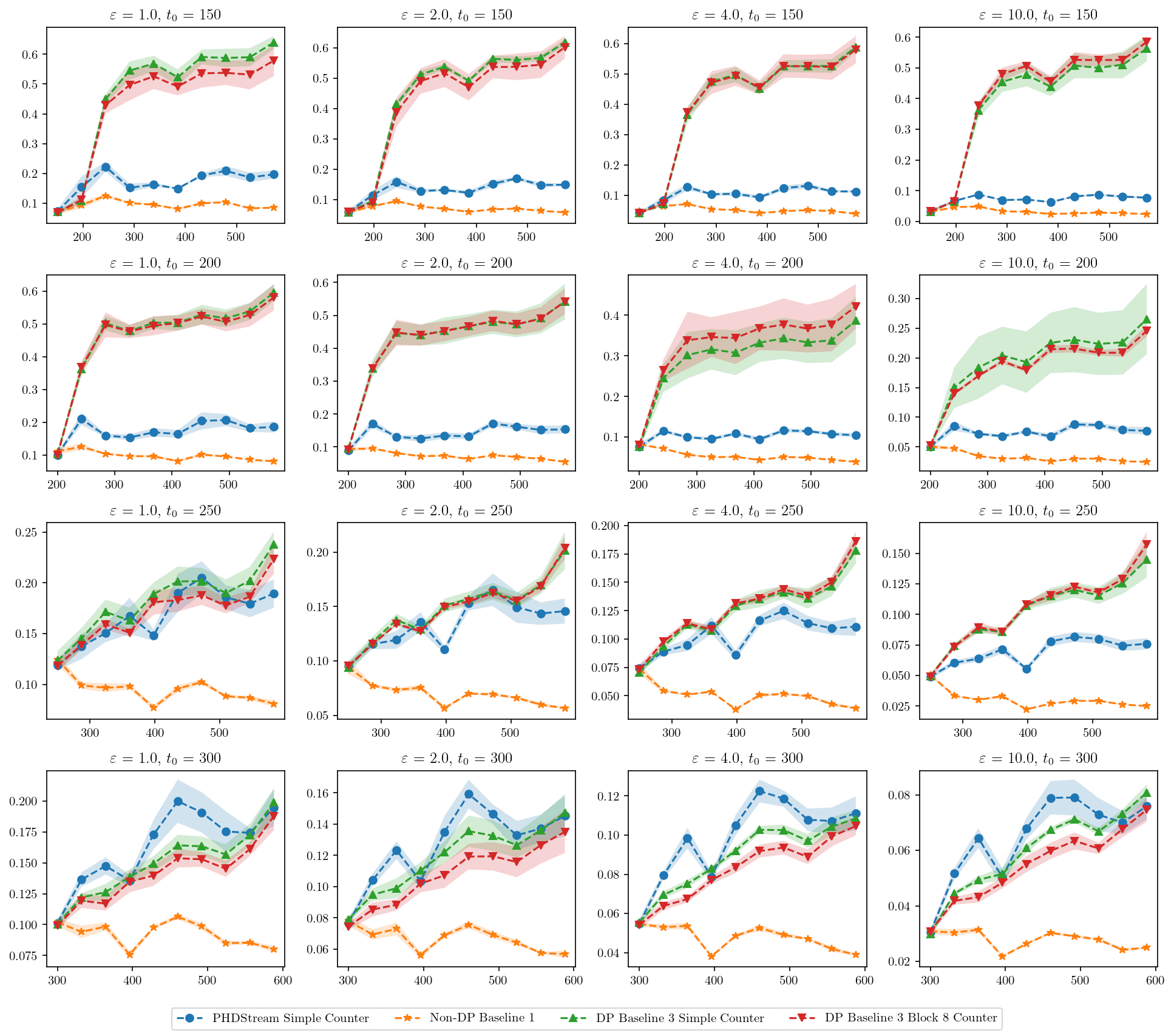
Our analysis indicates that PHDStream performs well across various datasets and hyper-parameter settings. We include some of the true and synthetic data images in Appendix H. Due to space constraints, we limit the discussion of the result to a particular setting in Figure 1 where we fix the privacy budget to $\varepsilon=1$, sensitivity to $2$, query set to small queries, and explore different values for initialization time $t_{0}$. For further discussion, refer to Appendices H and I.

PHDStream remains competitive to the challenging non-differentially private Baseline 1 and in almost all cases, it outperforms the differentially private Baseline 2. It also outperforms Baseline 3 if we initialize the algorithm sufficiently early. We discuss above mentioned observations together with the effect of various hyper-parameters below.

Initialization time: If the dataset grows without changing the underlying distribution too much, it seems redundant to update $T(t)$ with $\operatorname{PrivTree}_{T}$ at each time $t\in\mathbb{N}$. Moreover, when counting using fixed counters, we know that error in a counter grows with time so the performance of the overall algorithm should decrease with time. We observe the same for higher values of initialization time in Figure 1. Moreover, we see that Baseline 3, which uses PrivTree only once, outperforms PHDStream for such cases.

Counter type: In almost all cases, for the PHDStream algorithm, the Simple counter has better performance than the Block 8 counter. This can be explained by the fact that for these datasets, the majority of nodes had their counter activated only a few times in the entire algorithm. For example, when using the Gowalla dataset with $t_{0}=100$, on average, at least $90\%$ of total nodes created in the entire run of the algorithm had their counter activated less than $40$ times.

Sensitivity and batch size: We explore various values of sensitivity and batch size and the results are as expected - low sensitivity and large batch size improve the algorithm performance. For more details see Appendix I.