AMSS-Net: Audio Manipulation on User-Specified Sources with Textual Queries
Abstract.
This paper proposes a neural network that performs audio transformations to user-specified sources (e.g., vocals) of a given audio track according to a given description while preserving other sources not mentioned in the description. Audio Manipulation on a Specific Source (AMSS) is challenging because a sound object (i.e., a waveform sample or frequency bin) is ‘transparent’; it usually carries information from multiple sources, in contrast to a pixel in an image. To address this challenging problem, we propose AMSS-Net, which extracts latent sources and selectively manipulates them while preserving irrelevant sources. We also propose an evaluation benchmark for several AMSS tasks, and we show that AMSS-Net outperforms baselines on several AMSS tasks via objective metrics and empirical verification.
1. Introduction
In recent days, social media applications have attracted many users to create, edit, and share their audio, audio-visual, or other types of multimedia content. However, it is usually hard for non-experts to manipulate them, especially when they want to edit only the desired objects. For image manipulation, fortunately, recently proposed methods such as image inpainting (Yu et al., 2018), style transfer (Zhu et al., 2017), and text-guided image manipulation (Li et al., 2020; Liu et al., 2020) enables non-expert users to edit the desired objects while leaving other contents intact. These machine learned-based methods can reduce human labor for image editing and enable non-experts to manipulate their image without prior knowledge of tools that are often complicated to use.
On the other hand, little attention has been given to machine learning methods for automatic audio editing. It is challenging to edit specific sound objects (e.g., decrease the volume of cicada buzzing noise) with limited tools in the given audio. Considering that audio editing usually requires expert knowledge of audio engineering or signal processing, we explore a deep learning approach in conjunction with textual queries to lessen audio editing difficulty.
This paper addresses Audio Manipulation on Specific Sources (AMSS), which aims to edit only desired objects that correspond to specific sources, such as vocals and drums, according to a given description while preserving the content of sources that are not mentioned in the description. We formally define AMSS and a structured query language for AMSS in §2. AMSS can be used for many applications such as video creation tools making audio editing easy for non-experts. For example, users can decrease the volume of drums by typing simple textual instructions instead of time-consuming interactions with digital audio workstations.
Although many machine learning approaches have been proposed for audio processing (Ramírez and Reiss, 2018; Martínez Ramírez and Reiss, 2019; Martínez Ramírez et al., 2020; Steinmetz and Reiss, 2021; Wright et al., 2020; Mimilakis et al., 2016; Jansson et al., 2017; Meseguer-Brocal and Peeters, 2019; Choi et al., 2020a; Wisdom et al., 2020; Samuel et al., 2020), to the best of our knowledge, there is no existing method that can directly address AMSS (see §3). This paper proposes a novel end-to-end neural network that performs AMSS according to the given textual query. Designing a neural network for AMSS is straightforward if the sources of a given mixture track are observable. However, we assume that they are not observable because most audio data does not provide them in general. In the assumed environment, modeling AMSS is very challenging because a sound object (e.g., a sample in a wave, a frequency bin in a spectrogram) is ‘transparent’((Wyse, 2017)); a pixel in an image usually corresponds to only a single visual object, whereas a sound object carries information of multiple sources, as shown in Figure 1. Thus, we need different approaches for AMSS from the existing image manipulation techniques.

To address this challenge, we propose a neural network called AMSS-Net that extracts a feature map containing latent sources (see §5.4.1) from the given mixture audio and selectively manipulates them while preserving irrelevant latent sources. We describe the AMSS-Net architecture in §5.
Another challenge is that existing datasets cannot be directly used for supervised training AMSS-Net. If a training dataset of triples , where is an AMSS description, is a mixture, and is the manipulated audio according to is provided, we can train a neural network in a supervised manner by minimizing , where is a distance metric such as . Unfortunately, there were no datasets currently available that directly target AMSS. To address this issue, we propose a training framework for AMSS (see §4) that uses a ‘source observable multi-track dataset’ such as Musdb18 (Rafii et al., 2017). To generate an AMSS triple on-the-fly, we apply audio transformations onto specific sources of a given multi-track using common methods from Digital Signal Processing (DSP) libraries.
We summarize our contributions as follows:
-
•
Our work is a pioneer study on selective audio manipulation.
-
•
We propose a supervised training framework for AMSS based on source observable multi-track datasets and DSP libraries together with evaluation benchmarks for AMSS.
-
•
We propose AMSS-Net, which performs multiple tasks and outperforms baselines on several tasks.
2. Task Definition
2.1. Audio Manipulation on Specific Sources
We define Audio Manipulation on Specific Sources (AMSS) as follows: for a given audio track and a given description , AMSS aims to generate a manipulated audio track that semantically matches while preserving contents in that are not described in . contains multiple sources, and describes the desired audio transformation and the targets, which we want to manipulate. can be represented as a one-hot encoding or a textual query. In this paper, we assume that is a textual query written in the Audio Manipulation Language described in §2.2.
As a proof-of-concept, this paper aims to verify that it is possible to train a neural network for AMSS. Specifically, we focus on modifying specified sources’ sonic characteristics (e.g., loudness, panning, frequency content, and dereverberation). This paper does not address more complex manipulations such as distortion (see §6.7). Throughout the rest of the paper, we define an AMSS task to be a set of instructions dealing with the same manipulation method. Table 1 lists nine AMSS tasks we try to model in this paper. We also define an AMSS task class as a set of similar AMSS tasks.
| class | task | DSP operations |
|---|---|---|
| volume control | separate | masking the others |
| mute | masking targets | |
| increase vol | re-scaling (increase) | |
| decrease vol | re-scaling (decrease) | |
| volume control (multi channel) | pan left | re-scaling (left ¿ mean ¿ right) |
| pan right | re-scaling (left ¡ mean ¡ right) | |
| filter | lowpasss | Low-pass Filter |
| highpass | High-pass Filter | |
| delay | dereverb | reverb∗ |
2.2. Audio Manipulation Language
We assume that is given as a textual query, such as “apply light lowpass to drums”. We make this assumption because textual querying enables us to naturally describe any pair of a transformation function and its target sources with detailed options. For example, we can control the level of audio effects (which corresponds to the parameter settings of DSP functions) by simply inserting adjectives such as light, medium, or heavy into the query. It also can provide easy extensibility to natural language interfaces, which will be addressed in future works.
To this end, we propose an Audio Manipulation Language based on a probabilistic Context-Free Grammar (CFG) (Chomsky, 1956) for AMSS. Due to the page limit, we only present a subset of production rules (i.e., Rules (1a)-(1f)) that define the query language’s syntax for the filter class. The Full CFG is available online111https://kuielab.github.io/AMSS-Net/aml.html.
| (1a) | |||
| (1b) | |||
| (1c) | |||
| (1d) | |||
| (1e) | |||
| (1f) | |||
In the above rules, bold strings are terminal symbols, and strings enclosed in angle brackets are non-terminal symbols. Each rule is of the form , which means that can be replaced with or . In a CFG, we apply a rule to replace a single non-terminal symbol with one of the expressions. Starting from the first symbol , we can generate a valid query string by recursively applying rules until there is no non-terminal symbol.
For example, “apply medium lowpass to vocals, drums” can derived from by Rules (1a)-(1f). We can also produce “apply lowpass to vocals, drums” if we choose instead of . Since we set a default option for lowpass level to be medium, those two queries have the same meaning.
Rules (1b)-(1e) are dependant on a AMSS task class, and Rule (1f) is dependant on a given multi-track audio. In this work, we use four AMSS task classes as shown in Table 1. Since we use in the experiment Musdb18(Rafii et al., 2017) dataset of which track contains three named instruments (i.e., vocals, drums, bass), we set the right-hand side of Rule (1f) to have all the possible permutations (13 expressions in total)
3. Related Work
Since the past decade, data-driven approaches for audio manipulation have been active research fields. Meanwhile, there were virtually no studies that directly addressed AMSS. An exception was an early algorithmic method (Avendano, 2003), which proposed a framework that identifies and controls volumes of desired sources based on digital signal processing. Unlike (Avendano, 2003), this paper presents a machine learning-based approach for various AMSS tasks as well as volume controls. We review the literature related to machine learning-based studies for audio manipulation.
Audio Effect Modeling: As described in (Steinmetz and Reiss, 2021), audio effects are used to modify perceptual attributes of the given audio signal, such as loudness, spatialization, and timbre. Recently, several methods (Ramírez and Reiss, 2018; Martínez Ramírez and Reiss, 2019; Martínez Ramírez et al., 2020; Steinmetz and Reiss, 2021; Wright et al., 2020) have been proposed for audio effect modeling with deep neural networks. (Ramírez and Reiss, 2018) proposed a convolutional network performing equalization (i.e., an audio effect that changes the harmonic and timbral characteristics of audio signals). (Martínez Ramírez and Reiss, 2019; Martínez Ramírez et al., 2020) proposed convolutional and recurrent networks for nonlinear audio effects with Long and Short-Term Memory (Hochreiter and Schmidhuber, 1997), such as distortion and Leslie speaker cabinet. (Steinmetz and Reiss, 2021) presented an efficient neural network for modeling an analog dynamic range compressor enabling real-time operation on CPU.
All the methods above assume an audio input with a single source, while our method assumes a mixture of multiple sources as input. Also, they are task-specific (the trained model provides only one audio effect), while our approach can perform several manipulations with a single model.
Automatic Mixing: Audio mixing is a task that combines multi-track recordings into a single audio track. Before taking the sum of signals, mix engineers usually apply various audio signal processing techniques such as equalization and panning for a better hearing experience. Some approaches have attempted to automate audio mixing with deep neural networks. For example, (Martínez Ramírez et al., 2021a) trained end-to-end neural networks for automatic mixing of drums, where the audio waveform of individual drum recordings is the input of the model and the post-produced stereo mix is the output. (Steinmetz et al., 2020) proposed networks based on temporal dilated convolutions to learn neural proxies of specific audio effects and train them jointly to perform audio mixing. These methods mainly focus on developing expert-type mixing models that combine individual sources into a mixture track, regardless of user control or input for the desired type of transformation. On the other hand, AMSS-Net aims to manipulate user-specified sources in a desired manner, preserving others, where individual sources are not observable.
Unlike (Martínez Ramírez et al., 2021a, b), (Matz et al., 2015) assumed an environment where individual sources are not provided as input. They proposed an algorithmic framework that automatically remixes early jazz recordings, which are often perceived as irritating and disturbing from today’s perspective. It first decomposes the given input into individual tracks by means of acoustic source separation algorithms and remixes them using automatic mixing algorithms. (Mimilakis et al., 2016) proposed a replacement of the source separation and the mixing processes by deep neural networks. The environment assumed in (Mimilakis et al., 2016) is the most similar to ours. However, (Mimilakis et al., 2016) mainly focuses on remixing to change the audio mixing style, while this paper focuses on modifying specified sources in the desired manner. Thus, (Mimilakis et al., 2016) cannot directly address the AMSS problem.
Source Separation: Our work is also related to deep learning-based source separation methods (Jansson et al., 2017; Choi et al., 2020b; Yin et al., 2019; Liu and Yang, 2019; Meseguer-Brocal and Peeters, 2019; Choi et al., 2020a; Samuel et al., 2020). While early methods separate either a single source (Jansson et al., 2017; Choi et al., 2020b; Yin et al., 2019) or multiple sources once (Liu and Yang, 2019), conditioned source separation methods (Meseguer-Brocal and Peeters, 2019; Choi et al., 2020a; Samuel et al., 2020) isolate the source specified by an input symbol. A conditioned source separation task can be viewed as an AMSS task where we want to simply mute all the unwanted sources. We propose a method that can perform several AMSS tasks as well as source separation tasks using a single model, and controlled with a textual query.
We can design an algorithmic framework for AMSS using an existing separation method as a preprocessor, similar to (Matz et al., 2015). Such a method can perform some AMSS tasks by separating the individual sources and applying the appropriate DSP functions to target sources. However, source separation methods also generate minor artifacts, which are not present in the original source. Although they are negligible in each source, they can be large enough to be perceived when we sum the separated results for AMSS.
Instead of such a hybrid framework, we propose an end-to-end neural network since our approach can model more complex transformations such as dereverberation, which cannot be easily modeled with DSP algorithms. Still, our model must have the ability to extract the target sources to be manipulated. Inspired by recent deep learning-based methods, we design a novel model that extracts latent sources, selectively manipulates them, aggregates them, and outputs a mixture that follows a textual query.
The concept of latent source has been introduced in recent source separation methods (Wisdom et al., 2020; Choi et al., 2020a). (Wisdom et al., 2020) have trained their model to separate the given input into a variable number of latent sources, which can be remixed to approximate the original mixture. By carefully taking the weighted sum of separated latent sources, we can extract the desired source, such as clean speech. (Choi et al., 2020a) also use the concept of latent source for conditioned source separation. They proposed the Latent Source-Attentive Frequency Transformation (LaSAFT) method, which extracts the feature map for each latent source and takes the weighted sum of them by using an attention mechanism.
We also use the concept of latent sources in AMSS-Net, where each latent source deals with a more detailed aspect of acoustic features than a symbolic-level source (e.g., ‘vocals’). Similar to (Choi et al., 2020a), we assume that a weighted sum of latent sources can represent a source, while (Wisdom et al., 2020) assumed that latent sources are independent. Unlike previous works, our approach is based on channel-level separation as described in §5.4.1. Each decoding block of AMSS-Net extracts latent source channels from the given feature map so that each channel can be correlated to a latent source.

4. Training Framework for AMSS
We propose a novel training framework that uses a multi-track dataset. It generates an AMSS triple on the fly by applying DSP library transformations or audio effects onto target sources of a given multi-track audio file. For instance, suppose that we have a randomly generated query string ‘apply lowpass to drums’ using the CFG and a multi-track that consists of three sources, namely, a vocal track , a bass track , and a drum track . Our training framework takes the linear sum (i.e., ) to generate to generate corresponding input . For the target audio , it computes , where and is the set of target sources and DSP function described in , respectively. Our framework applies a Low-pass Filter (LPF) to , and takes the sum for as follows: . By doing so, it can generate an AMSS triple on-the-fly for a given description .
For audio restoration tasks such as dereverberation, we swap A and A’. For example, the framework applies reverb to , takes the sum for , and returns instead of for the description “remove reverb from drums.”
Input: multi-track , a set of triple generators
Output: a triple
The training framework has a set of triple generators. A generator has a subset of CFG for text query generation and the corresponding DSP function , which is used for computing . also has an indicator that describes whether is for applying or removing the effect. For a multi-track and a set of triple generators, our framework generates an AMSS triple by using Algorithm 1, where denotes the number of sources.
5. AMSS-Net Architecture
Our AMSS-Net takes as input an audio track with a text description and generates the manipulated audio track as shown in Figure 2. It consists of two sub-networks, i.e., a Description Encoder and a Spectrogram Encoder-Decoder Network . extracts word features from , where denotes the dimension of the word features and denotes the number of words, to analyze the meaning of . takes as input word features and the complex-valued spectrogram of the input audio . Conditioned on the word feature , it estimates the complex-valued spectrogram , from which can be reconstructed using iSTFT. We train the AMSS-Net by minimizing the loss between the ground-truth spectrogram of and the estimated .
5.1. Description Encoder
The description encoder encodes the given text description written in the Audio Manipulation Language (§2.2) to word features , where we denote the dimension of each word feature by and the number of words in by . It embeds each word to a dense vector using a word embedding layer and then encodes the embedded description using a bidirectional Recurrent Neural Network (Bi-RNN) (Schuster and Paliwal, 1997). We use pre-trained word embeddings such as GloVe(Pennington et al., 2014) to initialize the weight of the embedding layer since they were trained to capture the syntactic and semantic meaning of words.
5.2. Spectrogram Encoder-Decoder Network
The Spectrogram Encoder-Decoder Network estimates the complex-valued spectrogram , conditioned on the extracted word features . It is an encoder-decoder network that has the same number of down-sampling layers and up-sampling layers as depicted in Figure 2. It extracts down-sampled representations from in the encoding phase and generates up-sampled representations in the decoding phase. The output of the last decoding block is fed to the Aggregate PoCM (see §5.5) that generates the output .
As illustrated in Figure 2, it has direct connections between the encoding blocks and their counterpart decoding blocks, which help decoding blocks recover fine-grained details of the target. Instead of concatenation or summation commonly used in several U-Net-based architectures (Jansson et al., 2017; Choi et al., 2020b; Meseguer-Brocal and Peeters, 2019; Choi et al., 2020a), we propose a Channel-wise Skip Attention (CSA) mechanism (§5.4.4) that attentively aggregates latent source channels to reconstruct the original channels.
5.3. Spectrogram Encoding Block
uses multiple encoding blocks in the encoding phase to capture common sonic properties residing in the input spectrogram. The encoding block transforms an input spectrogram-like tensors into an equally-sized tensor. We adopt the encoding block called TFC-TDF proposed in (Choi et al., 2020b), which applies densely-connected 2-d convolutions to the given spectrogram-like representations followed by a fully connected layer that enhances features of frequency patterns observed in the frequency axis.

5.4. Spectrogram Decoding Block
In the decoding phase, uses multiple decoding blocks. Each decoding block first extracts a feature map in which each channel corresponds to a specific latent source. It selectively manipulates them conditioned on the AMSS description and aggregates channels using a channel-wise attention mechanism to minimize information loss during channel reconstruction.
As shown in Figure 3, the decoding block takes three inputs: (1) : features from the previous decoding block, (2) : features from the skip connection and (3) : word features. The first block takes the up-sampled features from the encoder instead because it has no previous decoding block.
Each decoding block consists of four components: Latent Source Channel (LSC) Extractor, Condition weight generator, Selective Manipulation via PoCMs (SMPoCM), and Channel-wise Skip Attention (CSA). We illustrate the overall workflow in Figure 3.
5.4.1. Latent Source Channel Extractor
We assume that we can learn representations of latent sources that deal with more detailed acoustic features than symbolic-level sources. The Latent Source Channel (LSC) extractor aims to generate a feature map , in which each channel deals with a latent source. Figure 4 visualizes the conceptual view of latent source channels. Each channel is a spectrogram-like representation of size dealing with a specific latent source. For example, the blue channel in Figure 4 deals with the acoustic features observed in the bass drum. We can also generate an audio track from a single latent source channel. In §6.4, we visualize and discuss results of the audio generation.

The LSC extractor takes as input and extracts feature maps with latent source channels, where refers to the number of channels, refers to the shape of the spectrogram-like features, and denotes the number of latent sources. It first concatenates and to obtain , and applies a TFC-TDF block (Choi et al., 2020b) to to obtain acoustic features for latent source separation.
To extract a feature map with latent source channels, it applies a convolution to . We denote this convolution as since its role is a value generator in the context of the channel-wise skip attention mechanism §5.4.4 as shown in Figure 3. Similar to , we apply another convolution called to , of which role is a key generator, to obtain . By the guide of the channel-wise skip attention mechanism, the LSC extractor is expected to extract latent source channels from the mixture features so that each channel deals with a latent source.
5.4.2. Selective Manipulation via PoCMs
Since we have to manipulate specific features while preserving other features, selective manipulation requires a more sophisticated modulation than existing methods such as Feature-wise Linear Modulation (FiLM) (Perez et al., 2018), or Point-wise Convolutional Modulation (PoCM) (Choi et al., 2020a).
We propose SMPoCM, an extension of PoCM, that aims to manipulate features for the given AMSS task selectively. As shown in Figure 3, it takes as input and condition parameters , generated by the LSC extractor and the condition weight generator, respectively. It outputs , a selectively manipulated feature.
Inspired by Long Short-term Memory (LSTM) (Hochreiter and Schmidhuber, 1997), the SMPoCM uses three different PoCMs: (1) a selective gate PoCM with to determine how much we should manipulate each latent source channel, (2) a manipulation PoCM with to manipulate specific features, and (3) an input gate PoCM with to determine how much we should emit the manipulated features.
Before defining SMPoCM formally, we summarize the behavior of PoCM as follows: a PoCM is a point-wise convolution (i.e., convolution) of which the condition weight generator provides parameters. We now give a definition of SMPoCM as follows: = , where is defined as , is defined as , is Hadamard product, and is a sigmoid function. The total number of parameters in is about (i.e., three point-wise convolutions).
SMPoCM naturally models the selective modulation required for modeling AMSS tasks. For example, if latent source should be preserved for the given input, then the channel of would be trained to have near-zero values.
5.4.3. Condition Weight Generator
Given , the condition weight generator generates parameters . We exploit the attention mechanism to determine which word should be attended to , , and respectively.
The weight generator has a learnable matrix , where we denote the cardinality of each PoCM task embedding by . It also has two linear layers and that embed to and respectively. To determine which word we should attend for each task, we compute the scaled attention (Vaswani et al., 2017) as follows: . Finally, it generates , , and as follows: , , and , where , , and are fully-connected layers.
5.4.4. Channel-wise Skip Attention
Inspired by skip attention (Yuan et al., 2019) and (Chen et al., 2017), we propose a Channel-wise Skip Attention (CSA) mechanism. It attentively aggregates latent source channels to restore the number of channels to the same as the input (i.e., ). The goal of CSA is to minimize information loss during channel reconstruction to preserve other features that are irrelevant to the description.
Figure 3 overviews the workflow required to prepare the query feature , key feature , and the value feature . To obtain , we apply , a convolution to .
For each frame, CSA aims to capture channel-to-channel dependencies between that encodes the original acoustic features of and the feature map of isolated latent sources obtained by the LSC extractor. It is worth noting that we use for computing attention matrix instead of since , which SMPoCM modulated, no longer has the same information as .
For and , we compute the scaled dot product attention matrix (Vaswani et al., 2017) as follows:
| (2) |
The attention weight represents the correlation between the channel of the original audio features and the latent source channel of the decoded audio features. Finally, we can obtain the decoding block’s output , where is defined as .
5.5. Aggregate PoCM
The Aggregate Pocm is similar to the SMPoCM other than two key differences. First, the Aggregate PoCM only has one PoCM that is not followed by any activation. Second, the Aggregate PoCM reduces the number of channels from to (i.e., the number of channels of the two-channeled complex-valued spectrogram) while the SMPoCM’s input and output have the same number of channels.
6. Experiments
6.1. Experiment Setup
We evaluate the proposed model both qualitatively and quantitatively on various AMSS tasks described in Table 1 using the Musdb18 dataset. We compare its performance with baselines to verify our architecture.
6.1.1. Training Framework
Musdb18 (Rafii et al., 2017) contains 86 tracks for training, 14 tracks for validation, and 50 tracks for the test. Each track is stereo, sampled at 44100 Hz, and each data tuple consists of the mixture and four sources: vocals, drums, bass, and other. We implemented the training framework based on Musdb18 and pysndfx222https://pypi.org/project/pysndfx/, a Python DSP library. We train all models based on this framework with 9 AMSS tasks listed in Table 1. For each task, we implement triple generators based on the Audio Manipulation Language (§2.2) and Musdb18. We exclude ‘other’ since it is not a single instrument. With the set of triple generators and randomly generated multi-tracks obtained by data augmentation (Uhlich et al., 2017), we generate AMSS triples using Algorithm 1 for training.
6.1.2. Training Environment
We train models using Adam (Kingma and Ba, 2015) with learning rate . Starting with a learning rate , we halved and restarted training when the current seemed to be too high. Each model is trained to minimize the loss between the ground-truth and estimated spectrograms. For validation, we use the loss of target and estimated signals. It takes about two weeks to converge when we train models with a single 2080Ti GPU.
6.2. Model Configurations
To validate the effectiveness of AMSS-Net, we compared it with the two baselines. One does not use CSA (AMSS-Net w/o CSA), and the other does not use SMPoCM in decoding blocks (AMSS-Net w/o SM). The baseline model without CSA uses an LSC extractor with LaSAFT block (Choi et al., 2020a) instead of TFC-TDF (Choi et al., 2020b) to compensate the absence of CSA. The model without SMPoCM uses a single PoCM with tanh activation in its decoding block. An AMSS-Net has about 4.3M, a baseline without CSA has about 4.9M, and a baseline without SMPoCM has about 2.4M.
For hyper-parameter setting, we use a similar configuration of models with an FFT window size of 2048 in (Choi et al., 2020a). Every model has three encoding blocks, two decoding blocks, an additional Aggregate PoCM block. We assume that there are eight latent sources (i.e., ). We also adopt the multi-head attention mechanism (Vaswani et al., 2017) for CSA, where we set the number of heads to 6. The STFT parameter of each model is as follows: an FFT window size of 2048 and a hop size of 1024.
| model | vocals | drums | bass | other | AVG | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Meta-TasNet | 6.40 | 5.91 | 5.58 | 4.19 | 5.52 | ||||||||||
| LaSAFT-GPoCM-Net12 | 7.33 | 5.68 | 5.63 | 4.87 | 5.88 | ||||||||||
| LaSAFT-GPoCM-Net11 | 6.96 | 5.84 | 5.24 | 4.54 | 5.64 | ||||||||||
| AMSS-Netseparate |
|
|
|
|
|
||||||||||
| AMSS-Net |
|
|
|
|
|
||||||||||
| w/o CSA |
|
|
|
|
|
||||||||||
| w/o SMPoCM |
|
|
|
|
|
| pan left | pan right | decrease volume | increase volume | |||||||||||||||||||||||||||||||||
| voc | drum | bass | voc | drum | bass | voc | drum | bass | voc | drum | bass | |||||||||||||||||||||||||
| reference loss | 4.62 | 8.20 | 2.18 | 4.66 | 8.30 | 2.13 | 4.06 | 6.99 | 2.00 | 6.68 | 9.70 | 3.48 | ||||||||||||||||||||||||
| AMSS-Net |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
| w/o CSA |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
| w/o SMPoCM |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
| lowpass filter | highpass filter | dereverberation | mean | |||||||||||||||||||||||||||||||||
| voc | drum | bass | voc | drum | bass | voc | drum | bass | voc | drum | bass | |||||||||||||||||||||||||
| reference loss | 9.02 | 16.27 | 1.12 | 6.72 | 8.22 | 4.74 | 9.43 | 11.07 | 5.61 | 6.46 | 9.82 | 3.04 | ||||||||||||||||||||||||
| AMSS-Net |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
| w/o CSA |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
| w/o SMPoCM |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
6.3. Quantitative Analysis
6.3.1. Evaluation of separate and mute tasks (Table 2)
To evaluate separate and mute tasks, we use Source-to-Distortion (SDR) (Vincent et al., 2006) metric by using the official tool333https://github.com/sigsep/sigsep-mus-eval. The Musdb18 tasks are separating vocals, drums, bass, and other, which corresponds to the following AMSS: ‘separate vocals,’ ‘separate drums,’ ‘separate bass,’ and ’mute vocals, drums, bass.’ Using the SDR metric for these two tasks allows us to compare our model’s source separation performance with other state-of-the-art models for conditioned source separation. Following the official guideline, we report the median SDR value over all the test set tracks for each run and report the mean SDR over three runs (with a different random seed).
Table 2 summarizes the result, where AMSS-Net shows comparable or and slightly inferior performance compared to state-of-the-art conditioned separation models, namely, Meta-TasNet (Samuel et al., 2020) and LaSAFT-GPoCM-Nets. AMSS-Net outperforms the baselines for all sources except for drums, where the gap is not significant. It is worth noting that ours can perform other AMSS tasks and show promising results on source separation tasks. If we train AMSS-Net solely for Musdb18 tasks (AMSS-Netseparate), then it shows comparable performance to LaSAFT-GPoCM-Net11 whose FFT window size is the same as ours.
6.3.2. Evaluation of other AMSS tasks (Table 3)
Since there is no reference evaluation metric for AMSS, we propose the new evaluation benchmark. The benchmark script is available online444https://github.com/kuielab/AMSS-Net/blob/main/task2_eval.py. For evaluation metric, we extract Mel-frequency Cepstral coefficients (MFCC) for and , and compute the Root Mean Square Error (RMSE) of them, since MFCC approximates the human perception of the given track. We refer to this metric as RMSE-MFCC. We report the mean RMSE-MFCC value over all the test set tracks for each run and report the mean RMSE-MFCC over three runs.
Table 3 summarizes the results, where reference loss is the RMSE-MFCC of and . Reference loss provides information about the amount of manipulation needed to model each AMSS task. As described in Table 3, AMSS-Net outperforms all the AMSS task but a task of “highpass filter to vocals”. Significantly, the model without SMPoCM is inferior to AMSS-Net for every task. It indicates that SMPoCM significantly contributes to improving the quality of AMSS results. CSA also improves the performance of AMSS-Net for most of the AMSS tasks. CSA might degrade the performance for more difficult AMSS tasks by forcing the model to over-correlate the latent source channels with the mixture channels. However, it reduces artifacts created during progressive manipulation as described in §6.5
6.4. Latent Source Channels
As mentioned in the LSC extractor (§5.4.1), we design AMSS-Net to perform latent source-level analysis. Such analysis enables AMSS-Net to perform delicate manipulation for the given AMSS task. To verify that AMSS-Net decoding blocks can extract a feature map in which each channel corresponds to a specific latent source, we generate an audio track from a single latent source channel. We mask all channels in the manipulated feature map except for a single latent source channel and fed it to the remaining sub-networks to generate the audio track during the last decoding block.
 |
 |
| (a) original | (b) kick drum |
 |
 |
| (c) high hat | (d) non-percussion |
Figure 5 shows interesting results of generated audios, which remind us the conceptual view of the latent source in Figure 4. For the given input track of Figure 5 (a), we generate an audio track after masking all channels except for the fifth channel in the second head group, then the result sounds similar to the low-frequency band of drums (i.e., kick drum) as illustrated in Figure 5 (b). AMSS-Net can keep this channel and drop other drum-related channels to process “apply lowpass to drums.” However, a latent source channel does not always contain a single class of instruments. For example, the latent channel of the fourth row in the table deals with several instruments. Some latent sources were not interpretable to the authors. Generated samples are available online.555https://kuielab.github.io/AMSS-Net/latent_source.html
6.5. Progressive Manipulation
We show that we can repeatedly apply the proposed method to manipulated audio tracks, which is also known as Progressive Manipulation used in conversational systems described in (Liu et al., 2020). Figure 6 shows an example of progressive manipulation.

However, methods based on neural networks sometimes suffer from artifacts (Vincent et al., 2006), which are not present in the original source. Although they sound negligible after a single manipulation task, they can be large enough to be perceived after progressively applying several. To investigate artifacts created by progressive manipulation, we apply the same AMSS task “apply highpass to drums” to a track in a progressive manner. Figure (a) shows the Mel-spectrogram of the ground-truth target. We can observe blurred areas in the high-frequency range in Mel-spectrograms of Figure 7 (c) and (d). Compared to them, Figure 7 (b) is more similar to the ground-truth target. Via hearing test, we observed perceivable artifacts 7 in the results of baselines. Our AMSS-Net contains minor artifacts compare to them because each decoding block of AMSS-Net has a CSA mechanism, a unique structure that prevents unwanted noise generated by intermediate manipulated features. Generated samples are available online666https://kuielab.github.io/AMSS-Net/progresive.html.
 |
 |
| (a) ground-truth target | (b) AMSS-Net |
 |
 |
| (c) w/o CSA | (d) w/o SMPoCM |
6.6. Controlling the level of audio effects
As mentioned in §2.2, we can train AMSS-Net to perform more detailed AMSS such as “apply heavy lowpass to vocals”. As shown in Figure 8, users can control the level of audio effects by simply injecting adverbs instead of a laborious search for an appropriate parameter configuration. Generated samples are available online777https://kuielab.github.io/AMSS-Net/control_level.html.
 |
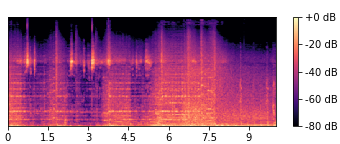 |
| (a) original | (b) heavy highpass to vocals |
 |
 |
| (c) separate vocals | (d) medium highpass to vocals |
 |
 |
| (e) mute vocals | (f) light highpass to vocals |
6.7. Discussion
AMSS-Net shows promising results on several AMSS tasks. AMSS-Net can also be trained with a more complicated AMSS training dataset based on a realistic audio mixing dataset such as IDMT-SMT-Audio-Effects dataset (Stein et al., 2010). However, this study is limited to model relatively simpler AMSS tasks. One can extend our work to provide more complex AMSS tasks such as distortion and reverberation. Each AMSS task in this paper only deals with a single type of manipulations, but one can also extend our work to provide multiple types of tasks such as “apply reverb to vocals and apply lowpass to drums” at once. Also, our work is easily extendable to support a more user-friendly interface. For example, adopting unsupervised training frameworks such as Mixture of Mixture (MoM) (Wisdom et al., 2020) to train AMSS on annotated audio datasets such as clotho(Drossos et al., 2020) might enable a natural language query interface.
7. Conclusion
In this paper, we define a novel task called AMSS. We propose AMSS-Net, which generates feature maps in which each channel deals with a latent source and selectively manipulates them while preserving irrelevant features. AMSS-Net can perform several AMSS tasks, unlike previous models such as LaSAFT-GPoCM-Net. The experimental results show that AMSS-Net outperforms baselines on several tasks. Future work will extend it to provide more complex AMSS tasks such as distortion and reverberation by adopting state-of-the-art methods such as Generative Adversarial Networks (GAN).
References
- (1)
- Avendano (2003) Carlos Avendano. 2003. Frequency-domain source identification and manipulation in stereo mixes for enhancement, suppression and re-panning applications. In 2003 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (IEEE Cat. No. 03TH8684). IEEE, 55–58.
- Chen et al. (2017) Long Chen, Hanwang Zhang, Jun Xiao, Liqiang Nie, Jian Shao, Wei Liu, and Tat-Seng Chua. 2017. Sca-cnn: Spatial and channel-wise attention in convolutional networks for image captioning. In Proceedings of the IEEE conference on computer vision and pattern recognition. 5659–5667.
- Choi et al. (2020a) Woosung Choi, Minseok Kim, Jaehwa Chung, and Soonyoung Jung. 2020a. LaSAFT: Latent Source Attentive Frequency Transformation for Conditioned Source Separation. arXiv preprint arXiv:2010.11631 (2020).
- Choi et al. (2020b) Woosung Choi, Minseok Kim, Jaehwa Chung, Daewon Lee, and Soonyoung Jung. 2020b. Investigating u-nets with various intermediate blocks for spectrogram-based singing voice separation. In Proceedings of the 21th International Society for Music Information Retrieval Conference.
- Chomsky (1956) N. Chomsky. 1956. Three models for the description of language. IRE Transactions on Information Theory 2, 3 (1956), 113–124. https://doi.org/10.1109/TIT.1956.1056813
- Drossos et al. (2020) Konstantinos Drossos, Samuel Lipping, and Tuomas Virtanen. 2020. Clotho: An audio captioning dataset. In ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 736–740.
- Hochreiter and Schmidhuber (1997) Sepp Hochreiter and Jürgen Schmidhuber. 1997. Long Short-Term Memory. Neural Computation 9, 8 (1997), 1735–1780.
- Jansson et al. (2017) Andreas Jansson, Eric Humphrey, Nicola Montecchio, Rachel Bittner, Aparna Kumar, and Tillman Weyde. 2017. Singing voice separation with deep u-net convolutional networks. In 18th International Society for Music Information Retrieval Conference. 745–751.
- Kingma and Ba (2015) Diederik P. Kingma and Jimmy Ba. 2015. Adam: A Method for Stochastic Optimization. In 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings, Yoshua Bengio and Yann LeCun (Eds.). http://arxiv.org/abs/1412.6980
- Li et al. (2020) Bowen Li, Xiaojuan Qi, Thomas Lukasiewicz, and Philip HS Torr. 2020. Manigan: Text-guided image manipulation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 7880–7889.
- Liu and Yang (2019) Jen-Yu Liu and Yi-Hsuan Yang. 2019. Dilated Convolution with Dilated GRU for Music Source Separation. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI-19. International Joint Conferences on Artificial Intelligence Organization, 4718–4724. https://doi.org/10.24963/ijcai.2019/655
- Liu et al. (2020) Yahui Liu, Marco De Nadai, Deng Cai, Huayang Li, Xavier Alameda-Pineda, Nicu Sebe, and Bruno Lepri. 2020. Describe What to Change: A Text-guided Unsupervised Image-to-Image Translation Approach. In Proceedings of the 28th ACM International Conference on Multimedia. 1357–1365.
- Martínez Ramírez et al. (2020) Marco A Martínez Ramírez, Emmanouil Benetos, and Joshua D Reiss. 2020. Deep learning for black-box modeling of audio effects. APPLIED SCIENCES-BASEL 10, 2 (2020).
- Martínez Ramírez and Reiss (2019) Marco A Martínez Ramírez and Joshua D Reiss. 2019. Modeling nonlinear audio effects with end-to-end deep neural networks. In ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 171–175.
- Martínez Ramírez et al. (2021a) Marco A Martínez Ramírez, Daniel Stoller, and David Moffat. 2021a. A Deep Learning Approach to Intelligent Drum Mixing with the Wave-U-Net. Journal of the Audio Engineering Society 69, 3 (2021), 142–151.
- Martínez Ramírez et al. (2021b) Marco A Martínez Ramírez, Daniel Stoller, and David Moffat. 2021b. A Deep Learning Approach to Intelligent Drum Mixing with the Wave-U-Net. Journal of the Audio Engineering Society 69, 3 (2021), 142–151.
- Matz et al. (2015) D. Matz, Estefanía Cano, and J. Abeßer. 2015. New Sonorities for Early Jazz Recordings Using Sound Source Separation and Automatic Mixing Tools. In ISMIR.
- Meseguer-Brocal and Peeters (2019) Gabriel Meseguer-Brocal and Geoffroy Peeters. 2019. CONDITIONED-U-NET: Introducing a Control Mechanism in the U-net For Multiple Source Separations.. In 20th International Society for Music Information Retrieval Conference, ISMIR (Ed.).
- Mimilakis et al. (2016) Stylianos Ioannis Mimilakis, Estefanıa Cano, Jakob Abeßer, and Gerald Schuller. 2016. New sonorities for jazz recordings: Separation and mixing using deep neural networks. In 2nd AES Workshop on Intelligent Music Production, Vol. 13.
- Pennington et al. (2014) Jeffrey Pennington, Richard Socher, and Christopher D Manning. 2014. Glove: Global Vectors for Word Representation.. In EMNLP, Vol. 14. 1532–1543.
- Perez et al. (2018) Ethan Perez, Florian Strub, Harm de Vries, Vincent Dumoulin, and Aaron C Courville. 2018. FiLM: Visual Reasoning with a General Conditioning Layer. In AAAI.
- Rafii et al. (2017) Zafar Rafii, Antoine Liutkus, Fabian-Robert Stöter, Stylianos Ioannis Mimilakis, and Rachel Bittner. 2017. MUSDB18 - a corpus for music separation. https://doi.org/10.5281/zenodo.1117371 MUSDB18: a corpus for music source separation.
- Ramírez and Reiss (2018) Martínez Ramírez and Joshua D Reiss. 2018. End-to-end equalization with convolutional neural networks. In 21st International Conference on Digital Audio Effects (DAFx-18).
- Samuel et al. (2020) David Samuel, Aditya Ganeshan, and Jason Naradowsky. 2020. Meta-learning Extractors for Music Source Separation. In ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 816–820.
- Schuster and Paliwal (1997) Mike Schuster and Kuldip K Paliwal. 1997. Bidirectional recurrent neural networks. IEEE transactions on Signal Processing 45, 11 (1997), 2673–2681.
- Stein et al. (2010) Michael Stein, Jakob Abeßer, Christian Dittmar, and Gerald Schuller. 2010. Automatic detection of audio effects in guitar and bass recordings. In Audio Engineering Society Convention 128. Audio Engineering Society.
- Steinmetz et al. (2020) Christian J Steinmetz, Jordi Pons, Santiago Pascual, and Joan Serrà. 2020. Automatic multitrack mixing with a differentiable mixing console of neural audio effects. arXiv preprint arXiv:2010.10291 (2020).
- Steinmetz and Reiss (2021) Christian J Steinmetz and Joshua D Reiss. 2021. Efficient Neural Networks for Real-time Analog Audio Effect Modeling. arXiv preprint arXiv:2102.06200 (2021).
- Uhlich et al. (2017) Stefan Uhlich, Marcello Porcu, Franck Giron, Michael Enenkl, Thomas Kemp, Naoya Takahashi, and Yuki Mitsufuji. 2017. Improving music source separation based on deep neural networks through data augmentation and network blending. In 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 261–265.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. In Advances in neural information processing systems. 5998–6008.
- Vincent et al. (2006) Emmanuel Vincent, Rémi Gribonval, and Cédric Févotte. 2006. Performance measurement in blind audio source separation. IEEE transactions on audio, speech, and language processing 14, 4 (2006), 1462–1469.
- Wisdom et al. (2020) Scott Wisdom, Efthymios Tzinis, Hakan Erdogan, Ron J. Weiss, Kevin Wilson, and John R. Hershey. 2020. Unsupervised Sound Separation Using Mixture Invariant Training. In NeurIPS. https://arxiv.org/pdf/2006.12701.pdf
- Wright et al. (2020) Alec Wright, Eero-Pekka Damskägg, Lauri Juvela, and Vesa Välimäki. 2020. Real-Time Guitar Amplifier Emulation with Deep Learning. Applied Sciences 10, 3 (2020). https://doi.org/10.3390/app10030766
- Wyse (2017) Lonce Wyse. 2017. Audio spectrogram representations for processing with convolutional neural networks. arXiv preprint arXiv:1706.09559 (2017).
- Yin et al. (2019) Dacheng Yin, Chong Luo, Zhiwei Xiong, and Wenjun Zeng. 2019. PHASEN: A Phase-and-Harmonics-Aware Speech Enhancement Network. arXiv preprint arXiv:1911.04697 (2019).
- Yu et al. (2018) Jiahui Yu, Zhe Lin, Jimei Yang, Xiaohui Shen, Xin Lu, and Thomas S Huang. 2018. Generative image inpainting with contextual attention. In Proceedings of the IEEE conference on computer vision and pattern recognition. 5505–5514.
- Yuan et al. (2019) Weitao Yuan, Shengbei Wang, Xiangrui Li, Masashi Unoki, and Wenwu Wang. 2019. A Skip Attention Mechanism for Monaural Singing Voice Separation. IEEE Signal Processing Letters 26, 10 (2019), 1481–1485.
- Zhu et al. (2017) Jun-Yan Zhu, Taesung Park, Phillip Isola, and Alexei A Efros. 2017. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE international conference on computer vision. 2223–2232.